Девятое задание из ЕГЭ по информатике нового формата 2021 основывается на работе с таблицами Excel.
Это задание выполняется на компьютере в новом формате ЕГЭ 2021 года. Будет выдан файл Excel, по которому нужно получить правильный ответ и записать его в бланк заданий.
Если Вам урок удобнее смотреть в видеоформате, то можете перейти на ролик по 9 заданию из ЕГЭ по информатике 2021 на Youtube. Подписывайтесь на канал!
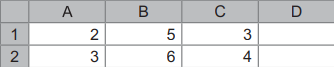
Здесь имеется столбец «Продукт». Другие столбцы: «Жиры», «Белки», «Углеводы», «Калорийность» – это характеристики этих продуктов.
В Excel можно каждой ячейке задавать какие-нибудь формулы. Например, пусть в ячейке F2 будет писаться СУММА из ячеек B2 (Жиры) и С2 (Белки).
Кликаем по ячейке F2, а затем на значок «вставить функцию».
Появится окно «Вставка функции«. Здесь все функции разбиты на категории: Финансовые, математические, логические и т.д. По умолчанию стоит категория «10 недавно используемых функций». В этой категории уже есть нужная нам функция СУММ. Выбираем её и кликаем «ОК». (Основная категория для функции СУММ является «математические»)
Появляется окно для функции СУММ.
Если мы напишем в поле Число1: «B2:E2» ,– то у нас суммируются три ячейки: B2, C2, E2. Таким образом, мы задали интервал.
Можно суммировать и вниз, т.е. ячейки одного столбца (B2:B1001).
Чтобы просуммировать отдельные ячейки, без интервала – необходимо уже использовать поле Число2.
Нам нужно просуммировать два числа: значение ячейки B2 и значение С2. Значит, пишем в поле Число1
— B2, а в поле Число2 — C2.
Нажимаем «Ок». Теперь у нас в ячейке F2 сумма значений ячеек B2 и С2.
Примечание 1: Мы могли сделать данную операцию с помощью интервала. Для этого нужно было написать в поле Число1: B2:C2.
Примечание 2: Так же мы могли суммировать и без вставки функции. Для этого нужно кликнуть по ячейке F2 и затем в поле, на которое показывает стрелка на рисунке, вписать формулу: «=B2+C2«. И нажать «Enter».
Необходимо подвести мышку к нижнему правому углу ячейки с формулой, чтобы появился чётный крестик:
И нажав левую кнопку мыши, тянем вниз. Таким образом, у нас формула распространится на весь столбец.
При изменении данных в ячейках столбцов В и С – значения в ячейках столбца F меняется автоматически.
Примерные задачи 9 задания ЕГЭ по информатике 2021
Задача (Среднее значение с условием)
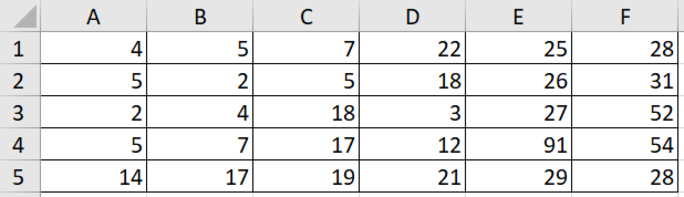
Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике и информатике. Каков средний балл по информатике среди участников тестирования, получивших зачётные баллы по этому предмету (т.е. не менее 44 баллов)?
В ответе округлить число до двух знаков после запятой.
Решение:
Для решения этой задачи будем использовать функцию =СРЗНАЧЕСЛИ().
Кликнем в свободную ближайшую ячейку E2. Здесь мы хотим получить ответ на задачу. Нажмём на кнопку «Вставить функцию«, выберем категорию «статистические«, а затем выберем функцию СРЗНАЧЕСЛИ.
В диапазоне нужно указать все ячейки с числами столбца «Информатика» (Столбец D). Значит, напишем: D2:D273 (Чтобы понять сколько строчек в таблице, нужно прокрутить всю таблицу до самого конца вниз.). В условии напишем: >=44 (Т.к. мы должны считать среднее значение для тех ячеек, где число не меньше 44).
Нажимаем «ОК» и получаем в ячейке E2 число 68,60851064. Нам его нужно округлить до 2 знаков после запятой. Воспользуемся инструментом в программе Excel для округления.
Найдём кнопки «Уменьшить разрядность» и «Увеличить разрядность«. Их можно применять к выделенной ячейке.
Уменьшим разрядность до 2 знаков. Получается число 68,61. Это и будет ответ!
Примечание 1: Если мы хотим найти среднее значение без условия, есть функция СРЗНАЧ.
Примечание 2: СРЗНАЧЕСЛИ (СРЗНАЧ)- это и есть среднее арифметическое значение.
Ответ: 68,61
Посмотрим ещё один важный пример 9 задания ЕГЭ по информатике нового формата 2021.
Задача (Количество с условием)
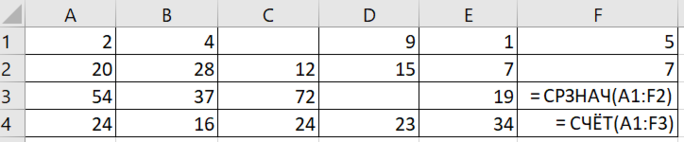
Откройте файл электронной таблицы, содержащей данные о сотрудниках одного из предприятий города Москвы. Сколько человек в таблице имеют возраст меньше 30 лет, и их вес превышает 100 кг?
В ответе напишите одно целое число.
Решение:
Сначала поставим 1 в столбце F в тех строчках, которые удовлетворяют нашему условию: человек имеет возраст меньше 30 лет, и его вес превышает 100 кг. Если строчка не удовлетворяет условию, значит, в ячейке столбца F поставим 0.
Сначала настроим формулу для одной строчки, а затем формулу распространим на весь столбец.
Кликаем по ячейке F2. Нажимаем на кнопку «Вставить функцию«. Выбираем функцию ЕСЛИ из категории «Логические«.
В поле «Лог_выражение» задаём условие : И(C2>100; E2<30). Т.к. сначала мы задаём формулу для второй строки, то пишем ячейки C2 и E2. Мы написали условие нашей задачи для второй строки. Столбец C — отвечает за Вес, а столбец E — за возраст.
В условии ставим вначале союз «И«, т.к. одновременно два условия должны выполняться. Если бы в задаче говорилось, что мы должны подсчитать количество строчек, где хотя бы одно условие сработало, тогда бы поставили союз «ИЛИ«.
В поле «Значение_если_истина» ставим 1. В поле «Значение_если_ложь» ставим 0. Нажимаем «ОК».
Получилось, что в ячейке F2 высветился ноль. Значит, первый сотрудник не удовлетворяет условию задачи.
Теперь распространим формулу на весь столбец F. Подводим мышку к ячейке F2 к правому нижнему углу. Когда появился чёрный крестик, нажимаем левую кнопку мыши и тянем вниз, распространяя формулу на весь столбец.
Где-то будут получатся нули, а где-то единицы. Всё зависит от характеристик сотрудника.
После того, как формула будет распространена на весь столбец F, нам нужно посчитать количество единиц в столбце F. Это количество и покажет число сотрудников, которые подходят под условие задачи.
Воспользуемся функцией СУММ. Кликнем по ячейке G2. Именно здесь получим ответ. Затем нажмём на кнопку «Вставить функцию» и выберем СУММ из категории «Математические«.
В поле Число1 зададим интервал F2:F301 (Ведь всего у нас 301 строчка в таблице).
Нажимаем «ОК» и получаем в ячейке G2 ответ на нашу задачу. В ответе напишем 14.
Примечание: Для подчёта количества с условием можно использовать функцию СЧЁТЕСЛИ. Попробуйте решить с помощью неё самостоятельно.
Ответ: 14
Продолжаем тренироваться решать 9 задания из ЕГЭ по информатике нового формата 2021.
Задача (Наименьшее значение + условие ИЛИ)
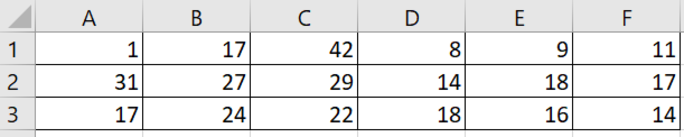
Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Чему равна наименьшая сумма баллов по математике и информатике среди школьников, получивших более 50 баллов по математике или информатике?
В ответе запишете целое число.
Решение:
В начале нужно выписать отдельно сумму баллов по математике и информатике для тех школьников, которые подходят под условие.
Выпишем сумму двух предметов, для удовлетворяющих условию строчек, в столбец F, с помощью функции ЕСЛИ.
В начале нужно задать формулу для одной ячейки F2. Кликаем по ячейке F2, нажимаем на кнопку «Вставить функцию«, выбираем функцию ЕСЛИ.
В поле «Лог_выражение» пишем: ИЛИ(C2>50; D2>50). В поле «Значение_если_истина«: C2+D2. В поле «Значение_если_ложь«: «» (Пустые двойные кавычки).
Важно: Здесь мы в поле «Значение_если_ложь» должны поставить пустые двойные кавычки, ведь, если поставить ноль, тогда, при поиске минимального значения будем находить всегда этот ноль. Мы ноль ставим в это поле только тогда, когда ищем количество строчек, ведь, тогда мы суммируем единицы, а ноль при суммировании не влияет на результат.
Нажимаем «ОК», и в ячейке F2 получается число 160. Это говорит о том, что первая строчка удовлетворяет условию задачи. И теперь в ячейке F2 лежит сумма баллов по математике и информатике для первого учащегося.
Распространим данную формулу на весь столбец F.
В основном получатся числа, но где-то ячейки останутся пустыми. Это значит, что эти строчки не подошли под условие задачи.
Теперь нужно с помощью функции МИН найти минимальное значение в столбце F.
Кликаем по ячейке G2, нажимаем «Вставить функцию«, выбираем функцию МИН из категории «Статистические«.
В поле Число1 пишем диапазон столбца F: F2:F273.
Получаем ответ 75.
Ответ: 75
Продолжаем оттачивать навыки работы с электронными таблицами в 9 задании из ЕГЭ по информатике нового формата 2021.
Задача (Среднее значение + сложное условие)
Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Каков средний балл по математике обучающихся, набравших не менее 60 баллов по информатике?
В ответе запишите только целую часть получившегося числа.
Решение:
Эту задачу решим двумя способами.
1 Способ
В этом способе решения будем снова использовать функцию СРЗНАЧЕСЛИ.
Кликаем по ячейке F2 и вставляем функцию СРЗНАЧЕСЛИ из категории «Статистические«.
Т.к. столбец, по которому мы будем проверять условие, отличается от того, по которому нужно искать среднее значение, то мы напишем следующие параметры:
В поле «Диапазон» пишем: D2:D273 (Это диапазон, который участвует в условии).
В поле «Условие«: >=60 (Это само условие, которое работает в диапазоне, написанный выше).
В поле «Диапазон_усреднения«: C2:C273 (Это диапазон, для которого будет найдено среднее арифметическое значение. Будут участвовать только те строчки, которые прошли условие).
Если последнее поле остаётся пустым, то среднее значение ищется по первому полю.
Нажимаем «ОК», и получаем число 60,0301205. Округлим это число до целых, получим число 60.
2 Способ
Этот способ подходит и для более запутанных ситуаций.
Для строчек, где выполняется условие задачи, перенесём значения столбца С в столбец F.
Кликаем в ячейку F2, нажимаем кнопку «Вставить функцию«, выбираем функцию Если.
Сначала нужно записать формулу для одной строки.
В поле «Лог_выражение» пишем: D2>=60 (Условие того, что человек набрал не менее 60 баллов по информатике)
В поле «Значение_если_истина» пишем: C2 (Переносим само значение столбца математики. Именно впоследствии мы должны найти среднее значение баллов по математике).
В поле «Значение_если_ложь» пишем: «» (Пустые кавычки. Нельзя писать ноль, иначе мы сильно занизим реальное среднее значение).
Нажимаем «ОК». Получается число 81 в ячейке F2.Оно перенеслось из ячейки C2, ведь значение по информатике больше 60 для этой строчки.
Распространяем формулу на весь столбец.
В строках, которые не удовлетворяют условию задачи, будут пустые ячейки.
Когда столбец готов, легко найти среднее значение для столбца F.
Кликаем в ячейку G2 и вставляем функцию СРЗНАЧ. В этой функции указываем диапазон F2:F273.
Получается число 60,0301205. Округляем его до целых, получается число 60.
Ответ: 60
Не редкий гость в примерных задачах 9 задания из ЕГЭ по информатике 2021.
Задача (Найти проценты)
Откройте файл электронной таблицы, содержащей данные о количестве белков, жиров и углеводов для различных продуктов. Сколько процентов от общего числа составили продукты, у которых более 10 г белка?
В ответе напишите одно целое число.
Решение:
Задачи на проценты обычно сводятся к нахождению количества.
Найдём сколько продуктов, у которых белка более 10 г.
Кликаем по полю E2. Применим функцию СЧЕТЕСЛИ из категории «Статестические«.
Диапазон указываем: C2:C1001 (Столбец белка).
В поле критерий пишем: >10.
Нажимаем кнопку «ОК». В поле E2 получается число 373.
Чтобы найти проценты, нужно это количество, которое мы нашли, разделить на всё количество продуктов и умножить на сто.
Кликаем по верхнему полю («строка формул»):
Дописываем: =СЧЁТЕСЛИ(C2:C1001;»>10″)/1000 * 100
Всего у нас 1000 наименований продуктов. Строчек 1001, но начинаются продукты со второй строчки. Поэтому делим на 1000 (1001 — 1). Умножаем на 100, чтобы найти проценты.
Нажимаем Enter. Получается число 37,3. Округлим до целого числа, ответом будет 37.
Ответ: 37
В следующей примерной задаче 9 задания ЕГЭ по информатике 2021 будем комбинировать уже изученные приёмы.
Задача (Комбинируем приёмы)
Откройте файл электронной таблицы, содержащей вещественные числа – ведомость продуктового магазина. Наценкой товара считается разность между закупочной ценой и ценой реализации. Прибыль – количество проданных товаров, умноженное на значение наценки. Найдите товар с наценкой выше среднего значения, который принесет максимальную прибыль после его полной продажи.
В качестве ответа укажите одно число – полученную после продажи найденного товара прибыль. Ответ округлите до целых чисел.
Сначала нужно найти среднее значение наценки. Запишем наценку в столбце E.
Запишем формулу сначала для одной ячейки E2. Кликаем по ячейки E2, затем кликаем по верхнему полю («строка формул») и пишем: =C2-B2.
Примечание: Формула начинается со знака «равно»!
Нажимаем Enter. Получается число 9,42.
Подводим курсор мышки к правому нижнему углу. После появления чёрного крестика, нажимаем левую кнопку мышку и тянем вниз. Тем самым распространим формулу на весь столбец.
Найдём среднее значение наценки, которая находится в столбце E.
Кликаем по ячейке F2, затем на кнопку «Вставить функцию«, выбираем СРЗНАЧ. Диапазон указываем: E2:E100. Нажимаем «ОК» и получаем число 58,25. Это и есть среднее значение для наценки.
Теперь напишем в столбец G прибыль, но только для тех товаров, у которых наценка выше среднего значения.
Сначала запишем формулу для одной строчки. Кликаем по ячейки G2, нажимаем «Вставить функцию«, выбираем ЕСЛИ.
В поле «Лог_выражение» пишем: E2>58,25. Если наценка выше среднего, то будем считать прибыль.
Т.к. в столбце E все числа имеют не более двух знаков после запятой и число 58,25 тоже имеет два знака после запятой, то мы не получим ошибок из-за округления среднего значения.
В поле «Значение_если_истина» : E2 * D2 (Умножаем наценку на количество проданных товаров. Получаем прибыль).
В поле «Значение_если_ложь«: «» (Пустые кавычки. Ведь мы потом будем искать максимальное значение для прибыли, для товаров, у которых наценка выше среднего значения).
Нажимаем «ОК». Получается в G2 пустое окошко. Значит, для этого товара наценка не выше среднего значения.
Распространим формулу на весь столбец G. Где-то окажутся числа, а где-то пустые ячейки.
Кликнем по ячейке H2 и найдём с помощью функции МАКС (категория «Статистические») максимальную прибыль, в диапазоне указав: G2:G100. Округлив до целых, в ячейке H2 получается ответ 10185.
Примечание: Мы могли при составлении условия E2>58,25 использовать название ячейки F2 вместо числа 58,25. Но тогда нужно её «зацементировать» т.е. E2>$F$2 (Использовать абсолютную адресацию). Если мы всё-таки решили написать число, то нужно следить, чтобы точность была одинаковая у среднего значения, и у тех ячеек, которые мы сравниваем с этим средним значением.
Ответ: 10185
Последнее. Если в задаче говорится о значении по абсолютной величине, т.е. о значении по модулю, то нужно использовать конструкцию ABS(). Например, разница по абсолютной величине двух ячеек A2 и B2 равна ABS(A2-B2). Это можно использовать при составлении формул.
Так же при подготовке к 9 заданию может быть полезна статья, которая была написана под старый формат ЕГЭ по информатике.
На этом всё. Комбинируйте приёмы, которые мы рассмотрели в этом уроке при подготовке к 9 заданию из ЕГЭ по информатике нового формата 2021. Удачи!
На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 9 задания. Объясняется тема о работе в электронных таблицах и базах данных.
Содержание:
- ЕГЭ по информатике 9 задания объяснение
- Анализ диаграмм и графиков в электронных таблицах
- Типы ссылок в ячейках
- Построение диаграмм
- Тренировочные задания 9 ЕГЭ по информатике и их решение
- Встроенные функции в электронных таблицах
- Задания с диаграммами (задания прошлых лет для тренировки)
9-е задание: «Электронные таблицы»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение обрабатывать числовую информацию в электронных таблицах
До ЕГЭ 2021 года — определенные типы этого задания были заданием № 7 ЕГЭ
Ниже рассмотрены наиболее часто встречающиеся функции и их смысл. Наводите курсор на пример для просмотра ответа.
Таблица: Наиболее часто используемые функции
| русский | англ. | действие | синтаксис |
|---|---|---|---|
| СУММ | SUM | Суммирует все числа в интервале ячеек | СУММ(число1;число2) |
| Пример: | |||
| =СУММ(3; 2) =СУММ(A2:A4) |
|||
| СЧЁТ | COUNT | Подсчитывает количество всех непустых значений указанных ячеек | СЧЁТ(значение1, [значение2],…) |
| Пример: | |||
| =СЧЁТ(A5:A8) | |||
| СРЗНАЧ | AVERAGE | Возвращает среднее значение всех непустых значений указанных ячеек | СРЕДНЕЕ(число1, [число2],…) |
| Пример: | |||
| =СРЗНАЧ(A2:A6) | |||
| МАКС | MAX | Возвращает наибольшее значение из набора значений | МАКС(число1;число2; …) |
| Пример: | |||
| =МАКС(A2:A6) | |||
| МИН | MIN | Возвращает наименьшее значение из набора значений | МИН(число1;число2; …) |
| Пример: | |||
| =МИН(A2:A6) | |||
| ЕСЛИ | IF | Проверка условия. Функция с тремя аргументами: первый аргумент — логическое выражение; если значение первого аргумента — истина, то результатом выполнения функции является второй аргумент. Если ложно — третий аргумент. | ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь) |
| Пример: | |||
| =ЕСЛИ(A2>B2;»Превышение»;»ОК») | |||
| СЧЁТЕСЛИ | COUNTIF | Количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СЧЁТЕСЛИ(диапазон, критерий) |
| Пример: | |||
| =СЧЁТЕСЛИ(A2:A5;»яблоки») | |||
| СУММЕСЛИ | SUMIF | Сумма непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СУММЕСЛИ (диапазон, критерий, [диапазон_суммирования]) |
| Пример: | |||
| =СУММЕСЛИ(B2:B25;»>5″) |
Анализ диаграмм и графиков в электронных таблицах
Типы ссылок в ячейках
Формулы, записанные в ячейках таблицы, бывают относительными, абсолютными и смешанными.
- Имена ячеек в относительной формуле автоматически меняются при переносе или копировании ячейки с формулой в другое место таблицы:
- Имена ячеек в абсолютной формуле не меняются при переносе или копировании ячейки с формулой в другое место таблицы.
- Для указания того, что не меняется столбец, ставится знак
$перед буквой столбца. Для указания того, что не меняется строка, ставится знак$перед номером строки: - В смешанных формулах меняется только относительная часть:
Относительная адресация:
имя столбца вправо на 1
номер строки вниз на 1
Абсолютная адресация:
имена столбцов и строк при копировании формулы остаются неизменными
Смешанные формулы
Построение диаграмм
- Диаграммы используются для наглядного представления табличных данных.
- Разные типы диаграмм используются в зависимости от необходимого эффекта визуализации.
- Так, круговая и кольцевая диаграммы отображают соотношение находящихся в выбранном диапазоне ячеек данных к их общей сумме. Иными словами, эти типы служат для представления доли отдельных составляющих в общей сумме.
- Соответствие секторов круговой диаграммы (если она намеренно НЕ перевернута) начинается с «севера»: верхний сектор соответствует первой ячейке диапазона.
- Типы диаграмм Линейчатая и Гистограмма (на левом рис.), а также График и Точечная (на рис. справа) отображают абсолютные значения в выбранном диапазоне ячеек.

Егифка ©:
* Некоторые изображения, представленные в изложении теоретического материала, заимствованны с сайта К. Полякова
Тренировочные задания 9 ЕГЭ по информатике и их решение
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Встроенные функции в электронных таблицах
9_00: 9 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры и её средним арифметическим значением.
В ответе запишите только целую часть получившегося числа.
Типовые задания для тренировки
9_01: Задание 1:
Задание выполняется с использованием прилагаемых файлов
Найдите разность между максимальным и минимальным числом в диапазоне C48:Y360. В ответе запишите только целую часть числа.
✍ Решение:
-
Добавим формулы в пустые ячейки:
- Ячейка A502
= МАКС(C48:Y360) - Ячейка B502
= МИН(C48:Y360) - любая пустая ячейка
=A502-B502 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 920
9_02: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл 9-J1.xls электронной таблицы, содержащей вещественные числа – показатели высот над уровнем моря географических точек.
Найдите среднее значение всех отрицательных показателей и максимальное положительное значение.
В качестве ответа укажите целую часть суммы найденных значений.
✍ Решение:
- Перейдите в пустую ячейку (например,
АО1). - Поскольку для вычисления среднего арифметического используется дополнительное условие (только отрицательные показатели), то проще использовать формулу
СРЗНАЧЕСЛИ. Внесите формулу в заготовленную ячейку:
=СРЗНАЧЕСЛИ(A1:AN500;"<0")
Здесь условие обязательно должно быть в кавычках.
МАКСЕСЛИ.AO2:=МАКСЕСЛИ(A1:AN500;A1:AN500;">0")
АО3:=СУММ(AO1;AO2)
Получилось 502,531856
Ответ: 502
9_03: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл 9-j2.xl s электронной таблицы, содержащей вещественные числа – успеваемость учеников школ города по учебным дисциплинам за четвертую четверть.
Найдите школы с максимальным и минимальным средними показателями.
В качестве ответа укажите два числа – номера найденных школ, сначала с наименьшим показателем, затем с наибольшим.
✍ Решение:
- Поскольку средние значения по дисциплинам расставлены по столбцам, то необходимо выполнить вычисление общего среднего арифметического по каждой школе в каждом столбце.
- Для этого в пустой ячейке
B18для школы №1 напишите формулу вычисления среднего арифметического:
=СРЗНАЧ(B2:B16)
B20 и введите формулу:=ЕСЛИ(МАКС($B$18:$AI$18)=B18;B1;"")
$), иначе при копировании диапазон изменится, а нам этого не надо.B21 и введите формулу:=ЕСЛИ(МИН($B$18:$AI$18)=B18;B1;"")
Ответ: 32 8
9_04: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры и её средним арифметическим значением в первой половине дня (до 12:00 включительно).
В ответе запишите только целую часть получившегося числа.
✍ Решение:
-
Добавим формулы в пустые ячейки:
- Ячейка A94
= МАКС(B2:N92)= 35,6 - Ячейка A95
=СРЗНАЧ(B2:N92)= 21,4 - любая пустая ячейка
=A94-A95= 14,2 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 14
9_05: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры в апреле и её средним арифметическим значением во второй половине дня (с 12:00) за тот же период.
В ответе запишите только целую часть получившегося числа.
✍ Решение:
-
Добавим формулы в пустые ячейки. Возьмем значения ячеек только за апрель (04 месяц). Для поиска среднего арифметического значения учтем также, что время должно быть с 12.00, то есть со столбца N:
- Ячейка A94
= МАКС(B2:Y31)= 26,0 - Ячейка A95
= СРЗНАЧ(N2:Y31)= 21,0 - любая пустая ячейка
=A94-A95= 5,0 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 5
9_06: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным и минимальным значением температуры среди измерений, сделанных в 17:00.
В ответе запишите только целую часть получившегося числа, округлять не нужно.
✍ Решение:
-
Добавим формулы в пустые ячейки. Возьмем значения ячеек только за 17.00, то есть со столбца S:
- Ячейка A94
=МАКС(S2:S92)= 37,8 - Ячейка A95
=МИН(S2:S92)= 22,4 - любая пустая ячейка
=A94-A95= 15,4 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 15
9_07: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Посчитайте сумму средних арифметических значений температур в 16:00 и в 23:00.
Округлите полученное число до целого и запишите его в ответ.
✍ Решение:
-
Добавим формулы в пустые ячейки. Возьмем значения ячеек только в 16.00, то есть со столбца R и в 23.00, то есть со столбца Y:
- Ячейка A94
=СРЗНАЧ(R2:R92)= 29,9 - Ячейка A95
=СРЗНАЧ(Y2:Y92)= 20,8 - любая пустая ячейка
=A94+A95= 50,7 - После округления получаем 51.
- Можно также решить данное задание, записав все в одну строку:
= СРЗНАЧ(R2:R92)+СРЗНАЧ(Y2:Y92)
Ответ: 51
9_08: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите результат деления суммы всех значений температуры на максимальное значение.
В ответе запишите только целую часть получившегося числа, округлять не нужно.
✍ Решение:
-
Добавим формулы в пустые ячейки. Используем в формулах вcю таблицу, то есть диапазон ячеек от
- Ячейка A94
=МАКС(B2:Y92)= 38,0 - Ячейка A95
=СУММ(B2:Y92)= 51807,0 - любая пустая ячейка (поделим сумму на максимальное значение)
=A95/A94= 1363,3 - Оставляем только целую часть = 1363.
B2 до Y92 (B2:Y92):
Ответ: 1363
9_09: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Посчитайте чему будет равно самое часто встречаемое значение температуры и среднее арифметическое значений температуры за всё время измерений. Найдите разницу между самым встречаемым значением и средним арифметическим значением.
В ответе запишите только целую часть числа (разницы).
✍ Решение:
-
Добавим формулы в пустые ячейки. Используем в формулах вcю таблицу, то есть диапазон ячеек от
- Для более достоверных расчетов будем использовать числа с тремя знаками после десятичной запятой. Воспользуемся кнопкой
- Ячейка A94
=СРЗНАЧ(B2:Y92)= 23,721 - Ячейка A95
=МОДА(B2:Y92)= 25,700 - любая пустая ячейка
=A95-A94= 1,979 - Оставляем только целую часть = 1.
B2 до Y92 (B2:Y92):
Для нахождения наиболее часто встречаемого значения используется функция МОДА ()
Ответ: 1
9_14: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
В каком количестве измерений температура оказалась выше 25 градусов?
✍ Решение:
- Поскольку нам необходимо посчитать количество, то будем использовать функцию
СЧЁТ(). Но так как считать надо количество измерений температуры выше 25 градусов, то нужно использовать функцию с критерием, а именно,СЧЁТЕСЛИ(). - Введите формулу в любую пустую ячейку:
=СЧЁТЕСЛИ(B2:Y92;">25")
Обратите внимание, что так как с условием сравнивается диапазон, а не единственная ячейка, то само условие необходимо разместить в кавычках.
Ответ: 942
9_15: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-j5.xls, содержащей вещественные числа – количество баллов, которое набрали участники тестирования. В первой строке указаны дисциплины, во второй – максимальный балл за тест по дисциплине, в левом столбце – фамилии участников. Считается, что тест пройден, если участник тестирования набрал больше 60% от максимального балла. В качестве ответа укажите, сколько участников тестирования прошли больше трёх тестов.
✍ Решение:
- Для начала будем сравнивать максимальный балл * 0,6 с баллом, набранным участником. Если балл участника больше, будем ставить в ячейку цифру
1, иначе —0. - В ячейку
B35введем формулу:
=ЕСЛИ(B4>B$2*0,6;1;0)
О включительно (последний столбец с данными).ЕСЛИ().А35:=ЕСЛИ(СУММ(B35:O35)>3;1;"")
B64.Ответ: 18
9_16: Задание:
Задание выполняется с использованием прилагаемых файлов
В электронной таблице в файле 9-j10.xls хранятся вещественные числа – результаты ежечасного измерения скорости ветра на протяжении трех месяцев.
Найдите количество дней, когда максимальная скорость ветра составляла не менее 90% от максимального значения за весь период.
✍ Решение:
- Сначала найдем максимальную скорость ветра за весь период. Введем формулу в ячейку
AB2:
=МАКС(B2:Y91)
AB2. Будем использовать функцию СЧЁТЕСЛИ(), так как считаем при условии.=СЧЁТЕСЛИ($Z$2:$Z$91;">="&AB2*0,9)
Обратите внимание, что в условии используются кавычки, но для добавления к условию рассчитанного значения в ячейке AB2, необходимо «приклеить» это значение с помощью знака &
Ответ: 80
Также можно посмотреть некоторые аналогичные задания ОГЭ
Задания с диаграммами (задания прошлых лет для тренировки)
9_7:
Задан фрагмент электронной таблицы:
Как изменится значение ячейки C3, если после ввода формул переместить содержимое ячейки B2 в B3?
(«+1» означает увеличение на 1, «-1» означает уменьшение на 1):
Варианты:
1) -2
2) -1
3) 0
4) +1
✍ Решение:
-
Проанализируем данные электронной таблицы до перемещения:
- В ячейке C2 будет находиться число 4, так как функция СЧЁТ подсчитывает количество непустых ячеек указанного диапазона.
- В ячейке С3 будет находиться число 3:
(1 + 2 + 2 + 6 + 4) / 5 = 3
Теперь посмотрим, что произойдет после перемещения:
(1 + 2 + 2 + 3) / 4 = 2
(нужно не забывать, что функция СРЗНАЧ не учитывает пустые ячейки, поэтому ячейка B2 не учтена).
Результат: 2
Подробное решение задания на видео:
📹 YouTube здесь (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
Задание:
В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3.
Чему равно значение формулы =СУММ(С2:С4), если значение ячейки С5 равно 5?
✍ Решение:
- Функция СРЗНАЧ предназначена для вычисления среднего арифметического значения указанного диапазона ячеек. Т.е. в нашем случае среднее значение ячеек C2, C3, C4, C5.
- Результат функции
=СРЗНАЧ(С2:С5)задан по условию, подставим его в формулу:
(C2 + C3 + C4 + C5)/4 = 3
x / 4 = 3
x = 3 * 4 = 12 -> C2 + C3 + C4 + C5 = 12
=СУММ(С2:С4). Зная значение в ячейке С5, вычтем его из полученной суммы и найдем ответ:C2 + C3 + C4 = C2 + C3 + C4 + C5 - C5 =
= 12 - 5 = 7
Результат: 7
Подробное решение смотрите на видео:
📹 YouTube здесь
Рассмотрим еще один пример решения 9 задания ЕГЭ по информатике:
9_10:
Дан фрагмент электронной таблицы:
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
✍ Решение:
- Круговая диаграмма отображает доли отдельных частей в общей сумме. В нашем случае в диаграмме отражаются результаты вычисления формул в ячейках А2:С2
- По диаграмме можно судить о том, что, скорее всего, полученные значения в формулах во всех ячейках должны быть равны (секторы диаграммы визуально равны).
- Получим выражения из формул ячеек, подставив вместо С1 -> x:
А2: х + 2 В2: 8/2 = 4 С2: х * 2
2 * х = 4 => x = 2
Результат: 2
Детальный разбор можно посмотреть в видеоуроке решения данного 9 задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
9_11:
Задан фрагмент электронной таблицы:
Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:C2 соответствовала рисунку:

✍ Решение:
- По диаграмме можно судить только о следующем: если она не перевернута, то значения в ячейках A2 и B2 должны быть равны, а значение ячейки C2 — в два раза больше каждой из них.
- Поскольку у нас неизвестны значения двух ячеек, то обозначим B1 за x, а C1 за y.
- Подставим неизвестные в формулы и получим:
- Исходя из первого пункта, получаем:
A2 = B2 = C2/2
4y = x - y 2 * 4y = x - y + 4
8y = 5y - y + 4 -> y = 1
Результат: 5
Подробное теоретическое решение смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
9_12:
Дан фрагмент электронной таблицы в режиме отображения формул:
После копирования диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 была построена диаграмма (график) по значениям столбцов диапазона ячеек В2:Е6.
Значениям D2:D6 соответствует график:
Варианты:
1) А 2) Б 3) В 4) Г
✍ Решение:
- Копирование диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 буквально означает выделение диапазона АЗ:ЕЗ и протягивание маркера копирования до конца указанного блока ячеек.
- Поскольку нас интересует только столбец D, то посмотрим, что там за формула, и что с ней произойдет при копировании:
- в ячейке D3 значение зависит от ячейки A3 и оно равно 2;
- при копировании формулы столбец остается тот же (D), поэтому и в формуле буквы остаются теми же (D и A), а вот строки копируются вниз, т.е. цифры в формуле увеличиваются на единицу при движении вниз на каждую строку; соответственно, нас интересуют еще ячейки A4, A5, A6;
- формулы ячеек A4, A5, A6 зависят от ячеек столбца B, поэтому рассмотрим получившиеся при копировании формулы столбцов A и B:
- Теперь вычислим значения в этих столбцах:
- Получаем точки по столбцу D: 1, -1, -1, -7, -15, что соответствует графику Г (ответ 4)
Результат: 4
Разбор задания смотрите на видео:
📹 YouTube здесьздесь (теоретическое решение)
9_13:
Дан фрагмент электронной таблицы:
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, положительные.
✍ Решение задания 7:
- На изображенной диаграмме (если она преднамеренно не перевернута) секторы соответствуют указанному диапазону ячеек при движении по часовой стрелке с «севера на юг»: т.е. А2 — синий сектор, B2 — красный и т.п. Таким образом, делаем следующий вывод:
А2 = B2 = 2 * C2 = 2 * D2
B2 = 2 * D2 2(x + 5) = x + 21 2x - x = 21 - 10 x = 11
Результат: 11
Видеоразбор задания:
📹 YouTube здесьздесь (теоретическое решение)
Технология обработки информации в электронных таблицах
Ввод и редактирование данных в электронных таблицах, операции над данными
Программа Excel — одно из самых популярных средств управления электронными таблицами.
Каждый документ представляет собой набор таблиц — рабочую книгу, которая состоит из одного или многих рабочих листов. Каждый рабочий лист имеет название — это как бы отдельная электронная таблица. По умолчанию первый документ называется Книга1. При сохранении в файле документа это имя можно изменить.
Таблица состоит из столбцов и строк. Столбцы обозначаются латинскими буквами A, B, C, D и т. д. Если букв алфавита не хватает — используют двухбуквенные обозначения AA, AB, AC,…, IV. Максимальное число столбцов — 256. Строки нумеруются целыми числами. Максимальное число строк — 65535.
Ячейки располагаются на пересечении столбцов и строк. Номер (адрес) ячейки формируется из номера столбца и номера строки без пробела между ними. Например, A1, D24, M355. Одна из ячеек на рабочем листе всегда является текущей (активной). Она обведена широкой рамкой; в поле имени выводится ее номер, а в строке формул — ее содержимое. Именно с этой ячейкой производится работа — считывание или запись.
Заполнение таблиц данными
Ячейка может содержать три вида данных:
- Текстовые данные — строка текста произвольной длины.
- Числовые данные — отдельное число (в допустимом формате). Как числа рассматриваются данные, определяющие даты или денежные суммы.
- Формулы — содержимое ячейки рассматривается как формула, если оно начинается со знака равенства «=». Ячейка, содержащая формулу, является вычисляемой, т. е. значение ее может зависеть от значений других ячеек таблицы. Формулы в ячейках не отображаются. Вместо формулы воспроизводится результат, полученный при ее вычислении. Чтобы увидеть формулу, хранящуюся в вычисляемой ячейке, нужно выделить эту ячейку (сделать текущей) и посмотреть в строку формул.
Возможна одновременная обработка нескольких ячеек (диапазона ячеек). Диапазон отображается на экране в инвертированном виде и обводится толстой рамкой. Бывают двумерные (строка, столбец) и трехмерные (строка, столбец, лист) диапазоны. Для обозначения диапазона используется разделитель « : ». Например, В:Е — диапазон столбцов от В до Е включительно, т. е. вертикальная полоса; 2:6 — диапазон строк со 2 по 6 включительно, т. е. горизонтальная полоса; B2:G12 — диапазон ячеек, левый верхний угол которого — ячейка В2, нижний правый угол — ячейка G12.
Данные вводятся в текущую ячейку и одновременно отображаются в строке формул. Вводимый текст автоматически выравнивается по левому краю, а числа — по правому. Необходимые данные можно вставить в электронную таблицу из других приложений с помощью команд группы Получить внешние данные вкладки Данные или обычным копированием с использованием буфера обмена Windows (здесь и далее приводятся команды для программы Excel из пакета MS Office 2007).
Редактирование введенных данных осуществляется следующим образом. Если в заполненную ячейку нужно ввести новые данные, то необходимо сделать ее текущей и начать вводить новые значения. Старое содержимое ячейки при этом утрачивается. Если же надо только откорректировать некоторые данные, то нужно, активизировав ячейку, нажать клавишу [F2] или выполнить двойной щелчок левой клавишей мыши по ячейке. При этом в ячейке появится текстовый курсор, и содержимое можно исправить. Также исправления можно ввести в строку формул активной ячейки.
В электронных таблицах реализована автоматизация ввода данных. Многие таблицы могут содержать в ячейках повторяющиеся данные. При заполнении таких таблиц Excel уже по первой букве «догадывается», что хочет ввести пользователь, и выводит подсвеченное значение в ячейку. Интеллектуальные способности программы можно развить и автоматизировать ввод не только повторяющихся данных, но и данных, поддающихся несложному закону изменения.
Чтобы размножить данные на несколько ячеек, нужно сделать активной первую ячейку диапазона и заполнить ее. Затем установить указатель мыши на маркер заполнения (правый нижний угол рамки текущей ячейки). Перетаскиванием маркера заполнения можно размножить содержимое текущей ячейки на несколько ячеек в столбце или строке. Если в первой ячейке были введены день недели или дата, то при перетаскивании вправо или вниз их значения будут увеличиваться на 1, а при перетаскивании влево или вверх — уменьшаться на 1. Если в ячейку было введено число или текст, то при перетаскивании маркера оно скопируется в другие ячейки. Для создания числового ряда при перетаскивании маркера заполнения следует удерживать нажатой клавишу [Ctrl]. По ходу перетаскивания содержимое последней ячейки отображается в небольшом всплывающем окне. Если для перетаскивания маркера использовать правую кнопку мыши, то при ее отпускании появится контекстное меню, позволяющее изменить способ заполнения диапазона.
Если требуется более сложный закон изменения последовательности значений, то после выбора первой ячейки и ввода в нее нужного значения надо выполнить команду Заполнить/Прогрессия из группы Редактирование вкладки Главная.
Автозаполнение ячеек данными можно также осуществить следующим образом. В первую ячейку надо ввести начальное значение ряда данных, а во вторую — следующее значение. Затем выделить эти две ячейки и перетащить маркер заполнения до конца нужного диапазона. Excel проанализирует данные двух исходных ячеек, определит, насколько отличаются их значения, и создаст такой же ряд. Если в исходную ячейку было введено смешанное значение, например текст и число, то автозаполнение копирует текстовую часть (если только это не месяц или день) и наращивает числовую часть, если число находится в начале или в конце значения (но не в середине).
Операции над данными
В Excel можно обрабатывать как одну ячейку, так и выделенный диапазон. Для отмены неверных действий можно пользоваться кнопками 
Удаление. При нажатии клавиши [Del] произойдет очистка содержимого ячейки. Реальное удаление ячейки сопровождается изменением структуры таблицы. По команде Удалить ячейки из группы Ячейки вкладки Главная откроется диалоговое окно Удаление ячеек, в котором нужно выбрать направление смещения ячеек, занимающих освобождающееся место. Аналогичное окно открывается и при выборе команды Удалить из контекстного меню ячейки. Для удаления строки (столбца) надо выделить какую-либо ячейку в удаляемой строке (столбце) и выполнить команду Удалить строки с листа (Удалить столбцы с листа) из группы Ячейки вкладки Главная. Удалить строку или столбец целиком можно также выделив строку или столбец щелчком мыши по маркеру строки или столбца и выбрав команду Удалить из контекстного меню.
Копирование или перемещение. Эти операции можно осуществить разными способами:
- Навести указатель мыши на границу текущей ячейки (диапазона) и перетащить при нажатой левой кнопке мыши на новое место. В результате произойдет перемещение ячейки (диапазона). Если при перетаскивании удерживать нажатой клавишу [Ctrl], то произойдет копирование ячейки. При перетаскивании появляется серая рамка, которая помогает правильно разместить блок на новом месте.
- Выделить ячейку (диапазон), перейти на вкладку Главная и выполнить команду Копировать
или Вырезать
из группы Буфер обмена, а затем щелкнуть в нужном месте и выполнить команду Вставить
.
- Выполнить специальное перетаскивание нужного блока ячеек (нажата правая кнопка мыши). При отпускании кнопки мыши будет выведено контекстное меню, содержащее перечень допустимых операций: копирование, перемещение, копирование только значений или только форматов, копирование или перемещение со сдвигом остальных ячеек в нужную сторону.
Вставка. Для вставки в таблицу столбца щелкнуть на заголовке столбца, перед которым будет вставлен новый столбец, чтобы выделить его. Затем выполнить команду Вставить из контекстного меню выделенного столбца. Аналогично можно вставить строку, ячейку или блок ячеек.
Если нужно скопировать только часть информации, можно воспользоваться специальной вставкой. Команда Вставить/Специальная вставка из группы Буфер обмена откроет диалоговое окно, в котором можно указать, какую часть информации следует вставить из Буфера обмена (например, только значения без формул, по которым они получены; только форматы или только примечания).
Для вставки в таблицу рисунков или видеоклипов следует выбрать соответствующие параметры из группы Иллюстрации вкладки Вставка. Простой рисунок можно сделать и самому, воспользовавшись параметрами Фигуры и SmartArtt из группы Иллюстрации. При добавлении фигуры на лист, открывается дополнительная вкладка Средства рисования, параметры которой позволяют изменить размеры и стиль фигуры, задать дополнительные эффекты, упорядочить, сгруппировать несколько фигур, добавить надписи и т. д.
Отформатировать ячейку (выделенный диапазон ячеек) и ее содержимое можно с помощью параметров групп Шрифт, Выравнивание, Число и Стили вкладки Главная. Щелчок мышью на кнопке с изображением стрелки рядом с названием группы открывает диалоговое окно Формат ячеек. На вкладке Число этого окна можно выбрать формат представления чисел и задать различные параметры, зависящие от выбранного формата; на вкладке Выравнивание установить способ вертикального и горизонтального выравнивания данных в ячейке, задать перенос по словам, объединение ячеек, автоподбор их ширины и т. д.; с помощью команд вкладки Шрифт задать гарнитуру шрифта и его параметров; на вкладках Граница и Вид задать способ обрамления ячейки, выбрать цвет фона и узор заполнения; с помощью команд вкладки Защита защитить ячейку паролем.
Типы и формат данных. Работа с формулами. Абсолютная и относительная ссылки. Использование функций
В работе с электронными таблицами выделяют три основных типа данных: числа, текст и формулы. В зависимости от решаемой задачи применяются различные форматы представления данных. Чтобы задать формат данных, нужно выбрать соответствующий параметр из группы Число вкладки Главная или щелчком мыши на кнопке с изображением стрелки рядом с названием группы открыть диалоговое окно Формат ячеек, в котором на вкладке Число выбрать желаемый формат представления данных и настроить его параметры.
Числа в Excel отображаются в таких категориях форматов, как Числовой, Экспоненциальный, Финансовый, Денежный, Процентный и Дробный. Если необходимо ввести числа без привязки к каким-либо форматам, можно использовать формат Общий. При использовании числового формата можно задавать количество десятичных знаков с помощью кнопок Формат с разделителями




Формат Дата и время позволяет хранить значения временных данных в удобном и привычном виде, например: 16.4; 16 апр; 16 Апрель 2009; апрель 2009; 16.04.09 1:30 РМ; 16.04.09 13:30 и т. д.
Текстом в Excel считается любая последовательность, состоящая из цифр, пробелов и нецифровых символов.
Формула должна начинаться со знака равенства и может включать в себя числа, имена ячеек, функции и знаки математических операций («+» — сложение; «–» — вычитание; «» — умножение; «/» — деление, «^» — возведение в степень).
Чтобы в формуле сделать ссылку на ячейку, нужно указать ее имя вручную или просто щелкнуть по ней мышью. При этом ячейка обводится цветной рамкой. Если содержимое ячейки, участвующей в формуле, изменится, то и значение формулы изменится.
Существуют следующие типы ссылок на адреса ячеек: относительные, абсолютные и смешанные. Различия между ними проявляются при копировании формулы из активной ячейки в другую ячейку.
Относительная ссылка указывает на ячейку, основываясь на ее положении относительно ячейки, в которой находится формула, например: «на две строки выше». Абсолютная ссылка использует для указания на ячейку ее фиксированное положение на листе, например: «ячейка находится в столбце А строки 2». Смешанная ссылка содержит относительную и абсолютную ссылки, например: «ячейка находится в столбце А и выше на две строки». Относительная ссылка на ячейку А1 записывается так: = А1.
Абсолютная ссылка на ячейку А1 имеет следующий вид: = $A$1.
Комбинируя абсолютные и относительные ссылки на ячейку А1, можно создать следующие смешанные ссылки: = $A1 = A$1.
Если символ «доллар» стоит перед буквой, то координата столбца абсолютная, а строки — относительная. Если же символ «доллар» стоит перед числом, то координата столбца относительная, а строки — абсолютная. С помощью клавиши [F4] можно быстро изменить тип ссылки по схеме: A1 → $A$1→ A$1 → $A1 → A1.
При перемещении или копировании формулы из активной ячейки относительные ссылки автоматически настраиваются, а абсолютные сохраняются. Например, если в ячейку С2 ввести формулу = А2 * В2 + $A$1, а затем перетащить маркер заполнения до ячейки С6, то в ячейках С3—С6 относительные ссылки А1 и В1 будут заменяться на А3, В3, А4, В4 и т. д., а ссылка $A$1 не изменится.
Формулы с текстовыми значениями
В большинстве случаев работа с текстовыми значениями происходит так же, как с числами. Например, если ячейка А1 содержит текст ABCDE и в ячейку А10 введена формула = А1, то в ячейке А10 также будет выведено ABCDE.
Для объединения текстовых значений используется текстовый оператор &. Например, если ячейка А1 содержит текст ABCDE, а ячейка А2 — текст WQRT, и в ячейку А3 введена формула = А1 & A2, то в ячейке А3 будет выведено ABCDEWQRT. Чтобы вставить пробел между двумя строками, нужно изменить формулу на следующую: = А1&» «&A2 && . Эта формула использует два текстовых оператора и текстовую константу — в данном случае пробел, заключенный в двойные кавычки.
С помощью оператора & можно объединять и числовые значения. Например, если ячейка А1 содержит числовое значение 123 и в ячейке А2 записано число 456, значением формулы =А1&А2 будет строка символов 123456. Эта строка выравнивается по левому краю, т. к. она является текстовым значением.
Кроме того, можно использовать оператор & для объединения текстовых и числовых значений. Например, если ячейка А1 содержит текст ABCDE, а ячейка А2 содержит числовое значение 123, то значением формулы = А1&А2 будет строка ABCDE123.
Если Excel не может вычислить результат формулы, то в ячейку выводится ошибочное значение, например: #Дел/0!, #ИМЯ?, #ЗНАЧ! и др.
Примеры решения задач
Пример 1. В ячейке С1 записана формула = 3 * $B1. Формулу скопировали в ячейку Е2. Какой вид приобретет формула в ячейке Е2?
Решение. В формуле используется смешанная ссылка на ячейку $B1: ссылка на столбец абсолютная, т. е. при копировании столбец не изменится; ссылка на строку относительная, т. е. при копировании номер строки настроится. В исходной формуле в качестве второго сомножителя выступают данные ячейки из той же строки, в которой находится и формула (из 1-й). Значит, и в скопированной формуле данные будут браться из той же строки (2-й).
Ответ: в ячейке Е2 будет записана формула = 3 * $B2.
Пример 2. Дан фрагмент электронной таблицы:
В ячейку D2 введена формула А2 * В1 + $C$1. Какое значение появится в ячейке D2 после вычисления формулы?
Решение. Значение ячейки А2 — 3, В1 — 5, $C$1 — 3. Подставим значения в формулу: 3 · 5 + 3 = 18.
Ответ: 18.
Использование функций
Функция — это заранее определенная формула, которая оперирует с одним или несколькими значениями и возвращает одно или несколько значений.
Одно из самых распространенных действий — вычисление суммы значений в столбцах или строках. Excel предлагает функцию =СУММ (диапазон). Например, для суммирования значений в ячейках А1:А10 в ячейку А11 нужно ввести функцию =СУММ (А1:А10). Для облегчения доступа к этой функции в группе Редактирование вкладки Главная есть кнопка Сумма
Функция состоит из двух частей:
- имя (СУММ, AVERAGE и др.) — описывает операцию, которую выполняет функция;
- аргументы — задают значения или ячейки, используемые функцией.
Например, СУММ (А1:А6). Здесь СУММ — имя, а диапазон М А1:А6 — ее единственный аргумент.
Между именем функции и ее аргументами не должно быть пробелов. Некоторые функции не имеют аргументов, но круглые скобки все равно нужно ставить. Например: =А1 ПИ().
При использовании в функции нескольких аргументов нужно отделять их друг от друга « ; ». Например: функция =ПРОИЗВ(С1;С2;С5) перемножает числа в ячейках С1, С2 и С5.
В функции можно использовать до 30 аргументов, если при этом общая длина формулы не превосходит 1024 символа. Однако любой аргумент может быть диапазоном, содержащим произвольное число ячеек листа. Например, функция =СУММ (А1:А5; С2:С10; D3:D17) содержит всего три аргумента, но суммирует 29 ячеек. Указанные в ссылке ячейки в свою очередь могут содержать формулы, которые ссылаются на другие ячейки и диапазоны. Используя аргументы, можно легко создавать длинные цепочки формул для выполнения сложных операций.
Аргументы функций могут представлять собой выражения из комбинаций функций. Например: =СУММ (SIN (A1ПИ ( ) ); 2 * COS (A2ПИ ( ) ) ). Здесь функции SIN, COS и ПИ сначала вычисляются, а затем используются в качестве аргументов функции СУММ.
Функцию можно вводить на рабочий лист прямо с клавиатуры. Но удобнее воспользоваться командой Вставить функцию из группы Библиотека функций вкладки Формулы. Excel выведет окно диалога Мастер функций — шаг 1 из 2. В этом окне сначала надо выбрать категорию в одноименном списке, а затем в алфавитном списке Выберите функцию указать нужную функцию и нажать кнопку ОК. Excel выведет в ячейке и в строке формул знак равенства, имя функции и пару круглых скобок, а затем откроет второе окно диалога мастера функций. В нем содержатся поля для ввода аргументов выбранной функции. Если функция имеет переменное число аргументов, то это окно диалога увеличивается при вводе дополнительных аргументов. Справа от каждого поля аргумента отображается его текущее значение. После ввода всех аргументов надо нажать кнопку ОКК — и созданная функция появится в строке формул.
Также окно мастера функций можно вызвать щелчком на кнопке Вставить функцию
Всего в Excel более 300 встроенных функций. Вот некоторые из них.
Математические функции:
= СУММ (числа) — функция суммирует множество чисел.
= ABS (число) — возвращает абсолютное значение числа или формулы.
= ОКРУГЛ (число; количество_цифр) — округляет число, задаваемое ее аргументом, до указанного количества десятичных разрядов.
= КОРЕНЬ (число) — возвращает положительный квадратный корень из числа. Аргумент должен быть положительным числом.
= ПРОИЗВЕД (число1; число2;…) — перемножает все числа, задаваемые ее аргументами.
= LOG (число; основание) — возвращает логарифм положительного числа по заданному основанию. Если аргумент основание не задан, то Excel примет его равным 10.
= СТЕПЕНЬ (число; степень) — возводит число в заданную степень. Эта функция является эквивалентом оператора ^. Например, формулы =СТЕПЕНЬ(3;2) и =3^2 равносильны.
= SIN (число), = COS (число), = TAN (число) — возвращают синус, косинус, тангенс угла. Число — это угол в радианах.
Текстовые функции:
= ЗНАЧЕН (текст) — преобразование текста в число. Текст — это числа или даты, введенные в текстовом формате, т. е. заключенные в кавычки.
= ДЛСТР (текст) — возвращает количество символов в текстовой строке.
= СИМВОЛ (число) — возвращает символ, который соответствует заданному числовому коду ASCII.
= КОДСИМВ (текст) — возвращает код ASCII для первого символа аргумента.
Логические функции:
= ЕСЛИ (логическое_выражение; значение_если_истина; значение_если_ложь). В качестве аргументов этой функции можно использовать другие функции.
= И (логическое_значение1; логическое_значение2; …; логическое_значение30). Принимает значение ИСТИНА тогда и только тогда, когда все аргументы имеют значение ИСТИНА.
= ИЛИ(логическое_значение1; логическое_значение2; …; логическое_значение30). Принимает значение ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА.
= НЕ (логическое_значение). Принимает значение ИСТИНА, если аргумент имеет значение ЛОЖЬ, и наоборот.
Функции даты и времени:
= ДАТА (год; месяц; день) — возвращает десятичное значение даты, которое представляет собой количество дней между базовой и заданной датой.
= СЕГОДНЯ () — возвращает десятичное значение текущей даты.
= ВРЕМЯ (часы; минуты; секунды) — возвращает десятичное значение, которое представляет собой долю суток между полуночью и заданным временем. Аргумент секунды является необязательным: его можно опустить, но точку с запятой после аргумента минуты все равно надо поставить.
Статистические функции:
= СРЗНАЧ (число1; число2;…) — вычисляет среднее арифметическое значение. Функция игнорирует пустые, логические и текстовые ячейки.
= МАКС (число1; число2;…), = МИН (число1; число2;…) — возвращают наибольшее и наименьшее значения из набора данных.
= СУММЕСЛИ (диапазон; критерий; диапазон_суммирования) — каждая ячейка диапазона проверяется на соответствие критерию, прежде чем прибавляется к итогу.
= СЧЕТЕСЛИ (диапазон; критерий) — вычисляется количество ячеек, которые удовлетворяют заданному критерию.
Типовое задание № 2
(базовый уровень,
время – 3 мин)
Тема:
Анализ таблиц истинности логических выражений.
Что проверяется:
Умение строить таблицы
истинности и логические схемы.
1.5.1.
Высказывания, логические операции, кванторы, истинность высказывания
1.1.6.
Умение строить модели объектов, систем и процессов в виде таблицы истинности
для логического высказывания
Про обозначения
К
сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной»
математической логике (Ù,Ú,¬), неудобны, интуитивно
непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему
стыду, до сих пор иногда путает Ù и Ú.
Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком
умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+»
(логическое сложение). В разных учебниках используют разные обозначения. К
счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù,Ú,¬), что еще раз подчеркивает проблему.
Что нужно знать:
условные
обозначения логических операций
¬ A, не
A (отрицание, инверсия)
A Ù B, A и B (логическое
умножение, конъюнкция)
A Ú B, A или B
(логическое сложение, дизъюнкция)
A → B импликация (следование)
A º B
эквивалентность (равносильность)
операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A → B = ¬ A Ú B или в других обозначениях A → B =
иногда для упрощения выражений полезны формулы де Моргана:
¬ (A Ù
B) = ¬ A Ú ¬ B
¬ (A Ú
B) = ¬ A Ù ¬ B
если в выражении нет скобок, сначала выполняются все операции
«НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя –
«эквивалентность»
таблица
истинности выражения определяет его значения при всех возможных комбинациях
исходных данных
если
известна только часть таблицы истинности, соответствующее логическое выражение
однозначно определить нельзя, поскольку частичной таблице могут соответствовать
несколько разных логических выражений (не совпадающих для других вариантов
входных данных);
количество
разных логических функций, удовлетворяющих неполной таблице истинности, равно , где
– число отсутствующих строк; например, полная
таблица истинности выражения с тремя переменными содержит 23=8 строчек, если
заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции,
удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
логическая
сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все
слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение
истинно)
логическое
произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда,
когда все сомножители одновременно равны единице, а в остальных случаях равно 0
(выражение ложно)
логическое
следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка)
истинна, а B (следствие) ложно
эквивалентность
АºB равна 1 тогда и только тогда,
когда оба значения одновременно равны 0 или одновременно равны 1
По материалам К.Ю. Полякова с сайта ЕГЭ по информатике: подготовка к
ЕГЭ-2022 по информатике, разбор задач ЕГЭ-2022 по информатике, материалы для
подготовки к ЕГЭ (kpolyakov.spb.ru)
Решение задач
второго типа в MS Excel
Алгоритм решения
1.
Составить таблицу входных значения, перечисляя все комбинации переменных в
порядке возрастания двоичного кода. Для этого подсчитать n число переменных в
исходном выражении, выписать наборы входных переменных. Количество
наборов входных переменных 2n.
2. Для каждой строки находим логическое решение. Для этого:
·
Подсчитать
общее число логических операций в выражении;
·
Установить последовательность
выполнения логических операций с учетом скобок и приоритетов.
3. Выполнить поиск значения функции,
отсортировать данное значение по искомой части (1 или 0).
4. Сопоставить исходную таблицу и вновь
полученную.
Используемые фукции в MS Excel
|
Операция |
Функция |
|
|
Отрицание |
=НЕ |
=ЕСЛИ(A2=1;0;1) |
|
Дизъюнкция |
=ИЛИ |
=ЕСЛИ(ИЛИ(A2=1;B2=1);1;0) |
|
Конъюнкция |
=И |
=ЕСЛИ(И(A2=1;B2=1);1;0) |
|
Импликация |
=ЕСЛИ(И(A2=1;B2=0);0;1) |
|
|
Эквиваленция |
=ЕСЛИ(A2=B2;1;0) |
Примеры:
1 (Задача 158 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением ¬x Ù y Ù (w ® z). На рисунке приведён фрагмент
таблицы истинности функции F, содержащий все наборы аргументов, при
которых функция F истинна. Определите, какому столбцу таблицы истинности
функции F соответствует каждая из переменных x, y, z,
w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |

z, w в том порядке, в котором идут соответствующие им столбцы.
Решение
1.
Подсчитаем количество переменных: x, y, z, w – 4 переменных, следовательно,
ищем количество наборов по формуле: 2n
= 24 = 16 наборов. Заполняем разными возможными вариантами (см.
рисунок)
2.
Определим наборы операций:
1) ¬x
2) (w ®
z)
3) ¬x Ù y Ù
(w ® z)
Ищем
результаты действий.
Результат вычислений Введенные
формулы
Следующий
шаг это отфильтровать значения 1 по столбцу H:
Сопоставим
с условием:

Анализируем:
0
– всегда X 1 – всегда Y 011 – Z 001
— W
|
y |
x |
z |
w |
F |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
Ответ:
YXZW
2(Задача 168 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением
x Ú (¬y
Ú z Ú ¬w) Ù (y Ú ¬z). На рисунке приведён фрагмент
таблицы истинности функции F, содержащий все наборы аргументов, при
которых функция F ложна. Определите, какому столбцу таблицы истинности
функции F соответствует каждая из переменных x, y, z,
w.
|
? |
? |
? |
? |
F |
|
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
В
ответе напишите буквы x, y, z, w в том порядке, в
котором идут соответствующие им столбцы.

|
W |
X |
Z |
Y |
F |
|
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
Ответ:
WXZY
3(Задача 178 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением (Øz ÚØ
y) ® (x º z). На рисунке приведён частично
заполненный фрагмент таблицы истинности функции F, содержащий
неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F
соответствует каждая из переменных x, y, z.
В
ответе напишите буквы x, y, z в том порядке, в котором
идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких
разделителей между буквами ставить не нужно.
Ответ:
YXZ
4 (Задача 188 с сайта К.Ю.
Полякова).
Логическая функция F задаётся выражением (w Ù y) Ú ((x ® w) º (y ® z)). На рисунке приведён частично
заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся
строки. Определите, какому столбцу таблицы истинности функции F соответствует
каждая из переменных x, y, z, w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
|||
|
1 |
1 |
0 |
||
|
1 |
1 |
1 |
0 |
В
ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие
им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами
ставить не нужно.
Ответ:
ZWYX
5 (Задача 198 с сайта К.Ю.
Полякова).
Логическая функция F задаётся выражением
(w ® y) Ù ((x ® z) º (y ® x)). На рисунке приведён частично заполненный фрагмент таблицы
истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу
таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
1 |
||
|
0 |
1 |
1 |
||
|
0 |
1 |
0 |
1 |
1 |
В
ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие
им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами
ставить не нужно.
Ответ:
WZXY
(Старый формат ЕГЭ) 7. Электронные таблицы
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Ниже приведен фрагмент электронной таблицы. Определите, чему будет равно значение, вычисленное по формуле =СРЗНАЧ(A2:B5) — D4 + E3*A5.
1. Вычислим значение формулы =СРЗНАЧ(A2:B5). Среднее значение – это сумма всех значений, деленное на их количество, то есть (cfrac{A2+A3+A4+A5+B2+B3+B4+B5}{8}) = (cfrac{5+2+5+14+2+4+7+17}{8}) = (cfrac{56}{8}) = 7.
2. Теперь вычислим значение всей формулы: =СРЗНАЧ(A2:B5)( — D4 + E3*A5 = 7 — 12 + 27 cdot 14 = 373).
Ответ: 373
В электронной таблице значение формулы =СРЗНАЧ(K4:K5) равно 5. Чему равно значение ячейки K6, если значение формулы =СУММ(К4:К6) равно 17? Считать, что все данные ячейки заполнены числовыми значениями.
Формула =СРЗНАЧ(К4:К5) считает среднее значение в ячейках К4 и К5, то есть (cfrac{K4 + K5}{2}). Значит, (cfrac{K4 + K5}{2}) = 5, то есть К4 + К5 = 10.
Формула =СУММ(К4:К6) считает сумму значений ячеек К4, К5, К6. То есть К4 + К5 + К6 = 17. Мы знаем, что К4 + К5 = 10, значит, К6 = 7.
Ответ: 7
В электронной таблице значение формулы =СУММ(B7:K7) равно 48. Чему равно значение формулы =CP3HAЧ(A7:K7), если значение ячейки А7 равно 18? Считать все значения данных ячеек числовыми.
Формула =СУММ(B7:K7) считает значение B7 + C7 + D7 + E7 + … + K7, то есть B7 + C7 + D7 + E7 + … + K7 = 48. Формула =CP3HAЧ(A7:K7) считает значение (cfrac{(A7 + B7 + C7 + D7 + E7 + … + K7)}{11}). Мы знаем, что значение A7 = 18, B7 + C7 + D7 + E7 + … + K7 = 48, то есть A7 + B7 + C7 + D7 + E7 + … + K7 = 18 + 48 = 66. Тогда значение формулы =CP3HAЧ(A7:K7) равно (cfrac{66}{11}) = 6.
Ответ: 6
Ниже приведен фрагмент электронной таблицы. Определите значение ячейки D2, если в нее записана формула =B3*C1-A1+B2.
Выполним указанные в формуле действия. По таблице определяем значения нужных ячеек:
B3 = 86
C1 = 37
A1 = 45
B2 = 43
И выполняем указанные действия: B3 (cdot) C1 — A1 + B2 = 86 (cdot) 37 — 45 + 43 = 3180.
Ответ: 3180
В электронной таблице значение формулы =СРЗНАЧ(K7:K19) равно 17. Определите значение формулы =СРЗНАЧ(K8:K19), если значение ячейки K7 равно 29?
Значение формулы =СРЗНАЧ(K7:K19) вычисляется так: (cfrac{K7+K8+…+K19}{13}). Отсюда знаем, что (cfrac{K7+K8+…+K19}{13}) = 17, то есть K7 + K8 + … + K19 = 17 (cdot) 13 = 221, откуда K8 + K9 + … + K19 = 221 — K7 = 221 — 29 = 192.
Значение формулы =СРЗНАЧ(K8:K19) – (cfrac{K8+K9+…+K19}{12}) = (cfrac{192}{12}) = 16.
Ответ: 16
Определите, на сколько изменится значение ячейки F4, если поменять местами содержимое ячеек C3 и C1?
Например, если значение изменится на -4, в ответе введите -4.
В этой задаче важно не делать лишнюю работу. Формула =СЧЁТ(A1:F3) считает количество ячеек в диапазоне A1:F3, которые содержат числа. Когда мы поменяем местами ячейки C3 и C1, значение ячейки F3 изменится (ведь среднее значение считается у ячеек из диапазона A1:F2, куда C3 не входит, а значит, при подсчете СРЗНАЧ(A1:F2) добавится значение 72). Но нам неважно, как изменится значение ячейки. Нам важно, что количество ячеек в диапазоне A1:F3, содержащих числовые значения, не изменится: и C1, и C3 есть в диапазоне, поэтому то, что они поменяются местами, никак не повлияет на количество заполненных числами ячеек, а в ячейке F3 по-прежнему будут числа. Значит, и значение =СЧЁТ(A1:F3) не изменится. Поэтому ответ 0.
Ответ: 0
Определите значение формулы =СУММ(B2:D2)/7+E2*C1-A1.
Функция СУММ(B2:D2) считает сумму значений в диапазоне B2:D2. Посчитаем ее. Получим 70. E2 (cdot) C1 = 18 (cdot) 42 = 756. A1 = 1, тогда значение всей формулы = 10 + 756 — 1 = 765.
Ответ: 765

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Информатика егэ 19 задание
На уроке рассмотрен разбор 19, 20, 21 задания ЕГЭ по информатике: дается подробное объяснение и решение задания.
Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
19-е задание: «Анализ алгоритма логической игры»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.
Проверяемые элементы содержания: Умение анализировать алгоритм логической игры
20-е задание: «Поиск выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.
Проверяемые элементы содержания: Умение найти выигрышную стратегию игры
21-е задание: «Дерево игры для выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 10 минут.
Проверяемые элементы содержания: Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию
Максимальный балл — 1,.
Examentv. ru
08.10.2020 22:20:21
2020-10-08 22:20:21
Источники:
Https://examentv. ru/informatika/4549-objasnenie-19-20-21-kege-po-informatike-reshenie-v-excel. html
ЕГЭ по информатике 2021 — Задание 19 (Играем и выигрываем) » /> » /> .keyword { color: red; } Информатика егэ 19 задание
ЕГЭ по информатике 2021 — Задание 19 (Играем и выигрываем)
ЕГЭ по информатике 2021 — Задание 19 (Играем и выигрываем)
Привет! Сегодня порешаем задачи из 19 задания ЕГЭ по информатике 2021.
Девятнадцатое задание связано с теорией игр.
Давайте приступим к практике решения.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может Добавить в кучу 2 камня или Добавить в кучу 3 камня или Увеличить количество камней в куче В два раза. Например, имея кучу из 8 камней, за один ход можно получить кучу из 10, 11, 16 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится Не менее 51. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 51 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 50.

При каких Минимальных значениях числа S Петя может выиграть первым ходом?
Распишем при каких значениях S первый игрок может выиграть сразу за один ход.
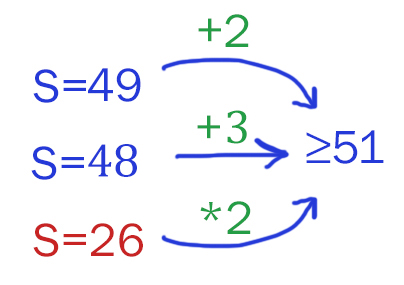
В ответ мы выберем значение 26, потому что оно Самое маленькое.
Продолжаем набирать обороты в 19 задании из ЕГЭ по информатике 2021.
Задача (Стандартная, 1 куча)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 47. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 47 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 46.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Известно, что Ваня точно должен выиграть, после Петиного хода. S1 — количество каменей после первого хода.

Чтобы найти Минимальное значение S, при котором будет выполняться ситуация, описанная в задаче, мы возьмём минимальное значение камней в куче после первого Петиного хода, когда Ваня будет точно выигрывать.
Т. е. первым ходом Петя должен получить 24 камня в куче. Как он это может сделать?

Видим, что, если в куче было изначально 12 камней, то возможная ситуация, которая описана в задаче. Значит, ответ будет 12.
Задание 19 из ЕГЭ по информатике 2021 в тренировочных задачах выглядит громоздким, но решается, как правило, при должной тренировке, не так сложно.
Задача (Стандартная, 2 кучи, Демонстрационный вариант ЕГЭ по информатике 2021)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было семь камней, во второй куче – S камней; 1 ≤ S ≤ 69.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Обозначим первую кучу за A, вторую кучу за B.
Распишем все комбинации для Суммы двух куч для каждого хода:
Блок 1
1. A + 1 + B (Добавляем камень к первой куче)
2. A + B + 1 (Добавляем камень ко второй куче)
3. 2*a + B (Удваиваем первую кучу)
4. A + 2*b (Удваиваем вторую кучу)
Ⅰ ход Пети.
S0 — первоначальное количество камней во второй куче.
Находим A и B после хода Пети.
1. A=8, B=S0
2. A=7, B=S0+1
3. A=14, B=S0
4. A=7, B=2*S0
ⅠⅠ ход Вани.
Разберём все варианты.
Снова подставляем A и B в блок 1.
Подставляем A и B в блок 1.
Подставляем A и B в блок 1.
Подставляем A и B в блок 1.
Теперь возле выражений, у которых коэффициент после переменной S0 равен Единице, поставим Синим цветом плюсик.
Возле выражений, у которых коэффициент после переменной S0 равен Двойке, поставим Оранжевым цветом плюсик.
Возле выражений, у которых коэффициент после переменной S0 равен Четвёрки, поставим Бордовым цветом плюсик.
Выберем из тех выражений, где стоят Синие плюсы, то выражение, где к S0 прибавляется Наибольшее число. Это выражение S0 + 28.
Найдём при каком наименьшем S0 это выражение будет больше или равно 77.
Аналогично для других цветов.
2*S0 + 14 ≥ 77
S0 ≥ (77 — 14) / 2 = 32
(округляем в большую сторону)
S0 = 32
И для последнего выражения.
4*S0 + 7 ≥ 77
S0 ≥ (77 — 7) / 4 = 18
(округляем в большую сторону)
S0 = 18
Берём Меньшее число среди всех трёх значений. Получается число 18.
Укажите минимальное значение S, когда такая ситуация возможна.
Code-enjoy. ru
13.05.2018 20:14:46
2018-05-13 20:14:46
Источники:
Https://code-enjoy. ru/ege_po_informatike_2021_zadanie_19_igraem_i_viigrivaem/
Информатика ЕГЭ вторая часть 19 задание разбор и объяснение » /> » /> .keyword { color: red; } Информатика егэ 19 задание
Информатика ЕГЭ 19, 20 и 21 задания разбор
Информатика ЕГЭ 19, 20 и 21 задания разбор
19-е задание: «Анализ алгоритма логической игры»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.
Проверяемые элементы содержания: Умение анализировать алгоритм логической игры
20-е задание: «Поиск выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.
Проверяемые элементы содержания: Умение найти выигрышную стратегию игры
21-е задание: «Дерево игры для выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 10 минут.
Проверяемые элементы содержания: Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию
Плейлист видеоразборов задания на YouTube:
Игра с двумя кучами камней или табличка
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) Один камень или увеличить количество камней в куче В два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится Не менее 59. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 59 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 53 .
Задание 19 ЕГЭ.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 20 ЕГЭ.
Найдите минимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Задание 21 ЕГЭ.
Найдите два значения S, при которых одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Найденные значения запишите в ответе в порядке возрастания.
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 53. Таблица пригодится для решения заданий 20 и 21:
Выигрышные позиции для первой строки ищем по принципу увеличения количества камней S в 2 два раза: 5 + S*2 >=59 . Получим S>=27
Ответ: 14
- Проанализируем таблицу, и для каждой строки найдем выигрышные позиции с одного хода. Т. е. которые позволят игроку, оказавшемуся «на них», выиграть за один ход (получить суммарно 59 и более камней):
При заполнении таблицы выигрышными позициями можно проследить закономерность «узора», а заполнять позиции по аналогии.
Ответ: 24
- Для решения этого задания найдем выигрышные позиции со второго хода, т. е. которые могут перевести соперника в проигрышную позицию (с минусом):
Ответ: 23 25
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат Две кучи камней. Игроки ходят по очереди, первый ход делает Петя.
За один ход игрок может Убрать из одной из куч Один камень или Уменьшить количество камней в куче В два раза (если количество камней в куче нечётно, остаётся на 1 камень больше, чем убирается).
Например, пусть в одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (5, 9), (3, 9), (6, 8), (6, 5).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой В кучах будет 20 или меньше камней. В начальный момент в первой куче было 10 камней, во второй куче – S камней, S > 10.
Задание 19 ЕГЭ.
Найдите значение S, при котором Ваня выигрывает своим первым ходом при любой игре Пети?
Задание 20 ЕГЭ.
Найдите минимальное и максимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21 ЕГЭ.
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Ответы:
21
22 44
24
- В столбце А отложим значения — количество камней в первой куче. Начнем с ячейки А2 , в которую внесем начальное количество камней, т. е. 10. Автозаполнением продлим значения вниз до 0:
При S=44 Пете необходимо уменьшить 2-ю кучу вдвое (44/2 = 22), чтобы оказаться в проигрышной позиции для соперника.
Ответ: 22 44
- Выделим все такие выигрышные позиции со второго хода:
При S = 24 Петя сможет уменьшить кучи на один камень, и тогда оказывается в выделенной зеленой области — выигрышные позиции со второго хода для Вани, либо уменьшить количество камней вдвое, и тогда Ваня оказывается в выигрышной позиции с первого хода (розовая область).
Ответ: 24
Два игрока, Петя и Ваня, играют в следующую игру. На табличке написаны два значения. Оба игрока в свой ход могут заменить одно из значений на сумму обеих (по своему выбору). Первый ход делает Петя. Игра считается законченной когда сумма обеих значений равняется не меньше 56. То есть Выигрывает игрок, получивший 56 или более в сумме. Начальное значение (10, S).
Задание 19 ЕГЭ.
Найдите максимальное S при котором Петя Не может выиграть первым ходом.
Задание 20 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (9, 15).
Задание 21 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (3,7)? Опишите эту стратегию и изобразите дерево всех возможных партий При этой стратегии.
- Задание 19.
Максимальное S при котором Петя НЕ может выиграть своим первым ходом S = 22. Петя проиграет, если в сумме получится 55 и меньше. Первое значение = 10, необходимо найти второе значение, при этом максимальное. Схематично отобразим варианты ходов:
Для того, чтобы сделать сумму большей, Петя заменит первое значение на сумму, так как оно меньше второго значения (10
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) Два камня или Увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится Не менее 44.
Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, что в кучах всего будет 44 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 38.
Задание 19.
При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
Задание 20.
Назовите одно любое значение S, при котором Петя может выиграть своим вторым ходом.
Задание 21.
Назовите значение S, при котором Ваня выигрывает своим первым или вторым ходом.
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 38:
Ответ 1 а): S = [20;38] (На ЕГЭ пояснить ходы, например: (5; 20) -> (Ход Пети)-> (5;40); 40 + 5 = 45)
Ответ 1 б): S = 19 (На ЕГЭ пояснить ходы, например: (5; 19) -> (Ходы Пети): (5;21),(5;28);(7;19);(7;28). Везде следующим ходом выиграет Ваня, см. предыдущ. пункт)
Ответ 2: S = 16, 17 или 18 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)
Видеорешение на RuTube здесь
Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
Игра с одной кучей камней
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу Один камень или увеличить количество камней в куче В два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится Не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии Не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.
Задание 19 ЕГЭ
А) Укажите такие значения числа S, при которых Петя может выиграть в один ход.
Б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 20 ЕГЭ
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причем:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанных значений S опишите выигрышную стратегию Пети.
Задание 21 ЕГЭ
Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции
Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, Первый ход делает Паша. За один ход игрок может добавить в кучу Один или Четыре камня или Увеличить количество камней в куче в пять раз. Игра завершается в тот момент, когда количество камней В куче становится не менее 69.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 69 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 68.
Задание 19 ЕГЭ.
А) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
Б)Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.
Задание 20 ЕГЭ. Укажите 2 таких значения S, при которых у Паши есть выигрышная стратегия, причём Паша не может выиграть за один ход и может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.
Задание 21 ЕГЭ. Укажите хотя бы одно значение S, при котором у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы).
- 19.
А)S ≥ 14. При количестве камней в куче от 14 и выше Паше необходимо увеличить их количество в пять раз, тем самым получив 70 или более камней.
Б) S = 13. Паша своим первым ходом может сделать 14, 17 или 65 камней, после этого Вася увеличивает количество в пять раз, получая 70, 85 или 325 камней в куче.
20. S = 9, 12. Для данных случаев Паше необходимо прибавить 4 камня к куче из 9 камней, либо 1 камень к куче из 12, и получить кучу из 13 камней.
После чего игра сводится к стратегии, описанной в пункте 1б.
21. S = 8. Своим первым ходом Паша может сделать количество камней в куче 9, 12 или 40. Если Паша увеличивает кол-во в пять раз, тогда Вася выигрывает своим первым ходом, увеличивая количество камней в пять раз.
Для случая 9 и 12 камней Вася использует стратегию, указанную в п.2.
Видеорешение на RuTube здесь
Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, Первый ход делает Паша. За один ход игрок может добавить в кучу Один камень или увеличить количество камней в куче В два раза. Например, имея кучу из 7 камней, за один ход можно получить кучу из 14 или 8 камней. У каждого игрока, чтобы сделать ход, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 28. Если при этом в куче осталось не более 44 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 23 камня, и Паша удвоит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1≤ S ≤ 27.
Задание 1
А) При каких значениях числа S Паша может выиграть в один ход? Укажите все такие значения и соответствующие ходы Паши.
Б) У кого из игроков есть выигрышная стратегия при S = 26, 25, 24? Опишите выигрышные стратегии для этих случаев.
Задание 2
У кого из игроков есть выигрышная стратегия при S = 13, 12? Опишите соответствующие выигрышные стратегии.
Задание 3
У кого из игроков есть выигрышная стратегия при S = 11? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции.
А) Паша имеет выигрышную стратегию и может выиграть за один ход, если S = 27: тогда ему достаточно добавить один камень, чтобы игра закончилась при 28 камнях в куче; или если S = 14, 15, 16, 17, 18, 19, 20, 21, 22 (44/2 = 22 и 28/2 = 14, т. е. от 14 до 22): тогда необходимо удвоить кучу.
Б) При S = 26 выигрышная стратегия есть у Вали. Паша делает ход первым, у него есть возможность либо удвоить количество камней в куче, и тогда количество превысит 44, — выигрывает Валя; либо увеличить количество на один камень, станет 27 камней: следующая Валя, — она может положить один камень и выиграть.
При S = 25 выигрышная стратегия есть у Паши. Удваивать количество камней нет смысла, т. к. количество превысит 44, значит, Паша добавит один камень, их станет 26, следующая Валя, — она может либо добавить камень (станет 27 камней, следующим ходом выиграет Паша) либо удвоить — и сразу проиграть, т. к. станет более 44 камней.
При S = 24 выигрышная стратегия есть у Вали. Паша делает ход первым: удваивать кучу нет смысла, т. к. в ней станет более 44, значит, Паша добавит один камень, их станет 25; следующая — Валя: она может только добавить один камень (станет 26 камней, следующим ходом Паша оказывается в проигрышной позиции, см. пункт при S = 26).
При S = 13 или S = 12 выигрышная стратегия есть у Паши. Паша удваивает количество и в куче остается 26 или 24 камня. Это проигрышная позиция для того, кто ходит (см. п. 1 б), а следующий ход за Валей.
Дерево возможных партий:
* Для Вали отображены только ходы по стратегии
** красный круг означает выигрыш
*** фиолетовый круг — конец игры (проигрыш)
📹 Видео (аналитическое решение)
Видеорешение на RuTube здесь
Задания с двумя кучами камней или табличка
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) Один камень или Увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится Не менее 73.
Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Задание 1.
Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2.
Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию.
Задание 3.
Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
- Задание 1. В начальных позициях (6, 33), (8, 32) выигрышная стратегия есть у Вани. Задание 2. В начальных позициях (6, 32), (7, 32) и (8, 31) выигрышная стратегия есть у Пети. Задание 3. В начальной позиции (7, 31) выигрышная стратегия есть у Вани.
Видеорешение на RuTube здесь
Игра с набором слов
Петя и Ваня играют в игру: есть набор слов, необходимо последовательно называть буквы этих слов. Побеждает тот игрок, который называет последнюю букву любого слова из набора. Петя ходит первым.
Например, есть набор слов ; для заданного набора слов Петя своим первым ходом может назвать букву В, И или С. Если Петя выберет букву В, то победит Ваня (следующие ходы: Петя — В, Ваня — О, Петя — Л, Ваня — К).
Б) Даны 2 слова ТРИТРИТРИ. ТРИ, РИТАРИТАРИТАРИТА. РИТА>. В первом слове 99 букв, во втором 164. Определить выигрышную стратегию.
Задание 2
Необходимо поменять две буквы местами из набора пункта 1А в слове с наименьшей длинной так, чтобы выигрышная стратегия была у другого игрока. Объяснить выигрышную стратегию.
Задание 3
Дан набор слов Ворона, Волк, Волна, Производная, Прохор, Просо>. У кого из игроков есть выигрышная стратегия? Обосновать ответ и написать дерево всех возможных партий для выигрышной стратегии.
А) Для выигрыша Пете достаточно выбрать первую букву слова с Нечетным количеством букв, тогда последний ход делает Петя. При исходном наборе слов Выигрышная стратегия есть у Пети. Она заключается в том, что своим первым ходом он должен выбрать букву И (слово ИКЛМНИКЛМНХ из 11 букв). Ване придется выбрать букву К. Таким образом, они последовательно будут называть буквы первого слова, пока Петя не выберет последнюю букву Х. На этом игра закончится выигрышем Пети. При данной стратегии возможна только одна партия. Заключением партии будет написано слово ИКЛМНИКЛМНХ.
Б) При исходном наборе слов Выигрышная стратегия есть у Пети. Она заключается в том, чтобы выбрать слово с нечетным количеством букв, т. к. при такой стратегии последнюю букву в любом случае записывает Петя. Т. о., Петя должен выбрать букву Т, т. к. в первом слове 99 букв.
Дерево возможных партий:
* Для Вани отображены только ходы по стратегии
** Красный круг означает выигрыш
- В столбце А отложим значения — количество камней в первой куче. Начнем с ячейки А2 , в которую внесем начальное количество камней, т. е. 10. Автозаполнением продлим значения вниз до 0:
Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу Один камень или увеличить количество камней в куче В два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится Не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии Не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.
Задание 19 ЕГЭ
А) Укажите такие значения числа S, при которых Петя может выиграть в один ход.
Б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 20 ЕГЭ
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причем:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанных значений S опишите выигрышную стратегию Пети.
Задание 21 ЕГЭ
Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции
Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, Первый ход делает Паша. За один ход игрок может добавить в кучу Один или Четыре камня или Увеличить количество камней в куче в пять раз. Игра завершается в тот момент, когда количество камней В куче становится не менее 69.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 69 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 68.
Задание 19 ЕГЭ.
А) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
Б)Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.
Задание 20 ЕГЭ. Укажите 2 таких значения S, при которых у Паши есть выигрышная стратегия, причём Паша не может выиграть за один ход и может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.
Задание 21 ЕГЭ. Укажите хотя бы одно значение S, при котором у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы).
- 19.
А)S ≥ 14. При количестве камней в куче от 14 и выше Паше необходимо увеличить их количество в пять раз, тем самым получив 70 или более камней.
Б) S = 13. Паша своим первым ходом может сделать 14, 17 или 65 камней, после этого Вася увеличивает количество в пять раз, получая 70, 85 или 325 камней в куче.
20. S = 9, 12. Для данных случаев Паше необходимо прибавить 4 камня к куче из 9 камней, либо 1 камень к куче из 12, и получить кучу из 13 камней.
После чего игра сводится к стратегии, описанной в пункте 1б.
21. S = 8. Своим первым ходом Паша может сделать количество камней в куче 9, 12 или 40. Если Паша увеличивает кол-во в пять раз, тогда Вася выигрывает своим первым ходом, увеличивая количество камней в пять раз.
Для случая 9 и 12 камней Вася использует стратегию, указанную в п.2.
Видеорешение на RuTube здесь
Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, Первый ход делает Паша. За один ход игрок может добавить в кучу Один камень или увеличить количество камней в куче В два раза. Например, имея кучу из 7 камней, за один ход можно получить кучу из 14 или 8 камней. У каждого игрока, чтобы сделать ход, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 28. Если при этом в куче осталось не более 44 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 23 камня, и Паша удвоит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1≤ S ≤ 27.
Задание 1
А) При каких значениях числа S Паша может выиграть в один ход? Укажите все такие значения и соответствующие ходы Паши.
Б) У кого из игроков есть выигрышная стратегия при S = 26, 25, 24? Опишите выигрышные стратегии для этих случаев.
Задание 2
У кого из игроков есть выигрышная стратегия при S = 13, 12? Опишите соответствующие выигрышные стратегии.
Задание 3
У кого из игроков есть выигрышная стратегия при S = 11? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции.
А) Паша имеет выигрышную стратегию и может выиграть за один ход, если S = 27: тогда ему достаточно добавить один камень, чтобы игра закончилась при 28 камнях в куче; или если S = 14, 15, 16, 17, 18, 19, 20, 21, 22 (44/2 = 22 и 28/2 = 14, т. е. от 14 до 22): тогда необходимо удвоить кучу.
Б) При S = 26 выигрышная стратегия есть у Вали. Паша делает ход первым, у него есть возможность либо удвоить количество камней в куче, и тогда количество превысит 44, — выигрывает Валя; либо увеличить количество на один камень, станет 27 камней: следующая Валя, — она может положить один камень и выиграть.
При S = 25 выигрышная стратегия есть у Паши. Удваивать количество камней нет смысла, т. к. количество превысит 44, значит, Паша добавит один камень, их станет 26, следующая Валя, — она может либо добавить камень (станет 27 камней, следующим ходом выиграет Паша) либо удвоить — и сразу проиграть, т. к. станет более 44 камней.
При S = 24 выигрышная стратегия есть у Вали. Паша делает ход первым: удваивать кучу нет смысла, т. к. в ней станет более 44, значит, Паша добавит один камень, их станет 25; следующая — Валя: она может только добавить один камень (станет 26 камней, следующим ходом Паша оказывается в проигрышной позиции, см. пункт при S = 26).
При S = 13 или S = 12 выигрышная стратегия есть у Паши. Паша удваивает количество и в куче остается 26 или 24 камня. Это проигрышная позиция для того, кто ходит (см. п. 1 б), а следующий ход за Валей.
Дерево возможных партий:
* Для Вали отображены только ходы по стратегии
** красный круг означает выигрыш
*** фиолетовый круг — конец игры (проигрыш)
📹 Видео (аналитическое решение)
Видеорешение на RuTube здесь
Задания с двумя кучами камней или табличка
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) Один камень или Увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится Не менее 73.
Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Задание 1.
Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2.
Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию.
Задание 3.
Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
- Задание 1. В начальных позициях (6, 33), (8, 32) выигрышная стратегия есть у Вани. Задание 2. В начальных позициях (6, 32), (7, 32) и (8, 31) выигрышная стратегия есть у Пети. Задание 3. В начальной позиции (7, 31) выигрышная стратегия есть у Вани.
Видеорешение на RuTube здесь
- Для решения этого задания найдем выигрышные позиции со второго хода, т. е. которые могут перевести соперника в проигрышную позицию (с минусом):
Удваивать количество камней нет смысла, т.
Labs-org. ru
28.07.2018 7:35:12
2018-07-28 07:35:12
Источники:
Https://labs-org. ru/ege-19-practice/
Автор материалов — Лада Борисовна Есакова.
Microsoft Excel (в дальнейшем просто — Excel) — это программа выполнения расчетов и управления так называемыми электронными таблицами.
Excel позволяет выполнять сложные расчеты, в которых могут использоваться данные, расположенные в разных областях электронной таблицы и связанные между собой определенной зависимостью. Для выполнения таких расчетов в Excel существует возможность вводить различные формулы в ячейки таблицы. Excel выполняет вычисления и отображает результат в ячейке с формулой.
Важной особенностью использования электронной таблицы является автоматический пересчет результатов при изменении значений ячеек. Excel также может строить и обновлять графики, основанные на введенных числах.
Адрес ячейки в электронных таблицах состоит из имени столбца и следующего за ним номера строки, например, C15.
Для написания формул используют адреса ячеек и знаки арифметических операций (+, -, *, /, ^). Формула начинается знаком =.
В Excel предусмотрены стандартные функции, которые могут быть использованы в формулах. Это математические, логические, текстовые, финансовые и другие функции. Однако, на экзамене Вам могут встретиться только самые простые функции: СЧЕТ (количество непустых ячеек), СУММ (сумма), СРЗНАЧ (среднее значение), МИН (минимальное значение), МАКС (максимальное значение).
Диапазон ячеек обозначается следующим образом: A1:D4 (все ячейки прямоугольника от A1 до D4.
Адреса ячеек бывают относительными, абсолютными и смешанными.
Они по-разному ведут себя при копировании формулы из ячейки в ячейку.
Относительная адресация:
Если в ячейке B2 мы напишем формулу =D1+3, то таблица воспримет это как «взять значение ячейки на две правее и на одну выше текущей, и прибавить к нему 3».
Т.е. адрес D1 воспринимается таблицей, как положение относительно ячейки, куда вводится формула. Такой адрес называется относительным. При копировании такой формулы в другую ячейку, таблица автоматически пересчитает адрес относительно нового расположения формулы:
Абсолютная адресация:
Если нам не нужно, чтобы адрес пересчитывался при копировании формулы, мы можем его «закрепить» в формуле — поставить знак $ перед буквой и индексом ячейки: =$D$1+3. Такой адрес называется абсолютным. Такая формула не будет изменяться при копировании:
Смешанная адресация:
Если же мы хотим, чтобы при копировании формулы автоматически пересчитывался, к примеру, только индекс ячейки, а буква оставалась неизменной, мы можем «закрепить» в формуле только букву (или наоборот): =$D1+3. Такой адрес называется смешанным. При копировании формулы будет меняться только индекс в адресе ячейки:
Электронные таблицы. Копирование формул.
Пример 1.
В ячейке C2 записана формула =$E$3+D2. Какой вид приобретет формула, после того как ячейку C2 скопируют в ячейку B1?
1) =$E$3+C1 2) =$D$3+D2 3) =$E$3+E3 4) =$F$4+D2
Решение:
Место расположения формулы меняется с C2 на B1, т.е. формула сдвигается на одну ячейку влево и на одну ячейку вверх (буква «уменьшается» на единицу и индекс уменьшается на единицу). Значит, так же изменятся все относительные адреса, а абсолютные (закрепленные знаком $) останутся неизменными:
=$E$3+С1.
Ответ: 1
Пример 2.
В ячейке В11 электронной таблицы записана формула. Эту формулу скопировали в ячейку А10. В результате значение в ячейке А10 вычисляется по формуле х—Зу, где х — значение в ячейке С22, а у — значение в ячейке D22. Укажите, какая формула могла быть написана в ячейке В11.
1) =C22-3*D22 2) =D$22-3*$D23 3) =C$22-3*D$22 4) =$C22-3*$D22
Решение:
Проанализируем поочередно каждую формулу:
Место расположения формулы меняется с B11 на A10, т.е. буква «уменьшается» на 1 и индекс уменьшается на 1.
Тогда при копировании формулы изменятся следующим образом:
1) =B21-3*C21
2) =C$22-3*$D22
3) =B$22-3*C$22
4) =$C21-3*$D21
Условию задачи соответствует формула 2).
Ответ: 2
Электронные таблицы. Определение значения формулы.
Пример 3.
Дан фрагмент электронной таблицы:
|
А |
В |
С |
D |
|
|
1 |
1 |
2 |
3 |
|
|
2 |
4 |
5 |
6 |
|
|
3 |
7 |
8 |
9 |
В ячейку D1 введена формула =$А$1*В1+С2, а затем скопирована в ячейку D2. Какое значение в результате появится в ячейке D2?
1) 10 2) 14 3) 16 4) 24
Решение:
Место расположения формулы меняется с D1 на D2, т.е. буква не меняется, а индекс увеличивается на 1.
Значит, формула примет вид: =$А$1*В2+С3. Подставим в формулу числовые значения ячеек:1*5+9=14. Правильный ответ указан под номером 2.
Ответ: 2
Пример 4.
В электронной таблице значение формулы =СРЗНАЧ(A6:C6) равно (-2). Чему равно значение формулы =СУММ(A6:D6), если значение ячейки D6 равно 5?
1) 1 2) -1 3) -3 4) 7
Решение:
По определению среднего значения:
СРЗНАЧ(A6:C6) = СУММ(A6:С6)/3 = -2
Значит, СУММ(A6:С6) = -6
СУММ(A6:D6) = СУММ(A6:С6)+D6 = -6+5 = -1
Ответ: 2
Электронные таблицы и диаграммы.
Пример 5.
Дан фрагмент электронной таблицы в режиме отображения формул.
После выполнения вычислений построили диаграмму по значениям диапазона A1:D1. Укажите полученную диаграмму:
Решение:
Вычислим по формулам значения ячеек A1:D1.
B1 = 3-2 =1
A1 = 2-1 =1
C1 = 1+2 =3
D1 = 1*3 =3
Этим данным соответствует диаграмма 3.
Ответ:3
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №7. Электронные таблицы. Абсолютная и относительная адресация. Графики и диаграммы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023


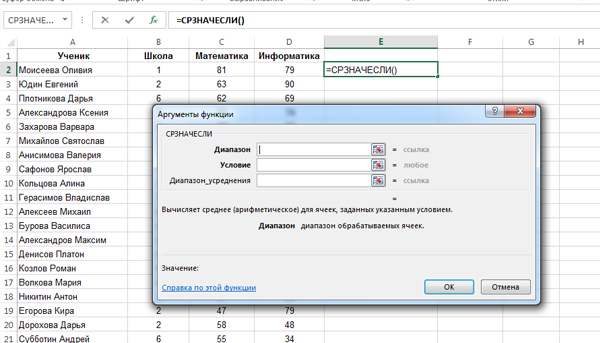
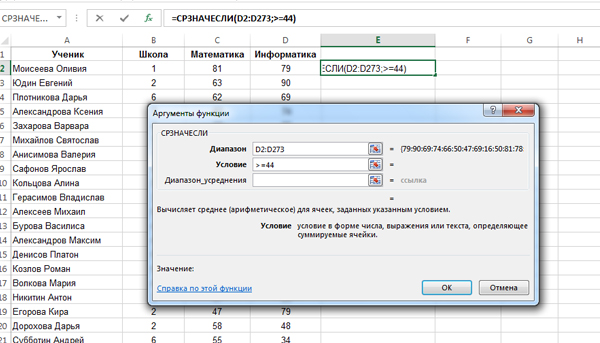
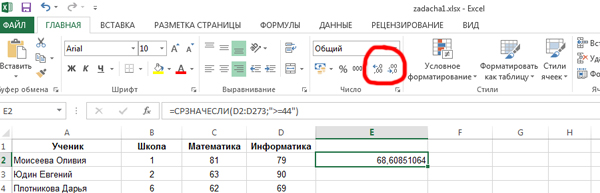
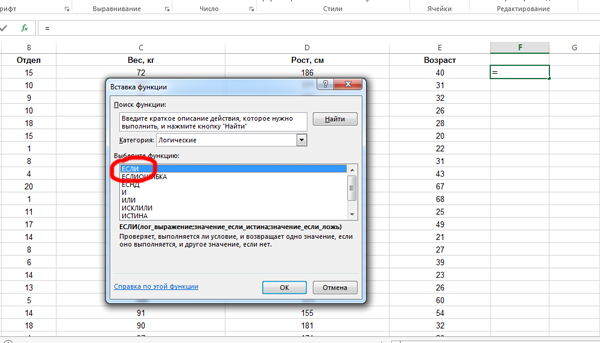
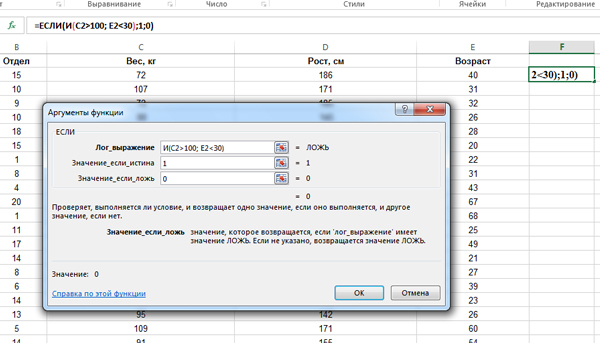
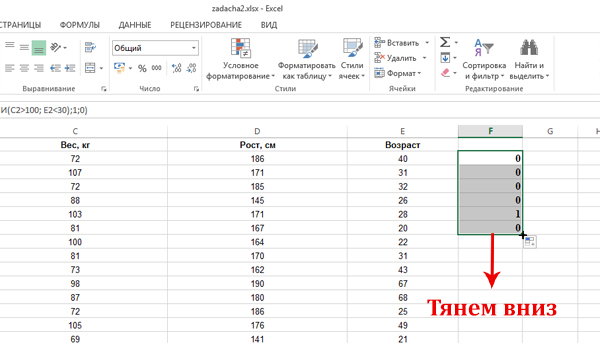
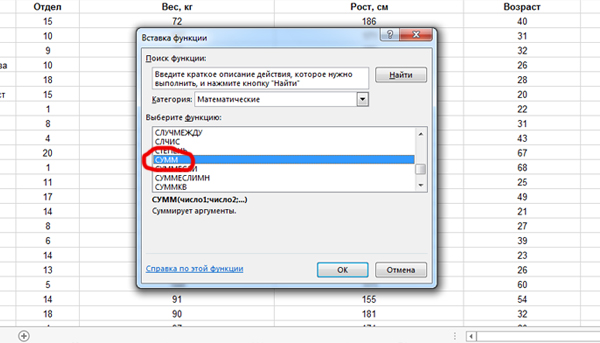
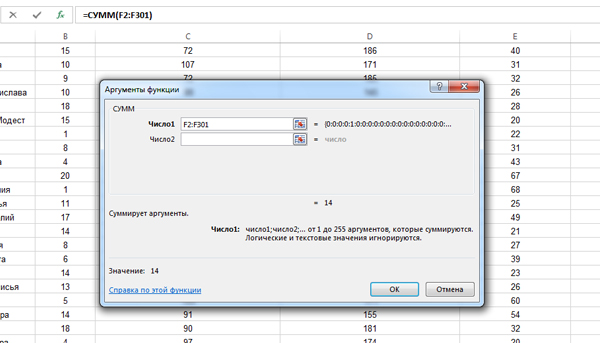
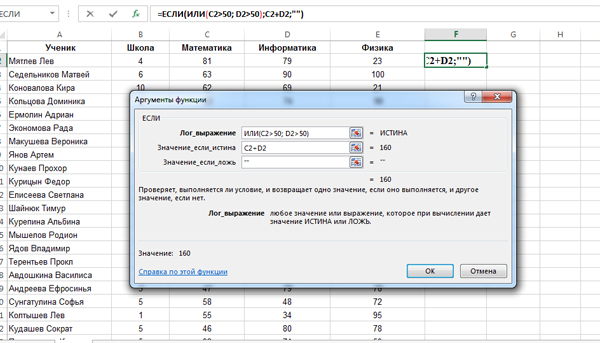
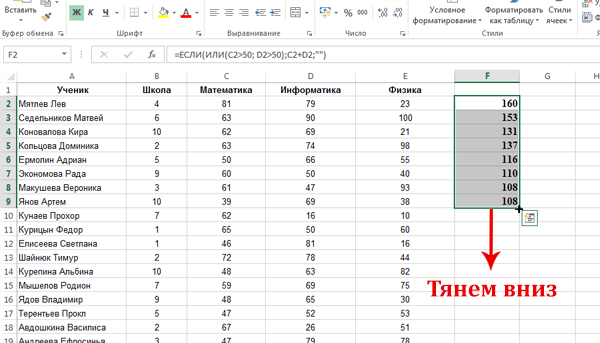
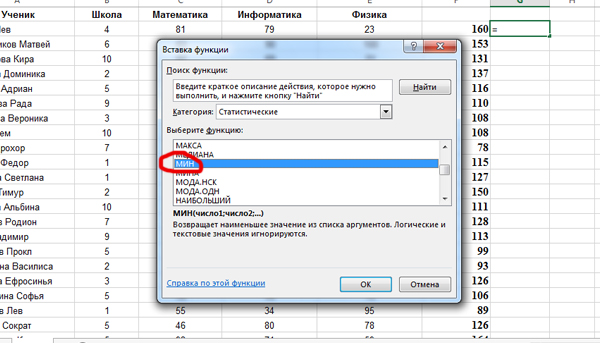
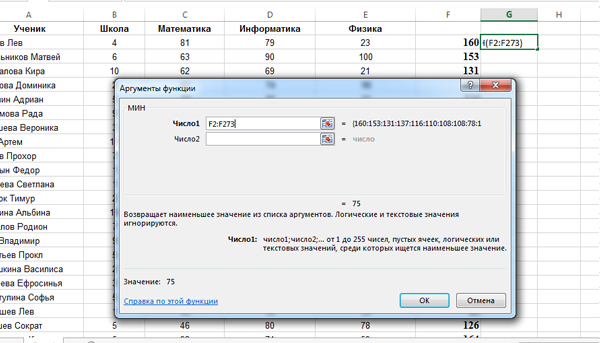
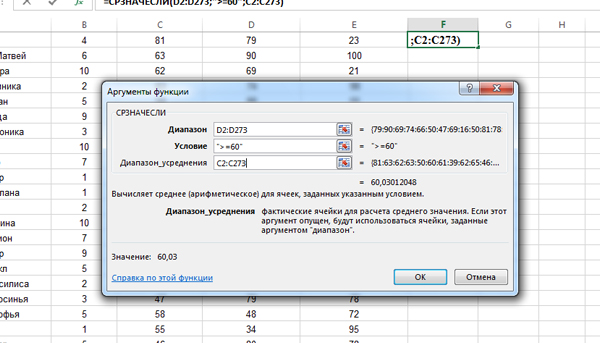
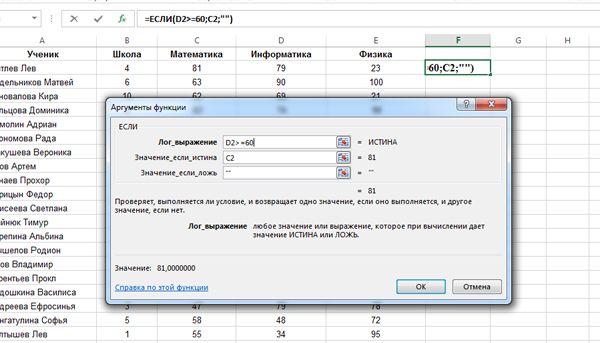
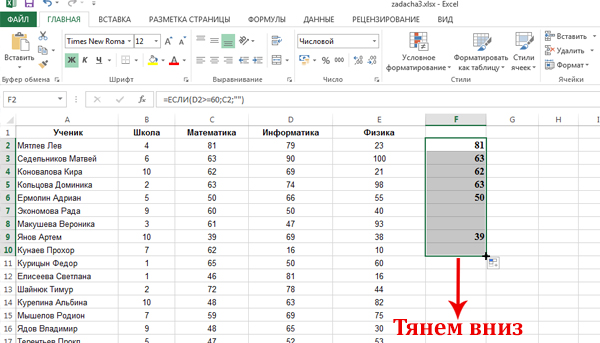
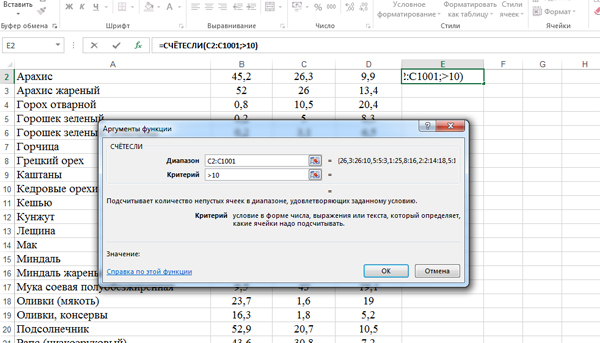
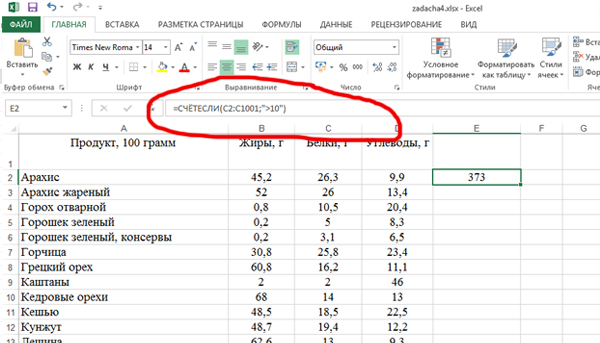
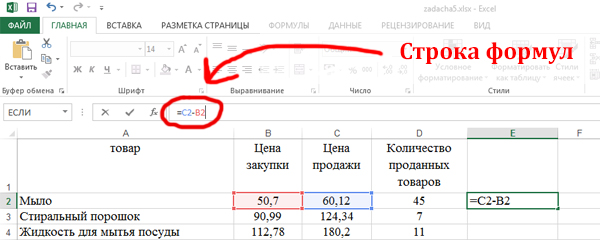
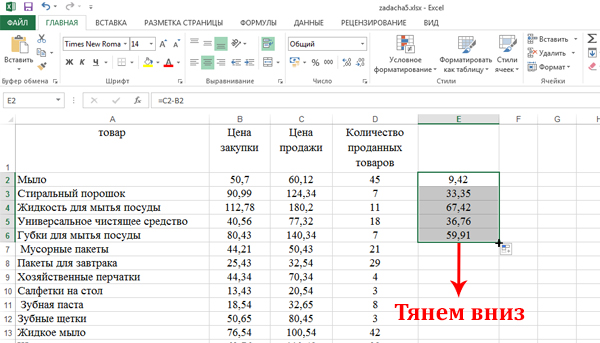
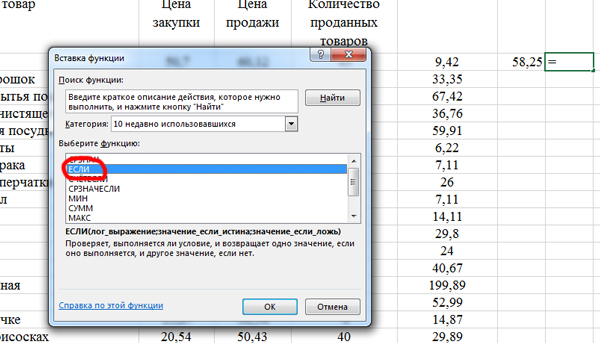
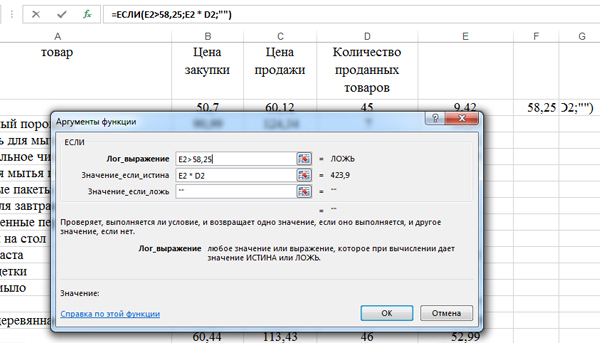
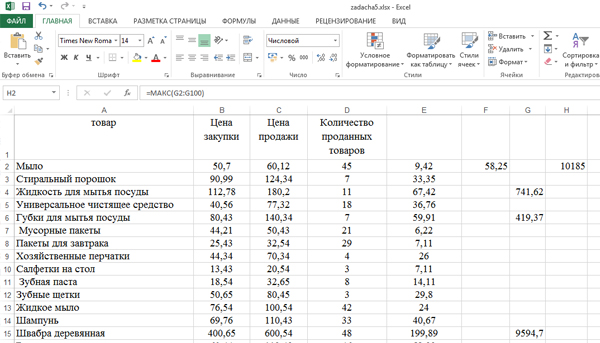




















 или Вырезать
или Вырезать из группы Буфер обмена, а затем щелкнуть в нужном месте и выполнить команду Вставить
из группы Буфер обмена, а затем щелкнуть в нужном месте и выполнить команду Вставить  .
.