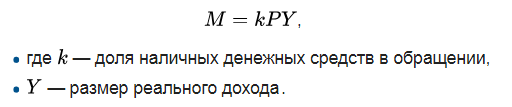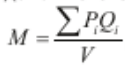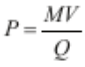Формулы
по экономической теории
-
Межотраслевой
баланс (МОБ) Леонтьева («затраты –
выпуск»): X=AX+Y,
где Х – это объём производства какой
– либо отрасли; Y
– это конечный продукт этой отрасли;
А – это матрица технологических
коэффициентов прямых затрат; -
Индекс
Потребительских Цен (ИПЦ): ИПЦ = Стоимость
потребительской корзины в текущем году
/ стоимость этой корзины в базовом году
* 100% -
Реальный
Валовой Внутренний Продукт (ВВП): ВВП
реал = ВВП номинальный / ИПЦ * 100%ВВП реал = ВВП номинальный / Дефлятор *
100% -
Чистый
Внутренний Продукт (ЧПВ): ЧПВ = ВВП – А,
где А-это Амортизационные отчисления; -
Чистый
Национальный Продукт (ЧНП): ЧНП= ВНП –
А, где А – Амортизационные отчисления; -
Внутренний
Доход (ВД): ВД = ЧПВ — косвенные налоги; -
Личный
Доход (ЛД): ЛД= ВД – взносы на социальное
страхование граждан, прибыль корпораций,
уплаченные проценты за кредит + дивиденды;
трансфертные платежи; процентный доход -
Личный
Располагаемый Доход (ЛРД): ЛРД = ЛД –
индивидуальные налоги -
Средняя
склонность к потреблению (АСР): АСР =
Потребление / Доход -
Предельная
склонность к потреблению (МРС): МРС =
Изменение в потреблении / Изменение в
доходе -
Средняя
склонность к сбережению (APS):
APS
= Сбережения / Доход -
Предельная
склонность к сбережению (MPS):
MPS
= изменения в сбережениях / Изменения
в доходе -
Темп
инфляции = Индекс цен текущего года –
Индекс цен базового года / Индекс цен
базового года * 100% -
Количественная
теория спроса на деньги (И.Фишер): M*V
= P*Y
, где: M- количество денег в обращении;
V
– скорость обращения денег; P-
уровень цен (Индекс цен); Y
– реальный объём производства; -
Спрос
на деньги: M
= P*Y/V -
Денежный
мультипликатор (М): М = 1/r
= Депозиты (D)/Резервы
(R) -
Скорость
обращения денег (V)
:V
= U/M,
где: V
– скорость обращения денег; U
– номинальный объём ВНП; М – масса
денег в обращении; -
Предельная
норма замещения: MPS
= -d
X
/ d
Y
, где : d-
это дельта -
Норма
замещения (НЗ): НЗ = d
q2
/ d
q1,
где: d-
это дельта; -
Совокупный
доход (TR):
TR
= P*Q
, где Р – цена на благо; Q
– количество благ; -
Средний
доход (AR):
AR
= TR
/ Q
= P*Q/
Q
= P -
Предельный
доход (MR):
MR
= d
TR
/ d
Q
= d(P*Q)
/ d
Q
= P,
где: d-
это дельта; -
Средние
постоянные издержки (AFC):
AFC
= FC
/ Q;
AFC
=TVC
/ Q; -
Средние
переменные издержки (AVC):
AVC
= VC
/ Q; -
Общие
(совокупные) издержки (ТС): ТС = FC+VC -
Средние
общие издержки (АТС): АТС = ТС / Q;
ATC
=N
(FC
+ VC)
/ Q; -
Предельные
издержки (МС): d
TC
/ d
Q;
MC
= d
TVC
/ d
Q
, где: d
– это дельта; -
Переменные
Предельные издержки (VMC):
VMC
= d
VC
/ d
Q
, где: d-
это дельта; -
Прибыль:
П = TR
– TC
, где: TR
– совокупный доход; TC
– совокупные издержки; -
Эластичность:
Ep
= d
Q
/ d
P
, где: d
Q
– изменение величины спроса, в процентах;
d
P
– изменение цены в процентах; Ep-
эластичность по цене; -
Мультипликатор
инвестиций = d
Y/
d
I
= изменение в реальном НД / изменение в
инвестиции -
Мультипликатор
автономных расходов (М а.р.): М а.р.=
1/1-МРС = к -
Акселератор
(V)
= i*t
/ Y
t-1
– Y
t-2,
где V-
акселератор; i-
чистые инвестиции в период времени;
t-год,
когда были осуществлены инвестиции; Y
– потребительский спрос дохода на
реальный ВВП; t-1
и t-2
– предшествующие года -
Реальный
курс акций = Дивиденд / Норма ссудного
процента * 100% -
Мультипликатор
денег (MD):
MD
= MS
/ M+1 -
Рентабельность
= Доход (результат)/ затраты (издержки) -
Эффективность
= прибыль / себестоимость -
Эластичность
предложения: Кр = объём предложения /
рост цен -
Дефлятор
ВНП = Номинальный ВНП / реальный ВНП *
100% -
Реальный
ВНП = номинальный ВНП / индекс цен -
Индекс
цен = цены текущего периода / цены
базового периода * 100% -
Валовой
Национальный продукт: ВНП = C+Y+G+X -
Валовой
национальный доход: ВНД = потребление
(С)+сбережение(S) -
Уравнение
Пигу: M=R*P*T,где
Т — физический объём производства -
Предельная
склонность к потреблению (МРС)+предельная
склонность к сбережению(MPS)=1;MPS=1-MPS
MPS=1-MPC
-
Коэффициент
эластичности=спрашиваемая
продукция/процентное изменение цены -
Экономическая
прибыль = совокупный доход(TR)-внутренние
издержки; -
Экономическая
прибыль=бухгалтерская прибыль —
внутренние издержки -
Бухгалтерская
прибыль=совокупный доход (TR)
–внешние издержки -
Бухгалтерская
прибыль = валовые издержки — внешние
издержки -
Формула
стоимости = C+V+m,
где: С — постоянный капитал;V-переменный
капитал; m-прибавочная
стоимость; -
Экономические
ресурсы = производство/факторы
производства -
Показатель
эффективности = выгоды/затраты -
Уровень
безработицы = количество
безработных/трудоспособное население*100%
Формулы
по экономической теории:
-
Межотраслевой
баланс (МОБ) Леонтьева («затраты –
выпуск»):
X=AX+Y,
где:
Х
– это объём производства какой – либо
отрасли; Y
– это конечный продукт этой отрасли; А
–
это матрица технологических коэффициентов
прямых затрат;
-
Индекс
Потребительских Цен (ИПЦ):
ИПЦ
=(Стоимость потребительской корзины в
текущем году / стоимость этой корзины
в базовом году) * 100%;
-
Реальный
Валовой Внутренний Продукт (ВВП):
ВВП
реал. =( ВВП номинальный / ИПЦ) * 100%
ВВП
реал. = (ВВП номинальный / Дефлятор)* 100%
-
Чистый
Внутренний Продукт (ЧПВ):
ЧПВ
= ВВП – А,
Где:
А
— Амортизационные отчисления;
-
Чистый
Национальный Продукт (ЧНП):
ЧНП=
ВНП – А,
Где:
А
– Амортизационные отчисления;
-
Внутренний
Доход (ВД):
ВД
= ЧПВ — косвенные налоги;
-
Личный
Доход (ЛД):
ЛД=
ВД – взносы на социальное страхование
граждан, прибыль корпораций, уплаченные
проценты за кредит + дивиденды, трансфертные
платежи, процентный доход;
-
Личный
Располагаемый Доход (ЛРД):
ЛРД
= ЛД – индивидуальные налоги;
-
Средняя
склонность к потреблению (АСР):
АСР
= Потребление / Доход;
-
Предельная
склонность к потреблению (МРС):
МРС
= Изменения в потреблении / Изменения в
доходе;
-
Средняя
склонность к сбережению (APS):
APS
= Сбережения / Доход;
-
Предельная
склонность к сбережению (MPS):
MPS
= изменения в сбережениях / Изменения в
доходе;
-
Темп
инфляции = ((Индекс цен текущего года –
Индекс цен базового года)/ Индекс цен
базового года) * 100%; -
Количественная
теория спроса на деньги (И.Фишер):
M*V
= P*Y,
где:
M—
количество денег в обращении; V
– скорость обращения денег; P—
уровень цен (индекс цен); Y
–
реальный объём производства;
-
Спрос
на деньги:
M
= P*Y/V;
-
Денежный
мультипликатор (М):
М
= 1/r
= Депозиты (D)/Резервы
(R);
-
Скорость
обращения денег (V):
V
= U/M,
где:
V
–
скорость обращения денег; U
– номинальный объём ВНП; М
– масса денег в обращении;
-
Предельная
норма замещения:
MPS
= —d
X
/ d
Y,
где:
d—
это дельта;
-
Норма
замещения (НЗ):
НЗ
= d
q2
/ d
q1,
где:
d—
это дельта;
-
Совокупный
доход (TR):
TR
= P*Q,
Где:
Р
– цена на благо; Q
–
количество благ;
-
Средний
доход (AR):
AR
= TR
/ Q
= P*Q/
Q
= P;
-
Предельный
доход (MR):
MR
= d TR / d Q = d(P*Q) / d Q = P,
где:
d—
это дельта;
-
Средние
постоянные издержки (AFC):
AFC
= FC
/ Q;
AFC
=TVC
/ Q;
-
Средние
переменные издержки (AVC):
AVC
= VC
/ Q;
-
Общие
(совокупные) издержки (ТС):
ТС
= FC+VC;
-
Средние
общие издержки (АТС):
АТС
= ТС / Q;
ATC
=N
(FC
+ VC)
/ Q;
-
Предельные
издержки (МС):
MC=d
TC / d Q;
MC
= d TVC / d Q,
где:
d
– это дельта;
-
Переменные
предельные издержки (VMC):
VMC
= d
VC
/ d
Q,
где:
d—
это дельта;
-
Прибыль:
П
= TR
– TC
,
где:
TR
– совокупный доход; TC
– совокупные издержки;
-
Эластичность:
Ep
= d
Q
/ d
P,
где:
d
Q
– изменение величины спроса, в процентах;
d
P
– изменение цены в процентах; Ep—
эластичность по цене;
-
Мультипликатор
инвестиций
= d
Y/
d
I
= Изменения в реальном НД / Изменения в
инвестициях; -
Мультипликатор
автономных расходов (М
а.р.):
М
а.р.= 1/1-МРС = к;
-
Акселератор
(V):
V=
i*t
/ Y
t-1
– Y
t-2,
где
V—
акселератор; i—
чистые инвестиции в период времени;
t-год,
когда были осуществлены инвестиции; Y
–
потребительский спрос дохода на реальный
ВВП; t-1
и t-2
– предшествующие года;
-
Реальный
курс акций
= Дивиденд
/ Норма ссудного процента * 100%; -
Мультипликатор
денег (MD):
MD
=
MS
/ M+1;
-
Рентабельность
= Доход (результат)/ затраты (издержки); -
Эффективность
= прибыль / себестоимость; -
Эластичность
предложения:
Кр
= Объём предложения / Рост цен;
-
Дефлятор
ВНП
= Номинальный ВНП / Реальный ВНП * 100%; -
Реальный
ВНП
= Номинальный ВНП / индекс цен; -
Индекс
цен
= (Цены текущего периода / Цены базового
периода)* 100%; -
Валовой
Национальный продукт:
ВНП
= C+Y+G+X;
-
Валовой
национальный доход:
ВНД
= Потребление (С)+Сбережение(S);
-
Уравнение
Пигу:
M=R*P*T,
где:
Т
— физический объём производства;
-
Предельная
склонность к потреблению (МРС)+предельная
склонность к сбережению(MPS)=1;
MPS=1-MPS;
MPS=1-MPC;
-
Коэффициент
эластичности
= Спрашиваемая продукция/Процентное
изменение цены; -
Экономическая
прибыль
= Совокупный доход(TR)-Внутренние
издержки; -
Экономическая
прибыль
= Бухгалтерская прибыль — Внутренние
издержки; -
Бухгалтерская
прибыль
= Совокупный доход (TR)
–Внешние издержки; -
Бухгалтерская
прибыль
= Валовые издержки — Внешние издержки; -
Формула
стоимости
= C+V+m,
где:
С
—
постоянный капитал;V-переменный
капитал; m-прибавочная
стоимость;
-
Экономические
ресурсы
= Производство/Факторы производства; -
Показатель
эффективности
= Выгоды/Затраты; -
Уровень
безработицы
=(Количество безработных/Трудоспособное
население)*100%.
Показатели
занятости и безработицы.
Состояние занятости
и безработицы характеризуют следующие
показатели:
-
неинституциональное
население
;
-
численность
занятых
;
-
численность
безработных
;
-
численность лиц,
не входящих в состав рабочей силы
;
Между данными
показателями существуют следующие
зависимости:
-
численность
рабочей силы

-
неинституциональное
население



-
уровень занятости
населения

-
уровень безработицы
населения

-
норма безработицы
-
уровень вовлеченности
населения в состав рабочей силы
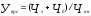
Исчисление
потенциальных потерь продукции и услуг
в результате роста безработицы
осуществляется на основе закона,
сформулированного американским
экономистом А. Оукеном:

где
– уровень
выпуска продукции при полной занятости;
– фактический
выпуск продукции;
– фактический
уровень безработицы;
– норма безработицы
при полной занятости (естественная
норма безработицы);
а – коэффициент,
рассчитанный эмпирическим путем, а
= 2,5.
Мультипликаторы.
Мультипликатор
(лат.
multiplicio
– умножать,
multiplier–
множитель
)
– коэффициент,
показывающий, во сколько раз возрастает
конечный результат при увеличении
исходных параметров.
-
Мультипликатор
автономных расходов –
показатель изменения равновесного
дохода (или ВВП) при увеличении любого
компонента автономных расходов:

где
–
мультипликатор;
– прирост
национального дохода (продукта);
– прирост автономных
расходов;
MPC
– предельная
склонность к потреблению;
MPS
– предельная
склонность к сбережению.
-
Мультипликатор
банковский (депозитный) (mb)
–
коэффициент,
который показывает, во сколько раз
увеличится количество денег в обращении
при первоначальном взносе в банковскую
систему:
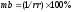
где rr
– норма
обязательных резервов в процентах.
-
Мультипликатор
внешней торговли –
процесс мультипликации в открытой
экономике осуществлялся через изменение
импорта. Формула мультипликатора
внешней торговли:
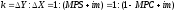
где

изменение
совокупного дохода;
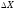
изменение экспорта;
im
– предельная
склонность к импорту.
-
Мультипликатор
государственных расходов (Mg)
– коэффициент,
который показывает, во сколько раз
конечный прирост совокупного дохода
(Y)
превосходит вызвавший его первоначальный
прирост государственных закупок товаров
и услуг (G):

-
Мультипликатор
инвестиционный –
коэффициент, который показывает, во
сколько раз конечный прирост совокупного
дохода (Y)
превосходит вызвавший его первоначальный
прирост автономных инвестиций (I):

-
Мультипликатор
налоговый –
коэффициент,
который показывает, во сколько раз
конечный прирост совокупного дохода
(Y)
превосходит первоначальное изменение
объема подоходных налогов (T):
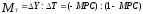
-
Мультипликатор
при наличии встроенных стабилизаторов
– при
наличии системы встроенных стабилизаторов,
например при пропорциональном
налогооблажении, все мультипликаторы
расходов меняются. Величина мультипликатора
снижается, что ослабляет воздействие
первоначального импульса (изменение
расходов) на объем производства и
совокупный доход. Например, мультипликатор
автономных расходов при наличии
встроенных стабилизаторов примет вид:

где MPC–предельная
склонность к потреблению;
t
– налоговая
ставка.
Соответственно
налоговый мультипликатор при наличии
встроенных стабилизаторов примет
вид:

-
Мультипликатор
сбалансированного бюджета равен
1, т.е. равный рост государственных
расходов и налогооблажения ведет к
росту совокупного продукта на ту же
величину.
-
Мультипликатор
фискальной политики ()
–
коэффициент,
который показывает, во сколько раз
результирующий рост национального
дохода превышает начальное увеличение
государственных расходов.
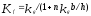
где
– мультипликатор
государственных расходов (с учетом
налогов на доходы);
n
– коэффициент,
показывающий степень реакции реального
спроса на деньги на изменение национального
дохода;
b
– коэффициент,
показывающий степень реакции инвестиций
на изменение ставки процента;
h
– коэффициент,
показывающий степень реакции реального
спроса на деньги на изменение ставки
процента.
-
Мультипликатор
денежной политики ()
–
коэффициент,
который показывает, во сколько раз
результирующий рост реального
национального дохода превышает начальное
увеличение реального денежного
предложения:

где а=
n
-
Мультипликатор
трансфертов ()–
коэффициент,
который показывает, во сколько раз
увеличится совокупный доход, если
трансферты увеличатся на единицу и
наоборот:

12
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные обозначения и формулы по
экономике:
I. Обозначения
1.
P — цена
2. Q —
количество
3. D –
спрос
4. S —
предложение
5.
QD – величина спроса
6.
QS – величина предложения
7.
Qдеф – дефицит (объем дефицита)
8.
Qпродаж – объём продаж
9.
QИЗБ – объём избытка (излишки)
10. EDP–
коэффициент эластичности спроса по цене
11.
ESP– коэффициент эластичности предложения по цене
12. I –
доход
13.
EDI— коэффициент эластичности спроса по доходу
14.
EDC— коэффициент перекрестной эластичности спроса
15. TR –
совокупный доход (выручка продавца)
16. TC –
общие затраты
17.
Pr – прибыль
18. PD –
цена спроса
19.
PS– цена предложения
20. PE–
равновесная цена
II. Формулы:
1.
y= k*x+b – уравнение описывающее функцию
спроса
2.
QD= k*P+b – функция
спроса
3.
EDP= Δ QD (%)/ΔP (%) –
коэффициент эластичности спроса по цене
4.
EDP= (Q2 –Q1): (Q2 + Q1)/
(P2 –P1): (P2 + P1) –
формула средней точки, где P1 – цена товара до изменения, P2 –
цена товара после изменения, Q1 – величина спроса
до изменения цены, Q2 – величина спроса после изменения цены;
5.
EDI= (Q2 –Q1): (Q2 + Q1)/
(I2 –I1): (I2 + I1) –
формула коэффициента эластичности спроса, где I1 – величина
дохода до изменения, I2 – величина дохода после
изменения, Q1 – величина спроса до изменения
дохода, Q2 – величина спроса после изменения дохода;
6.
EDС = (Q2 –Q1): (Q2 + Q1)/
(P2 –P1): (P2 + P1) –
формула средней точки, где P1 – цена второго товара до
изменения, P2 – цена второго товара после изменения, Q1 –
величина спроса первого товара до изменения цены, Q2 –
величина спроса первого товара после изменения цены;
7.
TR = P*Q – формула расчета выручки
продавца
8.
Pr= TR – TС – формула
расчета прибыли;
9.
QD= k*P+b – функция
предложения;
10. ESP=
(QS2 –QS1): (QS2 + QS1)/
(P2 –P1): (P2 + P1) –
формула коэффициента предложения, где P1 – цена товара до
изменения, P2 – цена товара после изменения, QS1 –
величина предложения до изменения цены, QS2 – величина
предложения после изменения цены;
11.
Qдеф = QD— QS–
формула для определения объема дефицита;
12. Qдеф = QS — QD–
формула для определения объема излиш
Формула
расчёта необходимого для обращения количества денег:
1)
КД — масса денег;
Ецт — сумма цен товаров;
К — товары, проданные в кредит;
СП — срочные платежи;
ВП — взаимопогашаемые платежи (бартерные сделки);
СО — скорость оборота денежной единицы (в год).
2)
M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Уравнение обмена:
M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Это уравнение показывает, что совокупные расходы в денежном выражении
равны стоимости всех товаров и услуг, произведенных экономикой. Формула для нахождения реального дохода:
ИПЦ — индекс потребительских цен. Формула для нахождения покупательной
способности денег:
Iпcд — покупательная способность денег;
Iц — индекс цен. Формула для нахождения индекса
потребительских цен:
Формула для расчёта стоимости
потребительской корзины:

P 1 — цена первого товара;
Р 2 — цена второго товара;
Р n — цена n-го товара;
Q 1 — количество первого товара;
Q 2 — количество второго товара;
Q n — количество n-го товара. Формула для расчёта темпа инфляции:
В зависимости от темпа инфляции различают несколько ее видов:
1.Мягкая (ползучая), когда цены растут в пределах 1—3% в год.
2.Умеренная — при росте цен до 10% в год.
3.Галопирующая — при росте цен от 20 до 200% в год.
4.Гиперинфляция, когда цены растут катастрофически — более чем 200% в
год. Формула для расчёта простого процента:
P — сумма долга с процентами;
S — сумма кредита;
n — число дней;
i — годовой процент в долях. Формула для расчёта сложного процента:
P — сумма долга с процентами;
S — сумма кредита;
n — число дней;
i — годовой процент в долях;
N — сколько раз начисляется в году. Формула для расчёта сложного процента начисляемого за несколько
лет:
P — сумма долга с процентами;
S — сумма кредита;
t — число лет;
i — годовой процент в долях. Формула для расчёта смешанного процента за дробное колличество лет:
P — сумма долга с процентами;
S — сумма кредита;
t — число лет;
i — годовой процент в долях;
n — число дней. Формула для расчёта банковских резервов:
S — норма обязательных резервов в процентах;
R — общая сумма резервов;
Д — величина депозитов на счету КБ. Формула расчёта уровня безработицы:
Формула расчёта уровня занятости:
Формула расчёта перекрёстной ценовой
эластичности:

Формула расчёта амортизации:
1)
2)
Формула расчёта личного дохода домохозяйств:
Формула расчёта ВНП по доходам:

Формула расчёта ЧНП:
Формула расчёта средних общих издержек:
1)
2)
Формула расчёта общих издержек:
Формула расчёта средних постоянных издержек:


1)
2)
Формула расчёта бухгалтерской прибыли:
Формула расчёта экономической прибыли:
1)
2)
Формула расчёта рентабельности продукции:



Формула расчёта величины циклической безработицы:
Формула расчёта величины естественной безработицы:
Формула расчёта производительности труда:
Формула расчёта дуговой эластичности по доходу:
<=»»
form=»»>
Коэффициент Джини
Самое краткое определение коэффициента Джини –коэффициент концентрации
богатства. Чем он выше – тем выше и
неравенство. Более полное
определение – мера
неравенства распределения доходов. Еще более полное определение – коэффициент
девиации экономики от абсолютного равенства в распределении доходов.
Коэффициент выводится из кривой Лоренца и представляет
собой отношение площади между этой кривой и линией абсолютного равенства к
общей площади под линией абсолютного равенства. Линия абсолютного равенства –
биссектриса между осями «доля домохозяйств» и «доля
доходов». Коэффициентможет быть рассчитан и по точной формуле.
Максимальное значение коэффициента равно единице и это –абсолютное неравенство.
Минимальное равно нулю и это абсолютное равенство
В силу социально-политической
значимости получаемых на основе коэффициента оценок, он активно рассчитывается,
дискутируется и используется для разного уровня выводов. Одна из наиболее
активных сфер использования – сравнительный межстрановой и временной анализ.
Например, коэффициент Джини
для России в 1991 году был
равен 0,24, в 2008 году 0,42. В так называемых «образцовых»
европейских и особенно североевропейских странах он находится в диапазоне от
0,2 до 0,3.
Но вряд ли уместны прямые
заключения из сравнения коэффициента по странам и по времени. У него есть ограничения, переходящие в
недостатки, что объясняется двумя обстоятельствами. Во-первых,
относительным характером этого показателя. Во-вторых, его диапазонной
асимметричностью: одно распределение может быть более равным, чем другое в
одном диапазоне, и менее равным в другом при одном том же значении коэффициента
для обоих распределений. Поэтому прямые выводы из сравнения коэффициента в
разных странах и во временной динамике могут привести к ошибочным оценкам.
Коэффициент назван в честь его автора – итальянца Коррадо Джини (Corradо Gini), преподавателя статистики,
социологии и демографии в университете Рима. Коэффициент был предложен им в 1912 году, поэтому у коэффициента
намечается знаменательная дата — 100 лет практического использования
Рассчитать коэффициент
Джини.
Рассчитать коэффициент
Джини:Всего население 1млн100тыс человек.
15%-богатые семьи месячный доход 200 тыс.
35%-средний класс месячный доход 30 тыс.
50%-бедные месячный доход 10 тыс.
Рассчитаем долю доходов бедных
семей.
Доход всех семей: 1.1млн*(0.15*200тыс+0.35*30тыс+0.5*10тыс)=1.1млн*(45.5тыс).
Значит доля доходов бедных семей =(1.1млн*(0.5*10тыс)/(1.1млн*(45.5тыс)=0.11.
Таким же образом находим долю доходов среднего класса в общих доходах ( равна
0.23).
Значит доля доходов бедных и среднего класса в общих доходах = 0.34.
Индекс Джини я рассчитывал как отношение площади фигуры(S), заключенной между
кривой абсолютного равенства и кривой Лоренца, к площади фигуры, заключенной
между кривой абсолютного равенства и кривой абсолютного неравенства(Sан=0.5)
S=0.5-S1-S2-S3-S4-S5
S1,S2,S3,S4,S5 можно легко найти по имеющимся данным,
а значит можно найти и индекс Джини.
Как найти данные
S1,S2,S3,S4,S5,чему они равны?И что делать дальше,как найти именно коэффициент
Джини?
·
S1,S3,S5 — это прямоугольные треугольники, их площадь находится
как половина произведения катетов
S2,S4 — это прямоугольники, их площадь — это произведение сторон
G = =
= 0.5865
·
Некое общество состоит из двух социальных групп, внутри каждой
из которых доход распределен равномерно. Известно, что среднедушевой доход в
первой группе составляет 5 тыс. руб. в месяц, во второй – 25 тыс. руб. в месяц,
а во всем обществе среднедушевой доход составляет 20 тыс. руб. в месяц.
Определите значение коэффициента Джини для этого общества.
·
·
Решение
и ответ
·
Обозначим
количество членов более бедной социальной группы за , более богатой —
за , а доходы
групп соответственно за и
. Тогда:

Кривая Лоренца будет иметь следующий вид:
·
·
Построив
ее, легко посчитать коэффициент Джини:
.
·
Ответ:
·
.
Четырехмерный коктейль
Для приготовления одной порции
коктейля «Неустойчивое равновесие» — фирменного коктейля бара
«Economics» — требуется 1 единица ингредиента A, 2 единицы
ингредиента B, 3 единицы ингредиента C и 4 единицы ингредиента D (названия
ингредиентов являются коммерческой тайной и не разглашаются). Однако владелец
бара, знаменитый бармен и экономист Сэм Полуэльсон, обладает лишь ограниченными
ресурсами для закупки дорогих ингредиентов. Так, на имеющиеся у него денежные
средства он может купить либо 100 единиц ингредиента A, либо 200 единиц
ингредиента B, либо 300 единиц ингредиента C, либо 400 единиц ингредиента D в
день.
Какое максимальное число порций фирменного коктейля сможет приготовить Сэм за
день?
Мне первым в голову пришло вообще
другое решение-логическое
Заметим тот факт,что для покупки любого ингредиента(А,B,C,D) на 1 порцию
коктейля нам надо потратить 1/100 всех денег,то-есть на 1 коктейль мы тратим
1/25 всех денег,поэтому всего можем сделать 25 коктейлей
·
Задача
на коэффициент Джини.
Всех жителей некоторой общины
можно условно разделить на три равные группы по численности: бедные, средние,
богатые. Доход Бедной группы составляет 20% от общего дохода всех жителей
данной общины. Доход средней группы составляет 30%. Рассчитайте коэффициент
Джини ().
В общине решили ввести налог на доходы богатой части общества в размере 30% от
их дохода. Полученная сумма налога распределяется следующим образом: две трети
полученной суммы идет бедным, одна треть — средней группе. Рассчитайте новое
значение коэффициенты Джини().
Решение: После введения налога
доход «богатых» составит: от
общего дохода всех жителей, то есть распределиться между оставшимися группами общего дохода, следовательно доходы
«бедных» составят: ;
доходы «средних» составят ,
что равно доходам «богатых», то есть теперь общество делиться на 2
группы: «бедные» ( населения
и от общего дохода) и
«средние-богатые»( населения и
от общего дохода).
Коэффициент Джини можно рассчитать, используя лемму о ломаной кривой Лоренца ,
имеющей два линейных участка (доказательство леммы в задаче, которая называется
«В некоторой стране», введите в поиске по сайту, ссылку вставить не
получилось), отсюда
Вычислите
коэффициент Джини, примерно отражающий общемировое неравенство доходов, если
ВВП развивающихся стран, в которых проживает 80 % населения Земли, в сумме
составляют только 20 % общемирового продукта (заметим, что это соотношение
держится уже много лет по данным Всемирного банка).
Решение и ответ
j=1-(0,8+(0,2+1))*0.2=1-2*0.2=0.6
Ответ:
0,6
В некоторой стране
В некоторой стране общество состоит
из двух неравных по численности и уровню доходов групп: богатых и бедных.
Допустим, бедные получают 40% совокупного дохода. Значение коэффициента Джини
составляет 0,3. Рассчитайте долю бедных и долю богатых от общей численности
населен
, где
-доля беднейшего
населения, — доля
дохода беднейшего населения. Теперь для полноправного использования выведем эту
формулу:
Ну или можно просто стандартно
рассчитать коэффициент Джини, что в конечном итоге даст аналогичный результат
результат))
·
Сложение
кривых Лоренца
В двух странах с одинаковым ВВП
на душу населения коэффициенты Джини отличаются на единицу. Государство с менее
равномерным распределением доходов – тоталитарное и милитаризованное – решило
развязать войну со своим более демократичным соседом. Однако, несмотря на
значительные расходы (на кампанию было потрачено около ВВП), агрессор потерпел явную неудачу.
В ходе кровопролитных боев погибло населения
нападающей страны. Для сравнения, демократическое государство потратило на
оборону только ВВП, пожертвовав жизнями
населения. В итоге страны решили
заключить мирный договор и образовать союзное государство. Оказалось, что
коэффициент Джини в объединенном государстве равен . Каков был бы
коэффициент Джини, если бы страны решили объединиться до войны?
Решение и ответ
Коэффициенты Джини отличаются на один из них равен
(в демократической стране), а другой –
(в тоталитарной).
Обозначим демократическую страну «D», а тоталитарную – «T», – ВВП,
– численность населения, момент до
войны – «0», момент после войны – «1».
Тогда
;
.
;
.
Отсюда
;
.
Но в силу равенства ВВП на душу населения до войны .
Значит,.
Обозначим .
Тогда .
Поймем, как будет выглядеть кривая Лоренца объединенного государства. Самые
бедные в новом государстве – это жители бывшего тоталитарного государства,
имеющие нулевые доходы. Их доля в населении нового государства равна , поэтому на
отрезке кривая
Лоренца нового государства будет совпадать с осью абсцисс. «Средний класс» в
новом государстве будут составлять бывшие жители демократического государства.
Вместе с бедными они будут составлять почти все население нового государства, а
суммарная доля доходов этих групп населения в общем ВВП равна . Кроме
того, внутри среднего класса распределение доходов абсолютно равномерно,
поэтому следующий участок общей кривой Лоренца будет отрезком прямой с концами
в точках и
. И, наконец, соединяя точку
с точкой
, получаем
отрезок общей кривой Лоренца, «ответственный» за богатых, то есть за ту самую
крайне малочисленную группу населения тоталитарной страны, располагавшую всем
ее ВВП. В итоге общая кривая Лоренца имеет вид:
Тогда коэффициент Джини равен .
Учитывая то, что , имеем:
Значит, .
Получается, что до войны страны имели одинаковый ВВП и одинаковую численность
населения!
Если бы страны объединились до войны, то общая кривая Лоренца имела бы
качественно такой же вид, как и в случае объединения после войны. Следуя
описанной выше логике построения этой кривой, нетрудно установить, что
совокупная кривая Лоренца до войны проходила бы через точки , и совокупный
коэффициент Джини был бы равен .
Ответ:
.
Неравенство
среднедушевых доходов
Некое общество состоит из двух
социальных групп, внутри каждой из которых доход распределен равномерно.
Известно, что среднедушевой доход в первой группе составляет 5 тыс. руб. в
месяц, во второй – 25 тыс. руб. в месяц, а во всем обществе среднедушевой доход
составляет 20 тыс. руб. в месяц. Определите значение коэффициента Джини для
этого общества.
Решение и
ответ
Обозначим количество членов более
бедной социальной группы за , более богатой — за
, а доходы групп соответственно за
и
. Тогда:

Кривая Лоренца будет иметь следующий вид:
Построив ее, легко посчитать
коэффициент Джини:
.
Ответ:
.
$«Три
поросенка и Серый волк»$
Жили-были на свете три
брата-поросенка: Ниф-Ниф, Нуф-Нуф и Наф-Наф. Все одинакового роста,
кругленькие, розовые, с одинаковыми веселыми хвостиками. Вот только навыки их
различались. За лето Ниф-Ниф мог построить три дома из соломы или два дома из
камня. Нуф-Нуф, более тщательный и аккуратный, мог построить за лето целых пять
соломенных домиков. И по лесу ходили слухи, что как-то, поспорив с братьями, он
смог за лето построить 2 домика из соломы и три дома из камня. Но самым
трудолюбивым из поросят был Наф-Наф: в июне он мог построить 2 соломенных
домика, в июльский зной его производительность снижалась, и его хватало лишь на
то, чтобы целиком построить один домик из соломы и начать еще один. Зато в
августе Наф-Наф работал, не покладая рук – не только мог доделать начатое в
июле, но и построить 4 новых соломенных домика. А каменщиком Наф-Наф был еще
более искусным: на каждый дом из камня он тратил на 40% времени меньше, чем на
соломенный.
Построенные домики поросята продавали жителям соседнего леса, которым покупка
домика из соломы обходилась в 10 монет, а домика из камня – в 15 монет.
Однажды, нежась в лужице, братья договорились, что будут заниматься
строительством вместе, создав девелоперскую компанию «ХрякДомСтрой».
— Но мы же всего лишь поросята, — сказал Наф-Наф, самый разумный из них, – нам
нужен бухгалтер, который будет учитывать все наши операции и составлять баланс.
— А давайте позовем Серого волка, — предложил Нуф-Нуф, — ведь после той
истории, сделавшей нас знаменитыми, он изменился, тоже работать хочет. Видимо
не зря мы его проучили!
Поросята согласились с предложением брата, но решили устроить волку экзамен,
чтобы проверить, не собирается ли он снова попытаться «надуть» их. Вот какие
задания были предложены Серому волку на экзамене:
1. Покажи, какими являются возможности каждого из братьев-поросят, если они
будут работать поодиночке. (5 баллов)
2. На стене одного из домов проиллюстрируй возможности строительства домиков,
которыми будет обладать компания «ХрякДомСтрой». (6 баллов)
3. Если надо будет построить несколько соломенных, и несколько каменных домов,
какие именно дома должен строить каждый из братьев? (5 баллов)
4. Скажи, какие домики стоит строить, чтобы «ХрякДомСтрой» смог получить
максимальный доход от их продажи жителям леса, если солома, необходимая для
постройки одного дома, обходится в 3 монеты, а камни – в 10 монет (10 баллов).
Серый волк решил задачки, но теперь перед поросятами встала новая проблема: как
проверить ответы волка? За верными ответами они обратились к нам. А мы – к вам.
1) Ниф-ниф :
Нуф-нуф :
Наф-наф :
3)Ниф-ниф строит соломенные
Нуф-нуфу всеравно какие
Наф-наф строит Каменные
4) Ниф-нифу и нуф-нуфу строить только соломенные а Наф-нафу строить Каменные
Прибыль получилась
А в чем проблема-то?
1) У Ниф-Нифа есть две крайние
точки на КПВ, у Нуф-Нуфа есть крайняя точка по оси соломы и точка (2;3) (если
строить КПВ в осях (соломенные домики;каменные домики)), у Наф-Нафа две крайние
точки 8 и по оси ординат и абсцисс
соответственно. Если чуть подробнее с Наф-Нафом, то у нас есть крайняя точка 8,
также известно, что на каменные домики тратится на 40% меньше, то есть 60%,
значит другая крайняя точка:
2) Здесь просто смотрите у кого меньшая альтернативная стоимость в производстве
какого-либо вида домиков, потом начинаете строить общую КПВ, начиная с
наименьшей а.с.
3) Опять же все сводится к альтернативной стоимости
4) Проверяете «краевые» точки суммарной КПВ, то есть 2 точки излома и
две крайние точки. Если более обоснованно, то тут вроде надо записать, что и пусть эта прямая «ездит»
по суммарной КПВ до тех пор, пока не будет
максимально.
Кстати, в задачнике Акимова есть очень похожие задачи на эту тему,просто там
вместо прибыли, надо было максимизировать выручку.
Задача
про зайцев
В темно-синем лесу, где трепещут
осины, компания «Зайцы Ltd.» является монополистом на рынке трын-травы и имеет
функцию издержек . Ежемесячно проводятся торги, каждый месяц
функция спроса на трын-траву одинакова и задается уравнением . Дед
Мазай, представляющий в лесу государство, собирается вмешаться в
ценообразование. Он хочет добиться снижения цены до определенного уровня , но, чтобы
вмешательство не казалось резким, Мазай будет проводить свою политику в три
этапа:
1.
Установит потолок цены на уровне ,
который выше , но при котором «Зайцы Ltd.» будут производить столько же,
сколько производили бы при .
2.
Снизит потолок до такого уровня ,
при котором оптимальный выпуск «Зайцев Ltd.» максимален.
3.
Наконец, снизит потолок до уровня .
Когда Дед Мазай спросил «Зайцев
Ltd.», выгодно ли им косить трын-траву при цене или лучше уйти с рынка, они ответили
своей знаменитой фразой: «А нам всё равно!».
1.
Какую прибыль получили бы «Зайцы Ltd.», если бы не было Деда
Мазая?
2.
Найдите цены, которые установятся на рынке после каждого этапа
вмешательства. Какую прибыль будут получать «Зайцы Ltd.» при каждой из этих
цен?
3.
Прокомментируйте действия Деда Мазая с точки зрения
общественного благосостояния.
Решение и ответ
Найдем прибыль «Зайцев Ltd.» до
государственного вмешательства:
|
|
Рассмотрим механизм выбора монополистом
объема производства при установке потолка цены . Новая
кривая спроса будет иметь два участка: ниже уровня она останется прежней, а на уровне
станет совершенно неэластичной. Исходя
из этого, левее
будет горизонтальной на уровне
, а правее
останется прежней (жирная линия на рисунке 1).
При каждом значении «Зайцы Ltd.» определяют уровень
выпуска, при котором пересекает
новую .
,
значит, речь идет о долгосрочном периоде. Поскольку при цене фирме безразлично, уйти из отрасли или
остаться, эта цена равна минимуму средних издержек (она получает нулевую
экономическую прибыль при оптимальном выпуске). Очевидно, что оптимальный объем
выпуска в этом случае лежит на горизонтальном участке кривой .
|
|
Какую цену может установить Дед Мазай, чтобы
объем производства тоже был равен 5? Такую, чтобы величина спроса при этой цене
была равна 5.
Осталось найти . Максимальный из
оптимальных объемов производства достигается при установке потолка на уровне
пересечения и
кривой спроса. (Кстати, именно такая цена и такой объем производства сложились
бы на рынке, если бы он был совершенно конкурентен.) Если потолок будет выше
или ниже этого уровня, «Зайцам Ltd.» будет выгодно снизить выпуск.
|
|
Говоря о последствиях действий
Деда Мазая для общества, можно заметить, что установка цен и
целесообразна, так
как снижает уровень цены и увеличивает объем продаж (при ситуация сходна с совершенной
конкуренцией), а снижение цены до вызывает появление
потерь общества от ценового регулирования и появления дефицита трын-травы на
рынке.
Примечание:
Подробно и с картинками поведение
монополиста в условиях ценового регулирования описано в известном учебнике
Роберта Пиндайка и Даниэля Рубинфельда в главе «Рыночная власть: монополия и
монопсония».
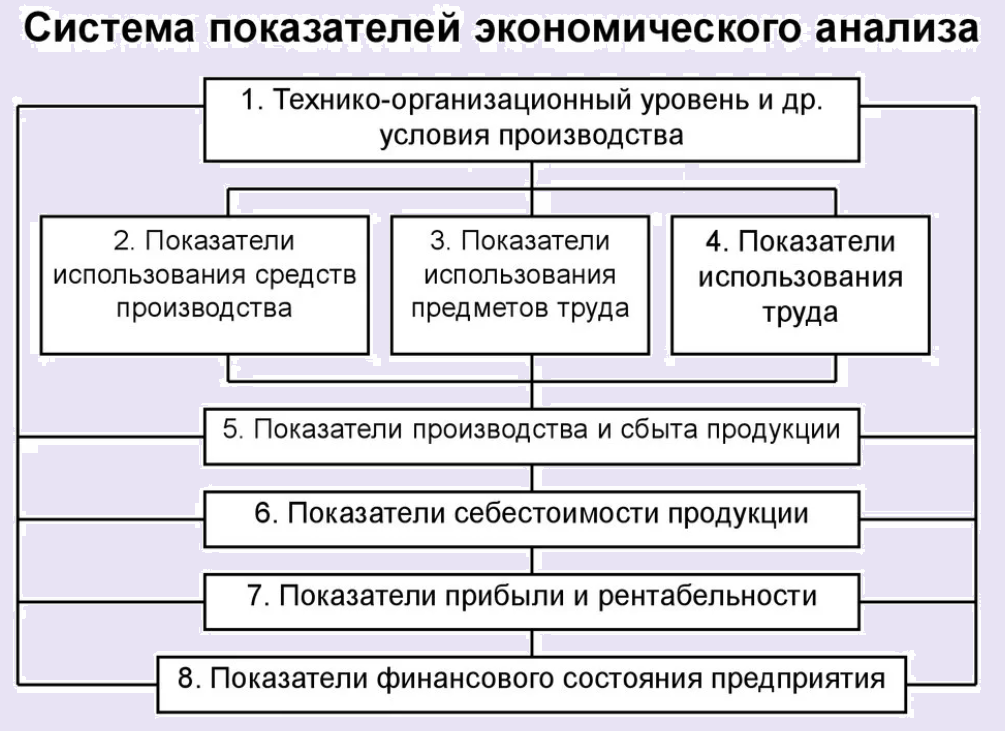
Выполнение экономических студенческих, научных работ и исследований сопровождается целым спектром точных расчётов и анализом полученных результатов, которые становятся аргументационной базой для принятия конкретного решения с учетом всевозможных факторов: возможности объекта, финансовое и правовое положение, воздействие внешней и внутренней среды, эффективность и пр.
Набор показателей и коэффициентов, применяемых в ходе исследования каждой конкретной ситуации, определятся автором самостоятельно с учетом действующих правил, ключевых понятий, имеющихся на руках материалах. При этом важно, чтобы исследуемый автором проекта набор коэффициентов и данных позволял получить конкретные сведения об объекте: общая характеристика, тенденции, сильные и слабые стороны, воздействующие на конечный результат или непосредственно объект факторы, перспективы решения проблемы с оценкой их эффективности, целесообразности и посильности.
На сегодняшний день существуют тысячи экономических показателей, методик анализа, но каждый автор имеет право «модифицировать» их с учетом собственных возможностей, нужд и пр., подбирая коэффициенты для расчетов и изучения. Чаще всего основными компонентами экономических работ выступает несколько групп показателей:
- Технико-экономическая (общая) характеристика объекта;
- Анализ ликвидности и платежеспособности;
- Анализ финансовой устойчивости;
- Оценка рентабельности компании;
- Исследование деловой активности предприятия;
- Инвестиционные критерии: окупаемость проекта, риск банкротства и пр.
Сегодня мы подробнее рассмотрим первую группу экономических формул, используемых в исследованиях студентами и учеными, экономистами-практиками.
Какие материалы потребуются для проведения расчетов и анализа?
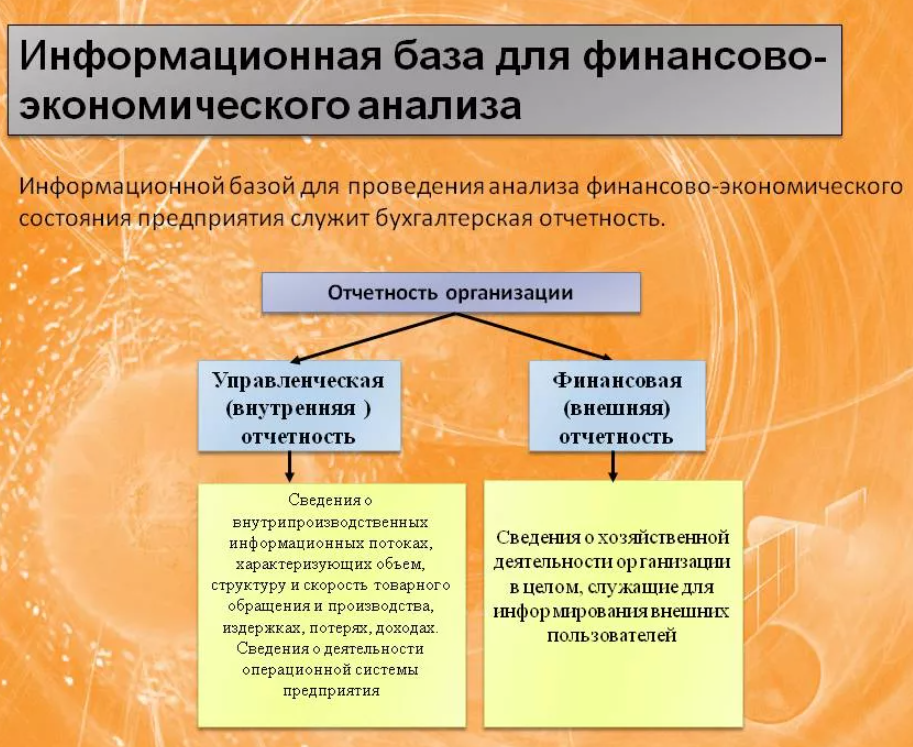
Для проведения расчетов и экономического анализа автору исследования потребуется доступ к концертным материалам об объекте исследования. С одной стороны, ими могут стать всем доступные данные – статьи из СМИ, данные официального сайта, отзывы потребителей и клиентов, отзывы сотрудников и пр.
С другой – в основу экономического анализа кладут исключительно точные, достоверные и проверенные факты, отраженные в бухгалтерской и финансовой отчетности. Поэтому для проведения расчётной деятельности целесообразно обратиться за необходимыми сведениями в бухгалтерию, отдел кадров, статистический отдел и др.
Основными документами, позволяющими провести аналитическую работу экономисту, являются: бухгалтерский баланс, отчет о прибылях и убытках, отчет о движении капитала (денежных средств), даны из отдела кадров о производственной и административной структуре компании устав организации, данные статистов или отдела продаж (уровень продаж, выручки, себестоимость и пр.) и пр.
Ниже мы детальнее рассмотрим правила расчета и анализа каждого конкретного показателя.
Основные экономические формулы для получения общей характеристики объекта
Основными формулами для проведения экономического анализа являются те показатели, которые позволяют исследователю получить первой преставление, обрести данные об общих и важных моментах деятельности предприятия, оценить степень его эффективности и важности в определенном сегменте и пр.
Возникли сложности?
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Строго набора показателей для оценки ситуации нет. Каждый автор самостоятельно комбинирует подходящие коэффициенты с учетом располагаемых первоисточников. Сложнее всего в проведении экономического анализа предприятия приходится практикантам, которым не желают предоставлять полноценные, достоверные и актуальные данные, отчетность.
Самыми популярными и простыми для расчетов и анализа выступают следующие показатели:
- Выручка от продаж и себестоимость в денежном выражении.
Как правило, здесь автору не требуется производить «ручной подсчет» доходов и расходов компании. Эти сведения можно легко найти в бухгалтерской отчётности в форме №2 – «Отчет о прибылях (убытках)» или «Отчет о финансовых результатах».
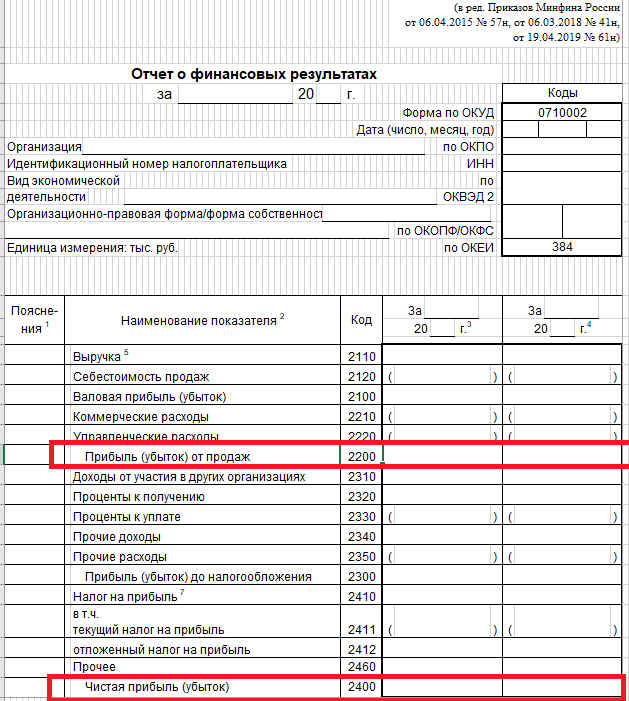
Первой строчкой в нем выступает «Выручка от продаж» — строка 2110. Данный показатель свидетельствует о том, какой доход компания получила от продажи определённого объема товаров с учетом действующей ценовой политики.
Вторая строка (код 2120) – Себестоимость. Она отражает уровень расходов на производство товаров/услуг.
Указанные показатели целесообразно анализировать в динамике. По экономическим правилам, положительная тенденция прослеживается если выручка с каждым годом растет, а себестоимость остается прежней или сокращается. Рост затрат на производство должен спровоцировать массу вопросов: причина роста, что повлияло на ценовой рост, как сократить расходы и увеличить доходность и пр.
Если себестоимость в значительной степени и на протяжении длительного времени превосходит выручку, то компания работает себе в убыток и требует срочных мер.
В идеале автору необходимо проанализировать динамику показателей за три последних года/квартала или месяца (в зависимости от анализируемого периода). Такой подход позволяет констатировать четкую тенденцию.
- Среднегодовая выработка одного работника (производительность труда).
Данный показатель свидетельствует о средней доли участия в производственном процессе каждого сотрудника: сколько произведенных и выпущенных в оборот товаров и услуг приходится на 1 задействованного человека.
Для подсчета этого коэффициента потребуется данные о выручке и среднесписочной численности персонала. Для получения этих материалов достаточно обратиться в бухгалтерию («Отчет о финансовых результатах», Строка 2110) и отдел кадров (справка или устные данные специалиста, годовой отчет предприятия).
Рост данного показателя считается положительной тенденцией, свидетельствующей о росте вклада каждого сотрудника в деятельности компании и конечный результат, ответственный подход или внедрение эффективных инноваций, позволивших нарастить выручку, привлечь всех работников и пр.
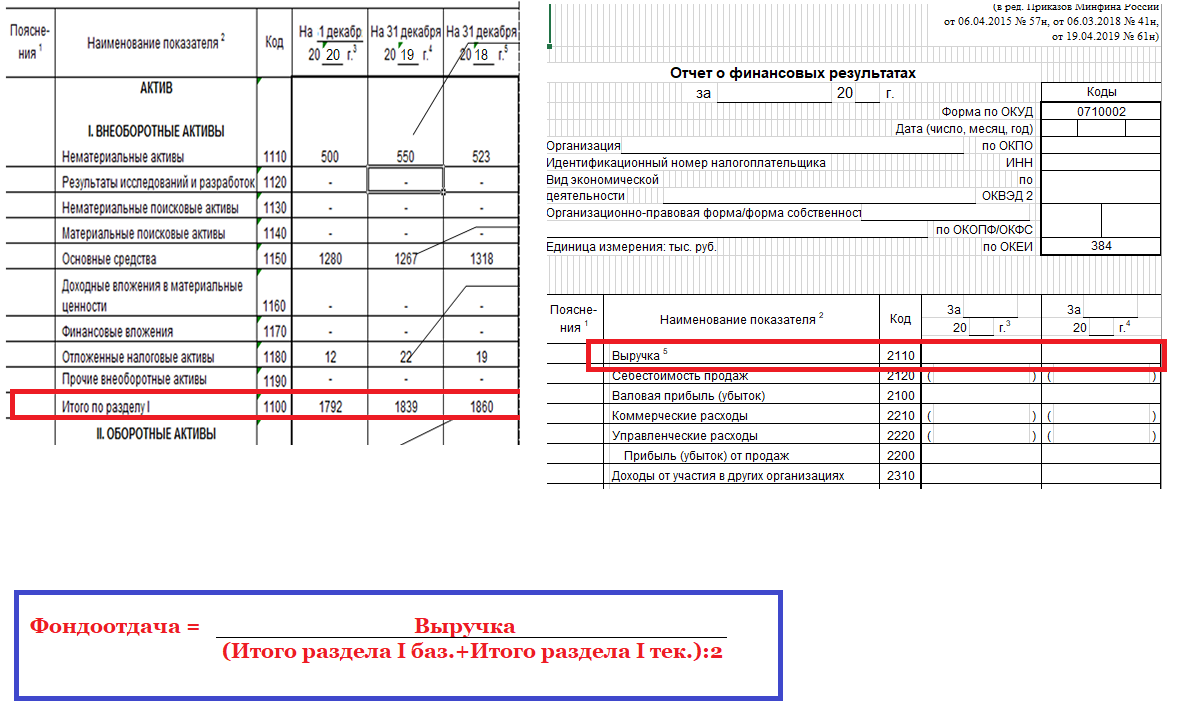
- Фондоотдача.
Данный показатель позволяет оценить эффективность использования основного капитала предприятия. Для его подсчета необходимо располагать следующими данными: выручка (отчет о прибылях и убытках строка 2110) и среднегодовая стоимость основного капитала (он представляет собой среднее арифметическое данных на начало и конец анализируемого периода по строке бухгалтерского баланса «Итого раздела I», строка 1100).
Соотношение полученной выгоды и объема задействованных основных фондов позволяет определить: степень окупаемости постоянных затрат. Конкретных норм у этого коэффициента нет. Его увеличение в динамике будет подчеркивать рост интенсивности использования основных средств, их пользу в производственном процессе.
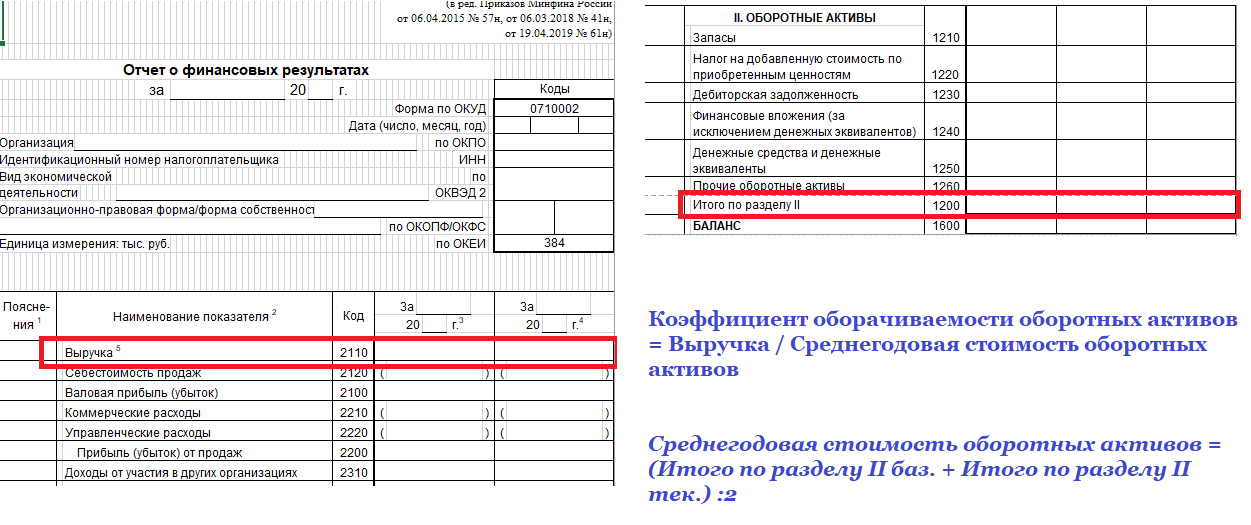
- Коэффициент оборачиваемости оборотных активов.
Данный показатель призван подчеркнуть уровень участия и эффективность использования оборотых активов. Под оборотным капиталом понимают те средства и предметы труда, которые однократно участвуют в производственном процессе: сырье, материалы и пр.
Его расчет основывается на следующих данных: выручка и среднее значение оборотных активов. Второй показатель рассчитывается как среднее арифметическое между данными на начало и конец исследуемого периода. Узнать точные сведения по нему можно в бухгалтерском балансе – строка «Итого по разделу II» (код 1200).
Этот показатель отражает количество оборотов, совершаемых оборотными средствами в течение анализируемого периода времени. Чтобы уточнить продолжительность одного оборота (в днях), необходимости разделит количество дней в анализируемом периода (30 – месяц, 90 – квартал, 180 – полгода, 36 – год) на коэффициент оборачиваемости. Данный показатель – своего рода «скорость» задействования и использования оборотного капитала. Чем короче продолжительность, тем быстрее запасы со склада превращаются в готовый товар.
- Прибыль от продаж и чистая прибыль.
Данные показатели отражают конечный финансовый результат от осуществляемой объектом исследования деятельности, то есть тот уровень доходов, которые они получили после всех операций, насколько выгодно производство товаров/оказание услуг.
Прибыль от продаж рассчитывается, как разница между выручкой и себестоимостью с учетом коммерческих и управленческих расходов.
Чистая прибыль – это тот остаток средств, который остается у предприятия после уплаты всевозможных налогов.
Экономисту-аналитику не придется калькулировать эти показатели вручную. Достаточно взглянуть на форму №2 – «Отчет о финансовых результатах» на соответствующие строки 2200 и 2400.
Динамика данных показателей свидетельствует о повышении доходности компании, получаемой ею выгоде.
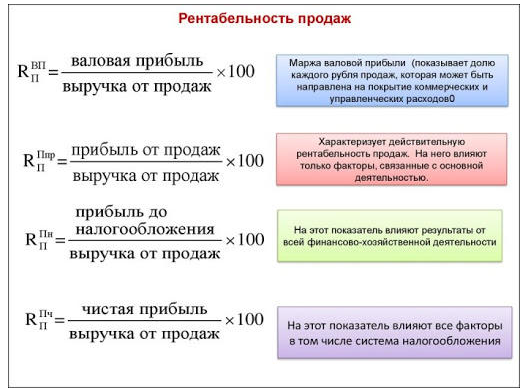
- Рентабельность продаж.
Данный показатель свидетельствует об общей эффективности предприятия. Она основывается на соотношении двух показателей: прибыль и выручка. Важно не путать указанные понятия и критерии: выручка – это объем реализованной продукции в денежном выражении, а прибыль – это доход, который остается по мере уплаты всех расходов и платежей.
Соотношение прибыли и выручки показывает, какая часть выручки приходится на каждый рубль полученного дохода. Притом данное соотношение рассчитывается в процентах.
Существует несколько вариаций расчета этого показателя в зависимости от вида прибыли: валовая, прибыль от продаж, прибыль до налогообложения, чистая прибыль и пр.
Для расчета этого показателя потребуется форма №2 – отчет о финансовых результатах.
Важно не просто следить за динамикой этого показателя с течением времени, но и соотносить его с рентабельностью затрат, которая рассчитывается, как соотношение прибыли и себестоимости. Если рентабельность затрат выше рентабельности продаж, то требуется в срочном порядке проанализировать расходные статьи и оптимизировать их (провести реструктуризацию затрат). В идеале рентабельность продаж в динамике должна расти, а рентабельность затрат – сокращаться. Суровых ограничений в этом плане нет.
- Среднесписочная численность работников.
Уточнит активную или общую численность сотрудников можно в отделе кадров. Есть же можно запросить более детальные сведения для анализа производственной и административной структуры предприятия: по полу, возрасту, образованию, опыту работы, квалификации и пр.
Динамика этого показателя свидетельствует о текучести кадров, действующих мерах оптимизации штата, наращивания или сокращения производств и пр. Данный для анализа средней численности сотрудников можно найти в отделе кадров.
Как оформить анализ данных?
Указанные показатели – не единственные в своем роде, но считаются самыми распространёнными и популярными в экономическом анализе, позволяющими получить общую характеристику о деятельности предприятия.
Конкретизировать порядок расчетов (что и как рассчитывалась) в исследовании не нужно. Достаточно привести сводную таблицу с показателями и результатами расчетов, а под ней проанализировать их, отметив выявленные тенденции, о чем они свидетельствуют. В выводах не стоит углубляться в числа. Они отражены в таблице. Главное – показать динамику наиболее важных или очевидных показателей, причину и возможности ее проявления (как и где сказывается, хорошо это или плохо), воздействие.
На основе анализа вышеуказанных показателей можно констатировать:
- Общее положение дел: уровень продаж, уровень затрат, динамика (их рост или сокращение);
- Эффективность использования активов;
- Соотношение прибыли и объем производства, прибыли и затрат;
- Потенциальные проблемы и перспективы развития (общие).
Результаты анализа общих экономических показателей должен подтолкнуть автора к углубленному анализу следующей группы коэффициентов, определить сильные и слабые стороны, проблему и причину ее возникновения.
Основные обозначения и формулы по экономике
Основные обозначения и формулы по экономике:
I. Обозначения
- P — цена
- Q — количество
- D – спрос
- S — предложение
- QD – величина спроса
- QS – величина предложения
- Qдеф – дефицит (объем дефицита)
- Qпродаж – объём продаж
- QИЗБ – объём избытка (излишки)
- EDP– коэффициент эластичности спроса по цене
- ESP– коэффициент эластичности предложения по цене
- I – доход
- EDI— коэффициент эластичности спроса по доходу
- EDC— коэффициент перекрестной эластичности спроса
- TR – совокупный доход (выручка продавца)
- TC – общие затраты
- Pr – прибыль
- PD – цена спроса
- P
S– цена предложения - PE– равновесная цена
II. Формулы:
- y= k*x+b – уравнение описывающее функцию спроса
- QD= k*P+b – функция спроса
- EDP= Δ QD (%)/ΔP (%) – коэффициент эластичности спроса по цене
- EDP= (Q2 –Q1): (Q2 + Q1)/ (P2 –P1): (P2 + P1) – формула средней точки, где P1 – цена товара до изменения, P2 – цена товара после изменения, Q1 – величина спроса до изменения цены, Q2
– величина спроса после изменения цены; - EDI= (Q2 –Q1): (Q2 + Q1)/ (I2 –I1): (I2 + I1) – формула коэффициента эластичности спроса, где I1 – величина дохода до изменения, I2 – величина дохода после изменения, Q1 – величина спроса до изменения дохода, Q2 – величина спроса после изменения дохода;
- EDС = (Q2 –Q1): (Q2 + Q1)/ (P2 –P1): (P2 + P1) – формула средней точки, где P1 – цена второго товара до изменения, P
2 – цена второго товара после изменения, Q1 – величина спроса первого товара до изменения цены, Q2 – величина спроса первого товара после изменения цены; - TR = P*Q – формула расчета выручки продавца
- Pr= TR – TС – формула расчета прибыли;
- QD= k*P+b – функция предложения;
- ESP= (QS2 –QS1): (QS2 + QS1)/ (P2 –P1): (P2 + P1) – формула коэффициента предложения, где P1 – цена товара до изменения, P2 – цена товара после изменения, Q
S1 – величина предложения до изменения цены, QS2 – величина предложения после изменения цены; - Qдеф = QD— QS– формула для определения объема дефицита;
- Qдеф = QS — QD– формула для определения объема излишек;
Вы должны ввойти чтобы оставить комментарий.
ekonomkan.ru
Формулы по экономике
Формулы спроса и эластичности
В первую очередь необходимо рассмотреть формулы по экономике, которые касаются спроса и предложения. Уравнение функции спроса можно представить в виде следующей формулы:
y= к*x+b
Сама функция спроса выглядит следующим образом:
QD= к*P+b
Функция предложения:
Qs= к*P+b
Если рассмотреть показатели эластичности, то можно выделить формулы по экономике, определяющие эластичность спроса по цене:
EDP= Δ QD (%) : Δ P (%)
EDP= (Q2 –Q1)/(Q2 + Q1) : (P2 –P1)/(P2 + P1)
Вторая формула представляет собой расчет средней точки, здесь значение P1 – цена продукции до изменения, P2 – цена продукции после изменения, Q1 – спрос до изменения цены, Q2 –спрос после изменения цены.
Формула коэффициента эластичности спроса в общем виде:
EDI= (Q2 –Q1)/ Q1 : (Р2 –Р1)/ Р1
Формулы макроэкономики
Формулы по экономике включают в себя формулы по микроэкономике (спрос и предложение, издержки фирмы и др.), а также формулы по макроэкономике. Важной формулой по макро экономике является формула расчета необходимого в обращении количества денег:
КД = ∑ ЦТ – К + СП – ВП / СО
КД — количество денег в обращении,
ЦТ — сумма цен на товары;
К — товары, продаваемые в кредит;
СП — срочные платежи;
ВП — взаимно погашаемые платежи по бартерным сделкам;
СО — годовая скорость оборота денежной единицы.
Для того чтобы определить денежную массу в обращении необходимо воспользоваться следующей формулой:
М = Р * Q / V
Здесь M — денежная масса, которая находится в обращении;
V — скорость обращения денег;
Р — средние цены на продукцию;
Q — количество выпущенной продукции в постоянных ценах.
Уравнение обмена может быть представлено следующим равенством:
M*V = P*Q
Это уравнение отражает, равенство совокупных расходов в денежном выражении и стоимости всех товаров и услуг, которые выпущены в государстве.
Другие формулы макроэкономики
Рассмотрим еще несколько формул по экономике, среди которых важное место занимает формула вычисления реального дохода:
РД = НД / ИПЦ * 100 %
Здесь РД – реальный доход,
НД – номинальный доход,
ИПЦ – показатель индекса потребительских цен.
Формула для вычисления индекса потребительских цен представлена следующим выражением:
ИПЦ = СТТГ / СТБГ
СТТГ – стоимость потребительской корзины в текущем году,
СТБГ – в базовом году.
В соответствии с показателем индексов цен можно определить темп инфляции по соответствующей формуле:
ТИ =(ИПЦ1 – ИПЦ0) / ИПЦ0 * 100 %
В соответствии с темпами инфляции можно выделить несколько видов:
1. Ползучая инфляция с ростом цен до 5 % годовых,
2. Умеренная инфляция до 10 % годовых,
3. Галопирующая инфляция с ростом цен 20-200% годовых,
4. Гиперинфляция с катастрофическим ростом цен более 200 % в год.
Формулы для расчета процентов
Экономические расчеты часто требуют расчета процентов. Формулы по экономике включают расчет, как сложного, так и простого процента. Формула расчета простого процента представлена следующим образом:
С = Р * (1 + in/360)
Здесь P — сумма долга, включая проценты;
С — общая сумма кредита;
n – количество дней;
i — годовой процент в долях.
Формула для вычисления сложного процента выглядит так:
С = Р (1 + in/360)k
K – количество лет.
Формула для расчёта сложного процента, который вычисляется за несколько лет:
С = Р (1+i)k
Формула безработицы, занятости и ВНП
Формулы по экономике также помогают рассчитать уровень безработицы:
УБ = Число безработных/ЧРС * 100%
Здесь ЧРС – численность рабочей силы.
Формула для вычисления уровня занятости выглядит следующим образом:
УЗ = Число занятых / ЧРС * 100 %
Формула для вычисления валового национального продукта вычисляется так:
ВНП = % + ЗП + Тр + КНал – ЧС + Р + Ам + ДС
Здесь Тр – корпорации,
Кнал – косвенные налоги,
ЧС – чистые субсидии,
Р – рента,
Ам – сумма амортизации,
ДС – доходы от собственности.
Формула расчёта ВНП в соответствии с расходами:
ВНП = ЛПР + ГЗ + ВЧВИ – ЧИ
Расчет выручки, прибыли и издержек
Формулы по экономике при расчете выручки и прибыли:
TR = P*Q
Прибыль = TR — TC
Формула для вычисления средних общих издержек выглядит так:
АС = AFC + AVC или
АС = TC / Q
Для того чтобы рассчитать общие издержки необходимо применить следующую формулу:
ТС = TFC + TVC
Формула для вычисления средних постоянных издержек:
AFC = TFC / Q
При расчете средних переменных издержек можно воспользоваться следующей формулой:
AVC = TVC / Q
Примеры решения задач
ru.solverbook.com
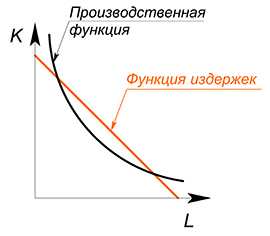
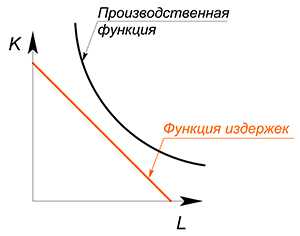
3.6 Производственная функция | Экономика для школьников
Фирма производит свою продукцию, следуя определенной технологии.
Производственная функция показывает налучшую технологическую зависимость между количеством используемых ресурсов и объемом выпуска.
$Q=f(L;K)$
Из производственной функции можно вывести функцию издержек.
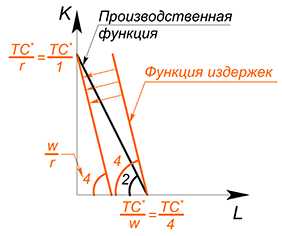
Пример 1
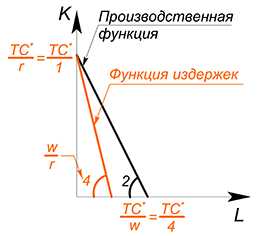
Дано: $Q= L cdot K$, $w=4$, $r=1$, найти функцию общих издержек.
В данном случае можно или минимизировать издержки при выбранном уровне $Q$, или максимизировать объем выпуска при данном уровне издержек.
Воспользуемся методом 2:
$TC=wL+rK$
$TC=4L+K$
Как уже не раз случалось, мы опять встречаем функцию, зависящую от двух переменных. Зафиксируем $TC$, выразим $L$ через $K$:
$K=TC^*-4L$
Что касается производственной функции — зафиксируем $Q$, выразим $L$ через $K$:
$K=dfrac{Q^*}{L}$
Имеем схожую ситуацию с задачей максимизации полезности, только в данном случае у нас цель — максимизировать объем выпускаемой продукции:
Возьмем производную обеих функций по $L$, найдем точку, в которой они равны, найдем точку касания графиков
(Почему именно касания? Если бы мы выбрали более низкий уровень $Q^*$, то мы получили бы более низкую производственную функцию, произвели бы меньше продукции с теми же издержками:
Если мы бы выбрали слишком высокий уровень $Q$, то данный объем производства был бы недостижим при данном уровне издержек:
$-4=-dfrac{Q^*}{L^2}$
Выразим $L$ ($L>0$):
$L=sqrt{dfrac{Q^*}{4}}=dfrac{sqrt {Q^*}}{2}$
Подставим в производственную функцию, выразим $K$:
$K=2sqrt{Q^*}$
Теперь подставим $L$ и $K$ в функцию издержек, $Q$ снова является переменной:
$TC=dfrac{4sqrt{Q}}{2}+2sqrt{Q}=4sqrt{Q}$
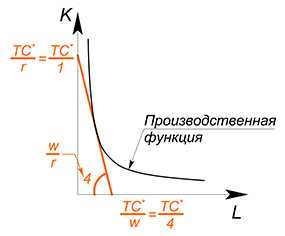
Производственная функция является линейной: $Q=2L+K$, $w=4$, $r=1$, $TC(Q)-?$
Действовать будем в целом аналогично предыдущему варианту, но в этот раз попробуем использовать метод 1: будем минимизировать издержки при выбранном уровне $Q$:
$TC=4L+K$
$K=TC^*-4L$
$K=Q^*-2L$
Имеем 2 линейные функции, будем двигать функцию издержек вниз, пока она не достигнет оптимального положения:
(Если мы выберем более высокий уровень издержек, то вступим нерационально — такой же объем выпуска при больших издержках. Зачем? Если выбрать более низкий уровень издержек, то невозможно будет произвести нужный объем продукции) .
Оптимальное положение будет достигнуто в точке, где количество капитала максимально, а труда равно нулю. Тогда:
$Q=K$
$TC=K$
$TC=Q$
$Q_{новое}(tL;tK)$ vs $tQ(L;K)$
Если $Q_{новое}(tL;tK) > tQ(L;K)$, то эффект масштаба положительный, если $Q_{новое}(tL;tK)=tQ(L;K)$, то постоянный, если $Q_{новое}(tL;tK) < tQ(L;K)$, то эффект масштаба отрицательный.
Пример 3
$Q=4L+K^2$, какой эффект масштаба наблюдается в данной ситуации?
$(tK)^2+4tL$ vs $t(K^2+4L)$
$t^2K^2+4tL$ vs $tK^2+4tL$
$t^2$ vs $t$
$t>1$, следовательно эффект масштаба положительный
TP — total product (он же Q), общий продукт труда — показывает зависимость объема выпуска продукции от количества переменного ресурса при прочих равных условиях.
Функция $TP$:
i участок — функция растет ускоряющимся темпом, при найме каждого последующего работника объем выпуска увеличивается на все большую и большую величину;
ii участок — функция растет замедляющимся темпом, при найме каждого дополнительного работника объем выпуска увеличивается на все меньшую величину;
iii участок — $TP$ убывает. При производстве товара может наступить такой момент, когда дополнительная единица переменного ресурса (труда обычно) уже не способствует увеличению производимой продукции. Дополнительно нанятый работник может только мешать. Например, если у нас имеется всего один станок, и мы наняли 50 рабочих, то они будут только мешать друг другу, стопившись у этого единственного механизма.
$AP_(L)$ average product, средний продукт (труда) — показывает, сколько в среднем единиц продукции приходится на одну единицу переменного ресурса:
$AP_L=dfrac{TP}{L}$ (бывает $AP_K=dfrac{TP}{K}$)
$AP_L(L)=dfrac{TP(L)}{L}$
Геометрический смысл среднего среднего продукта труда такой же как и у других средних величин — тангенс угла наклона луча, проведенного из начала координат (секущей) к точке на графике общего продукта труда.
$MP_(L)$ — marginal product, предельный продукт (труда) — показывает прирост общего продукта при увеличении переменного ресурса на единицу.
В дискретном случае $MP_L=dfrac{TP_2-TP_1}{L_2-L_1}$.
Геометрический смысл предельного продукта в данном случае — тангенс угла наклона секущей, соединяющей точки $(L_1;TP_1)$ и $(L_2;TP_2)$.
Если ресурс бесконечно делим, то $MP_L=TP'(L)$
Геометрический смысл предельного продукта в этой ситуации — тангенс угла наклона касательной, проведенной к графику $TP$ в интересующей нас нас точке.
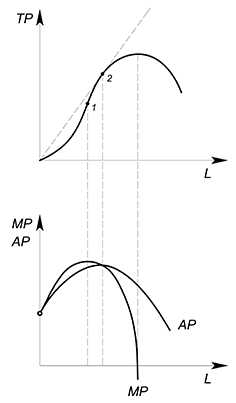
$Q(L)=30L-L^2$, найти $AP_L$, $MP_L$
$AP_L=dfrac{Q(L)}{L}=30-L$
$MP_L=Q'(L)=30-2L$
iloveeconomics.ru
Список обозначений и сокращений
|
Р |
– цена |
|
PL |
– цена |
|
PK |
– цена |
|
PZ |
– цена |
|
Q |
– объём |
|
Д |
– спрос, |
|
S |
– предложение, |
|
I |
– доход |
|
ТР |
– совокупный |
|
АР |
– средний |
|
МР |
– предельный |
|
МU |
– предельная |
|
TU |
– совокупная |
|
МRS |
– предельная |
|
МRTS |
– предельная |
|
TR |
– совокупный |
|
AR |
– средний |
|
МR |
– предельный |
|
ТС |
– совокупные |
|
ТFC |
– совокупные |
|
TVC |
– совокупные |
|
ATC |
– средние |
|
AFC |
– средние |
|
AVC |
– средние |
|
МС |
– предельные |
|
L |
– количество |
|
W |
– ставка |
|
К |
– количество |
|
i |
– ставка |
|
r |
– реальная |
|
π |
– ожидаемый |
|
R |
– доход |
|
П1 |
– прибыль |
|
П |
– совокупная |
|
|
– изменение, |
|
|
– коэффициент |
|
MRP |
– предельная |
|
MRC |
– предельные |
|
PV |
– |
|
NPV |
– чистая |
|
PC |
– частные |
|
EC |
– внешние |
|
SC |
– общественные |
|
MPC |
– предельные |
|
MEC |
– предельные |
|
MSC |
– предельные |
|
PB |
– частные |
|
EB |
– внешние |
|
SB |
– общественные |
|
MPB |
– предельные |
|
MEB |
– предельные |
|
MSB |
– предельные |
|
Е(х) |
– |
|
σ2 |
– дисперсия, |
|
σ |
– стандартное |
|
πi |
– вероятность |
Основные формулы для решения задач
Тема
2
I = px
X + pY
Y
Темы
3 – 6
TR
= р Q
TС
= АТС Q
П = TR
– TC
TC = TFC +
TVC
ATC = AFC +
AVC
МR
= МС
Тема 7
ТVCL
= W L
MRPL
=
MPL
p =
MRCL
=
MRPL
=
MRCL
=1
Тема 8
NPV = – I
+ PV
Пэк
= TR – TCэк
TCэк
= TCвнешние
+
TCвнутренние
Пбух
= TR
– TCвнешние
Пнорм
= TCвнутренние
Пэк
= Пбух
– Пнорм
Тема 9
i = r + π
Тема 10
Тема
11
MPC = ∆PC
/ ∆Q
MEC = ∆EC
/ ∆Q
MSC = ∆SC
/ ∆Q
MSC = MPC +
MEC
MPB = ∆PB
/ ∆Q
MEB = ∆EB
/ ∆Q
MSB = ∆SB
/ ∆Q
MSB = MPB +
MEB
Тема
12
Тема
13
СПИСОК ЛИТЕРАТУРЫ
ПО МИКРОЭКОНОМИКЕ
Основная
-
Микроэкономика
: практический подход / под ред. А. Г.
Грязновой, А. Ю. Юданова. – 4-е изд. –
Москва, 2008. – 704 с. -
Базылев,
Н. И. Микроэкономика / Н. И. Базылев. –
Минск, 2007. – 288 с. -
Зороастрова,
И. В. Микроэкономический анализ : задачи
и ситуации / И. В. Зороастрова, Н. М.
Розанова. – Ростов н/Д, 2007. – 293 с. -
Микроэкономика
/ А. В. Бондарь [и др.] ; под ред. А. В.
Бондаря, В. А. Воробьева. – Минск, 2009. –
415 с. -
Экономическая
теория . В 2-х ч. Ч. 1 / под ред. И. В. Новиковой,
Ю. М. Ясинского. – Минск, 2009. – 261 с. -
Авраменко,
А. И. Экономическая теория : практикум
/ А. И. Авраменко, Ю. Р. Тихонов, А. Я.
Коховец ; под ред. А. И. Авраменко. –
Минск, 2008. – 480 с. -
Ивашковский,
С. Н. Микроэкономика : учебник / С. Н.
Ивашковский. – Москва, 2001. – 415 с.
Дополнительная
-
Микроэкономика
: учебное пособие / под ред. М. И.
Плотницкого. – Минск, 2002. – 426 с. -
Тарануха,
Ю. В. Микроэкономика / Ю. В. Тарануха, Д.
Н. Земляков ; под общ. ред. А. В. Сидоровича.
– Москва, 2002. – 304 с. -
Гребенников,
П. И. Микроэкономика : учебник / П. И.
Гребенников, А. И. Чеусский, Л. С. Тарасевич.
– Москва, 2008. – 374 с. -
Плотницкий,
М. И. Микро- и макроэкономика : учебное
пособие / под ред. М. И. Плотницкого. –
Минск, 2004. – 185 с. -
Головачев,
А. С. Экономическая теория. Общие основы
: курс лекций / А. С. Головачев, И. В.
Головачева, Э. А. Лутохина. – 4-е изд. –
Минск, 2005. – 240 с. -
Современная
политическая экономия : учебное пособие
/ Т. И. Адамович, С. А. Бородич, П. С.
Лемещенко ; под общ. ред. П. С. Лемещенко.
– Минск, 2005. -
Мэнкью,
Н. Г. Принципы экономикс / Н. Г. Мэнкью.
– 2-е изд. – СПб, 2003. – 496 с. -
Пиндайк,
Р. Микроэкономика / Р. Пиндайк, Д.
Рубинфелльд. – СПб, 2002. – 606 с. -
Макконелл,
К. Экономикс : принципы, проблемы и
политика : учебник / К. Макконелл, С. Брю.
– 14-е изд. – Москва, 2003. – 970 с.
ВОПРОСЫ
К ЭКЗАМЕНУ ПО МИКРОЭКОНОМИКЕ
1.
Предмет микроэкономики и границы
микроэкономической теории.
2.
Методы микроэкономического анализа.
Предельный и функциональный анализ.
3.
Проблема оценки общей полезности в
кардинализме и ординализме.
4.
Аксиомы ординализма. Кривые безразличия.
5.
Бюджетные ограничения покупателя.
Равновесие
потребителя.
6.
Кривые «доход-потребление» и
«цена-потребление».
7.
Типы конкуренции и основные рыночные
структуры.
8.
Совершенная конкуренция, её основные
признаки.
9.
Равновесие конкурентной фирмы в
краткосрочном периоде.
10.
Равновесие конкурентного производителя
в долгосрочном периоде.
11.
Совершенная конкуренция и эффективность.
12.
Основные черты чистой монополии. Виды
монополии.
13.
Определение цены и объема производства
в условиях чистой монополии.
14.
Экономические последствия монополии.
Регулируемая монополия.
15.
Чистая монополия и эффективность.
16.
Основные черты монополистической
конкуренции.
17.
Равновесие фирмы в кратко- и долгосрочном
периодах при моно-полистической
конкуренции.
18.
Монополистическая конкуренция и
эффективность.
19.
Основные признаки олигополии.
20.
Типология моделей олигополии.
21.
Модель с ломаной кривой спроса.
22.
Олигополия и эффективность.
23.
Показатели монопольной власти.
Антимонопольное законодательство.
24.
Спрос на ресурсы: общий подход. Предельная
доходность ресурса. Предельные издержки
ресурса.
25.
Модель конкурентного рынка труда.
26.
Рынок труда в условиях несовершенной
конкуренции.
27.
Номинальная и реальная заработная
платы. Формы и системы заработной платы.
28.
Особенности функционирования рынка
труда в РБ.
29.
Рынок капитала и его структура. Рынок
капитальных благ.
30.
Рынок ссудного капитала и ссудный
процент. Номинальная и реальная ставка
процента.
31.
Дисконтирование будущих доходов.
Критерий чистой дисконтированной
стоимости.
32.
Рынок ценных бумаг. Цены и доходы на
рынке ценных бумаг.
33.
Предпринимательская способность и
экономическая прибыль. Функции и
источники экономической прибыли.
34.
Земля как фактор производства.
Ограниченность земли.
35.
Земельная рента и определение её размера.
Рента и арендная плата. Цена земли.
36.
Дифференциальная рента по плодородию
и местоположению.
37.
Формирование рынка земли в РБ.
38.
Частичное и общее равновесие. Взаимосвязи
на рынках продуктов и ресурсов.
39.
Общее экономическое равновесие и
общественное благосостояние.
40.
Фиаско рынка и необходимость
микроэкономического регулирования.
41.
Общественные и частные, положительные
и отрицательные внешние эффекты.
42.
Интернализация внешних эффектов. Теорема
Коуза.
43.
Регулирование внешних эффектов.
Использование теории внешних эффектов
в экономической практике.
44.
Выбор в условиях неопределенности.
Понятие асимметричной информации.
45.
Рынки с асимметричной информацией. Виды
рыночных сигналов.
46.
Моральный риск. Проблема «принципал-агент».
Гарантии и поручительства.
47.
Чистые частные и чистые общественные
блага. Свойства общественных благ.
48.
Особенности спроса на общественные
блага.
49.
Роль государства в обеспечении предложения
общественных благ.
50.
Методология анализа общественного
выбора. Политика как обмен.
51.
Политико-экономический цикл.
52.
Проблема эффективности государственного
вмешательства в экономику.
53.
Эффективность обмена. Кривая потребительских
возможностей.
54.
Эффективность производства. Кривая
производственных возможностей.
132
studfiles.net
Формулы
Основные
обозначения и формулы по экономике
Основные
обозначения и формулы по экономике:
I. Обозначения
-
P
— цена -
Q
— количество -
D
– спрос -
S
— предложение -
QD – величина
спроса -
QS –
величина предложения -
Qдеф –
дефицит (объем дефицита) -
Qпродаж –
объём продаж -
QИЗБ –
объём избытка (излишки) -
EDP–
коэффициент эластичности спроса по
цене -
ESP–
коэффициент эластичности предложения
по цене -
I
– доход -
EDI—
коэффициент эластичности спроса по
доходу -
EDC—
коэффициент перекрестной эластичности
спроса -
TR
– совокупный доход (выручка продавца) -
TC
– общие затраты -
Pr –
прибыль -
PD –
цена спроса -
PS–
цена предложения -
PE–
равновесная цена
II.
Формулы:
-
y= k*x+b –
уравнение описывающее функцию спроса -
QD= k*P+b –
функция спроса -
EDP=
Δ QD (%)/ΔP
(%) –
коэффициент эластичности спроса по
цене -
EDP=
(Q2 –Q1):
(Q2 + Q1)/
(P2 –P1):
(P2 + P1) –
формула средней точки, где P1 –
цена товара до изменения, P2 –
цена товара после изменения, Q1 –
величина спроса до изменения цены,
Q2 –
величина спроса после изменения цены; -
EDI=
(Q2 –Q1):
(Q2 + Q1)/
(I2 –I1):
(I2 + I1) –
формула коэффициента эластичности
спроса, где I1 –
величина дохода до изменения, I2 –
величина дохода после изменения,
Q1 –
величина спроса до изменения дохода,
Q2 –
величина спроса после изменения дохода; -
EDС =
(Q2 –Q1):
(Q2 + Q1)/
(P2 –P1):
(P2 + P1) –
формула средней точки, где P1 –
цена второго товара до изменения, P2 –
цена второго товара после изменения,
Q1 –
величина спроса первого товара до
изменения цены, Q2 –
величина спроса первого товара после
изменения цены; -
TR
= P*Q –
формула расчета выручки продавца -
Pr= TR
– TС –
формула расчета прибыли; -
QD= k*P+b –
функция предложения; -
ESP=
(QS2 –QS1):
(QS2 + QS1)/
(P2 –P1):
(P2 + P1) –
формула коэффициента предложения,
где P1 –
цена товара до изменения, P2 –
цена товара после изменения, QS1 –
величина предложения до изменения
цены, QS2 –
величина предложения после изменения
цены; -
Qдеф = QD— QS–
формула для определения объема дефицита; -
Qдеф = QS — QD–
формула для определения объема излишек;
studfiles.net
Что такое P&L и зачем он нужен собственнику бизнеса?
P&L (он же — отчет о прибыли и убытках, он же profit & loss report) входит в тройку самых главных финансовых отчетов для бизнеса. Вместе с ним в связке обычно идут отчет о движении денежных средств (cash flow) и баланс (balance sheet).
P&L составляется обычно по каждому месяцу и дает вам оперативную информацию о ваших доходах и расходах, а также показывает маржинальность бизнеса (в цифрах и процентах). Этот отчет вы будете постоянно видеть в отдельной закладке на рабочей панели вашего FourSoft Monitor.
Если говорить чуть подробнее, то P&L — это отчет, который отражает доходы и расходы компании по методу начисления, то есть «по актам». Это означает, что цифры в отчете появляются на основе факта отгрузки товара или подписания акта оказания услуг (а не на основе факта прихода денег от клиента).
Важно отметить, что этот отчет отражает только операции текущего бизнеса, которые ведут к получению либо прибыли, либо убытка. Например, если вы берете кредит, то тело кредита в таком отчете отражаться не будет, а проценты (как затрата) — будут. Также в этом отчете вы можете увидеть амортизацию (как основных материальных активов, среди них и обычные офисные компьютеры, так и нематериальных активов, если у компании есть торговые марки, лицензии, патенты, которые бухгалтер постепенно амортизирует).
Строго говоря, P&L не предназначен для анализа сумм налогов, которые необходимо уплатить, хотя собственник, понятное дело, хотел бы понимать, какие суммы необходимо зарезервировать для налоговой. Налоги будут появляться в P&L так часто, как бухгалтер будет их начислять. Бухгалтера небольших бизнесов начисляют налог зачастую тогда же, когда и платят. То есть, раз в квартал (если вы платите единый налог, то и начислите его один раз в квартал) или раз в год (если вы платите налог на прибыль предприятия). Тем не менее, по классике учета налоги можно начислять ежемесячно, а уплачивать согласно требований законодательства. Вопрос их регулярного начисления (чтобы вы регулярно, т.е. ежемесячно видели их в отчете на своей панели FourSoft Monitor) — это предмет уже предмет дискуссии между собственником и бухгалтером компании.
Нужен ли P&L малому бизнесу?
Такой отчет обязательно нужен и малому, и среднему, и даже крупному бизнесу. Каждый малый бизнес, который собирается расти, должен задуматься о том, чтобы своевременно анализировать свои финансовые результаты и принимать решения, которые предположительно приведут к росту компании.
Если вы — собственник малого бизнеса, который задумывается о правильном финансовом и управленческом учете, у вас наверняка уже были попытки вменить в обязанность бухгалтеру составлять таблицу P&L в екселе. И вы также уже знаете, что подготовка такого отчета занимает немало бухгалтерского времени. Кроме того, бухгалтер склонен очень ревностно охранять не до конца готовый P&L от посторонних глаз, даже от собственника, мотивируя это тем, что, мол, еще не все колонки заполнены.
Затягивание подготовки такого отчета бухгалтером и непонимание, прибылен твой бизнес или убыточен в этом конкретном месяце, может привести к принятию неверных управленческих решений. К примеру, к совершению затрат, без которых можно было бы обойтись, если бы собственнику вовремя показали реальное состояние финансов компании.
Черпая данные из вашей 1c, FourSoft Monitor автоматизирует P&L и позволяет освободить время бухгалтера для других задач. И кроме того, FourSoft Monitor обновляет данные каждый час, соответственно, вы будете видеть все колонки отчета, даже если он еще не полностью заполнен.
При этом FourSoft Monitor выполняет еще и контролирующую функцию — как только бухгалтер проводит тот или иной акт в системе, данные в P&L меняются (опять таки, обновления происходят 1 раз в час). Собственник сразу сможет оценить, насколько оперативно бухгалтерия работает с первичными документами (счетами и актами) и их проводками.
Что требовать от бухгалтера?
Но от бухгалтера можно и нужно требовать больше, нежели только своевременное проведение актов. Важно, чтобы статьи доходов и расходов в 1с, в которой работает ваш бухгалтер, были названы правильно, а не просто «доход операционной деятельности от реализации товаров и услуг (№ счета)» или, касательно затрат «прямые производственные затраты» и др. На основе таких названий, особенно если они повторяются в виде большого количества строк и отличаются только номером счета, собственник не сможет сделать никаких полезных выводов.
Попросите бухгалтера переназвать и детализировать в 1с статьи доходов и расходов, тогда автоматически в закладке P&L вашей программы FourSoft Monitor вы увидите не просто номера счетов, а названия видов работ, услуг или товаров, и рядом с ними в колонках количество денег, которое они принесли вам в том или ином месяце. Таким же образом детализируются и затраты.
Консолидированная финансовая отчетность и операции между собственными юрлицами
Что делать, если у вас несколько юридических лиц для обслуживания одного бизнеса? И хочется видеть консолидированный финансовый результат (доход и расход) в целом по ним всем? Если в базу 1с у вас заведено несколько юридических лиц, с которых клиентам выставляются счета и по которым идут затраты, ваш P&L будет консолидированным, то есть покажет общие доходы и общие затраты по всем вашим юрлицам. Налоги, если бухгалтер будет их начислять, также будут отражаться по каждому юрлицу, и вы будете видеть строчку общей (консолидированной) суммы налогов, которые нужно будет уплатить.
Обратите внимание, что операции между собственными юрлицами нужно исключить из отчета P&L, чтобы они не портили статистику, «задваивая» результат. Эту функцию также можно настроить при создании отчета P&L в FourSoft Monitor, а также настроить ее и у себя в 1с. Но об этом мы поговорим подробнее в следующих материалах.
4softbi.com
Задача № 86. Расчёт общего, среднего и предельного продукта
Заполнить пропуски в следующей таблице:
| Количество используемого труда | Общий продукт TP | Средний продукт AP | Предельный продукт MP |
|---|---|---|---|
| 3 | … | 20 | — |
| 4 | 80 | … | … |
| 5 | … | … | 10 |
| 6 | 95 | … | … |
Решение:
Общий продукт (TP, total product) — это объём продукции, произведённый фирмой за определённый период времени.
Средний продукт ресурса (AP, average product) — это выпуск продукции в расчёте на единицу переменного ресурса (при фиксированном количестве постоянного ресурса).
В данной задаче переменным ресурсом является труд L.
Средний продукт труда вычисляется по формуле:
Отсюда:
TP = APL * L
1 строка таблицы:
TP(3) = 20 * 3 = 60.
2 строка таблицы:
AP(4) = 80 / 4 = 20
Предельным продуктом (MP, marginal product) переменного ресурса называют прирост общего продукта в связи с увеличением применения данного переменного ресурса на единицу.
Предельный продукт труда определяется по формуле:
Так как ΔL в данной задаче равно единице, можно упростить эту формулу:
МРL = ΔТР
MP(4) = TP(4) — TP(3) = 80 — 60 = 20
3 строка таблицы:
ТР(5) = ТР(4) + МР(5) = 80 + 10 = 90
АР(5) = ТР(5) / 5 = 90 / 5 = 18
4 строка таблицы:
АР(6) = ТР(6) / 6 = 95 / 6 = 15,83
MP(6) = TP(6) — TP(5) = 95 — 90 = 5
| Количество используемого труда | Общий продукт TP | Средний продукт AP | Предельный продукт MP |
|---|---|---|---|
| 3 | 60 | 20 | — |
| 4 | 80 | 20 | 20 |
| 5 | 90 | 18 | 10 |
| 6 | 95 | 15,83 | 5 |
ecson.ru
No related posts.
Количественная теория денег и уравнение обмена
Управление уровнем цен и объемом денежной массы в обороте – один из главных способов влияния на экономическую систему рыночного типа. Взаимосвязь уровня ценообразования и количества денежной массы была выведена представителями монетаристской теории. Приверженцы рыночной экономики, предполагающей рынок, свободный от чьего-либо влияния, считают необходимым регулировать (не полностью) хозяйственные процессы. Практически во всем мире этим занимается государство, реже – специально сформированные органы. Прошедший XX век выявил глубокие взаимосвязи между массой денег в мировом обороте и основными экономическими показателями. Главным образом это процентная ставка Центробанка и уровень цен.
Зависимость Фишера
Как известно, ценовой уровень и денежная масса находятся в прямой зависимости друг от друга. Если вдруг, повинуясь различным влияниям, изменяется объем, находящейся в обороте денежной массы, то, как следствие, происходит колебание цен. С другой стороны, изменение ценовых показателей влечет за собой скачок денежного объема.

Знаменитый представитель количественной теории денег Ирвинг Фишер предложил некую формулу, которая, с его точки зрения, показывает зависимость денежного объема от уровня цен. Это уравнение обмена. Выглядит оно так:
m – масса наличных денег в обращении;
V – скорость оборота денежной наличности;
P – цена товаров;
Q – их количество.
Экономисты утверждают, что это равенство может применяться чисто теоретически, в практических целях оно не пригодно.
Использование формулы Фишера
Уравнение может иметь несколько интерпретаций. Одна из них, возможно, наиболее важная: При увеличении денежной массы (левая сторона уравнения) возможным результатом может стать как рост объема производства и товаров на рынке, так и рост уровня цен (правая сторона уравнения).
В реальной жизни могут происходить оба явления, но в разных пропорциях. И эти пропорции довольно качественно характеризуют свойства экономики. В развитых странах, где ВВП в основном складывается из промышленных и высоко технологичных продуктов и услуг, рынок спокойно «съедает» очередную порцию денег, напечатанную государством, без значительного роста цен. «Лишние» деньги, которые не может осовоить экономика напрямую, уходят в другие виды долгосрочных активов: акции, облигации, взаимные фонды, пенсионные накопления и т.п.
В других странах, зависящих от природных ресурсов с низкой зависимостью ВВП от реального сектора, наблюдается обратное явление. Сколько денег в экономику не вкачивай, на производство это не оказывает ни малейшего влияния.
Условия работа равенства
Формула уравнения обмена не предлагает исключительно верного решения. Она дает множество вариантов развития событий при некоторых условиях. Несомненно только одно: ценовой уровень находится в зависимости от объема денег, пребывающих в обращении. Верными считаются два условия:
- скорость оборота денежного потока – величина неизменная,
- производственно-хозяйственные мощности задействованы полностью.
Смысл принятия этих условий состоит в устранении возможного их воздействия на правую или левую стороны равенства. Но даже если учесть полное соблюдение условий, то все равно нельзя быть уверенным в том, что первичны изменения объема денежной массы, а цен – только вторичны. Зависимость здесь исключительно взаимная.
Объем денег в обороте является своеобразным регулятором ценового уровня, но только при условии устойчивого развития экономики. В случае стагнации или замедления роста экономического развития будет возможным сначала ценовое изменение, и только затем, как следствие, скачок денежной массы. Уравнение реакции обмена работает только с денежным объемом, участвующим в обращении. Так как деньги имеют еще несколько функций, то расчёт общей потребности денежной массы влечет за собой немаловажную коррекцию равенства Фишера.
Объем денежной массы в обращении
Денежный объем, находящийся в движении, и сумма цен на товары имеют следующее соотношение:
m – объем денежной массы, находящейся в движении;
V – скорость, с которой проходит оборот одна валютная единица;
T – объем совершившихся товарных операций;
P – общий уровень цен.
Появлению этого равенства способствовало уравнение обмена. Главный вывод, который был сделан представителями школы количественной теории денег, заключался в том, что в отдельной стране или союзе стран с единой валютой должен находиться в обороте определенный объем денежной массы, который напрямую зависит от количества произведенных товаров и услуг, а также полученных доходов. Это идеальная ситуация. В ней цены всегда стабильны. В случае смещения в сторону увеличения или уменьшения объема денежной массы с ценами происходит следующее:
mV PT – наступает инфляция (цены повышаются);
mV = PT – период стабильности.
Следовательно, устойчивое положение цен – наиглавнейшее условие, которое определяет оптимальный объем денежной массы в движении.
Количественная теория денег и уравнение обмена
Первое, что может ввести в заблуждение студента-экономиста при его попытках понять теорию денег, — это уравнение обмена. Это уравнение основывается на механистическом понимании количественной теории денег. Оно должно показать связь между предложением денег и ценами на товары. Это одна из фундаментальных ошибок современной экономики
Количественная теория денег сама по себе была важной вехой в развитии экономической теории. Ее корни уходят к итальянцу Бернардо Даванзати и поляку Копернику. Более известной версией количественной теории являются классические разработки Дэвида Юма и Дэвида Рикардо. Эти теоретики пытались объяснить связь между ценами и количеством денег на основе законов спроса и предложения. Их главный вывод — и центральная истина, установленная количественной теорией, — заключался в том, что увеличение количества денег обязательно ведет к росту цен. Следствием этого вывода является то, что увеличением количества денег нельзя ничего добиться; любое количество является достаточным для выполнения социальной функции денег.
Прогресс в теории денег состоял бы в исследовании того, как определяются спрос и предложение на деньги, что и сделал Мизес в своей “Теории денег и кредита” 1912 года. К сожалению, несмотря на новаторскую работу Мизеса широкую популярность получила другая и совершенно неполноценная разработка: механистическая версия количественной теории денег, обобщенная в так называемом уравнении обмена.
Анатомия уравнения обмена
Впервые уравнение обмена появилось в книге Ирвинга Фишера “Покупательная способность денег” 1911 года, и затем монетаристы широко распространили ее использование. Милтон Фридман, возможно, самый известный монетарист двадцатого века, даже напечатал его на своих номерных знаках. Существуют различные варианты уравнения (M • V = P • T, M • V = P • Y, M • V = P • Q, если взять простейший), но ни один из них существенно не отличается от исходной формулы Фишера: М • V = Р • Т. Каковы компоненты этой формулы?
М означает количество денег, или, вернее, среднее количество в данный период.
V — это скорость обращения денег, и, как мы увидим, это не вполне определенное понятие. Монетаристы обычно представляют это как “оборот” денег или показатель того, сколько “использований” приходится на каждую денежную единицу.
P — уровень цен, среднее значение всех цен, уплаченных за данный период.
Т — сумма транзакций за тот же период.
Утверждается, что это уравнение показывает связь между денежной и реальной сторонами экономики. Его сторонники утверждают, что уравнение ясно показывает связь между количеством денег и уровнем цен: если мы предположим, что V и T постоянны, то увеличение M обязательно приводит к увеличению P. Теперь у нас есть четкое доказательство количественной теории денег. Или нет?
Критика уравнения обмена
И Мизес, и Ротбард жестко критиковали уравнение обмена, и в дальнейшем мы будем опираться на их работы. С самого начала стоит отметить, что холистический подход, лежащий в основе монетаристской теории, совершенно недопустим. Как сказал Мизес в “Теории денег и кредита”:
Долгое время считалось, что спрос на деньги является величиной, определяемой объективными факторами и независим от субъективных соображений. Считалось, что спрос на деньги в экономическом сообществе определяется, с одной стороны, общим количеством товаров, которые должны были быть оплачены в течение определенного периода, а с другой — скоростью обращения денег … Недопустимо начинать с спроса на деньги сообщества в целом. Индивидуалистическое экономическое сообщество — единственное сообщество, в котором существует спрос на деньги, не является экономическим агентом. Оно предъявляет спрос на деньги только в том случае, если его отдельные члены предъявляют спрос на деньги. Спрос на деньги со стороны экономического сообщества есть не что иное, как сумма спроса на деньги отдельных экономических агентов, составляющих его. Но для отдельных экономических агентов невозможно использовать формулу: общий объем операций ÷ скорость обращения. Если мы хотим составить описание потребности человека в деньгах, мы должны начать с соображений о том, как он получает и тратит деньги.
Хотя этой основной ошибки должно быть более чем достаточно для того, чтобы дисквалифицировать уравнение, все же стоит и необходимо его детально изучить. Работает ли оно в своих собственных терминах? Давайте рассмотрим его компоненты.
М, количество денег, здесь нет проблем. Вопрос о том, какие требования и денежные заменители должны учитываться как часть денежной массы в экономике, открыт для обсуждения, но количество денег является четко определенной концепцией.
P и T более подозрительны. Каково истинное значение этих терминов? На самом деле они представляют собой ни что иное, как статистическое выражение всех сделок в экономике за определенный период. P. — это среднее значение уплаченных цен, а T — количество транзакций. Однако это означает, что P • T — это просто то, что продавцы получали в обмен на свои товары и услуги — их совокупные доходы или денежные доходы, которые традиционно обозначаются символом Y.
Это подводит нас к V. Как именно мы устанавливаем V? В отличие от других терминов уравнения, просто не существует способа независимого определения V. Это просто фактор, необходимый для того, чтобы уравнение M = P • T было верным.
Существует два способа найти V Один из них — просто разделить P • T на M. Другой — и тот, который использовал Фишер, — начать с суммы расходов за определенный период E и количества денег, M. Затем мы просто определяем V как отношение между этими двумя величинами: E / M = V. К сожалению, это все еще не решает проблему того, что Vне определяется независимо. Мы просто вводим другую переменную, E, в наше уравнение.
Более фундаментально, небольшой анализ показывает, что уравнение действительно абсурдно, если мы ожидаем от него, что оно должно сказать нам что-то о роли количества денег в экономике:
тогда M • V = M • E / M,
а затем M • E / M = E.
А поскольку мы уже знаем, что P • T = Y, уравнение M • V = P • T сводится к E = Y.
Таким образом, потрясающее откровение, заключенное в монетаристском уравнении обмена состоит в том, что сумма денежных расходов в данном периоде должна равняться сумме денежных доходов за тот же период. Безусловно, верно, что в любой сделке расходы покупателя обязательно равны доходам продавца, но возникает вопрос, почему это должно быть возведено в основу монетарной теории.
Как насчет инфляции? Защитники Фишера и его бесчисленные монетаристские эпигоны могут утверждать, что, по крайней мере, уравнение можно использовать, чтобы показать связь между количеством денег и уровнем цен. В известном изречении Фридман говорит, что “инфляция всегда и везде является монетарным явлением”. Однако это лишь повторяет то, что примитивная количественная теория уже установила без сложных атрибутов уравнения обмена. Фактически, уравнение отображает соотношение между количеством денег и инфляцией в упрощенной и вводящей в заблуждение форме, причем изменения уровня цен просто являются функцией изменений количества денег. И это явно ошибочно.
Альтернатива: денежная теория Мизеса
По сути, уравнение обмена опирается на ошибочный подход к экономической теории. Оно просто постулирует существование агрегированных концептов, таких как скорость и уровень цен, и то, что мы можем понять их, не глядя на то, что вызывает их к жизни и что заставляет их меняться. Любое рассмотрение причинности приносится в жертву в пользу впечатляющих формул.
Мизес и другие австрийцы давно показали, как следует думать о денежной теории, основанной на фундаментальном понимании роли человеческой деятельности и субъективных оценок в экономике. Вместо того, чтобы давать полное описание идей Мизеса, давайте кратко проиллюстрируем, как он представляет увеличение количества денег и как это в конечном итоге влияет на цены.
Прежде всего, до увеличения количества денег, у каждого человека есть определенный запас наличности, определяемый предельной полезностью денег для него. У каждого человека имеется денежный запас, большой настолько, чтобы полезность предельной денежной единицы перевешивала — оценивалась выше на его шкале ценностей, чем полезность, которую он ожидает получить от обмена ее на товары.
Что происходит, когда количество денег увеличивается? Это увеличение всегда означает, что некоторые люди получат больше денег, чем раньше. Предположим, что близкие личные друзья Дж. Пауэлла, экстраординарного производителя денег, мистер Голдман и миссис Сакс, внезапно обнаруживают, что их наличные средства увеличились. Теперь их оценка предельной денежной единицы изменилась, она стала меньше на их шкале ценности. Ценность предельной денежной единицы теперь ниже для миссис Сакс, и поэтому она будет использовать часть новых денег на товары и услуги, которые по ее шкале ценностей теперь оцениваются выше.
Таким образом, новые деньги начинают двигаться по экономике: первые получатели, г-н Голдман и миссис Сакс, тратят новые деньги до тех пор, пока их наличные средства снова не отражают их субъективную оценку предельной единицы. Между тем, дополнительный спрос на товары и услуги приводит к росту цен. Следующие получатели новых денег (те, кто снабжал мистера Голдмана и миссис Сакс товарами и услугами) теперь находятся в той же ситуации, что и первые получатели. Они тоже потратят свои дополнительные деньги, что приведет к росту цен на товары, на которые они их тратят. И так процесс продолжается, пока новые деньги не будут распределены по экономике. Некоторые цены растут, в то время как другие остаются прежними. Некоторые извлекли выгоду из этого процесса, а именно: те, кто получил новые деньги первыми, прежде чем цены были скорректированы; другие потеряли, а именно те, кто испытал увеличение своих денежных доходов только после роста цен, или кто вообще никогда не видел новых денег.
Вывод
Надеемся, что эта краткая критика уравнения обмена и контраст с мизесовской монетарной теорией сделают очевидным, что уравнение обмена является бессвязной и механистической версией количественной теории денег. К сожалению, плохие теории имеют долгую жизнь в социальных науках, и это, безусловно, относится к уравнению обмена. Тем не менее, если кто-то хочет понять денежные явления, отправной точкой должен стать полный отказ от механистической количественной теории.
Халява на elliottwave com. Европа: риск или возможность (бесплатный доступ)
Теперь настольную книгу волновиков «Волновой принцип Эллиотта» можно найти в бесплатном доступе здесь
И не забывайте подписываться на мой телеграм-канал и YouTube-канал
Бесплатное руководство «Как найти возможности для торговли с высокой вероятностью с помощью скользящих средних»
Если находите статью интересной, ставьте плюсики и добавляйте в избранное.
Уравнение обмена и показатель скорости обращения объема денег
Частота, с которой конкретная денежная наличная единица в общем движении денег участвует в реализации произведенных товаров (услуг) за отдельно взятый период, называется скоростью обращения денежной массы.
Приняв за базу уравнение обмена, скорость обращения денег (V) можно представить так:
Р – усредненный уровень цен на произведенные товары, услуги,
Q – физическая величина товаров (услуг), реализованных в отдельно взятом периоде, или национальный продукт, взятый в номинальном объеме,
М – средний объем денежной массы, который находится в обороте в отдельно взятом времени, или статистический объем денег.
Дальнейшая судьба уравнения
В более поздние годы существования формулы она не раз видоизменялась. В конечном итоге уравнение Фишера выглядело так: M=kPY, где k – обратная скорости обращения денежной единицы величина (k=1/V).
При всём этом средняя скорость оборота денежных средств – величина постоянная. На практике формула Фишера действительно несколько упрощает взаимосвязи, однако она не пригодна под условия высокой инфляции, изменения скорости денежного оборота.
Смотрите также: Акции Газпрома Акции Сбербанка Стоимость нефти сегодня
Интенсивность денежного потока
Выведенная величина возвратного движения денежной массы общепринята и считается признанным показателем государственной бизнес-активности. В связи с этим она находится в некоторой зависимости от:
- степени сформированности экономических механизмов страны (работы ценных бумаг, отлаженной работы банковского сектора, торговли и пр.);
- частоты операций с товарами (услугами) между участниками хозяйственных отношений и их объема;
- инфляционных процессов;
- развития экономических связей между субъектами хозяйствования;
- маркетинговых стратегий;
- баланса и стабильности предложения и спроса на рынке.
Отсюда следует, что выведенная через уравнение обмена величина V, дает возможность проследить, сколько раз в определённый период конкретная денежная единица участвует при покупке товара (услуги). То есть наглядно показана интенсивность движения денежной массы.
Конспект на тему «Формулы по экономике»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Основные обозначения и формулы по экономике:
Q D – величина спроса
Q S – величина предложения
Q деф – дефицит (объем дефицита)
Q продаж – объём продаж
Q ИЗБ – объём избытка (излишки)
E DP – коэффициент эластичности спроса по цене
E SP – коэффициент эластичности предложения по цене
E DI — коэффициент эластичности спроса по доходу
E DC — коэффициент перекрестной эластичности спроса
TR – совокупный доход (выручка продавца)
TC – общие затраты
P D – цена спроса
P S – цена предложения
P E – равновесная цена
y= k*x+b – уравнение описывающее функцию спроса
E DP = Δ Q D (%)/ΔP (%) – коэффициент эластичности спроса по цене
E DI = (Q 2 –Q 1 ): (Q 2 + Q 1 )/ (I 2 –I 1 ): (I 2 + I 1 ) – формула коэффициента эластичности спроса, где I 1 – величина дохода до изменения, I 2 – величина дохода после изменения, Q 1 – величина спроса до изменения дохода, Q 2 – величина спроса после изменения дохода;
E DС = (Q 2 –Q 1 ): (Q 2 + Q 1 )/ (P 2 –P 1 ): (P 2 + P 1 ) – формула средней точки, где P 1 – цена второго товара до изменения, P 2 – цена второго товара после изменения, Q 1 – величина спроса первого товара до изменения цены, Q 2 – величина спроса первого товара после изменения цены;
TR = P*Q – формула расчета выручки продавца
P r = TR – TС – формула расчета прибыли;
E SP = (Q S2 –Q S1 ): (Q S2 + Q S1 )/ (P 2 –P 1 ): (P 2 + P 1 ) – формула коэффициента предложения, где P 1 – цена товара до изменения, P 2 – цена товара после изменения, Q S1 – величина предложения до изменения цены, Q S2 – величина предложения после изменения цены;
Формула расчёта необходимого для обращения количества денег:
1)

КД — масса денег;
Ецт — сумма цен товаров;
К — товары, проданные в кредит;
СП — срочные платежи;
ВП — взаимопогашаемые платежи (бартерные сделки);
СО — скорость оборота денежной единицы (в год).
2)

M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Уравнение обмена:

M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Это уравнение показывает, что совокупные расходы в денежном выражении
равны стоимости всех товаров и услуг, произведенных экономикой.
Формула для нахождения реального дохода:

ИПЦ — индекс потребительских цен.
Формула для нахождения покупательной способности денег:

Iпcд — покупательная способность денег;
Iц — индекс цен.
Формула для расчёта стоимости потребительской корзины:

P 1 — цена первого товара;
Р 2 — цена второго товара;
Р n — цена n-го товара;
Q 1 — количество первого товара;
Q 2 — количество второго товара;
Q n — количество n-го товара.
Формула для расчёта темпа инфляции:

В зависимости от темпа инфляции различают несколько ее видов:
1.Мягкая (ползучая), когда цены растут в пределах 1—3% в год.
2.Умеренная — при росте цен до 10% в год.
3.Галопирующая — при росте цен от 20 до 200% в год.
4.Гиперинфляция, когда цены растут катастрофически — более чем 200% в год.
Формула для расчёта простого процента:

P — сумма долга с процентами;
S — сумма кредита;
n — число дней;
i — годовой процент в долях.
Формула для расчёта сложного процента:

P — сумма долга с процентами;
S — сумма кредита;
n — число дней;
i — годовой процент в долях;
N — сколько раз начисляется в году.
Формула для расчёта сложного процента начисляемого за несколько лет:

P — сумма долга с процентами;
S — сумма кредита;
t — число лет;
i — годовой процент в долях.
Формула для расчёта смешанного процента за дробное колличество лет:

P — сумма долга с процентами;
S — сумма кредита;
t — число лет;
i — годовой процент в долях;
n — число дней.
Формула для расчёта банковских резервов:

S — норма обязательных резервов в процентах;
R — общая сумма резервов;
Д — величина депозитов на счету КБ.
Формула расчёта дуговой эластичности по доходу:
Коэффициент Джини
Самое краткое определение коэффициента Джини –коэффициент концентрации богатства . Чем он выше – тем выше и неравенство. Более полное определение – мера неравенства распределения доходов. Еще более полное определение – коэффициент девиации экономики от абсолютного равенства в распределении доходов.
Коэффициент выводится из кривой Лоренца и представляет собой отношение площади между этой кривой и линией абсолютного равенства к общей площади под линией абсолютного равенства. Линия абсолютного равенства – биссектриса между осями «доля домохозяйств» и «доля доходов». Коэффициент может быть рассчитан и по точной формуле.
Максимальное значение коэффициента равно единице и это – абсолютное неравенство . Минимальное равно нулю и это абсолютное равенство
В силу социально-политической значимости получаемых на основе коэффициента оценок, он активно рассчитывается, дискутируется и используется для разного уровня выводов. Одна из наиболее активных сфер использования – сравнительный межстрановой и временной анализ. Например, коэффициент Джини для России в 1991 году был равен 0,24, в 2008 году 0,42. В так называемых «образцовых» европейских и особенно североевропейских странах он находится в диапазоне от 0,2 до 0,3.
Но вряд ли уместны прямые заключения из сравнения коэффициента по странам и по времени. У него есть ограничения, переходящие в недостатки , что объясняется двумя обстоятельствами. Во-первых, относительным характером этого показателя. Во-вторых, его диапазонной асимметричностью: одно распределение может быть более равным, чем другое в одном диапазоне, и менее равным в другом при одном том же значении коэффициента для обоих распределений. Поэтому прямые выводы из сравнения коэффициента в разных странах и во временной динамике могут привести к ошибочным оценкам.
Коэффициент назван в честь его автора – итальянца Коррадо Джини (Corradо Gini), преподавателя статистики, социологии и демографии в университете Рима. Коэффициент был предложен им в 1912 году, поэтому у коэффициента намечается знаменательная дата — 100 лет практического использования
Рассчитать коэффициент Джини.
Рассчитать коэффициент Джини:Всего население 1млн100тыс человек.
15%-богатые семьи месячный доход 200 тыс.
35%-средний класс месячный доход 30 тыс.
50%-бедные месячный доход 10 тыс.
Рассчитаем долю доходов бедных семей.
Доход всех семей: 1.1млн*(0.15*200тыс+0.35*30тыс+0.5*10тыс)=1.1млн*(45.5тыс).
Значит доля доходов бедных семей =(1.1млн*(0.5*10тыс)/(1.1млн*(45.5тыс)=0.11.
Таким же образом находим долю доходов среднего класса в общих доходах ( равна 0.23).
Значит доля доходов бедных и среднего класса в общих доходах = 0.34.
Индекс Джини я рассчитывал как отношение площади фигуры(S), заключенной между кривой абсолютного равенства и кривой Лоренца, к площади фигуры, заключенной между кривой абсолютного равенства и кривой абсолютного неравенства(Sан=0.5)
S=0.5-S 1 -S 2 -S 3 -S 4 -S 5
S 1 ,S 2 ,S 3 ,S 4 ,S 5 можно легко найти по имеющимся данным, а значит можно найти и индекс Джини.
Как найти данные S1,S2,S3,S4,S5,чему они равны?И что делать дальше,как найти именно коэффициент Джини?
S1,S3,S5 — это прямоугольные треугольники, их площадь находится как половина произведения катетов
S2,S4 — это прямоугольники, их площадь — это произведение сторон
G = 

Некое общество состоит из двух социальных групп, внутри каждой из которых доход распределен равномерно. Известно, что среднедушевой доход в первой группе составляет 5 тыс. руб. в месяц, во второй – 25 тыс. руб. в месяц, а во всем обществе среднедушевой доход составляет 20 тыс. руб. в месяц. Определите значение коэффициента Джини для этого общества.
Обозначим количество членов более бедной социальной группы за 




Кривая Лоренца будет иметь следующий вид:
Построив ее, легко посчитать коэффициент Джини:


Четырехмерный коктейль
Для приготовления одной порции коктейля «Неустойчивое равновесие» — фирменного коктейля бара «Economics» — требуется 1 единица ингредиента A, 2 единицы ингредиента B, 3 единицы ингредиента C и 4 единицы ингредиента D (названия ингредиентов являются коммерческой тайной и не разглашаются). Однако владелец бара, знаменитый бармен и экономист Сэм Полуэльсон, обладает лишь ограниченными ресурсами для закупки дорогих ингредиентов. Так, на имеющиеся у него денежные средства он может купить либо 100 единиц ингредиента A, либо 200 единиц ингредиента B, либо 300 единиц ингредиента C, либо 400 единиц ингредиента D в день.
Какое максимальное число порций фирменного коктейля сможет приготовить Сэм за день?
Мне первым в голову пришло вообще другое решение-логическое
Заметим тот факт,что для покупки любого ингредиента(А,B,C,D) на 1 порцию коктейля нам надо потратить 1/100 всех денег,то-есть на 1 коктейль мы тратим 1/25 всех денег,поэтому всего можем сделать 25 коктейлей
Задача на коэффициент Джини.
Всех жителей некоторой общины можно условно разделить на три равные группы по численности: бедные, средние, богатые. Доход Бедной группы составляет 20% от общего дохода всех жителей данной общины. Доход средней группы составляет 30%. Рассчитайте коэффициент Джини ( 
В общине решили ввести налог на доходы богатой части общества в размере 30% от их дохода. Полученная сумма налога распределяется следующим образом: две трети полученной суммы идет бедным, одна треть — средней группе. Рассчитайте новое значение коэффициенты Джини( 
Решение: После введения налога доход «богатых» составит: 







Коэффициент Джини можно рассчитать, используя лемму о ломаной кривой Лоренца , имеющей два линейных участка (доказательство леммы в задаче, которая называется «В некоторой стране», введите в поиске по сайту, ссылку вставить не получилось), отсюда
Вычислите коэффициент Джини, примерно отражающий общемировое неравенство доходов, если ВВП развивающихся стран, в которых проживает 80 % населения Земли, в сумме составляют только 20 % общемирового продукта (заметим, что это соотношение держится уже много лет по данным Всемирного банка).
В некоторой стране
В некоторой стране общество состоит из двух неравных по численности и уровню доходов групп: богатых и бедных. Допустим, бедные получают 40% совокупного дохода. Значение коэффициента Джини составляет 0,3. Рассчитайте долю бедных и долю богатых от общей численности населен



Ну или можно просто стандартно рассчитать коэффициент Джини, что в конечном итоге даст аналогичный результат результат))
Сложение кривых Лоренца
В двух странах с одинаковым ВВП на душу населения коэффициенты Джини отличаются на единицу. Государство с менее равномерным распределением доходов – тоталитарное и милитаризованное – решило развязать войну со своим более демократичным соседом. Однако, несмотря на значительные расходы (на кампанию было потрачено около 




Коэффициенты Джини отличаются на 


Обозначим демократическую страну «D», а тоталитарную – «T», 





Отсюда


Но в силу равенства ВВП на душу населения до войны 
Значит, 
Обозначим 

Поймем, как будет выглядеть кривая Лоренца объединенного государства. Самые бедные в новом государстве – это жители бывшего тоталитарного государства, имеющие нулевые доходы. Их доля в населении нового государства равна 






Тогда коэффициент Джини равен 
Учитывая то, что 
Значит, 
Получается, что до войны страны имели одинаковый ВВП и одинаковую численность населения!
Если бы страны объединились до войны, то общая кривая Лоренца имела бы качественно такой же вид, как и в случае объединения после войны. Следуя описанной выше логике построения этой кривой, нетрудно установить, что совокупная кривая Лоренца до войны проходила бы через точки 


Неравенство среднедушевых доходов
Некое общество состоит из двух социальных групп, внутри каждой из которых доход распределен равномерно. Известно, что среднедушевой доход в первой группе составляет 5 тыс. руб. в месяц, во второй – 25 тыс. руб. в месяц, а во всем обществе среднедушевой доход составляет 20 тыс. руб. в месяц. Определите значение коэффициента Джини для этого общества.
Обозначим количество членов более бедной социальной группы за 




Кривая Лоренца будет иметь следующий вид:
Построив ее, легко посчитать коэффициент Джини:


$«Три поросенка и Серый волк»$
Жили-были на свете три брата-поросенка: Ниф-Ниф, Нуф-Нуф и Наф-Наф. Все одинакового роста, кругленькие, розовые, с одинаковыми веселыми хвостиками. Вот только навыки их различались. За лето Ниф-Ниф мог построить три дома из соломы или два дома из камня. Нуф-Нуф, более тщательный и аккуратный, мог построить за лето целых пять соломенных домиков. И по лесу ходили слухи, что как-то, поспорив с братьями, он смог за лето построить 2 домика из соломы и три дома из камня. Но самым трудолюбивым из поросят был Наф-Наф: в июне он мог построить 2 соломенных домика, в июльский зной его производительность снижалась, и его хватало лишь на то, чтобы целиком построить один домик из соломы и начать еще один. Зато в августе Наф-Наф работал, не покладая рук – не только мог доделать начатое в июле, но и построить 4 новых соломенных домика. А каменщиком Наф-Наф был еще более искусным: на каждый дом из камня он тратил на 40% времени меньше, чем на соломенный.
Построенные домики поросята продавали жителям соседнего леса, которым покупка домика из соломы обходилась в 10 монет, а домика из камня – в 15 монет.
Однажды, нежась в лужице, братья договорились, что будут заниматься строительством вместе, создав девелоперскую компанию «ХрякДомСтрой».
— Но мы же всего лишь поросята, — сказал Наф-Наф, самый разумный из них, – нам нужен бухгалтер, который будет учитывать все наши операции и составлять баланс.
— А давайте позовем Серого волка, — предложил Нуф-Нуф, — ведь после той истории, сделавшей нас знаменитыми, он изменился, тоже работать хочет. Видимо не зря мы его проучили!
Поросята согласились с предложением брата, но решили устроить волку экзамен, чтобы проверить, не собирается ли он снова попытаться «надуть» их. Вот какие задания были предложены Серому волку на экзамене:
1. Покажи, какими являются возможности каждого из братьев-поросят, если они будут работать поодиночке. (5 баллов)
2. На стене одного из домов проиллюстрируй возможности строительства домиков, которыми будет обладать компания «ХрякДомСтрой». (6 баллов)
3. Если надо будет построить несколько соломенных, и несколько каменных домов, какие именно дома должен строить каждый из братьев? (5 баллов)
4. Скажи, какие домики стоит строить, чтобы «ХрякДомСтрой» смог получить максимальный доход от их продажи жителям леса, если солома, необходимая для постройки одного дома, обходится в 3 монеты, а камни – в 10 монет (10 баллов).
Серый волк решил задачки, но теперь перед поросятами встала новая проблема: как проверить ответы волка? За верными ответами они обратились к нам. А мы – к вам.
1) Ниф-ниф :
Нуф-нуф :
Наф-наф :
3)Ниф-ниф строит соломенные
Нуф-нуфу всеравно какие
Наф-наф строит Каменные
4) Ниф-нифу и нуф-нуфу строить только соломенные а Наф-нафу строить Каменные
Прибыль получилась
А в чем проблема-то?
1) У Ниф-Нифа есть две крайние точки на КПВ, у Нуф-Нуфа есть крайняя точка по оси соломы и точка (2;3) (если строить КПВ в осях (соломенные домики;каменные домики)), у Наф-Нафа две крайние точки 8 и 
2) Здесь просто смотрите у кого меньшая альтернативная стоимость в производстве какого-либо вида домиков, потом начинаете строить общую КПВ, начиная с наименьшей а.с.
3) Опять же все сводится к альтернативной стоимости
4) Проверяете «краевые» точки суммарной КПВ, то есть 2 точки излома и две крайние точки. Если более обоснованно, то тут вроде надо записать, что 

Кстати, в задачнике Акимова есть очень похожие задачи на эту тему,просто там вместо прибыли, надо было максимизировать выручку.
Задача про зайцев
В темно-синем лесу, где трепещут осины, компания «Зайцы Ltd.» является монополистом на рынке трын-травы и имеет функцию издержек 


Установит потолок цены на уровне 


Снизит потолок до такого уровня 
Наконец, снизит потолок до уровня 
Когда Дед Мазай спросил «Зайцев Ltd.», выгодно ли им косить трын-траву при цене 
Какую прибыль получили бы «Зайцы Ltd.», если бы не было Деда Мазая?
Найдите цены, которые установятся на рынке после каждого этапа вмешательства. Какую прибыль будут получать «Зайцы Ltd.» при каждой из этих цен?
Прокомментируйте действия Деда Мазая с точки зрения общественного благосостояния.
Найдем прибыль «Зайцев Ltd.» до государственного вмешательства:
Рассмотрим механизм выбора монополистом объема производства при установке потолка цены 





При каждом значении 





Какую цену 
Осталось найти 

Говоря о последствиях действий Деда Мазая для общества, можно заметить, что установка цен 



Подробно и с картинками поведение монополиста в условиях ценового регулирования описано в известном учебнике Роберта Пиндайка и Даниэля Рубинфельда в главе «Рыночная власть: монополия и монопсония».
Уравнение Фишера (уравнение обмена)
Иначе его еще иногда называют уравнением обмена или денежного потока. В общем своём виде, данное уравнение устанавливает взаимосвязь между такими величинами как:
- Количество денег находящееся в обращении (денежная масса);
- Скорость, с которой происходит оборот этой денежной массы. В общем случае она представляет собой ту среднюю частоту, с которой, в заданный промежуток времени, одна и таже денежная единица используется для обмена на услуги и товары отечественного производства. В краткосрочном периоде времени эта величина меняется очень медленно, поэтому её можно принять за константу;
- Текущий уровень цен;
- Текущий объём производства (выраженный в общем количестве произведённых товаров). Обычно, для данной формулы, принимается допущение о том, что все производственные мощности имеют полную загрузку.
Формула этой взаимосвязи выглядит так:
Как видно из приведённого уравнения, денежная масса находится в прямо пропорциональной зависимости от таких параметров как текущий уровень цен и текущий объём производства. И вместе с тем величина денежной массы обратно пропорциональна скорости её оборота.
Таким образом, данное уравнение представляет собой один и столпов, на которых базируется монетаристская доктрина в экономике.
Монетаризм – теория в современной макроэкономике, основным тезисом которой является утверждение о том, что основным фактором развития экономики является количество денег находящееся в обращении.
Формула была выведена ещё в 1911 году выдающимся представителем неоклассической школы экономики, американским экономистом Ирвингом Фишером.
По сути своей, данное уравнение представляет собой формальное выражение количественной теории денег.
Собственно говоря, сама формулировка количественной теории денег в экономике сводится к тому, что покупательная способность денег в купе с уровнем цен, полностью определяются тем количеством денег, которое находится в обороте.
Здесь следует отметить тот факт, что данная формулировка справедлива для условий стабильного (нормального) экономического развития. В данном случае, действительно, первичным выступает изменение денежной массы и лишь за ним, как следствие, происходит изменение покупательной способности и уровня цен.
В случае же, так называемой, диспропорции в экономическом развитии, может наблюдаться совершенно противоположная картина. В этом случае сначала происходит изменение уровня цен, а лишь за ним изменяется и величина денежной массы.
Кстати говоря, Кембриджская школа политэкономии даёт несколько иную трактовку количественной теории денег. В данном случае, большее значение придаётся выбору потребителей, в отличие от вышеописанной трактовки Ирвинга Фишера, в которой определяющими являются технологические факторы производства.
В формулировке Кембриджской школы, в основе количественной теории денег лежит следующее уравнение:
В рамках количественной теории денег была предложена ещё одна трактовка формулы Фишера:
Одним из выводов, проистекающих из данной трактовки, является то, что стабильность цен (в той или иной стране) напрямую зависит о того, насколько находящаяся в обороте денежная масса соответствует общему объёму товарных сделок (включающему в себя объёмы производства, сферы услуг, торговли и т.п.).
Нарушение этого баланса приводит к тому, что уровень цен начинает дестабилизироваться:
Следует иметь в виду, что формула Фишера, по большому счёту, представляет собой скорее теоретическое выражение количественной теории денег и не предназначена для проведения прямых расчётов по ней.
Критика формулы Фишера
В настоящее время уравнение Фишера признаётся верным далеко не всеми представителями современной экономической школы. В его обосновании обнаруживают целый ряд неточностей, благодаря которым конечная формула не может отражать истинное положение вещей в экономике.
В частности, в качестве примера такого рода критики можно привести статью Юрия Владимировича Лиференко, опубликованную в одном из выпусков журнала «Финансы и кредит» за 2015 год.
В этой статье, в частности, указывается на ошибки Банка России связанные с тем, что он, в процессе осуществлении своей регулирующей деятельности, во многом опирается на количественную теорию денег (иллюстрируемую, как раз, той самой формулой Фишера). Говорится о том, что его регулирующая функция является, мягко говоря, недостаточно эффективной вследствие факта ошибочности данной теории.
Далее приводится доказательство несостоятельности формулы Фишера и, как следствие этого, говорится о неприемлемости её использования (ни в теоретическом, ни в практическом виде) в качестве инструмента для регулирования реальной экономики.
В качестве основного аргумента ошибочности уравнения Фишера приводится тот факт, что правая часть формулы Фишера, представляющая собой выражение PQ, является некорректной. Приводится сравнение с формулой выведенной Карлом Марксом (иллюстрирующей закон денежного обращения) и имеющей следующий вид:
Как видите, внешне эта формула очень похожа на ту, которую впоследствии вывел Ирвинг Фишер. Естественно, он не мог не знать о её существовании (большую часть свей жизни, он преподавал политэкономию) и, предположительно, взял её в качестве основы для своих изысканий. Однако выводы из формулы К. Маркса делаются совершенно противоположные. Левая часть формулы, представленная количеством денег в экономике (денежной массой) М, в данном случае является функцией от её правой части, представленной уровнем цен и объёмом товаров.
Это, в свою очередь, означает, что уровень цен и объём товаров определяют то количество денег, которое необходимо для их обращения, а не наоборот, как утверждает количественная теория денег, выраженная уравнением Ирвинга Фишера.
По мнению автора статьи, Фишер, скорее всего, сознательно исказил некоторые факты для того чтобы представить неделимую составляющую формулы Маркса ΣPiQi в более простом и, самое главное, в математически разделимом виде простого произведения величин P и Q.
Такое представление позволило ему разделить правую часть и записать формулу в виде:
А это в корне меняет тот вывод, который делался Марксом. Теперь получается, что количество денег, в сущности, и определяет уровень цен в экономике. То есть мы видим не что иное, как формулировку количественной теории денег.
В действительности же, такое выражение как PQ не может существовать в принципе. Это объясняется тем, что не бывает понятия цены без привязки к конкретному товару (i). Равно как и не может быть такого понятия как объём производства в принципе, он также должен быть привязан к какому-либо определённому продукту (i).
Ну и наконец, невозможно отделить в этой формуле цену от количества товара (P от Q) поскольку цена любого товара всегда неразрывно связана с его количеством. Например, говорят, что цена хлеба составляет 20 руб/булка (двадцать рублей за одну булку) и её нельзя разорвать на два самостоятельных элемента, таких как 20 руб и 1 булка.
То есть, изначально правильным является всё-таки выражение в виде ΣPiQi, которое, кстати, лежит в основе формулы расчёта ВВП. А формула Фишера изначально построена на ошибочных предпосылках, что говорит не только о том, что она неверна в принципе, но и о несостоятельности всей количественной теории денег вообще.
источники:
http://infourok.ru/konspekt-na-temu-formuli-po-ekonomike-2484948.html
http://www.azbukatreydera.ru/uravnenie-fishera.html

 ;
; ;
; ;
;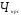 ;
;




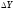
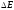

 )
)
 )
) )–
)–