В таблице представлены основные расчетные формулы по электротехнике для расчета тока, напряжения, сопротивления, мощности и других парметров электрических схем.
|
Измеряемые величины |
Формулы |
Обозначение и единицы измерения |
|
Сопротивление проводника омическое (при постоянном токе) |
|
s — сечение, мм2 |
|
Активное сопротивление при переменном токе |
|
r — активное сопротивление, Ом; k — коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках — также явление намагничивания |
|
Зависимость омического сопротивления проводника от температуры |
|
|
|
Индуктивное (реактивное) сопротивление |
|
сопротивление, Ом; f— частота, Гц; L — коэффициент самоиндукции (индуктивность), Гц; С — емкость, Ф; Z — полное сопротивление, Ом |
|
Емкостное (реактивное) сопротивление |
|
|
|
Полное реактивное сопротивление |
|
|
|
Полное сопротивление переменному току |
|
|
|
Емкость пластинчатого конденсатора |
|
С — емкость, Ф; S — площадь между двумя электродами, см n — число пластин; b — толщина слоя диэлектрика, см |
|
Общая емкость цепи: а) при последовательном соединении емкостей б) при параллельном соединении емкостей |
|
|
|
Закон Ома; цепь переменного тока с реактивным сопротивлением |
|
I — ток в цепи, А; U — напряжение цепи, В; |
|
1-й закон Кирхгофа (для узла) |
|
точке, А; i = 1, 2… n; Е — ЭДС, действующая в контуре, В; r — сопротивление отдельных участков, Ом |
|
2-й закон Кирхгофа (для замкнутого контура) |
|
|
|
Распределение тока в двух параллельных ветвях цепи переменного тока |
|
|
|
Закон электромагнитного индукции для синусоидального тока |
|
f — частота, Гц; w — число витков обмотки; В — индукция магнитного поля в стали, Тс; S — сечение магнитопровода, см2 |
|
Электродинамический эффект тока для двух параллельных проводников |
|
F — сила, действующая на 1 (см) длины проводника, кГ; а — расстояние между проводниками, си; |
|
Подъемная сила электромагнита |
|
Р — подъемная сила, кГ; В3 — индукция в воздушном зазоре; В3 = 1000 Гс (электромагниты для подъема стружки и мелких деталей); В3 = 8000 — 10 000 Гс (электромагниты для подъема крупных деталей) S — сечение стального сердечника, см2 |
|
Тепловой эффект тока |
|
тепла, кал; t— время протекания тока, сек; r — сопротивление, Ом; А — количество вещества, от- ложившегося на электроде, мг; α — электрохимический эквивалент вещества |
|
Химический эффект тока |
|
|
|
Зависимости в цепи переменного тока при частоте 50 Гц: а) период изменения тока б) угловая скорость |
|
Т — период изменения тока, сек; f — частота тока, Гц; |
|
Зависимости токов и напряжений в цепи переменного тока: а) ток в цепи б) напряжение в цепи |
|
I — полный ток в цепи, А; тока, А; U— напряжение в цепи, В; напряжения, В; |
|
Соотношения токов и напряжений в трехфазной системе: а) соединение в звезду б) соединение в треугольник |
|
|
|
Коэффициент мощности |
|
Р — активная мощность, Вт; Q — реактивная мощность, нар; S —полная мощность, B*А; r — активное сопротивление, z — полное сопротивление, Ом |
|
Мощность в цепи постоянного тока |
|
|
|
Мощность в цепи переменного тока: а) цепь однофазно тока б) цепь трехфазного тока |
|
|
|
Энергия в цепи постоянного тока |
|
t —время ч |
|
Энергия в цепи переменного тока: а) цепь однофазного тока б) цепь трехфазного тока |
|
меню сайта для мобильных приложений
ФОРМУЛЫ ТЕОРИИ ОСНОВ ЭЛЕКТРОТЕХНИКИ (ТОЭ)

Прежде чем перейти к формулам, обращу Ваше внимание на буквенное обозначение в ТОЭ, в разных учебниках по ТОЭ, мягко говоря, обозначение довольно произвольное, нет единого требования по данному вопросу в электротехнике. Особенно заметна разность обозначения в комплексных числах (как грибы в лесу, как только их не называют в разных местностях). Поэтому определимся сразу с буквенным обозначением:
При расчётах всегда приводить все значения в одну единицу, например если расчеты по мощности в ваттах, соответственно напряжение в вольтах, сопротивление в Омах и т.д.
Комплексная мощность обозначается буквой S с волнистым значком (тильда) над ней.
- А теперь формулы по электротехнике (ТОЭ) часто применяемые для расчетов (дома, на работе), рассмотрим в порядке от простых к очень простым, для студенческого сообщества выложу отдельно сложные и очень сложные, и напишу целую лекцию по ТОЭ.
ФОРМУЛЫ ПОСТОЯННОГО ТОКА
Закон Ома для участка цепи и всей цепи постоянного тока:
Пример для расчета сопротивления проводника (подробнее можете посмотреть, что такое величина удельного сопротивления проводника на стр. понятия и определения):
Мощность в цепи постоянного тока, здесь нет ничего сложного, как и все в постоянном токе, замечу только, что значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, единица мощности (Р) равна -1 кВт = 1000 Вт:
-
- На заметку для любознательных, можно например, электрическую мощность пересчитать в механическую и наоборот: 1 кВт*ч = 367000 кгс*м; 1кВт = 102кгс*м/с, т.е. за 1 кВтч. Т.е. можно поднять груз массой 367 кг на высоту 1 км, или 102 кг за 1 сек. на один метр.
ФОРМУЛЫ ПЕРЕМЕННОГО ТОКА
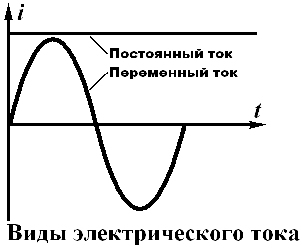
В отличие от постоянного тока, особенностью переменного тока является то, что электрический ток с течением времени изменяется по величине и направлению. Элементы такой электрической цепи влияют на амплитуду тока и на его фазу. Условное обозначение переменного тока на электроприборах ̴ (англ. alternating current и обозначается латинскими буквами АС):
Электромагнитные процессы, протекающие в электротехнических устройствах, как правило, достаточно сложны, поэтому далее формулы тоэ будут носить более учебный характер, чем практический, иначе говоря для учащихся и просто для любознательных.
Перевод (конвертировать) мощности (Р в Вт), тока (I в А), сопротивления (R в Ом) и напряжения (U в В) можно, как показано ниже на простом примере (см. рис. ниже):
При этом надо учитывать, если у Вас в цепи U 220 В есть электродвигатели, трансформаторы и т.д. (индуктивные или емкостные нагрузки — реактивные элементы), то тогда нужно учитывать cos φ , например:
I = P/(U*cos φ),
в цепи U 380 В подставляем ещё √3 (корень из трёх равен — 1,73), например:
для тока: I = P/(√3*U*cos φ), или I = P/(1,73*U*cos φ), для мощности: P = √3*U*I*cos φ.
Продолжение формулы тоэ:
См. также ниже продолжение раздела формулы:
перейти: формулы тоэ 1 краткое описание страницы — электрический ток (I, ампер), электродвижущая сила (ЭДС, E=A/q=Дж/Кл=В, вольт), электрическое напряжение (U, вольт), электрическая энергия и мощность (Eq, Дж, джоуль) и ватт (Р, Вт, ватт)…
перейти: формулы тоэ 2 краткое описание страницы — пассивные элементы цепи (резистор, катушка индуктивности и конденсатор), их основные характеристики и параметры…
-
Автор сайта надеяться, что информация Вам будет полезна, как доступно простая, так и более углублённая в других разделах сайта. Не забывайте просмотреть рекламу от гугл, реклама для Вас бесплатно, а мне развитие сайта, удачи.
P


=Pвх – условие максимальной мощности.
Pmax=U2abxx/4Rвх – максимальная мощность.
Pполн=UabxxI=U2abxx/(Rвх+R)
КПД=P/Pполн=R/(R+Rвх)
Закон Ома для участка цепи:
I=(U+E)/R
φ1=E φ2=φ1 – RI
i=Imsin(ωt+ψ)
f=1/T ω=2πf c-1
Iср=(2/π)*Im
эффективное
действительное средне-
квадратичное значение Im=Im/√2=0,707 Im
Количество теплоты: RIm2*(T/2); RIпост2T
Iпост=Im/√2 ejα=cosα+jsinα
Комплексная амплитуда:
I(.)m=Imejψ (ψ – начальная фаза)
Комплекс действ. значения I(.)=I(.)m/√2=Iejψ
Сопротивление цепи складывается
из сопротивлений элементов:
R, jωL, -j/ωC
Z=R+jX, модуль комплексного
сопротивления:
z=√R2+X2 tgφ=X/R
На векторной диаграмме U(.)L
должно опережать протекающий через нее ток на 90º, а на емкости наоборот отставать на 90º, на сопротивлении R совпадает по фазе. Если в схеме несколько контуров, то для них строится диаграмма по принципу обхода контура.
Мгновенные значения: U=RI, UL=L(di/dt),
Uc=(1/C)*∫idt. Если применять методы расчета цепей постоянного тока к синусоидальному току, то производят замену значений, в частности сопротивления на Z=R+jX, где комплексная часть получается из-за падений напряжений на L или C.
P=Uicosφ (активное) [Вт], Q=Uisinφ(реакт.)[ВАр]
S=UI (полная) [ВА], S2=P2+Q2 (прямоугольный треугольник, из него находим угол φ между PиS). Комплекс полной мощности при участке сопряженного комплексного тока I(*):
S(~)=U(.)I(*)=UIej(ψu – ψi)=UIejφ=Uicosφ+jUIsinφ=
=P+jQ P=ReU(.)I(*) Q=ImU(.)I(*)
U(.)=Uejψu I(*)=Ie-jψi φ=ψu — ψi – угол м/у u и i
U(.)=E(.) Z=R+jX=zejφ
Показания ваттметра Re(UabI(*)), цена деления UI/n[Вт/дел]. Сопротивление Z имеет характер:
X>0 – индуктивный, X<0 емкостный, X=0 чиста активный (резонанс!). Чтоб вывести формулу для резонанса в цепи используют 1ый закон Кирхгофа, Z заменяют на проводимость Y=1/Z. Получается I=U(.)Y, мнимую часть приравнивают к нулю. Ic=UωC – ток через конденсатор. Полоса пропускания – граничные частоты
ω1,2=(ω0/2Q)*(√1+4Q`±1). Постоянный ток через конденсатор не проходит. ω0 – резонансная частота. Резонанс напряжений наблюдается при последовательном соединении R,L,C. Условие наступления такого резонанса ωL=1/ωC. При этом I=E/R, UL=Uc=ωLI=ωLE/R, ωC/R=√L/C`/R=Q – добротность. ρ=QR – характеристическое сопротивление. Топографическая диаграмма – это даграмма токов и напряжений по осям +1 и +j
f(x)=A0+Σ[k=1, ∞] Ak‘sinkx + Σ[k=1,∞]Ak»coskx
f(x)=A0 + Σ[k=1,∞] Aksin(kx+ψk), tgψk=Ak»/Ak‘
A0=(1/2π)*∫[0-2π]f(x)dx,Ak‘=(1/π)*∫[0-2π]f(x)sinkxdx
Ak»=(1/π)*∫[0-2π]f(x)coskxdx, Ak2=Ak‘2+Ak» 2
Свойства периодических кривых: если удовлетворяет –f(x+π)=f(x), значит при разложении в ряд A0=Aчетное‘=Aчетное»=0. Если удовлетворяет f(-x)=f(x), то Ak‘=0. Если же
–f(-x)=f(x), то A0=Ak»=0.
Действующие значения U, I находятся как корень из суммы квадратов амплитуд деленных на 2.
P=U0I0+U1I1cosφ1+U2I2cosφ2+… (U0,I0 – ампл. зн.)
S=UI (U,I – действующие значения)
Несинусоидальные токи и напряжения, не содержащие постоянных составляющих, можно заменить эквивалентными синусоидальными. Действующее значение синусоидального тока принимают равным действующему значению несинусоидального напряжения. Угол сдвига фаз φ между между эквивалентными синусоидами напряжения и тока берут таким, чтобы cosφ=P/UI.
3-фазные цепи являются синусоидальными.
Провода, соединяющие точки A,B,C генера-
тора с нагрузкой, называются линейными.
Токи в них называются линейными. Модули
этих токов Iл. Модуль – коэффициент перед
ejφ. Фазные U – это U генератора.
Напряжение между линейными проводами называются линейными
U(.)AB. Модуль Uл.
При соединении генератора в звезду:Uл=UAB=Uф2cos30º=√3`Uф
Iл=Iф. При соединении генератора в ∆: Uл=Uф.
При соединении нагрузки в звезду: Iл=Iф
При соединении нагрузки в ∆ линейные токи опред. по 1 з.Кирхгофа.
Мощность: P=PA+PB+PC+P0. Q=QA+QB+QC+Q0
S2=P2+Q2. Если нагрузка равномерная, то P0=Q0=0
а все остальные составляющие равны:
P=3UфIфcosφф, Q=3UфIфsinφф, где φф – угол между U(.)ф на фазе и током I(.)ф фазы нагрузки. S=3UфIф
При равномерной нагрузке независимо от способа ее соединения в звезду или ∆: 3UфIф=√3`UлIл=S. Остальные мощности также при переходе ставим вместо тройки √.
4-полюсники бывают взаимные и не взаимные: для взаимных выполняется следующее соотношение: U(.)1/I(.)2=Zпер=U(.)2/I(.)1. Все пассивные являются взаимными.
В материале представлены задачи и основные формулы для экзамены по УД «Электротехника и электроника» для специальностей: «Техническое обслуживание и ремонт автомобильного транспорта» и «Организация превозок и управление на транспорте автомобильном».
Скачать:
Предварительный просмотр:
Уровень С.
Конденсаторы
- Определить эквивалентную емкость трех конденсаторов при их последовательном и параллельном соединении если: С1=2 мкФ; С2=4 мкФ, С3=6 мкФ. Начертите схему цепи.
- Определить эквивалентную емкость трех конденсаторов при их последовательном и параллельном соединении если: С1=12 мкФ; С2=12 мкФ, С3=12 мкФ. Начертите схему цепи.
Постоянный ток. Закон Ома для участка цепи. Законы последовательного и параллельного соединения потребителей.
- В электрическую цепь напряжением 220 В включено последовательно пять ламп сопротивлением 110 Ом каждая. Определить эквивалентное сопротивление ламп, силу тока, проходящего по цепи, и напряжение на каждой лампе. Начертите схему цепи.
- В электрическую цепь напряжением 120 В включено последовательно две лампы сопротивлением 20 Ом каждая. Определить эквивалентное сопротивление ламп, силу тока, проходящего по цепи, и напряжение на каждой лампе. Начертите схему цепи.
- К сети напряжением 220 В подключены параллельно 5 ламп сопротивлением 100 Ом каждая. Определить эквивалентное сопротивление цепи, силу тока в каждой лампе и общую силу тока, потребляемого всеми лампами. Начертите схему цепи.
- К сети напряжением 120 В подключены параллельно 2 лампы сопротивлением 100 Ом каждая. Определить эквивалентное сопротивление цепи, силу тока в каждой лампе и общую силу тока, потребляемого всеми лампами. Начертите схему цепи.
- Определить эквивалентное сопротивление трех резисторов при их последовательном и параллельном соединении если: R1=2 Ом; R2=4 Ом, R3=6 Ом. Начертите схему цепи.
- Определить эквивалентное сопротивление трех резисторов при их последовательном и параллельном соединении если: R1=4 Ом; R2=2 Ом, R3=3 Ом. Начертите схему цепи.
Постоянный ток. Закон Ома для полной цепи.
- Рассчитать ток в электрической цепи сопротивлением 2 Ом, источником с внутренним сопротивлением 0,1 Ом и ЭДС 20 В. Определить падение напряжение на источник. Начертите схему цепи.
- К источнику постоянного тока с ЭДС 1,5 В и внутренним сопротивлением 2,5 Ом подключен резистор сопротивления 10 Ом. Определить ток в цепи и падение напряжение на источник. Начертите схему цепи.
Мощность в цепи постоянного тока
- ЭДС источника энергии 100 В, его внутреннее сопротивление 2 Ом. К источнику подключен потребитель с сопротивлением 23 Ом. Определить мощность потерь внутри источника и его КПД. Начертите схему цепи.
- ЭДС источника энергии 55 В, его внутреннее сопротивление 1 Ом. К источнику подключен потребитель с сопротивлением 10 Ом. Определить мощность потерь внутри источника и его КПД. Начертите схему цепи.
Переменный ток. Расчет цепей переменного тока с индуктивностью
- Цепь с индуктивностью 0,02 Гн включена под напряжение 127 В и частотой 50 Гц. Определить индуктивное сопротивление цепи, силу тока и реактивную мощность. Начертите схему цепи.
- Цепь с индуктивностью 0,025 Гн включена под напряжение 220 В и частотой 50 Гц. Определить индуктивное сопротивление цепи, силу тока и реактивную мощность. Начертите схему цепи.
Переменный ток. Расчет цепей переменного тока с ёмкостью
- Конденсатор емкостью 80·10-6Ф включен в сеть с напряжением 380 В и частотой 50 Гц. Определить емкостное сопротивление в цепи, силу токаи реактивную мощность. Начертите схему цепи.
- Конденсатор емкостью 65·10-6Ф включен в сеть с напряжением 100 В и частотой 50 Гц. Определить емкостное сопротивление в цепи, силу токаи реактивную мощность. Начертите схему цепи.
Переменный ток. Последовательное соединение в цепи переменного тока.
- К цепи с последовательным соединением активного сопротивления 12 Ом и ёмкостного 16 Ом подведено напряжение 120 В. Определить ток цепи. активную, реактивную и полную мощности. Начертите схему цепи.
- К цепи с последовательным соединением активного сопротивления 8 Ом и ёмкостного 6 Ом подведено напряжение 220 В. Определить ток цепи, активную, реактивную и полную мощности. Начертите схему цепи.
Трёхфазные цепи переменного тока
- Линейное напряжение в сети 220 В, а линейный ток равен 8А.Определить фазное напряжение и фазный ток, если симметричная нагрузка соединена «треугольником» и «звездой».
- Линейное напряжение в сети 380В, а линейный ток равен 5А. Определить фазное напряжение и фазный ток, если симметричная нагрузка соединена «треугольником» и «звездой».
Трансформатор
- Входное напряжение трансформатора равно 6000 В и число витков первичной обмотки равно 150. Напряжение на вторичной обмотке при холостом ходе 400 Вольт. Определить число витков вторичной обмотки и коэффициент трансформации.
- Входное напряжение трансформатора равно 10 В и число витков первичной обмотки равно 16. Напряжение на вторичной обмотке при холостом ходе 50 Вольт. Определить число витков вторичной обмотки и коэффициент трансформации.
Параметры генератора переменного тока
- Генератор переменного тока имеет частоту вращения 6000 об/мин. Определить частоту и период электрического тока, если число полюсов генератора равно 12.
- Генератор переменного тока имеет частоту вращения 2800 об/мин. Определить частоту, период электрического тока, если число пар полюсов генератора равно 6.
Формулы
|
Конденсаторы |
Последовательное соединение конденсаторов Параллельное соединение конденсаторов |
|
Закон Ома для участка цепи. Законы последовательного и параллельного соединения потребителей. |
Закон Ома для участка цепи |
|
Последовательное соединение Сила тока Напряжение Сопротивление |
Параллельное соединение Сила тока Напряжение Сопротивление |
|
Постоянный ток. Закон Ома для полной цепи. |
Закон Ома для полной цепи |
|
Мощность в цепи постоянного тока |
Мощность, выделившаяся на внешнем участке Мощность потерь внутри источника тока КПД источника |
|
Расчет цепей переменного тока с индуктивностью |
Реактивно индуктивное сопротивление Сила тока Реактивная мощность QL =I2·XL |
|
Расчет цепей переменного тока с ёмкостью |
Цепь переменного тока с ёмкостью Сила тока Реактивная мощность QC= I2·XC |
|
Последовательное соединение в цепи переменного тока. |
Полное сопротивление цепи переменного тока Действующее значение тока в цепи Активная мощность Реактивная мощность QC= I2·XC Полная мощность |
|
Трехфазные цепи переменного тока |
Соединение звездой IЛ =IФ, Соединение треугольником UЛ =UФ , |
|
Трансформатор |
Коэффициент трансформации |
|
Параметры генератора переменного тока |
Частота вращения магнитного поля статора Период |
По теме: методические разработки, презентации и конспекты
- Мне нравится
Формулы, примеры решения задач: ТОЭ | Электрические машины | Высшая математика | Теоретическая механика
- Электрический ток, плотность тока, электрическое напряжение, энергия при протекании тока, мощность электрического тока
- Электрический ток
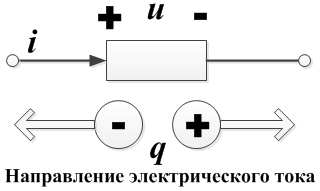
Электрический ток — это явление упорядоченного движения электрических зарядов. За направление электрического тока принимается направление движения положительных зарядов.
Формула электрического тока:
Электрический ток измеряется в амперах. СИ: А.
Электрический ток обозначается латинскими буквами i или I. Символом i(t) обозначается «мгновенное» значение тока, т.е. ток произвольного вида в любой момент времени. В частном случае он может быть постоянным или переменным.
Прописной латинской буквой I обозначается, как правило, постоянное значение тока.
В любом участке неразветвленной электрической цепи протекает одинаковый по величине ток, который прямо пропорционален напряжению на концах участка и обратно пропорционален его сопротивлению. Величина тока определяется по закону Ома:
1) для цепи постоянного тока
2) для цепи переменного тока,
где U — напряжение, В;
R — омическое сопротивление, Ом;
Z — полное сопротивление, Ом.
Омическое сопротивление проводника:
,
где l — длина проводника, м;
s — поперечное сечение, мм2;
ρ — удельное сопротивление, (Ом · мм2) / м.
Зависимость омического сопротивления от температуры:
Rt = R20 [1 + α(t — 20°)],
где R20 — сопротивление при 20°C, Ом;
Rt — сопротивление при t°C, Ом;
α — температурный коэффициент сопротивления.
Полное сопротивление цепи переменного тока:
,
где— активное сопротивление, Ом;
— индуктивное сопротивление, Ом;
— индуктивность, Гн;
— емкостное сопротивление, Ом;
— ёмкость, Ф.
Активное сопротивление больше омического сопротивления R:
,
где— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
При промышленной частоте, для нестальных проводников, принимаюти считают
.
- Плотность тока
Плотность тока (j) — это сила тока, рассчитанная на единицу площади поперечного сечения (s).
Для равномерного распределения плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, формула плотности тока принимает вид:,
где I — сила тока через поперечное сечение проводника площадью s.
СИ: А/м2 - Электрическое напряжение
При протекании тока, как и при всяком перемещении зарядов, происходит процесс преобразования энергии. Электрическое напряжение — количество энергии, которое необходимо затратить на перемещение единицы заряда из одной точки в другую.
Формула электрического напряжения:
Электрическое напряжение обозначается латинской буквой u. Символом u(t) обозначается «мгновенное» значение напряжения, а прописной латинской буквой U обозначается, как правило, постоянное напряжение.
Электрическое напряжение измеряется в вольтах. СИ: В. - Энергия при протекании электрического тока
Формула энергии, при протекании электрического тока:
СИ: Дж - Мощность при протекании электрического тока
Формула мощности, при протекании электрического тока:
СИ: Вт.
- Электрическая цепь
- Электрическая цепь — это совокупность устройств, предназначенных для протекания по ним электрического тока.
Эти устройства называются элементами цепи. - Источники электрической энергии — устройства, преобразующие различные виды энергии, например механическую или химическую, в энергию электрического тока.
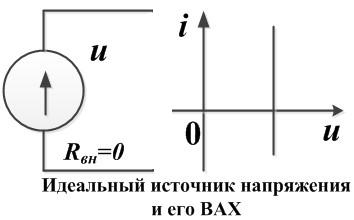
- Идеальный источник напряжения — источник, напряжение на зажимах которого не зависит от величины протекающего через него тока.
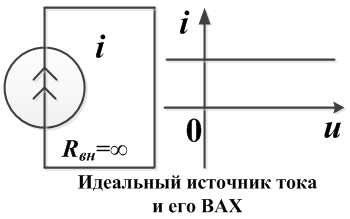
Внутреннее сопротивление идеального источника напряжения можно условно принять равным нулю. - Идеальный источник тока — источник, величина протекающего тока через который не зависит от напряжения на его зажимах.
Внутреннее сопротивление такого источника можно условно принять равным бесконечности. - Приемник — это устройство, потребляющее энергию или преобразующее электрическую энергию в другие виды энергии.
- Двухполюсник — это цепь, имеющая два зажима для подключения (полюса).
- Идеальный R-элемент (резистивный элемент, резистор) — это такой пассивный элемент цепи, в котором происходит необратимый процесс преобразования электрической энергии в тепловую.
Основной параметр резистора — это его сопротивление.
Сопротивление измеряется в омах. СИ: Ом
Проводимость — это обратная величина по отношению к сопротивлению..
Измеряется проводимость в сименсах. СИ: См.
Формула мощности R-элемента:.
Формула энергии R-элемента:
.
- Идеальный С-элемент (емкостной элемент, или конденсатор) — это такой пассивный элемент цепи, в котором происходит процесс преобразования энергии электрического тока в энергию электрического поля и наоборот. В идеальном C-элементе потери энергии отсутствуют.
Формула ёмкости:
. Примеры: задача 1, задача 2.
Ток в ёмкости:
Напряжения на ёмкости:
.
Закон коммутации для емкостного элемента. При токе конечной амплитуды заряд на C-элементе не может измениться скачком:.
.
При неизменной ёмкости, напряжение на емкостном элементе не может измениться скачком:.
Мощность C-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия C-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Емкость измеряется в фарадах. СИ: Ф. - Идеальный L-элемент (индуктивный элемент или катушка индуктивности) — это такой пассивный элемент цени, в котором происходит процесс преобразования энергии электрического тока в энергию магнитного поля и наоборот. В идеальном L-элементе потери энергии отсутствуют.
Для линейного L-элемента формула индуктивности (L) имеет вид:
,
где— потокосцепление.
Индуктивность обозначается буквойи играет роль коэффициента пропорциональности между потоком
и током
.
Напряжение на индуктивном элементе:
.
Ток в индуктивном элементе:
.
Закон коммутации для индуктивного элемента. При напряжении конечной амплитуды, потокосцепление не может измениться скачком:.
.
При неизменной индуктивности ток в индуктивном элементе не может измениться скачком:.
Мощность L-элемента:.
При p > 0 — энергия запасается, при p < 0 — энергия возвращается в источник.
Энергия L-элемента:
, или
.
Если к моменту времени, энергия равна 0, то
Индуктивность измеряется в генри. СИ: Гн
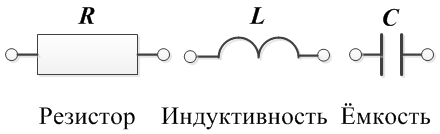
Пример: задача 3. - R, L, C — основные пассивные двухполюсные элементы электрических цепей.
- Основные законы электрических цепей
- Закон Ома для участка цепи, не содержащего источник ЭДС.
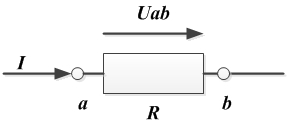
Закон Ома для участка цепи, не содержащего источник ЭДС, устанавливает связь между током и напряжением на этом участке.
Применительно к данному рисунку, математическое выражение закона Ома имеет вид:
, или
Формулируется это равенство так: при неизменном сопротивлении проводника напряжение на нем пропорционально току в проводнике. - Закон Ома для участка цепи, содержащего источник ЭДС
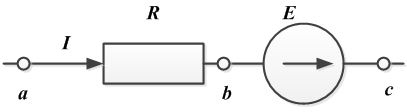
Для схемы
.
Для схемы
.
В общем случае
.
- Закон Джоуля-Ленца. Энергия, выделяемая на сопротивлении R при протекании по нему тока I, пропорциональна произведению квадрата силы тока и величины сопротивления:
- Законы Кирхгофа.
Топология (строение) цепи.
Электрическая схема — графическое изображение электрической цепи.
Ветвь ‐ участок цепи, содержащий один или несколько последовательно соединенных элементов и заключенный между двумя узлами.
Узел ‐ точка цепи, где сходится не менее трех ветвей. Узлы нумеруют произвольно, как правило, арабской цифрой. На схеме узел может быть обозначен точкой, а может и не быть обозначен. Как правило, не обозначают те узлы, расположение которых очевидно (т‐образные соединения). Если пересекающиеся ветви образуют узел, то он обозначается точкой. Если в месте пересечения ветвей точки нет, то и узла нет (провода лежат друг на друге).
Контур – замкнутый путь, проходящий по нескольким ветвям. Контуры независимы, если отличаются хотя бы одной ветвью. Контура обозначают стрелкой с указанным направлением обхода и римской цифрой. Направление обхода выбирают произвольно. Независимых контуров в схеме может быть много, при этом не все эти контура необходимы для составления достаточного для решения задачи количества уравнений.
Первый закон Кирхгофа:
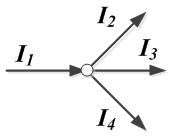
1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю:
;
2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов:
. Пример 1. Первый закон Кирхгофа.
Второй закон Кирхгофа:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
. Пример 2. Второй закон Кирхгофа.
- Матричная форма записи уравнений Кирхгофа:
,
где А, В — квадратные матрицы коэффициентов при токах и напряжениях порядка p х p (p — число ветвей схемы; q — число узлов схемы);
I, E — матрицы-столбцы неизвестных токов и заданных ЭДС
Элементами матрицы А являются коэффициенты при токах в левой части уравнений, составленных по первому и второму законам Кирхгофа. Первыестроки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
Элементы следующихстрок матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строки матрицы имеют нулевые элементы, так как ЭДС в правой части уравнений, записанных по первому закону Кирхгофа, отсутствуют. Остальные
строки содержат элементы +1, -1 в зависимости от того, с каким знаком входит ЭДС в уравнение, и 0, если ЭДС в уравнения не входит.
Общее решение уравнений, составленных по законам Кирхгофа:
,
где— матрица проводимостей.
.
Токи в каждой ветви:
;
;
.
- Режимы работы электрических цепей
- Номинальный режим работы элемента электрической цепи — это режим, при котором он работает с номинальными параметрами.
- Согласованный режим — это режим, при котором мощность, отдаваемая источником или потребляемая приемником, имеет максимальное значение. Такое значение получается при определенном соотношении (согласовании) параметров электрической цепи.
- Режим холостого хода — это такой режим, при котором через источник или приемник не протекает электрический ток. При этом источник не отдает энергию во внешнюю часть цепи, а приемник не потребляет ее. Для двигателя это будет режим без механической нагрузки навалу.
- Режим короткого замыкания — это режим, возникающий при соединении между собой разноименных зажимов источника или пассивного элемента, а также участка электрической цепи, находящегося под напряжением.
- Электрические цепи постоянного тока
- Если ток постоянный, то отсутствует явление самоиндукции и напряжение на катушке индуктивности равно нулю:
, так как
- Постоянный ток через емкость не проходит.
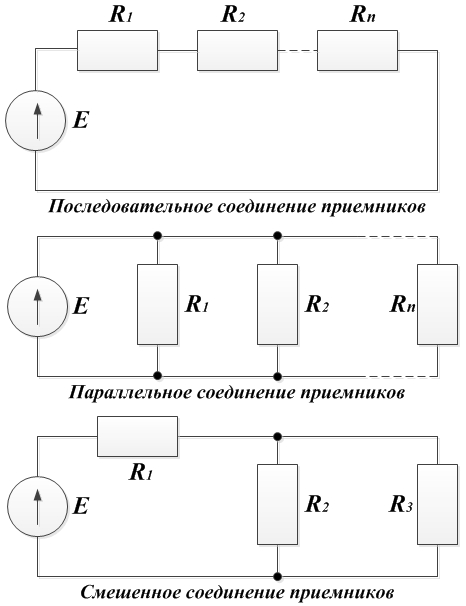
- Простая цепь постоянного тока — это цепь с одним источником при последовательном, параллельном или смешанном соединение приемников.
При последовательном соединении приемников:
I×Rэкв;
Rэкв=ΣRi.
При параллельном соединении приемников напряжение на всех приемниках одинаково.
По закону Ома токи в каждой ветви:
.
По первому закону Кирхгофа общий ток:
E×Gэкв;
Gэкв=G1+G2+…+Gn; Rэкв=1/Gэкв.
При смешанном соединении:
Rэкв=.
- Метод контурных токов.
Метод основан на применении второго закона Кирхгофа и позволяет сократить при расчете сложных систем число решаемых уравнений.
Во взаимно независимых контурах, где для каждого контура хотя бы одна ветвь входит только в этот контур, рассматривают условные контурные токи во всех ветвях контура.
Контурные токи, в отличие от токов ветвей, имеют следующие индексы:или
Уравнения составляют по второму закону Кирхгофа для контурных токов.
Токи ветвей выражают через контурные токи по первому закону Кирхгофа.
Число выбираемых контуров и число решаемых уравнений равно числу уравнений, составляемых по второму закону Кирхгофа:.
Сумма сопротивлений всех резистивных элементов каждого контура со знаком плюс является коэффициентом при токе контура, имеет следующие индексы:или
Знак коэффициента при токе смежных контуров зависит от совпадения или несовпадения направления смежных контурных токов. ЭДС входят в уравнение со знаком плюс, если направления ЭДС и направление тока контура совпадают. Пример 3. Метод контурных токов. - Метод узловых потенциалов.
Метод основан на применении первого закона Кирхгофа и позволяет сократить число решаемых уравнений при нахождении неизвестных токов до. При составлении уравнений потенциал одного из узлов схемы принимают равным нулю, а токи ветвей выражают через неизвестные потенциалы остальных
узлов схемы и для них записывают уравнения по первому закону Кирхгофа. Решение системы
уравнений позволяет определить неизвестные потенциалы, а через них найти токи ветвей.
Приследует отдавать предпочтение методу узловых потенциалов.
- Формула двух узлов:
.
Пример 4. Метод узловых потенциалов. - Метод пропорциональных величии.
Метод применяют для нахождения неизвестных токов при цепочечном соединении резистивных элементов в электрических цепях с одним источником. Токи и напряжения, а также и известную ЭДС цепи выражают через ток самой удаленной от источника ветви. Задача сводится к решению одного уравнения с одним неизвестным. - Баланс мощностей
На основании закона сохранения энергии мощность, развиваемая источниками электрической энергии, должна быть равна мощности преобразования в цепи электрической энергии в другие виды энергии:
.
— сумма мощностей, развиваемых источниками;
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
Баланс мощностей составляют, чтобы проверить правильность найденного решения. При этом сравнивают мощность, внесенную в цепь источниками энергии с мощностью, затрачиваемой потребителями.
Формула мощности для одного резистора:
Суммарная мощность потребителей:
PП=
Мощность источников:
Pист = PE + PJ,
где PE = ±EI — мощность источника ЭДС (определятся умножением его ЭДС на ток, протекающий в данной ветви. Ток берут со знаком, полученным в результате расчета. Минус перед произведением ставят, если направление тока и ЭДС не совпадают на схеме);
PJ = JUJ — мощность источника тока (определятся умножением тока источника на падение напряжения на нем).
Для определения UJ выбирают любой контур, который включал бы в себя источник тока. Обозначают падение UJ на схеме против тока источника, и записывают контурное уравнение. Все величины, кроме UJ, в данном уравнении уже известны, что позволяет рассчитать падение напряжения UJ.
Сравнение мощностей: Pист = PП. Если равенство соблюдено, значит, баланс сошелся и расчет токов верен. - Алгоритм расчета цепи по законам Кирхгофа
- Топология цепи.
- Определяем общее число ветвей p*.
- Определяем число ветвей с источниками тока pит. Токи в данных ветвях считаем известными и равными токам источников.
- Определяем число ветвей с неизвестными токами: p*‐pит
- Находим количество узлов q.
- Находим число уравнений, составляемых по первому закону Кирхгофа:
.
- Находим число уравнений, составляемых по второму закону Кирхгофа:
.
- Произвольно наносим на схему номера и направления неизвестных токов.
- Произвольно наносим на схему номера узлов.
- Составляем узловые уравнения для произвольно выбранных узлов (по первому закону).
- Обозначаем на схеме контура и выбираем направления их обхода.
- Количество обозначаемых контуров равно количеству уравнений, составляемых по второму закону Кирхгофа. При этом ни один из контуров не должен включать в себя ветвь с источником тока.
- Составляем контурные уравнения для выбранных контуров (по второму закону).
- Объединяем составленные уравнения в систему. Известные величины переносим в правую часть уравнений. Коэффициенты при искомых токах вносим в матрицу А (левые части уравнений)(о матрицах читаем здесь). Заполняем матрицу F, занося в нее правые части уравнений.
- Решаем полученную систему уравнений (примеры решения систем уравнений).
- Проверяем правильность решения составлением баланса мощностей.
Пример: задача 4.
- Электрические цепи переменного тока
- Электрическая цепь синусоидального тока — это электрическая цепь, в которой ЭДС, напряжения и и токи, изменяющиеся по синусоидальному закону:
- Переменный ток — это ток, периодически меняющийся по величине и направлению и характеризующийся амплитудой, периодом, частотой и фазой.
- Амплитуда переменного тока — это наибольшее значение, положительное или отрицательное, принимаемое переменным током.
- Период — это время, в течение которого происходит полное колебание тока в проводнике.
- Частота — это величина, обратная периоду.
- Фаза — это угол
или
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
- Периодический режим:
. К такому режиму может быть отнесен и синусоидальный:
,
где— амплитуда;
— начальная фаза;
— угловая скорость вращения ротора генератора.
При f = 50 Гцрад/с.
- Синусоидальный ток — это ток изменяющийся во времени по синусоидальному закону:
.
- Среднее значение синусоидального тока (ЭДС, напряжение), формула:
,
то есть среднее значение синусоидального тока составляетот амплитудного. Аналогично,
.
- Действующее значение синусоидального тока (ЭДС, напряжение), формула:
. Аналогично,
.
- Количество теплоты, выделенное за один период синусоидальным током, формула:
.
Действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты,что и синусоидальный ток.
=R×Iпост2×T или Iпост=I=
- Коэффициент амплитуды синусоидального тока (κa) — это отношение амплитуды синусоидального тока к действующему значению синусоидального тока:
.
- Коэффициент формы синусоидального тока (κф) — это отношение действующего значения синусоидального тока к среднему за пол периода значению синусоидального тока:
κф=.
Для несинусоидальных периодических токов κa≠, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
- Резонансные явления в электрических цепях
- Резонанс напряжений.
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю.
Режим резонанса может быть получен при изменении частоты ω питающего напряжения или изменением параметров L и C.
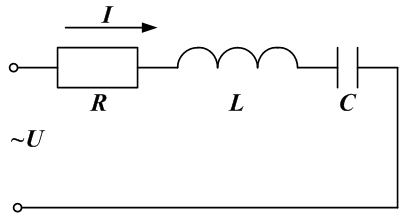
При последовательном соединении возникает резонанс напряжения.
Ток в схеме равен:
При совпадении вектора тока с вектором напряжения по фазе:
где— резонансная частота напряжения, определяемая из условия
Тогда
Волновое или характеристическое сопротивление последовательного контура:
Добротность контура — это отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса:
Добротность контура представляет собой коэффициент усиления по напряжению:
ULрез=IрезXрез=
В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции. - Резонанс токов.
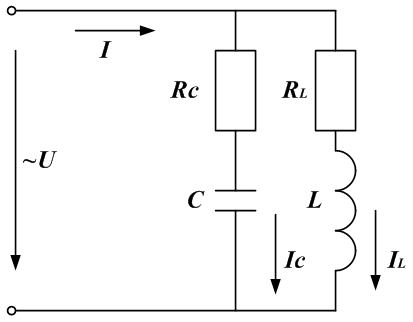
Резонанс токов может возникнуть при параллельном соединении реактивных элементов в цепях переменного тока. В этом случае:где
тогда
При резонансной частоте реактивные составляющие проводимости могут сравниться по модулю и суммарная проводимость будет минимальной. При этом общее сопротивление становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость:.
При g << bL ток в ветви с индуктивностью значительно больше общего тока, поэтому такое явление называется резонансом токов.
Резонансная частота:
ω*=
Из формулы следует:
1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если RL и RC больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс не возможен;
3) если RL = RC = ρ, то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при RL = RC << ρ резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам при резонансе напряжений.
Реактивная мощность при резонансе токов равна нулю. Подробно, реактивная мощность рассмотрена здесь.
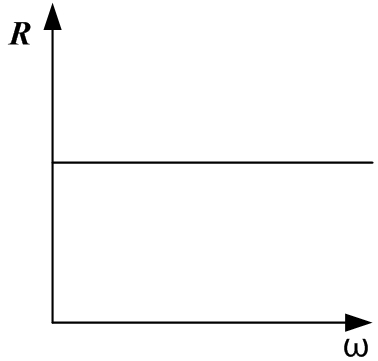
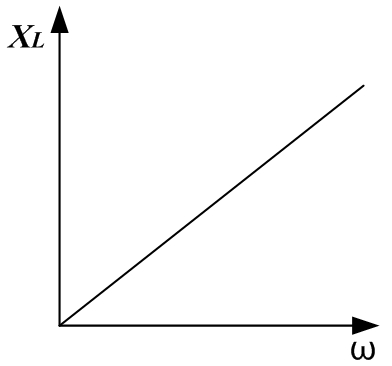
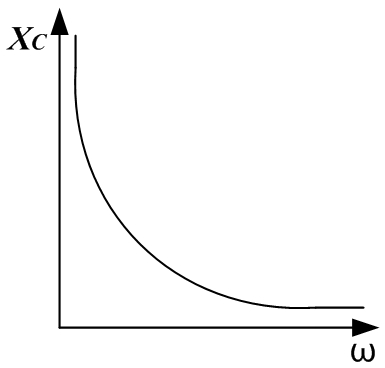
Идеальное активное сопротивление не зависит от частоты, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:

Основные законы электротехники для начинающих
Содержание
- 1 Великий Ом
- 2 Вычисление полного сопротивления цепи (Z)
- 3 Определение полной мощности (S) в электротехнике
- 4 Закон Джоуля-Ленца
- 5 Первый закон Кирхгофа
- 6 Второй закон Кирхгофа
- 7 Видео по теме
Сегодня сложно представить мир без электричества, а также приборов, машин и устройств, работающих на нем. Электротехника окружает нас в быту и на улицах. Без нее до сих пор бы на производствах преобладал ручной труд. Чтобы развивать эту отрасль, следует знать основные законы электротехники.
Великий Ом
Его закон признан самым главным в физике электроцепей, ведь без него невозможно рассчитать в них ни силу тока, ни степень падения напряжения, ни уровень сопротивления. Открытый немецким ученым Омом закон определяет соотношение в электрической цепи ее составляющих. Формулировка представлена ниже на картинке.
То есть, в электроцепи при высоком показателе напряжения показатели тока будут также высокие. С другой стороны, при высоком показателе сопротивления в ней меньше сила тока. Если сравнивать с потоком жидкости в трубе, то закон будет выглядеть так: при высоком давлении (в случае с током — напряжении) и малом сопротивлении стенок напор будет сильным, и наоборот.
Математически закон выглядит так: сопротивление (R) в цепи или на ее участке = 1 Ом, если по ней проходит ток с силой 1 Ампер при напряжении равном 1 Вольту. Величина тока (в А) определится, если напряжение (В) поделить на сопротивление (Ом).
Формула также может быть представлена в виде треугольника: если закрыть параметр, который требуется определить, оставшиеся два станут решением для его вычисления.
Использовать треугольник в качестве решения задач можно только в том случае, если параметры даются в вольтах (U), в омах (R) и в амперах (I).
Ниже приведен пример, как действует этот закон электротехники. В нем источником напряжения является аккумулятор. Через него пропущено два провода, которые подсоединены к резистору с разных сторон. Формула на рисунке отображает, как рассчитать R (сопротивление в омах), разделив U (напряжение в вольтах) на I (ток в амперах).
Под основной формулой в круге изображены ее варианты. Чтобы работать с ними, нужно закрыть любой параметр, проводя вычисления с оставшимися. Сделать это легко: если составляющие формулы расположены рядом, например, R и I, то их показатели нужно умножить, а если друг под другом, то производится деление.
Например, нужно найти величину R, используя показатели амперметра (I=2.6 А) и вольтметра (U=12 В). Сопротивление будет равно: R = 12:2.6 = 4.6 Ом.
Это основные формулы электротехники, благодаря им находим не только сопротивление в электрической цепи, но и напряжение, и силу тока (однофазного переменного с емкостным или индуктивным сопротивлением). Для начинающего электрика азами профессии является именно закон Ома.
Вычисление полного сопротивления цепи (Z)
Чтобы узнать показатель Z, нужно воспользоваться представленной ниже формулой:
Активное сопротивление — это какой-либо вид энергии, полученный путем перехода в нее электрической энергии в цепи или ее части. Например, она может превратиться в механическую, которая используется в электродвигателях, химическую или тепловую (электролиз и диэлектрики соответственно). Обозначается буквой R.
Емкостное сопротивление — это параметр, который обозначает уровень сопротивления электрической емкости цепи или ее части переменному току. То есть показатели тока или напряжения меняются из-за коэффициента самоиндукции или емкостного элемента. Обозначается Xc.
Индуктивное сопротивление — это степень сопротивления проводника, входящего в электрическую цепь переменного тока. То есть, индуктивность (обозначается L) в электроцепи создает состояние, когда электроток запаздывает по сравнению с электронапряжением. Обозначается XL.
Чтобы вычислить общее (полное) сопротивление Z в электрической цепи, необходимо знать параметры всех видов сопротивления. Все величины используются в ТОЭ для упрощения решения задач и проведения расчетов согласно формулам.
Определение полной мощности (S) в электротехнике
Мощность — важный показатель в электротехнике. Чтобы определить полную S, нужно использовать приведенную ниже формулу:
В данной формуле представлены:
- Активная мощность, то есть потребляемая, является частью полной. Обозначается P и выражается в Вт.
- Реактивная мощность — величина, которая обозначает колебания энергии в работающих электрических устройствах. Обозначается буквой Q, измеряется в ВАр (вольт/ампер реактивный).
- Полная мощность. Обозначается S и измеряется в ВА (вольт/ампер).
Чтобы определить уровень активной и реактивной мощностей, нужно воспользоваться приведенными ниже формулами:
В которых:
- U — напряжение;
- I — сила тока;
- cosΦ — коэффициент мощности.
Ниже представлены формулы для вычисления активной мощности для различных электрических цепей:
Чтобы определить S, нужно произвести расчеты активной и реактивной мощностей, после чего воспользоваться формулой:
Закон Джоуля-Ленца
Он применяется для определения теплового действия тока: Q = I2Rt. Благодаря этой формуле можно вычислить Q (теплоту в джоулях) при прохождении постоянного тока через проводник. При этом Q будет пропорционально силе тока в квадрате (I2 в амперах), сопротивлению проводника (R в омах) и времени прохождения тока (t в секундах).
Без определения уровня теплоты, выделяемого электротоком при прохождении через проводник, невозможно создание электрических нагревательных приборов и печей.
Первый закон Кирхгофа
Законы Кирхгофа универсальны для всех электротехнических задач, так как связаны с соотношением токов и напряжений в разветвленных цепях. Они подходят как для постоянных и переменных электротоков и электронапряжений, так и для линейных и нелинейных электрических цепей.
Первый закон представлен ниже:
Краткий вариант этого закона гласит: если по электроцепи проходит только постоянный электроток, то в ней нет ни единой точки, в которой бы мог накапливаться электрозаряд, в противном случае он не был бы постоянным. То есть, первый закон Кирхгофа дает определение непрерывности потока электрического тока. При этом входящие в узлы и исходящие из них электротоки имеют разные заряды: одни — положительные, а другие — отрицательные. В виде формулы этот закон выглядит так:
Ниже приведен пример использования первого закона:
Второй закон Кирхгофа
Это правило относится к замкнутым контурам. Закон гласит:
То есть суммы параметров электротоков и внешних/внутренних сопротивлений на всех участках контура будут равны сумме параметров сторонних электродвижущих сил (ЭДС), входящих в этот контур. Формула выглядит так:
При этом:
- Im и Rm — параметры падения напряжения;
- N — количество участков контура.
Ниже приведен пример применения законов:
Таково общее представление об основных законах электротехники.
Видео по теме
Основные формулы и законы электротехники
Измеряемые величины |
формулы |
Обозначения и единицы измерения. |
| Сопротивление проводника омическое (при постоянном токе) | ro – омическое сопротивление, ом;
ρ — удельное сопротивление, Ом мм2/м; l – длина, м; S – сечение, мм2; |
|
| Активное сопротивление при переменном токе | r =kro | r – активное сопротивление, ом;
k – коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках – также явление намагничивания; |
| Зависимость омического сопротивления проводника от температуры | r2=r1(1 + α (t2-t1)) | r2, r1 – сопротивление проводника в омах соответственно при температуре
t2,t1 OC |
| Индуктивное (реактивное) сопротивление | XL = |
XL_— индуктивное сопротивление, ом;
При f=50гц |
| Ёмкостное (реактивное) сопротивление | Xc= |
ХС – ёмкостное сопротивление, ом;
f – частота, гц; L – коэффициент самоиндукции (индуктивность), гн; С – ёмкость, ф; Z – полное сопротивление, ом. |
| Полное реактивное сопротивление | X = XL — XC | |
| Полное сопротивление переменному току | Z = Или Z = |
|
| Ёмкость пластинчатого конденсатора | C = |
С – ёмкость, ф;
S – площадь между двумя электродами, см2 n – число пластин;
b – толщина слоя диэлектрика, см. |
| Общая ёмкость цепи:
При последовательном соединении ёмкостей При параллельном соединении ёмкостей |
С = С1+С2+….. Сn |
Cn,С1,С2 – отдельные ёмкости. |
| Закон Ома; цепь переменного тока с реактивным сопротивлением | I = Или I = |
I – ток в цепи, а;
U – напряжение цепи, в |
| 1й закон Кирхгофа (для узла) | Ii – токи в отдельных ответвлениях, сходящихся в одной точке, а;
r – сопротивление отдельных участков, ом; Е – ЭДС, действующая в контуре, в |
|
| 2й закон Кирхгофа | ||
| Распределение тока в двух параллельных ветвях цепи переменного тока | I1 – ток первой ветви, а;
I2 – ток второй ветви, а; Z1 – сопротивление первой ветви, ом; Z2 – сопротивление второй ветви, ом. |
|
| Закон электромагнитной индукции для синусоидального тока | En = 4,44f |
En – наведённая ЭДС, в;
f – частота, гц;
B – индукция магнитного поля в стали, гс; S – сечение магнитопровода, см2 |
| Электродинамический эффект тока для двух параллельных проводников | F=2,04i1i2 |
F – сила, действующая на l (см) длины проводника, кГ;
i1,i2 – амплитудные значения токов в параллельных, а; a – расстояние между проводниками, см; l – длина проводника, см |
| Подъёмная сила электромагнита | Р = ( |
P – подъёмная сила, кГ;
B3 – индукция в воздушном зазоре; Вз = 1000гс (электромагниты для подъёма мелких деталей); Вз = 8000 – 10000 гс (для подъёма крупных деталей); S – сечение стального сердечника, см2 |
| Тепловой эффект тока | Q = 0,24I2rt
Или Q = 0,24UIt |
Q – количество выделяемого тепла, кал;
t – время протекания тока, сек; r – сопротивление, ом; A – количество вещества, отложившегося на электроде, мг;
|
| Химический эффект тока | А = |
|
| Зависимости в цепи переменного тока при частоте 50гц:
Период изменения тока Угловая скорость |
Т =
|
T- период изменения тока, сек;
f – частота тока, а;
|
| Зависимости токов и напряжений в цепи переменного тока:
Ток в цепи Напряжение в цепи |
I = Ia = Icos Ip = Isin U = Ua = Ucos Up = Usin |
I – полный ток в цепи, а;
Ia – активная составляющая тока; Ip – реактивная составляющая тока, а; U – напряжение в цепи, в; Ua – активная составляющая напряжения; в Up – реактивная составляющая напряжения, в;
|
| Соотношения токов и напряжений в трёхфазной системе:
Соединение в звезду Соединение в треугольник |
IЛ = IФ UЛ = 1,73UФ IЛ = 1,73IФ UЛ = UФ |
IЛ – ток линейный, а;
IФ – ток фазный, а; UЛ – напряжение линейное, в; UФ – напряжение фазное, в. |
| Коэффициент мощности |  |
P – активная мощность, вт;
Q – реактивная мощность, вар; S – кажущаяся (полная) мощность, ва; r – активное сопротивление, ом; z – полное сопротивление, ом |
| Мощность в цепи переменного тока:
Цепь однофазного тока Цепь трёхфазного тока |
P = UIcos Q = UIsin S = UI = P = 1,73UIcos Q = 1,73UIsin S = 1,73UI |
|
| Мощность в цепи постоянного тока | P = UI
P = I2R P = |
|
| Энергия в цепи постоянного тока | Wa = UIt
Wa = I2Rt Wa = |
Wa – активная энергия, втч;
Wp – реактивная энергия, варч; t – время, ч |
| Энергия в цепи переменного тока:
Цепь однофазного тока Цепь трёхфазного тока |
Wa = UIcos Wp = UIsin Wa = 1,73UIcos Wp = 1,73UIsin |

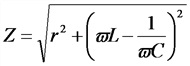
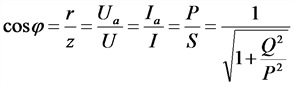








 перейти:
перейти: перейти:
перейти: 


 ,
, ,
, ,
, — активное сопротивление, Ом;
— активное сопротивление, Ом; — индуктивное сопротивление, Ом;
— индуктивное сопротивление, Ом; — индуктивность, Гн;
— индуктивность, Гн; — емкостное сопротивление, Ом;
— емкостное сопротивление, Ом; — ёмкость, Ф.
— ёмкость, Ф. ,
, — коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника.
— коэффициент, учитывающий увеличение сопротивления при переменном токе, зависящий от: частоты тока; магнитных свойств, проводимости и диаметра проводника. и считают
и считают  .
. .
. ,
,



 .
. .
. .
. . Примеры: задача 1, задача 2.
. Примеры: задача 1, задача 2.
 .
. .
. .
. .
. .
. , или
, или .
. , энергия равна 0, то
, энергия равна 0, то
 ,
, — потокосцепление.
— потокосцепление. .
. .
. .
. .
. .
. .
.
 , или
, или 
 .
.
 .
. .
.
 ;
;
 . Пример 1. Первый закон Кирхгофа.
. Пример 1. Первый закон Кирхгофа.
 . Пример 2. Второй закон Кирхгофа.
. Пример 2. Второй закон Кирхгофа. ,
, строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение.
строки матрицы А содержат коэффициенты при токах в уравнениях, составленных по первому закону Кирхгофа, и имеют элементы +1, -1, 0 в зависимости от того, с каким знаком входит данный ток в уравнение. строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые
строк матрицы А равны значениям сопротивлении при соответствующих токах в уравнениях, составленных по второму закону Кирхгофа, с соответствующим знаком. Элементы матрицы В равны коэффициентам при ЭДС в правой части уравнений, составленных по законам Кирхгофа. Первые  ,
, — матрица проводимостей.
— матрица проводимостей. .
. ;
; ;
;
 .
. , так как
, так как 
 I×Rэкв;
I×Rэкв; .
. E×Gэкв;
E×Gэкв; .
. или
или 
 .
. или
или 
 следует отдавать предпочтение методу узловых потенциалов.
следует отдавать предпочтение методу узловых потенциалов. .
. .
. — сумма мощностей, развиваемых источниками;
— сумма мощностей, развиваемых источниками; — сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.
— сумма мощностей всех приемников и необратимых преобразований энергии внутри источников.

 .
.
 или
или  , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной. . К такому режиму может быть отнесен и синусоидальный:
. К такому режиму может быть отнесен и синусоидальный: ,
, — амплитуда;
— амплитуда; — начальная фаза;
— начальная фаза; — угловая скорость вращения ротора генератора.
— угловая скорость вращения ротора генератора. рад/с.
рад/с. .
. ,
, от амплитудного. Аналогично,
от амплитудного. Аналогично, .
. . Аналогично,
. Аналогично, .
. .
. =R×Iпост2×T или Iпост=I=
=R×Iпост2×T или Iпост=I=
 .
. .
. , κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального.
, κф≠1,11. Это отклонение косвенно свидетельствует о том, насколько несинусоидальный ток отличается от синусоидального. .
.




 — резонансная частота напряжения, определяемая из условия
— резонансная частота напряжения, определяемая из условия




 где
где


 .
.
















