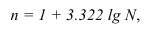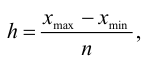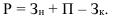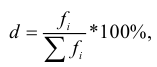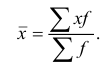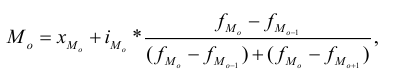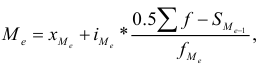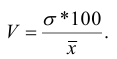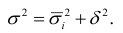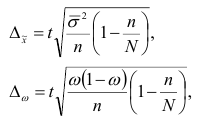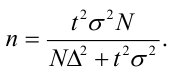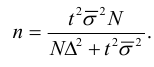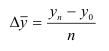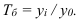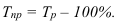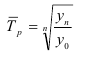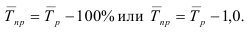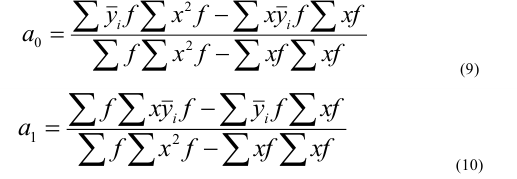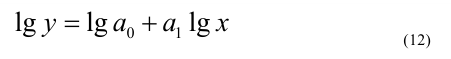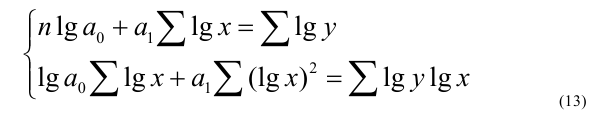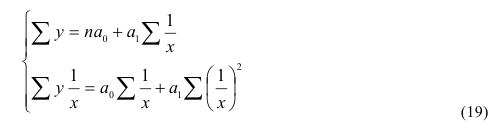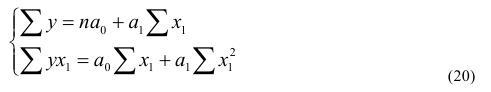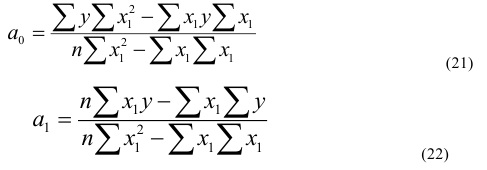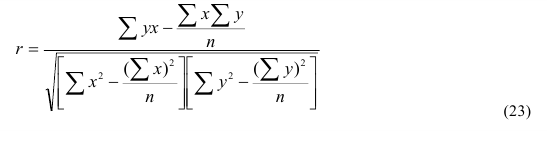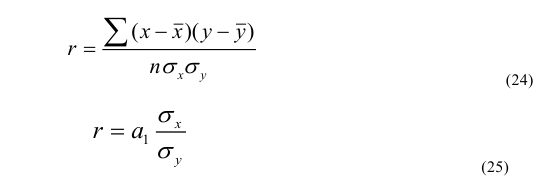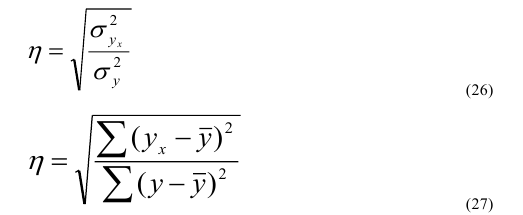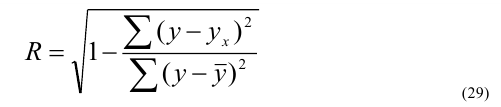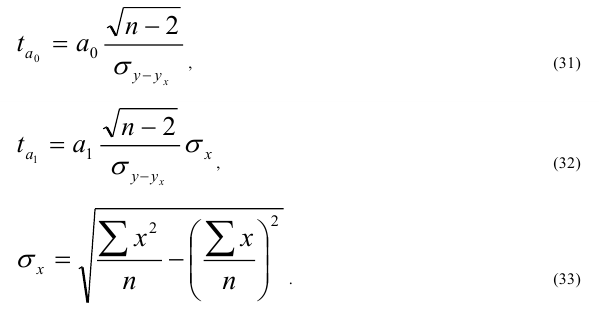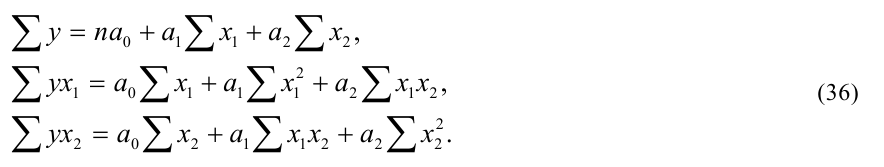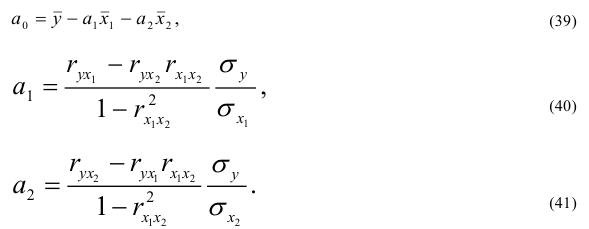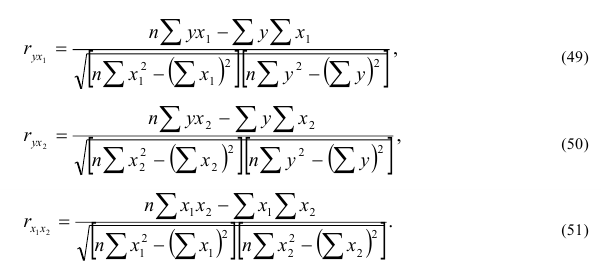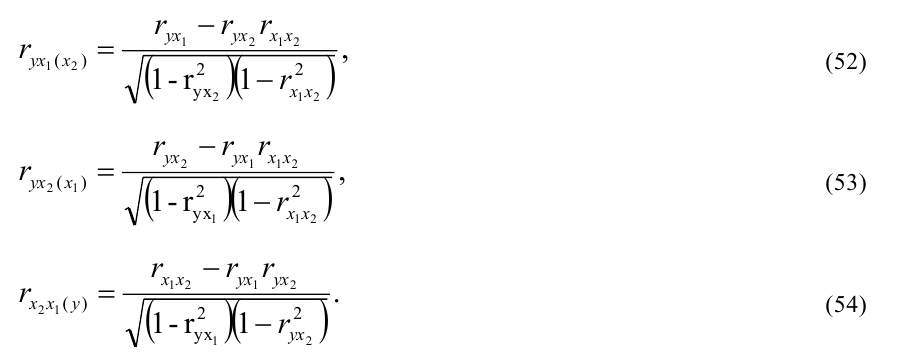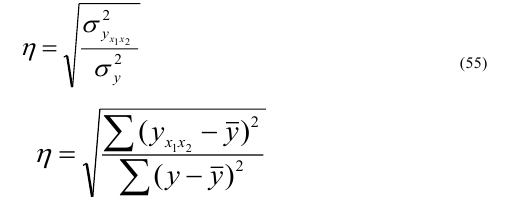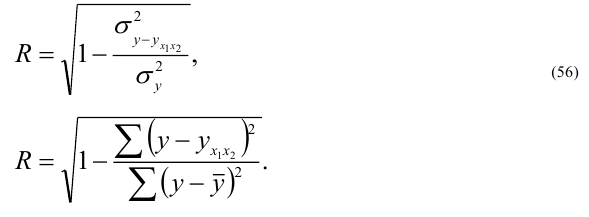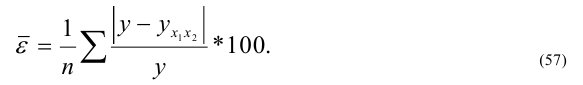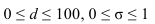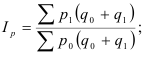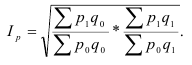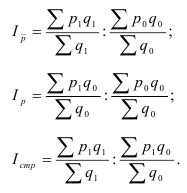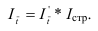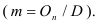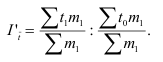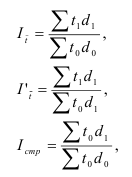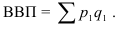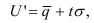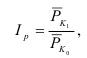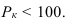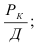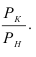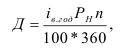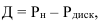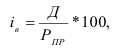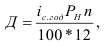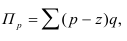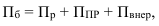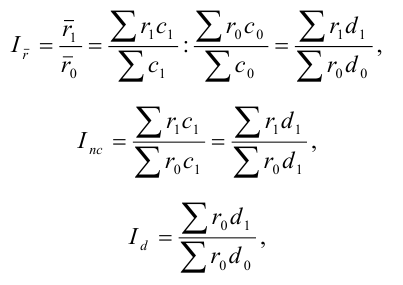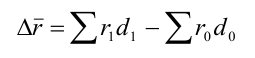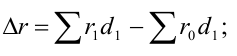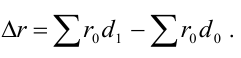~
7
~
Формулы по статистике
Тема 1: Группировка статистических данных
Определение
числа групп
(если группи-ка по непрер. приз-ку или
дискрет. со многими знач-ями)
Определение
величины равного интервала:
Тема 2: Абсолютные и относительные величины
Относительные
величины:
1)
относит.
вел-на структуры:
2)
относит.
вел-на планового задания:
3)
относит.
вел-на выполнения плана:
4)
относит.
вел-на динамики или темп роста:
5)
относит.
вел-на сравнения
6)
относит.
вел-на интенсивности
(пример: фондоотдача = объем/стоимость
(один год))
Тема 3: Средние величины и показатели вариации
Средняя
арифметическая
простая:
взвешенная:
Средняя
гармоническая
простая:
взвешенная:
, сумма
значений признака по группе
Свойства
средн. арифметической:
-
если
каждую вари-ту х
умен-ть
или увел-ть на одно и то же число, то ср.
вел-на умен-ется или увел-ется на это
же число; -
если
каждую вари-ту х
умен-ть
или увел-ть в одно и то же число раз, то
ср. вел-на умен-ется или увел-ется в одно
и то же число раз; -
если
каждую частоту f
умен-ть или увел-ть в одно и то же число
раз, то ср. вел-на не изменится.
Ср.
вел-на зависит
от
вар-ты х
и структуры совок-сти,
кот. харак-ется долями d.
Ряд
распределения имеет 3
центра:
1)
ср.
аримет-кое;
2)
мода
– наиболее часто встречающаяся вар-та
[M0];
3)
медиана
– вар-та, стоящая в середине ряда
распре-ния. Сначала находят N
медианы, кот. равен n/2,
если число еди-ц совок-сти n
– чётное, или
, если число еди-ц совок-сти нечетное
[Me].
Осн.
пока-ли вариации:
1)
размах
вариации:
2)
ср.
линейное отклонение
(ср. арифм-кая из абсолют. откл-ний отдел.
значений)
Для
несгруппир. данных:
Для
сгруппир. данных:
3)
ср.
квадратическое отклонение
(хар-ет ср. абсол. откл-ние вар-ты от ср.
вел-ны)
Для
несгруппир. данных:
Для
сгруппир. данных:
4)
Дисперсия
– квадрат среднеквадр-ного откл-ния
Для
несгруппир. данных:
Для
сгруппир. данных:
Общая
дисперсия:
(для сгрупп.)
(для несгрупп.)
– ср.
вел-на резул. приз-ка в сово-сти,
— частота (в совокупности!)
Внутригрупповая
дисперсия:
— кол-во вариант в группе i
Междугрупповая
дисперсия:
— кол-во вариант в группе i
Правило
сложения дисперсий:
Не
имеет еди-ц измерения.
5)
Коэффициент
вариации
хар-ет ср. относит. откл-ние вар-ты от
ср. вел-ны.
Способ
моментов
Часто
мы сталкиваемся с расчетом средней
арифметической упрощенным способом.
В
этом случае используются свойства
средней величины. Метод упрощенного
расчета называется способом моментов,
либо способом отсчета от условного
нуля.
Способ
моментов предполагает следующие
действия:
1)
Выбирается начало отсчета (из
х)
– условный нуль (A).
Обычно как можно ближе к середине
распре-ния.
2)
Находятся отклонения вариантов от
условного нуля ().
4)
Если эти отклонения содержат общий
множитель (k),
то рассчитанные
отклонения
делятся на этот множитель.
Способ
моментов:
Средняя:
Дисперсия:
Тема 4: Выборочное наблюдение
Обозначения
в теории выборки:
|
N |
n |
|
|
|
|
p |
w |
|
P(t) |
Генер.
средняя:
с
задан. уровнем вероя-сти P(t)
– ошибка
выборки для ср. вел-ны
, t
–
критерий
надеж-сти, его вел-на зав-т от уровня
задан. вероя-сти P(t)
Если
1)
P(t)
= 0,683, то t=1;
2)
P(t)
= 0,954, то t=2
; 3)
P(t)
= 0,997, то t=3
– среднеквадр. ошибка выборки
– верна для повторного отбора в выборке.
— для бесповторного отбора
Доказано:
с
задан. уровнем вероя-сти P(t)
– ошибка
выборки для доли
,
– среднеквадр. ошибка выборки для доли
–для повторного отбора
— для бесповторного отбора
Соседние файлы в папке 28-04-2013_17-44-42(1)
- #
21.03.2015476.16 Кб121.doc
- #
- #
- #
- #
- #
Статистика (шпора) — Формулы
Экономическая статистика (экзамен)
Тема 1. Сводка и группировка
Формула Стерджесса (для определения числа групп):
Интервалы группировки (если равные):
Частота-численность отдельных вариантов (
Частость-частоты, выражаемые в долях единицы или в процентах
Тема 2. Средние величины
Средняя арифметическая простая:
(несгруппиров.)
Средняя арифметическая взвешенная:
´x=∑xifi
∑fi
(
интервальн . ряд
)
Средняя гармоническая взвешенная:
(известен статистический
вес)
Мода:
Mo=xMo +dfMo −fMo−1
(
fMo−fMo −1
)
+(fMo−fMo+1)
— нижняя граница модального интервала
Медиана:
(не равные интервалы)
Квартили:
Q3=xQ3+dQ3
3∗∑fi
4−SQ3−1
fQ3
Д8=xД8+dД8
8∑fi
10 −SД8−1
fД8
Фондоотдача=продукция
осн . фонды
Фондооворужённость=осн . фонды
число рабочих
Тема 3. Показатели вариации
Размах вариации:
Простое среднее линейное отклонение:
(нет частоты)
Взвешенное среднее линейное отклонение:
∑¿xi− ´x∨¿fi
∑fi
´
dвзвеш.=¿
Лекция Формулы по статистике
Формулы по статистике
Содержание
Семестр 1_ 2
Группировка статистических данных и ее роль в анализе информации_ 2
Абсолютные, относительные, средние величины_ 2
Относительные величины_ 2
Средние величины_ 2
Статистические распределения и их характеристики_ 3
Показатели вариации (колеблемости) признака_ 4
Сложение дисперсий_ 4
Показатель асимметрии_ 5
Показатель эксцесса (островершинности) 5
Кривые распределения 5
Выборочное наблюдение 6
Формулы ошибок простой случайной выборки_ 7
Формулы для определения численности простой и случайной выборки_ 7
Типичная выборка_ 7
Серийная выборка_ 8
Малые выборки_ 8
Корреляционная связь_ 8
Уравнение регрессии_ 9
Ряды динамики_ 10
Показатели динамики_ 10
Средние показатели динамики_ 10
Тренды_ 11
Семестр 2 (Индексы) 11
Семестр 1
Группировка статистических данных и ее роль в анализе информации
Равный интервал, величина интервала — , M – число групп
Формула Стерджесса (величина интервала) — , N – число наблюдений
Абсолютные, относительные, средние величины
Относительные величины
Относительные величины (ОВ) динамики характеризуют изменение явления во времени. (Коэффициент роста)
Темп роста – с переменной базой — Yn – уровень явления за период (например, выпуск продукции по кварталам года)
С постоянной базой — , Yk – постоянная база сравнения
ОВ планового задания —
ОВ выполнения плана —
ОВ динамики —
ОВ структуры характеризуют долю отдельных частей в общем объеме совокупности (удельный вес) —
ОВ координации отражают отношение численности двух частей единого целого, т. е. показывают, сколько единиц одной группы приходится в среднем на одну, на 10 или на 100 единиц другой изучаемой совокупности.
ОВ координации —
ОВ наглядности (сравнения) отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду времени, но к разным объектам или территориям (например, сравнивается годовая производительность труда по 2-м предприятиям)
ОВ сравнения —
Средние величины
Степенные средние общего типового расчета:
Средняя степенная простая — 
— индивидуальное значение признака, по которому рассчитывается средняя, N – объем совокупности (число единиц)
СрЕдняя степенная взвешенная — 
=n)
|
Значе-ние k |
Наименование средней |
Формула средней |
|
|
Простая |
Средняя |
||
|
-1 |
Гармоническая |
|
|
|
0 |
Геометрическая |
|
|
|
1 |
Арифметическая |
|
|
|
2 |
Квадратическая |
|
|
Гарм. <
Геом <
Арифм <
Квадрат, x=w/f
Гармоническая простая – когда небольшая совокупность и индивидуальные значения не повторяются. Используется, если исчисляем среднюю из обратных величин.
Средняя квадратическая – для расчета среднего квадратического отклонения, являющегося показателем вариации признаков
Средняя геометрическая простая – для вычисления среднего коэффициента роста (темпа) в рядах динамики, если промежутки, к которым относятся коэффициенты роста, одинаковы.
Статистические распределения и их характеристики
Мода – значение признака, которое наиболее часто встречается в совокупности

— нижняя граница модального интервала (интервал с наибольшей частотой),
— величина интервала,
— частота в модальном интервале.
Медиана – значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
— положение медианы

— нижняя граница медианного интервала,
— накопленная частота интервала, предшествующего медианному,
— частота медианного интервала.
Квартель
,
,
Дециль
,
(от 1/10 до 9/10)
Показатели вариации (колеблемости) признака
Среднее линейное отклонение – на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
-для несгруппированных данных (первичного ряда):
-для вариационного ряда:
Среднее квадратическое отклонение
— для несгруппированных данных:
— для вариационного ряда:
Дисперсия
— для несгруппированных данных:
— для вариационного ряда:
Коэффициент вариации (используется для характеристики однородности совокупности по исследуемому признаку)
— до 17% – совокупность совершенно однородна, 17%-33% — достаточно однородна, >33% — неоднородна.
Сложение дисперсий
Величина общей дисперсии () характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности

— общая средняя арифметическая для всей совокупности
Межгрупповая дисперсия () отражает систематическую вариацию, т. е. различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки

— средняя в каждой группе,
— число единиц в каждой группе
Средняя внутригрупповая дисперсия () характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.


Или
Равенство:
Корреляционное отношение

>0,5 – связь между групповым фактором и результирующим признаком – тесная,
<0,5 – связь слабая
Показатель
асимметрии
,

Средняя квадратическая ошибка: , N – число наблюдений
Если , асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если
, асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств.
— правосторонняя асимметрия,
— левосторонняя асимметрия.
Показатель эксцесса (островершинности)
,

>0 – высоковершинное,
< 0 – низковершинное (
= -2 – предел)
Средняя квадратическая ошибка: N – число наблюдений
Кривые распределения
Кривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения.
Плотность распределения (расчет теоретических частот)
,
— нормированное отклонение
,
— определяется по таблице (приложение 1)
Критерий согласия К. Пирсона (Для проверки близости теоретического и эмпирического распределений, для проверки соответствия эмпирического распределения закону нормального распределения)
F – эмпирические частоты в интервале, F’ – теоретические частоты в интервале
Критерий согласия Романовского
, M – число групп, M-3 – число степеней свободы при исчислении частот нормального распределения
Если к<3, то можно принять гипотезу о нормальном характере эмпирического распределения
Критерий Колмогорова
, D – максимальное значение разности между накопленными эмпирическими и теоретическими частотами, N – сумма эмпирических частот
Распределение Пуассона (теоретические частоты)
, N – общее число независимых испытаний, λ – среднее число появления редкого события в N одинаковых независимых испытаниях, M – частота данного события, е=2,71828
Выборочное наблюдение
N – объем генеральной совокупности
N – объем выборочной совокупности (число единиц, попавших в выборку)
— генеральная средняя (среднее значение признака в генеральной совокупности)
— выборочная средняя
Р – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)
W – выборочная доля
— генеральная дисперсия
— выборочная дисперсия
— среднее квадратическое отклонение признака в генеральной совокупности
S – среднее квадратическое отклонение признака в выборочной совокупности.
Неравенство Чебышеба
При неограниченном числе наблюдений, независящих друг от друга из генеральной совокупности с вероятностью сколь угодно близкой к 1, можно утверждать, что расхождение между выборочной и генеральной средней будет сколь угодно малой величиной .
Теорема Ляпунова
Дает количественную оценку ошибки. При неограниченном объеме из генеральной совокупности с Р расхождения выборочной и генеральной средней равна интегралу Лапласа
,

Р – гарантированная вероятность
T – коэффициент доверия, зависящий от Р
|
Р |
0,683 |
0,954 |
0,997 |
|
T |
1 |
2 |
3 |
— предельная ошибка выборки
,
— стандартная среднеквадратическая ошибка
,
— предельная (максимально возможная) ошибка средней, T – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки
,
— предельная (максимально возможная) ошибка доли
Средняя ошибка (n>30) при случайной повторной выборке:
,
При случайной бесповторной выборке:
,
Формулы ошибок простой случайной выборки
|
Способ отбора единиц |
||
|
Повторный |
Бесповторный |
|
|
Средняя ошибка μ: Для средней |
|
|
|
Для доли |
|
|
|
Предельная ошибка Δ: Для средней |
|
|
|
Для доли |
|
|
Доверительные интервалы для генеральной средней –
Доверительные интервалы для генеральной доли –
Доверительная вероятность – функция от t, вероятность находится по приложению3
Формулы для определения численности простой и случайной выборки
|
Способ отбора единиц |
||
|
Повторный |
Бесповторный |
|
|
Численность выборки (n): Для средней |
|
|
|
Для доли* |
|
|
|
*В случае, когда частость w даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии доли, равную 0,25 (если w=0,5, то w(1-w)=0,25). |
Типичная выборка
Применяется в тех случаях, когда из генеральной совокупности можно выделить однокачественные группы единиц (или однородные), затем из каждой группы случайно отобрать определенное число единиц в выборку.
Стандартная среднеквадратическая ошибка:
Повторный отбор — 
— средняя из внутригрупповых
Бесповторный отбор —
Отбор единиц при типичной выборке из каждой типичной группы:
1.Равное число единиц ,
— число единиц, отобранных из I-ой типичной группы, N – общий объем, R – число групп
2.Пропорциональный отбор ,
— доля I-ой группы в общем объеме генеральной совокупности
3.Отбор единиц с учетом вариации случайного признака
Серийная выборка
Вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение.
Средняя стандартная ошибка:
Повторный отбор — ,
, M – число отобранных серий,
— средний уровень признака в серии,
— средний уровень признака для всей выборочной совокупности
Бесповторный отбор — , M – общее число серий
Малые выборки
Выборки, при которых наблюдением охватывается небольшое число единиц (n<30)
Средняя ошибка малой выборки ,
Вероятность того, что генеральная средняя находится в определенных границах, определяется по формуле ,
— значение функции Стьюдента (приложение 4)
Корреляционная связь
Для оценки однородности совокупности – коэффициент вариации по факторным признакам
, совокупность однородна, если
≤ 33%
Линейный коэффициент корреляции
Несгруппированные данные
Сгруппированные данные —
Оценка существенности линейного коэффициента корреляции
При большом объеме выборки ,
. Если это отношение больше значения t-критерия Стьюдента (приложение 6, k=n-2, вероятность – 1-α)
При недостаточно большом объеме выборки ,
Корреляционное отношение 


,
|
Признаки |
А(да) |
|
Итого |
|
В (да) |
A |
B |
A+b |
|
|
C |
D |
C+d |
|
Итого |
A+c |
B+d |
N |
|
A, b,c, d – частоты взаимного сочетания (комбинации) двух альтернативных признаков, n – общая сумма частот |
Коэффициент ассоциации
Коэффициент контингенции
Уравнение регрессии
Линейная
Гиперболичская
Параболическая
Показательная
Для проверки возможности использования линейной функции определяется разность , если она <0,1 то можно применить линейную функцию.
,M – число групп. Если
< F-критерия, то можно. (Значение F-критерия определяется по таблице (приложение 5) α=0,05, число степеней свободы числителя (k1 = m-2) и знаменателя (k2 =n-m))
Достоверность уравнения корреляционной зависимости ,

— значения результативного признака, рассчитанные по уравнению регрессии, L – число параметров в уравнении регрессии.
Если это отношение не превышает 10-15%, то уравнение хорошо отображает изучаемую взаимосвязь.
Ряды динамики
Показатели динамики
Показатель
|
Метод расчета |
||
|
С переменной базой (цепные) |
С постоянной базой (базисные) |
|
|
Абсолютный прирост (показывает, на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного) |
|
|
|
Коэффициент роста (показывает, во сколько раз уровень текущего периода больше (меньше) базисного) |
|
|
|
Темп роста, % (это коэффициент роста, выраженный в %, показывает, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периоа) |
|
|
|
Темп прироста, % (показывает, на сколько % уровень текущего периода больше (меньше) уровня базисного периода) |
|
|
|
Абсолютное значение 1% прироста (показывает, какая абсолютная величина скрывается за относительным показателем – одним процентом прироста) |
|
|
Средние показатели динамики
Показатель
|
Метод расчета |
|
|
Средний уровень ряда -Для интервального ряда |
|
|
-Для моментального ряда с равными интервалами |
|
|
-Для моментального ряда с неравными интервалами |
|
|
Средний абсолютный прирост |
|
|
Средний коэффициент рост |
|
|
Средний темп роста, % |
|
|
Средний темп прироста, % |
|
|
Средняя величина абсолютного значения 1% прироста |
|
Тренды
Линейный
Пусть =0, тогда если количество уровней в ряду динамики нечетное, то временные даты (t) будут (-2, -1, 0, 1, 2). Если четное, то (-5, -3, -1, 1, 3, 5)
Семестр 2 (Индексы)
Индекс – относительная величина, характеризующая изменение уровней сложных социально-экономических показателей во времени, в пространстве или по сравнению с планом.
Индивидуальный индекс физического объема выпуска продукции
Индивидуальный индекс цен
Индивидуальный индекс затрат на выпуск продукции
Индивидуальный индекс стоимости продукции
Агрегатный индекс физического объема продукции (Относительное изменение физического объема продукции в отчетном периоде по сравнению с базисным)
— характеризует абсолютное изменение физического объема в относительном выражении без влияния ценового фактора.
Средний взвешенный арифметический индекс физического объема продукции 
Средний взвешенный гармонический индекс физического объема продукции
Агрегатный индекс цен (характеризует среднее изменение цен по совокупности различных видов продукции)
— абсолютное изменение всей стоимости продукции за счет изменения цен
Агрегатный индекс цен (характеризует среднее изменение цен на потребительские товары)
Агрегатный индекс затрат на выпуск всей продукции
Двухфакторный индекс
Связь:
Индекс планового задания
Индекс степени выполнения плана
Связь:
Изменение себестоимости продукта А по фирме , средняя себестоимость —
Индекс влияния структурных сдвигов в объеме продукции 
Абсолютное изменение общей стоимости продукции за счет двух факторов: , за счет изменения физического объема продукции —
, за счет изменения цен на продукцию —
Абсолютное изменение общих затрат на выпуск продукции за счет двух факторов: , за счет изменения физического объема продукции —
, за счет среднего изменения себестоимости единицы продукции —
.
Выработка — W = Q/T, W – выработка, Q – физический объем реализованной продукции/услуг, T – затраты живого труда (среднесписочная численность работников/рабочих)
Трудоемкость (показатель, обратный выработке) — t = 1/W = T/Q Трудоемкость характеризует величину затрат рабочего времени на единицу произведенной продукции.
Индекс динамики выработки переменного состава, определяющий отношение выработки отчетного периода к выработке базисного периода — Iw = W1/W0
Этот индекс характеризует изменение производительности труда под влиянием всех факторов, а именно: НТП, человеческого фактора (квалификация и т. п.) и др.
Индекс динамики трудоемкости — It = t1/t0
Индекс динамики трудоёмкости характеризует изменение трудоёмкости в отчетном периоде по сравнению с базисным, и его величина зависит от изменения трудоёмкости производимой продукции и от изменения объемов производства этой продукции.
IQ = IW * IT – система связанных индексов, которая позволяет определить влияние интенсивных и экстенсивных факторов на изменение объема продукции, услуг.
Среднегодовая стоимость основных фондов в базисном и отчетном годах — ,
— введенные в эксплуатацию фонды в течение года,
— число месяцев эксплуатации фондов в данном году,
— фонды, выбывшие из эксплуатации в течение года,
— число месяцев, оставшихся до конца года после выбытия фондов из эксплуатации.
Фондоотдача —.
Фондоёмкость – показатель, обратный фондоотдаче, за базисный и отчетный годы по формуле
Индекс динамики фондоотдачи IVп. с.= =
Этот индекс характеризует изменение фондоотдачи под влиянием всех факторов, включая НТП (новая техника, технология), человеческий фактор, структурный фактор, который на уровне АО может выражаться в изменении состава основных фондов в отчетном по сравнению с базисным годом.
Индекс динамики фондоемкости
Влияние интенсивного (качественного) и экстенсивного (количественного) факторов на абсолютное изменение физического объема продукции/услуг. Под экстенсивным фактором обычно понимают абсолютное изменение основных фондов. Под интенсивным – абсолютное изменение показателя фондоотдачи.
Влияние экстенсивного фактора:
Влияние интенсивного фактора:
Влияние обоих факторов:
Показатели фондовооруженности рабочих ,
— среднесписочная численность рабочих.
Индекс динамики фондовооруженности:
Коэффициент износа основных фондов на конец отчетного года
Износ фондов на конец отчетного года
Сообщество Экспонента
- вопрос
- 22.09.2022
Математика и статистика,
Системы управления,
Изображения и видео,
Робототехника и беспилотники,
Глубокое и машинное обучение(ИИ),
Другое
Коллеги, добрый день.
Необходимо использовать corrcoef, а массивы разной длины.
Как сделать кол-во элементов одинаково?
Коллеги, добрый день.
Необходимо использовать corrcoef, а массивы разной длины.
Как сделать кол-во элементов одинаково?
7 Ответов
- вопрос
- 20.09.2022
Другое,
Встраиваемые системы,
Цифровая обработка сигналов,
Системы управления
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт.
Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
- MATLAB
20.09.2022
- Публикация
- 15.09.2022
Системы управления,
Другое
Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
- Публикация
- 10.09.2022
Системы управления,
Электропривод и силовая электроника,
Другое
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.
- Публикация
- 24.08.2022
Цифровая обработка сигналов,
Системы связи,
Математика и статистика
&…
Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.
- вопрос
- 23.08.2022
Математика и статистика,
Радиолокация,
Цифровая обработка сигналов
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
4 Ответа
- ЦОС
- цифровая обработка сигналов
23.08.2022
- Публикация
- 23.08.2022
Цифровая обработка сигналов,
Системы связи,
Математика и статистика
&.
Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.
- Публикация
- 16.08.2022
Цифровая обработка сигналов,
Системы связи,
Математика и статистика
Здесь собрана литература по методам множественного доступа с пространственным разделением.
- вопрос
- 22.07.2022
Изображения и видео,
Цифровая обработка сигналов,
Математика и статистика,
Биология,
Встраиваемые системы,
Глубокое и машинное обучение(ИИ),
Автоматизация испытаний,
ПЛИС и СнК,
Системы управления,
Другое
Здравствуйте.
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
Здравствуйте.
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
2 Ответа
- чтение
22.07.2022
- вопрос
- 17.07.2022
Математика и статистика,
Цифровая обработка сигналов
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера.
Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера.
Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
- MATLAB
- Signal Processing
17.07.2022
Формулы по статистике — n1.doc
приобрести
Формулы по статистике
скачать (97.
Доступные файлы (1):
| n1.doc | 357kb. | 21.04.2010 21:05 | скачать |
- Смотрите также:
- Справочник — Все формулы по математике за 11 класс (Справочник)
- Шпаргалка — Тригонометрия (Шпаргалка)
- Формулы по статистике с описанием (Документ)
- 90 тригонометрических формул (Документ)
- Формулы по статистике (Документ)
- Шпоры — Математика 10-11 класс (Шпаргалка)
- Лекции по статистике (Лекция)
- Основные формулы по математике (Документ)
- Шпаргалка — Основные формулы (Шпаргалка)
- Все формулы по математике и геометрии (Документ)
- Справочник — Все формулы по алгебре и геометрии в школе (Справочник)
- Формулы по Математике, Геометрии, Тригонометрии для подготовки к ЕГЭ и ГИА (Документ)
n1.doc
СОДЕРЖАНИЕ
Средние величины: 3
Простая формула: 3
Средняя гармоническая: 3
Средняя арифметическая 3
Средняя геометрическая 3
Среднее квадратическое 3
Средняя арифметическая взвешенная: 3
Средняя гармоническая взвешенная: 3
Показатели вариации 3
Среднее линейное отклонение: 3
Простая: 3
взвешенная: 3
Дисперсия 3
Среднее квадратическое отклонение: 3
Коэф.
Относительное линейное отклонение. 3
Коэф. вариации. 4
Дисперсия: 4
Способ моментов: 4
Межгрупповая дисперсия: 4
Внутригрупповая дисперсия: 4
Коэффициент детерминации: 4
Эмпирическое кореляц. отн-е. 4
Ряды динамики 4
Моментные РД – вычисление средней. 4
Абсолютный прирост 4
Темп роста базовый. 4
Темп роста цепной: 4
Темп прироста цепной: 5
Темп прироста базовый: 5
Абсолютное значение 1% прироста. 5
Ср. абсолютный прирост: 5
Ср. темп роста. 5
Ср. темп прироста. 5
Ср. значение 1% прироста. 5
Ур-е прямой: 5
Ошибка аппроксимации: 5
Индексы. 5
P — цен 5
Z – себест-ть ед. прод., т. е. затраты на пр-во ед. прод. 5
W – уровень производит. труда (ср. выработка на 1 раб) 5
t – трудоёмкость 5
Индекс физич. объёма. 6
Общий индекс товарооборота: 6
Индекс товарооборота: 6
Общий индекс физического объёма товарооборота: 6
Общая формула для вычисления всех Интегральных показателей: 6
Индекс Цен по Пааше.
Индекс Цен По Ласпейресу: 6
Индекс Цен По Фишеру: 6
Индекс переменного состава: 6
Индекс постоянного состава: 7
Индекс структурных сдвигов: 7
Выборочное наблюдение. 7
Предельная ошибка выборки: 7
Средний размер ошибки признака: 7
Средняя ошибка доли признака: 7
Средний размер ошибки признака: 7
Средняя ошибки доли признака: 7
Взаимосвязи м/у явлениями: 8
Лин. коэф корелляции: 8
Коэф. эластичности 8
Ошибка апроксимации: 8
Расчёт дисперсии: 8
C видов экономической деят-ти. 8
Коэф. роста выпуска товаров: 8
Темп роста выпуска: 8
Темп прироста выпуска товаров: 8
Среднегодовой коэффициент роста выпуска товаров: 8
Среднегодовой темп роста выпуска товаров: 8
Среднегодовой темп прироста выпуска товаров: 8
С рынка товаров и услуг. 9
Коэф неравномерности поставки продукции 9
Дисперсия: 9
Абсолютный размер отклонения (выполнения контракта) 9
Сумма переплаты населения: 9
Территориальный индекс цен: 9
Эмпирический коэф.
Эмпирический коэф. эластичности динамики: 9
Средний коэф. эластичности: 9
Теоретический коэф. эластичности. 9
По уравнению параболы: 9
С оборота торговли и товарных запасов: 9
Валовый оборот торговли: 9
Удельный вес продажи товара в объёме оборота торговли: 10
Виды Относительных Величин 10
Средние величины:
n – число единиц совокупности
xi – значение признака.
Простая формула:
Средняя гармоническая:
Средняя арифметическая
Средняя геометрическая
Среднее квадратическое
ИСС = суммарное значение или объём осредняемого признака/число единиц.
Средняя арифметическая взвешенная:
Средняя гармоническая взвешенная:
Показатели вариации
Среднее линейное отклонение:
Простая:
взвешенная:
Дисперсия
Среднее квадратическое отклонение:
Коэф.

Относительное линейное отклонение.
Коэф. вариации.
Дисперсия:
Способ моментов:
Межгрупповая дисперсия:
Внутригрупповая дисперсия:
Коэффициент детерминации:
Эмпирическое кореляц. отн-е.
Ряды динамики
Моментные РД – вычисление средней.
Если рас-е м/у датами и времени одинаковы:
неодинаково:
Абсолютный прирост
Темп роста базовый.
T=y1/y0
Темп роста цепной:
Темп прироста цепной:
Темп прироста базовый:
Абсолютное значение 1% прироста.
Ср. абсолютный прирост:
Ср. темп роста.
Ср. темп прироста.
Ср. значение 1% прироста.
Ур-е прямой:
Ошибка аппроксимации:
Индексы.
P — цен
P = Оборот торговли/кол-во прод. товаров.
Z – себест-ть ед. прод., т. е. затраты на пр-во ед. прод.
Z = Себестоимость прод., всего – затраты по отгр. прод. / кол-во прод.
W – уровень производит. труда (ср. выработка на 1 раб)
W = V произвед. прод. (WT) / число раб. (Т).
t – трудоёмкость
t = 1/N
T = t*q
Индекс физич. объёма.
Общий индекс товарооборота:
Индекс товарооборота:
Общий индекс физического объёма товарооборота:
Общая формула для вычисления всех Интегральных показателей:
Индекс Цен по Пааше.
Индекс Цен По Ласпейресу:
Индекс Цен По Фишеру:
Индекс переменного состава:
Индекс постоянного состава:
Индекс структурных сдвигов:
Выборочное наблюдение.
Предельная ошибка выборки:
— средняя ошибка репрезентативности;
t – коэффициент кратности ошибки.
Средний размер ошибки признака:
Средняя ошибка доли признака:
Средний размер ошибки признака:
Средняя ошибки доли признака:
Т – численность ген. сов-ти,
n – численность выборочной сов-ти
— доля данного признака в выборке.
Взаимосвязи м/у явлениями:
Лин. коэф корелляции:
Коэф. эластичности
Ошибка апроксимации:
Расчёт дисперсии:
C видов экономической деят-ти.
Коэф. роста выпуска товаров:
начальный уровень ряда.
Qn – конечный уровень ряда.
Темп роста выпуска:
Темп прироста выпуска товаров:
Среднегодовой коэффициент роста выпуска товаров:
Среднегодовой темп роста выпуска товаров:
Среднегодовой темп прироста выпуска товаров:
С рынка товаров и услуг.
Коэф неравномерности поставки продукции
— средняя величина поставки.
— простая
— взвешенная.
Дисперсия:
% выполнения плана = Факт/План (отч.)
Абсолютный размер отклонения (выполнения контракта)
Сумма переплаты населения:
Территориальный индекс цен:
pA – цены на товары по сравнимому объекту А
pb – цены на товары по сравнимому объекту В.
q – количество проданных товаров.
Эмпирический коэф. эластичности:
Эмпирический коэф. эластичности динамики:
Средний коэф. эластичности:
Теоретический коэф. эластичности.
а1 – первая производная соотв. ф-ии.
хi – значение I – фактора.
— теоретическое значение результативного признака.
По уравнению параболы:
С оборота торговли и товарных запасов:
Валовый оборот торговли:
ВОТ = ОРТ+ООТ
Розница+опт
Оборот розничной торговли = товарооборот
Оборот торговли в сопост.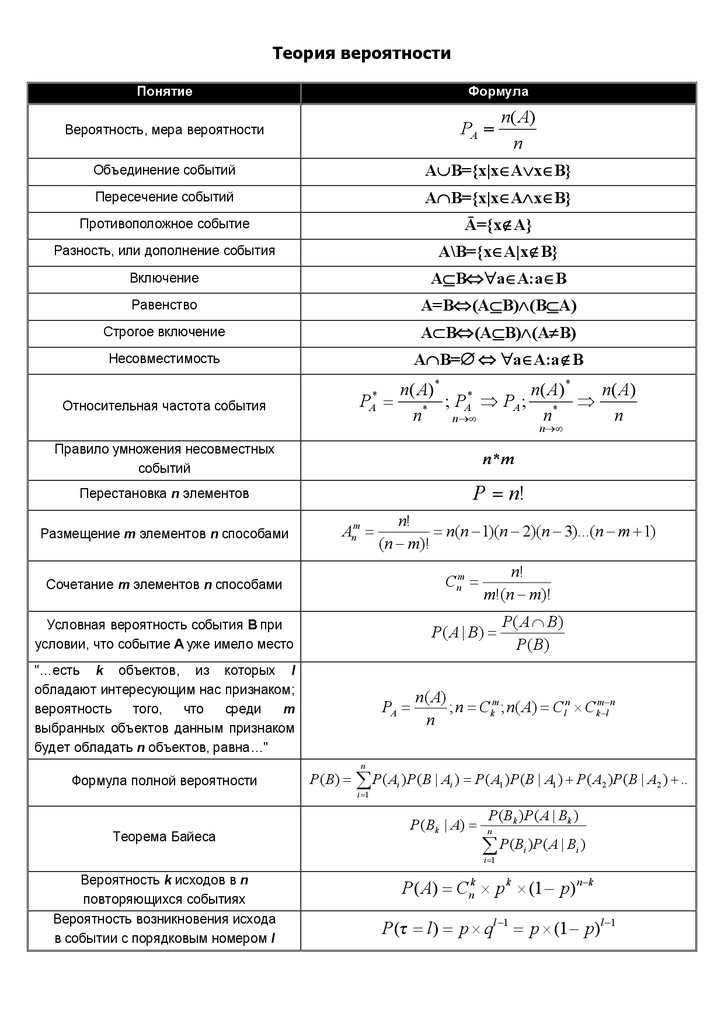
Удельный вес продажи товара в объёме оборота торговли:
— оборот торговли по i группе товаров
— общий объём оборота торговли.
Время обращения товаров в днях = Ср. сумма запасов за период/Однодневный оборот торговли.
Скорость обращения товаров = Оборот торговли за период/ср. сумма запасов за период.
С – скорость обращения в числе оборотов за период.
— средняя сумма запасов за период.
В – время обращения в днях
Виды Относительных Величин
ОВ выполнения плана = факт отчётного периода/Плановое задание (на отчётный период).
ОВ план. задания = план на тек. период/факт за баз. период.
ОВ динамики = Факт отчётного/факт базисного периода
ОВ план. задания*ОВ выполнения плана = ОВ динамики, всего.
ОВ структуры = 1 часть/вся сов-ть.
ОВ сравнения = показатели по объекту А/по В
ОВ интенсивности:
Фондоотдача основных средств (Н) = товарооборот/среднегодовая стоимость основных средств.
Excel. Часть 2. Статистика
Как с помощью математических и статистических функций получить выводы из данных
- Редакция
08.05.2020
Поделиться
В первом выпуске «Мастерской» об Excel «Важные истории» рассказали о том, как устроена программа, как импортировать и сохранять данные, что такое формулы и функции, как выполнить сортировку и фильтрацию данных. В этот раз – подробнее о списке функций, которые пригодятся журналистам для получения статистических выводов из данных.
Чаще всего дата-журналисты анализируют данные, чтобы найти в них новые тенденции и ответы на вопросы:
- Какие масштабы у явления?
- Какую часть целого составляет то или иное явление?
- Насколько изменилась ситуация по сравнению с предыдущим периодом?
- Ситуация ухудшилась или улучшилась, показали выросли или упали?
Получить ответы на эти вопросы помогают математические и статистические функции Excel.
- Для примера будем использовать набор данных по количеству заболевших коронавирусом в России, собранный Медиазоной на основе данных федерального Роспотребнадзора и его региональных штабов.
Исходные данные в формате json можно сказать здесь, а сводные данные по России, переведенные нами в формат xlsx, удобный для работы в Excel, здесь.
Процент от целого
Для того, чтобы получить представление о масштабах явления, принято считать, какую долю целого оно составляет. Например, в исследовании «Важных историй» о насилии над пожилыми говорится о том, что 82,5% таких преступлений совершаются родственниками пострадавших.
С помощью вычисления процента можно посчитать, какая доля выявленных заболевших выздоровела на сегодня в России, согласно официальным данным. Произвести такие расчеты позволяют Google Spreadsheets. Формула для подсчета процента выглядит так: =Часть / Целое * 100. В нашем примере: =Число выздоровевших / Число заболевших * 100.
Формула расчета процентного изменения
Прирост или падение.

Чтобы показать, как ситуация меняется со временем, считают изменение. Например, согласно официальным данным, 7 мая в России выявили на 702 заболевших больше, чем днем ранее – рост продолжается.
Прийти к такому выводу помогает простая формула вычитания: =Новое значение – Старое значение. Например: =Значение за этот год – Значение за предыдущий год. В нашем случае: =Значение за сегодня – значение за вчера. Если число получилось положительным, это указывает на прирост, если отрицательным – на падение.
Чаще всего абсолютные величины не дают нам представления о ситуации: 702 человека – это много или мало? А если днем ранее было выявлено на 471 человека больше, чем до этого, то темпы прироста увеличились или снизились?
В таких случаях показывают процентное изменение, которое тоже может быть положительным или отрицательным – сообщающем о росте или падении. Оно покажет, что 7 мая прирост составил 6,8%, и этот показатель остался на уровне предыдущего дня.
Процентное изменение рассчитывается по формуле: =(Новое значение – Старое значение) / Старое значение * 100. В нашем случае: =(Количество заболевших на сегодня – Количество заболевших на вчера) / Количество заболевших на вчера * 100.
Формула расчета процентного изменения
Среднее арифметическое
Еще одна распространенная операция над данными – это поиск среднего значения. Среднее необходимо, чтобы сделать обобщенный вывод из данных. Например, чтобы узнать, что, в среднем, за последнюю неделю в день выявляли 10 тыс. зараженных.
Формула среднего арифметического выглядит так: =Сумма всех значений / Количество значений. В нашем случае: = Сумма всех новых выявленных случаев заражения за неделю / 7. Чтобы не вводить формулу, можно воспользоваться функцией СРЗНАЧ, которая считает среднее арифметическое. В скобках после функции надо указать диапазон значений, среднее которых мы ищем: =СРЗНАЧ(диапазон).
Вычислять среднее нужно еще и для того, чтобы увидеть выпадающие значения в ряде чисел, как например, в расследовании «Важных историй» о закупках аппаратов ИВЛ. Если посчитать среднюю цену поставки аппарата ИВЛ и сравнить ее с остальными ценами, это позволит сделать вывод о том, какая часть закупок была совершена по завышенной цене.
Медиана
Существует несколько видов среднего, и не всегда для корректных выводов подходит среднее арифметическое. Иногда, когда значения в наборе данных сильно отличаются – например, в списке зарплат есть очень низкие и очень высокие, среднее арифметическое может искажать картину.
В таких случаях лучше считать медиану. Медиана показывает число в середине упорядоченного набора чисел. Это похоже на границу, которая делит данные пополам: половина данных находится выше нее, а половина – ниже. Рассчитывается она так: =МЕДИАНА(диапазон). В случае с количеством заболевших по дням медиана полезной не будет, но если бы мы работали с данными по возрастам заболевших, можно было бы посчитать не среднее, а медиану.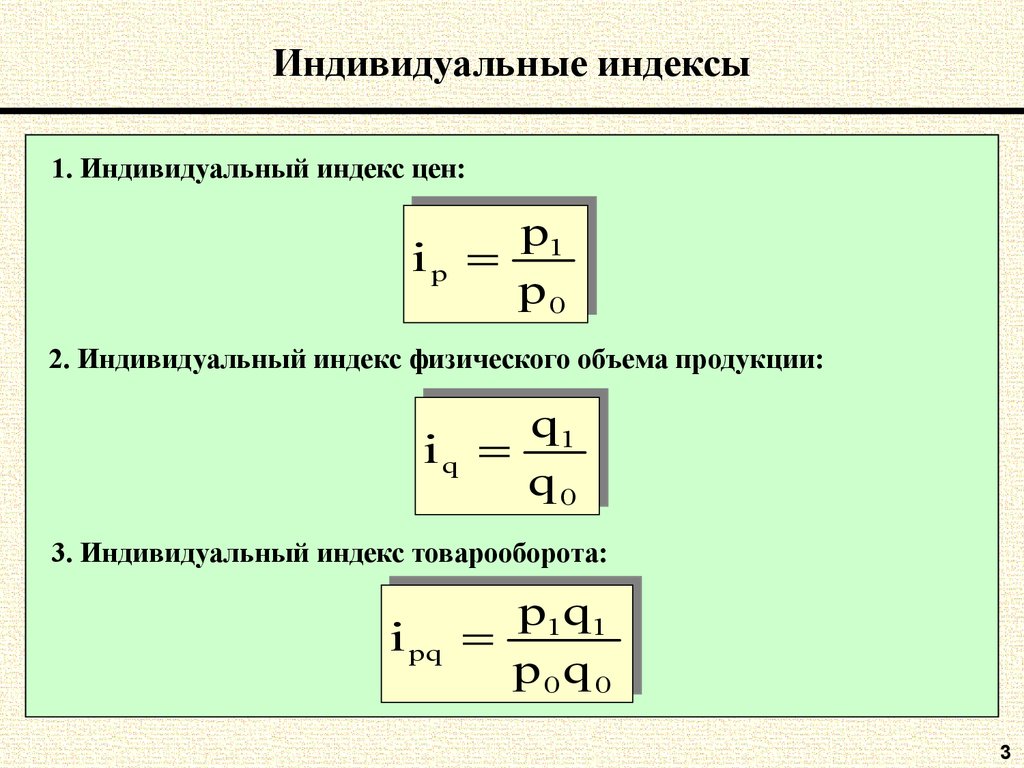
Мода
Мода в статистике – это еще один вид среднего, она показывает цифру, которая встречается в наборе данных чаще других. Она рассчитывается с помощью соответствующей функции, после которой указывается диапазон значений =МОДА(диапазон).
Среднее, медиана и мода
Вычислять моду из данных о количестве заболевших бесполезно, но если бы мы анализировали, например, данные об оценках студентов за экзамен, мода показала бы самую часто встречающуюся отметку. Если большинство сдали экзамен на пятерки и только пара студентов получили двойки, средняя успеваемость была бы меньше 5, но мода показала бы, что чаще всего студенты получали все-таки наивысшую оценку.
Максимум и минимум
Часто журналистов интересует, когда какое-либо явление достигало своего пика или наоборот оказывалось наименее заметным.
На душу населения
При сравнении данных из разных выборок, например, по разным странам или регионам важно учитывать, что в них проживает разное количество людей, и это влияет на результаты сопоставления. Например, сравнивая масштабы распространения коронавируса в разных странах, часто показывают не только абсолютное количество зараженных, но и показатель в пересчете на душу населения.
Пересчет на душу населения
Формула для подсчета количества случаев в пересчете на душу населения такая: = Количество выявленных заболевших / Численность населения * 100 000. В таком случае полученный результат будет показывать количество выявленных случаев на 100 тыс.
Статистика Формулы 1 по итогам прошлого сезона
В Формуле 1 опубликовали статистику по итогам прошлого сезона, отметив, что чемпионат входит в число наиболее динамично развивающихся крупных спортивных событий. Число подписчиков Формулы 1 достигло 49,1 миллионов человек, при этом у неё самый высокий коэффициент вовлечённости по сравнению с другими крупными спортивными соревнованиями в 2021 году.
Социальные сети и цифровые платформы
В прошлом году число подписчиков Формулы 1 в социальных сетях (Facebook, Twitter, Instagram, YouTube, Tiktok, Snapchat, Twitch и китайские социальные сети) выросло на 40% – до 49,1 миллионов, количество просмотров видео – на 50% до 7 миллиардов, а коэффициент вовлечённости – на 74% до 1,5 миллиардов.
При этом болельщики стали чаще смотреть видео на официальном сайте, в приложении и в социальных сетях – этот показатель достиг 7,04 миллиардов просмотров, что на 44% больше, чем в 2020 году.
Рейтинг телетрансляций
Финал сезона в Абу-Даби посмотрели 108,7 миллионов человек, что на 29% больше, чем у этой же гонки в 2020 году. Кроме того, Гран При Абу-Даби обладает самым высоким рейтингом среди всех гонок прошлого года.
Общая аудитория телевизионных трансляций в 2021 году составила 1,55 миллиардов человек – на 4% больше, чем в 2020 году. Довольно высокий рейтинг был у первой гонки сезона – Гран При Бахрейна посмотрели 84,5 миллионов человек – а также у Гран При Великобритании (79,5 миллионов человек), Италии (80,4 миллиона человек) и Бразилии (82,1 миллион), где проводили спринт.
На некоторых рынках увеличилась аудитория телевизионных трансляций, в первую очередь в Нидерландах, где рейтинг Формулы 1 вырос на 81% по сравнению с 2020 годом. Кроме того, выросла популярность спорта в США (на 58%), Франции (на 48%), Италии (на 40%) и в Великобритании (на 39%).
Общее количество уникальных просмотров телетрансляций (количество зрителей, которые посмотрели по меньшей мере одну гонку по ходу сезона) в 2021 году составило 445 миллионов, что на 3% больше, чем в 2020-м. Самым крупным рынком по этому показателю стал Китай (70,8 миллионов уникальных просмотров, что на 13% больше, чем в 2020-м), но зафиксирован также заметный рост в Испании (на 272%), в России (на 129%) и в США (на 53%) по сравнению с 2020 годом.
В целом среднее число зрителей на Гран При в 2021 году составило 70,3 миллиона человек. На рынках, где между 2020 и 2021 годами не менялись договорённости о трансляциях, этот показатель достиг 60,3 миллионов зрителей, то есть за год вырос на 13%, и считается лучшим показателем с 2013 года.
Посещаемость гонок
В 2021 году Гран При посетили 2,69 миллионов человек, что является довольно высоким показателем, учитывая, что во многих странах действовали ограничения по посещаемости, а некоторые гонки пришлось провести без зрителей из-за ситуации с Covid-19. Хотя это меньше, чем 4,16 миллионов человек в эпоху до пандемии, но такая посещаемость доказывает высокий спрос на гонки, и в Формуле 1 ждут, что после окончания пандемии этот показатель вернётся в норму.
На три гоночных уик-энда Гран При пришло более 300000: в США (400000 человек), Мексике (371000 человек) и в Великобритании (356000 человек) – при этом во всех этих странах посещаемость выросла по сравнению с 2019 годом, когда можно было проводить гонки без ограничений на количество зрителей.
Стефано Доменикали, президент Формулы 1: «Прошлый сезон стал особенным. Борьба за титул шла до последней гонки, при этом каждый гоночный уик-энд был необычайно интересным. Мы снова стали принимать зрителей, которых считаем сердцем и душой нашего спорта. Хотя наши возможности были ограничены из-за Covid-19, я рад увидеть 2,6 миллионов болельщиков на трибунах по всему миру.
Кроме того, мы зафиксировали очень высокие показатели в сфере телетрансляций и цифровых платформ, что в очередной раз доказало рост интереса к Формуле 1. Мы с нетерпением ждём начала сезона из 23 Гран При, который станет вызовом для всех команд и гонщиков, и где мы увидим новое поколение машин, построенных по новому регламенту. Я знаю, что наши болельщики считают дни до первой гонки».
Статистические функции (справка)
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|
СРОТКЛ |
Возвращает среднее арифметическое абсолютных значений отклонений точек данных от среднего. |
|
СРЗНАЧ |
Возвращает среднее арифметическое аргументов. |
|
СРЗНАЧА |
Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения. |
|
СРЗНАЧЕСЛИ |
Возвращает среднее значение (среднее арифметическое) всех ячеек в диапазоне, которые удовлетворяют заданному условию. |
|
СРЗНАЧЕСЛИМН |
Возвращает среднее значение (среднее арифметическое) всех ячеек, которые удовлетворяют нескольким условиям. |
|
БЕТА. |
Возвращает интегральную функцию бета-распределения. |
|
БЕТА.ОБР |
Возвращает обратную интегральную функцию указанного бета-распределения. |
|
БИНОМ.РАСП |
Возвращает отдельное значение вероятности биномиального распределения. |
|
БИНОМ.РАСП.ДИАП |
Возвращает вероятность пробного результата с помощью биномиального распределения. |
|
БИНОМ.ОБР |
Возвращает наименьшее значение, для которого интегральное биномиальное распределение меньше заданного значения или равно ему. |
|
ХИ2.РАСП |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.РАСП.ПХ |
Возвращает одностороннюю вероятность распределения хи-квадрат. |
|
ХИ2. |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.ОБР.ПХ |
Возвращает обратное значение односторонней вероятности распределения хи-квадрат. |
|
ХИ2.ТЕСТ |
Возвращает тест на независимость. |
|
ДОВЕРИТ.НОРМ |
Возвращает доверительный интервал для среднего значения по генеральной совокупности. |
|
ДОВЕРИТ.СТЬЮДЕНТ |
Возвращает доверительный интервал для среднего генеральной совокупности, используя t-распределение Стьюдента. |
|
КОРРЕЛ |
Возвращает коэффициент корреляции между двумя множествами данных. |
|
СЧЁТ |
Подсчитывает количество чисел в списке аргументов. |
|
СЧЁТЗ |
Подсчитывает количество значений в списке аргументов. |
|
СЧИТАТЬПУСТОТЫ |
Подсчитывает количество пустых ячеек в диапазоне. |
|
СЧЁТЕСЛИ |
Подсчитывает количество ячеек в диапазоне, удовлетворяющих заданному условию. |
|
СЧЁТЕСЛИМН |
Подсчитывает количество ячеек внутри диапазона, удовлетворяющих нескольким условиям. |
|
КОВАРИАЦИЯ.Г |
Возвращает ковариацию, среднее произведений парных отклонений. |
|
КОВАРИАЦИЯ.В |
Возвращает ковариацию выборки — среднее попарных произведений отклонений для всех точек данных в двух наборах данных. |
|
КВАДРОТКЛ |
Возвращает сумму квадратов отклонений. |
|
ЭКСП.РАСП |
Возвращает экспоненциальное распределение. |
|
F.РАСП |
Возвращает F-распределение вероятности. |
|
F.РАСП.ПХ |
Возвращает F-распределение вероятности. |
|
F.ОБР |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ОБР.ПХ |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ТЕСТ |
Возвращает результат F-теста. |
|
ФИШЕР |
Возвращает преобразование Фишера. |
|
ФИШЕРОБР |
Возвращает обратное преобразование Фишера. |
|
ПРЕДСКАЗ |
Возвращает значение линейного тренда. Примечание: В Excel 2016 эта функция заменена на ПРЕДСКАЗ.ЛИНЕЙН из нового набора функций прогнозирования. Однако она по-прежнему доступна для совместимости с предыдущими версиями. |
|
ПРЕДСКАЗ. |
Возвращает будущее значение на основе существующих (ретроспективных) данных с использованием версии AAA алгоритма экспоненциального сглаживания (ETS). |
|
ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ |
Возвращает доверительный интервал для прогнозной величины на указанную дату. |
|
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ |
Возвращает длину повторяющегося фрагмента, обнаруженного программой Excel в заданном временном ряду. |
|
ПРЕДСКАЗ. |
Возвращает статистическое значение, являющееся результатом прогнозирования временного ряда. |
|
ПРЕДСКАЗ.ЛИНЕЙН |
Возвращает будущее значение на основе существующих значений. |
|
ЧАСТОТА |
Возвращает распределение частот в виде вертикального массива. |
|
ГАММА |
Возвращает значение функции гамма |
|
ГАММА. |
Возвращает гамма-распределение. |
|
ГАММА.ОБР |
Возвращает обратное значение интегрального гамма-распределения. |
|
ГАММАНЛОГ |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАММАНЛОГ.ТОЧН |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАУСС |
Возвращает значение на 0,5 меньше стандартного нормального распределения. |
|
СРГЕОМ |
Возвращает среднее геометрическое. |
|
РОСТ |
Возвращает значения в соответствии с экспоненциальным трендом. |
|
СРГАРМ |
Возвращает среднее гармоническое. |
|
ГИПЕРГЕОМ.РАСП |
Возвращает гипергеометрическое распределение. |
|
ОТРЕЗОК |
Возвращает отрезок, отсекаемый на оси линией линейной регрессии. |
|
ЭКСЦЕСС |
Возвращает эксцесс множества данных. |
|
НАИБОЛЬШИЙ |
Возвращает k-ое наибольшее значение в множестве данных. |
|
ЛИНЕЙН |
Возвращает параметры линейного тренда. |
|
ЛГРФПРИБЛ |
Возвращает параметры экспоненциального тренда. |
|
ЛОГНОРМ.РАСП |
Возвращает интегральное логарифмическое нормальное распределение. |
|
ЛОГНОРМ.ОБР |
Возвращает обратное значение интегрального логарифмического нормального распределения. |
|
МАКС |
Возвращает наибольшее значение в списке аргументов. |
|
МАКСА |
Возвращает наибольшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МАКСЕСЛИ |
Возвращает максимальное значение из заданных определенными условиями или критериями ячеек. |
|
МЕДИАНА |
Возвращает медиану заданных чисел. |
|
МИН |
Возвращает наименьшее значение в списке аргументов. |
|
МИНЕСЛИ |
Возвращает минимальное значение из заданных определенными условиями или критериями ячеек. |
|
МИНА |
Возвращает наименьшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МОДА.НСК |
Возвращает вертикальный массив наиболее часто встречающихся или повторяющихся значений в массиве или диапазоне данных. |
|
МОДА. |
Возвращает значение моды набора данных. |
|
ОТРБИНОМ.РАСП |
Возвращает отрицательное биномиальное распределение. |
|
НОРМ.РАСП |
Возвращает нормальное интегральное распределение. |
|
НОРМ.ОБР |
Возвращает обратное значение нормального интегрального распределения. |
|
НОРМ. |
Возвращает стандартное нормальное интегральное распределение. |
|
НОРМ.СТ.ОБР |
Возвращает обратное значение стандартного нормального интегрального распределения. |
|
ПИРСОН |
Возвращает коэффициент корреляции Пирсона. |
|
ПРОЦЕНТИЛЬ.ИСКЛ |
Возвращает k-ю процентиль для значений диапазона, где k — число от 0 и 1 (не включая эти числа). |
|
ПРОЦЕНТИЛЬ.ВКЛ |
Возвращает k-ю процентиль для значений диапазона. |
|
ПРОЦЕНТРАНГ.ИСКЛ |
Возвращает ранг значения в наборе данных как процентную долю набора (от 0 до 1, исключая границы). |
|
ПРОЦЕНТРАНГ.ВКЛ |
Возвращает процентную норму значения в наборе данных. |
|
ПЕРЕСТ |
Возвращает количество перестановок для заданного числа объектов. |
|
ПЕРЕСТА |
Возвращает количество перестановок для заданного числа объектов (с повторами), которые можно выбрать из общего числа объектов. |
|
ФИ |
Возвращает значение функции плотности для стандартного нормального распределения. |
|
ПУАССОН.РАСП |
Возвращает распределение Пуассона. |
|
ВЕРОЯТНОСТЬ |
Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов. |
|
КВАРТИЛЬ.ИСКЛ |
Возвращает квартиль набора данных на основе значений процентили из диапазона от 0 до 1, исключая границы. |
|
КВАРТИЛЬ.ВКЛ |
Возвращает квартиль набора данных. |
|
РАНГ.СР |
Возвращает ранг числа в списке чисел. |
|
РАНГ.РВ |
Возвращает ранг числа в списке чисел. |
|
КВПИРСОН |
Возвращает квадрат коэффициента корреляции Пирсона. |
|
СКОС |
Возвращает асимметрию распределения. |
|
СКОС.Г |
Возвращает асимметрию распределения на основе заполнения: характеристика степени асимметрии распределения относительно его среднего. |
|
НАКЛОН |
Возвращает наклон линии линейной регрессии. |
|
НАИМЕНЬШИЙ |
Возвращает k-ое наименьшее значение в множестве данных. |
|
НОРМАЛИЗАЦИЯ |
Возвращает нормализованное значение. |
|
СТАНДОТКЛОН.Г |
Вычисляет стандартное отклонение по генеральной совокупности. |
|
СТАНДОТКЛОН.В |
Оценивает стандартное отклонение по выборке. |
|
СТАНДОТКЛОНА |
Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения. |
|
СТАНДОТКЛОНПА |
Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения. |
|
СТОШYX |
Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии. |
|
СТЬЮДРАСП |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.2Х |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.ПХ |
Возвращает t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ОБР |
Возвращает значение t для t-распределения Стьюдента как функцию вероятности и степеней свободы. |
|
СТЬЮДЕНТ. |
Возвращает обратное t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ТЕСТ |
Возвращает вероятность, соответствующую проверке по критерию Стьюдента. |
|
ТЕНДЕНЦИЯ |
Возвращает значения в соответствии с линейным трендом. |
|
УРЕЗСРЕДНЕЕ |
Возвращает среднее внутренности множества данных. |
|
ДИСП. |
Вычисляет дисперсию по генеральной совокупности. |
|
ДИСП.В |
Оценивает дисперсию по выборке. |
|
ДИСПА |
Оценивает дисперсию по выборке, включая числа, текст и логические значения. |
|
ДИСПРА |
Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения. |
|
ВЕЙБУЛЛ.РАСП |
Возвращает распределение Вейбулла. |
|
Z.ТЕСТ |
Возвращает одностороннее значение вероятности z-теста. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Excel (по категориям)
Excel (по алфавиту)
Основные статистические функции в Excel: использование, формулы
Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации.
- Использование статистических функций
- СРЗНАЧ
- МАКС
- МИН
- СРЗНАЧЕСЛИ
- МЕДИАНА
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
- Заключение
Использование статистических функций
Смотрите также: “Основные математические функции в Excel: использование, формулы”
Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.
Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:
- Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
- Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
- Используем сочетание клавиш Shift+F3.
Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.
Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.
На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.
Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.
Давайте теперь рассмотрим наиболее популярные функции.
СРЗНАЧ
Смотрите также: “Как посчитать среднее значение в Excel: формула, функции, инструменты”
Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:
=СРЗНАЧ(число1;число2;…)
В качестве аргументов функции можно указать:
- конкретные числа;
- ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
- диапазон ячеек – указывается вручную или путем выделения в таблице.
- переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.
МАКС
Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:
=МАКС(число1;число2;…)
В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.
МИН
Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:
=МИН(число1;число2;…)
Аргументы функции заполняются так же, как и для оператора МАКС.
СРЗНАЧЕСЛИ
Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:
=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)
В аргументах указываются:
- Диапазон ячеек – вручную или с помощью выделения в таблице;
- Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
- Диапазон_усреднения – не является обязательным аргументом для заполнения.
МЕДИАНА
Оператор находит медиану заданного диапазона значений. Синтаксис функции:
=МЕДИАНА(число1;число2;…)
В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.
НАИБОЛЬШИЙ
Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:
=НАИБОЛЬШИЙ(массив;k)
Аргумента функции два: массив и номер позиции – K.
Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.
НАИМЕНЬШИЙ
Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:
=НАИМЕНЬШИЙ(массив;k)
МОДА.ОДН
Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:
=МОДА.
В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.
Для вертикальных массивов, также, используется функция МОДА.НСК.
СТАНДОТКЛОН
Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:
- СТАДНОТКЛОН.В – находит стандартное отклонение выборки
- СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности
Формулы функций выглядят следующим образом:
- =СТАДНОТКЛОН.В(число1;число2;…)
- =СТАДНОТКЛОН.Г(число1;число2;…)
СРГЕОМ
Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:
=СРГЕОМ(число1;число2;…)
Заключение
В программе Excel более 100 статистических функций.
Смотрите также:
- Почему Эксель не считает формулу: что делать
- Сортировка и фильтрация данных в Excel
Формулы статистики
На этой веб-странице перечислены формулы статистики, используемые в Stat Trek
учебники. Каждая формула ссылается на веб-сайт
страница, которая объясняет, как использовать формулу.
Параметры
- Среднее значение населения =
μ = ( Σ X i ) / N - Стандартное отклонение населения =
σ = sqrt [ Σ ( X i
— μ ) 2 / N ] - Дисперсия населения =
σ 2 = Σ ( X i
— μ ) 2 / N - Дисперсия доли населения =
о P 2 = PQ / n - Стандартизированная оценка = Z = (X — μ) / σ
- Коэффициент корреляции населения =
ρ = [ 1 / N ] * Σ { [ (X i — μ X ) /
σ x ] * [ (Y i — μ Y ) /
σ y ] }
Статистика
Если не указано иное, эти формулы предполагают
простая случайная выборка.
- Выборочное среднее =
x = ( Σ x i ) / n - Стандартное отклонение выборки =
s = sqrt [ Σ ( x я
— x) 2 / (n — 1)] - Выборочная дисперсия =
с 2 = Σ ( х i
— x) 2 / (n — 1) - Дисперсия доли выборки =
s p 2 = pq / (n — 1) - Доля объединенной выборки =
p = (p 1 * n 1 + p 2 * n 2 )
/ (n 1 + n 2 ) - Стандартное отклонение объединенной выборки =
с р =
sqrt [ (n 1 — 1) * с 1 2
+ (n 2 — 1) * с 2 2 ]
/ (n 1 + n 2 — 2) ] - Выборочный коэффициент корреляции =
г = [ 1 / (п — 1) ] *
Σ { [ (х я — х) /
с x ] * [ (у я — у) /
s y ] }
Корреляция
- Корреляция Пирсона произведение-момент =
r = Σ (xy) / sqrt [ ( Σ x 2 ) * ( Σ y 2 ) ] - Линейная корреляция (выборочные данные) =
r = [ 1 / (n — 1) ] * Σ { [ (x i — x) / с x ] * [ (y i — y) / с y ] } - Линейная корреляция (данные населения) =
ρ = [ 1 / N ] * Σ { [ (X i — μ X ) / σ x ] * [ (Y i — μ Y ) / σ y ] 1 } 9004Простая линейная регрессия
- Линия простой линейной регрессии: ŷ = b 0 + b 1 x
- Коэффициент регрессии =
б 1 = Σ [ (х i — Икс)
(у я — у) ] /
Σ [ (х я —
x) 2 ] - Пересечение наклона регрессии =
b 0 = y — b 1 * x - Коэффициент регрессии =
b 1 = r * (s y / s x ) - Стандартная ошибка наклона регрессии =
с б 1 =
sqrt [ Σ(y i — ŷ i ) 2
/ (п — 2) ]
/ sqrt [ Σ(x я —
х) 2 ]
Подсчет
- n факториал:
н! = п * (п-1) * (п — 2) * .. . * 3 * 2 * 1. По соглашению,
0! = 1. - Перестановки n вещей, взятых r за один раз:
n P r = n! / (н — р)! - Комбинации из n вещей, взятых r за один раз:
n C r = n! / г!(п — г)! = n P r / r!
Вероятность
- Правило сложения:
Р (А ∪ В)
= Р(А) + Р(В)
— Р(А ∩ В) - Правило умножения:
Р (А ∩ В)
= P(A) P(B|A) - Правило вычитания: P(A’) = 1 — P(A)
Случайные величины
В следующих формулах X и Y являются случайными переменные и
a и b являются константами.- Ожидаемое значение X =
E(X) = μ x = Σ [ x i * P(x i ) ] - Дисперсия X = Var(X) = σ 2 =
Σ [ х i — Е(х) ] 2 * Р(х i ) =
Σ [ x i — μ x ] 2 * P(x i ) - Нормальная случайная величина = z-показатель = z = (X — μ)/σ
- Статистика хи-квадрат = Χ 2 =
[ ( n — 1 ) * s 2 ] / σ 2 - f статистика =
ж =
[ с 1 2 /σ 1 2 ] /
[ с 2 2 /σ 2 2 ] - Ожидаемое значение суммы случайных величин =
E(X + Y) = E(X) + E(Y) - Ожидаемое значение разницы между случайными величинами =
E(X — Y) = E(X) — E(Y) - Дисперсия суммы независимых случайных величин =
Var(X + Y) = Var(X) + Var(Y) - Дисперсия разности между независимыми случайными величинами =
Var(X — Y) = Var(X) + Var(Y)
Выборочные распределения
- Среднее выборочного распределения среднего = μ х =
μ - Среднее выборочное распределение доли =
μ p = P - Стандартное отклонение пропорции =
σ р =
sqrt[ P * (1 — P)/n ] = sqrt( PQ / n ) - Стандартное отклонение среднего =
σ x = σ/sqrt(n) - Стандартное отклонение разности выборочных средних =
σ d =
sqrt[ (σ 1 2 / n 1 ) +
(σ 2 2 / n 2 ) ] - Стандартное отклонение разности пропорций выборки =
о д =
sqrt{ [P 1 (1 — P 1 ) / номер 1 ] +
[P 2 (1 — P 2 ) / n 2 ] }
Стандартная ошибка
- Стандартная ошибка пропорции = SE p =
с р =
sqrt[ p * (1 — p)/n ] = sqrt( pq / n ) - Стандартная ошибка разности пропорций = SE p =
с р =
sqrt{ p * ( 1 — p ) * [ (1/n 1 )
+ (1/n 2 ) ] } - Стандартная ошибка среднего = SE х =
s x = s/sqrt(n) - Стандартная ошибка разности выборочных средних =
SE д = с д =
sqrt[ (s 1 2 / п 1 ) +
(s 2 2 / n 2 ) ] - Стандартная ошибка разности средних парных выборок =
SE д = с д =
{ квт [
(Σ(d i — d) 2
/ (n — 1) ] } / sqrt(n) - Стандартная ошибка объединенной выборки =
с в пуле знак равно
sqrt [ (n 1 — 1) * s 1 2
+ (n 2 — 1) * с 2 2 ]
/ (n 1 + n 2 — 2) ] - Стандартная ошибка разности пропорций выборки =
с д =
sqrt{ [p 1 (1 — p 1 ) / п 1 ] +
[p 2 (1 — p 2 ) / n 2 ] }
Дискретные вероятностные распределения
- Биномиальная формула: P(X = x) =
б( х ; н, Р ) =
n C x * P x * (1 — P) n — x =
n C x * P x * Q n — x - Среднее биномиального распределения =
μ x = n * P - Дисперсия биномиального распределения = σ x 2 =
n * P * ( 1 — P ) - Отрицательная биномиальная формула: P(X = x) =
b*( x ; r, P ) = x-1 С р-1
* P r * (1 — P) x — r - Среднее отрицательного биномиального распределения =
μ x = rQ / P - Дисперсия отрицательного биномиального распределения =
σ x 2 =
r * Q / P 2 - Геометрическая формула: P(X = x) =
g( x ; P ) = P * Q x — 1 - Среднее геометрическое распределение =
μ x = Q / P - Дисперсия геометрического распределения =
σ х 2 =
Q / P 2 - Гипергеометрическая формула: P(X = x) =
h( x ; N , n , k ) =
[ k C x ] [ N-k C n-x ]
/ [ N C n ] - Среднее значение гипергеометрического распределения =
μ x = n * k / N - Дисперсия гипергеометрического распределения =
σ x 2 =
п * к * ( Н — к ) * ( Н — п ) /
[Н 2 * ( Н — 1 ) ] - Формула Пуассона:
P( x; µ ) = (e -µ ) (µ x ) / x! - Среднее значение распределения Пуассона =
μ x = μ - Дисперсия распределения Пуассона =
σ x 2 = μ - Полиномиальная формула: P = [ n! / ( п 1 !
* п 2 ! * ... п к ! )]
* ( стр 1 п 1
* p 2 n 2 * . . .
* стр к п к )
Линейные преобразования
Для следующих формул предположим, что Y является
линейное преобразование
случайной величины X, определяемой уравнением: Y = aX + b.- Среднее линейного преобразования = E(Y) =
У = аХ + б. - Дисперсия линейного преобразования = Var(Y) =
а 2 * Вар(Х). - Стандартизированная оценка = z =
(x — μ x ) / σ x . - t статистика = t =
(x — μ x ) / [s/sqrt(n)].
Оценка
- Доверительный интервал:
Выборочная статистика +
Критическое значение * Стандартная ошибка статистики - Погрешность =
(Критическое значение) * (Стандартное отклонение статистики) - Погрешность =
(Критическое значение) * (Стандартная ошибка статистики)
Проверка гипотез
- Стандартизированная статистика испытаний =
(Статистика — Параметр) / (Стандартное отклонение статистики) - Одновыборочный z-критерий для пропорций:
z-оценка = z = (p — P 0 ) / sqrt( p * q / n ) - Двухвыборочный z-критерий для пропорций:
z-показатель = z = z = [(p 1 — p 2 ) — d ] / SE - Одновыборочный t-критерий для средних:
t статистика = t = (x — μ) / SE - Двухвыборочный t-критерий для средних значений:
t статистика = t = [ (x 1
— x 2 ) — d ] / SE - Стьюдентный критерий для средних значений:
t статистика = t = [ (x 1
— х 2 ) — Д ] / SE
= (d — D) / SE - Статистика критерия хи-квадрат = Χ 2 =
Σ[ (Наблюдаемое — Ожидаемое) 2 / Ожидаемое ]
Степени свободы
Правильная формула для степеней свободы (DF) зависит от ситуации
(характер тестовой статистики, количество образцов,
исходные предположения и др.).
- Одновыборочный t-критерий:
DF = n — 1 - Двухвыборочный t-критерий:
ДФ =
(s 1 2 /n 1 +
с 2 2 /n 2 ) 2 /
{ [ (с 1 2 / № 1 ) 2 /
(n 1 — 1) ] +
[ (с 2 2 / п 2 ) 2 /
(n 2 — 1) ] } - Двухвыборочный t-критерий, объединенная стандартная ошибка:
DF = n 1 + n 2 — 2 - Простая линейная регрессия, тестовый наклон:
DF = n — 2 - Критерий согласия хи-квадрат:
DF = k — 1 - Критерий хи-квадрат на однородность:
DF = (r — 1) * (c — 1) - Тест хи-квадрат на независимость:
DF = (r — 1) * (c — 1)
Размер выборки
Ниже первые две формулы находят наименьшие размеры выборки.
требуется для достижения фиксированной погрешности, используя простой
случайная выборка. Третья формула
распределяет выборку по стратам на основе пропорционального плана.
четвертая формула, распределение Неймана, использует стратифицированную выборку для
минимизировать дисперсию при фиксированном размере выборки. И последняя формула,
оптимальное распределение, использует стратифицированную выборку для минимизации дисперсии,
при фиксированном бюджете.- Среднее (простая случайная выборка):
п = { z 2 * о 2
* [Н/(Н-1)]}
/ {МЕ 2
+ [ z 2 * σ 2 / (N — 1) ] } - Доля (простая случайная выборка):
n = [(z 2 * p * q) + ME 2 ]
/ [ME 2 + z 2 * p * q / N ] - Пропорциональная стратифицированная выборка:
n h = ( N h / N ) * n - Распределение Неймана (стратифицированная выборка):
n ч = n * ( N ч * σ ч )
/ [ Σ ( N i * σ i ) ] - Оптимальное распределение (стратифицированная выборка):
n h = n * [ ( N h * σ h ) / sqrt( c h 9)
] / [ Σ ( N я * σ я ) /
sqrt( c i ) ]
10 лучших статистических формул — пустышки
Формулы — от них просто не уйти, когда изучаешь статистику.
Вот десять статистических формул, которые вы будете часто использовать, и шаги для их расчета.
Доля
Некоторые переменные являются категориальными и определяют, к какой категории или группе принадлежит человек. Например, «статус отношений» — это категориальная переменная, и человек может быть холостым, встречающимся, состоящим в браке, разведенным и т. д.
Фактическое количество людей в любой данной категории называется частотой для этой категории. Пропорция , или относительная частота представляет процент людей, попадающих в каждую категорию. Доля данной категории, обозначенная цифрой p — частота, деленная на общий размер выборки.
Итак, чтобы рассчитать пропорцию, вам
-
Подсчитайте всех лиц в выборке, попадающих в указанную категорию.
-
Разделите на n , количество особей в выборке.
Среднее
Среднее , или среднее набора данных — это один из способов измерения центра набора числовых данных.
Обозначение для среднего
Формула для среднего
, где x представляет каждое значение в наборе данных.
Чтобы вычислить среднее, вам
-
Сложите все числа в наборе данных.
-
Разделить на n количество значений в наборе данных.
Медиана
Медиана набора числовых данных — это еще один способ измерения центра. Медиана — это среднее значение после упорядочения данных от наименьшего к наибольшему.
Чтобы вычислить медиану, выполните следующие действия:
-
Расположите числа от меньшего к большему.
-
При нечетном количестве чисел выберите то, которое находится ровно посередине. Вы определили медиану.
-
Для четного количества чисел возьмите два числа точно посередине и усредните их, чтобы найти медиану.
Стандартное отклонение выборки
стандартное отклонение выборки является мерой степени изменчивости в выборке.
Вы можете думать об этом, в общих чертах, как о среднем расстоянии от среднего. Формула стандартного отклонения:
.
Чтобы рассчитать стандартное отклонение, вам
-
Найти среднее всех чисел,
-
Возьмите каждое число и вычтите из него среднее значение.
-
Возведение в квадрат каждого из полученных значений.
-
Сложите их все.
-
Разделить на n – 1.
-
Извлеките квадратный корень.
Процентиль
Процентили — это способ определения отдельного значения относительно всех других значений в наборе данных. При прохождении стандартизированного теста вы получаете индивидуальный необработанный балл и процентиль. Например, если вы попадаете в 90-й процентиль, 90 процентов результатов тестов всех учащихся такие же или ниже ваших (и 10 процентов выше ваших). В общем, находясь на k 90 299-й процентиль означает, что 90 298 k 90 299 процентов данных лежат в этой точке или ниже, а (100 – 90 298 k 90 299 ) процентов лежат выше нее.
Чтобы рассчитать процентиль, вам
-
Преобразование исходного значения в стандартную оценку с помощью формулы z ,
, где x — исходное значение,
— это среднее значение совокупности всех значений, а
— стандартное отклонение всех значений генеральной совокупности.
-
Используйте таблицу Z , чтобы найти соответствующий процентиль для стандартной оценки.
Погрешность выборочного среднего
Погрешность для вашего образца mea n ,
— это ожидаемая сумма, на которую среднее значение выборки будет варьироваться от выборки к выборке. Формула погрешности для
, относящийся к образцам размером 30 и более, равен
.
, где z * — стандартное нормальное значение для желаемого уровня достоверности.
Чтобы рассчитать погрешность для
ты
-
Определите доверительный уровень и найдите соответствующий z *.
-
Найти стандартное отклонение
и размер выборки n .
-
Умножить z * на
разделить на квадратный корень из n .
Необходимый размер образца
Если вы хотите рассчитать доверительный интервал для среднего значения совокупности с определенной погрешностью, вы можете определить необходимый размер выборки, прежде чем собирать какие-либо данные. Формула размера выборки для
это
, где z * — стандартное нормальное значение доверительного уровня, MOE — желаемая погрешность, а
— стандартное отклонение. Потому что
— это неизвестное значение, которое вам нужно, возможно, вам придется провести пилотное исследование (небольшое экспериментальное исследование), чтобы сделать предположение о значении стандартного отклонения.
Чтобы рассчитать размер выборки для
выполнить следующие шаги:
-
Умножить z * умножить на с .
-
Разделить на требуемый предел погрешности, MOE.
-
Квадрат ит.
-
Округлите любую дробную сумму до ближайшего целого числа (так вы достигнете желаемого MOE или выше).
Тестовая статистика для среднего
При проверке гипотезы для среднего значения генеральной совокупности вы берете среднее значение выборки и выясняете, насколько оно далеко от заявленного значения с точки зрения стандартного балла. Стандартная оценка называется тестовая статистика c . Формула тестовой статистики для среднего значения:
где
— заявленное значение для среднего значения совокупности (значение, которое находится в нулевой гипотезе).
Чтобы вычислить статистику теста для среднего значения выборки для выборок размером 30 и более, вы должны
-
Расчет выборочного среднего,
и стандартное отклонение выборки, s .
-
Дубль
-
Расчет стандартной ошибки,
-
Разделите результат шага 2 на стандартную ошибку, найденную в шаге 3.
Корреляция
Образец Корреляция является мерой силы и направления линейной зависимости между двумя количественными переменными X и Y . Он не измеряет никакие другие типы отношений и не применяется к категориальным переменным. Формула корреляции
Чтобы рассчитать корреляцию, вам
-
Найдите среднее значение всех значений x и назовите его
Найдите среднее значение всех значений и и назовите его
.
-
Найдите стандартное отклонение всех значений x и назовите его s x . Найдите стандартное отклонение всех значений y и назовите его s y .
-
Для каждой ( x , y ) пары в наборе данных возьмите x минус
и у минус
и умножьте их вместе.
-
Сложите все эти продукты вместе, чтобы получить сумму.
-
Разделите сумму на s x x s y .
-
Разделите результат на n – 1, где n это количество ( x , y ) пар. (Это то же самое, что умножить на единицу n – 1.)
Линия регрессии
Изучив диаграмму рассеяния между двумя числовыми переменными и вычислив выборочную корреляцию между двумя переменными, вы можете заметить линейную зависимость между ними. В этом случае было бы уместно оценить линию регрессии для оценки значения переменной отклика ( Y ) с учетом значения независимой переменной ( X ).
Перед расчетом линии регрессии необходимо пять сводных статистик:
-
Среднее значение x значений
-
Среднее значение и значений
-
Стандартное отклонение значений x (обозначается как с x )
-
Стандартное отклонение y значений (обозначается s y )
-
Корреляция между X и Y (обозначается как r )
Итак, чтобы рассчитать наиболее подходящую линию регрессии, вам
-
Найдите уклон по формуле
-
Найдите точку пересечения y- по формуле
-
Соедините результаты шагов 1 и 2, чтобы получить линию регрессии: y = m x + b .
Подробное руководство по базовой формуле статистики
Большинству учащихся трудно изучать статистику. Но вот несколько основных статистических формул, которые могут помочь учащимся начать работу со статистикой. Но прежде мы изучим эти формулы. Начнем со знакомства со статистикой.
Статистика — это один из разделов математики, который используется для изучения анализа данных. Методы статистики создаются для изучения больших данных и их свойств.
Статистические формулы используются несколькими компаниями для расчета отчетов людей или сотрудников. В следующих параграфах мы обсудим несколько статистических формул, которые используются для разных целей.
Прежде чем перейти к основным формулам статистики; давайте проверим, можете ли вы проанализировать, какое утверждение является статистическим, а какое нестатистическим.
Q1 . В зоопарке совиные обезьяны обычно весят больше, чем паукообразные?
(A) Статистические (B) Нестатистические Q2 .
В колледжах Нью-Йорка тренерам по футболу обычно платят больше, чем тренерам по теннису?
(A) Статистические (B) Нестатистические Q3. Сколько зубов у Алана во рту?»
(A) Статистические (B) Нестатистические Q4. Сколько дней в июле месяце?
(A) Статистические (B) Нестатистические Q5. Какова общая площадь ушей жирафа?
(A) Статистические (B) Нестатистические Q6. А вообще какой средний рост у жирафов?
(A) Статистические (B) Нестатистические Q7. Есть ли у Дева докторская степень? степень?
(A) Statistical (B) Not statistical Answers:–
- Statistical
- Statistical
- Not statistical
- Не статистически
- Статистический
- Статистический
- Нестатистический
После того, как вы проверили свои статистические знания, теперь вы можете приступить к проверке основных формул статистики.
Это поможет вам решить статистические задачи.
Какова цель использования статистики?
Содержание
Статистика — это наука об анализе, представлении, сборе, интерпретации, организации, анализе и представлении больших данных. Его можно определить как функцию заданных данных. Вот почему статистика сочетается с классификацией, представлением, сбором и упорядочиванием числовой информации. Это также облегчает интерпретацию нескольких результатов и прогнозирование различных возможностей для будущих приложений. С помощью статистики можно найти несколько показателей центральных данных и отклонений разнородных значений от основных значений.
Что такое формулы элементарной статистики?
Для всех статистических вычислений базовая концепция и формулы среднего, моды, стандартного отклонения, медианы и дисперсии являются ступеньками. Таким образом, мы представили все подробности по базовой формуле статистики:
где
x = данные наблюдений
x (бар) = среднее значение
n = общее количество наблюденийсреднее или среднее
Теоретически, это сумма компонентов набора, деленная на общее количество компонентов.
Вы можете легко понять всю концепцию вычисления среднего значения. Таким образом, формула среднего:
Среднее значение = (сумма всех данных элементов) / общее количество. элементов
Способность среднего используется для отображения всего набора данных с одним значением.
Медиана
Это центральное значение всего набора данных. Но если множество имеет нечетное число значений, то центральное значение множества можно рассматривать как медиану. С другой стороны, если конкретный набор содержит даже нет. наборов, то два центральных значения можно использовать для вычисления медианы.
Медиану можно использовать для разделения набора данных на две разные части. Чтобы вычислить медиану, вы должны расположить компоненты набора в порядке возрастания; только тогда вы можете найти медиану данных.
Медиана = (n+1)/2 ; , где n — нечетное число
Или
Медиана = [(n/2) член + ((n/2) + 1)] /2 ; , где n — четное число
Это формула базовой статистики для расчета медианы заданных данных.
Режим
Это значение часто используется в одном наборе данных. Или мы можем сказать, что мода — это сводка набора данных с одними данными.
Режим = Часто используемые данные в заданном наборе
Дисперсия
Используется для расчета отклонения набора данных по его среднему значению. Следовательно, это должно быть положительное значение, и оно также используется для измерения значения стандартного отклонения, которое считается основным понятием статистических значений.
Где дисперсия; х = заданные предметы; х бар = среднее значение; и n = общее количество элементов
Стандартное отклонение
Это квадратный корень из дисперсии данной информации.
S =
Где S = стандартное отклонение и квадратный корень из дисперсии.
Некоторые примеры основных статистических формул
Ниже приведены некоторые примеры основных статистических формул, которые вам следует знать:
Среднее: Найдите среднее значение данных 1,2,3,4,5.
Среднее значение = (сумма всех данных элементов) / общее количество.
Следовательно, среднее = (1+2+3+4+5)/5
15/5 =3
Следовательно, среднее = 3
Медиана: Если n нечетное число :
Найдите медиану данных 10,20,30,40,50.
Затем можно рассчитать медиану, записав набор данных в порядке возрастания, т.е.
10,20,30,40,50
Следовательно, 30 — это медиана, так как это центральное значение набора данных.
Или Медиана = (n+1)/2 ;
Где n=5, поэтому (5+1)/2 = 3, что означает, что третий член является медианой набора данных.
Если n четное число
Найдите медиану данных 4,10,15,2.
Затем можно рассчитать медиану, записав набор данных в порядке возрастания, т. е.
2,4,10,15
1310 Медиана = [(n/2) срок + ((n/2) + 1)] /2 ; , следовательно,
[(4/2) + (4/2)+1)]/2 = 2,5
Это означает, что 2-й и 3-й члены будут использоваться для медианы, т.
е.
(4+10)/2 = 7 , Медиана 7 .
Режим: Найти режим данных 1,1,2,2,2,3,3,3,3,4,4.
Поскольку число 3 повторяется 4 раза; поэтому мода данных равна 3.
ДисперсияНайдите дисперсию данных 10,5,-6,3,12.
]/5
[100+25+36+9+144]/5 = 62,8
Дисперсия равна 62,8.
Стандартное отклонение
В приведенном выше примере мы рассчитали дисперсию данных. Теперь, используя значение дисперсии, мы можем вычислить стандартное отклонение.
S = √ (дисперсия)
S = √ (62,8)
= 7,92
Следовательно, стандартное отклонение равно 7,92.
Ниже мы упомянули некоторые важные формулы статистики. Студенты могут использовать любой из них в соответствии со своими потребностями.
Термины статистики Базовая формула статистики Процентиль Преобразуйте исходную формулу с помощью стандартной формулы z. Затем используйте Z-таблицу для ее решения.
Здесь x — исходное значение, среднее значение генеральной совокупности, а σ — стандартное отклонение.Погрешность среднего значения выборки Здесь Z * – стандартное нормальное значение, σ – стандартное отклонение, а n – размер выборки. Объем выборки Здесь Z * — стандартное нормальное значение, σ — стандартное отклонение, а MOE — предел погрешности. Тестовая статистика для среднего Здесь — выборочное среднее, σ — стандартное отклонение и n выборочное среднее. Корреляция Здесь x — стандартное отклонение всех значений x и sy — стандартное отклонение всех значений x . Линия регрессии. Доля объединенной выборки p = (p1 * n1 + p2 * n2) / (n1 + n2)
Здесь n1 и n2 — размер выборки 1 и выборки 2, а p1 и p2 — доля выборки, взятая из совокупностей 1 и 2 соответственно.92
Здесь σ1 и σ2 — стандартные отклонения данной совокупности 1 и 2, с 1 и с 2 — стандартное отклонение совокупности 1 и 2 соответственно.Одновыборочный t-тест для среднего . Двухвыборочный t-критерий для средних значений t = [(x1 – x2) – d] / SE
Здесь x1 и x2 — среднее значение выборки 1 и 2, SE — стандартная ошибка, d — предполагаемая разница между средними значениями генеральной совокупности.Статистика критерия хи-квадрат уровень категориальной переменной. Среднее отрицательного биномиального распределения μ = r / P
Здесь r — количество успехов, μ — среднее число испытаний, а P — вероятность успеха.Стандартное нормальное распределение Z = ( x – 41310 x – 41310 x — μ) / µ µ). переменная, а σ — стандартное отклонение X.
Хи-квадрат критерия согласия DF = k – 1
Здесь DF — степень свободы, а K — уровни категориальной переменной.Заключение
В этом блоге есть актуальная информация о основных формулах статистики, которые могут помочь вам понять основную концепцию статистики. Поскольку статистика имеет разные термины, такие как среднее значение, медиана, мода, дисперсия и стандартное отклонение, вы можете использовать вышеупомянутый пример для решения проблемы этих статистических терминов.
Даже в этом случае, если у вас возникнут трудности с выполнением статистических заданий; то вы можете получить лучшую справку по назначению статистики прямо сейчас. Тем не менее, у нас есть команда экспертов, которые могут мгновенно помочь вам с вашими запросами, и мы доступны для вас 24 * 7 и доставляем данные без плагиата до истечения срока вместе с отчетом о плагиате.
Часто задаваемые вопросы
Q1.
Как рассчитать базовую статистику?
Вот некоторые из основных формул статистики:
1. Стандартное отклонение популяции = σ = sqrt [ Σ ( Xi – μ )2 / N ]
2. Среднее значение популяции = μ = ( Σ Xi ) / N.
3. Дисперсия доли популяции = σP2 = PQ / n .
4. Дисперсия населения = σ2 = Σ ( Xi – μ )2 / N.
5. Стандартизированная оценка = Z = (X – μ) / σQ2.
Типы статистики по математике ?
Статистика в основном подразделяется на два типа:
1. Описательная статистика
2. Логическая статистикаФормула статистики | Калькулятор (пример и шаблон Excel)
Формула статистики (оглавление)
- Формула
- Примеры
- Калькулятор
Термин «статистика» относится к разделу математики, который занимается анализом чисел и данных.
Формула статистики относится к набору мер дисперсии или центральной тенденции, которые помогают понять и интерпретировать определенный набор данных.
Формулы
Среднее x̄ = Σxi / N
Медиана = (N+1) th / 2 члена; когда N нечетно
[ N th / 2 член + ( N / 2 + 1) th член ] / 2 ; when N is evenMode = The value in the data set that occurs most frequently
Variance = Σ(xi – x̄) 2 / N
Where
- x i : i th Термин в наборе данных
- N : Количество переменных в наборе данных
Пример формулы статистики (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет формулы статистики.
Вы можете скачать этот шаблон формулы Excel для статистики здесь — Шаблон Excel для формулы статистики
Формула статистики — Пример № 1
Давайте возьмем пример набора данных с нечетным числом переменных, чтобы проиллюстрировать формулу статистики: 21, 27, 34, 39, 22, 45, 19, 27, 29, 43, 36, 24, 27, 31 , 25, 45, 21, 38, 30. Количество переменных, N = 19. Рассчитайте среднее значение, медиану, моду и дисперсию вышеуказанного набора данных.
Решение:
Среднее вычисляется по приведенной ниже формуле
Среднее0007 Среднее значение = (21 + 27 + 34 + 39 + 22 + 45 + 19 + 27 + 29 + 43 + 36 + 24 + 27 + 31 + 25 + 45 + 21 + 38 + 30) / 19
- Среднее = 30,7
Медиан рассчитывается с использованием формулы, приведенной ниже
(n + 1) TH /2 Срок
Медиан = (19 + 1)/ 2 = 10 TH Термин
- Median = 100014 TH -й срок, 19, 21, 21, 22, 24, 25, 27, 27, 27, 29, 30, 31, 34, 36, 38, 39, 43, 45, 45
- Медиана = 29
Мода рассчитывается по приведенной ниже формуле
Мода = Значение в наборе данных, которое встречается наиболее часто , 27, 29, 30, 31, 34, 36, 38, 39, 43, 45, 45
Дисперсия рассчитывается по формуле, приведенной ниже0002
- Дисперсия = {(21 – 30,7) 2 + (27 – 30,7) 2 + (34 – 30,7) 2 + (39 – 30,7) 2 0,74 – 20 (0,74 – 30,7) 20 (0,74)15 + (45 – 30,7) 2 + (19 – 30,7) 2 + (27 – 30,7) 2 + (29 – 30,7) 2 + (43 – 30,7) 4 – 3 (4 2 5) 30,7) 2 + (24 – 30,7) 2 + (27 – 30,7) 2 + (31 – 30,7) 2 + (25 – 30,7) 2 + (45 – 90) 3 + (21 – 30,7) 2 + (38 – 30,7) 2 + (30 – 30,7) 2 } / 19
- Разница = 65,5
Следовательно, среднее значение, медиана, мода и дисперсия данного набора данных равны 30,7, 29, 27 и 65,5 соответственно.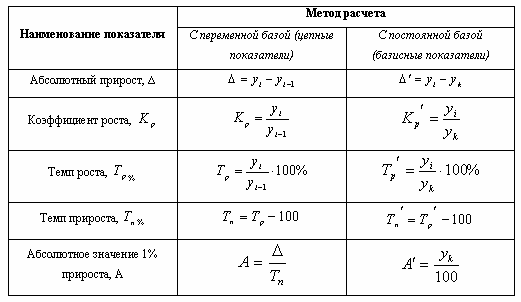
Формула статистики – пример №2
Теперь давайте возьмем пример набора данных с четным числом переменных и вычислим формулу статистики: 82, 76, 62, 78, 83, 89, 61, 76, 72 , 71, 91, 76, 62, 69, 77, 76, 85, 89, 71, 63, 68, 82. Количество переменных, N = 22. Вычисляет среднее значение, медиану, моду и дисперсию вышеуказанного набора данных. .
Solution:
Mean is calculated using the formula given below
Mean x̄ = Σxi / N
- Mean = (82 + 76 + 62 + 78 + 83 + 89 + 61 + 76 + 72 + 71 + 91 + 76 + 62 + 69 + 77 + 76 + 85 + 89 + 71 + 63 + 68 + 82) / 22
- Среднее значение = 75,4
Медиана рассчитывается по формуле, приведенной ниже0014 th term ] / 2
Медиана = (22/2 + (22/2 + 1)) / 2. Теперь расположите набор данных в порядке возрастания (или убывания), чтобы определить медиану, 11 -й -й терм 12 -й -й терм 61, 62, 62, 63, 68, 69, 71, 71, 72, 76, 76, 76, 76, 77, 78, 82, 82, 83, 85, 89, 89 , 91
- Медиана = (76 + 76) / 2
- Медиана = 76
Режим рассчитывается по приведенной ниже формуле
Режим = Значение в наборе данных, которое встречается чаще всего
- Режим = Набор данных равен 76, что встречается наиболее часто (4 раза) в этом наборе данных.
- Режим = 76
Дисперсия рассчитывается с использованием формулы, приведенной ниже
Дисперсия = σ (xi — x̄) 2 / n
- . ) 2 + (62 – 75,4) 2 + (78 – 75,4) 2 + (83 – 75,4) 2 + (89 – 75,4) 2 + (61 – 75,4) 2 + (76 – 90,14) 2 90 72 – 75,4) 2 + (71 – 75,4) 2 + (91 – 75,4) 2 + (76 – 75,4) 2 + (62 – 75,4) 2 19 – 015 + (6,4 ) 904 2 + (77 – 75,4) 2 + (76 – 75,4) 2 + (85 – 75,4) 2 + (89 – 75,4) 2 + (71 – 75,4) 4 2 – 75.4) 2 + (68 – 75,4) 2 + (82 – 75,4) 2 } / 22
- Отклонение = 78,5
Следовательно, среднее значение, медиана, мода и дисперсия данного набора данных равны 75,4, 76, 76 и 78,5 соответственно.
Объяснение
Формулу для статистики можно рассчитать, выполнив следующие шаги:
- Среднее значение: Это среднее значение всех чисел, доступных в наборе данных.
- Медиана: Если расположить в порядке возрастания или убывания, это точно середина набора данных. Например, если в наборе данных 100 чисел, то 50 -й -й и 51-й -й -й термины являются средними числами.
- Режим: Это число в наборе данных, которое встречается максимальное количество раз.
- Дисперсия: Он измеряет, насколько разбросаны числа в наборе данных, т. е. насколько далеко каждое число разбросано от среднего значения набора данных.
Актуальность и использование формулы статистики
С точки зрения статистика очень важно понимать концепцию формулы статистики, поскольку она помогает организовывать и анализировать большие объемы данных. Эти статистические методы также используются в различных инструментах для принятия решений, особенно для получения выводов на основе данных, собранных в ходе обследований.
Калькулятор формулы статистики
Вы можете использовать калькулятор формулы статистики
| Statistics Formula = | Σxi / N | |
| Σ0 / 0 = | 0 |
Рекомендуемые статьи
Это руководство по формуле статистики. Здесь мы обсуждаем, как рассчитать статистику вместе с практическими примерами. Мы также предоставляем калькулятор статистики с загружаемым шаблоном Excel. Вы также можете прочитать следующие статьи, чтобы узнать больше:
- Пример формулы среднего арифметического
- Как рассчитать медиану?
- Расчет формулы режима
- Что такое статистика Z-теста?
Статистические функции (справочник)
Чтобы получить подробную информацию о функции, щелкните ее имя в первом столбце.
Примечание. Маркеры версии указывают версию Excel, в которой была введена функция. Эти функции недоступны в более ранних версиях. Например, маркер версии 2013 указывает, что эта функция доступна в Excel 2013 и всех более поздних версиях.
|
Функция |
Описание |
|
функция АВЕДЕВ |
Возвращает среднее абсолютных отклонений точек данных от их среднего значения |
|
СРЕДНЯЯ функция |
Возвращает среднее значение своих аргументов |
|
Функция СРЗНАЧА |
Возвращает среднее значение аргументов, включая числа, текст и логические значения. |
|
СРЗНАЧЕСЛИ функция |
Возвращает среднее (среднее арифметическое) всех ячеек в диапазоне, соответствующих заданным критериям |
|
Функция СРЗНАЧЕСЛИ |
Возвращает среднее (среднее арифметическое) всех ячеек, соответствующих нескольким критериям |
|
БЕТА.РАСП |
Возвращает кумулятивную функцию бета-распределения |
|
БЕТА.ОБР функция |
Возвращает обратную интегральную функцию распределения для указанного бета-распределения |
|
БИНОМ. |
Возвращает вероятность биномиального распределения отдельного термина |
|
Функция БИНОМ.РАСП.ДИАПАЗОН |
Возвращает вероятность результата испытания с использованием биномиального распределения |
|
БИНОМ.ОБР функция |
Возвращает наименьшее значение, для которого кумулятивное биномиальное распределение меньше или равно значению критерия |
|
Функция ХИ.РАСП. |
Возвращает кумулятивную функцию плотности бета-вероятности |
|
Функция ХИ. |
Возвращает одностороннюю вероятность распределения хи-квадрат |
|
Функция ХИ.ОБР. |
Возвращает кумулятивную функцию плотности бета-вероятности |
|
Функция ХИСК.ОБР.ПХ |
Возвращает обратную одностороннюю вероятность распределения хи-квадрат |
|
Функция CHISQ.ТЕСТ |
Возвращает тест на независимость |
|
УВЕРЕННОСТЬ. |
Возвращает доверительный интервал для среднего значения генеральной совокупности. |
|
УВЕРЕННОСТЬ.T функция |
Возвращает доверительный интервал для среднего значения генеральной совокупности с использованием распределения Стьюдента |
|
КОРРЕЛ функция |
Возвращает коэффициент корреляции между двумя наборами данных |
|
СЧЕТ функция |
Подсчитывает количество чисел в списке аргументов |
|
Функция СЧЁТ |
Подсчитывает количество значений в списке аргументов |
|
СЧИТАТЬ ПУСТОТЫ |
Подсчитывает количество пустых ячеек в диапазоне |
|
СЧЁТЕСЛИ функция |
Подсчитывает количество ячеек в диапазоне, соответствующих заданным критериям |
|
СЧЁТЕСЛИМН функция |
Подсчитывает количество ячеек в диапазоне, соответствующих нескольким критериям |
|
Функция КОВАРИАЦИЯ. |
Возвращает ковариацию, среднее значение произведений парных отклонений |
|
Функция КОВАРИАЦИЯ.S |
Возвращает выборочную ковариацию, среднее значение отклонений произведений для каждой пары точек данных в двух наборах данных |
|
Функция DEVSQ |
Возвращает сумму квадратов отклонений |
|
Функция ЭКСП.РАСП. |
Возвращает экспоненциальное распределение |
|
Функция F. |
Возвращает F-распределение вероятностей |
|
Функция F.РАСП.ВП |
Возвращает F-распределение вероятностей |
|
Функция F.ОБР. |
Возвращает обратное F-распределение вероятностей |
|
Функция F.ОБР.ПХ |
Возвращает обратное F-распределение вероятностей |
|
Функция F. |
Возвращает результат F-теста |
|
функция ФИШЕР |
Возвращает преобразование Фишера |
|
функция РЫБАЛОБР |
Возвращает обратное преобразование Фишера |
|
ПРОГНОЗ |
Возвращает значение по линейному тренду Примечание. В Excel 2016 эта функция заменена на FORECAST.LINEAR как часть новых функций прогнозирования, но она по-прежнему доступна для совместимости с более ранними версиями. |
|
ПРОГНОЗ.ETS функция |
Возвращает будущее значение на основе существующих (исторических) значений с использованием версии AAA алгоритма экспоненциального сглаживания (ETS) |
|
ПРОГНОЗ.ETS.CONFINT функция |
Возвращает доверительный интервал для значения прогноза на указанную целевую дату |
|
ПРОГНОЗ.ETS.СЕЗОННОСТЬ функция |
Возвращает длину повторяющегося шаблона, обнаруженного Excel для указанного временного ряда |
|
ПРОГНОЗ. |
Возвращает статистическое значение в результате прогнозирования временных рядов |
|
ПРОГНОЗ.ЛИНЕЙНАЯ функция |
Возвращает будущее значение на основе существующих значений |
|
функция ЧАСТОТА |
Возвращает частотное распределение в виде вертикального массива |
|
ГАММА-функция |
Возвращает значение гамма-функции |
|
ГАММА. |
Возвращает гамма-распределение |
|
Функция ГАММА.ОБР |
Возвращает обратное суммарное гамма-распределение |
|
Функция ГАММАЛН |
Возвращает натуральный логарифм гамма-функции, Γ(x) |
|
ГАММАЛЬН.ТОЧНАЯ функция |
Возвращает натуральный логарифм гамма-функции, Γ(x) |
|
Функция ГАУССА |
Возвращает на 0,5 меньше стандартного нормального кумулятивного распределения |
|
Функция ГЕОМЕАН |
Возвращает среднее геометрическое |
|
функция РОСТА |
Возвращает значения по экспоненциальному тренду |
|
функция ХАРМАНА |
Возвращает среднее гармоническое |
|
Функция ГИПЕРГЕОМ. |
Возвращает гипергеометрическое распределение |
|
ПЕРЕХВАТ |
Возвращает точку пересечения линии линейной регрессии |
|
КУРТ функция |
Возвращает эксцесс набора данных |
|
БОЛЬШАЯ функция |
Возвращает k-е наибольшее значение в наборе данных |
|
Функция ЛИНЕЙН |
Возвращает параметры линейного тренда |
|
Функция ЛИНЕЙН |
Возвращает параметры экспоненциального тренда |
|
Функция ЛОГНОРМ. |
Возвращает кумулятивное логнормальное распределение |
|
функция ЛОГНОРМ.ОБР |
Возвращает обратное логарифмически нормальное кумулятивное распределение |
|
Функция МАКС. |
Возвращает максимальное значение в списке аргументов |
|
Функция МАКСА |
Возвращает максимальное значение в списке аргументов, включая числа, текст и логические значения |
|
Функция МАКСИФМН |
Возвращает максимальное значение среди ячеек, заданных заданным набором условий или критериев |
|
МЕДИАННАЯ функция |
Возвращает медиану заданных чисел |
|
Функция МИН. |
Возвращает минимальное значение в списке аргументов |
|
Функция МИНИФС |
Возвращает минимальное значение среди ячеек, заданных заданным набором условий или критериев. |
|
Функция МИНА |
Возвращает наименьшее значение в списке аргументов, включая числа, текст и логические значения |
|
РЕЖИМ.МУЛЬТФУНКЦИЯ |
Возвращает вертикальный массив наиболее часто встречающихся или повторяющихся значений в массиве или диапазоне данных |
|
Функция MODE. |
Возвращает наиболее распространенное значение в наборе данных |
|
ОТРБИНОМ.РАСП |
Возвращает отрицательное биномиальное распределение |
|
Функция НОРМ.РАСП. |
Возвращает нормальное кумулятивное распределение |
|
НОРМ.ОБР функция |
Возвращает обратное нормальное кумулятивное распределение |
|
Функция НОРМ. |
Возвращает стандартное нормальное кумулятивное распределение |
|
Функция НОРМ.С.ОБР. |
Возвращает обратное стандартному нормальному кумулятивному распределению |
|
Функция ПИРСОН |
Возвращает коэффициент корреляции момента продукта Пирсона |
|
ПРОЦЕНТИЛЬ.ИСКЛ функция |
Возвращает k-й процентиль значений в диапазоне, где k находится в диапазоне от 0 до 1, исключая. |
|
ПРОЦЕНТИЛЬ.ВКЛ функция |
Возвращает k-й процентиль значений в диапазоне |
|
Функция ПРОЦЕНТРАНГ.ИСКЛ. |
Возвращает ранг значения в наборе данных в процентах (0..1, исключая) набора данных |
|
Функция ПРОЦЕНТРАНГ.ВКЛ. |
Возвращает процентный ранг значения в наборе данных |
|
ПЕРЕСТАВИТЬ функцию |
Возвращает количество перестановок для заданного количества объектов |
|
функция ПЕРЕСТАНОВКА |
Возвращает количество перестановок для заданного количества объектов (с повторениями), которые можно выбрать из общего количества объектов |
|
функция PHI |
Возвращает значение функции плотности для стандартного нормального распределения |
|
Функция ПУАССОН. |
Возвращает распределение Пуассона |
|
ПРОБ функция |
Возвращает вероятность того, что значения в диапазоне находятся между двумя пределами |
|
КВАРТИЛЬ.ИСКЛ функция |
Возвращает квартиль набора данных на основе значений процентиля от 0 до 1, исключая |
|
КВАРТИЛЬ.ВКЛ функция |
Возвращает квартиль набора данных |
|
РАНГ. |
Возвращает ранг числа в списке чисел |
|
Функция РАНГ.ЭКВ. |
Возвращает ранг числа в списке чисел |
|
Функция RSQ |
Возвращает квадрат коэффициента корреляции момента произведения Пирсона |
|
Функция СКОС |
Возвращает асимметрию распределения |
|
Функция СКОС. |
Возвращает асимметрию распределения на основе генеральной совокупности: характеристика степени асимметрии распределения относительно его среднего значения |
|
НАКЛОН функция |
Возвращает наклон линии линейной регрессии |
|
МАЛЕНЬКАЯ функция |
Возвращает k-е наименьшее значение в наборе данных |
|
СТАНДАРТНАЯ функция |
Возвращает нормализованное значение |
|
Функция СТАНДОТКЛОН. |
Вычисляет стандартное отклонение на основе всей совокупности |
|
Функция СТАНДОТКЛОН.С |
Оценивает стандартное отклонение на основе выборки |
|
СТАНДОТКЛОН функция |
Оценивает стандартное отклонение на основе выборки, включая числа, текст и логические значения |
|
Функция СТАНДОТКЛОНПА |
Вычисляет стандартное отклонение на основе всей совокупности, включая числа, текст и логические значения |
|
Функция СТЕЙКС |
Возвращает стандартную ошибку предсказанного значения y для каждого x в регрессии |
|
Функция Т. |
Возвращает процентные пункты (вероятность) для t-распределения Стьюдента |
|
Функция Т.РАСП.2T |
Возвращает процентные пункты (вероятность) для t-распределения Стьюдента |
|
Функция Т.РАСП.ВП |
Возвращает t-распределение Стьюдента |
|
Функция Т.ОБР. |
Возвращает t-значение распределения Стьюдента как функцию вероятности и степеней свободы |
|
Функция Т. |
Возвращает обратное распределение Стьюдента |
|
Функция Т.ТЕСТ |
Возвращает вероятность, связанную с критерием Стьюдента |
|
Функция ТРЕНД |
Возвращает значения по линейному тренду |
|
функция ОБРЕЗАТЬСРЕДНЕЕ |
Возвращает среднее значение внутренней части набора данных |
|
Функция VAR. |
Вычисляет дисперсию на основе всего населения |
|
Функция VAR.S |
Оценивает дисперсию на основе выборки |
|
Функция ВАРА |
Оценивает дисперсию на основе выборки, включая числа, текст и логические значения |
|
Функция ВАРПА |
Вычисляет дисперсию на основе всей совокупности, включая числа, текст и логические значения |
|
Функция WEIBULL. |
Возвращает распределение Вейбулла |
|
Функция Z.ТЕСТ |
Возвращает одностороннее значение вероятности z-критерия |
Важно: Результаты расчетов формул и некоторых функций рабочего листа Excel могут незначительно отличаться на ПК с Windows с архитектурой x86 или x86-64 и ПК с Windows RT с архитектурой ARM. Узнайте больше о различиях.
Функции Excel (по категориям)
функций Excel (по алфавиту)
Выучить формулы для среднего, медианы и моды
- Автор: Ритеш Кумар Гупта
- Последнее изменение 20-07-2022
- Автор
Ритеш Кумар Гупта - Последнее изменение 20-07-2022
Статистические формулы : Статистика — это раздел математики, который занимается сбором, организацией, анализом, интерпретацией и представлением данных.
Используя статистику, мы можем получить несколько показателей центральной тенденции и отклонения отдельных значений от центра. Мы можем использовать статистику для изучения данных в различных областях, чтобы отслеживать развивающиеся закономерности, а затем использовать результаты для разработки выводов и прогнозов. Давайте узнаем о формулах статистики класса 10 на их примерах.
Статистика — это дисциплина математики, которая занимается анализом данных и числами. Изучение сбора, анализа, интерпретации, представления и организации данных известно как статистика.
Статистика связана со сбором, классификацией, организацией и представлением числовых данных в заданном контексте.
Изучение концепций экзамена на Embibe
Основные понятия среднего, медианы, моды, дисперсии и стандартного отклонения являются ступеньками практически для всех статистических вычислений. Давайте подробно рассмотрим базовую статистику всех формул класса 10. 9n {{f_i} = } )Общее количество частот
Практические экзаменационные вопросы
Медиана
Среднее число или центральное значение в наборе данных называется медианой. Середина множества также известна как медиана. Чтобы найти медиану, расположите данные в порядке возрастания/убывания от наименьшего к наибольшему или от наибольшего к наименьшему значению. Медиана — это число, которое разделяет верхнюю и нижнюю половины выборки данных, генеральной совокупности или распределения вероятностей.
9{{rm{th}}}}{rm{term}}}}{2})
Аналогично, для сгруппированных данных:
Медиана ( = l + left( {frac {{frac {N}{2} – c}}{f}} right) times h)
Где,
(l = )нижний предел среднего класса
(c = )кумулятивная частота класса, предшествующего среднему классу
(f = )частота среднего класса
(N = )общее количество частота
(h=)высота медианного класса
Попытка пробных тестов
Режим
В наборе данных режим данных — это наблюдение с наибольшей частотой.
Режим ( = l + left( { frac {{{f_1} – {f_0}}}{{2,{f_1} – {f_0} – {f_2}}}} right) times h )
Где,
(l = )нижняя граница модального класса
({f_0} = )частота класса, предшествующего модальному классу
({f_1} = )частота модального класса
( {f_2} = ) частота класса, следующего за модальным классом
(h = )высота модального класса
Существует одна эмпирическая формула среди среднего, медианы и моды:
({rm{Mean}} — {rm{Mode}} = 3left( {{rm{Mean}} — {rm{Median}}} right))
Изучите все концепции статистики
Диапазон
Разница между самым высоким и самым низким значением среди заданного набора данных называется диапазоном.
Где,
(MDleft( A right) = ) Среднее отклонение относительно (A)
(A = ) Среднее/медиана/мода
(n = ) количество данных или наблюдений
Дисперсия
Дисперсия точек данных является мерой того, насколько они отличаются от среднего. Чем выше значение дисперсии, тем больше разброс данных от среднего, а чем меньше значение дисперсии, тем меньше разброс данных от среднего. Ожидание случайного набора квадратов отклонений данных от их среднего значения называется дисперсией. 92}} }}{N}} )
(N = )Общее количество частот
Применение статистики в реальной жизни
Вот несколько примеров использования статистики в повседневной жизни.
1. Все медицинские исследования опираются на статистику. Врачи используют статистику, чтобы отслеживать, где должен быть младенец с точки зрения умственного развития. Врачи также используют статистику для оценки эффективности лечения.
2.
3. Ежедневно корпорация производит тысячи товаров и следит за тем, чтобы продавались только самые качественные вещи. Корпорация не может протестировать каждый продукт. В результате организация применяет статистически обоснованное тестирование качества.
4. Для анализа акций фондовый рынок также использует статистические компьютерные модели. Биржевые аналитики используют статистические методы для сбора информации об экономике.
5. Розничные торговцы используют статистику для отслеживания всего, что они продают, и для отслеживания своих запасов. Ведущие ритейлеры по всему миру используют аналитику, чтобы определить, какие товары поставляются в какие магазины и когда. 9{{rm{th}}}}{rm{наблюдение}}}}{2} = frac{{2 + 3}}{2} = 2,5)
Следовательно, медиана данных равна ( 2.
Q.4. Вычислите среднее отклонение от среднего для следующих данных:
4,7,8,9,10,12,13,17
Ответ: среднее значение заданных данных.
(overline x = frac{{4 + 7 + 8 + 9 + 10 + 12 + 13 + 17}} {8} = 10)
2 1 3 9132 (3) 9133 (17) 9п { слева | {{d_i}} right|} )
Q.5. Найдите стандартное отклонение и дисперсию для следующих данных:
| ({x_i}) | (left| {{d_i}} right| = left| {{x_i} – overline x } right|) |
| (4) | (6) |
| (7) | (3) |
| (8) | (2) |
| (9) | (1) |
| (10) | (0) |
| (12) | (2) |
| (13) | (7) |
(поэтому MD = frac{1}{8} times 24 = 3) (f:)
| (x:) | (3) | (8) | (13) | (18) | (23) | (7) | (10) | (15) | (10) | (6) |
2 913 An 3 9132) (3) (7) (21) (63) (8) ) (80) (640) (13) (15) (195) (2532) 913 93 ) (10) (180) (3240) (23) (6) (1323) 9 3174) 92}} справа) = 37,49)
Подведение итогов
В этой статье мы узнали о статистике, формулах и решенных примерах и их применении в реальной жизни.
Статистика широко используется в области медицинских исследований, прогнозов погоды, проверки качества, фондового рынка и т. д. Мы можем узнать о том, что произошло в прошлом и что может произойти в будущем, используя статистику.
Изучение показателей центральной тенденции
Часто задаваемые вопросы по формулам статистики
Вот некоторые из часто задаваемых вопросов о формулах статистики:
Q.1: Как запомнить формулы статистики?
Ответ: Чтобы запомнить формулы статистики, нам нужно продолжать практиковаться в ежедневном решении множества вопросов. Регулярное решение множества задач поможет запомнить формулы статистики.
Q.2: Что такое формула моды в статистике?
Ответ: В наборе данных модой данных является наблюдение с наибольшей частотой.
Здравствуйте, на этой странице я собрала краткий курс лекций по предмету «Статистика».
Лекции подготовлены для студентов любых специальностей и охватывает курс предмета «Статистика».
В лекциях вы найдёте основные законы, теоремы, формулы и примеры с решением.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Стати́стика — отрасль знаний, наука, в которой излагаются общие вопросы сбора, измерения, мониторинга, анализа массовых статистических (количественных или качественных) данных и их сравнение; изучение количественной стороны массовых общественных явлений в числовой форме. wikipedia.org/wiki/Статистика
Статистическое наблюдение, сводка и группировка
Статистическое наблюдение – это сбор данных (фактов, сведений) об изучаемых явлениях. При подготовке к проведению статистического наблюдения решаются программно-методологические и организационные вопросы.
Программно-методологические вопросы включают в себя формулировку задачи наблюдения, определение объекта и единиц наблюдения, а также составление программы наблюдения.
Объектом наблюдения называют явление или совокупность явлений, информацию о которых собирают в процессе наблюдения.
Единицы наблюдения – первичные элементы объекта, являющиеся носителями признаков, подлежащих регистрации.
Программа наблюдения – перечень вопросов, ответы на которые получают в процессе наблюдения.
Для решения организационных вопросов составляется организационный план статистического наблюдения, определяющий цель, вид, форму, способ наблюдения, место и сроки его проведения.
В результате статистического наблюдения получают первичные данные о единицах совокупности, которые на следующем этапе статистического исследования – этапе сводки – обобщаются в группы, систематизируются. Статистическая сводка – это приведение собранной информации к виду, удобному для проведения анализа. Простая сводка заключается в простом подсчете общих итогов, сложная – в группировке единичных данных по однородному признаку, подсчете итогов по ним и представлении результатов в виде статистических таблиц.
Статистические группировки в зависимости от решаемых задач подразделяются на типологические, структурные и аналитические.
Статистическая группировка позволяет дать характеристику размеров, структуры и взаимосвязи изучаемых явлений, выявить их закономерности.
Важным направлением в статистической сводке является построение рядов распределения, одно из назначений которых состоит в изучении структуры исследуемой совокупности, характера и закономерности распределения.
Ряд распределения – это простейшая группировка, представляющая собой распределение численности единиц совокупности по значению какого-либо признака.
Вариантами ряда распределения являются отдельные значения признака, а численности отдельных вариантов или групп ряда, показывающие, как часто встречаются те или иные варианты в ряду распределения, называют частотами.
Ряды распределения, в основе которых лежит качественный признак, называют атрибутивными. Если ряд построен по количественному признаку, его называют вариационным.
Различают дискретные (признак – целое число) и интервальные вариационные ряды (признак принимает разные значения в пределах интервала).
При построении вариационного ряда с равными интервалами определяют число групп 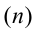
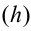
где N – число единиц совокупности.
Величина равного интервала рассчитывается по формуле:
где 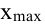
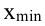
Для изучения связи между явлениями и их признаками строят корреляционную таблицу и аналитическую группировку.
Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному.
Концентрация частот около диагоналей матрицы данных свидетельствует о наличии корреляционной связи между признаками.
Аналитическая группировка позволяет изучать взаимосвязь факторного и результативного признаков.
Основные этапы проведения аналитической группировки – обоснование и выбор факторного и результативного признаков, подсчет числа единиц в каждой из образованных групп, определение объема варьирующих признаков в пределах созданных групп, а также исчисление средних размеров результативного показателя. Результаты группировки оформляются в таблице.
Абсолютные и относительные показатели
Абсолютные и относительные величины являются обобщающими показателями, характеризующими количественную сторону общественных явлений. Различают два вида обобщающих показателей: абсолютные и относительные величины.
Абсолютные величины – именованные числа, имеющие определенную размерность и единицы измерения. Они характеризуют показатели на момент времени или за период. В зависимости от различных причин и целей анализа применяются натуральные, условнонатуральные, денежные и трудовые единицы измерения.
В практической деятельности при отсутствии необходимой информации абсолютные величины получают расчетным путем, например на основе балансовой увязки:
где 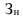
П – поступление за период;
Р – расход за период; 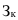
Отсюда:
Абсолютные статистические величины широко используют в анализе и прогнозировании состояния и развития явлений общественной жизни. На основе абсолютных величин исчисляют относительные величины.
Относительные величины характеризуют количественное соотношение сравниваемых абсолютных величин.
Числитель – сравниваемая величина, ее называют текущей или отчетной величиной; знаменатель называют базой сравнения или основанием сравнения. Как правило, базу сравнения принимают равной 1, 100, 1000, 10000. Если отношение равно 1, то относительная величина показывает, во сколько раз текущая величина больше базисной или какую долю от базисной она составляет, и выражается в коэффициентах. Если база сравнения равна 100, то относительная величина выражена а процентах (%), если база сравнения равна 1000 – в промилле (‰), 10000 – в продецимилле (‰0).
Различают следующие виды относительных показателей: планового задания и выполнения плана, динамики, структуры, интенсивности, координации, сравнения.
1. Относительные показатели планового задания (ОППЗ) – отношение уровня, запланированного на предстоящий период (П), уровню показателя, достигнутого в предыдущем периоде 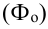
Относительные показатели выполнения плана (ОПВП) – отношение фактически достигнутого уровня в текущем периоде 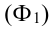
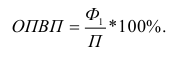
2. Относительные показатели динамики характеризуют изменение уровня развития какого-либо явления во времени. Показатели этого вида получаются делением уровня признака за определенный период или момент времени на уровень этого же показателя в предыдущий период или момент. Относительные величины динамики иначе называют темпами роста. Они могут быть выражены в коэффициентах или процентах и определяются с использованием переменной базы сравнения – цепные и постоянной базы сравнения – базисные.
3. Относительные показатели структуры характеризуют состав изучаемой совокупности, доли, удельные веса элементов совокупности в общем итоге и представляют собой отношение части единиц совокупности 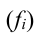
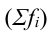
где d – удельный вес частей совокупности.
4. Относительные показатели интенсивности характеризуют степень насыщенности или развития данного явления в определенной среде, являются именованными показателями и могут выражаться в кратных отношениях, процентах, промилле и других формах.
5. Относительные показатели координации (ОПК) характеризуют отношения частей изучаемой совокупности к одной из них, принятой за базу сравнения. Они показывают, во сколько раз одна часть совокупности больше другой или сколько единиц одной части приходится на 1, 10, 100, 1000 единиц другой части. Эти относительные величины могут быть исчислены как по абсолютным показателям, так и по показателям структуры.
6. Относительные показатели сравнения (ОПС) характеризуют отношения одноименных абсолютных показателей, соответствующих одному и тому же периоду или моменту времени, но к различным объектам или территориям.
Средние величины и показатели вариации
Средняя является обобщающей характеристикой совокупности единиц по качественно однородному признаку. В статистике применяются различные виды средних: арифметическая, гармоническая, квадратическая, геометрическая и структурные средние – мода, медиана. Средние, кроме моды и медианы, исчисляются в двух формах: простой и взвешенной. Выбор формы средней зависит от исходных данных и содержания определяемого показателя. Наибольшее распространение получила средняя арифметическая, как простая, так и взвешенная.
Средняя арифметическая простая равна сумме значений признака, деленной на их число:
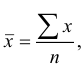
где х – значение признака (вариант);
n – число единиц признака.
Средняя арифметическая простая применяется в случаях, когда варианты представлены индивидуально в виде их перечня в любом порядке или ранжированного ряда.
Если данные представлены в виде дискретных или интервальных рядов распределения, в которых одинаковые значения признака (х) объединены в группы, имеющие различное число единиц (f), называемое частотой (весом), применяется средняя арифметическая взвешенная:
В качестве весов могут быть использованы относительные величины, выраженные в процентах (d). Метод расчета средней не изменяется:
Если проценты заменить коэффициентами 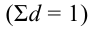
В статистике приходится вычислять средние по вариантам, которые являются групповыми (частными) средними. В таких случаях общая средняя определяется как средняя арифметическая взвешенная из групповых средних, в которой весами являются объемы единиц в группах.
Наряду со средней арифметической применяется средняя гармоническая, которая вычисляется из обратных значений осредняемого признака и по форме может быть простой и взвешенной.
Мода – значение признака, наиболее часто встречающееся в изучаемой совокупности. Для дискретных рядов распределения модой является вариант с наибольшей частотой. Для интервальных вариационных рядов распределения мода рассчитывается по формуле:
где 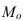
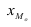
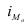
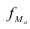
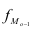
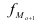
Медианой называется вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части. Для интервальных вариационных рядов медиана рассчитывается по формуле:
где 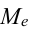
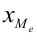
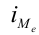
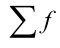
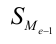
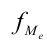
Показатели вариации. Для измерения степени колеблемости отдельных значений признака от средней исчисляются основные обобщающие показатели вариации: дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Дисперсия 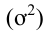
В зависимости от исходных данных дисперсия вычисляется по формуле средней арифметической простой или взвешенной:
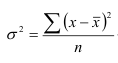
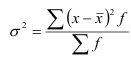
Среднее квадратическое отклонение 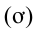
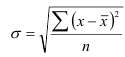
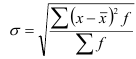
В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака (рублях, тоннах, процентах и т.д.).
Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации (V), который представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.
Правило сложения дисперсий (вариаций). Для статистической совокупности, сгруппированной по изучаемому признаку, возможно вычисление трех видов дисперсий: общей 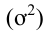
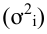
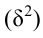
Если основанием группировки является факторный признак, то с помощью правила сложения дисперсий можно измерить силу его влияния на результативный признак, вычислив коэффициент детерминации и эмпирическое корреляционное отношение.
Коэффициент детерминации равен отношению межгрупповой дисперсии к общей:
и показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака.
Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением:
По абсолютной величине он может изменяться от 0 до 1. Если 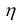
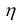
Возможно эта страница вам будет полезна:
Выборочное наблюдение
Целью выборочного наблюдения является определение характеристик генеральной совокупности – генеральной средней 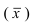
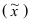
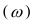
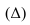
Собственно-случайная и механическая выборки. При случайном повторном отборе предельная ошибка выборки для средней 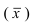
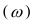
где 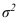
n – численность выборки;
t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности (Р).
При бесповторном случайном и механическом отборе предельная ошибка выборки определяется по формулам:
где N – численность генеральной совокупности.
Типическая выборка. При типическом (районированном) отборе генеральная совокупность разбивается на однородные типические группы, районы. Отбор единиц наблюдения в выборочную совокупность производится различными методами. Рассмотрим типическую выборку с пропорциональным отбором внутри типических групп.
Объем выборки из типической группы при отборе, пропорциональном численности типических групп, определяется по формуле
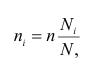
где 
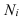
Предельная ошибка выборочной средней и доли при бесповторном случайном и механическом способе отбора внутри типических групп рассчитывается по формулам:
где 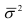
Серийная выборка. При серийном способе отбора генеральную совокупность делят на одинаковые по объему группы – серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию.
При бесповторном отборе серий предельные ошибки выборочной средней и доли определяются по формуле
где 
R – число серий в генеральной совокупности;
r – число отобранных серий.
В практике проектирования выборочного наблюдения возникает потребность в нахождении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли.
Предельная ошибка выборки, вероятность ее появления и вариации признака предварительны известны.
При случайном повторном отборе численность выборки определяется по формуле:
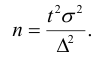
При случайном бесповторном и механическом отборе численность выборки вычисляется по формуле:
Для типической выборки
Для серийной выборки
Ряды динамики
Ряды динамики характеризуют изменение уровней показателя во времени. Ряды динамики подразделяют на ряды динамики абсолютных, средних и относительных величин. По признаку времени ряды динамики абсолютных величин подразделяют на моментные и интервальные ряды динамики. Каждый ряд динамики состоит из двух элементов: 1) периодов или моментов времени; 2) уровней.
Уровни ряда динамики должны сопоставимы по методологии расчета показателя, территории, продолжительности периодов, охватываемого объекта, единицам измерения и другим признакам.
В тех случаях, когда вначале имеются уровни ряда, исчисляемые по одной методологии или в одних границах, а затем уровни, исчисляемые по другой методологии или в других границах, уровни ряда динамики оказываются несопоставимы между собой. Чтобы привести уровни в ряду динамики к сопоставимому, годному для анализа виду, необходимо применить прием, который называют смыканием рядов динамики.
В статистике для сравнения базисных темпов роста изучаемых рядов динамики за анализируемый период принято исчислять коэффициент опережения 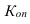
где 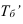
Для интервального ряда динамики средний уровень 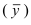
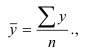
где у – уровни ряда.
Для моментного рядя динамики с равными интервалами средний уровень ряда исчисляется по формуле средней хронологической:
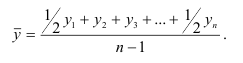
Для моментного ряда динамики с неравными интервалами средний уровень ряда исчисляется по формуле:
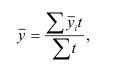
где 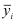
t – интервал времени (число месяцев между моментами времени).
Аналитические показатели ряда динамики
1. Абсолютный прирост (Δу) – это разность между последующим уровнем ряда и предыдущим (или базисным). цепной – 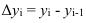
Средний абсолютный прирост исчисляется двумя способами: а) как средняя арифметическая простая годовых (цепных) приростов:
б) как отношение базисного прироста к числу периодов:
2. Темп роста 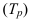
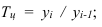
Между цепными и базисными темпами роста имеется взаимосвязь: произведение соответствующих цепных темпов роста равна базисному. Зная базисные темпы, можно исчислить цепные делением каждого последующего базисного темпа роста на каждый предыдущий.
3. Темп прироста 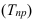
а) как отношение абсолютного прироста к предыдущему уровню:
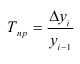
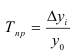
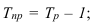
4. Абсолютное значение одного процента прироста (А1%) равно отношению абсолютного прироста цепного к темпу прироста цепному.
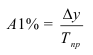
Этот показатель может быть исчислен иначе: как одна сотая часть предыдущего уровня.
Расчет среднего абсолютного значения одного процента прироста за несколько лет производится по формуле:
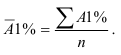
Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
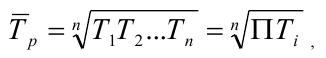
где n – число коэффициентов;
П — знак произведения.
Среднегодовой темп роста может быть исчислен из отношения конечного 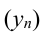
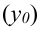
Среднегодовой темп прироста исчисляется следующим образом:
Выявление основной тенденции развития показателей может определяться следующими методами:
1) методом скользящей средней;
2) методом аналитического выравнивания.
2. Метод аналитического выравнивания ряда динамики по прямой. Уравнение прямой имеет вид
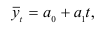
где 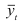
t – показатель времени (дни, месяцы, годы и т.д.).
Для нахождения параметров
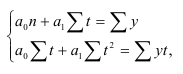
где у – фактические уровни ряда динамики;
n – число уровней.
После решения уравнения наносим на график фактические уровни и исчисленную прямую линию, характеризующую тенденцию динамического ряда.
Индексы сезонности.
Для исчисления индексов сезонности применяют различные методы, выбор которых зависит от характера общей тенденции ряда динамики. Если ряд динамики не содержит ярко выраженной тенденции развития, то индексы сезонности исчисляют непосредственно по эмпирическим данным без их предварительного выравнивания.
Для расчета индексов сезонности необходимо иметь помесячные данные минимум за три года. Для каждого месяца рассчитывается средний уровень 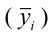
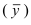
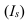
где 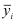
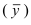
Когда уровни ряда динамики проявляют тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях фактические данные сопоставляются с выравненными.
Для расчета индекса сезонности в таких рядах динамики применяется формула:
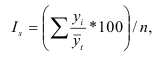
где 
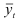
n – число лет.
Индексы
Индексы – обобщающие показатели сравнения во времени и в пространстве не только однотипных (одноименных) явлений, но и совокупностей, состоящих из несоизмеримых элементов.
Методики построения и расчета индексов как для временных, так и для пространственных сравнений одинаковы. Не различаются между собой и методы построения индексов различных явлений. Поэтому в данной главе формулы для расчета индексов приведены на примере индексируемых цен (р), объемов продаж (производства) (q), товарооборота (рq), изменяющихся во времени.
Динамика одноименных явлений изучается с помощью индивидуальных индексов (i), которые представляют собой известные относительные величины сравнения, динамики и выполнения плана (обязательств):
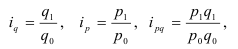
где подстрочное обозначение «0» соответствует уровню базисного периода (с которым сравнивают) или момент времени, «1» — уровню отчетного (сравниваемого) периода или момента времени.
Изменения совокупностей, состоящих из элементов, непосредственно не сопоставимых (например, различных видов продукции), изучают с помощью групповых, или общих, индексов (I). Последние по методам построения подразделяются на агрегатные индексы и средневзвешенные из индивидуальных индексов.
Формулы агрегатных индексов:
1) физического объема:
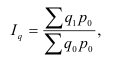
где q – индексируемая величина; 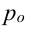
В случае индексов объемных показателей весами являются качественные показатели (цена, себестоимость и др.), зафиксированные на уровне базисного периода.
Разница между числителем и знаменателем индекса
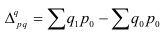
в данном случае означает абсолютное изменение товарооборота (прирост или снижение) за счет изменения физического объема;
2) цен и других качественных показателей:
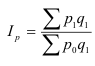
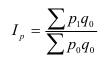
где q – объемы (количества) являются весами, взятыми на одинаковом уровне (отчетном или базисном).
Разница между числителем и знаменателем индексов
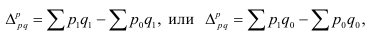
означает:
— в первом случае – абсолютный прирост товарооборота (выручки от продаж) в результате изменения цен или экономию (перерасход_ денежных средств населения в результате среднего снижения (повышения) цен;
— во втором случае – условный абсолютный прирост товарооборота, если бы объемы продаж в отчетном периоде совпали с объемами продаж в базисном периоде;
3) товарооборота (выручки от реализации или продаж):
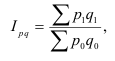
где pq – индексируемое сложное явление, в состав которого входят соизмеримые элементы совокупности. Разница между числителем и знаменателем индекса 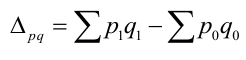
Формулы средних индексов из индивидуальных:
1) физического объема:
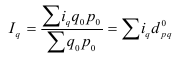
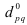
2) цен:
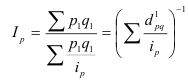
где 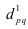
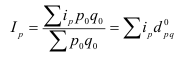
Если индексы качественных показателей построены на основе весов, взятых на уровне отчетного периода (например, по формуле Пааше), то рассмотренные выше агрегатные индексы, а также их элементы взаимосвязаны между собой: 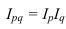
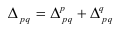
Участие каждого фактора в формировании общего прироста товарооборота в относительном выражении может быть определено так:
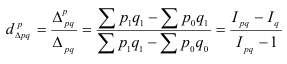
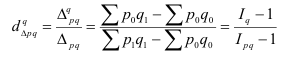
При этом 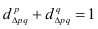
Если сравнивают друг с другом не два периода (момента), а более, то выделяют цепную и базисную системы индексов.
Цепные и базисные индивидуальные индексы взаимосвязаны между собой:
— произведение цепных индексов равно конечному базисному;
— частное от деления двух смежных базисных индексов равно промежуточному цепному.
Между цепными и базисными общими индексами, построенными на основе постоянных весов, существует взаимосвязь, аналогичная взаимосвязи между индивидуальными индексами.
Индексы, построенные на основе переменных весов, непосредственно перемножать и делить нельзя.
Индексный метод широко применяется также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующее изменение индексируемого (осредняемого) показателя.
Индекс переменного состава для любых качественных показателей имеет следующий вид:
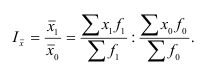
Величина этого индекса характеризует изменение средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного (фиксированного) состава представляет собой отношение средних взвешенных с одними и теми же весами (при постоянной структуре). Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя (х) у единиц совокупности. В общем виде он может быть записан следующим образом:
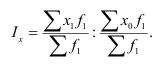
Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:
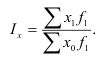
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:
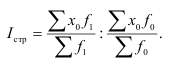
Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d). Система взаимосвязанных индексов при анализе динамики среднего уровня качественного показателя имеет вид:
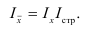
В индексах средних уровней в качестве весов могут быть взяты удельные веса единиц совокупности 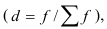
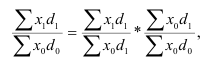
или

Аналогично приведенным формулам строятся индексы средних уровней: цен, себестоимости продукции, фондоотдачи, производительности труда, оплаты труда и др.
Возможно эта страница вам будет полезна:
Статистические методы изучения взаимосвязей
При статистическом исследовании корреляционных связей одной из основных задач является определение их формы, т.е. построение модели связи.
Построение регрессионной модели проходит несколько этапов: предварительный теоретический анализ, определение объекта, отбор факторов, сбор и подготовка информации, выбор модели связи, исчисление показателей тесноты корреляционной связи, оценка адекватности регрессионной модели.
Вычисление параметров корреляционных линейных уравнений по первичным данным. Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость является линейной и выражается уравнением прямой
(1)
где у — индивидуальные значения результативного признака;
х — индивидуальные значения факторного признака;
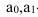
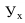
Параметры уравнения прямой 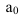
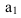
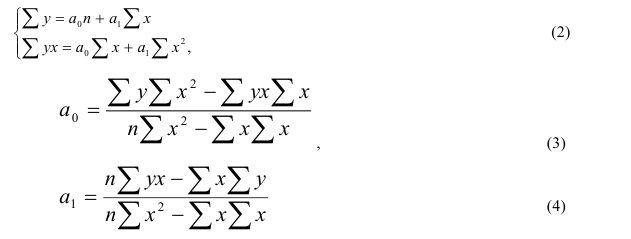
Что касается параметра уравнения регрессии в виде свободного члена, то возможен и такой подсчет:
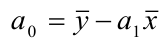
Ясно, что практически приемлемым является наименее трудоемкий вариант расчета (возможно производить расчеты на компьютере).
В уравнении прямой параметр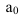
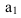

где 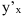
Средний коэффициент эластичности определяется для уравнения прямой по формуле
Коэффициент эластичности показывает, насколько процентов изменяется результативный признак при изменении факторного признака на 1%.
Определение параметров линейного однофакторного уравнения регрессии по сгруппированным данным. Если данные сгруппированы и представлены в виде корреляционной таблицы, то параметры линейного уравнения регрессии могут быть определены путем решения следующей системы нормальных уравнений:
или по формулам
где 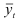
Параметр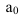
Расчет параметров степенной функции. Если значения факторного признака расположены в порядке геометрической прогрессии и соответствующие значения результативного признака также образуют геометрическую прогрессию, то связь между признаками может быть представлена степенной функцией вида
Для определения параметров степенной функции методом наименьших квадратов необходимо привести ее к линейному виду путем логарифмирования:
Система нормальных уравнений имеет вид
Параметры можно определить, решая систему нормальных уравнений или по формулам
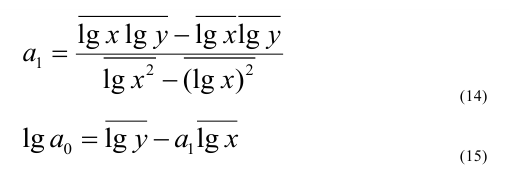
или
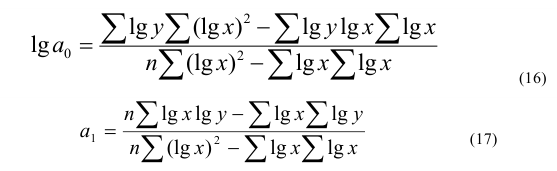
Параметр 
Расчет параметров уравнения гиперболы. Если результативный признак с увеличением факторного признака возрастает (или убывает) не бесконечно, а стремится к конечному пределу, то для анализа такого признака применяется уравнение гиперболы вида
Для определения параметров этого уравнения используется система нормальных уравнений
Чтобы определить параметры уравнения гиперболы методом наименьших квадратов, необходимо привести его к линейному виду. Для этого произведем замену переменных 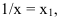
Параметры уравнения гиперболы можно вычислить по формулам
Статистические методы измерения тесноты корреляционной связи между двумя признаками. Одним из важнейших этапов исследования корреляционной связи является измерение ее тесноты. Для этого применяются: линейный коэффициент корреляции, теоретическое корреляционное отношение, индекс корреляции.
Линейный коэффициент корреляции вычисляется по формулам и применяется для измерения тесноты связи только при линейной форме связи:
Теоретическое корреляционное отношение и индекс корреляции применяются для измерения тесноты корреляционной связи между признаками при любой форме связи, как линейной, так и нелинейной.
Оба показателя можно вычислять только после того, как определена форма связи и исчислена теоретическая линия регрессии.
Теоретическое корреляционное отношение рассчитывается по формулам
где 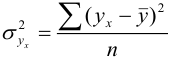
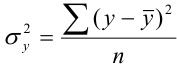
Теоретическое корреляционное отношение изменяется от 0 до 1: чем ближе корреляционное отношение к 1, тем теснее связь между признаками.
Для упрощения расчетов меры тесноты корреляционной связи часто применяется индекс корреляционной связи, который определяется по следующим формулам:
, где 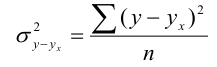
Проверка адекватности однофакторной регрессионной модели и значимости показателей тесноты корреляционной связи. Адекватность регрессионной модели при малой выборке можно оценить F-критерием Фишера:
, где m — число параметров модели;
n — число единиц наблюдения.
Эмпирическое значение критерия 
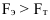
Значимость коэффициентов линейного уравнения регрессии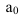
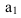
Эмпирическое значение t — критерия сравнивается с критическим (табличным) значением t — распределения Стьюдента с уровнем значимости 0,01 или 0,05 и числом степеней свободы (n — 2). Параметр признается значимым, если эмпирическое значение t больше табличного.
Аналогично проводится оценка коэффициента корреляции r с помощью t критерия, который определяется по формуле
где (n — 2) — число степеней свободы.
Если эмпирическое значение t оказывается больше табличного, то линейный коэффициент корреляции признается значимым.
Построение моделей связи в виде уравнения множественной регрессии. Изменение экономических явлений происходит под влиянием не одного, а большого числа самых разнообразных факторов. Связь между результативным признаком и двумя и более факторами принято выражать уравнением множественной регрессии.
Уравнения множественной регрессии могут быть линейные, криволинейные и комбинированные.
Наиболее простым видом уравнения множественной регрессии является линейное уравнение с двумя независимыми переменными:
Параметры уравнения множественной регрессии определяются методом наименьших квадратов путем решения системы нормальных уравнений:
Параметры уравнения множественной регрессии показывают изменение результативного признака при изменении факторного признака на единицу. Для оценки влияния факторных признаков на результативный рассчитываются частные коэффициенты эластичности и бета-коэффициенты.
Частный коэффициент эластичности (Э) вычисляется по формуле
где 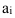
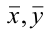
Частный коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1% при фиксированных значениях других факторов.
Бета-коэффициент (β) вычисляется по формуле
Бета-коэффициент показывает, на какую часть сигмы изменяется результативный признак при изменении факторного признака на величину его сигмы.
Сравнение бета-коэффициентов при различных факторах дает возможность оценить силу их воздействия на результативный признак.
Параметры уравнения регрессии можно определять по формулам через коэффициенты корреляции и средние квадратические отклонения:
Парные коэффициенты корреляции можно вычислить по следующим формулам:
Средние квадратические отклонения определяются по формулам
Статистические методы измерения тесноты корреляционной связи в многофакторных моделях. При проведении многофакторного корреляционного анализа возникает необходимость расчета множественных, парных и частных коэффициентов корреляции. Для измерения тесноты корреляционной связи между результативным признаком и несколькими факторными при линейной форме связи рассчитывается множественный коэффициент корреляции по формуле
где 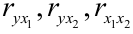
Множественный коэффициент корреляции изменяется от 0 до +1. Он показывает тесноту корреляционной связи между результативным признаком и факторными признаками, включенными в уравнение множественной регрессии.
Парные коэффициенты корреляции вычисляются по формулам
или по формулам (42), (43), (44).
Парные коэффициенты корреляции показывают тесноту корреляционной связи как между факторными и результативными признаками, так и между признаками-факторами.
Для исследования тесноты корреляционной связи между признаками при построении моделей множественной регрессии применяются частные (парные) коэффициенты корреляции, которые характеризуют тесноту корреляционной связи между факторным и результативным признаками, при элиминировании влияния учтенных факторов.
Возможно эта страница вам будет полезна:
Частные коэффициенты корреляции вычисляются по формулам
Теоретическое корреляционное отношение и совокупный индекс корреляции. Эти показатели имеют такой же экономический смысл, что и при парной регрессии, и определяются по формулам
Вместо теоретического корреляционного отношения может быть использован адекватный ему показатель — совокупный индекс корреляции:
Проверка адекватности многофакторной регрессионной модели. Построенное уравнение множественной регрессии необходимо содержательно интерпретировать и оценить его с точки зрения адекватности реальной действительности. Прежде всего следует установить, соответствуют ли полученные данные тем гипотетическим представлениям, которые сложились в результате анализа, и показывают ли они причинно-следственные связи, которые ожидались. Для оценки адекватности модели можно вычислить отклонение теоретических данных от эмпирических, остаточную дисперсию, также ошибку аппроксимации, которая определяется по формуле
Особое внимание необходимо обратить на интерпретацию и оценку параметров уравнения. Параметры уравнения регрессии следует проверить на их значимость.
Для оценки значимости параметров при малых выборках уравнения множественной регрессии используется t -критерий Стьюдента при (n — m- 1) степенях свободы:
Значения 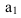
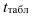
Адекватность уравнения регрессии оценивается с помощью F-критерия Фишера, который определяется по формуле
Если 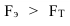
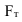
Существенность совокупного коэффициента корреляции также оценивается с помощью t-критерия Стьюдента:
Если 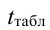
Статистика населения и трудовых ресурсов
Экономически активное население (рабочая сила) – часть населения, обеспечивающая предложение рабочей силы для производства товаров и услуг. Численность экономически активного населения включает занятых и безработных.
Коэффициент экономической активности населения определяется отношением численности экономически активного населения к общей численности населения:
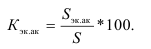
Коэффициент занятости населения определяется отношением численности занятого населения к численности экономически активного населения:
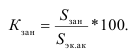
Коэффициент безработицы определяется отношением численности безработных к численности экономически активного населения:
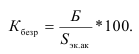
Численность трудовых ресурсов определяется как численность трудоспособного населения в трудоспособном возрасте и работающих лиц за пределами трудоспособного возраста (лица пенсионного возраста и подростки).
Статистика национального богатства
По определению, принятому в отечественной статистике, национальное богатство представляет собой совокупность ресурсов страны – экономических активов, создающих необходимые условия для производства товаров, оказания услуг и обеспечения жизни людей.
Экономические активы, включаемые в состав национального богатства, подразделяются на финансовые и нефинансовые.
Объем национального богатства определяется, как правило, в стоимостном выражении в текущих и постоянных ценах на начало и конец года.
Значительный удельный вес в составе накопленного богатства занимают основные производственные фонды. Статистика характеризует фонды системой показателей, среди которых показатели объема, состава фондов, коэффициенты состояния, движения основных фондов, показатели их использования, показатели динамики.
К коэффициентам состояния основных фондов относятся:
— коэффициент износа основных фондов;

— коэффициент годности основных фондов:
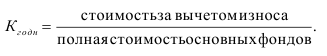
Эти коэффициенты являются моментными показателями, то есть характеризуют степень физического состояния фондов на определенную дату.
Расширенное воспроизводство основных фондов характеризуют коэффициенты выбытия и обновления за период.
Коэффициент выбытия рассчитывается как отношение стоимости фондов, выбывших за год, к стоимости фондов на начало года.
Коэффициент обновления представляет собой отношение стоимости введенных за год новых фондов к их полной стоимости на конец года.
Для характеристики простого и расширенного воспроизводства основных фондов составляют балансы основных фондов по полной стоимости и по стоимости за вычетом износа. В балансах основных фондов показывается их наличие на начало года, поступление по источникам, выбытие по направлениям, наличие на конец года. При составлении баланса основных фондов по стоимости за вычетом износа, кроме того. учитывают сумму амортизации, уменьшающей стоимость основных фондов.
Эффективность использования основных фондов характеризует показатель фондоотдачи, рассчитываемый как отношение объема выпуска продукции за год к среднегодовой полной стоимости основных фондов.
Статистика рассчитывает ряд показателей для характеристики оборотных фондов. Основными из них являются коэффициент оборачиваемости (количество оборотов) оборотных средств и продолжительность одного оборота.
Коэффициент оборачиваемости есть отношение объема реализации к оборотным средствам. Продолжительность одного оборота может быть рассчитана как отношение числа дней в периоде к числу оборотов.
При ускорении оборачиваемости оборотных средств часть их высвобождается из оборота. Эта высвобождающаяся в результате ускорения оборачиваемости часть может быть рассчитана по формуле
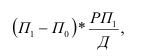
где 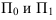
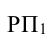
Д — продолжительность периода (месяц — 30 дней, квартал — 90 дней, год — 360 дней).
Возможно эта страница вам будет полезна:
Статистика макроэкономических показателей
Система показателей, характеризующих развитие экономики, включает результаты деятельности на всех уровнях производства. Оценка конечных результатов деятельности осуществляется на уровне отдельного предприятия, организации, учреждения и других хозяйствующих субъектов, а также в разрезе секторов отраслей и экономики в целом.
Система статистических показателей необходима для достоверной оценки результатов функционирования и прогнозирования дальнейшего развития экономики страны.
Показатели результатов функционирования экономики в целом на макроуровне принято называть макроэкономическими показателями. Они определяются на основе системы национальных счетов (СНС) и характеризуют различные стадии экономической деятельности: производство товаров и услуг, образование и распределение доходов и их конечное использование.
Стадия производства характеризуется следующими показателями: валовой выпуск (ВВ), промежуточное потребление (ПП), валовая добавленная стоимость (ВДС) и валовой внутренний продукт (ВВП).
Валовой выпуск — это суммарная стоимость всех произведенных товаров и услуг за год в экономике, имеющих рыночный и нерыночный характер.
Товары и услуги оцениваются по основным ценам, т.е. ценам, по которым они продаются, поэтому валовой выпуск в отраслевом разрезе исчисляется в основных ценах.
Промежуточное потребление определяется как стоимость товаров и рыночных услуг, которые трансформируются или полностью потребляются в течение данного периода с целью производства других товаров и услуг. Потребление основного капитала (амортизация) не входит в промежуточное потребление.
Валовая добавленная стоимость (ВДС) исчисляется на уровне отраслей экономики как разность между валовым выпуском товаров, услуг и промежуточным потреблением. Термин «валовая» означает то, что показатель включает потребленную в процессе производства стоимость основного капитала.
В системе национальных счетов валовая добавленная стоимость оценивается в основных ценах, т.е. в ценах, включающих субсидии на продукты, но не включающих налоги на продукты.
Налоги на продукты включают платежи, размер которых прямо зависит от стоимости произведенной продукции и оказанных услуг: налог на добавленную стоимость, налог с продаж, акцизы и др. Налоги на импорт — это налоги на импортируемые товары и услуги.
Термин «чистые» налоги на продукты и импорт (ЧНП) и (ЧНИ) в данном случае означает, что налоги показаны за вычетом соответствующих субсидий.
Субсидии (С) — текущие некомпенсируемые выплаты из федерального бюджета предприятиям при условии производства ими определенного вида продукции или услуг.
ВДС (в основных ценах) = (ВВ — ПП) — косвенно измеряемые услуги финансового посредничества.
ВДС (в рыночных ценах) = ВДС (в основных ценах) + ЧНП + ЧНИ, ЧНП = НП — С, ЧНИ = НИ — С,
где ЧНП, ЧНИ — чистые налоги на продукты и импорт,
НП и НИ — налоги на продукты и импорт,
С — субсидии.
Валовой внутренний продукт (ВВП) является основным экономическим индикатором в зарубежной и отечественной статистике. ВВП — показатель стоимости товаров и услуг, созданной в результате производственной деятельности институциональных единиц на экономической территории данной страны, как правило, за год.
ВВП на стадии производства рассчитывается как сумма валовой добавленной стоимости всех отраслей и секторов экономики в рыночных ценах (включая налоги на продукты и импорт без НДС):
ВВП = Σ ВДС.
ВВП исчисляется также в рыночных ценах:
ВВП = Σ ВДС + ЧНП + ЧНИ.
Стадия образования доходов в СНС характеризуется следующими показателями:
• оплата труда наемных работников (ОТ);
• налоги на производство и импорт (включая налоги на продукты) (НП);
• другие налоги на производство (ДНП);
• субсидии на производство и импорт;
• валовая прибыль экономики (ВПЭ). Таким образом, ВВП на стадии образования доходов равен сумме:
ВВП = ОТ + ЧНП + ЧНИ + ДНП + ВПЭ.
Валовая прибыль экономики (ВПЭ) — макроэкономический показатель, характеризующий превышение доходов над расходами, которые предприятия имеют в результате производства до вычета явных или скрытых процентных издержек, арендной платы или других доходов от собственности.
Показатель ВПЭ рассчитывается балансовым путем и определяется как валовая добавленная стоимость (ВДС) за вычетом оплаты труда наемных работников (ОТ) и других чистых налогов на производство (ДЧНП):
ВПЭ = ВДС — ОТ — ДЧНП.
Чистая прибыль экономики (ЧПЭ) — это показатель макроэкономической прибыли в СНС, который рассчитывается путем вычитания потребления основного капитала (ПОК) из валовой прибыли экономики:
ЧПЭ = ВПЭ — ПОК.
На стадии использования ВВП рассчитывается как сумма конечного потребления продуктов и услуг (КП), валового накопления (ВН) и чистого экспорта товаров и услуг, который представляет разницу между экспортом и импортом (Э — И):
ВВП = КП + ВН + (Э — И).
Конечное потребление продуктов и услуг складывается из расходов на конечное потребление домашних хозяйств, государственных учреждений, некоммерческих организаций, обслуживающих домашние хозяйства. Валовое накопление рассчитывается как сумма валового накопления основного капитала, изменения запасов материальных оборотных средств и чистого приобретения ценностей. Прирост основного капитала приравнивается к общему объему капитальных вложений за счет всех источников финансирования.
Чистый экспорт товаров и услуг рассчитывается во внутренних ценах как разница между экспортом и импортом и включает в себя оборот российской торговли со странами как дальнего, так и ближнего зарубежья.
Для оценки качества расчетов, проводимых в СНС, используют специфический показатель — статистическое расхождение между произведенным и использованным ВВП. Он показывает расхождение между объемами ВВП, рассчитанными различными способами: на стадии производства и на стадии использования. Расхождение может возникнуть из-за многих объективных и субъективных причин. К основным причинам возникновения статистического расхождения относятся: недостаток необходимой информации, определенные методологические неточности, связанные с переходным характером современной российской экономики и общей незавершенностью системы национальных счетов. В международной практике принято считать допустимым уровнем погрешности статистическое расхождение, составляющее не более 5% ВВП.
Индекс-дефлятор ВВП — отношение ВВП измеренного в текущих ценах к объему ВВП, исчисленного в постоянных ценах базисного периода. Индекс-дефлятор ВВП рассчитывается по структуре веса отчетного периода, характеризует среднее изменение цен на добавленную стоимость, созданную во всех отраслях экономики (включая рыночные и нерыночные услуги), и чистых налогов на продукты и импорт.
Для обобщающей характеристики экономики региона рассчитывается показатель валовой региональный продукт (ВРП). Расчеты ВРП осуществляются производственным методом как сумма валовой добавленной стоимости, произведенной на территории региона за определенный период.
Валовой национальный доход (ВИД) равен сумме ВВП в рыночных ценах плюс доходы от собственности, полученные от «остальною мира», минус соответствующие им потоки, переданные «остальному миру».
Чистый национальный доход (ЧНД) в рыночных ценах получается в результате вычитания потребления основного капитала (ПОК) из валового национального дохода:
ЧНД = ВНД — ПОК.
Потребление основного капитала представляет собой уменьшение стоимости основного капитала в течение отчетного периода в результате его физического и морального износа, случайных повреждений.
Располагаемый доход образуется в результате распределения и перераспределения доходов и предназначен для конечного потребления и сбережения.
Располагаемый национальный доход (РНД) в рыночных ценах представляет собой ЧНД плюс чистые текущие трансферты из-за границы (т.е. дарения, пожертвования, гуманитарная помощь, а также аналогичные перераспределительные поступления из-за границы за вычетом аналогичных трансфертов, переданных за границу).
Валовой располагаемый доход (ВРД) равен ВНД в рыночных ценах плюс (минус) текущие трансферты, полученные от «остального мира» и переданные «остальному миру».
Чистый располагаемый доход (ЧРД) представляет собой разность между ВРД и потреблением основного капитала (ПОК):
ЧРД = ВРД — ПОК.
Сбережение — часть ВРД, которая не входит в конечное потребление товаров и услуг. В экономическом смысле она соответствует сложившемуся в отечественной практике показателю «Накопление». Сбережение определяется как разность между суммой текущих доходов и расходов.
Валовое сбережение (ВС) — сбережение до вычета потребления основного капитала, равное сумме валовых сбережений всех секторов экономики.
Валовое накопление в целом по экономике включает валовое накопление основного капитала, изменение запасов материальных оборотных средств и чистое приобретение ценностей.
Социальная статистика
К основным социально-экономическим индикаторам уровня жизни населения относятся денежные доходы и расходы населения, их состав и использование; динамика реальных располагаемых доходов населения; показатели потребления товаров и услуг; показатели дифференциации доходов; уровень бедности и др.
Среднедушевые денежные доходы населения (или средние по домашним хозяйствам) исчисляются делением общей суммы денежного дохода за год на среднегодовую численность населения (или число домохозяйств).
Располагаемые доходы — это номинальные денежные доходы за вычетом обязательных платежей и взносов.
Среднемесячная начисленная заработная плата работников в отраслях экономики рассчитывается делением начисленного месячного фонда заработной платы на среднесписочную численность работающих (занятых в экономике) в расчете на месяц.
С целью устранения фактора изменений цен номинальные и располагаемые денежные доходы (расходы) населения рассчитываются в реальном выражении с корректировкой на индексы потребительских цен (сводный и субиндексы на отдельные товарные группы).
Расчет показателей в реальном выражении осуществляется делением соответствующих показателей текущего периода на индекс потребительских цен.
Индекс реальной заработной платы исчисляется по формуле
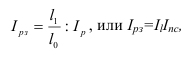
где 
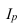
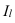
Реальные располагаемые денежные доходы определяются исходя из денежных доходов текущего года за минусом обязательных платежей и взносов, скорректированных на индекс потребительских цен.
Для оценки интенсивности изменения структуры доходов (расходов) населения, а также потребительских расходов домашних хозяйств по группам населения в одном из исследуемых периодов используют:
1) линейный коэффициент структурных различий (сдвигов)
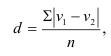
где 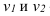
n — число структурных составляющих:
2) квадратический коэффициент структурных сдвигов (в том случае, если показатели измерены в процентах,
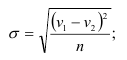
3) интегральный коэффициент К. Гатева
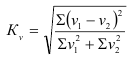
изменяется в пределах
4) индекс Салаи
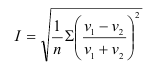
изменяется в пределах
Динамика общего объема потребления населением товаров и услуг, а также динамика потребления по отдельным товарным группам или услугам изучается индексным методом.
Стоимость реализованных населению товаров и услуг в фактических ценах пересчитывается в цены и тарифы базисного периода методом дефлятирования. При этом общий объем потребления населением товаров и услуг отчетного периода делят на средний индекс потребительских цен товаров и услуг:
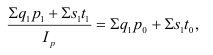
где 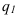
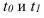
Расчет агрегатного индекса физического объема потребления осуществляется по формуле
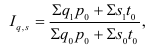
где 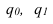
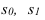
Для изучения динамики потребления отдельных групп товаров или услуг применяется средний гармонический индекс физического объема следующего вида:
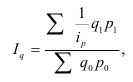
где 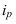
В социальной статистике на практике используется коэффициент эластичности потребления в зависимости от изменения доходов, который рассчитывается по формуле
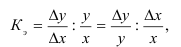
где х и у — начальные доход и потребление;
Δх и Δy — их приращения за некоторый период (или при переходе от одной группы к другой).
Он позволяет определить, на сколько процентов возрастает (или снижается) потребление товаров или услуг при росте дохода на 1%.
Если коэффициент эластичности отрицательный, то качество товара принято квалифицировать как низкое, т.е. потребление товара уменьшается с повышением доходов. Если 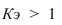
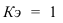
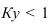
К основным характеристикам дифференциации доходов населения и уровня бедности относятся следующие показатели:
• модальный, медианный и средний доход;
• коэффициент фондов, децильный коэффициент дифференциации;
• коэффициент концентрации доходов Джини;
• уровень бедности, среднедушевой доход бедного населения, дефицит дохода.
Их исчисляют на основе распределения численности (или долей) населения по размеру среднедушевого (среднего на домохозяйство) денежного дохода, сгруппированного по интервалам с заданными (фиксированными) границами, децильным (10%-м) и другим интервалам.
Коэффициент фондов 
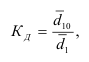
где 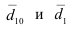
При расчете среднего дохода 10% населения в знаменателе показателей 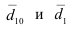
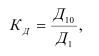
где 
Децильные коэффициенты доходов и потребления населения 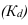
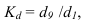
где 
Коэффициент концентрации доходов Джини 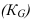
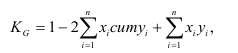
где 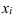
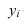
n — число социальных групп; 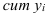
При равномерном распределении доходов коэффициент Джини стремится к нулю. Чем выше поляризация доходов в обществе, тем ближе этот коэффициент к единице.
Для графического изображения степени неравномерности в распределении доходов строится кривая Лоренца. При равномерном распределении доходов каждая 20%-я группа населения имела бы пятую часть доходов общества. На графике это изображается диагональю квадрата, что означает равномерное распределение. При неравномерном распределении «линия концентрации» представляет собой вогнутую вниз кривую. Чем больше отклонение кривой Лоренца от диагонали квадрата, тем выше поляризация доходов общества. Коэффициент Джини можно рассчитать но кривой Лоренца как отношение площади фигуры, образуемой кривой Лоренца и линией равномерного распределения 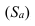
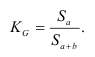
Уровень бедности — это удельный вес населения с доходами ниже прожиточного минимума в общей численности населения. Прожиточный минимум представляет собой стоимость минимальной продовольственной «корзины», а также расходы на непродовольственные товары и услуги, налоги и обязательные платежи, исходя из доли затрат на эти цели в бюджетах у 10% низкодоходных домашних хозяйств.
Показатель дефицита дохода равен суммарному доходу населения, недостающему до величины прожиточного минимума.
Возможно эта страница вам будет полезна:
Система национальных счетов
Система национальных счетов (СНС) — это современная информационная база, адекватная реальному хозяйственному механизму и используемая для описания и анализа процессов рыночной экономики на макроуровне. СНС представляет собой развернутую статистическую макроэкономическую модель экономики.
СНС — основа национального счетоводства. Для экономического анализа деятельности хозяйствующих субъектов и для макроэкономического анализа на национальном уровне экономические операции представляются в виде отдельных счетов. Счета используются для регистрации экономических операций, осуществляемых институциональными единицами, а именно предприятиями, учреждениями, организациями, домашними хозяйствами и др., которые являются резидентами данной страны. Отражаются также и операции между резидентами данной страны и нерезидентами.
Национальные счета — набор взаимосвязанных таблиц, имеющих вид балансовых построений. По методу построения национальные счета аналогичны бухгалтерским счетам. Каждый счет представляет собой баланс в виде двухсторонней таблицы, в которой каждая операция отражается дважды: один раз — в ресурсах, другой — в использовании. Итоги операций на каждой стороне счета балансируются или по определению, или с помощью балансирующей статьи, которая является ресурсной статьей следующего счета.
Балансирующая статья счета, обеспечивающая баланс (равенство) его правой и левой частей, рассчитывается как разность между объемами ресурсов и их использованием. Иначе говоря, балансирующая статья предыдущего счета, отраженная в разделе «Использование», является исходным показателем раздела «Ресурсы» последующего счета (табл. 12.1). Этим достигается увязка счетов между собой и образование системы национальных счетов. Таблица 12.1 — Балансирующие статьи счетов
Реализуемая в отечественной статистике Система национальных счетов основана на методологии, рекомендованной ООН, но категории и понятия СНС ООН приняты с учетом специфики организации и функционирования экономики страны. В ходе построения счетов использовались некоторые рекомендации новой версии Системы национальных счетов ООН, пересмотренной и принятой Статистической комиссией ООН в 1993 г. (СНС-93). Система национальных счетов, реализуемая в Российской Федерации, включает следующие счета:
Счета внутренней экономики:
• счет производства;
• счет образования доходов;
• счет распределения доходов:
а) счет распределения первичных доходов;
б) счет вторичного распределения доходов;
• счет использования располагаемого дохода;
• счет операций с капиталом;
• счет товаров и услуг.
Счета внешнеэкономических связей («остального мира»):
• счет текущих операций;
• счет капитальных затрат;
• финансовый счет.
Все счета являются консолидированными, т.е. построенными для экономики в целом, и отражают, с одной стороны, отношения между национальной экономикой и зарубежными странами, а с другой — взаимосвязь различных показателей системы счетов.
Для каждого сектора внутренней экономики предусматривается составление набора счетов — от счета производства до финансового счета. Счета разрабатываются также по секторам и регионам.
Статистика цен
Статистика уровня и структуры цен. Обобщающей характеристикой уровня цен на одноименный товар является его средняя цена. Наилучшая характеристика средней цены — средняя взвешенная:
• арифметическая, когда весами являются объемы продаж в натуральном выражении:
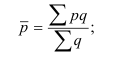
• гармоническая, когда весами служат объемы продаж в стоимостном выражении (выручка от продаж, или товарооборот):
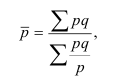
где р — индивидуальные значения цен на определенный момент времени (временные интервалы) регистрации или на конкурентных субрынках;
q — объемы продаж в натуральном выражении;
pq — выручка от продажи, или товарооборот.
Если данные об указанных весах недоступны, то в качестве весов могут использоваться другие показатели, например численность населения или число семей, проживающих на территориях, обслуживаемых субрынком. Здесь применяется средняя арифметическая взвешенная. Если, например, известно число дней непрерывной торговли при данном уровне цен, то используется средняя гармоническая взвешенная.
В тех случаях, когда сведения о весах отсутствуют вообще, допускается применение средних невзвешенных (простых) величин. Предпочтение при этом чаще всего отдается средней арифметической. Так, например, рассчитывается средняя цена конкретного товара, реализуемого различными торговыми точками за торговый день. Таким же образом определяют и среднюю цену товара на конкретном торговом месте за определенный период па основе данных о ежедневных значениях цен или одинаковых значениях цен в течение равных промежутков времени. Однако если цена резко возрастает в течение изучаемого периода, что вызывает заметное снижение объема продаж товара, то средняя арифметическая дает завышенное значение обобщающего показателя. Меньшее значение средней цены получается при использовании средней гармонической простой.
Средние цены в п. 2 и 3 совпали между собой. Они представляют собой наиболее точный уровень, истинное значение обобщающей характеристики цен торгового дня.
Остальные значения отличаются от найденного выше, поскольку были вычислены либо без взвешивания (п.1), либо с использованием не прямых, а косвенных показателей в качестве весов.
При этом завышение средней цены, найденной без взвешивания, объясняется отрицательной корреляцией между уровнями цен и объемами продаж — по более низким ценам продается больше товара, чем по более высокой цене.
Завышение цен, найденных в п. 4 и 5, вызвано неодинаковой структурой объема продаж товара и структурой населения, обслуживаемого различными субрынками. В данном случае доля населения, проживающего на территории субрынка I, выше, чем доля этого субрынка по количеству продаж. На данном субрынке цена самая высокая, что и приводит к завышению общей средней цены.
Средняя цена, вычисленная в п. 4, больше, чем в п. 5. Объясняется это различиями в структуре семейных образований между территориями. Здесь средний размер семьи на территории, обслуживаемой субрынком II, меньше, чем на территории субрынка I, a число семей больше. При этом цена товара на субрынке II ниже, что и занижает общую среднюю характеристику цены.
Структура цен изучается с помощью традиционных статистических методов на основе расчета и анализа во времени и в пространстве удельных весов или долей (относительных величин структуры) отдельных элементов общего уровня цен, выделяемых по различным признакам, исходя из целей исследования. Наиболее общую методику такого изучения см. в гл. 2.
Специфические особенности изучения структуры в статистике цен состоят в анализе числа и роли посреднических звеньев в формировании конечной (например, розничной) цены.
Определение числа посреднических звеньев связано с расчетом коэффициента звенности 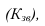
Роль звеньев-посредников в нарастании конечной цены товара характеризуется соотношением этой цены с оптовой ценой производителя товара.
Статистика вариации цен. Для изучения собственно вариации (дифференциации) цен используются традиционные методы анализа, основанные на вычислении таких показателей, как размах вариации, среднее линейное (арифметическое) отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Методику их расчета и решение типовой задачи см. в гл. 3.
Связанная (зависимая от факторов) вариация цен изучается с помощью дисперсионного анализа, проводимого на основе аналитической группировки с расчетом показателей тесноты взаимосвязи, например коэффициента детерминации и эмпирического корреляционного отношения.
Если наличие эмпирической зависимости между уровнем цен и влияющим на него фактором установлено, то анализ дополняется расчетом коэффициентов эластичности. Применяемый для фактических данных эмпирический коэффициент эластичности А. Маршала вычисляется по формуле
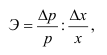
где Δх и Δр — абсолютные приросты факторного признака и цены; х и р — базовые значения факторного признака и цены соответственно.
Если, например, при изучении изменения цен в зависимости от уровня доходов населения по территориям коэффициент эластичности составил +1,1, то это означает, что прирост денежных доходов на один процент вызывает увеличение уровня цен на 1,1%.
Статистика динамики цен. Методику традиционного анализа динамических рядов любых явлений, включая цены, а также вычисления индексов с решением типовых задач см. в гл. 5 и 6.
Однако помимо традиционных методик для расчета индексов цен используются и другие.
Например, для однородных товаров (услуг) могут быть вычислены простейшие агрегатные индексы (субиндексы) по методикам:
Дюто —
Карли —
средней геометрической —
Для разноименных товаров (услуг) помимо общеизвестных также вычисляют индексы по методикам:
Эджворта — Маршалла —
Фишера (так называемая «идеальная» формула) —
Если при изучении динамики средней цены традиционная методика не дает положительных результатов оценки влияния структурного сдвига, то вычисления индексов цен переменного состава 
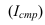
Статистика кредита
Статистика кредита использует различные показатели, изучающие объем, состав, структурные сдвиги, динамику, взаимосвязи и эффективность кредитный вложений.
Для характеристики объема кредитных вложений используются следующие показатели: остатки задолженности и размер выданных и погашенных ссуд (оборот по погашению и выдаче), средний размер ссуды, средний размер задолженности но кредиту, средний срок ссуды, средняя процентная ставка (доходность кредита) и др.
Состав кредитных вложений изучают по целевому назначению, формам собственности, территориям, категориям заемщиков, экономическим секторам, срокам погашения, видам остатков задолженности и другим признакам.
Большое внимание статистика уделяет изучению просроченных ссуд по их объему, составу и динамике.
Для анализа и прогноза кредитных вложений статистика кредита рассматривает тенденции их изменения, интенсивность изменений кредита во времени с использованием показателей анализа ряда динамики, а также трендовых и факторных динамических моделей.
Для выявления статистических закономерностей статистика изучает взаимосвязи кредитных вложений с показателями объема производства, капитальных вложений и т.д. при помощи однофакторного и многофакторного регрессионного анализа и индексного метода. Особое внимание уделяется эффективности кредитных вложений, т.е. анализу оборачиваемости кредитов, оценке влияния отдельных факторов на изменения оборачиваемости ссуд и др.
Структура, динамика, взаимосвязи кредитных вложений рассматриваются в гл. 2 «Абсолютные и относительные показатели», гл. 5 «Ряды динамики», гл. 6 «Индексы», гл. 7 «Статистические методы изучения взаимосвязей».
В данной главе изучаются объем и эффективность кредитных вложений.
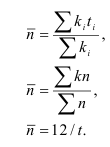
Для изучения влияния отдельных факторов на изменение средней длительности пользования кредитом строится система взаимосвязанных индексов
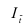
1) изменения длительности пользования кредитом в отраслях;
2) структурных сдвигов в однодневном обороте
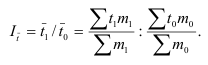
Абсолютное изменение средней длительности пользования кредитом за счет двух факторов:
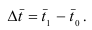
Далее, 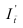
Абсолютное изменение средней длительности пользования кредитом за счет снижения длительности пользования кредитом в отраслях составит:
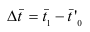
И, наконец, 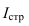
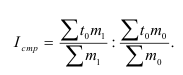
Абсолютное изменение средней длительности пользования кредитам за счет структурных сдвигов в однодневном обороте составит:
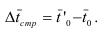
Общее изменение средней длительности пользования кредитом
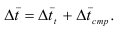
Индексы средней длительности пользования кредитом можно определить и по формулам
где 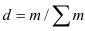
Возможно эта страница вам будет полезна:
Статистика денежного обращения
Система показателей статистики денежного обращения включает: денежный оборот, денежную массу, наличные деньги внебанковской системы, безналичные средства, скорость обращения, продолжительность оборота, купюрное строение денежной массы, индекс-дефлятор, покупательную способность рубля и др.
Денежная масса является важным количественным показателем движения денег, ее величина зависит от количества денег в обращении и от скорости их обращения.
Скорость обращения денег измеряется двумя показателями:
1) количеством оборотов (V) денег в обращении за рассматриваемый период, которое рассчитывается по формуле
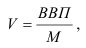
где ВВП — валовой внутренний продукт в текущих ценах;
М — общая масса денег, рассчитанная как остатки денег за изучаемый период.
Этот показатель характеризует скорость оборота денежной единицы. На практике в качестве универсального показателя денежной массы применяется денежный агрегат М2, который представляет собой объем наличных денег в обращении (вне банков) и остатков средств в национальной валюте на расчетных, текущих счетах и депозитах нефинансовых предприятий, организаций и физических лиц, являющихся резидентами Российской Федерации;
2) продолжительностью одного оборота денежной массы, которая рассчитывается по формуле
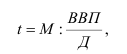
где Д — число календарных дней в периоде.
Рассмотренные показатели взаимосвязаны, поэтому если известна величина одного из них, то можно определить и другой показатель:
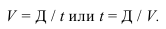
Скорость обращения денег зависит от величины валового внутреннего продукта, или совокупности созданных продуктов и услуг, и денежной массы.
Из известного уравнения денежного обмена MV = PQ, которое означает, что произведение денежной массы на скорость обращения денег равно произведению уровня цен на объем произведенных товаров и услуг (ВВП в текущих ценах), можно записать: MV = ВВП Тогда скорость обращения денег определяется по формуле
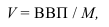
где
Этот показатель находится в прямой зависимости от объема ВВП и динамики цен на товары и услуги и обратно пропорционален денежной массе.
Изучение данных показателей в динамике позволяет установить их взаимосвязь:
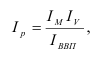
где 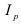
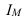
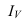
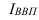
На практике индекс-дефлятор ВВП рассчитывается по формуле
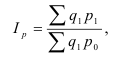
где 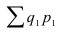
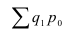
При увеличении числа оборотов скорость обращения денежной массы возрастает; при сокращении числа дней, необходимых для одного оборота денег, требуется меньшая денежная масса.
Для определения изменения скорости обращения денежной массы используется взаимосвязь следующих индексов:
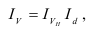
где 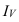
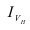
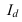
Абсолютное изменение скорости обращения денежной массы, определяемое индексным метолом, обусловлено влиянием следующих факторов:
1) изменением скорости обращения наличной денежной массы
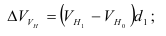
2) изменением доли наличности в общем объеме денежной массы
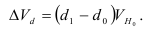
Таким образом, абсолютное изменение скорости обращения массы денег равно
Для контроля за динамикой денежной массы и анализа объемов кредитных вложений коммерческих банков в экономику используется показатель, называемый денежным мультипликатором 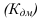
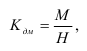
где М — денежная масса в обращении; Н — денежная база.
При этом денежная масса определяется по денежному агрегату М2, а показатель «денежная база» включает в себя наличные деньги н обращении (в том числе остатки средств в кассах коммерческих банков), остатки средств коммерческих банков на корреспондентских счетах в Банке России, фонд обязательных резервов коммерческих банков в Банке России. Денежный мультипликатор представляет собой коэффициент, характеризующий увеличение денежной массы в обороте в результате роста банковских резервов.
Для характеристики динамики купюрного строения денежной массы и выявления тенденции его изменения необходимы данные о величине средней купюры, которую можно рассчитать но формуле средней арифметической взвешенной:
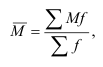
где М — достоинство купюр; f — число купюр.
В случае когда происходит переполнение каналов денежного обращения избыточной денежной массы при отсутствии увеличения произведенных товаров и услуг, возникает проблема опенки инфляции. Инфляция, как правило, измеряется с помощью индекса-дефлятора ВВП и индекса потребительских цен. На практике чаще всего для измерения инсоляции применяется индекс потребительских цен или индекс покупательной способности денежной единицы, определяемый как величина, обратная индексу потребительских цен:
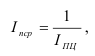
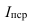
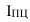
Индекс покупательной способности рубля показывает, во сколько раз обесценились деньги, т.е. характеризует инфляцию, и может исчисляться по отношению к денежной единице текущего и базисного периодов. Если индекс цен за анализируемый период повысится, то индекс покупательной способности рубля снизится, и наоборот, если индекс цен за рассматриваемый период понизится, то индекс покупательной способности рубля возрастет. Относительные показатели инсоляции рассчитывают как темпы роста или снижения покупательной способности рубля. Относительный показатель инфляции можно представить также как величину, обратную индексу потребительских цен.
При исчислении индекса изменения цен на товары и услуги необходимо учитывать также изменение курса рубля (по отношению к иностранным валютам, в частности к доллару США), соответственно должен корректироваться и индекс покупательной способности рубля. При этом корректировка номинального индекса покупательной способности должна осуществляться пропорционально доле денежного оборота в иностранной валюте в общем денежном обороте страны.
Обратная величина индекса курса рубля по отношению к доллару США и другим иностранным валютам, котирующимся в России, представляет собой индекс цен на покупку долларов в России.
Статистика страхования
Страховой рынок подразделяется на отрасли имущественного, личного страхования, страхования ответственности и социального страхования.
Объектами имущественного страхования являются основные и оборотные фонды предприятий, организаций, домашнее имущество граждан. К основным абсолютным показателям этой отрасли относятся: страховое поле 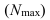
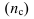
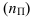
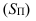
Нетто-ставка исчисляется по формуле
где 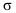
3. Брутто-ставка определяется по формуле
где f — доля нагрузки к нетто-ставке:
Важнейшей задачей статистики личного страхования является расчет единовременных тарифных ставок на дожитие, на случай смерти с различным сроком договора и выдачи платежей.
Единовременная нетто-ставка на дожитие определяется по формуле
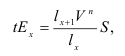
где 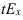
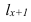
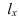
V — дисконтный множитель;
S — страховая сумма.
Единовременная ставка на случай смерти — временная, т.е. на определенный срок. Она равна
где 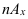
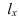
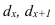
Расчет тарифных нетто-ставок производится с использованием таблиц смертности и средней продолжительности жизни.
Для практических расчетов разработаны специальные таблицы коммутационных чисел, в которых содержатся показатели, взятые из таблиц смертности, дисконтирующие множители и расчетные показатели (коммутационные числа). Таблицы составлены в двух видах: на дожитие и на случай смерти. Для удобства вычислений они могут быть объединены в одну показатели уровня травматизма:
1) частоту травматизма;
2) тяжесть травматизма;
3) коэффициент нетрудоспособности (количество человеко-дней нетрудоспособности на одного работающего).
Статистика ценных бумаг
Рынок ценных бумаг — часть финансового рынка, на котором обращаются средне- и долгосрочные бумаги. К ценным бумагам относятся акции, облигации, сертификаты, векселя, казначейские обязательства и др. Рынок ценных бумаг складывается из спроса и предложения и уравновешивающих их цен. Существуют различные виды ценных бумаг: с нефиксированным доходом, с фиксированным доходом. Смешанные формы.
Акции не имеют установленного срока обращения, их владельцы получают дивиденды в течение всего срока существования акционерного общества (АО).
В зависимости от длительности обращения ценных бумаг на рынке устанавливаются цены на акции: номинальная, эмиссионная, рыночная. На акции указывается номинальная стоимость, которая определяется путем деления величины уставного капитала на количество выпущенных акций:
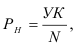
где 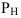
УК — величина уставного капитала;
N — количество выпущенных акций.
На основе номинальной стоимости устанавливается эмиссионная цена, по которой осуществляется первичное размещение акций. На рынке ценных бумаг акции реализуются по рыночной цене, зависящей от соотношения спроса и предложения.
Активность бирж базируется на биржевых индексах цен, характеризующих динамику цен и средний уровень цены на акции.
Индекс цены на акцию определенного наименования исчисляется по формуле
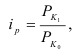
где 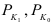
Индекс средних уровней
где 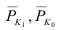
Доходность акции определяется двумя факторами: получением части распределяемой прибыли АО (дивидендом) и дополнительным доходом, который равен разнице между курсовой ценой и ценой приобретения (∆ = РК — РПР).
Годовая ставка дивиденда рассчитывается по формуле
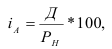
где
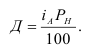
Д — абсолютный уровень дивиденда. Сумма годового дохода акции определяется по формуле
Для оценки дохода по акции, приобретенной по курсу, используют показатель рендит, который характеризует процент прибыли от цены приобретения акции:
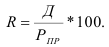
Совокупная доходность исчисляется отношением совокупного дохода (СД = Д + ∆д ) к цене приобретения:
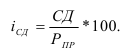
Доходность облигации определяется двумя факторами: купонными выплатами, которые производятся ежегодно (иногда раз в квартал или полугодие), и разницей между ценой погашения и приобретения бумаги:
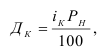
где 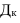
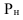
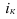
Разница между ценой погашения и приобретения бумаги определяет величину прироста или убытка капитала за весь срок займа. Если погашение производится по номиналу, а облигация куплена с дисконтом, инвестор имеет прирост капитала. При покупке облигации по цене с премией владелец, погашая бумагу, терпит убыток. Облигация с премией имеет доходность ниже указанной на купоне. Сумма купонных выплат и годового прироста (убытка) капитала определяет величину совокупного годового дохода по облигации. Совокупная годовая доходность облигации представляет собой отношение совокупного годового дохода к цене приобретения облигации:
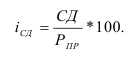
Текущая доходность облигации без выплаты процентов исчисляется по формуле
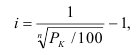
где 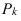
n — срок от момента приобретения до выкупа облигации.
При этом, если облигация приобретена с дисконтом, до ее выкупа
Доходность облигации с выплатой процентов в конце срока рассчитывается по формуле
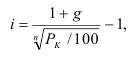
где g — объявленная годовая норма доходности по облигации.
Доходность облигации с периодической выплатой процентов, погашаемой в конце срока, определяется по формулам:
а) сложных процентов:
где g — норма доходности по купонам;
Р — рыночная цена;
б) простых процентов:
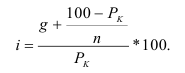
Текущая доходность облигаций с учетом налоговых льгот исчисляется по формуле
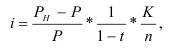
где t — ставка налоговых льгот;
n — срок от даты приобретения до погашения облигации;
К — количество дней в году.
Стоимость облигации без обязательного погашения с периодической выплатой процентов определяется по формулам:
а) современная стоимость:
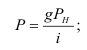
б) курсовая цена:
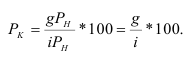
Для сравнительной оценки акций используются следующие показатели:
ценность акции =
коэффициент котировки =
Ожидаемая доходность акций рассчитывается по эффективной ставке процентов:
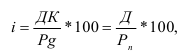
где Д — ожидаемый доход;
n — срок операций;
Р — ожидаемая цена акции.
При расчете доходности векселей необходимо учитывать следующее:
1) если владелец векселя держит документ до даты его погашения, причем вексель размещен по номинальной цене с доходом в виде процента, то векселедержатель сверх номинала получает сумму дохода, равную
где 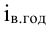
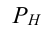
n — число дней от даты выставления векселя до даты погашения.
2) если вексель размещен с дисконтом, а погашение производится по номиналу, доход владельца составляет
где 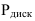
Доходность векселя
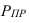
Абсолютный размер дохода по сертификату определяется по формуле
где 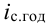
n — число месяцев, на которое выпущен сертификат.
Доходность сертификата исчисляется по формуле
Кстати тут дополнительная теория из учебников.
Статистика финансов предприятий и организаций
В условиях рыночной экономики, когда развитие предприятий и организаций осуществляется в основном за счет собственных средств, важное значение имеет устойчивое финансовое состояние, которое характеризуется системой показателей. Эта система содержит четыре группы показателей: ликвидность, оборачиваемость активов, привлечение средств, прибыльность.
Первая группа — показатели ликвидности: коэффициент ликвидности, который определяется как отношение быстрореализуемых активов (денежные средства, отгруженные товары, дебиторская задолженность) к краткосрочным обязательствам (краткосрочные ссуды, задолженность рабочим и служащим по заработной плате и социальным выплатам, кредиторская задолженность); коэффициент покрытия, который рассчитывается как отношение всех ликвидных активов к краткосрочным обязательствам.
Вторая группа — коэффициенты оборачиваемости активов (оборачиваемость всех активов основных средств, дебиторских счетов, средств в расчетах и запасов).
Третья группа — степень покрытия фиксированных платежей — определяется как отношение балансовой прибыли к сумме фиксированных платежей.
Четвертая группа — показатели прибыли и рентабельности.
Прибыль oт реализации продукции определяется как разница между выручкой, полученной от реализации продукции, и затратами на ее производство:
где р — цена единицы продукции;
z — затраты па производство единицы продукции:
q -объем продукции.
Балансовая прибыль предприятия
где 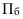
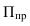
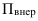
Чистая прибыль представляет собой разность между балансовой прибылью и суммой платежей в бюджет.
Прибыльность предприятия определяется показателями рентабельности.
Рассчитывают рентабельность продукции и предприятия.
Рентабельность продукции (r) исчисляют как отношение прибыли 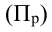
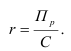
Рентабельность предприятия (R) определяется по формуле
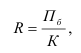
где К — величина капитала.
Анализируя показатели прибыли и рентабельности, статистика дает не только общую оценку их размера, но и характеризует их изменение под влиянием отдельных факторов.
Относительное изменение среднего уровня рентабельности продукции определяется системой индексов:
где 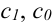
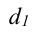
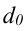
Абсолютное изменение среднего уровня рентабельности
обусловлено влиянием следующих факторов:
а) рентабельности:
б) структуры:
Оборачиваемость оборотных средств характеризуется двумя показателями: числом оборотов и продолжительностью одного оборота.
Количество (n) оборотов оборотных средств определяется отношением стоимости реализованной продукции (РП) к средним
остаткам оборотных средств 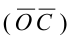
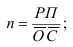
продолжительность (t) одного оборота оборотных средств равна
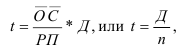
где Д — количество календарных дней.
Финансовые вычисления
Методы финансовых расчетов подразделяются на общие и специфические, применяемые при выполнении особого класса финансовых операций и сделок, требующих адаптации общих методов, их видоизменения применительно к сути финансовых операций и сделок, исполнения на основе документарных данных.
Ввиду очевидной специфики указанных методов примеры их применения приводятся отдельно в виде решения актуарных и инвестиционных задач, исчисления биржевых индексов, проведения приближенных расчетов и т.д.
К наиболее распространенным относятся методы исчисления простых и сложных процентов, математического и банковского дисконтирования, консолидированных и рентных расчетов.
Ниже представлены основные формулы, по которым производится подавляющее большинство расчетов в современной практике финансовых вычислений.
Здесь S — наращенная сумма (стоимость);
Р — первоначальная сумма;
n— число периодов;
i — процентная ставка:
m — число случаев начисления в периоде:
d — учетная ставка:
R — член ренты.
В зарубежной практике к этим широко применяемым формулам добавляются, как правило, следующие шесть дополнительных, предназначенных для определения различных норм эффективности.
1. Срок окупаемости
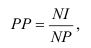
где NI — чистые инвестиции (приведенные затраты):
NP — чистая прибыль (годовая).
2. Норма эффективности (окупаемости инвестиций)
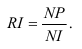
3. Чистая текущая (дисконтированная) стоимость
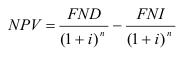
где FND — чистая сумма будущих доходов;
FNI — чистая сумма будущих расходов.
4. Внутренняя ставка доходности
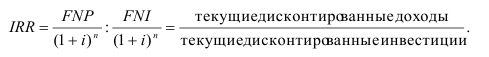
5. Ставка доходности дисконтированных денежных потоков
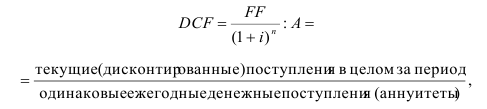
где FF — объем будущих поступлений;
А — аннуитеты.
6. Учетная ставка доходности
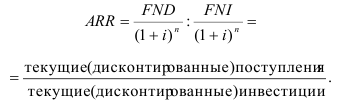

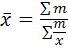
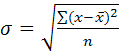

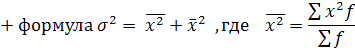

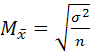

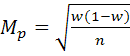
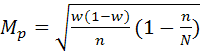

 ,
, 




























 Исходные данные в формате json можно сказать здесь, а сводные данные по России, переведенные нами в формат xlsx, удобный для работы в Excel, здесь.
Исходные данные в формате json можно сказать здесь, а сводные данные по России, переведенные нами в формат xlsx, удобный для работы в Excel, здесь.
 РАСП
РАСП
 ОБР
ОБР




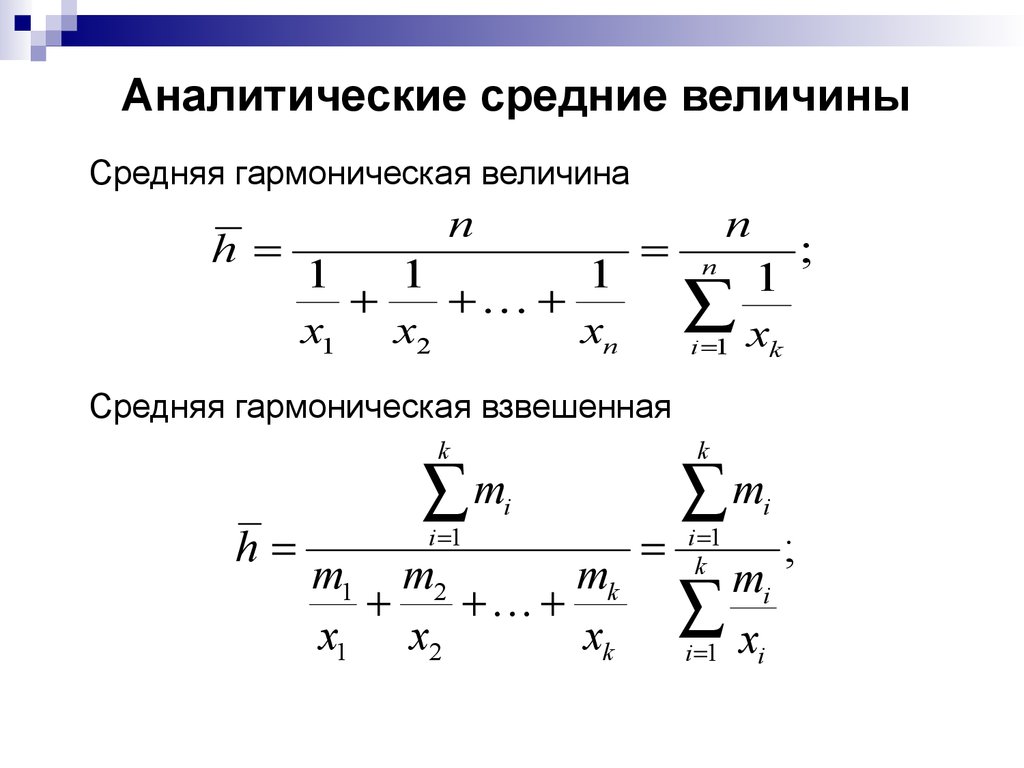 ETS
ETS ETS.СТАТ
ETS.СТАТ РАСП
РАСП

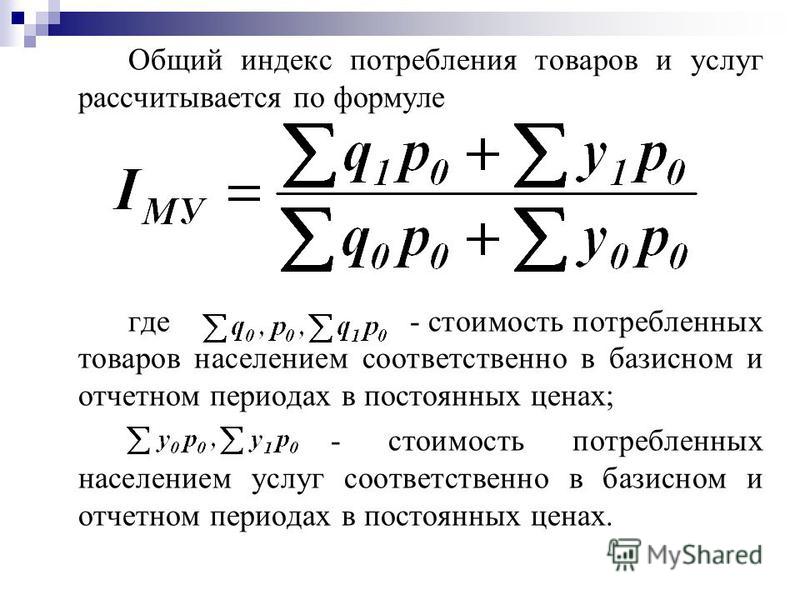

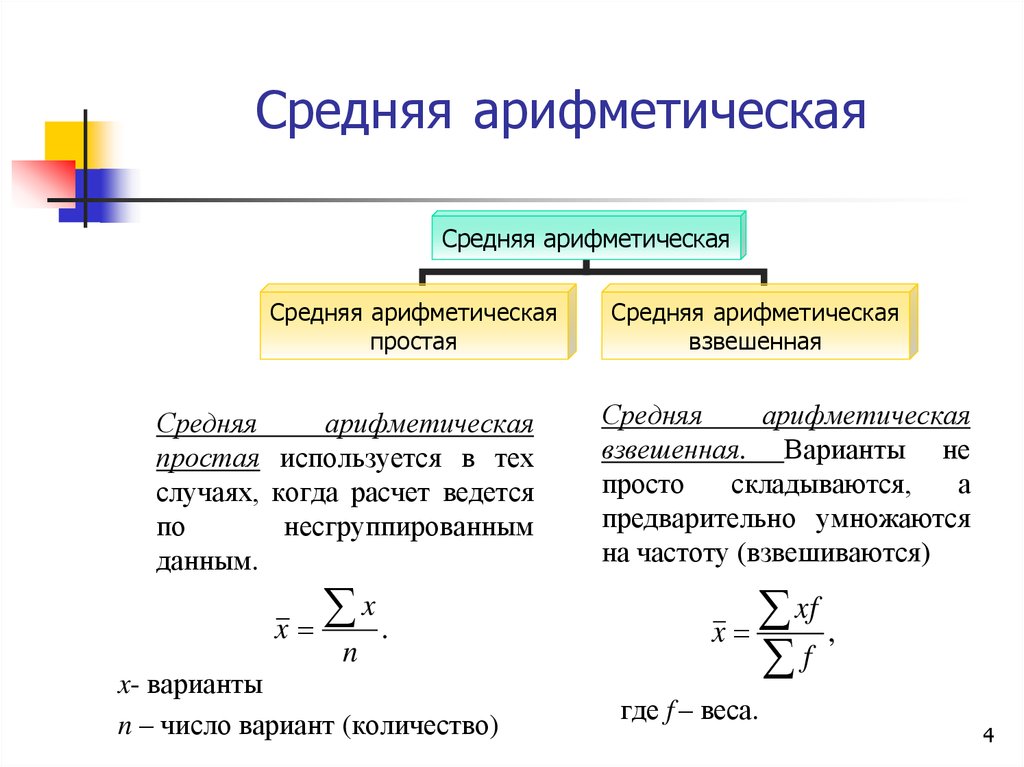
 ОДН
ОДН СТ.РАСП
СТ.РАСП






 ОБР.2Х
ОБР.2Х Г
Г

 . . * 3 * 2 * 1. По соглашению,
. . * 3 * 2 * 1. По соглашению, .. п к ! )]
.. п к ! )] ).
). 
 Вот десять статистических формул, которые вы будете часто использовать, и шаги для их расчета.
Вот десять статистических формул, которые вы будете часто использовать, и шаги для их расчета.  Обозначение для среднего
Обозначение для среднего  Вы можете думать об этом, в общих чертах, как о среднем расстоянии от среднего. Формула стандартного отклонения:
Вы можете думать об этом, в общих чертах, как о среднем расстоянии от среднего. Формула стандартного отклонения: 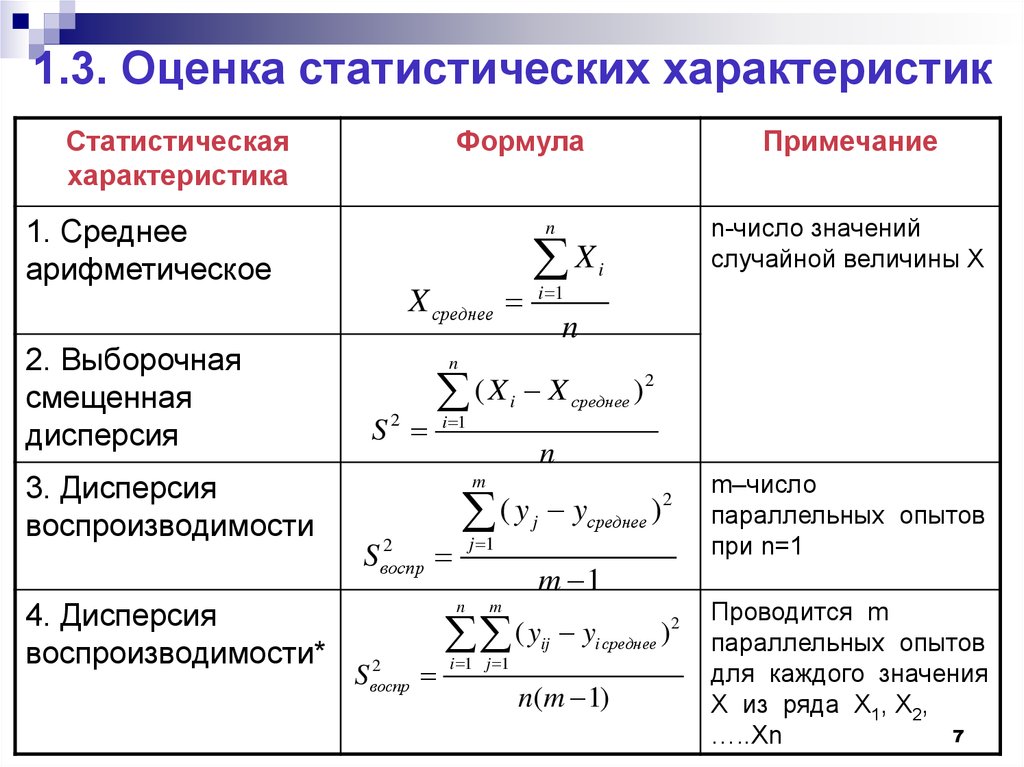





 В колледжах Нью-Йорка тренерам по футболу обычно платят больше, чем тренерам по теннису?
В колледжах Нью-Йорка тренерам по футболу обычно платят больше, чем тренерам по теннису?  Это поможет вам решить статистические задачи.
Это поможет вам решить статистические задачи.  Вы можете легко понять всю концепцию вычисления среднего значения. Таким образом, формула среднего:
Вы можете легко понять всю концепцию вычисления среднего значения. Таким образом, формула среднего: 

 е.
е.  Затем используйте Z-таблицу для ее решения.
Затем используйте Z-таблицу для ее решения.  92
92  переменная, а σ — стандартное отклонение X.
переменная, а σ — стандартное отклонение X. 
 Формула статистики относится к набору мер дисперсии или центральной тенденции, которые помогают понять и интерпретировать определенный набор данных.
Формула статистики относится к набору мер дисперсии или центральной тенденции, которые помогают понять и интерпретировать определенный набор данных. 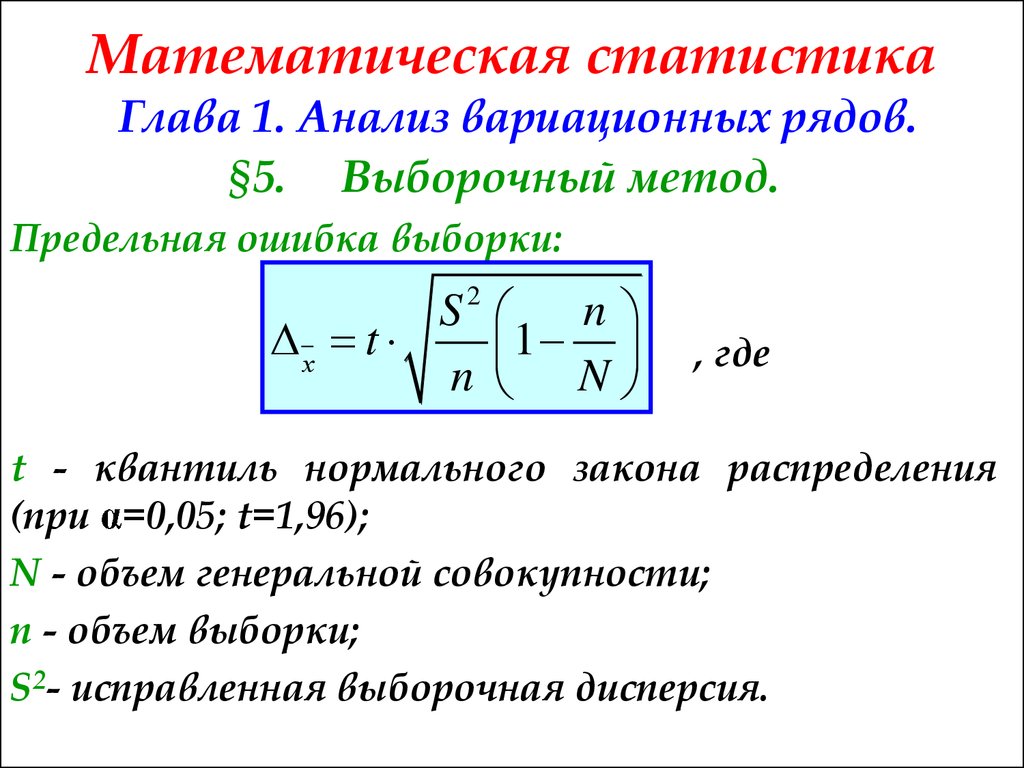
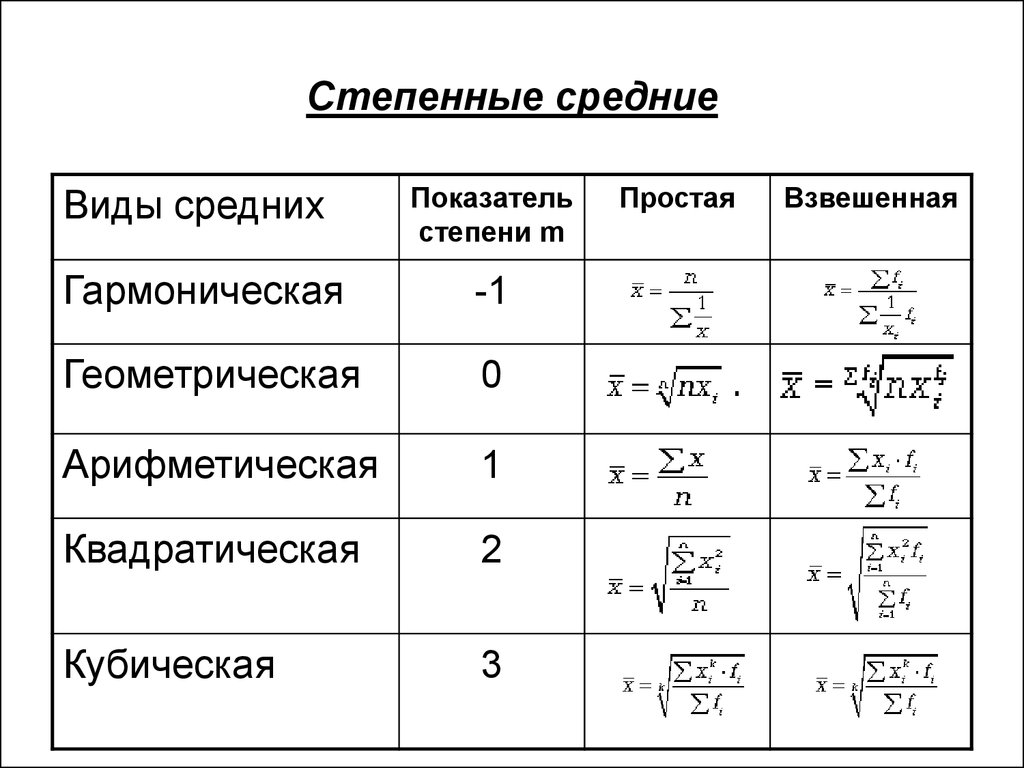

 РАСП функция
РАСП функция РАСП.ВП
РАСП.ВП НОРМ функция
НОРМ функция P
P РАСП
РАСП ТЕСТ
ТЕСТ
 ETS.СТАТ функция
ETS.СТАТ функция РАСП
РАСП РАСП.
РАСП.
 РАСП
РАСП
 SNGL
SNGL СТ.РАСП
СТ.РАСП
 РАСП
РАСП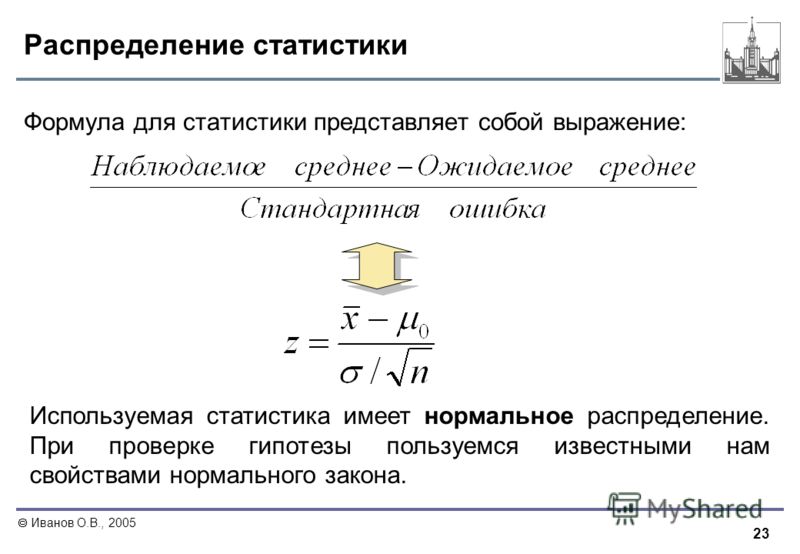 СРЕДНЯЯ функция
СРЕДНЯЯ функция П
П П
П РАСП
РАСП ОБР.2Т
ОБР.2Т P
P DIST
DIST