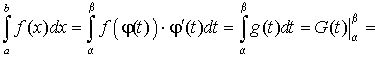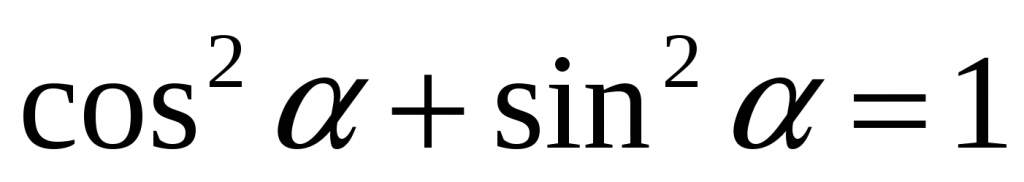1.
Матрица
Это
прямоугольная таблица, состоящая из
m×n
элементов и содержащая m
строк и n
столбцов.
Числовая
матрица
– все элементы матрицы числа.
Квадратная
матрица
– m=n.
Операции
над матрицами
Сложение
– складываются все элементы, стоящие
на одинаковых местах (только у
равноразмерных).
Произведение
– каждый элемент матрицы умножается
на число (с).
2
Транспонирование
Транспонированная
матрица – это матрица, полученная из
матрицы А заменой строк столбцами.
Умножение
матриц
Вводится
только для согласованных матриц (число
столбцов м-цы А должно совпадать со
строками м-цы В).
При
умножении матриц появляется новая
матрица, элементы которой вычисляются
по формуле: c11=a11b11+a12b21+…(1
элемент 1 строки умножаем на 1 э-т 1
столбца + 2 э-т 1 с-ки на 2 э-т 2 с-ца, и т.д.)
3.
Определители
2 и 3 порядков
Определители
вводятся только для квадратных матриц.
Определителем (Δ) или детерминалом
матрицы А называется число det
A.
Для
2-го порядка Δ вычисляется по формуле:
a11a22-a12a21
(крест накрест).
Для
3-го порядка по правилу треугольников.
Свойства:
1)
Δ
единичной матрицы =1. 2) Δ треугольной
матрицы = произведению элементов,
стоящих на главной диагонали. 3)
det(A*B)=detA*detB.
4) если строка или столбец = 0, то Δ=0.
4.Определитель
n-го порядка
Определитель
n-го
порядка находится либо разложением по
элементам строки (столбца), либо
приведением определителя к треугольному
виду.
Миноры
и алгебраические дополнения
Минор
матрицы А соответствующей элементу
Aij
– это Δ
(n-1)
порядка, получаемый путём вычёркивания
i-ой
строки или j-го
столбца. Aij=(-1)i+jMij
называется алгебраическим дополнением
к элементу aij.
Разложение
определителя
Δ
раскладывается по элементам i-ой
строки или j-го
столбца по формуле:
Δ = ai1Ai1+
ai2Ai2+…+
ainAin
5.
Обратная
матрица. Теорема о существовании
обратной матрицы
Обратная
матрица существует только для квадратных
матриц.
Если
обратная матрица существует, то она
единственна.
Матрица
А-1
обратная
А,
если выполняется условие: А-1А=А
А-1=Е
(единичная матрица).
Для
того чтобы матрица А была обратной,
необходимо чтобы она была невырожденной
(Δ не должен =0).
Матрица,
состоящая из алгебр. дополнений,
полученная путём транспонирования
называется союзной
(Ас).
Вычисление
обратной матрицы: 1) Находим Δ
2) Вычислем алгебр. доп., 3) Строим Ас
и
вычисляем:
А-1=
Ас
, 4) Делаем проверку А-1А=Е
6.
Ранг
матрицы
Ранг
матрицы
– это максимальный порядок минора,
отличный от нуля. Способы вычисления:
1)Если существует минор Mk
(k
— какой-то порядок минора) и все Mk+1=0,
то ранг М=k.
2) Метод элементарных преобразований
(матрицу приводят к треугольной и
трапециевидной форме).
Элементарные
преобразования
1)
сложение 2-х любых строк матрицы. 2)
Умножение элементов строки на число.
Теорема
о базисном миноре
Базисный
минор – это минор, не равный 0, порядок
которого равен рангу матрицы.
7.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Решение
систем по формулам Крамера
Сначала
находим Δ
и убеждаемся, что он не равен 0. Затем
по формулам Крамера находим определители
уже как бы новых матриц с заменой
определённого столбца на столбец
свободных членов. Находим переменные
(x,
y,
z)
по формулам Δx
Δ
и
т.д. Делаем проверку.
8.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Матричный
метод
Сначала
находим Δ
и убеждаемся, что он не равен 0. Находим
союзную матрицу, а затем обратную по
формуле А-1=
Ас.
Затем находим переменные (x,
y,
z)
и делаем проверку.
9.
Решение
произвольных СЛАУ
Берём
обычную систему уравнений, где А –
матрица системы, а добавление к матрице
А столбец свободных членов даёт нам
расширенную матрицу

Теорема
Кренекера-Капелли
Для
того, чтобы система уравнений была
совместна, необходимо чтобы ранг А =
рангу

Если:
1) rA=
то система имеет единственное решение.
n
– последний член элемента (a1n)
2)
rA=
то система имеет бесконечное кол-во
решений.
10.
Векторы
в пространстве
Вектор
– это направленный отрезок.
– свободный;
– имеющий точку приложения. Длина
вектора – модуль.
Линейные
операции над векторами
1)
сложение (по правилу треугольника и
параллелограмма). Суммой 2 векторов
и
явл.
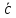
начало которого совпадает с началом 1
вектора (
а конец — с концом 2 вектора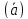
2)
вычитание (
Разностью
и
явл.

конец которого совпадает с концом

а начало — с концом
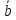
3)
умножение на число (Условия: 1) существует

2)
и
направлены одинаково если с
11.
Координаты
вектора в пространстве.
3
вектора (
образую
базис в пространстве если они взаимно
⊥
и имеют единичную длину.


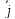
=
(x2—x1,
y2—y1,
z2—z1).

– длина
вектора
Направляющие
косинусы вектора
ax
= ПрOx
=

= ПрOy
=
cosβ;
az
= ПрOz
=
cosγ;
cosα=
Проекции
вектора на ось
образованный
с помощью осей Ox,
Oy,
Oz,
образует углы
α,
β, γ.
12.
Скалярное
произведение 2 векторов
Это
число, равное произведению длин этих
векторов на cos
угла между ними.
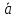
=
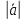

Свойство:
1)

=

2)
(
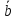
=



3)
Скалярное произведение на число =
произведение числа на один из векторов
и * на 2 вектор.
4)

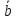
если
вектора
и
явл. Ортогональными (
⊥

13.
Векторное
произведение 2 векторов

произведением 2 векторов
и
явл.
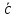
который удовлетворяет условиям: 1)
⊥


2)


– правая тройка векторов. 3)
=


(модуль произв. 2 векторов – площадь
параллелограмма)
Свойство:
1)

—

2)
=

3)

0 если
//
14.
Смешанное
произведение 3 векторов
Это
число = скалярному произведению 3-го
вектора на векторное произведение 2-х
первых векторов.
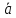

= (
—
объём параллелепипеда.
Свойство:
1)
От перемены мест множителей произведение
не меняется.
=
=
2)
Если умножить на число, то оно умножается
с одним из членов произведения.
3)
(α-
β)(
= α(
β (
15.
Базис
в пространстве
Компланарные
векторы лежат в одной плоскости.
3
любых некомпланарных вектора образуют
базис в пространстве.
Разложение
вектора по базису
Любой
вектор можно разложить по базису таким
способом: допустим B
(

– базис, а (α,
β, γ)
координаты определённого вектора,
например

Тогда разложение
по базису имеет вид:
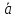
α
β
γ
16.
Прямая
на плоскости
Вектором
нормали
называется вектор перпендикулярный
плоскости. Пусть вектор
= (𝐴,
𝐵)
является вектором нормали к прямой 𝑙.
Произвольная точка плоскости 𝑀(𝑥,
𝑦)
принадлежит прямой 𝑙
тогда и только тогда, когда
⊥
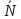
т.е. скалярное произведение этих векторов


0
Её
уравнения
1)
Уравнение прямой, проходящей через
заданную точку и имеющей заданный
вектор нормали 𝐴(𝑥–𝑥0)+𝐵(𝑦−𝑦0)=0
2)
Общее уравнение прямой: 𝐴𝑥
+ 𝐵𝑦
+ 𝐶
= 0
17.
Различные
уравнения плоскости
а)
Общее уравнение плоскости: Ax
+ By + Cz + D = 0
б)
Уравнение проходящее через точку
M0(x0,y0,z0)
и ⊥
вектору нормали

A(x—x0)
+ B(y—y0)
+C(z—z0)=0
в)
Уравнение плоскости, проходящей через
3 заданные точки.
г)
Уравнение плоскости в отрезках:
18.
Угол
между плоскостями
Допустим,
мы имеем 2 уравнения плоскости (α: A1x
+ B1y
+ C1z
+ D1
= 0
и β: A2x
+ B2y
+ C2z
+ D2
= 0)
и нам нужно вычислить угол между 2
плоскостями – двугранный
угол.
Он вычисляется по формуле: cos
(отношение произведения


к произведению модулей векторов
нормали).
Взаимное
расположение плоскостей
Две
плоскости в пространстве либо
параллельны, либо пересекаются.
α1//α2
– коллинеарные ⇒


– условие
параллельности.
α1⊥α2
⇒

⇒

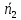

– условие
⊥.
19.
Прямая
в пространстве.
Различные
уравнения прямой в пространстве
1)
Параметрическое уравнение: x=x0+mt,
y=y0+nt,
z=z0+pt
(m,n,p)
– направляющий вектор прямой (l),
который параллелен этой прямой. M0(x0,
y0,
z0)
∈l.
2)
Каноническое уравнение:
=
=
3)
Уравнение прямой проходящей через 2
точки:
=
=
4)
Общее уравнение прямой в пространстве:
20.
Угол
между прямыми и их взаимное расположение
Допустим,
мы имеем 2 (канонических) уравнения
прямых, а также их направляющие векторы

и

Тогда угол между 2 прямыми
можно найти по формуле: cos
Условие
//-ти:

//
⇒


Условие
⊥—ти:
Расстояние
от точки до прямой в пространстве
У
нас есть уравнение прямой
=
=

её направляющий вектор
(m,n,p)
и точка не принадлежащая этой прямой
M(x1,y1,z1).
Расстояние от точки до прямой определяется
по формуле:
21.
Угол
между прямой и плоскостью.
Допустим,
у нас есть каноническое уравнение
прямой
=
=
и уравнение плоскости Ax
+ By
+ Cz
+ D
= 0.
Тогда угол между прямой и плоскостью
можно найти по формуле: Sin
=
22.
Взаимное
расположение прямой и плоскости
Условие
//-ти:
Am+Bn+Cp
= 0
Условие
⊥—ти:
Плоскости
могут совпадать, быть параллельными
или пересекаться по прямой.
23.
Эллипс
Эллипс
– это геометрическое место точек
плоскости, расстоянием от которых до
2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения

= 1
Геометрические
свойства
1)
Эллипс является кривой 2-го порядка.
2)
Является ограниченной фигурой.
3)
Является симметричной фигурой, оси
симметрии Ox,
Oy.
4)
a – большая ось; b
– малая ось; Вершины: А1(а,0);
А2(-а,0);
В1(0,
b);
В2(0,
—b);
5)
=
– эксцентриситет эллипса; 0
1.
6)
Прямые
x
=
– директриса эллипса. При
=1 ⇒
а=с; а=b
– уравнение окружности.


24.
Гипербола
Гипербола
– геометрическое место точек на
плоскости, модуль разности расстояний
для 2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения
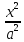
= 1
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Является неограниченной кривой.
3)
Является симметричной фигурой.
4)
Пересекает Ox
в 2 точках, не пересекает ось Oy.
a – действительная полуось; b
– мнимая полуось;
5)
=
– эксцентриситет эллипса;

6)
x
=
– директриса.
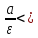
7)
y
=

– асимптоты
25.
Парабола
Парабола
– геометрическое место точек плоскости,
расстояние каждой из которых до заданной
точки называется фокусом и до определённой
прямой L,
называемой директрисой. (F∉L)
Вывод
канонического уравнения
p-
(параметр) расстояние от F
до L.
F(
– фокус параболы. x=
Уравнение: y2=2px
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Симметричная фигура, ось симметрии –
Ox.
3)
Неограниченная фигура
4)
= 1
– эксцентриситет
26.
Числовая
последовательность
Если
каждому натуральному числу из множества
N
поставлено в соответствие некоторое
число или величина, то множество
последних образует последовательность.
xn
– числовая последовательность.
Предел
Число
a
называется пределом числовой
последовательности, если для любого
положительного числа существует
N-число,
такое, что для всех номеров N
последующий больше, чем это число по
модулю.
Теорема
о сходимости
Если
xn
имеет
предел, то он единственный. xn
наз.
ограниченной, если существует n
и все члены удовлетворяют

n
27.
Предел
функции
Если
к каждому числу из множества x
поставлено в соответствие одно число
и множество y,
то на множестве x
задана функция y=f(x)
Число
b
называется пределом функции f(x)
при x→a,
если для любого положительного
существует положительная дельта,
зависящая от
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
28.
Односторонние
пределы функции
Левый
и правый пределы называют односторонними
пределами.
1)
Число b
называется правым пределом функции
при x→a
справа если для всех

существует дельта от
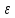
такой что 0
модуль f(x)-b

следовательно x
2)
Число b
называется левым пределом функции при
x→a
слева если для всех

существует дельта от

такой что —b
следовательно модуль f(x)-b
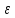
следовательно x
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
29.
Бесконечно-малые
и их свойства.
Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю. Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.
При
x→a
lim
=
предел не существует.
Основные
свойства
1°
Сумма конечного числа б.м функций
является функцией б.м.
3°
Произведение двух б.м функций есть
функция б.м.
4°
Произведение б.м функции на константу
является б.м функцией.
5°
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция б.м.
6°
Функция 
обратная
к б.м функции α(x)
0,
есть функция бесконечно большая. Верно
и обратное.
30.
Бесконечно-большие
функции.
Бесконечно
большая функция
– это функция, предел которой
стремится к
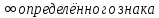
Теорема
о связи бесконечно-большой и
бесконечно-малой функции
Теорема.
Функция обратная бесконечно малой,
является бесконечно большой и наоборот.
Доказательство: Пусть предел функции
равен 0, а сама функция не = 0, при x→a,
т.е. задаём бесконечно-малую функцию

Тогда для любого числа 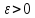
такое число дельта

что для всех x,
удовлетворяющих неравенству

выполняется неравенство 
т.е.

А из этого следует, что функция 
бесконечно большая.
1. Линейная алгебра
1.1. Определители (детерминанты)
1.2. Матрицы
1.3. Системы линейных уравнений
2. Векторная алгебра
3. Аналитическая геометрия
3.1. Линейные образы
3.1.1. Прямая на плоскости
3.1.2. Плоскость в пространстве
3.1.3. Прямая в пространстве
3.2. Кривые второго порядка
3.2.1. Окружность
3.2.2. Эллипс
3.2.3. Гипербола
3.2.4. Парабола
3.3. Поверхности второго порядка
3.4. Преобразование координат
3.4.1. Преобразование координат на плоскости
3.4.2. Преобразование координат в пространстве
4. Комплексные числа
4.1. Алгебраическая форма комплексного числа
4.2. Действия над комплексными числами в алгебраической форме
4.3. Тригонометрическая форма комплексного числа
4.4. Показательная форма комплексного числа
4.5. Действия над комплексными числами в тригонометрической и показательной форме
5. Введение в анализ
5.1. Функции. Общие свойства
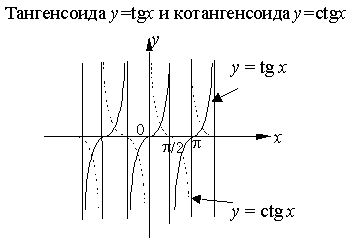
5.2. Основные элементарные функции
5.3. Теория пределов
5.4. Непрерывность функции
6. Дифференциальное исчисление
6.1. Определение производной
6.2. Основные правила дифференцирования
6.3. Производные основных элементарных функций
6.4. Гиперболические функции
6.5. Производные высших порядков и формула Тейлора
6.6. Исследование функций
7. Интегральное исчисление
7.1. Неопределенный интеграл
7.1.1. Определения и свойства
7.1.2. Основные методы интегрирования
7.1.3. Таблица интегралов
7.2. Определенный интеграл
7.2.1. Определения и свойства
7.2.2. Приложения определенного интеграла
1. Линейная алгебра
1.1. Определители (детерминанты)
Обозначения определителя матрицы А: D , det A, .
Определитель второго порядка: 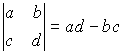
Определитель третьего порядка:
Разложение определителя n-го порядка по i-й строке:
Разложение определителя n-го порядка по j-ому столбцу:
-алгебраическое дополнение элемента
,
,
-минор элемента
, т.е. определитель, получаемый из исходного определителя вычёркиванием i-й строки и j-го столбца.
1.2. Матрицы
| Матрица размерами n x m (n строк и m столбцов): | 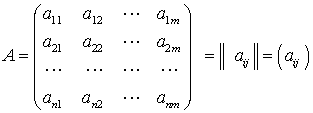 , ,
где |
Равенство матриц: , если эти матрицы одного размера и
.
Квадратная матрица порядка n: .
Сложение матриц: , где
.
Свойства сложения матриц:
1) ассоциативность: ;
2) коммутативность: ;
Умножение матрицы на число: .
Умножение матриц: 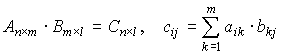
Свойства умножения матриц:
-
- ассоциативность:
;
- некоммутативность.
- определитель произведения квадратных матриц:
.
- ассоциативность:
Транспонирование матрицы: .
Свойство транспонирования произведения матриц: .
Невырожденная (неособая) матрица: .
Обратная матрица для невырожденной матрицы A: .
Свойства обратной матрицы:
1) ;
2) .
Виды матриц:
единичная матрица:
симметрическая матрица:
ортогональная матрица: A — невырождена и
кососимметрическая матрица: ;
матрица-строка:
матрица-столбец: .
Ранг матрицы — наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
1.3. Системы линейных уравнений
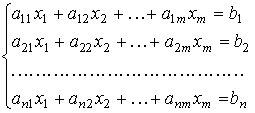 |
|
Матричный вид: ,
— матрица системы,
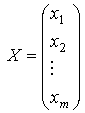 |
— столбец неизвестных, |
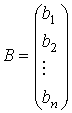 |
— столбец свободных членов. |
Совместность системы: , где
— расширенная матрица системы (теорема Кронекера-Капелли).
Формулы Крамера (n=m): ,
— определитель матрицы системы;
-определитель, полученный при замене i-го столбца матрица A на столбец В.
Однородная система (B=0):
2. Векторная алгебра
|
Наименование |
Обозначение, формула |
|
Вектор и его выражение в декартовых координатах |
a=ax i+ay j+az k=(ax, ay, az) |
|
Модуль (длина) вектора |
|
|
Направляющие косинусы вектора |
|
|
Сложение двух векторов |
a+b=(ax+bx, |
|
Умножение вектора на скаляр |
ka=(kax, |
|
Скалярное произведение двух векторов |
|
| Скалярное произведение в декартовых координатах |
ab=axbx+ayby+azbz |
|
Условие ортогональности двух ненулевых векторов |
ab=0 |
|
Векторное произведение двух векторов |
|
|
Векторное произведение в декартовых координатах |
|
|
Условие коллинеарности двух ненулевых векторов |
|
|
Смешанное произведение трех векторов |
|
|
Смешанное произведение в декартовых координатах |
|
|
Условие компланарности трех ненулевых векторов |
abc=0 векторы (лежат в одной плоскости) |
| Линейно независимая система векторов | {a1,a2,…,an} — линейно независима 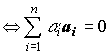 только при условии только при условии |
3. Аналитическая геометрия
3.1. Линейные образы
3.1.1. Прямая на плоскости
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
| общее уравнение прямой на плоскости | n=(A,B) — нормальный вектор прямой;
k — a — отрезок, отсекаемый прямой на оси х; b — отрезок, отсекаемый прямой на оси y; q=(l,m) — направляющий вектор прямой |
|
| уравнение прямой, проходящей через данную точку | ||
| уравнение прямой с данным угловым коэффициентом | ||
| уравнение прямой, проходящей через данную точку с данным угловым коэффициентом | ||
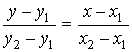 |
уравнение прямой, проходящей через две точки | |
| уравнение прямой в отрезках | ||
| каноническое уравнение прямой |
Формулы для вычисления угла между двумя прямыми на плоскости:
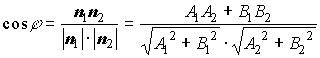
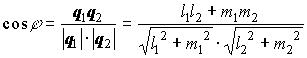
где и
-нормальный и направляющий векторы первой прямой;
и
— нормальный и направляющий векторы второй прямой.
Условия параллельности двух прямых на плоскости:
;
;
, где
и
— угловые коэффициенты прямых.
Условия перпендикулярности двух прямых на плоскости:
- n1
n2
n1
n2=0 или A1A2+B1B2=0;
- q1
q2
q1
q2=0 или l1l2+m1m2=0;
3.1.2. Плоскость в пространстве
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
| общее уравнение плоскости в пространстве |
a,b,c – отрезки, отсекаемые плоскостью
p — длина перпендикуляра, опущенного |
|
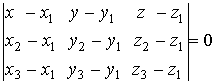 |
уравнение плоскости, проходящей через три точки |
|
| уравнение плоскости в отрезках | ||
| нормальное уравнение плоскости |
Выражение направляющих косинусов через координаты нормального вектора:
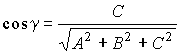
Формулы для вычисления угла между двумя плоскостями:
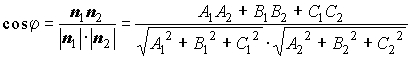
где и
-нормальные векторы плоскостей.
Условие параллельности двух плоскостей:
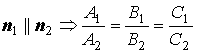
Условие перпендикулярности двух плоскостей:
n1 n2
n1
n2=0 или A1A2+B1B2+С1С2=0.
3.1.3. Прямая в пространстве
Виды уравнений
Формулы для вычисления угла между двумя прямыми в пространстве:
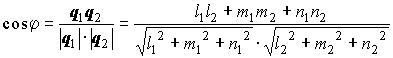
где и
— направляющие векторы прямых.
Условие параллельности двух прямых в пространстве:
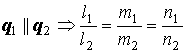
Условие ортогональности двух прямых в пространстве:
q1 q2
q1
q2=0 или l1l2+m1m2+n1n2=0.
3.2. Кривые второго порядка
Общее уравнение кривой второго порядка:
.
3.2.1. Окружность
3.2.2. Эллипс
|
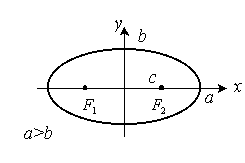
Каноническое уравнение:
Полуоси эллипса: |
 |
||
|
Эксцентриситет: |
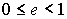 . . |
Параметрическое уравнение: | 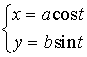 . . |
3.2.3. Гипербола
3.2.4. Парабола
| Каноническое уравнение:
Параметр: p. |
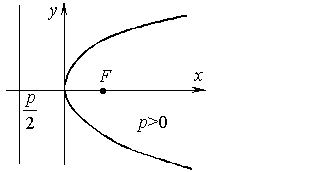 |
3.3. Поверхности второго порядка
|
Каноническое уравнение |
Наименование |
Параметры |
Чертеж |
|
|
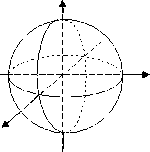
сфера |
a – |
 |
|
|
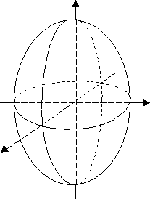
эллипсоид |
|
 |
|
|
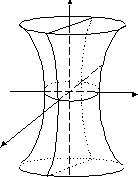
однополостный гиперболоид |
|
 |
|
|
двуполостный гиперболоид |
|
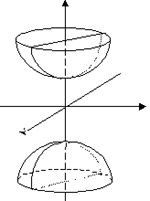 |
|
|
эллиптический параболоид |
|
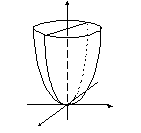 |
|
|
гиперболический параболоид |
|
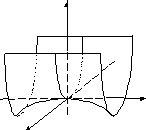 |
|
|
конус |
|
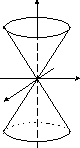 |
|
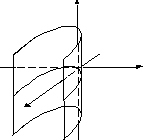
|
параболический цилиндр |
р — параметр |
 |
|
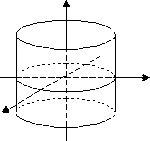
|
эллиптический цилиндр |
|
 |
|
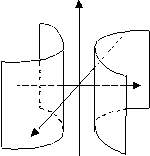
|
гиперболический цилиндр |
|
 |
3.4. Преобразование координат
3.4.1. Преобразование координат на плоскости
Преобразование декартовой прямоугольной системы координат.
Параллельный перенос: 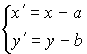 , ,
|
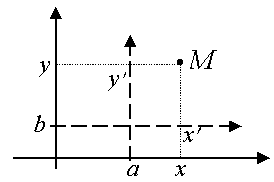 |
где координаты точки M в старой системе координат: ;
координаты точки M в новой системе координат: ;
координаты нового начала координат: .
Поворот: 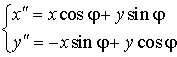 , ,
|
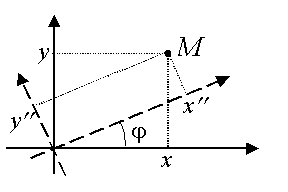 |
где координаты точки M в старой системе координат: ;
координаты точки M в новой системе координат: ;
угол поворота: j .
3.4.2. Преобразование координат в пространстве
Переход от декартовых координат к цилиндрическим координатам
и обратно:
Переход от декартовых координат к сферическим координатам
и обратно:
4. Комплексные числа
Мнимая единица .
4.1. Алгебраическая форма комплексного числа
, где a, b – действительные числа; a — действительная часть комплексного числа, b — мнимая часть комплексного числа;
Обозначения действительной и мнимой части: .
Модуль комплексного числа: .
Сопряжённые комплексные числа: и
.
4.2. Действия над комплексными числами в алгебраической форме
;
;
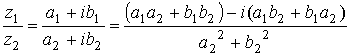
4.3. Тригонометрическая форма комплексного числа
,
где — аргумент комплексного числа,
.
4.4. Показательная форма комплексного числа
.
Формула Эйлера: .
4.5. Действия над комплексными числами в тригонометрической и показательной форме
,
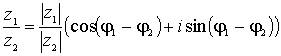
, где
.
Формула Муавра: .
5. Введение в анализ
5.1. Функции. Общие свойства
Числовая функция определена на множестве D действительных чисел, если каждому значению переменной поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
Аналитическое представление функции:
в явном виде: ;
в неявном виде: ;
в параметрической форме: 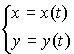
разными формулами в области определения (a,c]: 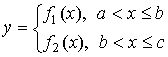
Четная функция: .
Нечетная функция: .
Периодическая функция: , где T – период функции,
.
5.2. Основные элементарные функции
|
Название |
Формула |
Частные случаи |
|
|
1 |
Постоянная | ||
|
2 |
Степенная функция |
|
|
|
3 |
Показательная функция | ||
|
4 |
Логарифмическая функция | ||
|
5 |
Тригонометрические функции |
|
|
|
6 |
Обратные тригонометрические функции |
|
Графики основных элементарных функций:
|
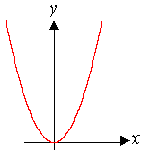
Парабола |
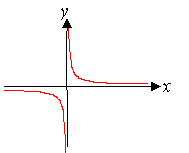
Гипербола |
|
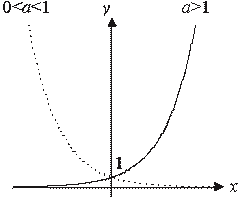
График показательной функции |
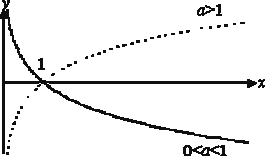
График логарифмической фунгкции |
|
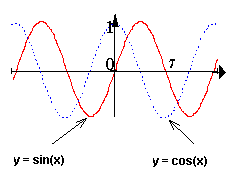
Синусоида |
|
|
|
5.3. Теория пределов
Пределом функции при
называется число b, если для любого
(e -сколь угодно малое положительное число) можно найти такое значение аргумента
,
начиная с которого выполняется неравенство .
Обозначение: .
Пределом функции при
называется число b, если для любого
(e -сколь угодно малое положительное число) существует такое положительное число d , что для всех значений x, удовлетворяющих неравенству
выполняется неравенство
.
Обозначение:
.
Формула для вычисления предела элементарной функции в точке
, где
:
.
Бесконечно малая величина при есть функция
такая, что
.
Бесконечно большая величина при есть функция
такая, что
.
Первый замечательный предел: .
Следствия: ;
;
Второй замечательный предел: 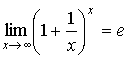
Следствия: ;
;
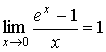
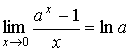
Эквивалентные бесконечно малые величины при :
x ~sinx ~ tgx
~ arcsinx ~
arctgx ~
ex-1~ ln(1+x).
Виды неопределенностей:
|
Символическое обозначение |
Содержание неопределенности |
Пределы компонент при x ® a |
|
|
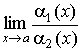 |
a 1(x) a 2(x) |
|
|
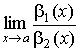 |
b 1(x) b 2(x) |
|
|
a b |
|
|
|
b 1(x) b 2(x) |
|
|
|
g b |
|
|
|
a 1(x) a 2(x) |
|
|
|
a b |
5.4. Непрерывность функции
Функция непрерывна в точке
, где
, если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке.
Эквивалентные условия:
-
;
,
где;
;
.
Классификация точек разрыва:
разрыв I рода:
— устранимый – односторонние пределы существуют и равны;
— неустранимый (скачок) – односторонние пределы не равны;
разрыв II рода: предел функции в точке не существует.
6. Дифференциальное исчисление
6.1. Определение производной
Пусть — определена и непрерывна в окрестности x0
Производная функции в точке x0 и ее обозначения:
6.2. Основные правила дифференцирования
|
Наименование |
Функция |
Производная |
| Линейная комбинация двух функций
Частные случаи: a) умножение б) сумма (разность) двух функций |
|
|
| Произведение
а) двух функций б) трех функций |
|
|
| Частное двух функций |
|
|
| Сложная функция |
y=F(u), u=j (x) |
|
| Обратная функция |
|
|
| Параметрическое задание функции |
|
|
| Логарифмическое дифференцирование |
|
|
6.3. Производные основных элементарных функций
|
№ п/п |
Наименование функции |
Функция и её производная |
|
1 |
константа | |
|
2 |
степенная функция
частные случаи |
|
|
3 |
показательная функция
частный случай |
|
|
4 |
логарифмическая функция
частный случай |
|
|
5 |
тригонометрические функции | |
|
6 |
обратные тригонометрические функции |
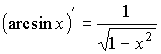 ; ;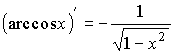 ; ;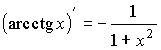 |
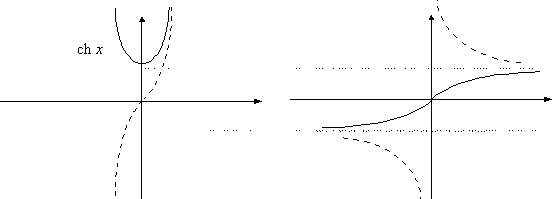
6.4. Гиперболические функции
Обратные гиперболические функции
Графики гиперболических функций:
6.5. Производные высших порядков и формула Тейлора
Производная второго порядка функции y=f(x) :
Производная n-го порядка (n-ая производная) функции y=f(x):
Формула Тейлора:
где
— остаточный член в форме Лагранжа.
Формула Маклорена (a=0):
6.6. Исследование функций
План полного исследования функции:
1. Элементарное исследование:
— найти область определения и область значений;
— выяснить общие свойства: четность(нечетность), периодичность;
— найти точки пересечения с осями координат;
— определить участки знакопостоянства.
2. Исследование с помощью предела:
— найти точки разрыва и выяснить их характер;
— найти область непрерывности;
— найти вертикальные и наклонные асимптоты.
3. Исследование с помощью
:
— найти критические точки;
— определить интервалы возрастания и убывания функции;
— определить экстремумы.
4. Исследование с помощью
:
— найти точки, в которых
или не существует;
— найти участки выпуклости и вогнутости;
— определить точки перегиба.
5. Построение графика функции.
Рекомендации по применению плана исследования функции:
- Отдельные элементы исследования наносятся на график постепенно, по мере их нахождения.
- Если появляются затруднения с построением графика функции, то находятся значения функции в некоторых дополнительных точках.
- Целью исследования является описание характера поведения функции. Поэтому строится не точный график, а его приближение, на котором четко обозначены найденные элементы (экстремумы, точки перегиба, асимптоты и т.д.).
- Строго придерживаться приведенного плана необязательно; важно не упустить характерные элементы поведения функции.
7. Интегральное исчисление
7.1. Неопределенный интеграл
7.1.1. Определения и свойства
Функция называется первообразной для
, если
.
Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.
Обозначение: , где
— произвольная постоянная.
Свойства неопределенного интеграла
-
- Производная неопределенного интеграла:
.
- Дифференциал неопределенного интеграла:
.
- Неопределенный интеграл от дифференциала:
.
- Производная неопределенного интеграла:
- Неопределенный интеграл от линейной комбинации функций:
;
4а. Неопределенный интеграл от суммы (разности) двух функций:;
4б. Вынесение постоянного множителя за знак неопределенного интеграла:
7.1.2. Основные методы интегрирования
-
- использование свойств неопределенного интеграла;
- подведение под знак дифференциала;
- метод замены переменной:
а) замена в интеграле
:
где
— функция, интегрируемая легче, чем исходная;
— функция, обратная функции
;
— первообразная функции
;
б) замена в интеграле вида
:
;
-
- метод интегрирования по частям:
.
- метод интегрирования по частям:
7.1.3. Таблица интегралов
- Степенная функция
частные случаи
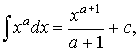
,
2. Показательная функция
частный случай
3. Рациональные функции
4. Иррациональные функции
5. Тригонометрические функции
6. Содержит тригонометрические функции
7.2. Определенный интеграл
7.2.1. Определения и свойства
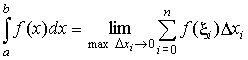
где
Свойства определенного интеграла
-
- Интеграл от суммы или разности двух функций:
.
- Интеграл от суммы или разности двух функций:
- Внесение или вынесение постоянного множителя за знак интеграла:
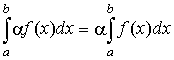
а)
, где
,
,
и
непрерывна на
, а
непрерывна и монотонна на
б) 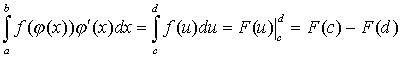
7.2.2. Приложения определенного
интеграла
Ученики, сдающие базовую математику, почти не тратят времени на подготовку к ней, ведь в экзамене нужно решить лишь задания, которые требуют самых основ. Тем же выпускникам, которые хотят поступать в технические вузы, предстоит готовиться не только к предметам по выбору, но и к профилю. В этой статье мы расскажем, какие формулы для ЕГЭ по математике (профильный уровень) сделают подготовку легче, а баллы на экзамене — выше.
Какие формулы необходимы для сдачи ЕГЭ по профильной математике?
Помимо очевидного, что для сдачи профиля нужно уметь складывать, вычитать и умножать, необходимы еще некоторые знания. Все это проходится в течение школы, но повторить или заполнить пробелы перед экзаменом нужно обязательно. Вот, что пригодится:
- Формулы сокращенного умножения;
- Арифметическая и геометрическая прогрессии;
- Вероятность;
- Свойства степеней;
- Свойства логарифмов;
- Тригонометрия;
- Производные;
- Первообразные.
Список внушительный, но вполне реальный, чтобы его выучить. Для того, чтобы лишний раз не гуглить в интернете «формулы для ЕГЭ по математике профильный уровень», приложим их ниже. А начнем по порядку из списка выше.
Формулы сокращённого умножения
Первые в нашем списке – формулы сокращенного умножения – нужны для решения задания №9 из профильного уровня. Вам встретятся задачи на преобразование выражений, поэтому умение это делать будет вознаграждено баллами.
Вот то, что будет вашим спасательным кругом:
Есть те, которые знать не обязательно. Но чем большими знаниями вы будете обладать, тем легче вам будет на экзамене. Вот они:
Умея применять эти формулы для ЕГЭ по математике, профильный уровень вам уже будет решить легче. Но это далеко не все, что нужно знать, чтобы получить сто баллов за ЕГЭ.
Арифметическая и геометрическая прогрессии
Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:
Вероятность
Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:
Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.
Свойства степеней
Эти свойства нужно знать и для того, чтобы решить «базу», так что гуманитарии тоже могут обратить внимание на это:
Как вы видите, запоминать не очень много, зато формулы не самые простые. Но есть еще сложнее, и сейчас узнаем, какие они.
Свойства логарифмов
Формулы логарифмов лучше всего начать с их определения:
Теперь перейдем к более сложному:
Тригонометрия
Тригонометрические уравнения встречаются в задании №13. Для того, чтобы заработать баллы, нужно знать это:
Но это еще не все. Есть такая вещь, как основное тригонометрическое тождество. Вот оно:
Формулы двойного угла:
Формулы суммы и разности аргументов:
Преобразование суммы и разности в произведение:
Формулы половинного аргумента:
На этом с тригонометрией все.
Производные
Начнем с основных правил дифференцирования:
Уравнение касательной:
Производные элементарных функций:
Закончим эту статью первообразными.
Первообразные
Она выглядит так:
Таблица первообразных:
Итог
То, что работа предстоит колоссальная — и правда, и нет. Да, придется хорошо постараться, чтобы набрать высокие баллы, так как составители ЕГЭ все больше усложняют экзамен. С другой стороны, хотя бы часть формул, описанных выше, вы уже знаете. А значит, работы хоть на немного, но меньше. А это ли не счастье в такие тяжелые времена подготовки?
Оглавление:
- Формулы сокращенного умножения
- Квадратное уравнение и формула разложения квадратного трехчлена на множители
- Свойства степеней и корней
- Формулы с логарифмами
- Арифметическая прогрессия
- Геометрическая прогрессия
- Тригонометрия
- Тригонометрические уравнения
- Геометрия на плоскости (планиметрия)
- Геометрия в пространстве (стереометрия)
- Координаты
- Таблица умножения
- Таблица квадратов двухзначных чисел
- Расширенная PDF версия документа «Все главные формулы по школьной математике»
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению…
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа «Все главные формулы по школьной математике»:
К оглавлению…

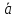







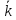
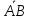



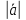

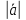


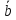




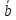


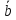
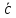






















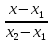




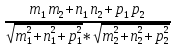


























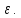
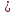







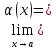

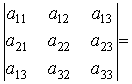
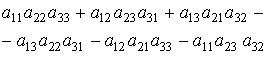
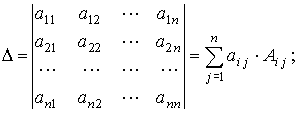
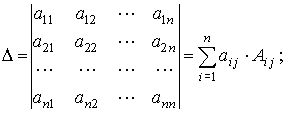
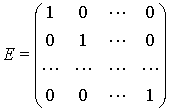
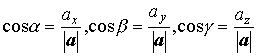
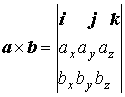
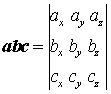
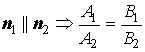 ;
;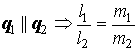 ;
;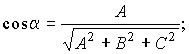
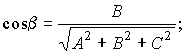
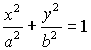 .
.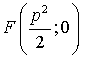 ;
;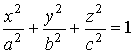 .
.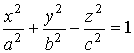
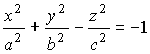
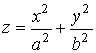
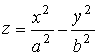
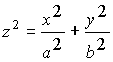
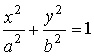
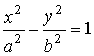
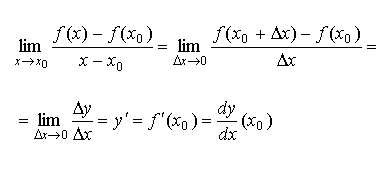
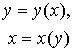
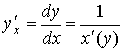
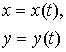
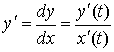
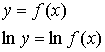
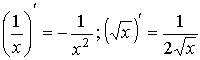
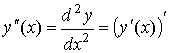
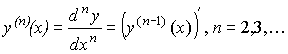
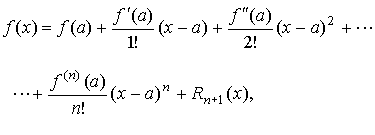
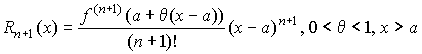
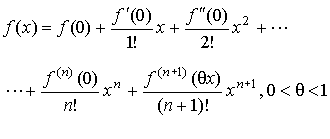
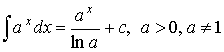
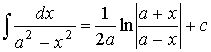
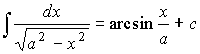
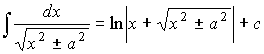
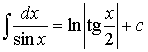
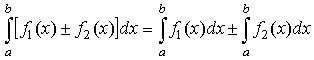 .
.