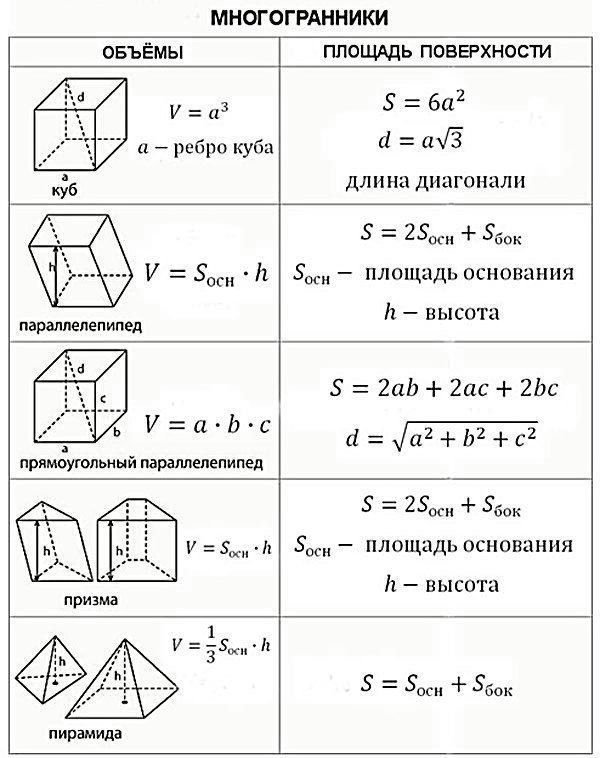
Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.
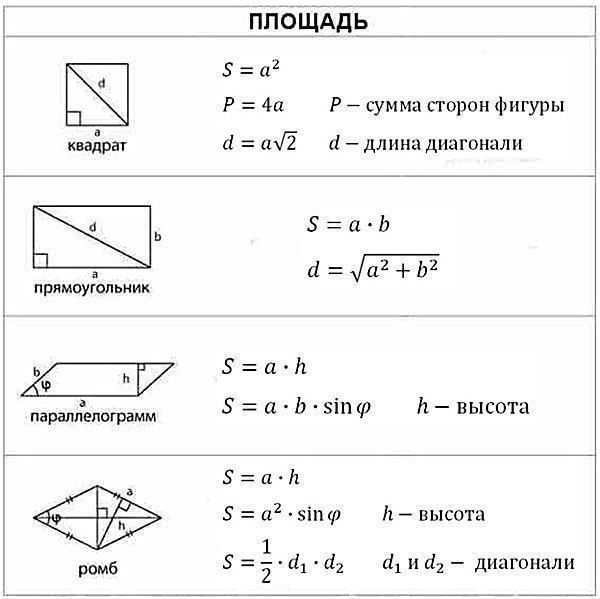
Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.
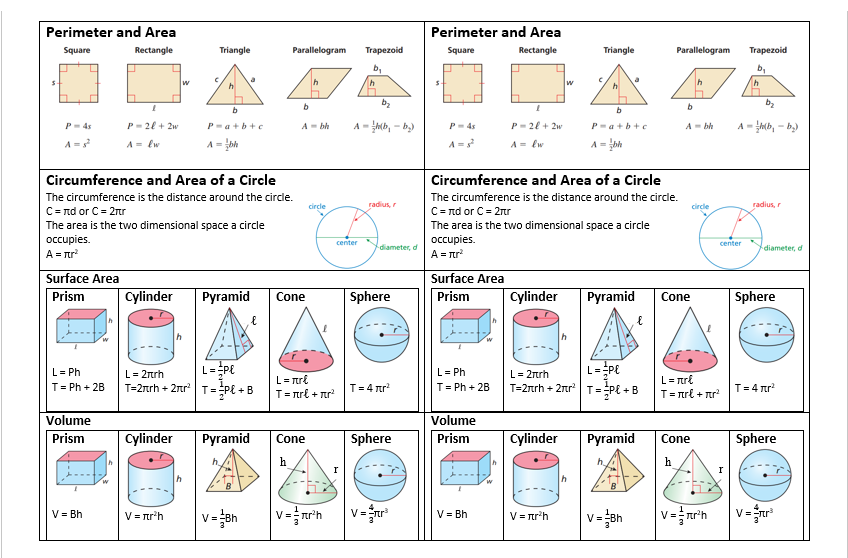
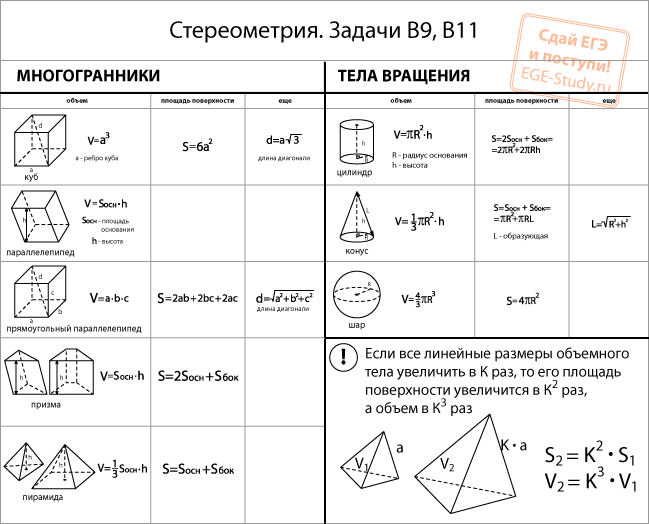
В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом.
Формулы для профильного ЕГЭ-2022 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c``a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
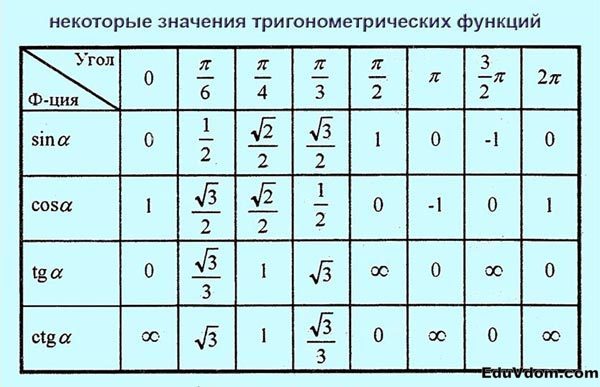
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` |
`kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
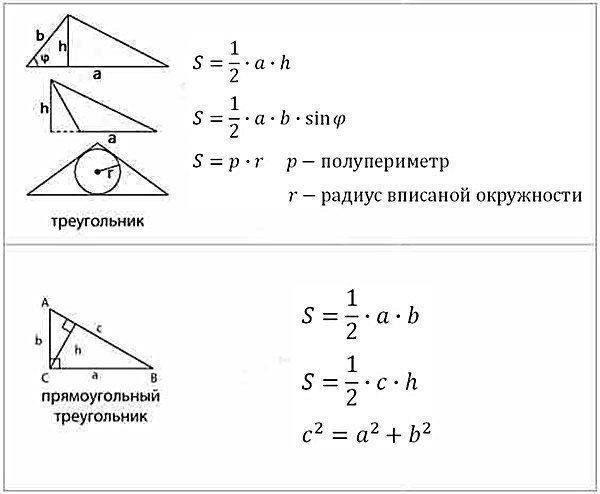
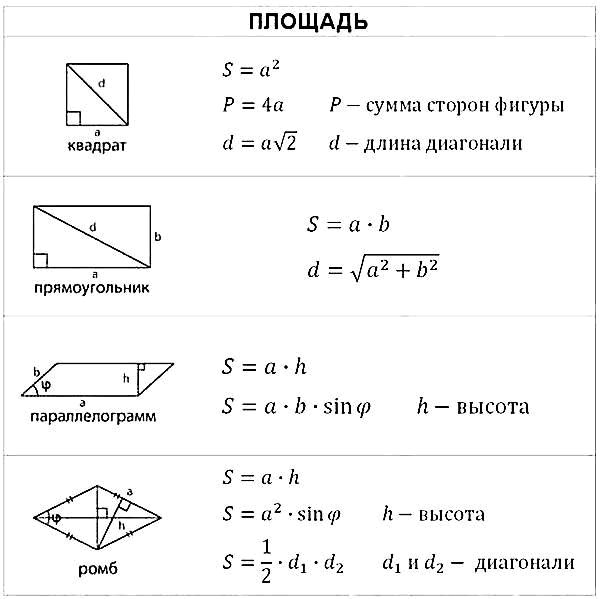
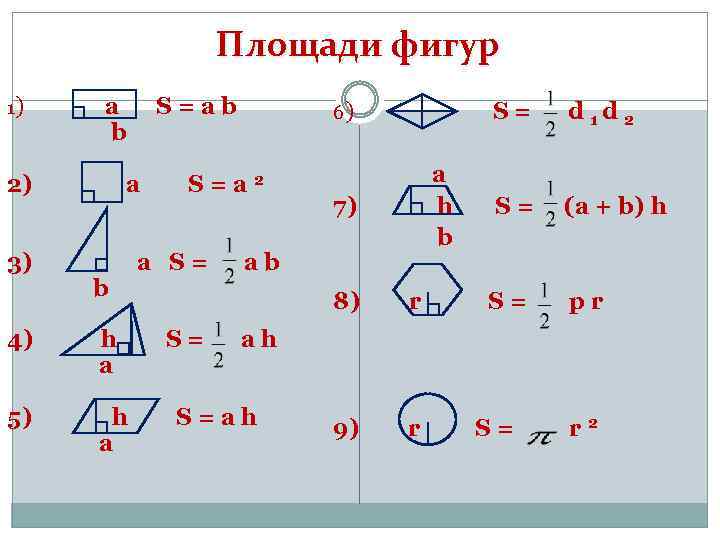
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
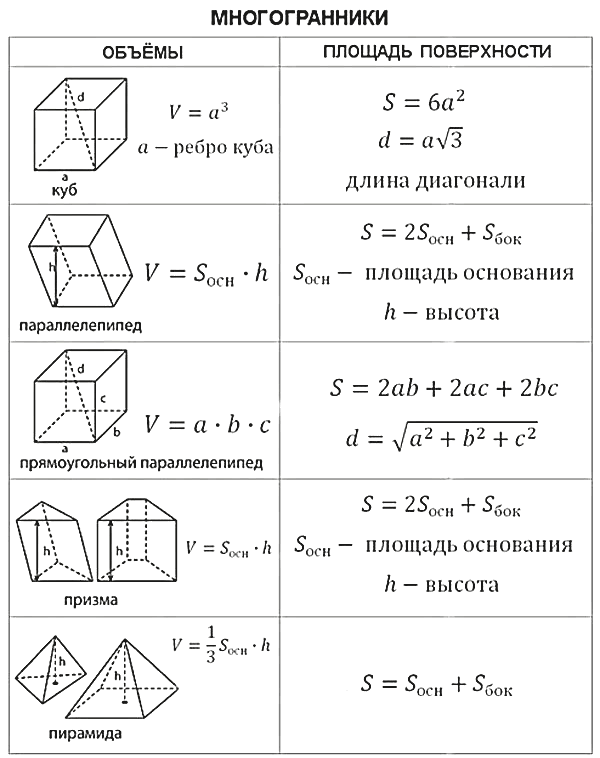
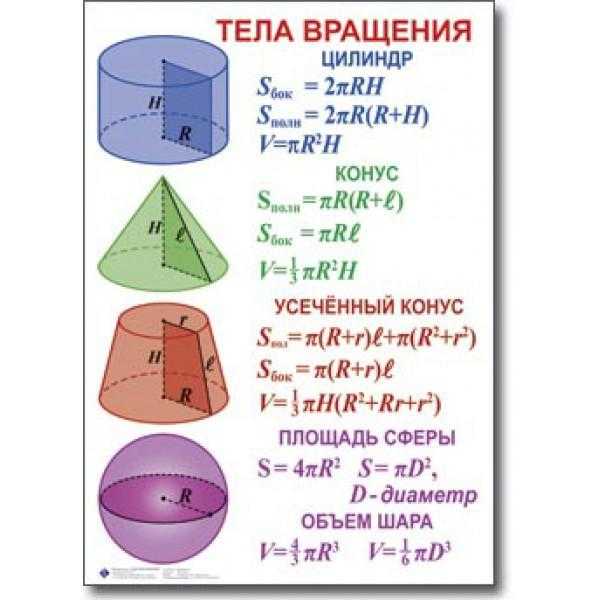
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.
Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.
В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом.
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF: Скачайте pdf файл.
Можете записаться на занятия к репетитору математики, если что-то не понятно.
По разделам:
Степени и корни:
Сокращенное умножение
:
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:
Логарифмы:
Формулы тригонометрии, тождества:
Тригонометрические уравнения:
Значения тригонометрических функций:
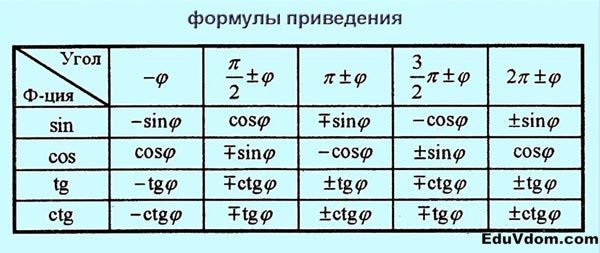
Формулы приведения:
Сумма и разность углов:
Формулы двойного и тройного аргумента:
Формулы половинного аргумента:
Сумма и разность тригонометрических функций:
Произведение тригонометрических функций:
Производная: признаки возрастания, убывания, минимума функции:
Дифференциальное исчисление:
Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:
Стереометрия: объёмы, площади поверхностей:
Обратиться к репетитору по математике.
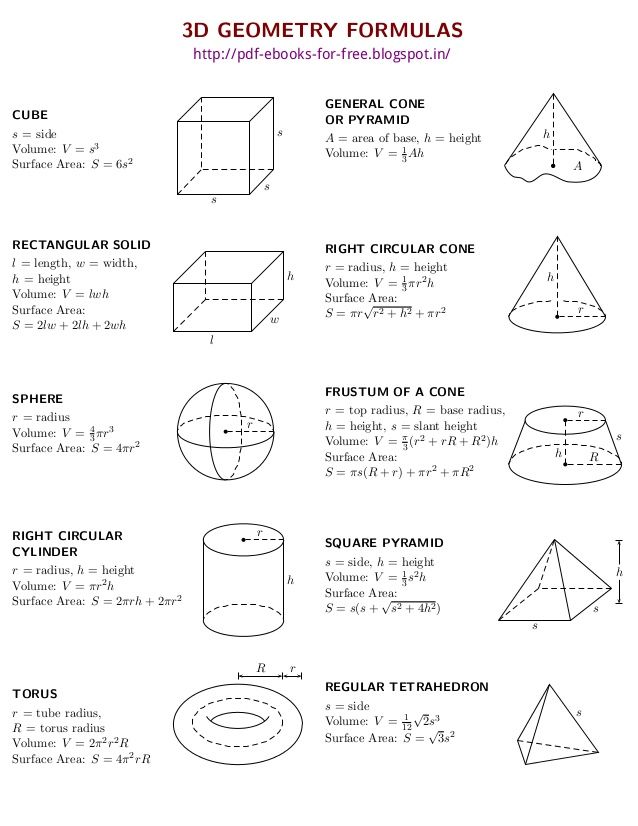
В данной теме выложены вспомогательные картинки для учеников и студентов с формулами площадей и объемов фигур. Ниже расположены основные формулы, которые потребуются при решении задач по геометрии на нахождение объемов и площадей поверхности таких фигур, как квадрат, прямоугольник, параллелограмм, ромб, треугольник, прямоугольный треугольник, трапеция, круг, куб, параллелепипед, прямоугольный параллелепипед, призма, пирамида, цилиндр, конус и шар.
Удержать в голове абсолютно все изученные в курсе алгебры и геометрии формулы к моменту сдачи ЕГЭ по математике практически невозможно. Поэтому, чтобы подойти к экзамену во всеоружии, стоит «вычислить» и запомнить те из них, которые могут понадобиться для решения типовых заданий КИМов.
Формулы по базовой математике для ЕГЭ
Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:
- таблица квадратных чисел от 0 до 99;
- свойства арифметического квадратного корня;
- формулы сокращенного умножения;
- корни квадратного уравнения;
- свойства степени и логарифма;
- теорема Пифагора;
- формула расчета длины окружности и площади круга;
- расчет средней линии треугольника и трапеции;
- радиус вписанной и описанной окружности правильного треугольника;
- формулы расчета площади планиметрических фигур;
- вычисление поверхностей и объемов тел;
- основные тригонометрические функции и тождества;
- график линейной функции;
- геометрический смысл производной.
Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.
Основные формулы для профильного ЕГЭ
Выпускники, планирующие сдавать профиль, ставятся в более жесткие условия, чем те, кто выбрал базовый уровень. Учитывая то, что они видят перспективу своего дальнейшего обучения по направлениям, тесно или напрямую связанным с математикой, к их знаниям предъявляются повышенные требования. В частности, на официальные справочные материалы особенно рассчитывать не приходится. Все, что в них есть, это 5 тригонометрических тождеств.
Естественно, чтобы сдать профильную математику, для ЕГЭ потребуется запомнить намного больше формул. Выяснить, на какие темы нужно обратить внимание, можно по тому же алгоритму, что и для базы (из КЭС или, решая тренировочные задания).
Основываясь на данных, опубликованных на сайте ФИПИ, с большой долей вероятности потребуется знание следующих формул для сдачи ЕГЭ по профильной математике:
- правила сокращенного умножения;
- арифметическая и геометрическая прогрессии;
- основы вероятностной теории;
- свойства степеней и логарифмов;
- азы тригонометрии (формулы двойного угла, суммы и разности аргументов; алгоритм преобразования разности и суммы в произведение; обратные функции);
- производная (правила дифференцирования, элементарнее функции и уравнение касательной);
- первообразная;
- двухмерная планиметрия;
- правила нахождения площадей геометрических фигур;
- трехмерная стереометрия.
Опытные учителя и репетиторы собрали все формулы по математике, которые приходилось использовать на ЕГЭ в последние три года:
- ЕГЭ по математике – формулы для алгебры и начал анализа
- Формулы ЕГЭ – математика, раздел геометрия
Материалы для скачивания – в формате pdf.
Выученные назубок формулы к ЕГЭ по математике – это только часть пути к успешной сдаче, надо еще научиться правильно применять их. Хорошую практику даст решение сложных задач.
Математика
+27
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по математике
Русский язык
+30
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по русскому языку
Обществознание
+25
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по обществознанию
Физика
+31
балл
к ЕГЭ
Курсы подготовки к ЕГЭ по физике
Английский язык
+24
балла
к ЕГЭ
Курсы подготовки к ЕГЭ по английскому языку
Биология
+29
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по биологии
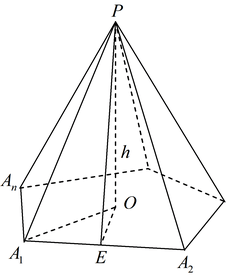
Объем правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).
( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).
Вспомним, как искать эту площадь. Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma ).
У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle H).
По теореме Пифагора для ( displaystyle Delta SOC)
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}).
Чему же равно ( displaystyle OC)? Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамидаправильная и, значит, ( displaystyle O) – центр ( displaystyle Delta ABC).
Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).
( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) – точка пересечения и медиан тоже.
( displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}) (теорема Пифагора для ( displaystyle Delta ACK))
( displaystyle C{{K}^{2}}-{{a}^{2}}-frac{{{a}^{2}}}{4}=frac{3{{a}^{2}}}{4}); ( displaystyle CK=frac{asqrt{3}}{2})
Значит, ( displaystyle OC=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})
Подставим ( displaystyle OC) в формулу для ( displaystyle H).
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{left( frac{asqrt{3}}{3} right)}^{2}}={{b}^{2}}-frac{{{a}^{2}}}{3})
И подставим все в формулу объема:
( displaystyle V=frac{1}{3}{{S}_{ABC}}cdot H=frac{1}{3}cdot frac{{{a}^{2}}sqrt{3}}{4}cdot sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}})
( displaystyle V=frac{{{a}^{2}}sqrt{3}}{12}sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}}).
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).
Объемы и площади объемных фигур. Формулы для нахождения объема параллелепипеда
Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора
гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно.
Пример задания и оформления его решения приведен на рисунке ниже.
Примечание 1
. Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).
Примечание 2
. Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике.
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13.
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
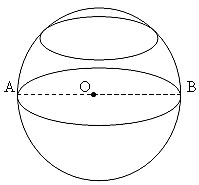
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности.
Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
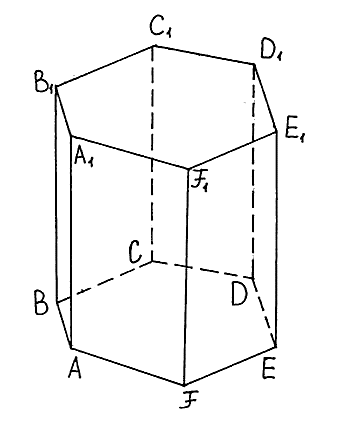
Формула расчета объема шестиугольной призмы. Объемы геометрических фигур
Все фигуры, которые ограничены гранями, находящимися в разных плоскостях в пространстве, обладают некоторым объемом. Вычислением этой величины занимается специальный геометрический раздел — стереометрия. В данной статье приведем формулу объема шестиугольной призмы.
Что такое призма?
Очевидно, что прежде чем находить объем геометрической фигуры, следует познакомиться с ней и понять, какими свойствами она обладает.
Построить фигуру несложно. Для этого следует взять произвольный многоугольник и с помощью одинаковых параллельных друг другу отрезков перенести его в другую плоскость. Получившаяся фигура будет призмой. Отметим, что она, в отличие от конуса, цилиндра и сферы, не является фигурой вращения, то есть ее нельзя получить с помощью вращения вокруг оси какой-либо плоской фигуры.
Выше на рисунке приведен для примера параллелепипед, который является четырехугольной призмой.
Свойства правильной призмы. Формулы площади, объема и длины…
Пространственная геометрическая фигура призма является объектом изучения стереометрии. Ее…
Призма шестиугольная и ее виды
Далее в статье приведем формулу объема призмы шестиугольной.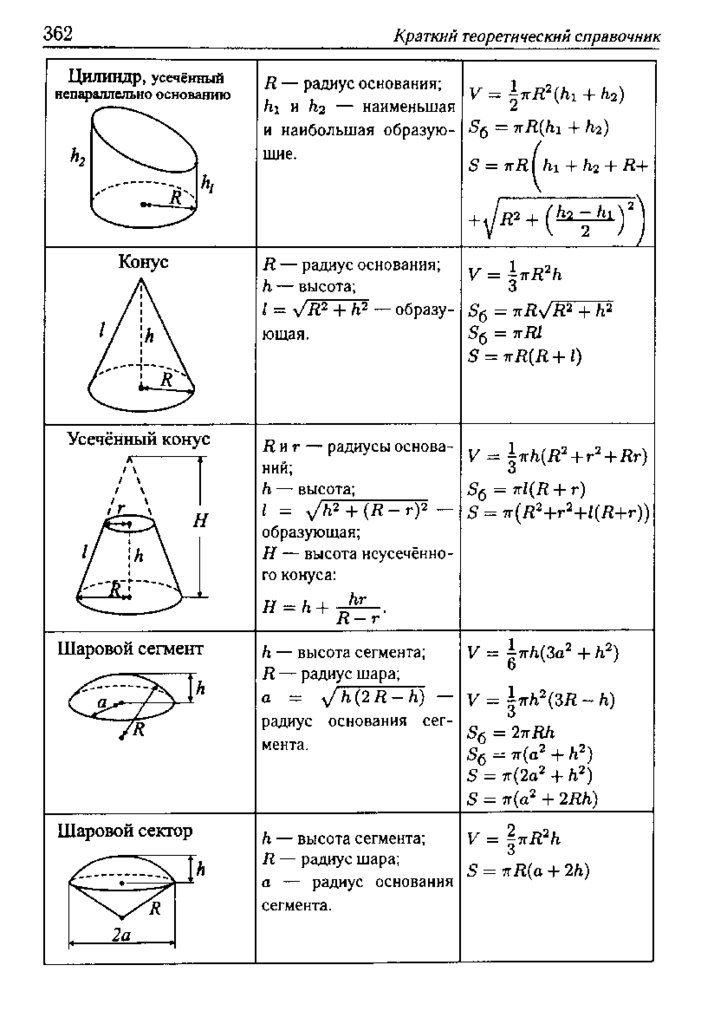
Она образована двумя шестиугольниками в основаниях и шестью параллелограммами, совокупность которых составляет боковую площадь фигуры. Эта призма имеет 12 вершин, 8 граней или сторон и 18 ребер, 2/3 из которых принадлежат основаниям.
Приведенному описанию элементов соответствуют несколько видов шестиугольной призмы. Во-первых, эта фигура может быть выпуклой или вогнутой, что зависит от шестиугольника в основаниях, во-вторых, призма может быть наклонной и прямой. Разница между ними заключается в том, что в прямой фигуре любая боковая сторона будет перпендикулярна основаниям, а в наклонной фигуре боковые стороны пересекают основания под некоторыми углами, которые отличны от 90o. Обе призмы показаны на рисунке.
Заметим, что условие перпендикулярности боковых сторон и оснований приводит к тому, что параллелограммы прямой призмы становятся прямоугольниками.
Наконец, в-третьих, шестиугольная призма бывает правильной и неправильной. Последней будет любая фигура, которая не является прямой и не обладает правильным шестиугольным основанием. Далее основное внимание будем уделять именно правильной призме.
Свойства правильной призмы. Формулы площади, объема и длины…
Пространственная геометрическая фигура призма является объектом изучения стереометрии. Ее…
Правильный шестиугольник
Для определения объемов геометрических фигур многих классов необходимо знать значение площади их основания. Этот факт справедлив для пирамид, цилиндров, конусов. Призмы тоже не являются исключением.
Чтобы найти площадь основания шестиугольной призмы, следует рассчитать площадь шестиугольника. Проще всего сделать это для правильной фигуры. Для наглядности покажем, что такое правильный шестиугольник.
Видно, что представляет он многоугольник, образованный шестью одинаковыми сторонами, которые пересекаются под углами 120o.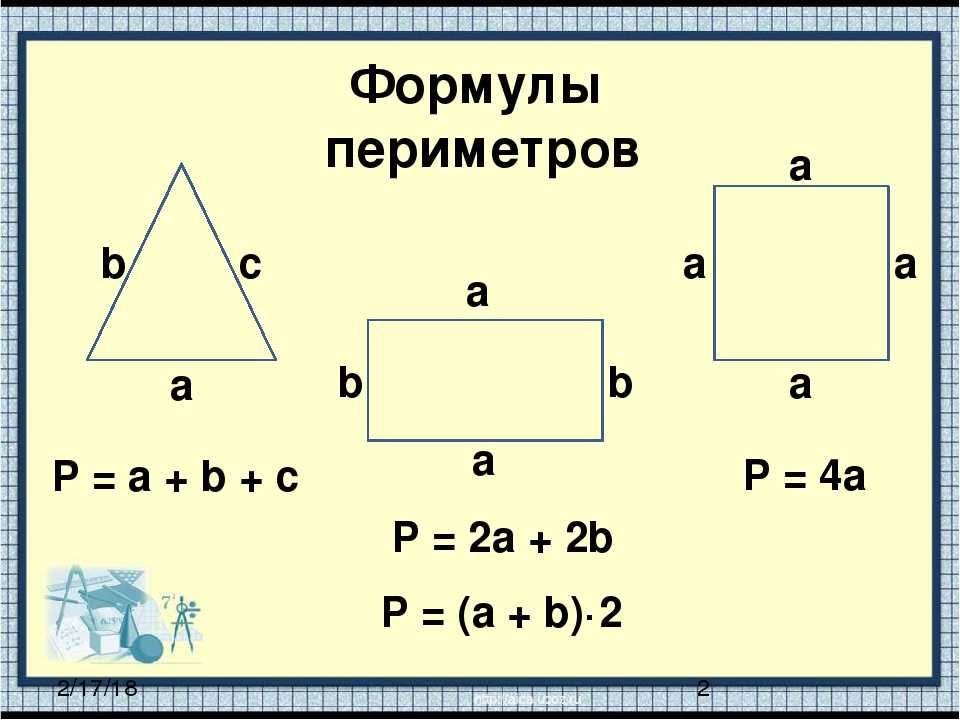
Вычисление площади основания призмы шестиугольной правильной сводится к определению площади приведенной выше фигуры. Если шестиугольник разбить на равносторонние треугольники так, как показано на рисунке, то его площадь будет равна умноженной на 6 площади одного треугольника. Обозначим длину стороны шестиугольника буквой a, тогда для площади S шестиугольника получаем:
S = 6*1/2*a*√3/2*a = 3*√3/2*a2.
Для любого другого шестиугольника, который не является правильным, эта формула будет несправедливой.
Объем правильной шестиугольной призмы. Объем шестиугольной…
Призма — это одна из объемных фигур, свойства которой изучают в школе в курсе пространственной…
Вычислить объем любой призмы несложно, для этого следует знать всего два ее параметра: высоту h и основания площадь S. Расчет объема V осуществляется по следующей формуле:
V = h*S.

Отметим важную вещь: записанное выражение справедливо для любых видов призм, включая вогнутые и наклонные. Тем не менее для произвольной призмы, несмотря на простоту формулы, применять ее бывает сложно. Сложность связана с определением обоих параметров в выражении.
В связи с вышесказанным, рассмотрим конкретную правильную призму с правильным шестиугольным основанием. Если ее высота равна h, а длина стороны равна a, тогда формула объема шестиугольной призмы правильной примет вид:
V = 3*√3/2*h*a2.
При записи этого выражения была подставлена формула для S, приведенная в предыдущем пункте.
Далее решим две задачи, в которых покажем, как найти объем шестиугольной призмы для конкретных случаев.
Задача с известной диагональю
Ниже на рисунке показана правильная призма. Известно, что сторона ее основания равна 9 см. Чему равен объем шестиугольной призмы, если диагональ AB имеет длину 21 см.
Не сложно догадаться, взглянув на рисунок, что треугольник ABC является прямоугольным, причем сторона AB — это гипотенуза.
h = AC = √(AB2-CB2) = √(212-182) ≈ 10,82 см.
Значение высоты мы округлили до сотых долей сантиметра.
Поскольку нам известна высота h и сторона основания a, то можно применить формулу для V. Получаем:
V = 3*√3/2*h*a2 = 3*√3/2*10,82*92 = 2277 см3.
Таким образом, рассмотренная призма имеет объем почти 2,3 литра.
Задача с вписанным в призму цилиндром
Известно, что цилиндр с радиусом 12 см вписан в правильную шестиугольную призму. Объем цилиндра равен 1360 см3. Чему равен объем призмы?
Как было показано, определить объем призмы можно, если знать ее высоту и сторону основания.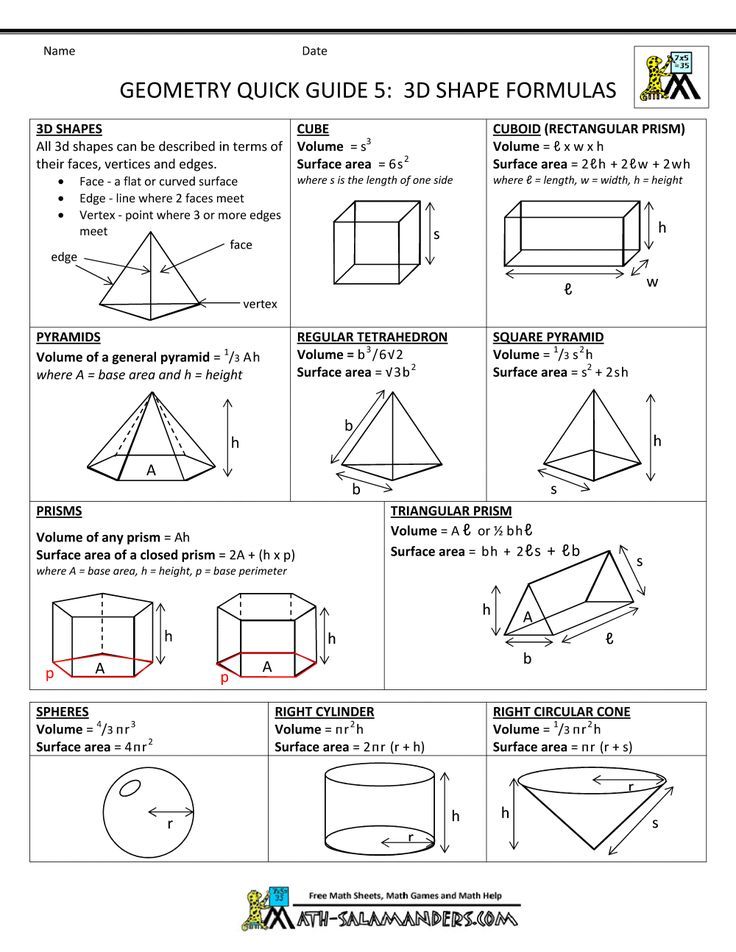
a = 2*r/√3.
Понять, откуда взялась эта формула, можно, если учесть, что радиус r является высотой одного из шести равносторонних треугольников шестиугольника.
Теперь вычислим высоту h призмы. Согласно условию задачи, она должна совпадать с высотой цилиндра. Объем же цилиндра рассчитывается по той же формуле, что и для призмы. Имеем:
Vc = So*h = pi*r2*h =>
h = Vc/(pi*r2).
Подставляем выражения для a и h в формулу для V призмы, получаем:
V = 3*√3/2*h*a2 = 3*√3/2*Vc/(pi*r2)*(2*r/√3)**2 = 2*√3*Vc/pi.
Мы пришли к интересному результату: оказывается, объем шестиугольной призмы не зависит от радиуса вписанного цилиндра, а однозначно определяется его объемом.
Volume Formulas — Etsy.de
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное,
присоединяйтесь к сообществу, делающему добро.
(40 релевантных результатов)
Разница между площадью и объемом
Как мы знаем, геометрия изучает формы.
Площадь
Площадь — это измерение области, покрытой любыми двумерными геометрическими фигурами. Площадь любой формы зависит от ее размеров. Различные формы имеют разные области. Например, площадь квадрата отличается от площади прямоугольника. Площадь фигуры рассчитывается в квадратных единицах (квадратных единицах).
Предположим, если вы хотите покрасить прямоугольную стену своего дома, вам нужно знать площадь стены, чтобы рассчитать количество краски, необходимой для покраски стены, и стоимость покраски.
Если две фигуры имеют одинаковую форму, нет необходимости, чтобы они имели одинаковую площадь до тех пор, пока их размеры не станут равными. Предположим, что два квадрата имеют стороны s и s1, поэтому площади двух квадратов будут равны, если s = s 1
Объем
Пространство, занимаемое трехмерным объектом, измеряется с точки зрения объема этого объекта. . Объем твердой формы является произведением трех измерений, поэтому объем выражается в кубических единицах. Предположим, объем куба измеряется произведением его длины, ширины и высоты.
Внутренняя часть полого объекта может быть заполнена воздухом или какой-либо жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренность предмета, называется вместимостью полого предмета. Таким образом, мы можем сказать, что объем объекта — это мера пространства, которое он занимает, а вместимость объекта — это объем вещества, которое может вместить его внутренность.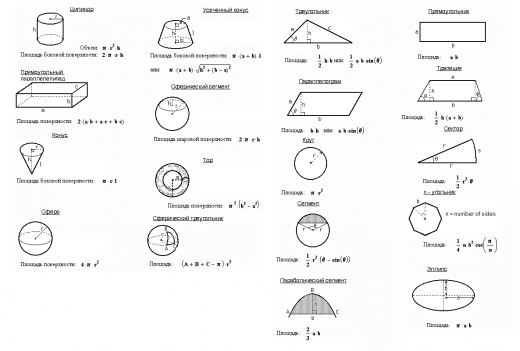
Площадь и объем Определение
Площадь относится к области, охватываемой объектом. И объем относится к количеству или мощности объекта. Площадь — это двумерный объект, а объем — трехмерный объект. Площадь — это обычная фигура, а Объем — сплошная фигура. Площадь охватывает внешнее пространство, а Объем охватывает внутреннюю емкость. Площадь измеряется в квадратных единицах, а объем измеряется в кубических единицах.
Обычно площадь вычисляется для двухмерных объектов, а объем — для трехмерных.
Вот графическое изображение площади и объема, показывающее соотношение между площадью и объемом.
(Изображение будет загружено в ближайшее время)
Давайте попробуем разобраться в связи между Площадью и Объемом и в чем разница между Площадью и Объемом в деталях.
Таблица формул площади для 2D-фигур
999999999999999999999999999999999999999999999999999999
|
Name of Geometric Shapes |
Area Formula |
Variables |
|
Rectangle |
Area = l [times] w |
l = length w = width |
|
Square |
Area = a 2 |
a = sides of the square |
|
Triangle |
область = ½ [ times ] b [ times ] h |
B = основание H = высота |
|
Trapezoid 9999 |
||
|
. |
a =base 1 b = base 2 h = vertical height |
|
|
Parallelogram |
Area = b [times] h |
a = сторона b=основание h=вертикальная высота
|
|
Rhombus |
Area = a [times] h |
a = side of rhombus h = height |
|
Circle |
Area = πr 2 |
r = radius of the circle = (22)/7 or 3.1416 |
|
Semicircle |
Area = ½ πr 2
|
r = radius of круг |
Volume Formula Chart for 3D Shapes(Solid Shapes)
H = высота
H = высота
H = высота
|
Name of Geometric Shapes |
Volume Formula |
Abbreviations Used |
|
Cuboid |
L [times] b[times] h |
h = высота, l = длина b=ширина |
| Куб 9910003 |
a 3 |
a = length of the sides |
|
Right Prism |
Area of Base [times] Height |
. |
|
Правый круглый цилиндр |
πr 2 H |
R = радиус H = высота |
| H = высота | ||
| H = высота | ||
|
. ] Высота |
.. |
|
|
Right Circular Cone |
⅓ (πr 2 h) |
r = radius l = length |
|
Sphere |
4/3πr 3 |
r = radius |
|
Hemisphere |
⅔ (πr 3 ) |
r = radius |
Разница между площадью и объемом
Некоторые ключевые различия между площадью и объемом в математике:
Площадь и объем объемные геометрические фигуры.
Объем – это пространство, занимаемое трехмерным объектом.
Площадь измерена для простых фигур
Объем измеряется для трехмерных (сплошных) фигур.
Площадь измеряется в двух измерениях: длине и ширине.
Объем измеряется в трех измерениях: длина, ширина и высота.
Площадь измеряется в квадратных единицах
Объем измеряется в кубических единицах.
Площадь охватывает космическое пространство объекта
Объем — это вместимость объекта
Пример: квадрат, прямоугольник, круг и т. д.
Пример: куб, прямоугольный параллелепипед, сфера и т. д.
Эти различия показывают соотношение между площадью и объемом.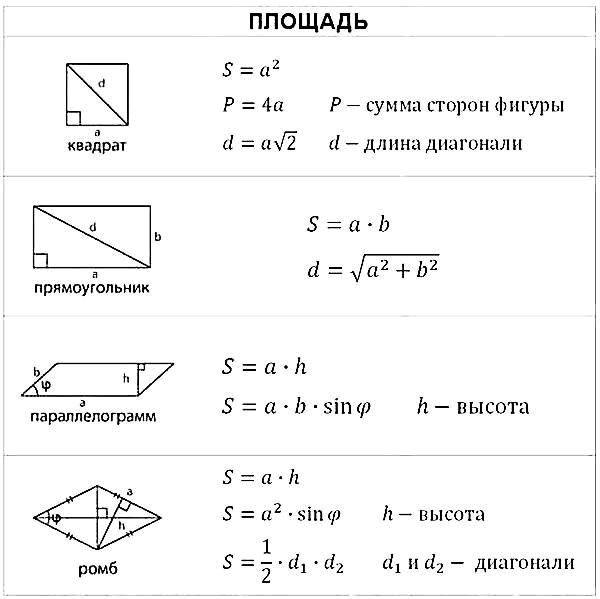
Решенные примеры
1. Стороны квадратного участка равны 9м. Найдите площадь квадратного участка.
Ответ: Дано, Сторона = a = 9 м
По формуле площади квадрата мы знаем, что
Площадь = a2
A = 9 x 9
A = 81 кв.м или 81
2. Сторона куба 9м. Найдите Объем кубического ящика.
Ответ: Дано, Сторона = a = 9м
По формуле Объема куба мы знаем, что
V = a3
V = 9 x 9 x 9
V = 729 кв.м или 729м2
Площадь и объем объекта зависят от размера конкретной формы или фигуры. В то время как площадь — это объем пространства, которое объект занимает в двухмерном пространстве, объем — это емкость формы или фигуры в трехмерном пространстве. Площадь формы — это количество места, которое занимает объект, а объем может быть определен как емкость или количество пространства, которое объект или форма имеет в себе.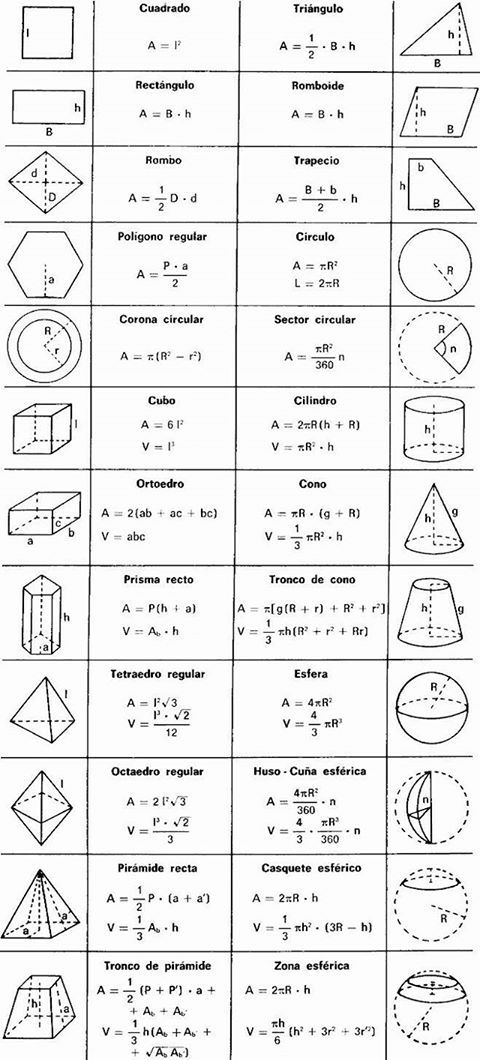
Область твердого тела Форма с определенной стороны или направления может быть объяснена как тень этой сплошной фигуры на определенной плоскости. Например, на определенной плоскости тень сферы с любого направления или стороны представляет собой круг, и, таким образом, площадь сферы с определенного направления представляет собой площадь круга с диаметром, равным диаметру сферы. Однако общая площадь поверхности сферы является отдельной величиной и равна площади четырех таких кругов, если смотреть с четырех перпендикулярных направлений.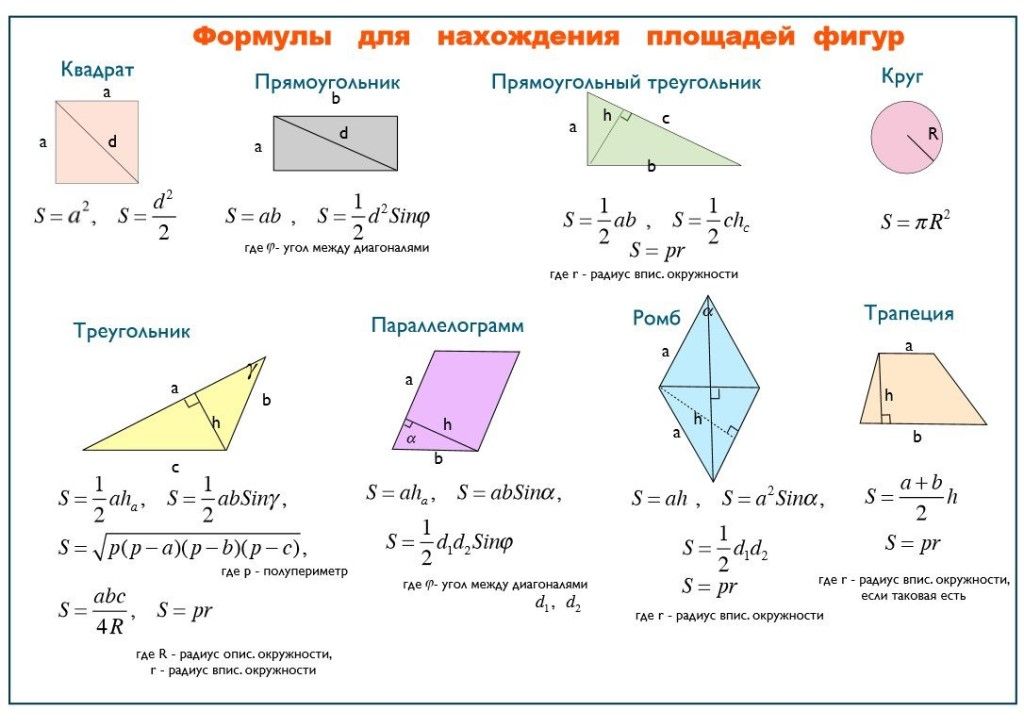
Объем сплошных фигур не зависит от направления, с которого они анализируются. Объем куба имеет фиксированное значение независимо от того, с какой стороны его можно анализировать. Куб будет иметь ту же емкость и займет такое же количество места в трехмерной геометрии. Различные формулы для расчета площади, общей площади поверхности и объема различных форм и тел показаны в таблицах выше. Как видно из таблицы, площадь представляет собой двухмерное понятие и, соответственно, имеет единицу измерения (Длина) 9.0212 2 ., с другой стороны, Объем является трехмерным понятием и, следовательно, имеет единицу измерения (Длина) 3 .
Как связаны площадь и объем?
Площадь и Объем связаны в том смысле, что удлинение, расширение или вращение двухмерных Площадей в другом (третьем) измерении приведет к образованию цельной фигуры, имеющей Объем. Например, расширение круга по измерению высоты приведет к образованию цилиндра, расширение квадрата приведет к образованию куба определенного объема, вращение треугольника по любой из его осей приведет к формирование конуса определенного объема.
Можно ли рассчитать объем по площади?
Некоторые фигуры имеют один параметр, который требуется для расчета площади и объема объекта. Таким образом, если кто-то знает одну из Площади или Объема объекта, можно вычислить другую. Например, сфера имеет параметр радиуса, и с его помощью можно рассчитать как площадь, так и объем сферы, или, если кто-то знает одну из площади сферы или объема сферы, можно вычислить другой.
Однако это возможно не для всех рисунков.
|
Таблицы и формулы 2
|
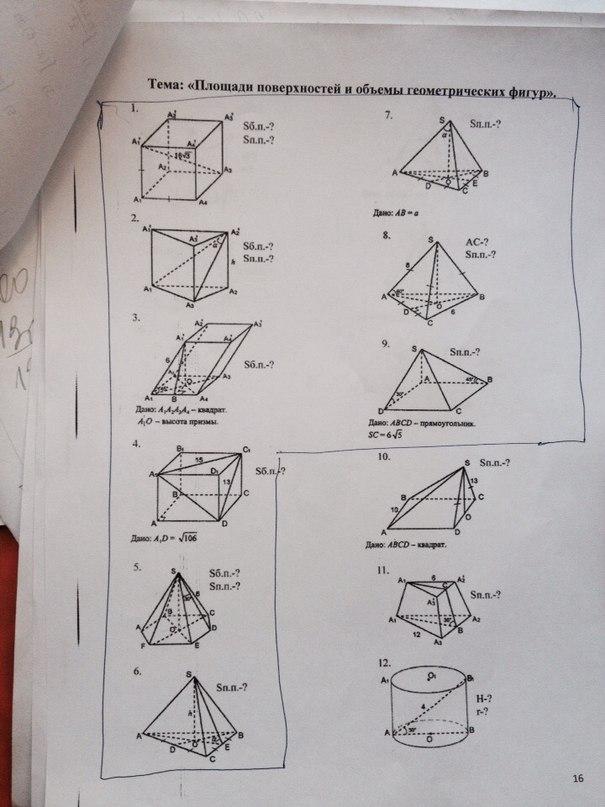
Формулы нахождения площадей поверхностей и объемов фигур.
- Sбок =Pсеч*l;
- V = Sосн*H;
- V=Sсеч*l;
- Sполн= Sсеч + 2* Sосн;
Прямая призма
- Sбок =P*H;
- V = Sосн*H;
- Sполн=Sсеч + 2*Sосн;
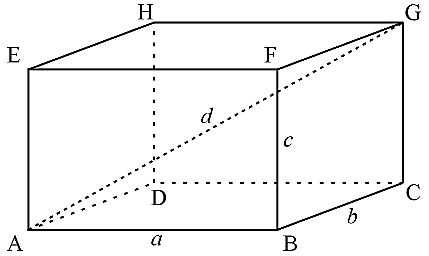
- Sбок =P*H=2(a + b)c;
- V = abc;
- Sполн =2(ab + bc +ac);
- d2 = a2 + b2 + c2;
- Sполн =Sбок+Sосн;
- V = frac{1}{3}V=31 Sосн * H
Правильная пирамида
- Sбок =frac{1}{2}P*h; 21 P∗ h;
- Sбок = Sосн : cos α;
- Sполн = Sбок + Sосн ;
- V = frac{1}{3}Sосн * HV=31 Sосн∗ H
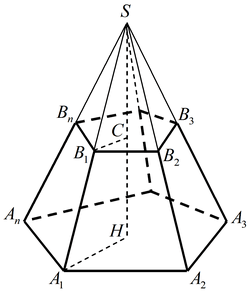
- V=frac{H}{3}(S_1 + S_2 + sqrt{S_1S_2})V=3H (S1 +S2 +S1 S2 )
Правильная усеченная пирамида
- Sбок = frac{1}{2}(P_1 + P_2)21 (P1 +P2 ), где P1 и Р2 — периметры оснований
- Sполн = Sбок + S1 + S2, где S1 и S2 — площади оснований
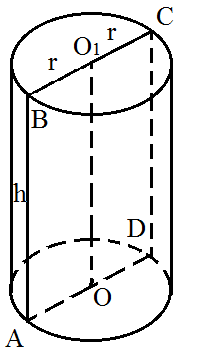
- Sбок= 2 pi RH; 2π RH;
- Sполн = Sбок + 2Sосн;
- Sполн =2 pi R(R+H); 2π R(R+H);
- V=pi R^{2}HV=π R2H
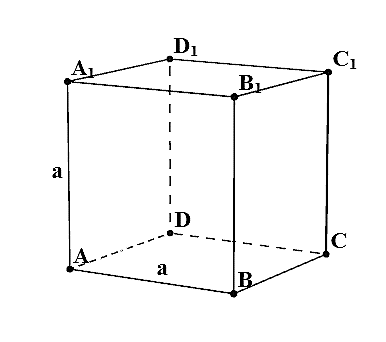
- Если а — ребро куба, то V = a3;
- Sполн =6a^2; d = asqrt{3}; =6a2; d=a3;
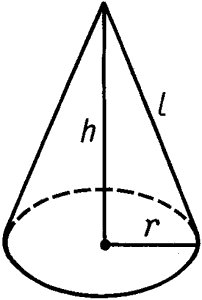
- Sбок= pi Rl; π Rl;
- Sполн = Sбок + Sосн;
- Sполн =pi R(R+l); π R(R+l);
- V=frac{1}{3} pi R^{2}HV=31 π R2H
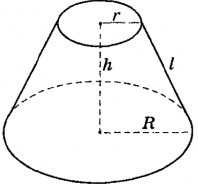
- Sбок=pi l(R+ r); π l(R+r);
- Sполн = Sбок+ S_1 + S_2; +S1 +S2;
- S_1 = pi R^2; S1 =π R2;
- S_2 = pi r^2; S2 =π r2;
- V = frac{pi H}{3}(R^2 + Rr + r^2)V=3π H (R2+Rr+r2)
- Sшара = 4pi R^2 = pi D^24π R2=π D2
- Vшара= frac{4}{3}pi R^3 = frac{1}{6}pi D^334 π R3=61 π D3


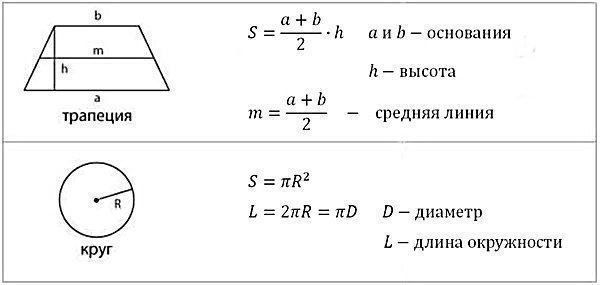










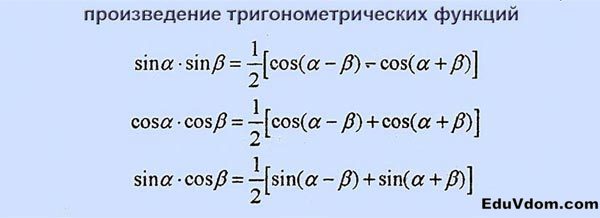




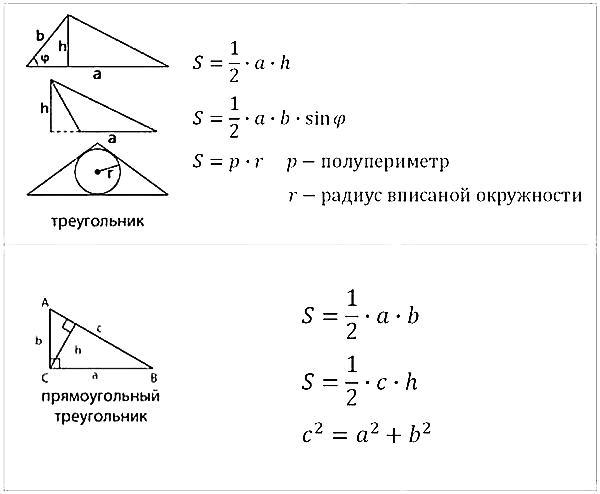
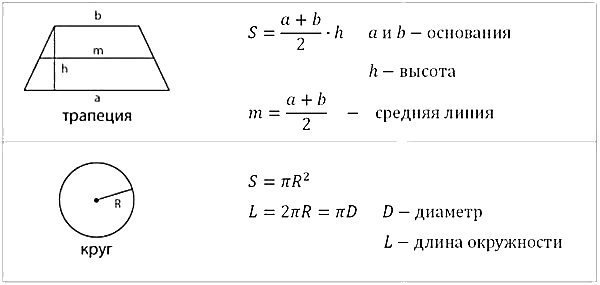



 a + b)h
a + b)h 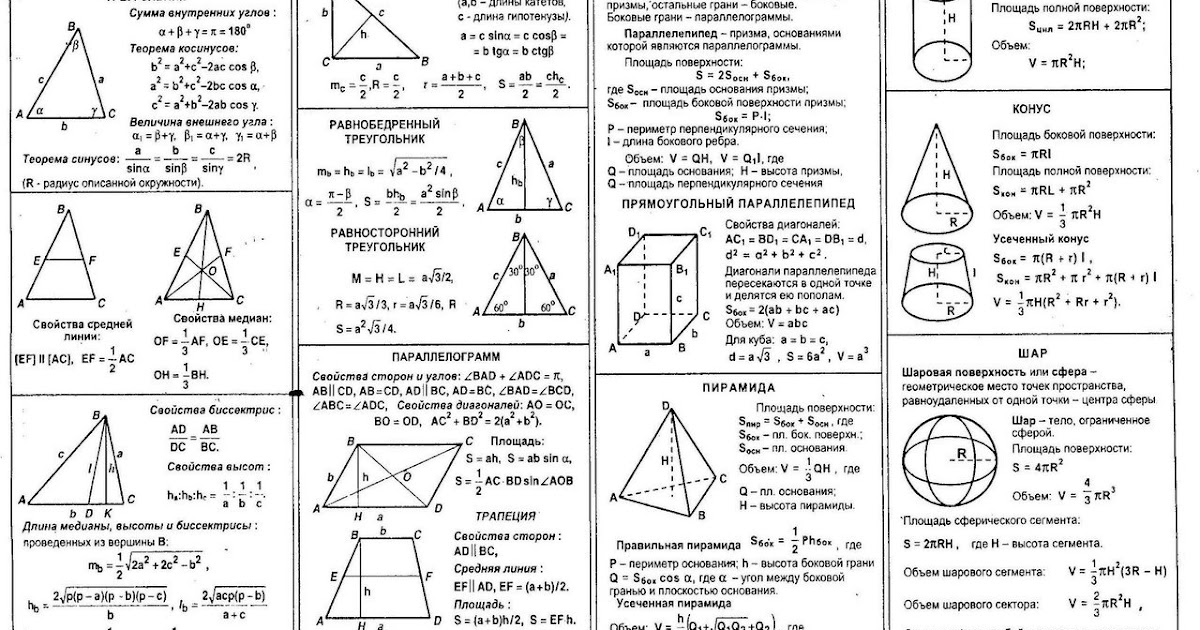 .
.