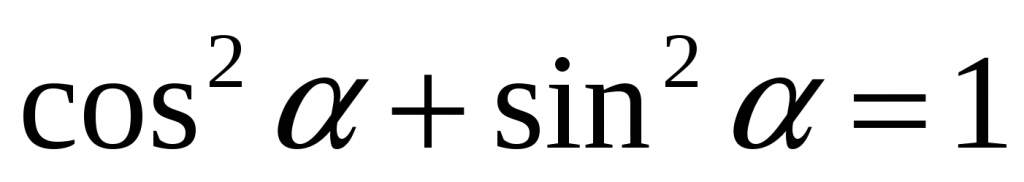Формулы для подготовки к экзамену по математике

Оглавление:

• Формулы сокращенного умножения
• Квадратное уравнение и формула разложения квадратного трехчлена на множители
• Свойства степеней и корней
• Формулы с логарифмами
• Арифметическая прогрессия
• Геометрическая прогрессия
• Тригонометрия
• Тригонометрические уравнения
• Геометрия на плоскости (планиметрия)
• Геометрия в пространстве (стереометрия)
• Координаты
• Таблица умножения
• Таблица квадратов двухзначных чисел
• Расширенная PDF версия документа «Все главные формулы по школьной математике»

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты

К оглавлению…

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

К оглавлению…

Ученики, сдающие базовую математику, почти не тратят времени на подготовку к ней, ведь в экзамене нужно решить лишь задания, которые требуют самых основ. Тем же выпускникам, которые хотят поступать в технические вузы, предстоит готовиться не только к предметам по выбору, но и к профилю. В этой статье мы расскажем, какие формулы для ЕГЭ по математике (профильный уровень) сделают подготовку легче, а баллы на экзамене — выше.

Какие формулы необходимы для сдачи ЕГЭ по профильной математике?

Помимо очевидного, что для сдачи профиля нужно уметь складывать, вычитать и умножать, необходимы еще некоторые знания. Все это проходится в течение школы, но повторить или заполнить пробелы перед экзаменом нужно обязательно. Вот, что пригодится:

• Формулы сокращенного умножения;
• Арифметическая и геометрическая прогрессии;
• Вероятность;
• Свойства степеней;
• Свойства логарифмов;
• Тригонометрия;
• Производные;
• Первообразные.

Список внушительный, но вполне реальный, чтобы его выучить. Для того, чтобы лишний раз не гуглить в интернете «формулы для ЕГЭ по математике профильный уровень», приложим их ниже. А начнем по порядку из списка выше.

Формулы сокращённого умножения

Первые в нашем списке – формулы сокращенного умножения – нужны для решения задания №9 из профильного уровня. Вам встретятся задачи на преобразование выражений, поэтому умение это делать будет вознаграждено баллами.

Вот то, что будет вашим спасательным кругом:

Есть те, которые знать не обязательно. Но чем большими знаниями вы будете обладать, тем легче вам будет на экзамене. Вот они:

Умея применять эти формулы для ЕГЭ по математике, профильный уровень вам уже будет решить легче. Но это далеко не все, что нужно знать, чтобы получить сто баллов за ЕГЭ.

Арифметическая и геометрическая прогрессии

Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:

Вероятность

Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:

Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.

Свойства степеней

Эти свойства нужно знать и для того, чтобы решить «базу», так что гуманитарии тоже могут обратить внимание на это:

Как вы видите, запоминать не очень много, зато формулы не самые простые. Но есть еще сложнее, и сейчас узнаем, какие они.

Свойства логарифмов

Формулы логарифмов лучше всего начать с их определения:

Теперь перейдем к более сложному:

Тригонометрия

Тригонометрические уравнения встречаются в задании №13. Для того, чтобы заработать баллы, нужно знать это:

Но это еще не все. Есть такая вещь, как основное тригонометрическое тождество. Вот оно:

Формулы двойного угла:

Формулы суммы и разности аргументов:

Преобразование суммы и разности в произведение:

Формулы половинного аргумента:

На этом с тригонометрией все.

Производные

Начнем с основных правил дифференцирования:

Уравнение касательной: 

Производные элементарных функций:

Закончим эту статью первообразными.

Первообразные

Она выглядит так:

Таблица первообразных:

Итог

То, что работа предстоит колоссальная — и правда, и нет. Да, придется хорошо постараться, чтобы набрать высокие баллы, так как составители ЕГЭ все больше усложняют экзамен. С другой стороны, хотя бы часть формул, описанных выше, вы уже знаете. А значит, работы хоть на немного, но меньше. А это ли не счастье в такие тяжелые времена подготовки?