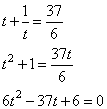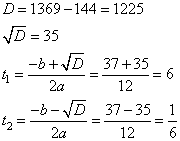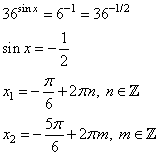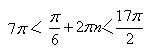Задание 13 Профильного ЕГЭ (Стереометрия) многие старшеклассники считают самой сложной задачей в варианте. И напрасно! Ничего особенного в ней нет. Просто начинать надо вовремя, лучше всего в десятом классе. И конечно, не с самых сложных задач. Действуем по порядку!
1. Подготовительный этап — решение задач по стереометрии из первой части ЕГЭ. Повторите формулы объемов и площадей поверхности многогранников и тел вращения. Посмотрите, как решаются типовые задачи.
2. Повторите необходимую теорию. Вот краткая Программа по стереометрии. Проверьте себя. Все ли вы знаете? В освоении стереометрии вам поможет наш ЕГЭ-Справочник.
3. Посмотрите, как правильно строить чертежи.
4. Выучили теорию? Применяем на практике — строим сечения.
5. Решаем простые задачи по стереометрии. И после этого — переходим к реальным задачам ЕГЭ.
6. Задачи 13 по стереометрии из Профильного ЕГЭ по математике обычно относятся к одному из типов. Смотрите нашу Классификацию задач по стереометрии и методы их решения.
Вот примеры простых подготовительных задач по стереометрии:
1. Высота правильной треугольной пирамиды равна 4, а угол между боковой гранью и плоскостью основания равен 60 градусов. Найдите расстояние от вершины основания до плоскости противолежащей ей боковой грани.
Посмотреть решение
2. В правильной шестиугольной призме , все ребра которой равны 1, точка G — середина ребра
Найдите угол между прямой АG и плоскостью
Посмотреть решение
3. В правильной шестиугольной призме все рёбра равны 1. Найдите расстояние от точки В до плоскости
Посмотреть решение
4. В основании прямой призмы лежит ромб. Найти угол между прямыми
и
Посмотреть решение
5. Точка E — середина ребра куба
Найдите угол между прямыми
и
Посмотреть решение
6. В правильной треугольной призме , все рёбра которой равны
. Найдите расстояние между прямыми
и
Посмотреть решение
7. Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 5. Найдите площадь сечения конуса плоскостью ABP.
Посмотреть решение
А теперь — реальные задачи по стереометрии, встретившиеся выпускникам на Профильном ЕГЭ по математике.
8. Точки М и N — середины ребер соответственно АВ и СD треугольной пирамиды АВСD, О — точка пересечения медиан грани АВС.
а) Докажите, что прямая DO проходит через середину отрезка MN.
б) Найдите угол между прямыми MN и ВС, если АВСD — правильный тетраэдр.
Посмотреть решение
9. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка , причём
— образующая цилиндра, а AC — диаметр основания. Известно, что
а) Докажите, что угол между прямыми и
равен
б)Найдите объём цилиндра.
Посмотреть решение
10. В основании призмы лежит правильный треугольник, вершина
проецируется в центр Q основания АВС.
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите угол между прямой и плоскостью
если боковое ребро призмы равно стороне основания.
Посмотреть решение
11. Сечением прямоугольного параллелепипеда плоскостью
, содержащей прямую
и параллельной прямой АС, является ромб.
а) Докажите, что грань ABCD — квадрат.
б) Найдите угол между плоскостями и
, если
Посмотреть решение
12. На ребрах АВ и ВС треугольной пирамиды АВСD отмечены точки М и N соответственно, причем
Точки P и Q — середины ребер DA и DC соответственно.
а) Докажите, что точки P, Q, M и N лежат в одной плоскости.
б) Найдите, в каком отношении эта плоскость делит объем пирамиды.
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 14
7 лайфхаков для решения задач по стереометрии:
1. Задача по стереометрии не решается без хорошего чертежа! Чертеж строим по линейке, черной ручкой, на клетчатой бумаге, по правилам построения чертежей. На ЕГЭ можно и нужно пользоваться линейкой! А бланк будет в клеточку.
2. Все, что нужно, на чертеже должно быть хорошо видно! Если вам не понравился чертеж — не сидите над ним, бросьте и нарисуйте другой. Одного объемного чертежа будет недостаточно — понадобится один или несколько плоских.
3. Учимся записывать решение кратко. Вспомним основные обозначения
— точка M принадлежит плоскости АВС.
— прямые а и b пересекаются в точке О.
— прямые а и b параллельны.
— прямые а и b перпендикулярны.
4. Почти в каждой задаче по стереометрии встречаются «особенные треугольники»
Давайте вспомним:
— В прямоугольном равнобедренном треугольнике гипотенуза в раз больше катета.
— В треугольнике с углами 30, 60 и 90 градусов гипотенуза в 2 раза больше меньшего катета, а больший катет в раз больше меньшего.
5. Формула для площади прямоугольной проекции фигуры помогает найти угол между плоскостями. Здесь
— угол между плоскостью фигуры и плоскостью проекции.
6. Метод объемов помогает найти расстояние от точки до плоскости. Надо выбрать треугольную пирамиду, записать ее объем двумя способами и найти из полученного уравнения нужное расстояние.
7. Сначала изучаем «классику». После этого, если время есть, можно браться и за координатный метод
Почему именно в таком порядке?
Конечно, координатный метод удобен. Однако большинство задач по стереометрии из вариантов ЕГЭ «заточены» под классику.
И если в решении задачи координатным методом вы сделаете арифметическую ошибку — можете потерять все баллы. Эксперт не будет разбираться, правильно ли вы посчитали определитель или смешанное произведение векторов. Потому что эти темы не входят в школьную программу, и составители «конструировали» задачи по стереометрии так, чтобы они решались обычными, «классическими» способами.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 13 Профильного ЕГЭ по математике. Стереометрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
ЕГЭ Профиль №13. Тригонометрические уравнения
13 задания профильного ЕГЭ по математике представляет собой уравнение с отбором корней принадлежащих заданному промежутку. Одним из видов уравнений которое может оказаться в 13 задание является тригонометрическое уравнение. Как правило, это достаточно простое тригонометрическое уравнение для решения которого потребуется знания основных тригонометрических формул, и умение решать простейшие тригонометрические уравнения. Отбор корней тригонометрического уравнения принадлежащих заданному промежутку можно производить одним из четырех способов: методом перебора, с помощью тригонометрической окружности, с помощью двойного неравенства и графическим способом. В данном разделе представлены тригонометрические уравнения (всего 226) разбитые на три уровня сложности. Уровень А — это простейшие тригонометрические уравнения, которые являются подготовительными для решения реальных тригонометрических уравнений предлагаемых на экзамене. Уровень В — состоит из уравнений, которые предлагали на реальных ЕГЭ и диагностических работах прошлых лет. Уровень С — задачи повышенной сложности.
Задание №13 ЕГЭ по математике профильного уровня
Уравнения
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем
Простейшие (Protozoa) — тип одноклеточных животных.
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
сos2x = 1 – sin x.
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
Получаем такое уравнение: 1−sin 2 x=1− sinx Теперь в уравнении присутствует только одна тригонометрическая функция sinx. 2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:
3. Делаем обратную замену:
Решаем эти уравнения:
Следовательно, получаем два семейства решений. Пункт б):
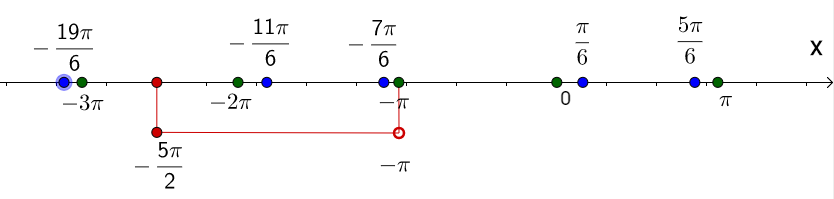
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Второй вариант задания (из Ященко, №1)
Алгоритм решения:
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
D=b 2 – c = 81 – 4∙4∙2 =49,
3. Возвращаемся к переменной х: 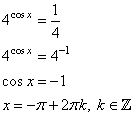
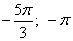
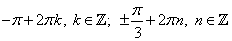
Третий вариант задания (из Ященко, № 6)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
- Решаем неравенства для каждого случая.
- Записываем ответ.
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
источники:
http://spadilo.ru/zadanie-13-ege-po-matematike-profilnyj/
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
Уравнения
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
[su_note note_color=”#defae6″]
а) Решите уравнение cos2x = 1-cos(п/2-x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-5п/2;-п].
[/su_note]
Алгоритм решения:
Пункт а)
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие тригонометрические уравнения.
Пункт б)
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
Пункт а)
1. Преобразуем правую часть равенства, используя формулу приведения cos(π/2−x)=sinx. Имеем:
сos2x = 1 – sin x.
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
cos(2х)=1−2sin2 х
Получаем такое уравнение: 1−sin 2x=1− sinx
Теперь в уравнении присутствует только одна тригонометрическая функция sinx.
2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:
1−2t2=1−t,
−2t2+t=0,
t (−2t+1)=0,
t = 0 или -2t + 1 = 0,
t1 = 0 t2 = 1/2.
3. Делаем обратную замену:
sin x = 0 или sin x = ½
Решаем эти уравнения:
sin x =0↔x=πn, nЄZ
sin(x)=1/2↔x= (-1)n∙(π/6)+ πn, nЄZ.
Следовательно, получаем два семейства решений.
Пункт б):
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).
3. Красным цветом помечаем концы промежутка.
4. В указанном промежутке расположены три корня что три корня: −2π;−11π/6 и −7π/6.
Ответ:
а) πn, nЄZ; (-1)n∙(π/6)+ πn, nЄZ
б) −2π;−11π6;−7π6
Второй вариант задания (из Ященко, №1)
[su_note note_color=”#defae6″]
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку .
[/su_note]
Алгоритм решения:
Пункт а)
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
Пункт б)
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
Пункт а)
1. Вводим замену t = 4cos х. тогда уравнение примет вид:
Решаем квадратное уравнение с помощью формул дискриминанта и корней:
D=b2 – c = 81 – 4∙4∙2 =49,
t1= (9 – 7)/8= ¼, t2 = (9+7)/8=2.
3. Возвращаемся к переменной х:
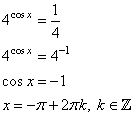
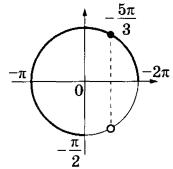
Пункт б)
1. Строим координатную плоскость и окружность единичного радиуса на ней.
2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка..
Это корни . Их два.
Ответ:
а)
б)
Третий вариант задания (из Ященко, № 6)
[su_note note_color=”#defae6″]
а) Решите уравнение 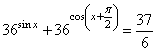
б) Найдите все корни этого уравнения, принадлежащие отрезку .
[/su_note]
Алгоритм решения:
Пункт а)
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
Пункт б)
- Решаем неравенства для каждого случая.
- Записываем ответ.
Решение:
а)
1. По формулам приведения .
2. Тогда данное уравнение примет вид:
3. Вводим замену . Получаем:
Решаем обычное квадратное уравнение с помощью формул дискриминанта и корней:
Оба корня положительны.
3. Возвращаемся к переменной х:
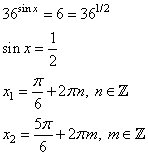
Получили четыре семейства корней. Их бесконечно много.
б)
4. С помощью неравенств находим те корни, которые принадлежащие отрезку :
Для корней
Получаем одно значение .
Для корней
ни одного значения корней нет.
Для корней
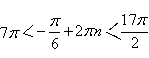
;
Для корней
есть одно значение
.
Ответ:
а) ;
;
б) .
Даниил Романович | Просмотров: 16k
-
Главная
-
Теория ЕГЭ
-
Математика — теория ЕГЭ
-
Задание 13 ЕГЭ 2021 по математике, теория
- 08.10.2018
Необходимая теория для успешного освоения и решения заданий №13 по математике профильного уровня на ЕГЭ в 2021 году.
Представлена вся теория и алгоритм решения различных заданий такого типа.
- Тренировочные кимы ЕГЭ по математике
- Практика — примеры для решения каждого типа заданий
Обсудить решение конкретных заданий вы можете в комментариях ниже.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
«Использование метода координат в пространстве для решения задачи №13 Единого государственного экзамена»
Как всем известно, для учеников старших классов самой насущной проблемой является Единый государственный экзамен. Причём, тех учеников, которые с уверенностью могут сказать: «Я могу решить 13 или 16 задачу», всего единицы. Да и те, кто действительно могут решить их, об этом громко не заявляют.
Анализируя данную проблему, можно сказать, что большая часть выпускников ограничивается заданием 13 пункта а). А при решении пункта б) уже возникают проблемы.
Как вы знаете, в задании 13 чаще всего требуется найти:
1) угол между двумя скрещивающимися прямыми, между прямой и плоскостью, между двумя плоскостями;
2) расстояние между двумя скрещивающимися прямыми, расстояние от точки до прямой, от точки до плоскости.
В своей работе я предлагаю использовать один из универсальных приёмов решения геометрических задач – метод координат в пространстве. Мы уже хорошо знакомы с векторами, координатами и их свойствами. Цель моей работы: научиться применять знания для решения задач стереометрии.
Однако формальное применение координатно-векторного метода может значительно затруднить решение даже самой простой задачи. Поэтому я привожу несколько общих указаний, которые помогут сориентироваться и решить, можно ли в данной задаче использовать векторы и координаты.
Во-первых, естественно, нужно применять координатный или векторный метод, если в условиях задачи говорится о векторах или координатах;
Во-вторых, очень полезно применить координатный метод, если из условия задачи не понятно, как расположены те или иные точки;
В-третьих, что для нас особенно важно, полезно и удобно применять координаты и векторы для вычисления углов и расстояний;
В-четвертых, вообще, часто, когда не видно ни каких подходов к решению задачи, можно попробовать применить координатный метод. Он не обязательно даст решение, но поможет разобраться с условиями и даст толчок к поиску другого решения.
2.1. Кратко из теории4
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Существует множество систем координат: аффинная, полярная, биполярная, коническая, параболическая, проективная, сферическая, цилиндрическая и др. Наиболее используемая из них — прямоугольная система координат (также известная как декартова система координат). Ею мы и будем пользоваться для решения задач.
Прямоугольная (декартова) система координат – совокупность точки О (называемой началом координат), единицы измерения и трёх попарно перпендикулярных прямых Ox, Oy и Oz (называемых осями координат: Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано направление положительного отсчёта. Плоскости хОу, уОz и zOx называют координатными плоскостями. Каждой точке пространства ставится в соответствие тройка чисел, называемых её координатами.
Применение метода координат даёт нам множество возможностей для решения задач.
- Нахождение расстояния между двумя точками, заданными своими координатами.
где d=AB, A(x1; y1; z1), B(x2; y2; z2)
2. Нахождение координаты середины С(x; y; z) отрезка АВ, A(x1; y1; z1), B(x2; y2; z2). 


где .
4. Нахождение угла между плоскостями путем составления уравнения каждой плоскости Ах+Ву+Сz+D=0 и определения угла между нормалями к плоскостям. Нормаль n при этом имеет координаты .
5.Нахождение расстояния от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно.
6. Координаты x, y, z точки М, которая делит отрезок 












2.2. Нахождение угла между скрещивающимися прямыми
- Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку.
- 0˚<(a,α)<90˚.
При нахождении угла между прямыми используют:
формулу или в координатной форме
для нахождения угла φ между прямыми m и l, если векторы и параллельны соотвественно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы или .
Пример 1.5 Сторона основания правильной четырехугольной призмы ABCDA1B1C1 D1 равна 2, высота — 4. Точка E — середина отрезка CD, точка F — середина отрезка AD. Найдите угол между прямыми CF и B1E.
х
у
z
B1
A1
C1
D1
B C
A E
F D
Решение.
Для начала сделаем чертёж и проанализируем задачу.
Прямые CF и B1E являются скрещивающимися, поэтому, чтобы найти угол между ними геометрическим способом, было бы необходимо параллельно перенести одну из прямых так, чтобы обе прямые лежали на одной плоскости. При этом было бы довольно сложно определить, в каком соотношении они будут пересекаться, и решить эту задачу поэтапно-вычислительным методом.
Я предлагаю поместить параллелепипед в прямоугольную систему координат, как показано на рисунке, и найти искомый угол как угол между векторами.
Выпишем координаты точек B1, E, C, F в этой системе координат:
B1 (0; 0; 4), E(1; 2; 0), C(0; 2; 0), F (2; 1; 0).
Тогда {2; -1; 0}, {1; 2; -4}. Найдём угол между этими векторами по формуле:
То есть искомый угол α=90˚.
Как видите, задачу, которую довольно-таки сложно решить геометрическим путём, можно быстро и красиво решить аналитически.
Ответ: 90˚.
Пример 2.2 Точка О лежит на ребре DD1 куба ABCDA1B1C1 D1, точка Р является точкой пересечения диагоналей грани ABCD. DO : DD1 = 1 : 5. Найдите косинус угла между прямой ОР и прямой, содержащей диагональ куба, выходящую из вершины С.

Поместим куб в прямоугольную систему координат, как показано на рисунке. Условно обозначим грани куба за единицу. Если обозначить её какой-либо буквой, она всё равно сократится. Определим координаты точек Р, О, С и А1:
О
Р
Р(0,5; 0,5; 0), О(1; 1; 0,5), С(0; 1; 0), А1(1; 0; 1).
Отсюда .
Ответ: .
Пример 3.5 Основанием пирамиды SABC является равносторонний треугольник ABC, сторона которого равна . Боковое ребро SC перпендикулярно плоскости основания и равно 1. Найдите угол между скрещивающимися прямыми, одна из которых проходит через точку S и и середину ребра DC, а другая проходит через точку C и середину ребра AB.

Поместим пирамиду в декартову систему координат. Найдём координаты точек S, L, C и M: S(0;0;1), L(0;;0), C(0;0;0). Чтобы найти координаты точки М, воспользуемся геометрией: в равностороннем треугольнике все углы равны 60˚, а т.М, которая делит сторону АВ пополам, является не только медианой, но и биссектрисой, поэтому .
Для равностороннего треугольника , х(СМ)=СМ·соs60˚=, у(СМ)=СМ·соs30˚=, {}, SL{0;;-1}
Решая аналогично предыдущим примерам, находим, что .
Ответ: 45˚.
2.3. Нахождение угла между прямой и плоскостью
- Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
- 0˚<(a,α)<90˚.
Угол между прямой l и плоскостью α можно вычислить:
по формуле или в координатах , где
— вектор нормали к плоскости α,
— направляющий векор прямой l;

Решение. Для решения этой задачи необходимо воспользоваться уравнением плоскости, имеющим общий вид
ах+bу+cz+d=0, где a, b и c – координаты нормали к плоскости.
Чтобы составить это уравнение, необходимо определить координаты трёх точек, лежащих в данной плоскости: А(1; 0; 0), В1(0;0;1), С(0;2;0).
Решая систему
находим коэффициенты а, b и с уравнения ах+bу+cz+d=0: а= -d, b=,
c=-d. Таким образом, уравнение примет вид или, после упрощения, 2х+у+2z-2=0. Значит нормаль n к этой плоскости имеет координаты .
Длину вектора легко найти геометрически: . Но его координаты нам всё равно необходимы. Из простых вычислений находим, что .
Найдем угол между вектором и нормалью к плоскости по формуле скалярного произведения векторов:
.
Ответ: 45˚
2.4. Нахождение угла между двумя плоскостями
- Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
- Величина двугранного угла принадлежит промежутку(0˚; 180˚)
- Величина угла между пересекающимися плоскостями принадлежит промежутку (0˚; 90˚].
- Угол между двумя параллельными плоскостями считается равным 0˚.
Угол между двумя пересекающимися плоскостями можно вычислить:
как угол между нормалями по формуле или в координатной форме , где — вектор нормали плоскости А1х+В1у+С1z+D1=0, — вектор нормали плоскости A2x+B2y+C2z+D2=0.

Решение.
Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0), D1(1;0;1), E(0;0,5;1), F(0,5;1;1).
1) Решая систему
, составляем уравнение плоскости (АD1E): x+2y-z=0.
2) плоскость CFD1:
отсюда находим уравнение 2x+y+z-3=0. Найдём искомый угол как угол между нормалями плоскостей.
, , откуда φ=60˚ Ответ: 60˚
2.5. Нахождение расстояния между двумя точками.
Расстояние между точками А и В можно вычислить:
по формуле ,
где A(x1; y1; z1), B(x2; y2; z2);
по формуле .
Пример 6.6 В основании пирамиды SABCD лежит ромб со стороной 2 и острым углом в 60˚. Боковое ребро SA перпендикулярно основанию пирамиды и равно 4. Найдите расстояние от середины Н ребра SD и серединой М ребра ВС.

Найдём координаты точки Н как координаты середины отрезка SD: S(0; 0; 4), D(0; 2; 0).
Чтобы найти координаты точек В и С, найдём координаты их проекций на оси. АВх=ACx=2·cos30˚=, ABy=ACу–2=2·cos60˚=1.
Отсюда В(; 1; 0), С(; 3;0). Тогда координаты точки М равняются:
.
Теперь находим расстояние между точками, заданными своими координатами:
Ответ: .
Пример 7.1 В единичном кубе АВСDA1В1С1D1 точки Е и К – середины ребер АА1 и СD соответственно, а точка М расположена на диагонали В1D1 так, что В1М = 2МD1. Найдите расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML=2LK
Решение. Введём декартову систему координат. E(1;0;0,5), K(0,5;1,0), В1(0;0;1), D1(1;1;1). Чтобы вычислить координаты т.М, воспользуемся формулой для нахождения координат точки, которая делит отрезок B1D1 в отношении λ=2:1:



Аналогично находим координаты точки L:
.
Координаты точки Q находим по формуле координат середины отрезка:



Ответ: .
2.6. Нахождение расстояния от точки до плоскости.
Расстояние от точки до плоскости , не содержащей эту точку , есть длина отрезка перпендикуляра , опущенного из этой точки на плоскость .
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
Расстояние от точки М до плоскости α
вычисляется по формуле , где М(х0;у0;z0), плоскость α задана уравнением ax+by+cz+d=0;
Пример 8.2 В кубе АВСDA1B1C1D1 проведена диагональ B1D. В каком отношении, считая от вершины B1, плоскость А1BC1 делит диагональ B1D?
Решение. Составим уравнение плоскости А1BC1 и найдём расстояние от этой плоскости до каждой из точек B1 и D. Пусть l – ребро куба.
В(0;0;0), А1(l;0;l), С1(0;l;l).
Решив систему определяем, что уравнение плоскости имеет вид: x+y–z=0 → а=1, b=1, c= –1. B1(0;0;1), D(1;1;0).
Теперь найдём расстояние от каждой точки до плоскости по формуле
:
Ответ: 2:1.
Пример 9.5 Основание прямой призмы АВСА1В1С1 – равнобедренный треугольник АВС, основание АС и высота ВD которого равны 4. Боковое ребро равно 2. Через середину К отрезка В1С проведена плоскость, перпендикулярная к этому отрезку. Найдите расстояние от вершины А до этой плоскости.

Теперь находим расстояние от т.А(0;-2;0) до плоскости:
. Ответ: .
Заключение
Представляю вашему вниманию свою работу, которой я занималась в течение последних месяцев: я искала формулы, подбирала для каждого случая именно те задачи, геометрическое решение которых перегружено формулами, редко используемыми теоремами, сложными преобразованиями и вычислениями.
Конечно, эту работу нельзя считать авторитетным пособием по решению задания 13 ЕГЭ, так как в ней рассмотрено лишь небольшое количество задач, и ограниченное количество приёмов.
Конечно, я не настаиваю на том, что все задачи стереометрии надо решать методом координат, иногда это просто нецелесообразно. Но согласитесь, настолько простое и изящное решение не только освободит время для решения других заданий, но и будет высоко оцениваться проверяющим учителем.
Список использованной литературы
1. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010: Математика /авт.-сост . И.Р.Высоцкий, Д.Д.Гущин, П.И.Захаров и др.; под ред. А.Л.Семенова, И.В.Ященко. – М.: АСТ: Астрель , 2009. – (ФИПИ).
2. Математика. Подготовка к ЕГЭ-2011: учебно-методическое пособие/ под ред. Ф.Ф.Лысенко, С.Ю.Калабухова. – Ростов-на-Дону: Легион – М., 2010.
3. Единый государственный экзамен 2010. Математика. Универсальные материалы для подготовки учащихся / ФИПИ – М.: Интеллект -Центр, 2010.
4. Большая универсальная школьная энциклопедия/ гл. редактор М.Аксёнова – М.: Мир энциклопедий Аванта+, Астрель, 2008.
5. www.fmclass.ru – образовательный портал «Физ/мат класс»
6. www.mathege.ru – открытый банк заданий.
7. www.problems.ru – каталог задач.
ЕГЭ Профиль №13. Тригонометрические уравнения
Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.
13 задания профильного ЕГЭ по математике представляет собой уравнение с отбором корней принадлежащих заданному промежутку. Одним из видов уравнений которое может оказаться в 13 задание является тригонометрическое уравнение. Как правило, это достаточно простое тригонометрическое уравнение для решения которого потребуется знания основных тригонометрических формул, и умение решать простейшие тригонометрические уравнения. Отбор корней тригонометрического уравнения принадлежащих заданному промежутку можно производить одним из четырех способов: методом перебора, с помощью тригонометрической окружности, с помощью двойного неравенства и графическим способом. В данном разделе представлены тригонометрические уравнения (всего 226) разбитые на три уровня сложности. Уровень А — это простейшие тригонометрические уравнения, которые являются подготовительными для решения реальных тригонометрических уравнений предлагаемых на экзамене. Уровень В — состоит из уравнений, которые предлагали на реальных ЕГЭ и диагностических работах прошлых лет. Уровень С — задачи повышенной сложности.
Задание №13 (С1) ЕГЭ профильного уровня по математике – это тригонометрическое, логарифмическое, иррациональное или показательное уравнение. Каждое задание состоит из пунктов а и б. При отсутствии в решении уравнения ответа на вопрос пункта а задание С1 оценивается 0 баллов.
Пункт а предполагает решение предложенного уравнения.
Пункт б предполагает отбор корней любым доступным ученику способом: отбор на тригонометрическом круге, аналитическим методом (подбор значений n), решением двойного неравенства, построением графика
Общие правила заполнения бланков ЕГЭ
Таблица математических символов и обозначений
Критерии оценивания
Задание С1
Оформление решения задания С1
Задание С1 – это тригонометрическое, логарифмическое, иррациональное или показательное уравнение. Каждое задание состоит из пунктов а и б. При отсутствии в решении уравнения ответа на вопрос пункта а задание С1 оценивается 0 баллов.
Основные ошибки при выполнении задания С1 допускаются при нахождении корней простейших тригонометрических уравнений, применении формул, определении знака, отборе корней. Зачастую ошибки связаны с невнимательностью учеников. Многих из них можно избежать, если следовать правилам оформления задания:
- Писать аккуратно, разборчивым почерком;
- Записывать исходное уравнение, предложенное для решения;
- Записывать область допустимых значений;
- Делать проверку корней в иррациональном уравнении;
- Соблюдать последовательность решения;
- Использовать знак равенства при решении уравнения только один раз в каждой строчке;
- Грамотно использовать математические символы;
- Не пренебрегать записью формул перед их использованием;
- Выделять нужную дугу заданного промежутка при отборе корней тригонометрического уравнения с использованием числовой окружности;
- Указывать точки при отборе корней на числовой окружности в тригонометрическом уравнении;
- Записывать ответ.
Логарифмические уравнения
Иррационнальные уравнения
Тригонометрические уравнения
Показательное уравнение
Задания для самопроверки

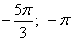


.png)