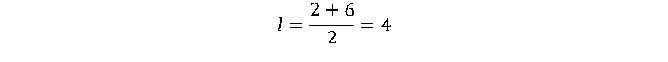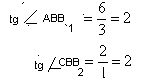- ЕГЭ по математике профиль
Задание №3 ЕГЭ-2021 (профильный уровень). Простейшая геометрия (задачи на клетчатой бумаге или координатной плоскости). Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы:
— формулы площадей фигур: треугольника, параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга;
— формулы длины окружности, длины дуги и площади сектора;
— формулы средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения.
К данному конспекту смотрите приложения, содержащие все необходимые формулы для решения задания 3 ЕГЭ по математике профильного уровня и о том, как быстро выучить формулы.
→ скачать конспект
Автор: Алькаева Л. Р.
Практический материал:
→ задание 3 из банка ФИПИ
→ задание 3 — окружность и круг
→ задание 3 — вычисление площади
→ задание 3 — вычисление площади на координатной плоскости
→ задание 3 — вычисления углов и длин
Связанные страницы:
Задание 3. Теория вероятностей на ЕГЭ по математике.
Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…
Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.
Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?
Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.
Орел и решка — два возможных исхода испытания.
Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна .
Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.
Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.
Вероятность выпадения тройки равна (один благоприятный исход из шести возможных).
Вероятность четверки — тоже .
А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность не может быть больше единицы.
Вот другой пример. В пакете яблок, из них
— красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна
, а зеленое —
.
Вероятность достать красное или зеленое яблоко равна .
БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ
Определение вероятности. Простые задачи из вариантов ЕГЭ.
Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.
В фирме такси в данный момент свободно
машин:
красных,
желтых и
зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.
Всего имеется машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна
, то есть
.
В сборнике билетов по биологии всего
билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Очевидно, вероятность вытащить билет без вопроса о грибах равна , то есть
.
Родительский комитет закупил
пазлов для подарков детям на окончание учебного года, из них
с картинами известных художников и
с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.
Задача решается аналогично.
Ответ: .
В чемпионате по гимнастике участвуют
спортсменок:
— из России,
— из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.
Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен (поскольку из Китая —
спортсменок). Ответ:
.
Ученика попросили назвать число от
до
. Какова вероятность того, что он назовет число кратное пяти?
Каждое пятое число из данного множества делится на . Значит, вероятность равна
.
Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.
— нечетные числа;
— четные. Вероятность нечетного числа очков равна
.
Ответ: .
Монета брошена три раза. Какова вероятность двух «орлов» и одной «решки»?
Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.
Как вы думаете, сколько здесь возможных исходов?
Бросаем монету. У этого действия два возможных исхода: орел и решка.
Две монеты — уже четыре исхода:
| орел | орел |
| орел | решка |
| решка | орел |
| решка | решка |
Три монеты? Правильно, исходов, так как
.
Вот они:
| орел | орел | орел |
| орел | орел | решка |
| орел | решка | орел |
| решка | орел | орел |
| орел | решка | решка |
| решка | орел | решка |
| решка | решка | орел |
| решка | решка | решка |
Два орла и одна решка выпадают в трех случаях из восьми.
Ответ: .
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет
очков. Результат округлите до сотых.
Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.
Получаем, что у данного действия — бросания двух игральных костей — всего возможных исходов, так как
.
А теперь — благоприятные исходы:
Вероятность выпадения восьми очков равна .
Стрелок попадает в цель с вероятностью
. Найдите вероятность того, что он попадёт в цель четыре выстрела подряд.
Если вероятность попадания равна — следовательно, вероятность промаха
. Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна
. А вероятность четырех попаданий подряд равна
.
Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей
ПОДРОБНЕЕ
Вероятность: логика перебора.
В кармане у Пети было
монеты по
рублей и
монеты по
рублей. Петя не глядя переложил какие-то
монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?
Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами
— а затем посчитать, сколькими способами можно выбрать три элемента из набора
.
Однако есть более простое решение:
Кодируем монеты числами: ,
(это пятирублёвые),
(это десятирублёвые). Условие задачи можно теперь сформулировать так:
Есть шесть фишек с номерами от до
. Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами
и
не оказались вместе?
Давайте запишем, что у нас в первом кармане.
Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях
и
— это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:
…
А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — , а затем:
.
Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:
.
Всего возможных исходов.
У нас есть условие — фишки с номерами и
не должны оказаться вместе. Это значит, например, что комбинация
нам не подходит — она означает, что фишки
и
обе оказались не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только
, либо только
. Вот они:
134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего благоприятных исходов.
Тогда искомая вероятность равна .
Ответ: .
Сумма событий, произведение событий и их комбинации
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.
– вероятность того, что он сломается на второй год,
– вероятность того, что он прослужит больше двух лет.
Очевидно,
Тогда
Ответ: 0,06.
События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.
Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.
В нашей задаче события «чайник сломался на второй год работы» и «чайник работает больше двух лет» — несовместные. Чайник или сломался, или остается в рабочем состоянии.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.
Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.
Он может либо выйти в выход D, и вероятность этого события равна Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью
На каждой развилке вероятность свернуть в ту или другую сторону равна
а поскольку развилок пять, вероятность выбраться через выход А равна
то есть 0,03125.
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.
Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.
(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?
Вероятность для первого грузовика благополучно одолеть горку Для второго
Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.
Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.
Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна
.
Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.
Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.
Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей:
Вероятность того, что яйцо из второго хозяйства и высшей категории, равна
Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.
Мы получили уравнение:
Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).
Пациенту делают анализ. Покажем на схеме все возможные исходы:
Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.
Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.
Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна ), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна
). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна
Ответ: 0,0545.
Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознание или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна
Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна
В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.
Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.
Еще задачи ЕГЭ по теме «Теория вероятностей».
Смотрите также: парадокс Монти Холла.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 3. Теория вероятностей на ЕГЭ по математике.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
-
Главная
-
Теория ЕГЭ
-
Математика — теория ЕГЭ
-
Задание 3 ЕГЭ 2021 по математике, теория
- 08.10.2018
Необходимая теория для успешного освоения и решения заданий №3 по математике профильного уровня на ЕГЭ в 2021 году.
Представлена вся теория и алгоритм решения различных заданий такого типа.
- Тренировочные кимы ЕГЭ по математике
- Практика — примеры для решения каждого типа заданий
Обсудить решение конкретных заданий вы можете в комментариях ниже.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 3
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 3 рассчитано на умение использовать геометрические понятия и теоремы для решения практических задач, связанных с нахождением геометрических величин (длин, углов, площадей).
Задание состоит из текстовой задачи и рисунка. Необходимо внимательно прочитать текст, решить задачу и записать результат в поле ответа в тексте работы и бланк ответов. Если в итоге получилась обыкновенная дробь, её нужно перевести в десятичную.
Чтобы успешно справиться с данным заданием, нужно повторить определения и свойства плоских фигур:
- треугольники:
- четырёхугольники, в частности параллелограмм, прямоугольник, ромб, квадрат, трапеция;
- многоугольники, в частности правильные многоугольники;
- окружность и круг, описанные и вписанные в многоугольник окружности;
- площади треугольника, параллелограмма, трапеции, круга, сектора.
План выполнения:
- Внимательно прочитайте задачу.
- При необходимости выполните на чертеже дополнительные построения.
- Выполните арифметические вычисления.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Задачи на Прямоугольные треугольники
При подготовке следует повторить значение синуса, косинуса и тангенса основных углов; отношения между сторонами прямоугольника; теорему Пифагора.
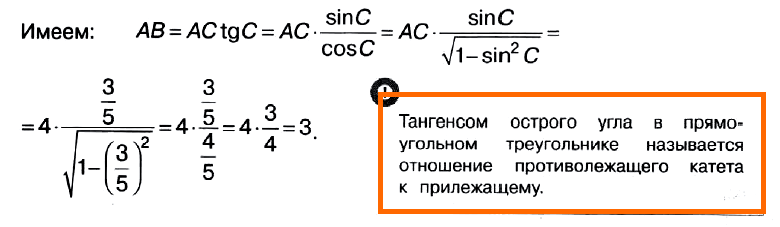
Задача № 3 (1). В треугольнике АВС угол А равен 90°, АС = 4, sin C = 3/5. Найдите АВ.
Решение:
Ответ: 3.
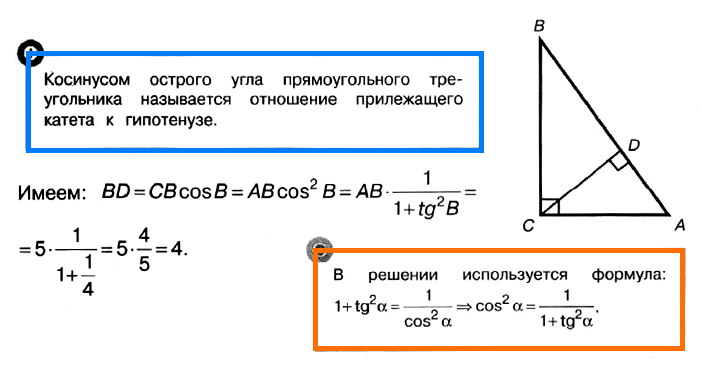
Задача № 3 (2). В треугольнике АВС угол С равен 90°, CD – высота, АВ = 5, tg B = 1/2. Найдите BD.
Решение:
Ответ: 4.
Задачи на Равнобедренные треугольники
Задача № 3 (3). В треугольнике АВС АС = ВС = 10, sin А = 3/5. Найдите АВ.
Решение:
Ответ: 16.
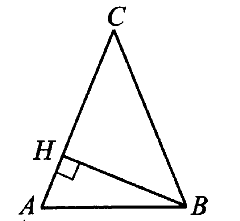
Задача № 3 (4). В треугольнике АВС АС = ВС = 25, sin BAC = 3/5. Найдите высоту АН.
Решение:
Ответ: 24.
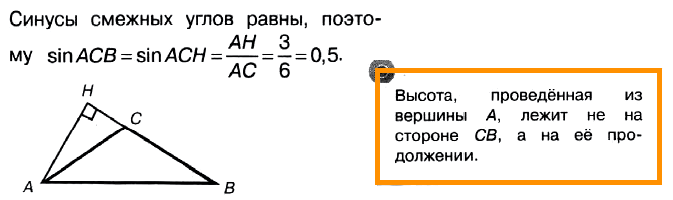
Задача № 3 (5). В тупоугольном треугольнике АВС АС = ВС = 6, высота АН = 3. Найдите sin АСВ.
Решение:
Ответ: 0,5.
Задачи на Разносторонние треугольники
Задача № 3 (6). Площадь треугольника АВС равна 8. DE — средняя линия CDE.
Решение:
Ответ: 2.
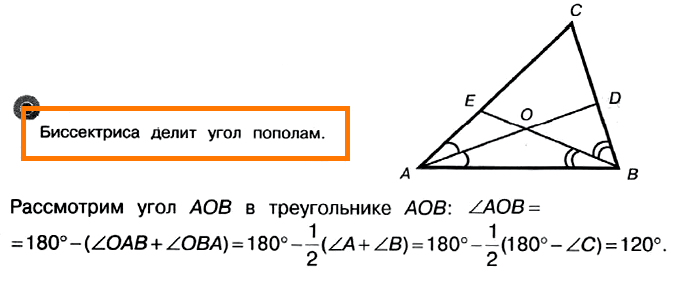
Задача № 3 (7). В треугольнике АВС угол С равен 60°, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.
Решение:
Ответ: 120.
Задачи на Параллелограммы
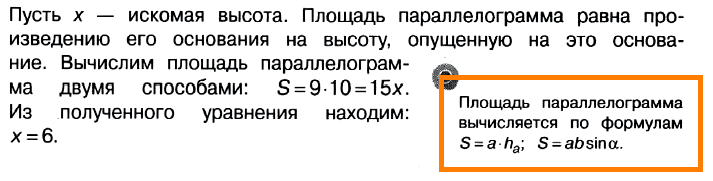
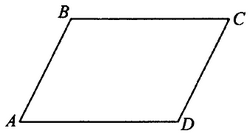
Задача № 3 (8). Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
Решение:
Ответ: 6.
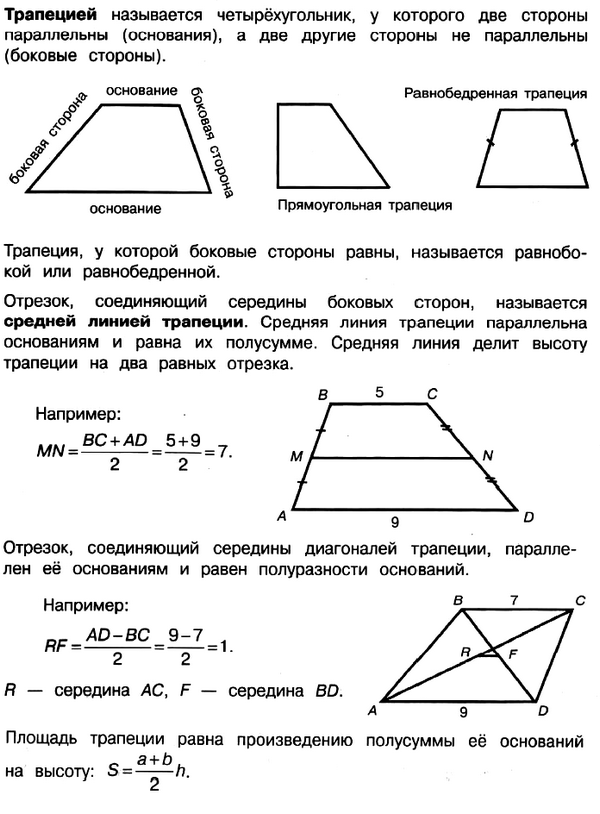
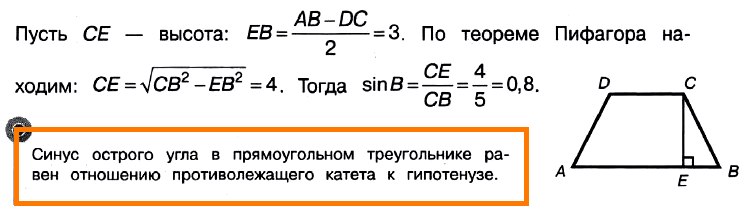
Задачи на Трапецию
Задача № 3 (9).
Решение:
Ответ: 0,8.
Задачи на Центральные и вписанные углы
При подготовке нужно повторить свойства центральных и вписанных углов, понятия хорды, касательной и секущей к окружности; знать правила нахождения величин центральных и вписанных углов, дуг окружностей.
Задача № 3 (10). Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 158° и 38°. Ответ дайте в градусах.
Решение:
Ответ: 60.
Задачи на Вписанные и описанные окружности
Задача № 3 (11). В четырёхугольник ABCD вписана окружность, АВ = 4, CD = 6. Найдите периметр четырёхугольника ABCD.
Решение:
Ответ: 20.
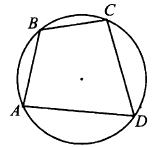
Задача № 3 (12).
Решение:
Ответ: 1.
Тренировочные задания с самопроверкой
№ 3.1. Стороны АВ, ВС, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129° (см. рис.). Найдите угол BCD. Ответ дайте в градусах.
Открыть ОТВЕТ
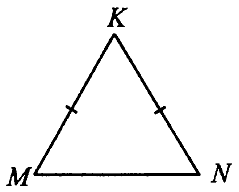
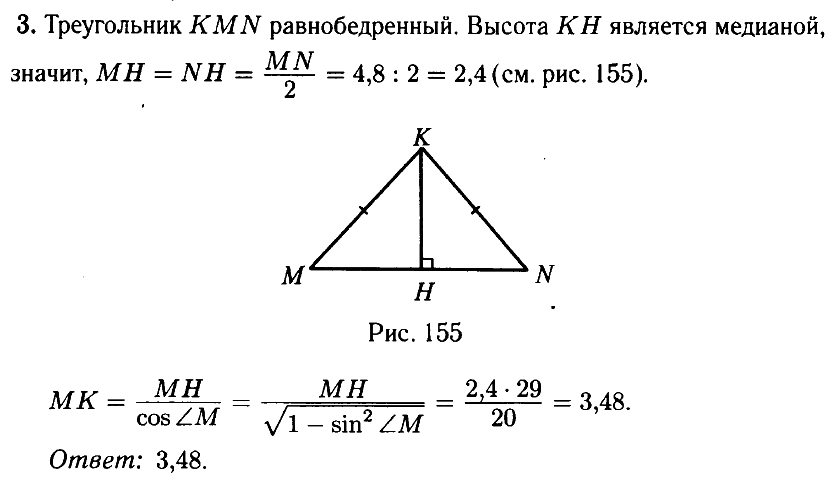
№ 3.2. В треугольнике MNK известно, что МК = NK, MN = 4,8, sin М = 21/29 (см. рис.). Найдите МК.
Открыть ОТВЕТ
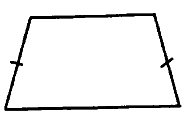
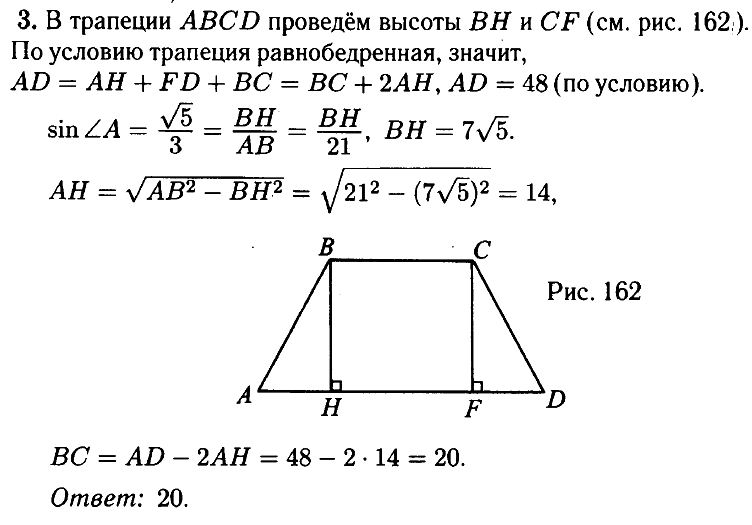
№ 3.3. Большее основание равнобедренной трапеции равно 48. Боковая сторона равна 21. Синус острого угла равен √5/3 (см. рис.). Найдите меньшее основание.
Открыть ОТВЕТ
№ 3.4. В треугольнике АВС известно, что АС = ВС, высота ВН равна 9, АВ = 3√13 (см. рис.). Найдите tg АВС.
Открыть ОТВЕТ
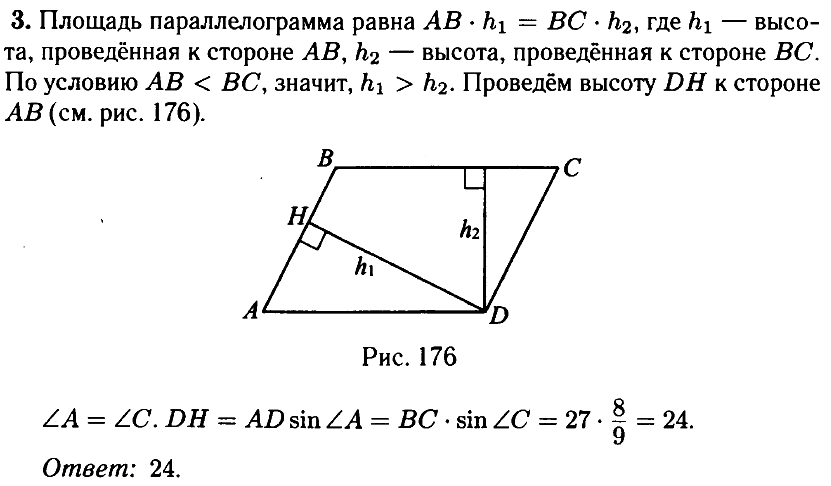
№ 3.5. В параллелограмме ABCD известно, что АВ = 18, ВС = 27, sin ∠C = 8/9 (см. рис.). Найдите большую высоту параллелограмма.
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
18 632
Квадратная решетка и координатная плоскость
В задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках – вычислять параметры фигур – стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов.
Разбор типовых вариантов заданий №3 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=”#defae6″]
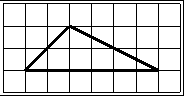
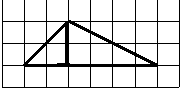
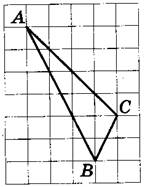
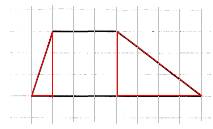
На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь.
[/su_note]
Алгоритм решения:
- Подсчитываем длину основания и высоты.
- Записываем формулу вычисления площади.
- Вычисляем площадь.
- Записываем ответ.
Решение:
1. Подсчитываем длины основания и высоты:
основание = 6,
высота = 2.
2. Записываем формулу площади треугольника: S= ah|2.
3. Вычисляем площадь: S= 6∙2/2=6
Ответ: 6.
Второй вариант задания (из Ященко, №1)
[su_note note_color=”#defae6″]
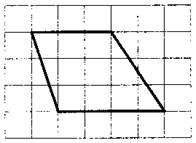
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
[/su_note]
Алгоритм решения:
- Подсчитываем длину каждого основания и высоты трапеции.
- Записываем формулу длины средней линии трапеции.
- Вычисляем среднюю линию.
- Записываем ответ.
Решение:
1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4.
2. Длина средней линии трапеции находится по формуле
, где a и b – длина верхнего и нижнего оснований трапеции.
3. Имеем:
.
4. Значит, средняя линия равна 3,5.
Ответ: 3,5.
Третий вариант задания (из Ященко, №2)
[su_note note_color=”#defae6″]
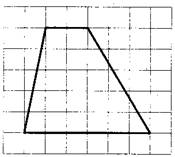
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
[/su_note]
Алгоритм решения:
- Подсчитываем длину каждого основания и высоты трапеции.
- Записываем формулу длины средней линии трапеции.
- Вычисляем среднюю линию.
- Записываем ответ.
Решение:
1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6.
2. Длина средней линии трапеции находится по формуле
, где a и b – длина верхнего и нижнего оснований трапеции.
3. Имеем:
4. Значит, средняя линия равна 4.
Ответ: 4.
Четвертый вариант задания (из Ященко, №4)
[su_note note_color=”#defae6″]
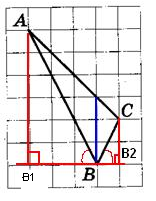
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.
[/su_note]
Алгоритм решения:
- Проведем перпендикуряры из вершин Аи С.
- Построим биссектрису угла В.
- Покажем, что биссектриса параллельна высотам.
- Измерим длину биссектрисы.
- Запишем ответ.
Решение:
1. Проведем из вершин А и С отрезки АВ1 иСВ2, перпендикулярные прямой, содержащей вершину В на рисунке.
2. Построим биссектрису угла B.
3. Рассмотрим треугольники АВВ1 иВВ2С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках
Это означает, что углы АВB1 и СВB2 равны, так как равны тангенсы этих углов.
Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3.
Ответ: 3.
Пятый вариант задания (из Ященко, №7)
[su_note note_color=”#defae6″]
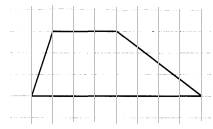
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
[/su_note]
Алгоритм решения:
- Рассмотрим рисунок и измерим основания.
- Проведем высоту.
- Запишем формулу площади трапеции.
- Вычислим площадь по формуле.
Решение:
1. На рисунке основания равны 3 и 8.
2. Опустим высоту. Она рана 3.
3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота.
4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5
Следовательно, площадь данной трапеции равна 16,5.
Ответ: 16,5.
Даниил Романович | Просмотров: 12.1k
На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.
Содержание
Формулы для ЕГЭ по профильной математике. Алгебра
Формулы сокращенного умножения
Квадрат суммы: (a + b)² = a² + 2ab + b²
Квадрат разности: (a – b)² = a² – 2ab + b²
Разность квадратов: a² – b² = (a + b)(a – b)
Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)
Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)
Прогрессия
Арифметическая
Геометрическая
Таблица степеней
Свойства степеней
Таблица квадратов
Интенсивы по подготовке к региональному этапу ВсОШ
Все, что нужно знать
для победы, за 7 дней!
Свойства корней
Тригонометрия
Таблица значений тригонометрических функций
Тригонометрическая окружность
Тригонометрические формулы
Обратные тригонометрические функции
Преобразование суммы и разности в произведение
Регулярные курсы по подготовке к олимпиадам и ЕГЭ
Поступаем в вуз мечты без проблем!
Вероятность
Вероятность события А: m – благоприятные, n – общее число событий
P(A) = m/n
События А и В происходят одновременно: A · B
Независимые события: P(A · B) = P(A) · P(B)
Зависимые события: P(A · B) = P(A) · P(B | A)
Происходит или А, или В: A + B
Несовместные события: P(A + B) = P(A) + P(B)
Совместные события: P(A + B) = P(A) + P(B) – P(A · B)
Свойства модуля
Производные
Основные правила дифференцирования
Таблица производных
Первообразные
Логарифмы
Квадратные уравнения
Дискриминант
Теорема Виета
Разложение на множители
Формулы для ЕГЭ по профильной математике. Геометрия
Планиметрия
Треугольник
Следствие из теоремы косинусов:
Длина биссектрисы (через угол):
Длина биссектрисы (через отрезки):
Прямоугольный треугольник
24 декабря – 20 января
5-11 классы
Онлайн-олимпиада Коалиции
Равносторонний треугольник
Аргументы для итогового сочинения
Подборка лучших аргументов
Равносторонний шестиугольник
Площадь внутреннего треугольника:
Площадь внутреннего прямоугольника:
Ромб
Трапеция
Произвольный четырёхугольник
Окружность
Стереометрия
Выводы
Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.
А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.
Поделиться в социальных сетях
Какими формулами вам приходится пользоваться чаще всего?
Межтекстовые Отзывы
Посмотреть все комментарии
Читайте также
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 95%
Ответом к заданию 3 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Перед началом первого тура чемпионата по спортивным нардам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует $56$ игроков, среди которых $12$ спортсменов из России, в том числе Евгений Победкин. Найдите вероятность того, что в первом туре Евгений Победкин будет играть с каким-либо игроком из России.
Решение
Будем считать случайным экспериментом выбор соперника Евгения Победкина. Этот эксперимент имеет $56-1 = 55$ равновозможных исходов (сам с собой он играть не может!). При этом $12 — 1 = 11$ исходов благо приятствуют событию «Евгений Победкин будет играть со спортсменом из России» (так как есть $11$ спортсменов из России, не считая самого Евгения Победкина). По определению искомая вероятность равна ${11}/{55} = 0.2$.
Ответ: 0.2
Задача 2
Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует $76$ спортсменов, среди которых $46$ спортсменов из России, в том числе Григорий Соколенко. Найдите вероятность того, что в первом туре Григорий Соколенко будет играть с каким-либо теннисистом из России.
Решение
Будем считать случайным экспериментом выбор соперника Григория Соколенко. Этот эксперимент имеет $76-1=75$ равновозможных исходов (сам с собой он играть не может!). При этом $46-1=45$ исходов благоприятствуют событию «Григорий Соколенко будет играть со спортсменом из России» (так как есть $45$ спортсменов из России, не считая самого Григория Соколенко). По определению, искомая вероятность равна ${45} / {75}=0{,}6$.
Ответ: 0.6
Задача 3
Вероятность того, что новая электрическая кофемашина прослужит больше года, равна $0{,}92$. Вероятность того, что она прослужит больше двух лет, равна $0{,}85$. Найдите вероятность того, что она прослужит меньше двух лет, но больше года.
Решение
Заметим, что из событий «кофемашина прослужит меньше года», «кофемашина прослужит от 1 до 2 лет» и «кофемашина прослужит больше двух лет» произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение — достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.
При этом события «кофемашина прослужит меньше года» и «кофемашина прослужит больше года» противоположны, поэтому вероятность события «кофемашина прослужит меньше года» равна 1 — 0.92 = 0.08. Заполним таблицу.
| Событие | Прослужит меньше года | Прослужит от 1 до 2 лет | Прослужит больше двух лет |
| Вероятность | 0.08 | ? | 0.85 |
Отсюда искомая вероятность равна 1 — 0.08 — 0.85 = 0.07.
Ответ: 0.07
Задача 4
В некотором городе из $5000$ появившихся на свет младенцев $2075$ мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до сотых.
Решение
Из каждых $5000$ появившихся на свет младенцев девочек $5000 — 2075 = 2925$. По определению искомая частота равна ${2925}/{5000} = 0.585 ≈ 0.59$.
Ответ: 0.59
Задача 5
На экзамене по физике студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Элект-
ричество», равна $0{,}3$. Вероятность того, что это вопрос по теме «Механика», равна $0{,}42$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.
Решение
Из условия следует, что события A = «достанется вопрос по теме Электричество» и B = «достанется вопрос по теме Механика» несовместны. Действительно, нет билетов, относящихся к обоим этим темам одновременно. Событие «достанется вопрос по одной из этих двух тем» — это объединение событий A и B (A $∪$ B). По формуле вероятности объединения несовместных событий получим, что искомая вероятность равна P(A $∪$ B) = P(A) + P(B) = 0.3 + 0.42 = 0.72.
Ответ: 0.72
Задача 6
При производстве в среднем на каждые $468$ исправных телефонов приходится $32$ неисправных. Найдите вероятность того, что случайно выбранный телефон окажется неисправным.
Решение
Из условия следует, что в среднем из каждых $468 + 32 = 500$ телефонов $32$ неисправных. По определению искомая вероятность равна ${32}/{500} = 0.064$.
Ответ: 0.064
Задача 7
Завод выпускает съёмные жёсткие диски. В среднем $15$ дисков из $300$ имеют скрытые дефекты. Найдите вероятность того, что купленный диск окажется без дефектов.
Решение
По определению вероятность покупки диска с дефектом равна ${15}/{300} = 0.05$. Тогда по формуле вероятности противоположного события вероятность купить диск без дефекта равна $1 — 0.05 = 0.95$.
Ответ: 0.95
Задача 8
Фабрика выпускает туфли. В среднем $12$ пар туфель из $200$ пар имеют скрытые дефекты. Найдите вероятность того, что купленная пара туфель окажется без дефектов.
Решение
Из условия следует, что в среднем из каждых $200$ пар $200 — 12 = 188$ не имеют дефектов. Тогда искомая вероятность равна ${188}/{200} = 0.94$.
Ответ: 0.94
Задача 9
В чемпионате мира участвуют $16$ команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: $1$, $1$, $1$, $1$, $2$, $2$, $2$, $2$, $3$, $3$, $3$, $3$, $4$, $4$, $4$, $4$. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда «Плутон», участвующая в чемпионате, окажется во второй группе?
Решение
Будем считать, что случайный эксперимент заключается в том, что капитан команды «Плутон» тянет карточку с номером группы. У этого эксперимента $16$ равновозможных исходов (по числу карточек). Событию «Команда „ Плутон“ окажется во второй группе» благоприятствуют $4$ исхода (количество карточек с номером $2$). По определению вероятности искомая вероятность равна ${4} / {16}=0{,}25$.
Ответ: 0.25
Задача 10
На конференцию приехали $7$ учёных из Китая, $5$ — из России и $8$ — из Египта. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад учёного из России.
Решение
Будем считать, что случайный эксперимент заключается в том, что выбирается учёный, который будет выступать восьмым. Всего существует $20$ равновозможных исходов ($7+5+8=20$ учёных, все имеют равные шансы выступить восьмыми). Событию «Восьмым будет выступать учёный из России» благоприятствуют $5$ исходов. По определению искомая вероятность равна ${5}/{20} = {1}/{4} = 0.25$.
Ответ: 0.25
Задача 11
В чемпионате по спортивной гимнастике участвуют $40$ спортсменов: $16$ — из России, $9$ — из Франции, остальные — из Беларуси. Порядок, в котором выступают гимнасты, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Беларуси.
Решение
Из Беларуси $40-16-9 = 15$ спортсменов. Будем считать, что случайный эксперимент заключается в том, что выбирается спортсмен, который будет выступать первым. Всего существует $40$ равновозможных исходов ($40$ спортсменов, все имеют равные шансы выступить первыми). Событию Первым будет выступать спортсмен из Беларуси благоприятствуют $15$ исходов. По определению искомая вероятность равна ${15}/{40} = {3}/{8} = 0.375$.
Ответ: 0.375
Задача 12
В кармане у Валерия было пять конфет — «Птичье молоко», «Ромашка», «Черноморочка», «Мишка косолапый» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Валерий случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Ромашка».
Решение
Валерий мог с одинаковой вероятностью выронить каждую из пяти конфет, значит, искомая вероятность равна ${1}/{5} = 0.2$.
Ответ: 0.2
Задача 13
Света, Марина, Оля и Ксюша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет Света.
Решение
Жребий имеет $4$ равновозможных исхода (все девочки имеют равные шансы начинать игру). Значит, вероятность события «Игру будет начинать Света» равна ${1} / {4}=0{,}25$.
Ответ: 0.25