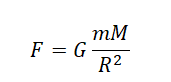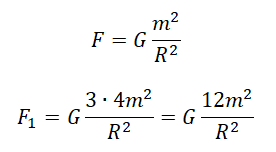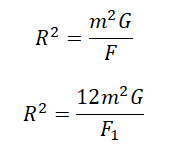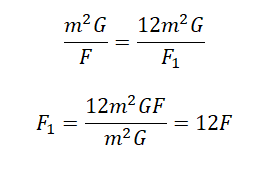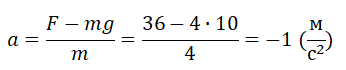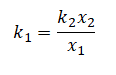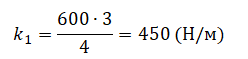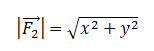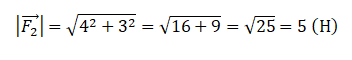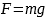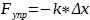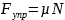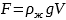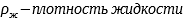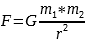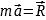Формулы для второго задания егэ по физике

2 задание в ЕГЭ по физике связано с основными силами в природе: трением, тяжестью и упругостью, законами Ньютона и законом всемирного тяготения. Теории по этим темам несложные, а вот решение задач часто вызывает у школьников затруднения. Дело в том, что нужно не просто знать формулы, но и уметь правильно их применять, понимать особенности разных физических процессов. Всему этому учат на курсах подготовки к ЕГЭ. Там вам расскажут, как решать 2 задание из ЕГЭ по физике. А если вы хотите понять основы этой темы, читайте нашу статью.

Первый закон Ньютона

Первый закон Ньютона существует только в инерциальных системах отсчета. Это такие системы, в которых материальная точка без воздействия внешних сил не двигается, либо двигается равномерно и прямолинейно. На самом деле, настоящие инерциальные системы невозможны. Для существования системы нужна связь с каким-то объектом, например, полом. Но любые объекты во Вселенной движутся с определенным ускорением, поэтому деление систем на инерциальные и неинерциальные носит условный характер. Эта информация не нужна для 2 задания по физике, но ее нужно понимать. 

Сам первый закон Ньютона (закон инерции) звучит так: «До тех пор, пока к телу не приложится сила извне, оно находится в покое или движется равномерно и прямолинейно». Это один из трех основных законов механики. Он не определяется формулами, поэтому не используется в задачах 2 задания физики. Но, он дает понимание того, что в механике изучаются только инерциальные системы отсчета. 

Принцип относительности Галилея

Галилей занимался изучением разных инерциальных систем. В частности, он создал так называемые преобразования Галилея, которые показывают, как меняются координаты при переходе из одной системы отсчета в другую. При этом основные уравнения, объясняющие законы механики, не изменяются. Принцип относительности выглядит так: «Законы механики одинаковы для всех инерциальных систем отсчета». Сами преобразования довольно сложны, они не нужны для решения 2 задания из ЕГЭ по физике, поэтому здесь мы их приводить не будем. Галилей доказал, что невозможно изучать движение одной системы координат относительно другой. Мы не можем понять, как двигается поезд, находясь внутри него. Для нас он неподвижен, а для людей, стоящих на перроне, быстро проезжает мимо. Нужно понимать и то, что тождественно не само движение, а лишь его законы. Если мы встанем у окна движущегося поезда и подкинем камень, относительно поезда его траектория будет вертикальной. Люди, заглянувшие к нам в окно, увидят параболу. 

Взаимодействие

Тела и частицы постоянно сталкиваются и действуют друг на друга. Это приводит к изменению траектории движения. Это явление физики называют взаимодействием. Оно осуществляется через поля (электромагнитное, гравитационное), действующие на все объекты во Вселенной. Существуют фундаментальные взаимодействия. Они являются основой всех процессов, их нельзя свести к еще более простым явлениям. Некоторые ученые предполагают, что фундаментальные взаимодействия — лишь частный случай одного объединенного. Для решения 2 задания по физике нужно знать, что из себя представляют эти взаимодействия: 

• гравитационное. Распространяется на все объекты во Вселенной, от мельчайших частиц до огромных планет. Радиус действия бесконечен, а относительную интенсивность принимают за единицу. Но, для небольших объектов эти взаимодействия столь незначительны, что ими принято пренебрегать. Они приобретает значение при изучении небесных объектов;
• слабое. Присуще всем частицам кроме фотона. Благодаря этому взаимодействию проходят почти все ядерные реакции. Радиус равен 10^-17 (поэтому не ощущается человеком и влияет лишь на мельчайшие частицы), а относительная интенсивность — 10³²; 
• электромагнитное. Связывает электроны с ядром, объединяет атомы в молекулы, а молекулы в вещества. Это взаимодействие объясняет многие механические процессы. У него бесконечный радиус действия, но оно почти не оказывает влияния на макрообъекты, так как они нейтральны. Относительная интенсивность — 10³⁶;
• сильное. Действует только на адроны, обеспечивает нахождение нуклонов в ядре. Радиус действия — 10^-15, а относительная интенсивность равна 10³⁸. 

Сила

Следующая часть теории ко 2 заданию по физике связана с понятием силы. Это величина, которая показывает, как тела влияют друг на друга. Силы в механике обусловлены только теми взаимодействиями, у которых есть неограниченный радиус действия. Сильные и слабые существуют при таких малых масштабах, что законы Ньютона к ним неприменимы. В рамках механики считается, что возникновение силы приводит к изменению скорости. Она может действовать напрямую или посредством образования полей. Кроме того, она придает объекту ускорение. Величина обозначается как F и измеряется в Ньютонах (Н). При решении задач нужно указывать точку приложения.

Принцип суперпозиции

В реальном мире тела подвержены воздействию нескольких сил одновременно. В таком случае гораздо удобнее пользоваться суммарной силой. Она равна векторной сумме всех сил, действующих на предмет или частицу. В этом и заключается принцип суперпозиции тел. Не забывайте, что при расчете нужно пользоваться правилами векторного сложения. Запомните это правило, оно пригодится при решении 2 задания по физике.

Второй закон Ньютона

Второй закон Ньютона называют также законом ускорения. Он позволяет связать силу, ускорение и массу тела. Закон также представляет собой важнейшую формулу для 2 задания ЕГЭ по физике: a = F / m. Получается, что ускорение растет с увеличением приложенной к телу силы. Увеличение массы, наоборот, уменьшает ускорение. 

Третий закон Ньютона

Объектом исследования первых двух законов Ньютона является одно тело, на которое действует бесконечное количество других. В третьем анализируется система, состоящая из двух тел, действующих друг на друга. Ньютон доказал, что сила этих взаимодействий равна, потому что иначе система потеряла бы устойчивость. Закон сформулирован так: «У каждой силы есть противодействующая, они равны и противоположны по направлению». Но нужно понимать, что силы при этом не могут уравновесить друг друга, так как относятся к разным телам. В математическом виде это записывается так: F₁ = -F₂. Для решения 2 задания по физике может пригодиться и другая форма записи: a₁ / a₂ = m₁ / m₂. 

Упругость

Упругость — свойство, которое позволяет телам деформироваться (менять форму и размер), а потом возвращаться в первоначальное состояние. Деформации при этом могут быть любыми, упругость есть и у твердых тел, и у жидкостей, и у газов. Деформированное тело стремится вернуть свою привычную форму и размер, при этом возникает сила упругости. Она часто встречается во 2 задании. 

Закон Гука

Закон Гука тоже связан с упругостью. Для решения задач нужно знать его математическое отражение, оно является еще одной формулой для 2 задания ЕГЭ по физике: F_упр = -kx. x означает удлинение тела (в случае с пружиной), а минус показывает, что удлинение направлено против силы упругости. k — это коэффициент пропорциональности или жесткость. Она своя для каждого тела. Чем выше ее значение, тем сложнее деформировать объект. Еще один важный момент: закон Гука можно использовать, только если деформации незначительные. Если они большие, зависимость перестает быть линейной, а при дальнейшем воздействии тело разрушается. 

Трение

Еще одна часть теории для 2 задания ЕГЭ по физике — сила трения. Трение возникает при соприкосновении тел, оно препятствует их движению. При этом возникает сила трения. Она имеет электромагнитную природу и бывает трех типов: 

• трение покоя возникает, если тела не двигаются. Оно не дает шнуркам развязываться, а гвоздям — выпадать из стены. Иными словами, оно мешает одному телу двигаться относительно другого. Она направлена против силы предполагаемого движения, но имеет максимальное значение. В какой-то момент трение покоя не сможет уравновешивать внешнюю силу, и тела начнут перемещаться. Максимальное значение зависит от свойств предметов и определяется формулой F_{тр. пок. макс.} = μпN, где N — сила реакции опоры, а μ_п — коэффициент трения покоя;
• трение скольжения возникает при переходе через F_{тр. пок. макс.}. При этом объект начинает перемещаться, а трение направлено против этого движения. Сама сила определяется формулой F _{тр. скольж.} = μN, где μ — коэффициент трения скольжения. Величина силы трения скольжения определяется также скоростями тел, но если их значения невелики, то этим фактором можно пренебречь;
• трение качения возникает, когда предмет катится по поверхности, как колесо или цилиндр. При этом оно как бы вдавливается в землю, поэтому при каждом обороте телу нужно пересечь небольшое возвышение. Получается, сила трения растет с уменьшением твердости опоры. Она определяется формулой F _тр.кач. = μ_кач.N, где μ_кач — коэффициент трения качения. μ_кач << μ — сила трения качения значительно меньше силы трения скольжения, поэтому катить что-то всегда проще, чем просто тащить по земле. 

Сопротивление твердого тела, движущегося в жидкости и газе

Разбираем последнюю тему для 2 задания по физике. Когда тело перемещается внутри жидкости или газа, оно сталкивается с сопротивлением среды. Оно похоже на силу трения, но появляется только когда объект начинает движение. Аналога силы трения покоя нет, поэтому перемещать предметы в воде проще, чем на суше. При малых скоростях F_c = k₁v, а при больших F_c = k₂v². k₁ и k₂ — коэффициенты, отличные друг от друга. k₁ — коэффициент, зависящий от размеров, формы, состояния поверхности тела и вязкости среды; k₂ — коэффициент сопротивления.

Примеры задач

А теперь проведем разбор 2 задания ЕГЭ по физике. 

Задание 1. Брусок массой 5 кг перемещается по горизонтальной поверхности. На него действует сила трения скольжения, равная 10 Н. Рассчитайте силу трения скольжения при уменьшении массы бруска в 2 раза, если учитывать, что коэффициент трения не изменился. 

Решение. Сила трения скольжения определяется формулой F = μN. Брусок находится на горизонтальной поверхности, поэтому силу реакции опоры можно определить через второй закон Ньютона: N = mg. Таким образом, F = mgμ. Первые две величины не меняются, значит, на силу будет влиять только уменьшение массы. Необходимо 10 Н разделить на 2. 

Ответ: 5 Н.

Задание 2. Мальчик взял камень массой 200 г и бросил его вверх под углом 60° к горизонту. Рассчитайте, чему равна сила тяжести в момент броска. Ускорение свободного падения равно 10 м/с².

Решение. Сила тяжести постоянна. Она не зависит от угла наклона и скорости. Сила тяжести в момент броска равна силе в любой другой момент времени и определяется формулой F = mg. Следовательно, F = 0,2 кг • 10 м/с² = 2 Н.

Ответ: 2 Н. 

Мы провели разбор 2 задания по физике, причем как по теории, так и по практике. Этот материал представляет собой лишь основы предмета, но он обязательно поможет подготовиться к ЕГЭ. А если вы хотите знать больше, записывайтесь на курсы. Лучше всего выбрать комплексный вариант, например, русский + математика + физика. Так у вас будет больше шансов получить хорошие баллы. А мы желаем вам удачи на экзамене. 

Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения

В. З. Шапиро

Второе задание ЕГЭ по физике проверяет знания по разделу «Динамика». Это задание базового уровня сложности, без возможности выбора ответа. Для его решения необходимо знать законы Ньютона, формулы, которые выражают силу тяжести, силу всемирного тяготения, силу упругости, вес тела, силу трения, силу реакции опоры на горизонтальной поверхности и на наклонной плоскости. Во многих задачах применяется одна и та же формула, но в различных ситуациях. Как правило, необходимо составить и решить систему из двух уравнений.

Применение закона всемирного тяготения

Необходимая теория: Сила тяготения

1. Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Во сколько раз больше будет модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами в два раза больше, а массы звёзд равны 2m и 3m?

Ответ: в _________________________ раз(а).

В этой задаче необходимо записать формулу закона всемирного тяготения для двух случаев:

(1).

(2).

Разделив (2) на (1), получим:

Ответ: в 1,5 раза.

Подобные задачи проверяют знания основных физических формул. Их необходимо записать в общем виде и в случае, когда происходит изменение какой-либо физической величины. Полученную систему уравнений решаем любым удобным способом. Задания такого типа часто встречаются в различных разделах курса физики.

Применение II закона Ньютона

Необходимая теория: Второй и третий законы Ньютона

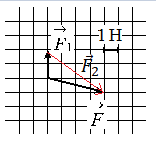
2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей сил, приложенных к телу.

Равнодействующая сила равна геометрической сумме сил, приложенных к телу.

Следующий шаг – найти сумму проекций сил на оси OX и OY.

Сумма проекций сил на ось OX равна:

Сумма проекций сил на вертикальную ось равна:

По теореме Пифагора, модуль равнодействующей силы определяется:

 Ответ: 2 Н.

Секрет решения: Многие задачи по динамике требует прочных знаний по геометрии. Теорема Пифагора, а также соотношения в прямоугольном треугольнике являются обязательными инструментами для тех, кто собирается сдавать экзамен по физике.

Применение формулы силы упругости (закон Гука)

Необходимая теория: Сила упругости

3. Подвешенная к потолку пружина под действием силы 5 Н удлинилась на 10 см. Чему равно удлинение этой пружины под действием силы 8 Н?

Ответ: ___________________________ см.

Запишем формулу закона Гука для двух случаев:

(1)

(2)

Разделим (2) на (1).

(м).

Ответ: 16 см.

Задача решается стандартным применением физической формулы для двух случаев. Обратите внимание на единицы измерения, которые требуются в ответе.

Применение формул для силы реакции опоры и силы трения

Необходимая теория: Сила трения

4. Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.

Ответ: ___________________________.

Общая формула для силы трения имеет вид:

 где N  — сила реакции опоры.

Отсюда коэффициент трения можно выразить 

Проведем расчет: 

Ответ: 0,25.

Секрет решения: Помним, что коэффициент трения находится в интервале от 0 до 1. Это поможет вам более уверенно решать задачи на расчет коэффициента трения.

Во втором задании ЕГЭ по физике необходимо решить задачу на законы ньютона или связанную с действием сил. Ниже мы приводим теорию с формулами, которые необходимы для успешного решения задач по этой тематике.

Задание EF17569

Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?

а) 7F

б) 9F

в) 12F

г) 16F

---

Алгоритм решения

1.Записать закон всемирного тяготения.

2.Применить закон всемирного тяготения для первой и второй пары звезд.

3.Из каждого выражения выразить расстояние между звездами.

4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.

Решение

Закон всемирного тяготения выглядит так:

Примерим этот закон для первой и второй пары звезд:

Выразим квадраты радиусов, так как они в обоих случаях одинаковые:

Приравняем правые части выражений и выразим силу притяжения во втором случае:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18738

Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см². Какое давление человек оказывает на пол?

---

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Выполнить решение в общем виде.

3.Вычислить искомую величину, подставив исходные данные.

Решение

Запишем исходные данные:

• Масса человека: m = 80 кг.

• Вес сумки, которую держит человек: P_c = 100 Н.

• Площадь соприкосновения подошвы ботинок с полом: S = 600 кв. см.

600 кв. см = 600/10000 кв. м = 0,06 кв. м

Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:

F = mg + P_c

Поэтому давление, оказываемое человеком с сумкой на пол, равно:

P=mg+PCS=80·10+1000,06=15000 (Па)

Ответ: 15000

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF19052

Кирпич массой 4 кг лежит на горизонтальной кладке стены, покрытой раствором, оказывая на неё давление 1250 Па. Какова площадь грани, на которой лежит кирпич? Ответ запишите в квадратных сантиметрах.

---

Алгоритм решения

1.Записать исходные данные.

2.Выполнить решение в общем виде.

3.Вычислить искомую величину, подставив исходные данные.

Решение

Запишем исходные данные:

• Масса кирпича: m = 4 кг.

• Давление, оказываемое кирпичом на раствор: P = 1250 Па.

Площадь можно выразить из формулы давления твердого тела. Она будет равна:

S=FP

В данном случае под силой будет подразумеваться сила тяжести кирпича. Поэтому:

S=mgP=4·101250=0,032 (м2)=320 (см2)

Ответ: 320

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17624

Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅10³ H. На канат со стороны груза действует сила, которая:

а) 8∙10³ Н

б) меньше 8∙10³ Н

в) больше 8∙10³ Н

г) равна силе тяжести, действующей на груз

---

Алгоритм решения

1.Сформулировать третий закон Ньютона.

2.Применить закон Ньютона к канату и грузу.

3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.

Решение

Третий закон Ньютона формулируется так:

«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».

Математически он записывается так:

F_A = –F_B

Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙10³ Н.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22586

Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:

а) больше 100 Н, направленной вниз

б) меньше 100 Н, направленной вверх

в) 100 Н, направленной вниз

г) 100 Н, направленной вверх

 

---

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж, иллюстрирующий ситуацию.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций.

5.Вычислить силу, с которой гиря действует на руку мальчика.

Решение

Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.

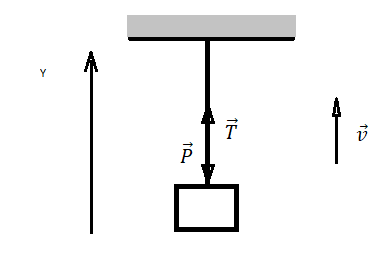
Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.

На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:

P + T = 0

Запишем этот же закон в проекции на ось ОУ:

–P + T = 0

Отсюда:

P = T

Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.

Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17555

Груз массой 4 кг подвешен к укреплённому в лифте динамометру. Лифт начинает спускаться с верхнего этажа с постоянным ускорением. Показания динамометра при этом равны 36 Н. Чему равно и куда направлено ускорение лифта?

а) 1 м/с², вниз

б) 1 м/с², вверх

в) 9 м/с², вниз

г) 9 м/с², вверх

---

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж с указанием известных сил, действующих на груз, их направлений и выбором системы координат.

3.Определить, какая сила действует на тело.

4.Записать второй закон Ньютона в векторной форме.

5.Записать второй закон Ньютона в виде проекций на оси.

6.Выразить из формулы проекцию ускорения лифта и рассчитать ее.

7.По знаку проекции ускорения лифта определить, в какую сторону оно направлено.

Решение

Запишем исходные данные:

• Масса груза равна: m = 4 кг.

• Показания динамометра во время спуска: F = 36 Н.

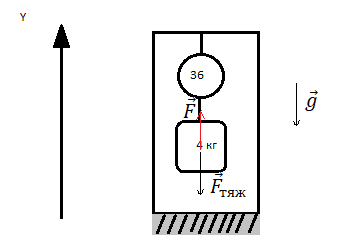
Сделаем чертеж:

Направление силы, действующей на тело, обратно силе, которую оказывает тело на подвес в виде динамометра. Поэтому сила F равна по модулю весу тела во время спуска, но направлена противоположно ему (вверх). Направление ускорения лифта пока остается неизвестным.

Второй закон Ньютона в векторной форме:

F + mg = ma

Второй закон Ньютона в виде проекции сил на ось ОУ:

F – mg = ma

Выразим отсюда ускорение лифта и вычислим его, подставив известные данные:

Перед проекцией ускорения стоит знак «–». Это значит, что оно направлено противопроложно оси ОУ (т.е. вниз).

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17589

Система отсчёта, связанная с Землёй, считается инерциальной. В этом случае систему отсчёта, связанную с самолётом, можно считать инерциальной, если самолёт движется:

а) равномерно и прямолинейно, набирая высоту

б) с постоянным ускорением по горизонтали

в) равномерно, выполняя поворот

г) по взлетной полосе при взлете

---

Алгоритм решения

1. Сформулировать первый закон Ньютона об инерциальных системах отсчета.
2. На основании закона сделать вывод, при каких условиях система отсчета, связанная с самолетом, может считаться инерциальной.
3. Проанализировать все 4 ситуации, приведенные в вариантах ответа.
4. Выбрать тот вариант, который описывает ситуацию, не противоречащую условию, выведенному в шаге 2.

Решение

Первый закон Ньютона формулируется так:

«Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано».

Чтобы система отсчета, связанная с самолетом, была инерциальной, она должна быть неподвижной или двигаться относительно Земли — инерциальной системы отсчета — равномерно и прямолинейно.

Когда самолет движется равномерно и прямолинейно, набирая высоту, самолет движется с собственным ускорением, которое компенсируется ускорением свободного падения. И это единственный верный ответ, так как:

• Самолет, двигаясь с постоянным ускорением по горизонтали, движется неравномерно, что противоречит условию.
• Самолет, двигаясь равномерно во время поворота, движется непрямолинейно (с центростремительным ускорением).
• Самолет, двигаясь по взлетной полосе при взлете, движется прямолинейно, но неравномерно, так как он разгоняется из состояния покоя.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17484

Тело массой m скользит по шероховатой наклонной опоре с углом α к горизонту (см. рисунок). На него действуют 3 силы: сила тяжести mg, сила упругости опоры N и сила трения F_тр. Если скорость тела не меняется, то модуль равнодействующей сил F_тр и mg равен:

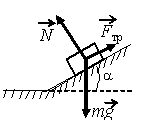
а) N cosα

б) N

в) N sinα

г) mg + F_тр

---

Алгоритм решения

1. Запись второго закона Ньютона в векторном виде.
2. Вывод формулы равнодействующей силы трения и силы тяжести.
3. Нахождение модуля равнодействующей силы трения и силы тяжести.

Решение

Записываем второй закон Ньютона в векторном виде с учетом того, сто скорость тела не меняется (ускорение равно 0):

N + mg + F_тр = 0

Отсюда равнодействующая силы трения и силы тяжести равна:

mg + F_тр = –N

Следовательно, равнодействующая силы трения и силы тяжести направлена противоположно силе реакции опоры, но равна ей по модулю. Отсюда:

|mg + F_тр| = N

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

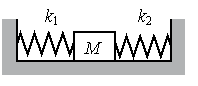
Задание EF18489

Кубик массой 1 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рисунок). Первая пружина сжата на 4 см, а вторая сжата на 3 см. Жёсткость второй пружины k₂ = 600 Н/м. Чему равна жёсткость первой пружины k₁?

---

Алгоритм решения

1. Записать исходные данные.
2. Записать закон Гука.
3. Применить закон Гука к обеим пружинам.
4. Применить третий закон Ньютона.
5. Выразить жесткость первой пружины.
6. Вычислить искомую величину.

Решение

Запишем исходные данные:

• Сжатие первой пружины x₁ — 4 см.
• Сжатие второй пружины x₂ — 3 см.
• Жесткость второй пружины k₂ — 600 Н/м.

Запишем закон Гука:

F_упр = kx

Применим этот закон к обеим пружинам:

F_упр1 = k₁x₁

F_упр2 = k₂x₂

Силы упругости обеих пружин уравновешены, так как тело между ними покоится. Согласно третьему закону Ньютона:

F_упр1 = F_упр2

Отсюда:

k₁x₁ = k₂x₂

Выразим отсюда жесткость первой пружины:

Подставим известные данные и вычислим:

Внимание! В данном случае переводить единицы измерения в СИ не нужно. Отношение длин постоянно независимо от выбранной единицы измерения.

Ответ: 450

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18548

На тело действуют две силы: F₁ и F₂. По силе F₁ и равнодействующей двух сил F = F₁ + F₂ найдите модуль второй силы (см. рисунок).

---

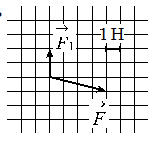
Алгоритм решения

1. Изобразить на рисунке второй вектор с учетом правил сложения векторов.
2. Записать геометрическую формулу для расчета модуля вектора по его проекциям.
3. Выбрать систему координат и построить проекции второй силы на оси ОХ и ОУ.
4. По рисунку определить проекции второй силы на оси.
5. Используя полученные данные, применить формулу для расчета вектора по его проекциям.

Решение

Построим вектор второй силы. Его начало должно совпадать с концом вектора первой силы, а его конец — с концов равнодействующей этих сил. Этот вывод следует из сложения векторов правилом треугольника.

Модуль вектора равен корню из суммы квадратов его проекций на оси ОХ и ОУ:

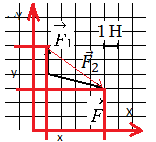
Выберем систему координат и построим проекции второй силы на оси ОХ и ОУ:

Согласно рисунку, проекция второй силы на ось ОХ равна: x = 4 (Н). Ее проекция на ось ОУ равна: y = 3 (Н).

Подставим известные данные в формулу и вычислим модуль вектора второй силы:

Ответ: 5

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17520

Две упругие пружины растягиваются силами одной и той же величины F. Удлинение второй пружины Δl₂ в 2 раза меньше, чем удлинение первой пружины Δl₁. Жёсткость первой пружины равна k₁, а жёсткость второй k₂ равна…

а) 0,25k₁

б) 2k₁

в) 0,5k₁

г) 4k₁

---

Алгоритм решения

1. Записать исходные данные.
2. Записать закон Гука.
3. Применить закон Гука к обеим пружинам.
4. Выразить величину жесткости второй пружины.

Решение

Записываем исходные данные:

• Первая и вторая пружины растягиваются под действием одной и той же силы. Поэтому: F₁ = F₂ = F.
• Удлинение первой пружины равно: Δl₁ = 2l.
• Удлинение второй пружины вдвое меньше удлинения первой. Поэтому: Δl₂ = l.

Закон Гука выглядит следующим образом:

F = k Δl

Применим закон Гука для обеих пружин:

F₁ = k₁ Δl₁

F₂ = k₂ Δl₂

Так как первая и вторая силы равны, можем приравнять правые части выражений. Получим:

k₁ Δl₁ = k₂ Δl₂

Перепишем выражение с учетом значения удлинений первой и второй пружин:

k₁ 2l = k₂ l

«l» в левой и правой частях выражения взаимоуничтожаются, отсюда жесткость второй пружины равна:

k₂ = 2k₁

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Представляем вашему вниманию разбор 2 задания ЕГЭ-2019 по физике

09 октября 2018

Задание 2

Это задание относится к динамике и чаще всего содержит задание, в котором рассматривается действие различных сил на тело. Формулы основных сил и два основных закона, которые могут пригодиться ученикам при выполнении данного задания приведены на слайде. И снова отмечу – второй закон Ньютона в каждой конкретной задаче применяется не для векторных расчётов, а для составления соответствующего уравнения с проекциями сил, действующих на тело. Закон всемирного тяготения в задании 2 так же может встретиться учащимся на ЕГЭ, хотя в демоверсии в этом задании его и нет.

 Какой подход желательно выработать у учащихся при решении подобных заданий? На мой взгляд, они должны действовать в соответствии с простой схемой: если в задаче тело движется под действием нескольких сил, то сделай рисунок, указав вектора всех сил, действующих на это тело, вектор его ускорения и оси координат, затем, спроецируй все векторные величины на оси координат и составь уравнение в соответствии с 2 законом Ньютона, где под Fобщ имеется в виду сумма проекций всех сил на эту ось. Далее замени в составленном уравнении силы на их формулы и найди неизвестное, решив уравнение. Вроде бы всё просто. Тем более, для задания 2, достаточно составить всего одно уравнение для проекций на одну ось, в отличие от задания 25 или 29, где таких уравнений может быть 2 и более. Плюс такого подхода в том, что дети привыкают действовать по схеме: рисунок-проекции-уравнение, а в дальнейшем они смогут решать и более сложные задачи.

K = 50 Н/м   m = 200 г   Найти изменение длины пружины

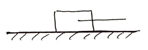
Найти коэффициент трения, если для того, чтобы равномерно тянуть груз массой 4 кг требуется сила 8 Н.

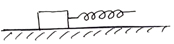
μ = 0,4  m = 500 г  K = 40 Н/м  Каково изменение длины пружины при равномерном движении груза?

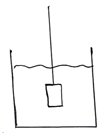
Какова сила натяжения нити, если груз массой 5 кг висит в воде, а объем груза 2 дм3

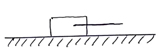
При какой силе тяги груз массой 4 кг будет двигаться с ускорением 2 м/с2, если коэффициент трения равен 0,8?

Рассмотрим примеры.

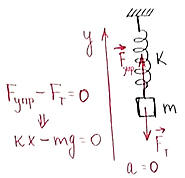
K = 50 Н/м   m = 200 г   Найти изменение длины пружины

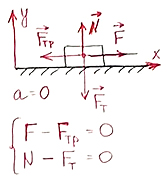
Найти коэффициент трения, если для того, чтобы равномерно тянуть груз массой 4 кг требуется сила 8 Н.

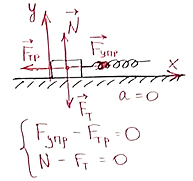
μ = 0,4  m = 500 г  K = 40 Н/м  Каково изменение длины пружины при равномерном движении груза?

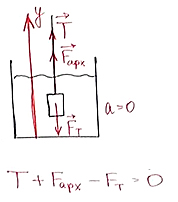
Какова сила натяжения нити, если груз массой 5 кг висит в воде, а объем груза 2 дм3

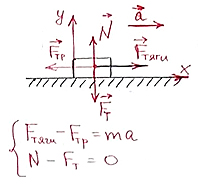
При какой силе тяги груз массой 4 кг будет двигаться с ускорением 2 м/с2, если коэффициент трения равен 0,8?

Из последних КИМов ЕГЭ по физике следует, что задание 2 относится к разделу «Динамика» и может содержать расчетные задачи по следующим темам: «Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения».

Основные формулы, которые необходимо знать для успешного решения задания 2.

Сила тяжести		m — масса тела g=10 м/с2 – ускорение свободного падения
Сила упругости		Δx – удлинение пружины k – коэффициент жесткости пружины
Сила трения		µ — коэффициент трения N – сила реакции опоры
Сила Архимеда (выталкивающая сила)		V – объём погруженной части тела g=10 м/с2 – ускорение свободного падения
Сила притяжения между телами (закон Всемирного тяготения)		G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная m1 и m2 — массы взаимодействующих тел r – расстояние между телами
Второй закон Ньютона		m – масса тела R – равнодействующая всех сил, действующих на тело a – ускорение, с которым движется тело под действием этих сил

Алгоритм решения

При решении задач из раздела «Динамика» желательно придерживаться следующего алгоритма решения:

1. Сделать рисунок, на котором указать вектора всех сил, действующих на тело.

2. Если тело двигается с ускорением, указать направление этого ускорения. Если тело покоится или двигается равномерно, его ускорение a=0.

3. Составить уравнение движения (второй закон Ньютона) для рассматриваемого тела в его векторном виде.

3. Выбрать систему координат и спроецировать полученное уравнение на выбранные оси координат.

4. Расшифровать неизвестные величины, вошедшие в уравнение движения.

5. Решить полученную систему уравнений.

Задание 2
– это расчётные задачи базового уровня сложности, и для решения некоторых из них этот алгоритм будет чересчур подробным и перегруженным, так как их можно решить и без вспомогательного рисунка или даже без записи второго закона Ньютона. Это касается, например, заданий, в которых на тело действует только одна сила. Но привычка решать задания по приведенному выше алгоритму поможет ученикам успешно справиться с расчетными задачами по разделу «Динамика» повышенного и высокого уровней сложности – такие задания могут стоять в ЕГЭ под номерами 25 и 29.

Ответом на задание 2 является число, именно его нужно вписать в бланк ответов 1, не указывая единицы измерения.

Примеры решения с разбором

Пример решения 2 задания по физике (ЕГЭ-2019)

Пружина жёсткостью 2*10⁴
Н/м одним концом закреплена в штативе. На какую величину она растянется под действием силы 400 Н?

Ответ: ___________________________ см.

Решение:

Сделаем чертёж

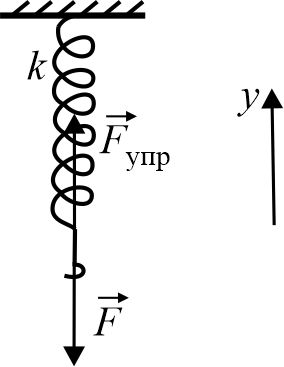
Пружина под действием силы F
привели в растянутое состояние. Кроме растягивающей силы F
и силы упругости
, стремящейся вернуть пружину в нерастянутое состояние, больше никакие силы на нее не действуют.

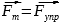
Запишем проекции сил на вертикальную ось Oy

F=F_упр

По закону Гука, сила упругости F_упр = k
*Δx, следовательно,

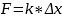
k
— коэффициент жёсткости пружины, Δx
– её удлинение.

Выразим величину растяжения пружины

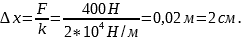
Ответ: 2

Пример решения 2 задания по физике (ЕГЭ – 2020. Вариант 1 досрочного ЕГЭ)

Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.

Ответ: _______ .

Решение:

Силу трения можно найти по формуле

F_тр= µN,

где N – сила реакции опоры, или по-другому нормальная составляющая силы воздействия тела на плоскость.

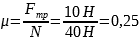
Ответ: 0,25.

Пример решения 2 задания по физике (ЕГЭ – 2020. Демонстрационный вариант)

Два одинаковых маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них равна 2m, а расстояние между их центрами равно 2r?

Ответ: _______ пН.

Решение:

По закону Всемирного тяготения шары массами m₁и m₂, находящиеся друг от друга на расстоянии r,
притягиваются друг к другу с силой

.

В первом случае

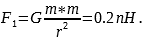
Во втором случае

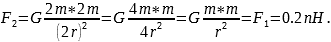
Ответ: 0,2

Пример решения 2 задания по физике (ЕГЭ – 2019. Демонстрационный вариант)

По горизонтальному полу по прямой равномерно тянут ящик, приложив к нему горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и ящиком равен 0,25. Чему равна масса ящика?

Ответ _______ кг.

Решение:

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

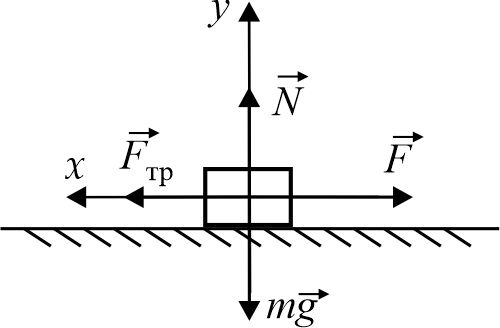
По второму закону Ньютона, равнодействующая всех сил, действующих на тело, будет равна нулю, так как по условию задачи тело движется равномерно, то есть ускорение тела a=0.

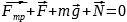
Запишем это в проекциях на оси Ox и Oy

Ox: F_тр
– F = 0,

Oy: N — m g=0.

Откуда N = mg, следовательно,

F_тр = µ N = µ mg.

Масса тела

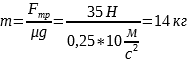
Ответ: 14

Пример решения 2 задания по физике (ЕГЭ – 2018)

К пружине подвесили груз массой 150 г, вследствие чего пружина удлинилась на 1 см. Чему будет равно удлинение этой пружины, если к ней подвесить груз 450 г?

Ответ: __________ см.

Решение:

Переведём единицы измерения физических величин в систему СИ

m₁ = 150 г = 0,15 кг, m₂ = 450 г = 0,45 кг, Δx=1 см = 0,01 м.

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

На тело действует сила тяжести (F_т
= mg), направленная вертикально вниз, и сила упругости со стороны пружины (F_упр
= k Δx), направленная вертикально вверх.

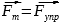
В проекции на вертикальную ось Oy.

F_т
=F_упр

mg = kΔx (1)

k
— коэффициент жёсткости пружины, Δx
– её удлинение.

Найдём, чему равен коэффициент жёсткости пружины

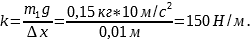
Выразим из выражения (1) удлинение пружины во втором случае

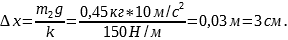
Ответ: 3

Инерциальные системы отсчета. Первый закон Ньютона. Принцип относительности Галилея

Инерциальная система отсчета — это система отсчета, в которой справедлив закон инерции: материальная точка, когда на нее не действуют никакие силы (или действуют силы, взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.

Закон этот был открыт Галилеем в 1632 г. и сформулирован Ньютоном в 1687 г. как первый закон механики.

Любая система отсчета, движущаяся по отношению к инерциальной системе отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета, т. е. в ней выполняется первый закон Ньютона. Следовательно, инерциальных систем отсчета может быть сколь угодно много. Система отсчета, движущаяся с ускорением по отношению к инерциальной системе отсчета, неинерциальна и закон инерции в ней не выполняется.

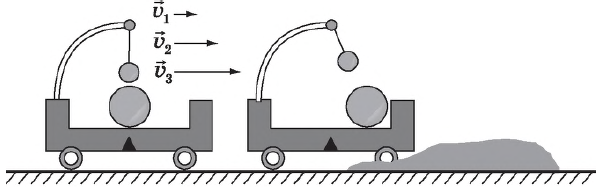
Сказанное подтверждается опытом, изображенным на рисунке. Сначала тележка движется прямолинейно и равномерно относительно земли. На ней находятся два шарика, один из которых лежит на горизонтальной поверхности, а другой подвешен на нити. Силы, действующие на каждый шарик по вертикали, уравновешены, по горизонтали никакие силы на шарики не действуют (силой сопротивления воздуха в данном случае можно пренебречь).

Шарики будут находиться в покое относительно тележки при любой скорости ее движения ($υ_1, υ_2, υ_3$ и т. д.) относительно Земли — главное, чтобы эта скорость была постоянна.

Но когда тележка попадает на песчаную насыпь, ее скорость быстро уменьшается, в результате чего тележка останавливается. Во время торможения тележки оба шарика приходят в движение, т. е. изменяют свою скорость относительно тележки, хотя нет никаких сил, которые толкали бы их.

Здесь первой (условно неподвижной) системой отсчета является Земля. Второй системой отсчета, движущейся относительно первой, является тележка. Пока тележка двигалась прямолинейно и равномерно, шарики находились в состоянии покоя относительно тележки, т. е. закон инерции выполнялся. Как только тележка начала тормозить, т. е. начала двигаться с ускорением относительно первой инерциальной системы отсчета (Земли), закон инерции перестал выполняться.

Если относительно какой-нибудь системы отсчета тело движется с ускорением, не вызванным действием на него других тел, то такую систему называют неинерциальной.

В неинерциальных системах отсчета основное положение механики о том, что ускорение тела вызывается воздействием на него других тел, не выполняется.

Следует отметить, что невозможно найти строго инерциальную систему отсчета. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом (Землей, корпусом корабля или самолета и т. и.), по отношению к которому и изучается движение различных объектов. Поскольку все реальные тела движутся с тем или иным ускорением, любая реальная система отсчета может рассматриваться как инерциальная лишь приближенно.

С очень высокой степенью точности инерциальной можно считать гелиоцентрическую систему, связанную с центром Солнца и с координатными осями, направленными на три далекие звезды. Эта система используется в задачах небесной механики и космонавтики. Для решения большинства технических задач инерциальной системой отсчета можно считать любую систему, жестко связанную с Землей (или с любым телом, которое покоится или движется равномерно и прямолинейно относительно поверхности Земли).

Первый закон Ньютона

Любое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Так был сформулирован Ньютоном в 1687 г. первый закон механики, или закон инерции.

Суть закона инерции впервые была изложена в одной из книг итальянского ученого Галилео Галилея, опубликованной в начале XVII в.

Ньютон обобщил выводы Галилея, сформулировав закон инерции, и включил его в качестве первого из трех законов в основу механики. Поэтому данный закон называют первым законом Ньютона.

Однако со временем выяснилось, что первый закон Ньютона выполняется не во всех системах отсчета, а только в инерциальных. Поэтому с точки зрения современных представлений первый закон Ньютона формулируется так:

Существуют системы отсчета, называемые инерциальными, относительно которых свободные тела движутся прямолинейно и равномерно.

Под свободным телом здесь понимают тело, на которое не оказывают воздействие другие тела.

Следует помнить, что в первом законе Ньютона речь идет о телах, которые могут рассматриваться как материальные точки.

Принцип относительности Галилея

Принцип относительности Галилея гласит:

Во всех инерциальных системах отсчета законы механики имеют одинаковый вид.

Это означает, что уравнения, выражающие законы механики, не меняются (инвариантны) при преобразованиях Галилея.

Преобразования Галилея заключаются в преобразовании координат $r↖{→} (х, у, z)$ и времени $t$ движущейся материальной точки при переходе от одной инерциальной системы отсчета (ИСО) к другой:

$r↖{→}={r’}↖{→}+υ↖{→}t, t=t’$ (1.47)

Для координаты $х$, например, это означает:

$x=x’+υt, t=t’,$

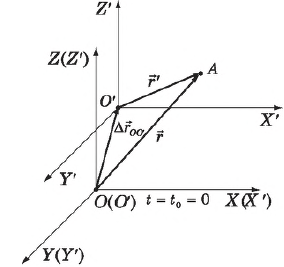
где $υ$ — относительная скорость (постоянная) движения двух ИСО, $r↖{→}$ и ${r’}↖{→}$ — радиус-векторы, а х и х1 — координаты точки в этих двух ИСО. Согласно преобразованию Галилея (1.47), время не изменяется при переходе из одной ИСО в другую: принцип относительности Галилея основан на представлениях об абсолютном времени и абсолютном пространстве, что означает одинаковость (одновременность) протекания событий во всех ИСО. Преобразования координат легко понять, если в некоторый момент времени $t_0$, принятый за начальный $t_0=0$, одну из систем координат $К(ХYZ)$ — неподвижную — совместить с другой — $К'(Х’Y’Z’)$ — подвижной и зафиксировать систему $К$.

Тогда в любой последующий момент времени положение некоторой точки $А$, движущейся относительно обеих систем координат, определяется в системе $К$ радиус-вектором $r↖{→}$, а в системе $К’$ — радиус-вектором ${r’}↖{→}$. Вектор, соединяющий начала координат $О$ неподвижной и $О’$ — подвижной систем координат, равен вектору перемещения системы $К’$ относительно $К:{OO’}↖{-}=∆r↖{→}{OO}$. Согласно правилу сложения векторов

$r↖{→}={r’}↖{→}+∆r↖{→}{OO}$

Однако вектор перемещения можно выразить через скорость движение системы $К’$ относительно $К: ∆r↖{→}{OO}=υ↖{→}t$. Поэтому

$r↖{→}={r’}↖{→}+υ↖{→}t$

что совпадает с (1.47).

Из уравнения (1.47) вытекает закон сложения скоростей:

$u↖{→}={u’}↖{→}+υ↖{→},$

где $u$ и $u’$ — скорости точки относительно систем $К$ и $К’$ соответственно.

Принцип относительности Галилея означает, что никакими механическими опытами нельзя обнаружить движение одной инерциальной системы координат относительно другой. Именно поэтому, находясь в салоне сверхзвукового самолета, пассажиры могут спокойно передвигаться, не чувствуя его скорости.

Не нужно, однако, думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела относительно разных инерциальных систем координат. Тождественны лишь законы движения. Характер же движения определяется начальными условиями (начальными скоростями и координатами тела), которые различны в разных системах отсчета.

Так, камень, выпущенный из рук в движущемся вагоне поезда, будет падать вертикально лишь относительно стен вагона, а для наблюдателя, находящегося на платформе, он будет двигаться по параболе. Объясняется это тем, что начальные скорости разные: относительно стен вагона начальная скорость равна нулю, а относительно Земли она равна скорости движения вагона.

Взаимодействие. Сила. Принцип суперпозиции сил

Взаимодействие в физике — это воздействие тел или частиц друг на друга, приводящее к изменению их движения.

Близкодействие и дальнодействие (или действие на расстоянии). О том, как осуществляется взаимодействие тел, в физике издавна существовали две точки зрения. Первая из них предполагала наличие некоторого агента (например, эфира), через который одно тело передает свое влияние на другое, причем с конечной скоростью. Это теория близкодействия. Вторая предполагала, что взаимодействие между телами осуществляется через пустое пространство, не принимающее никакого участия в передаче взаимодействия, причем передача происходит мгновенно. Это теория дальнодействия. Она, казалось бы, окончательно победила после открытия Ньютоном закона всемирного тяготения. Так, например, считалось, что перемещение Земли должно сразу же приводить к изменению силы тяготения, действующей на Луну. Кроме самого Ньютона, позднее концепции дальнодействия придерживались Кулон и Ампер.

После открытия и исследования электромагнитного поля теория дальнодействия была отвергнута, так как было доказано, что взаимодействие электрически заряженных тел осуществляется не мгновенно, а с конечной скоростью (равной скорости света: $c=3·10^8$ м/с) и перемещение одного из зарядов приводит к изменению сил, действующих на другие заряды, не мгновенно, а спустя некоторое время. Возникла новая теория близкодействия, которая была затем распространена и на все другие виды взаимодействий. Согласно теории близкодействия взаимодействие осуществляется посредством соответствующих полей, окружающих тела и непрерывно распределенных в пространстве (т. е. поле является тем посредником, который передает действие одного тела на другое). Взаимодействие электрических зарядов — посредством электромагнитного поля, всемирное тяготение — посредством гравитационного поля.

На сегодняшний день физике известны четыре типа фундаментальных взаимодействий, существующих в природе (в порядке возрастания интенсивности): гравитационное, слабое, электромагнитное и сильное взаимодействия.

Фундаментальными называются взаимодействия, которые нельзя свести к другим типам взаимодействий.

Фундаментальные взаимодействия отличаются интенсивностью ж радиусом действия. Под радиусом действия понимают максимальное расстояние между частицами, за пределами которого их взаимодействием можно пренебречь.

По радиусу действия фундаментальные взаимодействия делятся на дальнодействующие (гравитационное и электромагнитное) и короткодействующие (слабое и сильное).

Гравитационное взаимодействие универсально: в нем участвуют все тела в природе — от звезд, планет и галактик до микрочастиц: атомов, электронов, ядер. Его радиус действия равен бесконечности. Однако как для элементарных частиц микромира, так и для окружающих нас предметов макромира силы гравитационного взаимодействия настолько малы, что ими можно пренебречь. Оно становится заметным с увеличением массы взаимодействующих тел и потому определяющим в поведении небесных тел и образовании и эволюции звезд.

Основные характеристики фундаментальных взаимодействий

Взаимодействие	Взаимодействующие частицы	Радиус действия, $м$	Относительная интенсивность
Гравитационное	Все	$∞$	1
Слабое	Все, кроме фотона	$10^{-17}$	$10^{32}$
Электромагнитное	Заряженные частицы	$∞$	$10^{36}$
Сильное	Адроны	$10^{-15}$	$10^{38}$

Слабое взаимодействие присуще всем элементарным частицам, кроме фотона. Оно отвечает за большинство ядерных реакций распада и многие превращения элементарных частиц.

Электромагнитное взаимодействие определяет структуру вещества, связывая электроны и ядра в атомах и молекулах, объединяя атомы и молекулы в различные вещества. Оно определяет химические и биологические процессы. Электромагнитное взаимодействие является причиной таких явлений, как упругость, трение, вязкость, магнетизм и составляет природу соответствующих сил. На движение макроскопических электронейтральных тел оно существенного влияния не оказывает.

Сильное взаимодействие осуществляется между адронами, именно оно удерживает нуклоны в ядре.

В 1967 г. Шелдон Глэшоу, Абдус Салам и Стивен Вайнберг создали теорию, объединяющую электромагнитное и слабое взаимодействия в единое электрослабое взаимодействие с радиусом действия $10^{-17} м$, в пределах которого исчезает различие между слабым и электромагнитным взаимодействиями.

В настоящее время выдвинута теория великого объединения, согласно которой существуют лишь два типа взаимодействий: объединенное, куда входят сильное, слабое и электромагнитное взаимодействия, и гравитационное взаимодействие.

Есть также предположение, что все четыре взаимодействия являются частными случаями проявления единого взаимодействия.

В механике взаимное действие тел друг на друга характеризуется силой. Более общей характеристикой взаимодействия является потенциальная энергия.

Силы в механике делятся на гравитационные, упругости и трения. Как уже упоминалось выше, природа механических сил обусловлена гравитационным и электромагнитным взаимодействиями. Только эти взаимодействия можно рассматривать как силы в смысле механики Ньютона. Сильные (ядерные) и слабые взаимодействия проявляются на таких малых расстояниях, при которых законы механики Ньютона, а вместе с ними и понятие механической силы теряют смысл. Поэтому термин «сила» в этих случаях следует воспринимать как «взаимодействие».

Сила

Сила в механике — это величина, являющаяся мерой взаимодействия тел.

При механическом движении проявляются следующие виды сил: силы упругости, силы трения и гравитационные силы (всемирного тяготения).

Действие одного тела на другое приводит как к изменению скорости всего тела как целого, так и к изменению скорости отдельных его частей.

Мерой этого действия является сила. Часто не указывают, какое тело и как действовало на данное тело. Просто говорят, что на тело действует сила, или к нему приложена сила.

Действие одного тела на другое может производиться как при непосредственном контакте (давление, трение), так и посредством создаваемых телами полей (электромагнитное поле, гравитационное поле).

Проявлением действия силы является изменение ускорения тела.

Сила, как и скорость, — векторная величина, т. е. имеет не только численное значение, но и направление. Сила обычно обозначается буквой $F↖{→}$, модуль силы — буквой $F$ (без стрелки). Прямая, вдоль которой направлена сила, называется линией действия силы. Когда говорят о силе, важно указать, к какой точке тела приложена действующая на него сила. Если речь идет об абсолютно твердом (недеформируемом) теле, то можно считать, что сила приложена к любой точке на линии ее действия.

Итак, результат действия силы на тело зависит от ее модуля, направления и точки приложения.

Иначе говоря, сила — векторная величина, характеризующаяся численным значением, направлением в пространстве и точкой приложения.

Единицей силы в СИ является ньютон (H). Один ньютон (1 H) — это сила, которая за $1$с изменяет скорость тела массой $1$ кг на $1$ м/с. Эта единица названа в честь великого английского ученого Исаака Ньютона (1642-1727). На практике применяются также килоньютоны и миллиньютоны:

$1кH|=1000H, 1мH=0.001H.$

Принцип суперпозиции сил

Обычно на любое движущееся тело действует не одна, а сразу несколько сил. Так, например, на парашютиста, спускающегося на землю, действуют сила тяжести и сила сопротивления воздуха. На тело, висящее на пружине, действуют две силы: сила тяжести и сила упругости пружины.

В каждом подобном случае несколько сил, приложенных к телу, можно заменить одной суммарной силой $F↖{→}$, равноценной по своему действию этим силам. Сила, производящая на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил:

$F↖{→}=∑↙{i=1}↖{n}{F_i}↖{→}={F_1}↖{→}+{F_2}↖{→}+…+{F_n}↖{→}$

В этом состоит принцип суперпозиции (наложения) сил.

Равнодействующая сила, действующая на частицу со стороны других тел, равна векторной сумме сил, с которыми каждое из этих тел действует на частицу.

Для нахождения равнодействующей силы пользуются правилами сложения векторов (поскольку сила — векторная величина), в частности, сложение двух сил производится по правилу параллелограмма.

О двух силах, равных по величине и направленных вдоль одной прямой в противоположные стороны, говорят, что они уравновешивают, или компенсируют друг друга. Равнодействующая $F$ таких сил всегда равна нулю и потому изменить скорость тела не может.

Для изменения скорости тела относительно Земли необходимо, чтобы равнодействующая всех приложенных к телу сил была отлична от нуля. В том случае, когда тело движется в направлении равнодействующей силы, его скорость возрастает; при движении в противоположном направлении скорость тела убывает. Таким образом, направление скорости не всегда совпадает с направлением действующей силы $F$, а вот изменение направления скорости (а следовательно, и направление ускорения) всегда совпадает с направлением действующей силы.

Второй закон Ньютона

Второй закон Ньютона формулируется так:

Ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально его массе. Направление ускорения совпадает с направлением равнодействующей всех сил.

Следует помнить, что во втором законе Ньютона, так же, как и в первом, под телом подразумевается материальная точка, движение которой рассматривается в инерциальной системе отсчета.

Математически второй закон Ньютона выражается формулой:

$a↖{→}={F↖{→}}/{m}$

В скалярном виде второй закон можно записать:

${a_x}↖{→}={{F_x}↖{→}}/{m}$

$a={F}/{m}$

Отсюда можно вывести два следствия:

1. Чем больше сила, приложенная к телу, тем больше его ускорение, и следовательно, тем быстрее изменяется скорость движения этого тела.
2. Чем больше масса тела, тем меньшее ускорение оно получает в результате действия данной силы и потому тем медленнее изменяет свою скорость.

Из формулы $a↖{→}={F↖{→}}/{m}$ следует:

$F↖{→}=a↖{→}m$

Формулировка второго закона механики, данная самим Ньютоном, такова:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

В современном виде закон этот записывается следующим образом:

${d(mυ↖{→})}/{dt}=F↖{→}$

где $mυ↖{→}$ — количество движения тела. Количество движения называют также импульсом тела $p↖{→}$:

$p↖{→}=mυ↖{→}$

Когда равнодействующая сил, приложенных к телу, постоянна ($F↖{→}=const$), дифференцирование в ${d(mυ↖{→})}/{dt}=F↖{→}$ можно заменить разностью $∆$, поскольку изменение скорости (ускорение) постоянно:

$∆p↖{→}=F↖{→}∆t$

Второй закон Ньютона иногда называют основным законом динамики. После его открытия стало возможным решать такие задачи о движении тел, которые до Ньютона казались неразрешимыми. Многие казавшиеся ранее непонятными явления теперь были объяснены на основе открытых законов физики.

На основании второго закона Ньютона вводится единица силы в СИ — ньютон (Н). Один ньютон ($1Н$) — это сила, с которой нужно действовать на тело массой в $1$ кг, чтобы сообщить ему ускорение в $1$ м/$с^2$.

Подставив в формулу значения ускорения и массы с их размерностями из приведенного определения, выразим размерность силы в $1Н$ через основные единицы СИ:

$1H=1кг·1$м/$с^2=1кг·$м/$с^2$

Третий закон Ньютона

Третий закон Ньютона гласит:

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

В своем первом законе Ньютон описал движение тела, не подверженного действию других тел. В этом случае тело либо сохраняет свое состояние покоя, либо движется равномерно и прямолинейно (относительно инерциальной системы отсчета).

Во втором законе Ньютона речь идет о прямо противоположной ситуации. Теперь на данное тело действуют внешние тела, причем их количество может быть произвольным. Под действием окружающих тел рассматриваемое тело начинает двигаться с ускорением, причем произведение массы данного тела на его ускорение оказывается равным действующей силе.

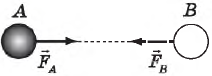
Сформулировав эти два закона, Ньютон обратился к анализу ситуации, когда во взаимодействии участвуют только два тела. Допустим, имеются два тела $А$ и $В$, которые притягивают друг друга с силами $F$ и $F’$, Может ли одна из этих сил быть больше другой? Размышление над этой проблемой привело Ньютона к выводу, что такого быть не может: силы взаимодействия двух тел всегда равны друг другу. Каким образом Ньютон пришел к такому заключению? Вот как он рассуждал: «Относительно притяжения дело может быть изложено вкратце следующим образом: между двумя взаимно притягивающимися телами надо вообразить какое-либо препятствие, мешающее их сближению. Если бы одно из тел $А$ притягивалось телом $В$ сильнее, нежели тело $В$ притягивается телом $А$, то препятствие испытывало бы со стороны тела $А$ большее давление, нежели со стороны тела $В$, и, следовательно, не осталось бы равновесия. Преобладающее давление вызвало бы движение системы, состоящей из этих двух тел и препятствия, в сторону тела $В$, ив свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону. Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же».

Следует помнить, что силы, о которых говорится в законе Ньютона, никогда не уравновешивают друг друга, поскольку они приложены к разным телам. Две равные по модулю и противоположно направленные силы уравновешивают друг друга в том случае, если они приложены к одному телу. Тогда их равнодействующая равна нулю, и тело при этом находится в равновесии, т. е. либо покоится, либо движется равномерно и прямолинейно.

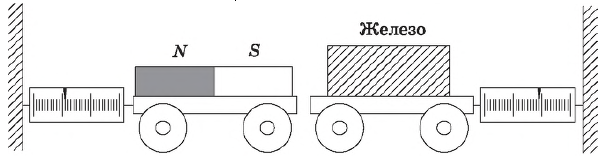
Опыты подтверждают вывод Ньютона. Если, например, взять две тележки и на одной из них закрепить магнит, а на другой кусок железа, а затем соединить их с динамометрами, то мы увидим, что показания этих приборов совпадут. Это означает, что сила, с которой магнит притягивает к себе железо, равна по величине силе, с которой железо притягивает к себе магнит. Эти силы равны по абсолютной величине и противоположны по направлению: сила притяжения к магниту направлена влево, а сила притяжения к железу вправо.

Итак, третий закон Ньютона на более привычном для нас языке может быть сформулирован так:

Силы, с которыми взаимодействуют любые два тела, всегда равны по величине и противоположны по направлению.

Математически он записывается в следующем виде:

${F_1}↖{→}=-{F_2}↖{→}$

Знак «минус» показывает, что векторы сил направлены в противоположные стороны. Используя второй закон Ньютона, можно записать:

$m_1{a_1}↖{→}=-m_2{a_2}↖{→}$

Отсюда следует, что

${a_1}/{a_2}={m_2}/{m_1}$

Таким образом, отношение модулей ускорений двух взаимодействующих тел определяется исключительно их массами (чем меньше масса тела, тем большее ускорение оно приобретает) и не зависит от природы сил взаимодействия.

Третий закон Ньютона обосновывает введение самого термина «взаимодействие»: если одно тело действует на другое, то второе также действует на первое. Другими словами, не может быть такого, чтобы одно тело на другое действовало, а второе на первое — нет. Как писал сам Ньютон, «если кто нажимает пальцем на камень, то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и обратно (если можно так выразиться) она с равным усилием оттягивается к камню».