Формулы для задач по геометрии егэ

Алгебра — ЕГЭ                Тригонометрия — ЕГЭ                Геометрия — ЕГЭ                Стереометрия — ЕГЭ                Алгебра — ОГЭ                Геометрия — ОГЭ

Шпаргалка по геометрии для ЕГЭ

Формулы по геометрии для ЕГЭ

Сборник формул по геометрии

Формулы для четырехугольников

Формулы для окружности

Больше
половины всех задач В3 из вариантов ЕГЭ
— это задачи, в которых надо посчитать
площадь фигуры. Чтобы решить их, надо
знать формулы по геометрии — такие, как
площадь треугольника или площадь
параллелограмма — а также простые
приёмы, о которых мы расскажем.

Для
начала стоит выучить формулы площадей
фигур. Мы специально собрали их в удобную
таблицу. Распечатайте, выучите и
применяйте!

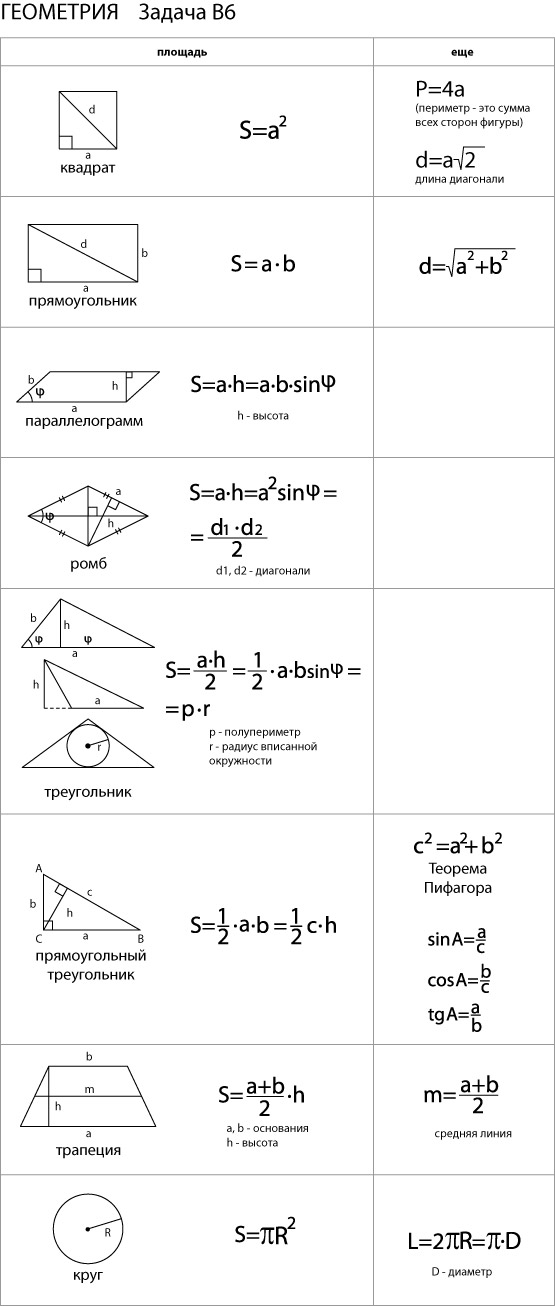
Конечно
же, не все формулы по геометрии есть в
нашей таблице. Например, для решения
задачи С4 применяются и другие формулы
площади треугольника. О них мы обязательно
расскажем.

А
что делать, если надо найти не площадь
трапеции или треугольника, а площадь
какой-либо сложной фигуры? Есть
универсальные способы! Покажем их на
примерах из банка заданий ФИПИ.

1. Как
   найти площадь нестандартной фигуры?
   Например, произвольного четырёхугольника?
   Простой приём — разобьём эту фигуру
   на такие, о которых мы всё знаем, и найдем
   её площадь — как сумму площадей этих
   фигур.

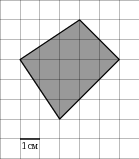
Разделим
этот четырёхугольник горизонтальной
линией на два треугольника с общим
основанием, равным 5. Высоты этих
треугольников равны 2 и 3. Тогда площадь
четырёхугольника равна сумме площадей
двух треугольников:

S
= 5 + 7,5 = 12,5.

Ответ:
12,5.

1. В
   некоторых случаях площадь фигуры можно
   представить как разность каких-либо
   площадей.

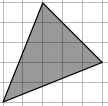
Не
так-то просто посчитать, чему равны
основание и высота в этом треугольнике!
Зато мы можем сказать, что его площадь
равна разности площадей квадрата со
стороной 5 и трёх прямоугольных
треугольников. Видите их на рисунке?
Получаем:

S
= 25 – 5 – 5 – 4,5 = 10,5.

Ответ:
10,5.

1. Иногда
   в задании В3 надо найти площадь не всей
   фигуры, а её части. Обычно речь здесь
   идет о площади сектора — части круга.

Найдите
площадь сектора круга радиуса 1, длина
дуги которого равна 2.

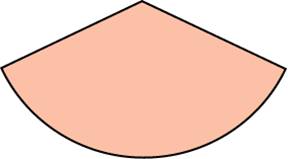
На
этом рисунке мы видим часть круга.
Площадь всего круга равна πR² = π, так
как R=1. Остается узнать, какая часть
круга изображена. Поскольку длина всей
окружности равна 2πR = 2π (так как R=1), а
длина дуги данного сектора равна 2,
следовательно, длина дуги в π раз меньше,
чем длина всей окружности. Угол, на
который опирается эта дуга, также в π
раз меньше, чем полный круг (то есть 360
градусов). Значит, и площадь сектора
будет в π раз меньше, чем площадь всего
круга.

Ответ:
1.

И
ещё примерно половина прототипов задачи
В3 — это простые задачи на тему «Координаты
и векторы». Для их решения вспомните,
что такое абсцисса точки (это ее координата
по Х) и что такое ордината (координата
по Y). Пригодятся также такие понятия,
как координаты вектора и длина вектора
(она находится по теореме Пифагора),
синус и косинус угла, угловой коэффициент
прямой, уравнение прямой, а также сумма,
разность и скалярное произведение
векторов, угол между векторами. Все
прототипы задачи В3 можно найти на сайте
mathege.ru.

Геометрия на егэ по математике

Геометрия
на ЕГЭ по математике — одна
из сложных тем для абитуриентов. Дело
в том, что когда-то экзамен по геометрии
в школе был обязательным, а сейчас —
нет. В результате у большинства
абитуриентов знания по геометрии
близки к нулю.

Геометрия
на ЕГЭ — это четыре задачи в части
и В (две по планиметрии и две
по стереометрии), а также задача
С2 и для многих недосягаемая С4.
Как же научиться их решать?

Начнем
с планиметрии. Прежде всего, вам нужно
выучить основные формулы
геометрии.

На нашем
сайте вы найдете курс геометрии
с нуля — основные определения,
формулы и теоремы, а также разбор
множества экзаменационных задач
по геометрии из части В.

Для
решения задачи С4 нужна более серьезная
подготовка.

Первый этап — теория.
Необходимый материал есть в учебнике
по геометрии за 7-9 класс (автор —
А. В. Погорелов или Л. С. Атанасян).
Выпишите в тетрадь определения
и формулировки теорем. Сделайте
чертежи. Доказывать теоремы старайтесь
самостоятельно.

Программа
по геометрии.

1.
Треугольники. Элементы треугольника.
Вершины и стороны. Высоты, медианы,
биссектрисы (определения).

2.
Построение треугольника: практические
задания.

а) Три стороны треугольника
АВС равны 4, 6 и 8 сантиметров
соответственно. Постройте треугольник
АВС с помощью циркуля и линейки.

б)
В треугольнике АВС угол В равен
48 градусов, сторона АВ равна двум,
ВС равна 9. Постройте треугольник
АВС.

в) В треугольнике АВС сторона ВС
равна 5, угол В равен 26°, угол С
равен 58°. Постройте треугольник АВС.

3.
Три признака равенства треугольников.
Неравенство треугольника.

4.
Постройте с помощью циркуля и линейки:

а) серединный перпендикуляр
к отрезку;

б) биссектрису угла.

5.
Углы при параллельных прямых и секущей.
Вертикальные, смежные, соответственные,
односторонние и накрест лежащие
углы. Их определение и свойства.

6.
Теорема о сумме углов треугольника.

7.
Внешний угол треугольника.

8.
Постройте в одном и том же
треугольнике

а) три высоты. Рассмотрите
также случаи тупоугольного
и прямоугольного треугольника.

б) три биссектрисы.

в) три медианы.

9.
Равнобедренный треугольник. Определение
и свойства. Высота в равнобедренном
треугольнике.

10.
Средняя линия треугольника и ее свойства.

11.
Прямоугольный треугольник. Теорема
Пифагора.

12.
Определения синуса, косинуса и тангенса

— для острого угла прямоугольного
треугольника

— для произвольного
угла.

13.
Четырехугольники. Сумма углов
четырехугольника.

14.
Параллелограмм. Определение и свойства.
Площадь параллелограмма.

15.
Виды параллелограммов и их свойства.
(ромб, прямоугольник, квадрат).

16.
Трапеция. Средняя линия трапеции. Площадь
трапеции.

17.
Подобные треугольники. Три признака
подобия треугольников.

18.
Площадь треугольника. Формулы  

 и 

.

19.
Теоремы синусов и косинусов.

20.
Чему равно отношение площадей подобных
фигур.

21.
Свойство медианы (в каком отношении
делятся медианы в точке пересечения?)

22.
Свойство биссектрисы (в каком отношении
биссектриса делит противоположную
сторону?)

23.
Окружность и круг. Длина окружности.
Площадь круга. Длина дуги и площадь
сектора.

24.
Теорема о радиусе, проведенном в точку
касания.

25.
Центральный и вписанный углы. Связь
между ними.

26.
Теоремы о вписанных углах.

27.
Теорема о пересекающихся хордах.

28.
Теорема об отрезках длин касательных,
проведенных из одной точки.

29.
Теорема о секущей и касательной.

30.
Дан треугольник АВС. Постройте

а)
окружность, вписанную в данный
треугольник

б) окружность, описанную
вокруг данного треугольника.

Где
находятся центры этих окружностей?

31.
Еще три формулы площади треугольника
(через радиус вписанной окружности,
через радиус описанной окружности
и формула Герона).

32.
Когда можно вписать окружность
в четырехугольник? Когда — описать
вокруг четырехугольника?

(Программа
по стереометрии будет размещена в
ближайшее время.)

Отдельно —
тема «Векторы». Напомним, что на ЕГЭ
по математике векторы встречаются
в задаче В3. Они также пригодятся вам
в решении задачи С2.

Освоив
теорию, можно приступать к решению
сложных задач по геометрии, входящих
в часть С ЕГЭ. Мы рекомендуем
вам сборники:

Р. К. Гордин «ЕГЭ
2012. Математика. Задача С4. Геометрия.
Планиметрия» и

А. Г. Корянов
и А. А. Прокофьев «Пособие
по решению заданий типа С4». Можно
найти на сайте alexlarin.net.

Разбирая
и решая задания ЕГЭ по геометрии,
вы заметите очень интересную вещь.
Простые задачи из части В, разобранные
на нашем сайте, часто оказываются
базовыми схемами, на которых строятся
сложные С4.

Решая
на ЕГЭ задачи С4 по геометрии,
обращайте особое внимание на оформление.
Помните совет, который дал абитуриентам
автор бестселлера «Математика —
абитуриенту» В. В. Ткачук. Вот он,
этот ценнейший совет:

«Подробность
решения должна быть такова, чтобы его
мог понять человек в 10 (десять)
раз глупее вас

Синус,
косинус и тангенс острого угла
прямоугольного треугольника

Изучение
тригонометрии мы начнем с прямоугольного
треугольника. Определим, что такое синус
и косинус, а также тангенс и котангенс
острого угла. Это основы тригонометрии.

Напомним,
что прямой
угол —
это угол, равный 90º. Другими словами,
половина развернутого угла.

Острый
угол —
меньший 90º.

Тупой
угол —
больший 90º. Применительно к такому
углу «тупой» — не оскорбление,
а математический термин

Нарисуем
прямоугольный треугольник. Прямой угол
обычно обозначается С. Обратим
внимание, что сторона, лежащая напротив
угла, обозначается той же буквой,
только маленькой. Так, сторона, лежащая
напротив угла А, обозначается а.

Угол
А обозначается соответствующей греческой
буквой α.

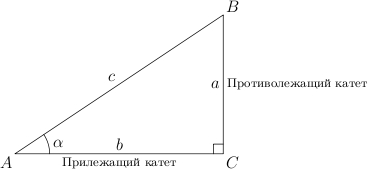
Гипотенуза
прямоугольного треугольника — это
сторона, лежащая напротив прямого угла.

Катеты —
стороны, лежащие напротив острых углов.

Катет а,
лежащий напротив угла α, называется
противолежащим
(по отношению к углу α). Другой
катет b, который лежит на одной
из сторон угла α, называется прилежащим.

Синус
острого угла в прямоугольном
треугольнике — это отношение
противолежащего катета к гипотенузе:

Косинус
острого угла в прямоугольном
треугольнике — отношение прилежащего
катета к гипотенузе:

Тангенс
острого угла в прямоугольном
треугольнике — отношение противолежащего
катета к прилежащему:

Другое
(равносильное) определение: тангенсом
острого угла называется отношение
синуса угла к его косинусу:

Котангенс
острого угла в прямоугольном
треугольнике — отношение прилежащего
катета к противолежащему (или, что
то же самое, отношение косинуса к синусу):

Обратите
внимание на основные соотношения
для синуса, косинуса, тангенса и
котангенса, которые приведены ниже. Они
пригодятся нам при решении задач.

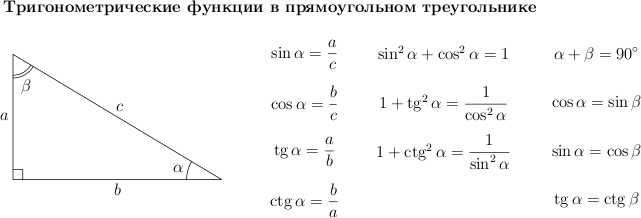
Давайте
докажем некоторые из них.

1. Сумма
   углов любого треугольника равна 180º.
   Значит, сумма
   двух острых углов прямоугольного
   треугольника равнa 90º.

2. С
   одной стороны,

   как
   отношение противолежащего катета
   к гипотенузе. С другой стороны,

   
   ,
   поскольку для угла β катет а будет
   прилежащим.

Получаем,
что cos β = sin A. Иными словами, cos (90º —
А) = sin A.

1. Возьмем
   теорему Пифагора: a²
   + b²
   = c².

Поделим
обе части на cos² A:

Мы
получили основное
тригонометрическое тождество:

1. Поделив
   обе части основного тригонометрического
   тождества на cos² A,
   получим:

Это
значит, что если нам дан тангенс острого
угла α, то мы сразу можем найти его
косинус.

Аналогично,

Хорошо,
мы дали определения и записали
формулы. А для чего все-таки нужны
синус, косинус, тангенс и котангенс?

Мы знаем,
что сумма
углов любого треугольника равна 180°.

Знаем
соотношение между сторонами
прямоугольного треугольника. Это теорема
Пифагора: a²
+ b²
= с².

Получается,
что зная два угла в треугольнике,
можно найти третий. Зная две стороны
в прямоугольном треугольнике, можно
найти третью. Значит, для углов —
свое соотношение, для сторон — свое.
А что делать, если в прямоугольном
треугольнике известен один угол (кроме
прямого) и одна сторона, а найти
надо другие стороны?

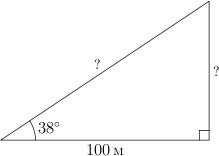
С этим
и столкнулись люди в прошлом,
составляя карты местности и звездного
неба. Ведь не всегда можно непосредственно
измерить все стороны треугольника.

Синус,
косинус и тангенс — их еще
называют тригонометрическими
функциями угла —
дают соотношения между сторонами
и углами
треугольника. Зная угол, можно найти
все его тригонометрические функции
по специальным таблицам. А зная
синусы, косинусы и тангенсы углов
треугольника и одну из его сторон,
можно найти остальные.

Мы тоже
нарисуем таблицу значений синуса,
косинуса, тангенса и котангенса для
«хороших» углов от 0 до 90°.

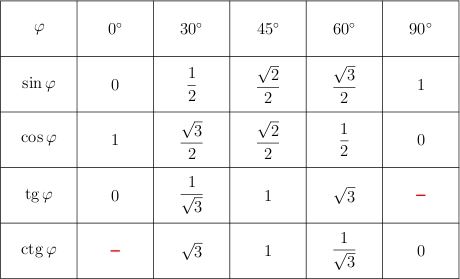
Обратите
внимание на два красных прочерка в
таблице. При соответствующих значениях
углов тангенс и котангенс не существуют.

Разберем
несколько задач по тригонометрии
из Банка заданий ФИПИ.

1.
В треугольнике ABC угол C равен 90°,
sin A = 0,1. Найдите cos B.

Задача
решается за четыре секунды.

Поскольку
А+В = 90°, sin A = cos B = 0,1.

2.
В треугольнике ABC угол C равен 90°, АВ
= 5,

.
Найдите AC.

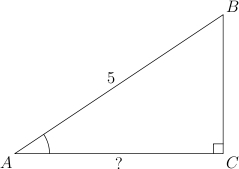
Имеем:

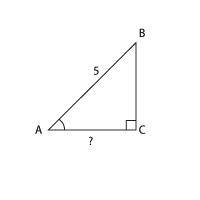
Отсюда

Найдем
АС по теореме Пифагора.

Задача
решена.

Часто
в задачах встречаются треугольники
с углами 90°, 30° и 60° или
с углами 90°, 45° и 45°. Основные
соотношения для них запоминайте наизусть!

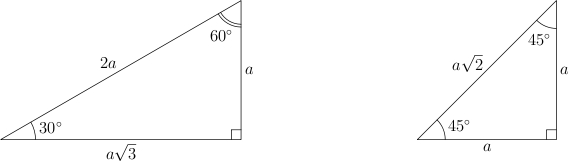
Для
треугольника с углами 90°, 30° и 60°
катет, лежащий напротив угла в 30°,
равен половине
гипотенузы.

Треугольник
с углами 90°, 45° и 45° —
равнобедренный. В нем гипотенуза в

раз
больше катета.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #