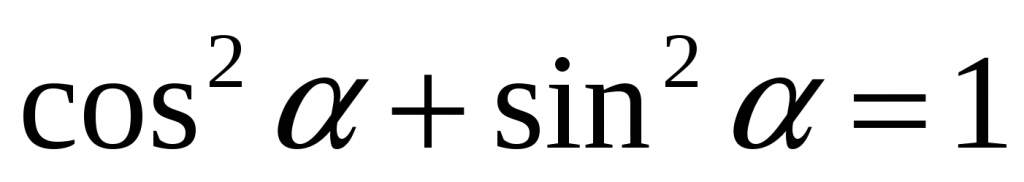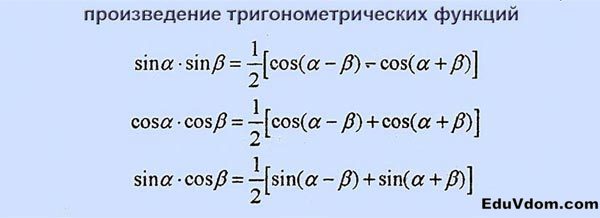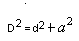На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.
Содержание
Формулы для ЕГЭ по профильной математике. Алгебра
Формулы сокращенного умножения
Квадрат суммы: (a + b)² = a² + 2ab + b²
Квадрат разности: (a – b)² = a² – 2ab + b²
Разность квадратов: a² – b² = (a + b)(a – b)
Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)
Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)
Прогрессия
Арифметическая
Геометрическая
Таблица степеней
Свойства степеней
Таблица квадратов
Интенсивы по подготовке к региональному этапу ВсОШ
Все, что нужно знать
для победы, за 7 дней!
Свойства корней
Тригонометрия
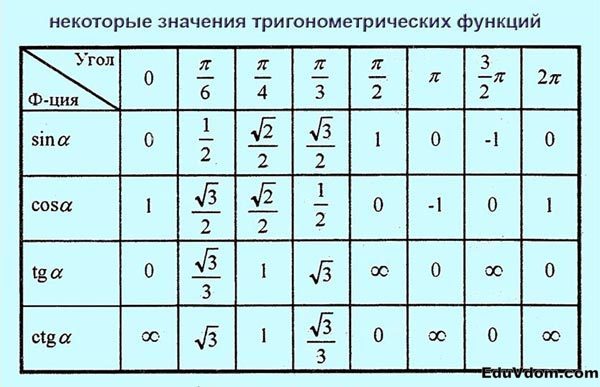
Таблица значений тригонометрических функций
Тригонометрическая окружность
Тригонометрические формулы
Обратные тригонометрические функции
Преобразование суммы и разности в произведение
Регулярные курсы по подготовке к олимпиадам и ЕГЭ
Поступаем в вуз мечты без проблем!
Вероятность
Вероятность события А: m – благоприятные, n – общее число событий
P(A) = m/n
События А и В происходят одновременно: A · B
Независимые события: P(A · B) = P(A) · P(B)
Зависимые события: P(A · B) = P(A) · P(B | A)
Происходит или А, или В: A + B
Несовместные события: P(A + B) = P(A) + P(B)
Совместные события: P(A + B) = P(A) + P(B) – P(A · B)
Свойства модуля
Производные
Основные правила дифференцирования
Таблица производных
Первообразные
Логарифмы
Квадратные уравнения
Дискриминант
Теорема Виета
Разложение на множители
Формулы для ЕГЭ по профильной математике. Геометрия
Планиметрия
Треугольник
Следствие из теоремы косинусов:
Длина биссектрисы (через угол):
Длина биссектрисы (через отрезки):
Прямоугольный треугольник
24 декабря – 20 января
5-11 классы
Онлайн-олимпиада Коалиции
Равносторонний треугольник
Аргументы для итогового сочинения
Подборка лучших аргументов
Равносторонний шестиугольник
Площадь внутреннего треугольника:
Площадь внутреннего прямоугольника:
Ромб
Трапеция
Произвольный четырёхугольник
Окружность
Стереометрия
Выводы
Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.
А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.
Поделиться в социальных сетях
Какими формулами вам приходится пользоваться чаще всего?
Межтекстовые Отзывы
Посмотреть все комментарии
Читайте также
Ученики, сдающие базовую математику, почти не тратят времени на подготовку к ней, ведь в экзамене нужно решить лишь задания, которые требуют самых основ. Тем же выпускникам, которые хотят поступать в технические вузы, предстоит готовиться не только к предметам по выбору, но и к профилю. В этой статье мы расскажем, какие формулы для ЕГЭ по математике (профильный уровень) сделают подготовку легче, а баллы на экзамене — выше.
Какие формулы необходимы для сдачи ЕГЭ по профильной математике?
Помимо очевидного, что для сдачи профиля нужно уметь складывать, вычитать и умножать, необходимы еще некоторые знания. Все это проходится в течение школы, но повторить или заполнить пробелы перед экзаменом нужно обязательно. Вот, что пригодится:
- Формулы сокращенного умножения;
- Арифметическая и геометрическая прогрессии;
- Вероятность;
- Свойства степеней;
- Свойства логарифмов;
- Тригонометрия;
- Производные;
- Первообразные.
Список внушительный, но вполне реальный, чтобы его выучить. Для того, чтобы лишний раз не гуглить в интернете «формулы для ЕГЭ по математике профильный уровень», приложим их ниже. А начнем по порядку из списка выше.
Формулы сокращённого умножения
Первые в нашем списке – формулы сокращенного умножения – нужны для решения задания №9 из профильного уровня. Вам встретятся задачи на преобразование выражений, поэтому умение это делать будет вознаграждено баллами.
Вот то, что будет вашим спасательным кругом:
Есть те, которые знать не обязательно. Но чем большими знаниями вы будете обладать, тем легче вам будет на экзамене. Вот они:
Умея применять эти формулы для ЕГЭ по математике, профильный уровень вам уже будет решить легче. Но это далеко не все, что нужно знать, чтобы получить сто баллов за ЕГЭ.
Арифметическая и геометрическая прогрессии
Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:
Вероятность
Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:
Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.
Свойства степеней
Эти свойства нужно знать и для того, чтобы решить «базу», так что гуманитарии тоже могут обратить внимание на это:
Как вы видите, запоминать не очень много, зато формулы не самые простые. Но есть еще сложнее, и сейчас узнаем, какие они.
Свойства логарифмов
Формулы логарифмов лучше всего начать с их определения:
Теперь перейдем к более сложному:
Тригонометрия
Тригонометрические уравнения встречаются в задании №13. Для того, чтобы заработать баллы, нужно знать это:
Но это еще не все. Есть такая вещь, как основное тригонометрическое тождество. Вот оно:
Формулы двойного угла:
Формулы суммы и разности аргументов:
Преобразование суммы и разности в произведение:
Формулы половинного аргумента:
На этом с тригонометрией все.
Производные
Начнем с основных правил дифференцирования:
Уравнение касательной:
Производные элементарных функций:
Закончим эту статью первообразными.
Первообразные
Она выглядит так:
Таблица первообразных:
Итог
То, что работа предстоит колоссальная — и правда, и нет. Да, придется хорошо постараться, чтобы набрать высокие баллы, так как составители ЕГЭ все больше усложняют экзамен. С другой стороны, хотя бы часть формул, описанных выше, вы уже знаете. А значит, работы хоть на немного, но меньше. А это ли не счастье в такие тяжелые времена подготовки?
- Треугольник
- Четырехугольники
- Окружность и круг
- Призма
- Пирамида
- Усеченная пирамида
- Цилиндр
- Конус
- Усеченный конус
- Сфера и шар
1. Формулы сокращённого умножения
Наверх
2. Модуль числа
Определение:
Основные свойства модуля:
Наверх
3. Степень с действительным показателем
Свойства степени с действительным показателем
Пусть Тогда верны следующие соотношения:
Наверх
4. Корень n-ой степени из числа
Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
Основные свойства арифметического корня:
Наверх
5. Логарифмы
Определение логарифма:
Основное логарифмическое тождество:
Основные свойства логарифмов
Пусть
Тогда верны следующие соотношения:
Наверх
6. Арифметическая прогрессия
Формула n-го члена арифметической прогрессии:
Характеристическое свойство арифметической прогрессии:
Сумма n первых членов арифметической прогрессии:
При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
7. Геометрическая прогрессия
Формула n-го члена геометрической прогрессии:
Характеристическое свойство геометрической прогрессии:
Сумма n первых членов геометрической прогрессии:
При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
8. Бесконечно убывающая геометрическая прогрессия
Сумма бесконечно убывающей геометрической прогрессии:
Наверх
9. Основные формулы тригонометрии
Зависимость между тригонометрическими функциями одного аргумента:
Формулы сложения:
Формулы тригонометрических функций двойного аргумента:
Формулы понижения степени:
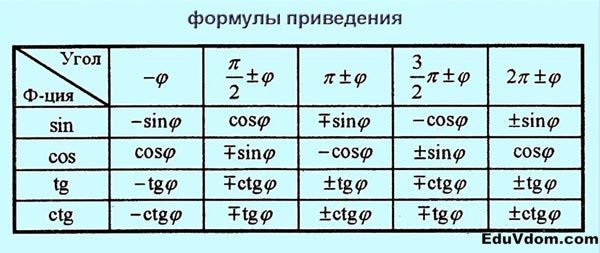
Формулы приведения
Все формулы приведения получаются из соответствующих формул сложения. Например:
Применение формул приведения укладывается в следующую схему:
— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;
— определяется знак приводимой функции;
— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или
, то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид
, то функция названия не меняет.
Например, получим формулу :
— — IV четверть;
— в IV четверти тангенс отрицательный;
— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,
Формулы преобразования суммы тригонометрических функций в произведение:
Формулы преобразования произведения тригонометрических функций в сумму:
Наверх
10. Производная и интеграл
Таблица производных некоторых элементарных функций
Правила дифференцирования:
1.
2.
3.
4.
5.
Уравнение касательной к графику функции в его точке
:
Таблица первообразных для некоторых элементарных функций
Правила нахождения первообразных
Пусть ― первообразные для функций
и
соответственно, a, b, k ― постоянные,
Тогда:
— ― первообразная для функции
— ― первообразная для функции
— ― первообразная для функции
— Формула Ньютона-Лейбница:
1. Треугольник
Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно;
― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно;
― длины высот AA2, BB2, CC2 треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC;
― площадь треугольника ABC. Тогда имеют место следующие соотношения:
(теорема синусов);
(теорема косинусов);
Наверх
2. Четырёхугольники
Параллелограмм
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.
Площадь четырехугольника
Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Наверх
3. Окружность и круг
Соотношения между элементами окружности и круга
Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга, — длина дуги в
градусов,
— длина дуги в
радиан,
— площадь сектора, ограниченного дугой в n градусов,
— площадь сектора, ограниченного дугой в
радиан. Тогда имеют место следующие соотношения:
Вписанный угол
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, — прямой.
Вписанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Описанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.
Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны
Наверх
4. Призма
Пусть H ― высота призмы, AA1 ― боковое ребро призмы, ― периметр основания призмы,
― площадь основания призмы,
― площадь боковой поверхности призмы,
― площадь полной поверхности призмы, V ― объем призмы,
― периметр перпендикулярного сечения призмы,
― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
Свойства параллелепипеда:
— противоположные грани параллелепипеда равны и параллельны;
— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;
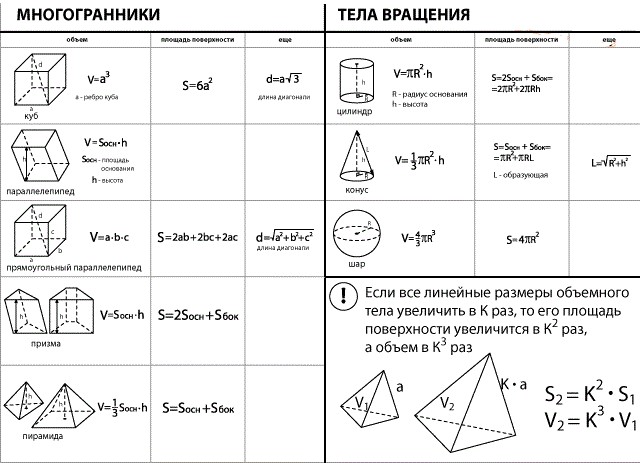
— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Наверх
5. Пирамида
Пусть H ― высота пирамиды, ― периметр основания пирамиды,
― площадь основания пирамиды,
― площадь боковой поверхности пирамиды,
― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:
;
.
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то
Наверх
6. Усечённая пирамида
Пусть H ― высота усеченной пирамиды, и
― периметры оснований усеченной пирамиды,
и
― площади оснований усеченной пирамиды,
― площадь боковой поверхности усеченной пирамиды,
― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.
Тогда имеют место следующие соотношения:
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то:
Наверх
7. Цилиндр
Пусть h ― высота цилиндра, r ― радиус цилиндра, ― площадь боковой поверхности цилиндра,
― площадь полной поверхности цилиндра, V ― объем цилиндра.
Тогда имеют место следующие соотношения:
Наверх
8. Конус
Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса, ― площадь боковой поверхности конуса,
― площадь полной поверхности конуса, V ― объем конуса.
Тогда имеют место следующие соотношения:
Наверх
9. Усечённый конус
Пусть h ― высота усеченного конуса, r и ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,
― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:
Наверх
10. Сфера и шар
Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы, ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,
― объем сегмента, высота которого равна h,
― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:
Наверх
Формулы для профильного ЕГЭ-2022 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c``a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` |
`kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Математика – обязательный предмет на ЕГЭ, ее придется сдавать всем выпускникам – по базовому или профильному уровню. Какие требования предъявляются к школьнику на ЕГЭ по математике, что можно и что нельзя с собой брать на экзамен: разъяснения Рособрнадзора.
Выпускники российских школ в среду, 29 мая будут сдавать ЕГЭ по математике. Минпросвещения в 2019 году изменило порядок проведения этого экзамена: если раньше школьник мог выбрать для сдачи и базовый, и профильный уровень, то сейчас такой возможности нет. Эксперты решили, что проходить тестирование сразу по двум уровням не имеет смысла: те, кто выбирает профиль, легко выполнит и базу, и наоборот – выбравшие базовый уровень с профильным просто не справятся.
Изменения в правилах проведения ЕГЭ по математике вызывают вопросы у школьников и родителей: что можно с собой брать на экзамен того или другого уровня, и есть ли какие-либо отличия в правилах проведения экзамена.
Предметы, разрешенные на ЕГЭ по профильной математике
Перечень того, что допускается проносить на ЕГЭ, ежегодно устанавливается Рособрнадзором и Минпросом. В 2019 году список совсем небольшой, с собой можно взять только ручку (гелевую, черную) и линейку. Справочники, которым разрешено пользоваться, выпускники могут попросить непосредственно на экзамене.
Категорически не разрешается проносить:
- смартфоны;
- планшеты;
- калькуляторы;
- справочные материалы.
Нарушение установленных правил может привести к тому, что ученика выгонят.
Задания ЕГЭ по математике профильного уровня
Выпускники, выбравшие профиль, должны будут выполнить 19 заданий разного уровня сложности, самые сложные помечаются звездочкой. Эксперты отмечают, что в 2019 году задания стали сложнее, особенно во второй части (с 13 по 19 пункты). Так, 14-я задача сформулирована таким образом, что школьнику потребуется произвести дополнительные построения, подразумевающие хорошее пространственное воображение и безусловное понимание материала. 17-я и 18-я задачи также требует уверенного владения предметом и способностью видеть, какие графические процессы скрываются за формулами: просто подставить данные под какую-либо формулу не получится.
Разработчики заданий для ЕГЭ по математике профильного уровня подчеркивают, что с каждым годом они изменяются таким образом, чтобы как можно точнее выявить способность учеников к самостоятельному мышлению и нестандартным решениям.
Экзамен по профильной математике продлится 253 минуты.
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF: Скачайте pdf файл.
Можете записаться на занятия к репетитору математики, если что-то не понятно.
По разделам:
Степени и корни:
Сокращенное умножение
:
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:
Логарифмы:
Формулы тригонометрии, тождества:
Тригонометрические уравнения:
Значения тригонометрических функций:
Формулы приведения:
Сумма и разность углов:
Формулы двойного и тройного аргумента:
Формулы половинного аргумента:
Сумма и разность тригонометрических функций:
Произведение тригонометрических функций:
Производная: признаки возрастания, убывания, минимума функции:
Дифференциальное исчисление:
Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:
Стереометрия: объёмы, площади поверхностей:
Обратиться к репетитору по математике.
На ЕГЭ формулами пользоваться нельзя, нужно их помнить!
В этой подборке формул использованы 3 основных принципа, для упрощения запоминания:
- Выбраны только те формулы, которые могут встретиться на ЕГЭ по математике (это лишь часть того, что изучено в школе);
- Формулы разобраны на тематические блоки;
- Блоки формул выделены цветовым фоном, который позволяет, всего после нескольких обращений, вспоминать картинку и буквально читать с нее нужную формулу.
Как легко запомнить именно нужные формулы из всего курса математики?
Для подготовки нужно выбрать такое оформление математических формул, чтобы они отложились в памятки наиболее эффективно.
Обобщающий тест по русскому языку
Рейтинговый контроль по русскому языку (10-11 классы).
Минпросвещения вводит исполнение гимна России во всех школах с 1 сентября
Образование | Сегодня, 15:00
Исполнение гимна РФ и поднятие государственного флага в начале учебной недели будут проводиться в каждой школе с 1 сентября следующего учебного года, заявил во вторник глава министерства просвещения Сергей Кравцов на первом всероссийском школьном историческом форуме «Сила в правде!» в Музее Победы.
Консультация по биологии
Биология | Сегодня, 14:58
Разработчики экзаменационных материалов, учителя и выпускники, расскажут, как подготовиться к экзамену, об особенностях заданий в ЕГЭ и ответят на вопросы старшеклассников.
Главные формулы для егэ по профильной математике
Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:
- таблица квадратных чисел от 0 до 99;
- свойства арифметического квадратного корня;
- формулы сокращенного умножения;
- корни квадратного уравнения;
- свойства степени и логарифма;
- теорема Пифагора;
- формула расчета длины окружности и площади круга;
- расчет средней линии треугольника и трапеции;
- радиус вписанной и описанной окружности правильного треугольника;
- формулы расчета площади планиметрических фигур;
- вычисление поверхностей и объемов тел;
- основные тригонометрические функции и тождества;
- график линейной функции;
- геометрический смысл производной.
Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.
Дробно рациональные уравнения
- Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
- Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые не удовлетворяют условию ОДЗ.
Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения
Тригонометрия
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Тригонометрические формулы преобразования суммы в произведение
Произведение синуса и косинуса:
Формулы понижения степени
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Формулы приведения задаются в виде таблицы:
Особенности уровней ЕГЭ по математике
В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.
Базовый уровень ЕГЭ по математике
Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.
Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.
В ЕГЭ по математике базового уровня 6 тематических блоков:
Тематические блоки, ЕГЭ по математике 2022, базовый уровень
Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.
Профильный уровень ЕГЭ по математике
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.
Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.
Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.
База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались
Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!
Несовместные события
Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)
Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:
На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:
Теория к заданию 4 из ЕГЭ по математике (профильной)
Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов
$P(A)=/$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.
Вероятность события — это число из отрезка $$
В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.
Найдем количество желтых автомобилей:
Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна $<15>/<50>=<3>/<10>=0,3$
Противоположные события
Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
$<(А)><->$.
Независимые события
Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.
Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:
Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.
Вероятность $Р(А)$ — выиграет первый билет.
Вероятность $Р(В)$ — выиграет второй билет.
События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей
Несовместные события
Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)
Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:
На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:
Совместные события
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.
Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:
В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.
Обозначим события, пусть:
$А$ = кофе закончится в первом автомате,
$В$ = кофе закончится во втором автомате.
$A·B =$ кофе закончится в обоих автоматах,
$A + B =$ кофе закончится хотя бы в одном автомате.
По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.
События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:
$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$
Формулы для базового ЕГЭ-2022 по математике
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | Эти две формулы заучивать не обязательно, но желательно |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | m — число благоприятных событийn — общее число событий |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | Когда вероятность одного события (А) не зависит от другого события (B) |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | `P(B|A)` — вероятность события B при условии, что событие A наступило |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | Когда невозможно наступление обоих событий одновременно, т.е. `P(A*B)=0` |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` | Когда оба события могут наступить одновременно |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c«a^c=b` | Определение логарифма |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Геометрия
Планиметрия (2D)
| Тригонометрия: | `sinA=a/c` `cosA=b/c` | |
| `text(tg)A=sinA/cosA=a/b` | ||
| Теорема косинусов: | `c^2=a^2+b^2-2ab*cosC` | |
| Теорема синусов: | `a/sinA=b/sinB=c/sinC=2R` | где R — радиус описанной окружности |
| Уравнение окружности: | `(x-x_0)^2+(y-y_0)^2=R^2` | где `(x_0;y_0)` — координаты центра окружности |
| Соотношение вписанного и центрального углов: | `beta=alpha/2=(uualpha)/2` | |
| Описанная окружность, треугольник: | `R=(abc)/(4S)` | См. также теорему синусов. Центр лежит на пересечении срединных перпендикуляров. |
| Вписанная окружность, треугольник: | `r=S/p` | где p — полупериметр многоугольника. Центр лежит на пересечении биссектрис. |
| Описанная окружность, четырёхугольник: | `alpha+gamma=beta+delta=180^circ` | |
| Вписанная окружность, четырёхугольник: | `a+c=b+d` | |
| Свойство биссектрисы: | `a/x=b/y` | |
| Теорема о пересекающихся хордах: | `AM*BM=CM*DM` | Эти теоремы необходимо уметь выводить |
| Теорема об угле между касательной и хордой: | `alpha=1/2uuAB` | |
| Теорема о касательной и секущей: | `CM^2=AM*BM` | |
| Теорема об отрезках касательных: | `AB=AC` |
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | У ромба `varphi=90^@` |
| Трапеция: | `S=(a+b)/2*h` |
Обратные тригонометрические функции и простейшие тригонометрические уравнения
Арккосинус
Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $$, косинус которого равен $а$.
$arcos(-a) = π-arccosa$, где $0≤а≤1$
Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение
$t=±arccos a+2πk; k∈Z$
Частные случаи
$cos t =1, t = 2πk;k∈Z$
$cos t = 0, t = <π>/<2>+πk;k∈Z$
$cos t = -1, t=π+2πk;k∈Z$
Найдите наименьший положительный корень уравнения $сos<2πx>/<3>=-<√3>/<2>$
Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на $<2π>/<3>$
Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения
Нам подходит $1,25$ – это и есть результат
Арксинус
Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-<π>/<2>;<π>/<2>]$, синус которого равен $а$.
$arcsin(-a)= — arcsin a$, где $0≤а≤1$
Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:
$1. t_1 = arcsin a+2πk;k∈Z$
$t_2 = (π- arcsin a)+ 2πk;k∈Z$
$2. t=(-1)^n arcsin a+πn; n∈Z$
$3.$ Частные случаи
Арктангенс
$arctg a$ — это такое число, из отрезка $[-<π>/<2>;<π>/<2>]$, тангенс которого равен $а$.
Основные формулы для профильного ЕГЭ
Выпускники, планирующие сдавать профиль, ставятся в более жесткие условия, чем те, кто выбрал базовый уровень. Учитывая то, что они видят перспективу своего дальнейшего обучения по направлениям, тесно или напрямую связанным с математикой, к их знаниям предъявляются повышенные требования. В частности, на официальные справочные материалы особенно рассчитывать не приходится. Все, что в них есть, это 5 тригонометрических тождеств.
Основываясь на данных, опубликованных на сайте ФИПИ, с большой долей вероятности потребуется знание следующих формул для сдачи ЕГЭ по профильной математике:
- правила сокращенного умножения;
- арифметическая и геометрическая прогрессии;
- основы вероятностной теории;
- свойства степеней и логарифмов;
- азы тригонометрии (формулы двойного угла, суммы и разности аргументов; алгоритм преобразования разности и суммы в произведение; обратные функции);
- производная (правила дифференцирования, элементарнее функции и уравнение касательной);
- первообразная;
- двухмерная планиметрия;
- правила нахождения площадей геометрических фигур;
- трехмерная стереометрия.
Опытные учителя и репетиторы собрали все формулы по математике, которые приходилось использовать на ЕГЭ в последние три года:
- ЕГЭ по математике – формулы для алгебры и начал анализа
- Формулы ЕГЭ – математика, раздел геометрия
Материалы для скачивания – в формате pdf.
Выученные назубок формулы к ЕГЭ по математике – это только часть пути к успешной сдаче, надо еще научиться правильно применять их. Хорошую практику даст решение сложных задач.
Квадратное уравнение и формула разложения квадратного трехчлена на множители
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Игрек вершины параболы:
Независимые события
Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.
Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:
Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.
Вероятность $Р(А)$ — выиграет первый билет.
Вероятность $Р(В)$ — выиграет второй билет.
События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей
Формулы для ОГЭ-2022 по математике
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | Эти две формулы заучивать не обязательно, но желательно |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | m — число благоприятных событийn — общее число событий |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | Когда вероятность одного события (А) не зависит от другого события (B) |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | `P(B|A)` — вероятность события B при условии, что событие A наступило |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | Когда невозможно наступление обоих событий одновременно, т.е. `P(A*B)=0` |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` | Когда оба события могут наступить одновременно |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Геометрия
Планиметрия (2D)
| Тригонометрия: | `sinA=a/c` `cosA=b/c` | |
| `text(tg)A=sinA/cosA=a/b` | ||
| Теорема косинусов: | `c^2=a^2+b^2-2ab*cosC` | |
| Теорема синусов: | `a/sinA=b/sinB=c/sinC=2R` | где R — радиус описанной окружности |
| Уравнение окружности: | `(x-x_0)^2+(y-y_0)^2=R^2` | где `(x_0;y_0)` — координаты центра окружности |
| Соотношение вписанного и центрального углов: | `beta=alpha/2=(uualpha)/2` | |
| Описанная окружность, треугольник: | `R=(abc)/(4S)` | См. также теорему синусов. Центр лежит на пересечении срединных перпендикуляров. |
| Вписанная окружность, треугольник: | `r=S/p` | где p — полупериметр многоугольника. Центр лежит на пересечении биссектрис. |
| Описанная окружность, четырёхугольник: | `alpha+gamma=beta+delta=180^circ` | |
| Вписанная окружность, четырёхугольник: | `a+c=b+d` | |
| Свойство биссектрисы: | `a/x=b/y` | |
| Теорема о пересекающихся хордах: | `AM*BM=CM*DM` | Эти теоремы необходимо уметь выводить |
| Теорема об угле между касательной и хордой: | `alpha=1/2uuAB` | |
| Теорема о касательной и секущей: | `CM^2=AM*BM` | |
| Теорема об отрезках касательных: | `AB=AC` |
Площади фигур:
Применение формул сокращенного умножения
1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.
2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.
3. Разность квадратов раскладывается на произведение разности чисел и их сумму.
4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.
5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.
6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.
7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.
Задание №8 ЕГЭ по математике профильного уровня
Тогда диагональ куба
3 комментариев
откуда берем 4 первоначально?
Радиус (R) – это диаметр (D) поделить на 2, следовательно, R^2 = (D/2)^2 (возводим числитель и знаменатель в квадрат), получаем D^2/4
Формула диагонали квадрата = а√3 значит а√3=√48,; а=√48:3=√16=4, сторона равна 4, значит Vкуба равно а*а*а=64.
Какие формулы понадобятся на егэ по математике профильный уровень

● краткая теория по базовому курсу;
● теория по вычислениям и преобразованиям (базовый уровень);
● теория по профильному уровню
● решение каждого задания профильного курса
● основные формулы по планиметрии и стереометрии;
● решение геометрических задач;
● задачи по алгебре:
• на движение;
• на совместную работу;
• на проценты;
• на сплавы и смеси;
● материалы по алгебре и геометрии;
● теория по каждому заданию (1-12);
● основные теоремы и определения по геометрии;
● теория по 86 темам:
• Графики числовых функций
1-3. Преобразование графиков
4. Чтение графиков
• Неравенства (1)
1. Числовые неравенства и их свойства
2. Графическое решение неравенств
3. Двойное неравенство
4. Числовые промежутки
5. Линейные неравенства
6. Системы линейных неравенств
7. Квадратные неравенства
8. Дробно — рациональные неравенства
• Неравенства (2)
1. Метод интервалов
2. Показательные неравенства
3. Логарифмические неравенства
4. Тригонометрические неравенства
5. Графическое решение неравенств
6. Неравенства с двумя переменными
• Производные
1. Производные основных функций
2. Вычисление производной
3. Исследование функции с помощью производной
4. Касательная к графику функции
5. Наибольшее и наименьшее значения функций
6. График производной функции
7. Вторая производная функции. Выпуклость функции, точки экстремумов и перегиба
• Решение уравнений (1)
1. Линейные уравнение с одной переменной
2-3. Системы уравнений с двумя переменными
4. Неполные квадратные уравнения
5. Квадратные уравнения
6. Теорема Виета
7. Дробные уравнения
8. Уравнения с двумя переменными и их графики
9. Графическое решение уравнений
10. Графическое решение систем линейных уравнений
11. Графическое решение систем НЕлинейных уравнений
12. Выражения. Тождества. Уравнения
• Решение уравнений (2)
1. Методы решения уравнений
2-3. Иррациональные уравнение
4. Показательные уравнения
5. Логарифмические уравнения
6. Тригонометрические уравнения
7-8. Решение тригонометрических уравнений
9. Графическое решение уравнений
• Тригонометрия и логарифмы
1-3. Формулы тригонометрии
4-6. Логарифм и его свойства
• Формулы и преобразование выражений
1-2. Формулы сокращенного умножения
3. Степени с натуральным и целым показателями
4. Степень с рациональным показателем
5. Квадратный корень и его свойства
6. Действия с квадратными корнями
7. Корни натуральной степени
8. Одночлены и многочлены
9. Действия с многочленами
10. Разложение многочлена на множители
• Функции (1)
1. Прямая пропорциональность
2. Обратная пропорциональность
3. Линейная функция
4. Функции y=x2 и y=x3
5. Функции с корнем
6-7. Квадратичная функция
8. Функции и их графики
• Функции (2)
1. Тригонометрическая окружность. Синус и косинус угла
2. Тригонометрическая окружность. Тангенс и котангенс угла
3. Тригонометрические функции — синус и косинус
4. Тригонометрические функции — тангенс и котангенс
5. Обратные тригонометрические функции — арксинус и арккосинус
6. Обратные тригонометрические функции — арктангенс и арккотангенс
7. Степенная функция
8. Показательная функция
9. Логарифмическая функция
10. Графики функций
11. Взаимно-обратные функции
12. Свойства функций
13. Асимптоты графиков функций
• Числа, последовательности, проценты
1. Числовые множества
2. Числовые последовательности
3. Арифметическая прогрессия
4-5. Геометрическая прогрессия
6. Сложные проценты
• Многоугольник
1. Свойства параллелограммов
2. Трапеция
3. Признаки параллелограмма и его видов
4. Свойства многоугольников
5. Теорема Фалеса
6. Правильные треугольник и четырехугольник
7. Правильные шестиугольник и восьмиугольник
8-9. Площадь многоугольника
• Окружность
1. Окружность. Хорды и касательные
2. Окружность, описанная около треугольника
3. Окружность, вписанная в треугольник
4. Центральные и вписанные углы
5. Свойства хорд и секущих
6. Вписанные и описанные четырехугольники
7. Длина окружности и площадь круга
• Треугольник
1. Виды треугольников. Равные треугольники
2. Признаки равенства треугольников
3. Основные линии в треугольнике
4. Равнобедренный треугольник
5. Отношения отрезков в треугольнике
6. Прямоугольный треугольник
7. Теорема Пифагора
8. Синус, косинус, тангенс прямоугольного треугольника
9. Подобие треугольников
10. Теорема косинусов
11. Теорема синусов
12-13. Площадь треугольника
• Углы
1. Измерение отрезков и углов
2. Смежные и вертикальные углы
3. Биссектриса угла. Перпендикулярные прямые
4. Признаки параллельности прямых
5. Свойства параллельных прямых
6. Сумма углов треугольника. Внешний угол