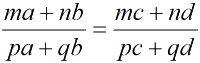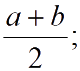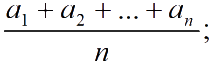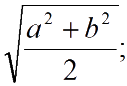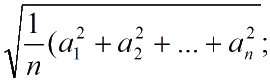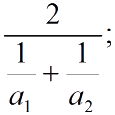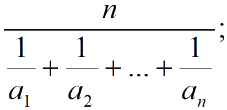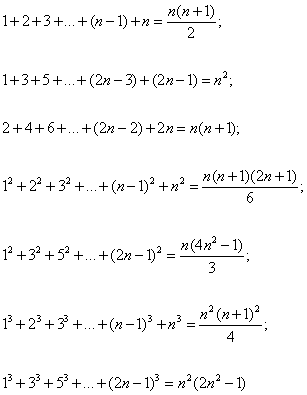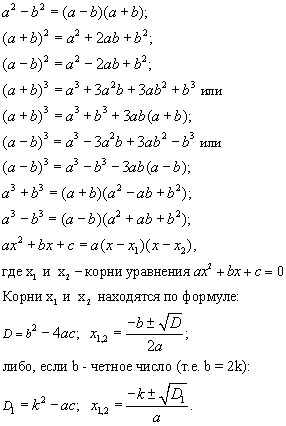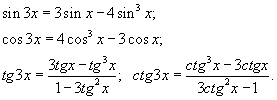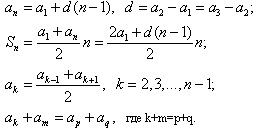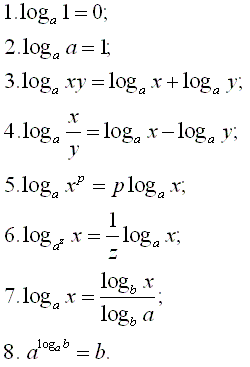Оглавление:
- Формулы сокращенного умножения
- Квадратное уравнение и формула разложения квадратного трехчлена на множители
- Свойства степеней и корней
- Формулы с логарифмами
- Арифметическая прогрессия
- Геометрическая прогрессия
- Тригонометрия
- Тригонометрические уравнения
- Геометрия на плоскости (планиметрия)
- Геометрия в пространстве (стереометрия)
- Координаты
- Таблица умножения
- Таблица квадратов двухзначных чисел
- Расширенная PDF версия документа «Все главные формулы по школьной математике»
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению…
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа «Все главные формулы по школьной математике»:
К оглавлению…
На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.
Содержание
Формулы для ЕГЭ по профильной математике. Алгебра
Формулы сокращенного умножения
Квадрат суммы: (a + b)² = a² + 2ab + b²
Квадрат разности: (a – b)² = a² – 2ab + b²
Разность квадратов: a² – b² = (a + b)(a – b)
Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)
Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)
Прогрессия
Арифметическая
Геометрическая
Таблица степеней
Свойства степеней
Таблица квадратов
Интенсивы по подготовке к региональному этапу ВсОШ
Все, что нужно знать
для победы, за 7 дней!
Свойства корней
Тригонометрия
Таблица значений тригонометрических функций
Тригонометрическая окружность
Тригонометрические формулы
Обратные тригонометрические функции
Преобразование суммы и разности в произведение
Регулярные курсы по подготовке к олимпиадам и ЕГЭ
Поступаем в вуз мечты без проблем!
Вероятность
Вероятность события А: m – благоприятные, n – общее число событий
P(A) = m/n
События А и В происходят одновременно: A · B
Независимые события: P(A · B) = P(A) · P(B)
Зависимые события: P(A · B) = P(A) · P(B | A)
Происходит или А, или В: A + B
Несовместные события: P(A + B) = P(A) + P(B)
Совместные события: P(A + B) = P(A) + P(B) – P(A · B)
Свойства модуля
Производные
Основные правила дифференцирования
Таблица производных
Первообразные
Логарифмы
Квадратные уравнения
Дискриминант
Теорема Виета
Разложение на множители
Формулы для ЕГЭ по профильной математике. Геометрия
Планиметрия
Треугольник
Следствие из теоремы косинусов:
Длина биссектрисы (через угол):
Длина биссектрисы (через отрезки):
Прямоугольный треугольник
24 декабря – 20 января
5-11 классы
Онлайн-олимпиада Коалиции
Равносторонний треугольник
Аргументы для итогового сочинения
Подборка лучших аргументов
Равносторонний шестиугольник
Площадь внутреннего треугольника:
Площадь внутреннего прямоугольника:
Ромб
Трапеция
Произвольный четырёхугольник
Окружность
Стереометрия
Выводы
Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.
А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.
Поделиться в социальных сетях
Какими формулами вам приходится пользоваться чаще всего?
Межтекстовые Отзывы
Посмотреть все комментарии
Читайте также
Формулы ЕГЭ по математике
- 27.09.2013
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF:
Скачайте в pdf файле.
По разделам:
Комментарии
+30
#1
Плотников А.
04.06.2014 20:58
Класный сайт!
Цитировать
-4
#2
Гость
18.09.2014 11:22
Цитирую лоло:
школоло не осилило
Цитировать
+10
#6
Ann
10.04.2015 19:04
Благодарю за формулы 
Цитировать
+6
#7
Мария
25.04.2015 08:05
Спасибо огромное за такой хороший сайт! 
Цитировать
+1
#9
настюша
16.05.2015 10:03
не все формулы по заданиям 
Цитировать
+20
#10
Алина
30.05.2015 10:52
Очень помогли формулы. Ребята, кто ссдает ЕГЭ, удачи нам!
Цитировать
+2
#12
Анон
02.08.2015 12:30
Спасибо.
Прошу выложить так же и в разрешении .jpg
Так удобнее просматривать и использовать на разных девайсах.
Цитировать
-2
#13
Анон
02.08.2015 12:32
Цитирую Анон:
Спасибо.
Прошу выложить так же и в разрешении .jpg
Так удобнее просматривать и использовать на разных девайсах.
Оказалось они под катом, я имел в виду весь pdf-файл в формате .jpg КАЖДУЮ картинку.
Спасибо.
Цитировать
+5
#15
Мария
30.09.2015 06:52
Здравствуйте! Спасибо за формулы и такое яркое цветное оформление — это помогает запомнить. Не могли бы вы еще дополнить свой список формул формулами, связанными с прогрессиями — это тоже очень важно.
Цитировать
+4
#16
Мария
30.09.2015 07:18
и еще нет формул поверхности, боковой и общей, у пирамиды.
Цитировать
0
#17
настя
01.03.2016 15:18
Цитирую galaxe:
спасиб большое

кто сдает гиа тому сюда
Цитировать
+4
#18
настя
01.03.2016 15:18
думаю мне пригодится для подготовки к гиа
Цитировать
-4
#21
а
03.03.2017 18:44
а это на профильный матан ил на базу?
Цитировать
+2
#23
Саша
28.01.2019 20:56
спасибо большое, очень помогли 
Цитировать
+3
#24
Алексей Алексеевич
05.02.2019 14:23
Спасибо. А то нихера не помню а ЕГЭ уже скороо!!!!
Цитировать
-2
#25
Glebasta_Rhymes
13.05.2019 19:41
а где формулы призмы????????? ???????? 
Цитировать
0
#26
Татьяна
16.05.2019 04:06
А векторная часть? В 9 классе есть раздел векторов, координат векторов. Не нашла у вас этот раздел(((
Цитировать
+5
#27
Татьяна
16.05.2019 04:13
Не сказала вам огромное спасибо!!!! Работа проделана очень большая, поэтому благодарность вам за помощь 
Цитировать
+1
#28
Мария
11.06.2019 12:07
Интересно ,мне эта информация поможет на экзамене по математике профиль?
Цитировать
0
#29
Нико
26.04.2022 06:55
Ещё бы среднюю линию, и было бы прекрасно
Цитировать
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.
Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.
Можно так же распечатать необходимые сборники математических формул.
Успехов в учебе!
Формулы Арифметики:
- Законы действий над числами
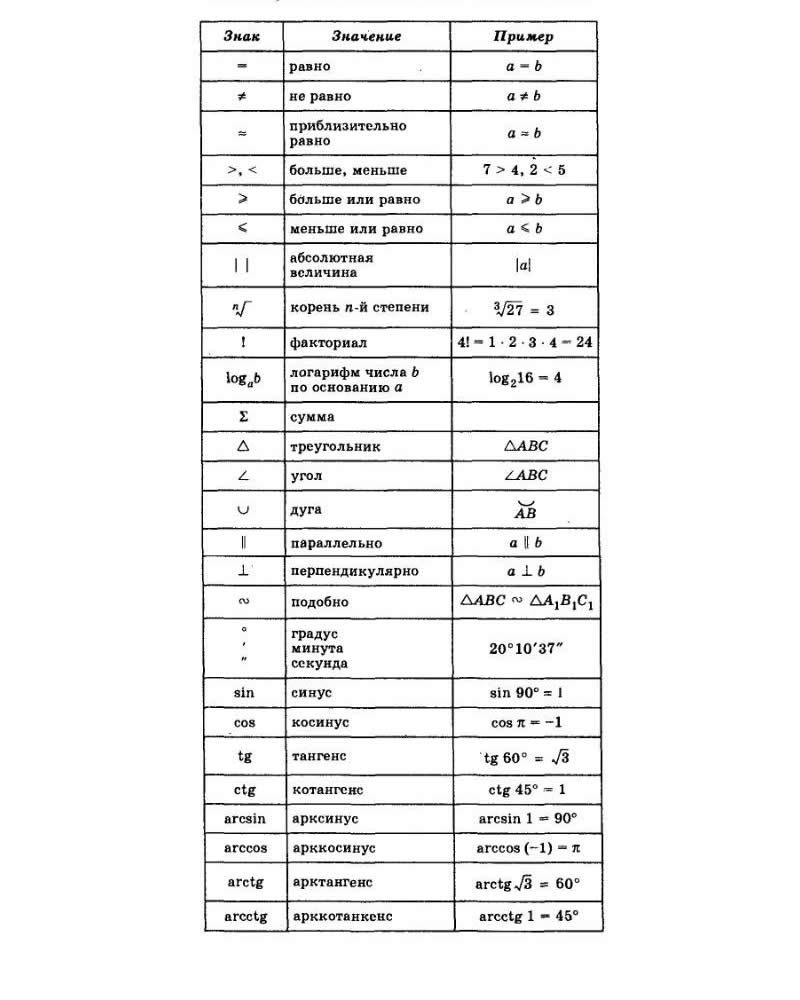
- Некоторые математические обозначения
- Признаки делимости натуральных чисел
- Модуль
- Действия с дробями
- Пропорции
- Средние величины
- Некоторые конечные числовые ряды
Формулы Алгебры:
- Тождественные преобразования
- Тригонометрические формулы
- Прогрессии
- Производная
- Логарифмы
- Координаты и векторы
- Комбинаторика и бином Ньютона
- Пределы
- Интегралы
Геометрические Формулы:
- Планиметрия
- Стереометрия
Арифметические формулы:
Законы действий над числами
Переместительный закон сложения: a + b = b + a.
Сочетательный закон сложения: (a + b) + с = a + (b + c).
Переместительный закон умножения: ab = ba.
Сочетательный закон умножения: (ab)с = a(bc).
Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.
Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.
Некоторые математические обозначения и сокращения:
Признаки делимости
Признаки делимости на «2»
- Число, делящееся на «2» без остатка называется чётным, не делящееся – нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6,
или ноль
Признаки делимости на «4»
- Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»
Признаки делимости на «8»
- Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и.т.д.)
Признаки делимости на «3» и на «9»
- Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»
Признаки делимости на «5»
- Без остатка на «5» делятся числа, последняя цифра которых «0» или «5»
Признаки делимости на «25»
- Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»
Признаки делимости на «10», «100» и на «1 000»
- Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули
Признаки делимости на «11»
- Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»
Абсолютная величина — формулы (модуль)
|a| ? 0, причём |a| = 0 только если a = 0;
|-a|=|a|
|a2|=|a|2=a2
|ab|=|a|*|b|
|a/b|=|a|/|b|, причём b ? 0;
|a+b|?|a|+|b|
|a-b|?|a|-|b|
Формулы Действия с дробями
Пропорции
<span «>Два равных отношения образуют пропорцию:
Основное свойство пропорции
ad = bc
Нахождение членов пропорции
Пропорции, равносильные пропорции
:
Производная пропорция — следствие данной пропорции
в виде

Средние величины
Среднее арифметическое
Двух величин:
n величин:
Среднее геометрическое
(среднее пропорциональное)Двух величин:
n величин:
Среднее квадратичное
Двух величин:
n величин:
Среднее гармоническое
Двух величин:
n величин:
Некоторые конечные числовые ряды
Алгебра:
-
Тождественные преобразования алгебраических и тригонометрических выражений
-
Для любых a, b и c верны равенства:
Свойства числовых неравенств
1) Если a < b, то при любом c: a + с < b + с.
2) Если a < b и c > 0, то aс < bс.
3) Если a < b и c < 0, то aс > bс.
4) Если a < b, a и b одного знака, то 1/a > 1/b.
5) Если a < b и c < d, то a + с < b + d, a — d < b — c.
6) Если a < b, c < d, a > 0, b > 0, c > 0, d > 0, то ac < bd.
7) Если a < b, a > 0, b > 0, то
Если
, то
-
Формулы Прогрессии:
-
-
Арифметическая прогрессия
-
(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):
-
Геометрическая прогрессия
-
(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):
-
-
Производная
- Логарифмы:
- Координаты и векторы
1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:
2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:
3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:
y = kx + q.
Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
4. Общее уравнение прямой имеет вид:
ax + by + c = 0.
5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:
ax + by + c = 0.
6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2
соответственно имеют вид:7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:
8. Уравнение:
представляет собой уравнение параболы с вершиной в точке, абсцисса которой
- Прямоугольная декартова система координат в пространстве
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:
2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:
3. Модуль вектора
заданного своими координатами, находится по формуле:
4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы:
5. Единичный вектор
сонаправленный с вектором
находится по формуле:
6. Скалярным произведением
векторов
называется число:
где
— угол между векторами.
7. Скалярное произведение векторов
8. Косинус угла между векторами
и
находится по формуле:
9. Необходимое и достаточное условие перпендикулярности векторов
и
имеет вид:
10. Общее уравнение плоскости, перпендикулярной вектору
имеет вид:
ax + by + cz + d = 0.
11. Уравнение плоскости, перпендикулярной вектору
и проходящей через точку (xo;yo;zo), имеет вид:
a(x — xo) + b(y — yo) + c(z — zo) = 0.
12. Уравнение сферы с центром O(0;0;0) записывается в виде:
- Комбинаторика и бином Ньютона
1) Число перестановок из n элементов находится по формуле:
2) Число размещений из n элементов по m находится по формуле:
3) Число сочетаний из n элементов по m находится по формуле:
4) Справедливы следующие свойства сочетаний:
5) Формула бинома Ньютона имеет вид:
Сумма показателей чисел a и b равна n.
6) (k+1)-й член находится по формуле:
7) Число сочетаний
также можно найти по треугольнику Паскаля.
Треугольник Паскаля (до n=7):
Сумма биномиальных коэффициентов равна 2n.
9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.
- Пределы
- Неопределенные интегралы
Геометрия
- Планиметрия1. Произвольный треугольник:
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Центр вписанной окружности – точка пересечения биссектрис.
(a,b,c – стороны:— противолежащие им углы; p – полупериметр; R – радиус описанной окружности; r – радиус вписанной окружности; S – площадь; ha – высота, проведенная к стороне a):
2. Прямоугольный треугольник:
Центр описанной окружности совпадает с центром гипотенузы.
(a,b – катеты; c – гипотенуза; ac, bc – проекции катетов на гипотенузу):3. Равносторонний треугольник:
Медиана = биссектрисе. OR = Or.
4. Произвольный выпуклый четырехугольник
(d1 и d2 – диагонали;
– угол между ними; S — площадь):
5. Параллелограмм
(a и b – смежные стороны;
– угол между ними; ha – высота, проведенная к стороне a):
6. Ромб:
В любой ромб можно вписать окружность.
7. Прямоугольник:
Около любого прямоугольника можно описать окружность.
8. Квадрат
(d – диагональ):
9. Трапеция
(a и b – основания; h – расстояние между ними; l – средняя линия):
10. Описанный многоугольник
(p – полупериметр; r – радиус вписанной окружности):
S = pr.
11. Правильный многоугольник
(an – сторона правильного n-угольника; R – радиус описанной окружности; r – радиус вписанной окружности):
12. Окружность, круг
(r — радиус; C – длина окружности; S – площадь круга):
13. Сектор
(l – длина дуги, ограничивающей сектор;
— градусная мера центрального угла;
— радианная мера центрального угла):
- Стереометрия1. Произвольная призма
(l – боковое ребро; P – периметр основания; S – площадь основания; H – высота; Pсеч – периметр перпендикулярного сечения; Sбок – площадь боковой поверхности; V — объем):
2. Прямая призма:
3. Прямоугольный параллелепипед
(a,b,c – его измерения; V — диагональ):
4. Куб
(a — ребро):
5. Произвольная пирамида
(S – площадь основания; H – высота; V — объем):
6. Правильная пирамида
(P – периметр основания; l – апофема; Sбок – площадь боковой поверхности):
7. Произвольная усеченная пирамида
(S1 и S1 – площади оснований; h – высота; V — объем):
8. Правильная усеченная пирамида
(P1 и P2 – периметры оснований; l – апофема; Sбок – площадь боковой поверхности):
9. Цилиндр
(R – радиус основания; H – высота; Sбок – площадь боковой поверхности; V — объем):
10. Конус
(R – радиус основания; H – высота; l – образующая; Sбок – площадь боковой поверхности; V — объем):
11. Шар, сфера
(R – радиус шара; S – площадь сферической поверхности; V — объем):
12. Шаровой сегмент
(R – радиус шара; h – высота сегмента; S – площадь сферической поверхности сегмента; V — объем):
13. Шаровой сектор
(R – радиус шара; h – высота сегмента; V — объем):
-
Настоящий материал опубликован пользователем Буракова Юлия Дмитриевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Пожаловаться на материал
-
Автор материала
- На сайте: 6 лет и 5 месяцев
- Подписчики: 5
- Всего просмотров: 582336
- Всего материалов:
19
По теме: методические разработки, презентации и конспекты
Личностно ориентированный интегрированный урок по физике, математике, информатике «Графическое представление физических формул.Создание графиков в текстовом редакторе MS Word»
Тема урока:«Графическое представление физических формул. Создание графиков с использованием средств текстового редактора MSWord»Цели урока:используя математические знания, помочь учен…
Интегрированный урок по математики и информатики 9 класс Тема «Прогрессия. Применение формул алгебраической и геометрической прогрессии в электронных таблицах»
Интегрированный урок по математики и информатики 9 классТема «Прогрессия. Применение формул алгебраической и геометрической прогрессии в электронных таблицах»…
план урока по теме «задание функции с помощью формулы», математика, 6 класс.
Учащиеся, уходя из дома в школу, тратят там большую часть активного времени. Поэтому в школе нам необходимо создавать условия для развития не только когнитивных навыков, но и научить…
Интегрированный урок (математика + химия), 10-й класс «Решение задач на вывод формул органических веществ» Учитель математики: Гугняева АА(МАОУ СОШ №107г.Пермь) Учитель химии: Коковина ЛЕ(МАОУ СОШ
Интегрированный урок (математика + химия), 10-й класс «Решение задач на вывод формул органических веществ» …
А сейчас мы начнем наш путь с повторения формул и правил. На доске записана левая честь формулы, нужно продолжить формулу, назвать её и рассказать правило Формула Словесная формулировка (а + в) 2 = а2 + 2ав + в2 квадрат суммы двух выражений Квадрат сум
Тема урока: Формулы сокращённого умноженияЦель урока: научить учащихся применять формулы сокращенного умножения при выполнении упражнений различной сложности и творческих заданий.Задачи урока:Образова…
Методическая разработка внеурочного занятия по математике «МАТЕМАТИКА БЕЗ ФОРМУЛ»
Развитие личностных, регулятивных, коммуникативных и познавательных универсальных учебных действий; раскрытие способностей и поддержка одарённости обучающихся; организация интеллектуальных и творчески…
формулы приведения. формулы сложения. формулы двойного и половинного угла
формулы приведения. формулы сложения. формулы двойного и половинного угла…
Этапы закрепощения крестьян в России
Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.
Задания 12-18 досрочного ЕГЭ по математике
3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.
ОГЭ по математике. Тренировочный вариант СтатГрад
Видеоуроки ОГЭ | Вчера, 21:46
Решение тестовой части (№1-19) тренировочной работы по математике от 18 апреля 2022 года.
|
Для у спешной сдачи математики ОГЭ нужно знать основные формулы, которые школьники изучают на уроках. Все формулы, которые пригодятся на экзамене размещены здесь, их можно скачать и распечатать. Обязательно нужно знать формулы сокращенного умножения, не помешает знание формул степеней, ещё пригодится знание формул последовательностей и прогрессий, с таблицей квадратов и степеней так же не помешает ознакомиться. Так же нужно будет знать формулы нахождения площадей различных фигур. автор вопроса выбрал этот ответ лучшим 88SkyWalker88 4 года назад Подготовка к экзамену по математике в девятом классе включает в себя повторение материала за седьмой, восьмой, девятый классы. В том числе и формулы. Помимо уже упомянутых, могут также встретиться формулы арифметической и геометрической прогрессии, определение модуля, которые ученики скорее всего знают, но повторить не мешало бы. Единый гос. экзамен по математике надо сдавать в обязательном порядке всем учащимся в 9-м классе, впрочем как дальше и в 11-м, но этот предмет не сдать если не знать базовых и нужных формул по которым можно решить задачи по геометрии и алгебре. Ниже представлю нужные формулы чтобы экзамен была возможно сдать. Перед экзаменом обязательно повторите все эти формулы. Скачать их полностью все можно с этого сайта источника. Основные — это сокращенное умножение, степени, прогрессии, геометрические и т.п. Для тех у кого гуманитарный склад ума знание формул это уже 50% успешной сдачи экзамена ОГЭ, к сожалению без него никуда. hufrcw43bkr 3 года назад Экзамены не за горами, многие ученики сейчас очень тщательно готовятся и вспоминают всю школьную программу, чтобы успешно сдать все экзамены. Такой предмет как математика один из самых сложных, но он считается обязательным, поэтому к нему готовится очень хорошо, чтобы получить хорошие отметки (баллы). Вот хорошая шпаргалка для экзамена по математике, тут и формулы степени, и формулы сокращенного умножения (как ни странно, но такое задание часто попадается на экзаменах), и логарифмы и квадратное уравнение, и производная. Из геометрии важно помнить формулы тригонометрии, это формулы косинусов и синусов, тангенсов и котангенсов. Еще больше формул можно посмотреть на этом сайте. 127771 3 года назад ОГЭ является основным государственным экзаменом для учеников девятого класса. Математика является обязательным экзаменом, поэтому ее сдают все ученики Для многих ОГЭ по математике является самым сложным экзаменов среди всех и не зря. Для экзамена необходимо не только выучить формулы, но и знать как их применять. На самом каждому необходимо составить свою шпаргалку, так кто точно эту формулу забудет, кто-то другую формулу. Ниже представлены основные формулы, которые необходимо знать успешной сдачи экзамена по математике: Также удалась найти еще один вариант формул, которые могут пригодится для подготовки к экзамену: VeneraD 3 года назад Вот и пришла пора ОГЭ, теперь все ученики пытаются наверстать все пробелы в учебе и подготовится. Чтобы сдать математику, конечно нужно знать ряд формул. В принципе все эти формулы изучают на уроках. Начинают с легкого, и в 9 классах уже конечно все сложнее. Если все темы запоминать и понимать сразу, то и на ОГЭ будет легче. Особо на шпаргалки рассчитывать не стоит, так как с каждым годом сдача ОГЭ все строже контролируется. Ниже добавлю ряд формул, есть там и степени, и квадратные корни. А еще больше формул тут. Jean Montibus-Citri 3 года назад ОГЭ — основной государственный экзамен. Его должны в обязательном порядке сдавать ученики по окончанию 9 класса, не зависимо продолжат ли они обучение в школе, или выберут профессиональное образование. ОГЭ является аналогом ЕГЭ, так что во многом задачи экзаменов перекликаются и запоминать информацию стоит всерьез и надолго. Математика и русский язык являются обязательными дисциплинами ОГЭ. Формулы, которые ученик должен знать, что бы сдать экзамен, выглядят так: Так же можно подсказать девятиклассникам вот этот сайт. Здесь представлена та же информация, но в более расширенном варианте. Те, кто запомнить все эти сочетания значков не в силах, смогут просто распечатать формулы и смастерить шпаргалку. Бархатные лапки 3 года назад Экзамены уже совсем скоро, поэтому школьникам стоит подготовиться, особенно это касается такого предмета, как математика. Ведь это один из основных предметов, по которому обязательно сдают экзамены. Итак, начнем с формул, которые нужно знать в первую очередь, это формула сокращенного умножения, такие формулы часто встречаются в различных задачах. По геометрии нам нужно знать формулы площади различных геометрических фигур. Также необходимо помнить и знать тригонометрические функции, все что касается косинусов, синусов, тангенсов и котангенсов. Не помешает знать и и такие формулы прогрессии. Все формулы и шпаргалки смотрим на этом сайте. дольфаника 4 года назад Для успешной сдачи ОГЭ 9-классники должны знать определения и формулы по следующим темам степень и корни, преобразование многочленов, квадраты и кубы чисел, св-ва обратной пропорциональности, свойства прогрессии, свойства функции обязательно и другие. Весь список формул для ОГЭ можно посмотреть здесь. Все, что учили с первого по 9 класс по математике и геометрии, нужно знать. На основе одного правила и формулы вытекает решение задач. Незнание одной формулы ставит под угрозу сдачу всего экзамена. Поэтому перед экзаменом нужно повторить слабые места в математике, особенно проценты, в которых многие путаются. Ниже приведены все основные формулы, которые необходимо знать учащемуся общеобразовательной школы, желающему быть уверенным в своих знаниях при сдаче Основного Государственного экзамена (ОГЭ) Эти формулы — все они известны нам из курса математики пройденных девяти классов. Остается только повторить их и освежить память. Удачи на экзамене! Знаете ответ? |
- Треугольник
- Четырехугольники
- Окружность и круг
- Призма
- Пирамида
- Усеченная пирамида
- Цилиндр
- Конус
- Усеченный конус
- Сфера и шар
1. Формулы сокращённого умножения
Наверх
2. Модуль числа
Определение:
Основные свойства модуля:
Наверх
3. Степень с действительным показателем
Свойства степени с действительным показателем
Пусть Тогда верны следующие соотношения:
Наверх
4. Корень n-ой степени из числа
Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
Основные свойства арифметического корня:
Наверх
5. Логарифмы
Определение логарифма:
Основное логарифмическое тождество:
Основные свойства логарифмов
Пусть
Тогда верны следующие соотношения:
Наверх
6. Арифметическая прогрессия
Формула n-го члена арифметической прогрессии:
Характеристическое свойство арифметической прогрессии:
Сумма n первых членов арифметической прогрессии:
При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
7. Геометрическая прогрессия
Формула n-го члена геометрической прогрессии:
Характеристическое свойство геометрической прогрессии:
Сумма n первых членов геометрической прогрессии:
При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
8. Бесконечно убывающая геометрическая прогрессия
Сумма бесконечно убывающей геометрической прогрессии:
Наверх
9. Основные формулы тригонометрии
Зависимость между тригонометрическими функциями одного аргумента:
Формулы сложения:
Формулы тригонометрических функций двойного аргумента:
Формулы понижения степени:
Формулы приведения
Все формулы приведения получаются из соответствующих формул сложения. Например:
Применение формул приведения укладывается в следующую схему:
— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;
— определяется знак приводимой функции;
— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или
, то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид
, то функция названия не меняет.
Например, получим формулу :
— — IV четверть;
— в IV четверти тангенс отрицательный;
— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,
Формулы преобразования суммы тригонометрических функций в произведение:
Формулы преобразования произведения тригонометрических функций в сумму:
Наверх
10. Производная и интеграл
Таблица производных некоторых элементарных функций
Правила дифференцирования:
1.
2.
3.
4.
5.
Уравнение касательной к графику функции в его точке
:
Таблица первообразных для некоторых элементарных функций
Правила нахождения первообразных
Пусть ― первообразные для функций
и
соответственно, a, b, k ― постоянные,
Тогда:
— ― первообразная для функции
— ― первообразная для функции
— ― первообразная для функции
— Формула Ньютона-Лейбница:
1. Треугольник
Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно;
― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно;
― длины высот AA2, BB2, CC2 треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC;
― площадь треугольника ABC. Тогда имеют место следующие соотношения:
(теорема синусов);
(теорема косинусов);
Наверх
2. Четырёхугольники
Параллелограмм
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.
Площадь четырехугольника
Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Наверх
3. Окружность и круг
Соотношения между элементами окружности и круга
Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга, — длина дуги в
градусов,
— длина дуги в
радиан,
— площадь сектора, ограниченного дугой в n градусов,
— площадь сектора, ограниченного дугой в
радиан. Тогда имеют место следующие соотношения:
Вписанный угол
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, — прямой.
Вписанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Описанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.
Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны
Наверх
4. Призма
Пусть H ― высота призмы, AA1 ― боковое ребро призмы, ― периметр основания призмы,
― площадь основания призмы,
― площадь боковой поверхности призмы,
― площадь полной поверхности призмы, V ― объем призмы,
― периметр перпендикулярного сечения призмы,
― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
Свойства параллелепипеда:
— противоположные грани параллелепипеда равны и параллельны;
— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;
— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Наверх
5. Пирамида
Пусть H ― высота пирамиды, ― периметр основания пирамиды,
― площадь основания пирамиды,
― площадь боковой поверхности пирамиды,
― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:
;
.
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то
Наверх
6. Усечённая пирамида
Пусть H ― высота усеченной пирамиды, и
― периметры оснований усеченной пирамиды,
и
― площади оснований усеченной пирамиды,
― площадь боковой поверхности усеченной пирамиды,
― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.
Тогда имеют место следующие соотношения:
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то:
Наверх
7. Цилиндр
Пусть h ― высота цилиндра, r ― радиус цилиндра, ― площадь боковой поверхности цилиндра,
― площадь полной поверхности цилиндра, V ― объем цилиндра.
Тогда имеют место следующие соотношения:
Наверх
8. Конус
Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса, ― площадь боковой поверхности конуса,
― площадь полной поверхности конуса, V ― объем конуса.
Тогда имеют место следующие соотношения:
Наверх
9. Усечённый конус
Пусть h ― высота усеченного конуса, r и ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,
― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:
Наверх
10. Сфера и шар
Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы, ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,
― объем сегмента, высота которого равна h,
― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:
Наверх




















































































































































































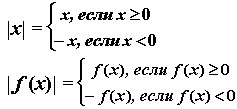
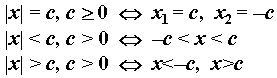
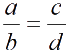 Основное свойство пропорции
Основное свойство пропорции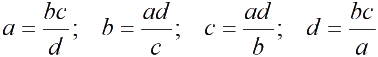 Пропорции, равносильные пропорции
Пропорции, равносильные пропорции 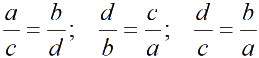 Производная пропорция — следствие данной пропорции
Производная пропорция — следствие данной пропорции