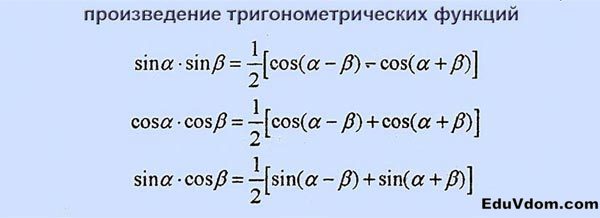На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.
Содержание
Формулы для ЕГЭ по профильной математике. Алгебра
Формулы сокращенного умножения
Квадрат суммы: (a + b)² = a² + 2ab + b²
Квадрат разности: (a – b)² = a² – 2ab + b²
Разность квадратов: a² – b² = (a + b)(a – b)
Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)
Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)
Прогрессия
Арифметическая
Геометрическая
Таблица степеней
Свойства степеней
Таблица квадратов
Интенсивы по подготовке к региональному этапу ВсОШ
Все, что нужно знать
для победы, за 7 дней!
Свойства корней
Тригонометрия
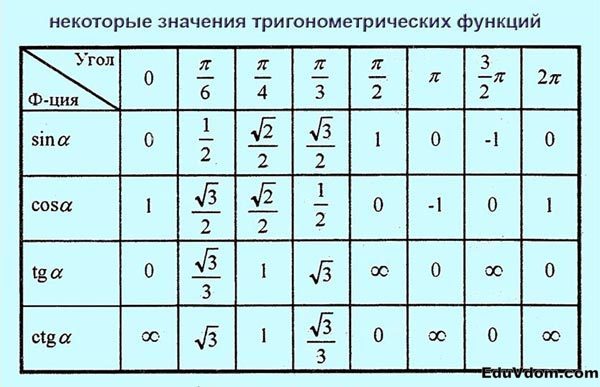
Таблица значений тригонометрических функций
Тригонометрическая окружность
Тригонометрические формулы
Обратные тригонометрические функции
Преобразование суммы и разности в произведение
Регулярные курсы по подготовке к олимпиадам и ЕГЭ
Поступаем в вуз мечты без проблем!
Вероятность
Вероятность события А: m – благоприятные, n – общее число событий
P(A) = m/n
События А и В происходят одновременно: A · B
Независимые события: P(A · B) = P(A) · P(B)
Зависимые события: P(A · B) = P(A) · P(B | A)
Происходит или А, или В: A + B
Несовместные события: P(A + B) = P(A) + P(B)
Совместные события: P(A + B) = P(A) + P(B) – P(A · B)
Свойства модуля
Производные
Основные правила дифференцирования
Таблица производных
Первообразные
Логарифмы
Квадратные уравнения
Дискриминант
Теорема Виета
Разложение на множители
Формулы для ЕГЭ по профильной математике. Геометрия
Планиметрия
Треугольник
Следствие из теоремы косинусов:
Длина биссектрисы (через угол):
Длина биссектрисы (через отрезки):
Прямоугольный треугольник
24 декабря – 20 января
5-11 классы
Онлайн-олимпиада Коалиции
Равносторонний треугольник
Аргументы для итогового сочинения
Подборка лучших аргументов
Равносторонний шестиугольник
Площадь внутреннего треугольника:
Площадь внутреннего прямоугольника:
Ромб
Трапеция
Произвольный четырёхугольник
Окружность
Стереометрия
Выводы
Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.
А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.
Поделиться в социальных сетях
Какими формулами вам приходится пользоваться чаще всего?
Межтекстовые Отзывы
Посмотреть все комментарии
Читайте также
Формулы ЕГЭ по математике
- 27.09.2013
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF:
Скачайте в pdf файле.
По разделам:
Комментарии
+30
#1
Плотников А.
04.06.2014 20:58
Класный сайт!
Цитировать
-4
#2
Гость
18.09.2014 11:22
Цитирую лоло:
школоло не осилило
Цитировать
+10
#6
Ann
10.04.2015 19:04
Благодарю за формулы 
Цитировать
+6
#7
Мария
25.04.2015 08:05
Спасибо огромное за такой хороший сайт! 
Цитировать
+1
#9
настюша
16.05.2015 10:03
не все формулы по заданиям 
Цитировать
+20
#10
Алина
30.05.2015 10:52
Очень помогли формулы. Ребята, кто ссдает ЕГЭ, удачи нам!
Цитировать
+2
#12
Анон
02.08.2015 12:30
Спасибо.
Прошу выложить так же и в разрешении .jpg
Так удобнее просматривать и использовать на разных девайсах.
Цитировать
-2
#13
Анон
02.08.2015 12:32
Цитирую Анон:
Спасибо.
Прошу выложить так же и в разрешении .jpg
Так удобнее просматривать и использовать на разных девайсах.
Оказалось они под катом, я имел в виду весь pdf-файл в формате .jpg КАЖДУЮ картинку.
Спасибо.
Цитировать
+5
#15
Мария
30.09.2015 06:52
Здравствуйте! Спасибо за формулы и такое яркое цветное оформление — это помогает запомнить. Не могли бы вы еще дополнить свой список формул формулами, связанными с прогрессиями — это тоже очень важно.
Цитировать
+4
#16
Мария
30.09.2015 07:18
и еще нет формул поверхности, боковой и общей, у пирамиды.
Цитировать
0
#17
настя
01.03.2016 15:18
Цитирую galaxe:
спасиб большое

кто сдает гиа тому сюда
Цитировать
+4
#18
настя
01.03.2016 15:18
думаю мне пригодится для подготовки к гиа
Цитировать
-4
#21
а
03.03.2017 18:44
а это на профильный матан ил на базу?
Цитировать
+2
#23
Саша
28.01.2019 20:56
спасибо большое, очень помогли 
Цитировать
+3
#24
Алексей Алексеевич
05.02.2019 14:23
Спасибо. А то нихера не помню а ЕГЭ уже скороо!!!!
Цитировать
-2
#25
Glebasta_Rhymes
13.05.2019 19:41
а где формулы призмы????????? ???????? 
Цитировать
0
#26
Татьяна
16.05.2019 04:06
А векторная часть? В 9 классе есть раздел векторов, координат векторов. Не нашла у вас этот раздел(((
Цитировать
+5
#27
Татьяна
16.05.2019 04:13
Не сказала вам огромное спасибо!!!! Работа проделана очень большая, поэтому благодарность вам за помощь 
Цитировать
+1
#28
Мария
11.06.2019 12:07
Интересно ,мне эта информация поможет на экзамене по математике профиль?
Цитировать
0
#29
Нико
26.04.2022 06:55
Ещё бы среднюю линию, и было бы прекрасно
Цитировать
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Формулы для профильного ЕГЭ-2022 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c``a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` |
`kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Как выучить все формулы по математике к ЕГЭ
Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.
Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.
Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.
Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.
Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.
Математические формулы школьного курса алгебры
Степени и корни
Формулы сокращенного умножения
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители
Логарифмические формулы
Формулы тригонометрии
Основные формулы тригонометрии
Тригонометрические уравнения
Значения тригонометрических функций
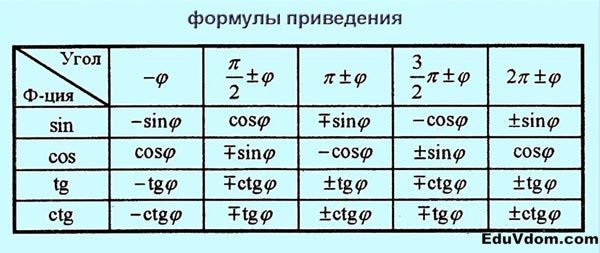
Формулы приведения
Сумма и разность углов
Формулы двойного и тройного аргумента
Формулы половинного аргумента
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы дифференциального исчисления
Формулы векторной алгебры из школьного курса математики
Формулы арифметической и геометрической прогрессии
Геометрические формулы школьного курса математики для ЕГЭ
Планиметрия
Стереометрия
Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.
Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!
DOC-шпаргалка — подборка всех основных формул по разделам, которые нужны при решении заданий ЕГЭ по математике базового или профильного уровня…
Скачать шпаргалку
Скриншот:
Рейтинг: 3.6 из 5.0
Проголосовало: 17
Комментарии
Всего комментариев: 0
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF: Скачайте pdf файл.
Можете записаться на занятия к репетитору математики, если что-то не понятно.
По разделам:
Степени и корни:
Сокращенное умножение
:
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:
Логарифмы:
Формулы тригонометрии, тождества:
Тригонометрические уравнения:
Значения тригонометрических функций:
Формулы приведения:
Сумма и разность углов:
Формулы двойного и тройного аргумента:
Формулы половинного аргумента:
Сумма и разность тригонометрических функций:
Произведение тригонометрических функций:
Производная: признаки возрастания, убывания, минимума функции:
Дифференциальное исчисление:
Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:
Стереометрия: объёмы, площади поверхностей:
Обратиться к репетитору по математике.
На ЕГЭ формулами пользоваться нельзя, нужно их помнить!
В этой подборке формул использованы 3 основных принципа, для упрощения запоминания:
- Выбраны только те формулы, которые могут встретиться на ЕГЭ по математике (это лишь часть того, что изучено в школе);
- Формулы разобраны на тематические блоки;
- Блоки формул выделены цветовым фоном, который позволяет, всего после нескольких обращений, вспоминать картинку и буквально читать с нее нужную формулу.
Как легко запомнить именно нужные формулы из всего курса математики?
Для подготовки нужно выбрать такое оформление математических формул, чтобы они отложились в памятки наиболее эффективно.
Формулы к ЕГЭ по математике!
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF: Скачайте pdf файл.
Можете записаться на занятия к репетитору математики, если что-то не понятно.
По разделам:
Степени и корни:
Сокращенное умножение
:
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:
Логарифмы:
Формулы тригонометрии, тождества:
Тригонометрические уравнения:
Значения тригонометрических функций:
Формулы приведения:
Сумма и разность углов:
Формулы двойного и тройного аргумента:
Формулы половинного аргумента:
Сумма и разность тригонометрических функций:
Произведение тригонометрических функций:
Производная: признаки возрастания, убывания, минимума функции:
Дифференциальное исчисление:
Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:
Стереометрия: объёмы, площади поверхностей:
Обратиться к репетитору по математике.
- ЕГЭ по математике профиль
Для профильной математики на ЕГЭ в компактном виде для распечатки на принтере.
→ скачать docx
→ скачать pdf
Включены основные формулы:
— по алгебре (Формулы сокращенного умножения, Арифметическая прогрессия, Делимость натуральных чисел, Правила вычисления первообразной функции и т.д.)
— основные тригонометрические формулы (Формулы суммы функций, Формулы суммы аргументов, Формулы произведения функций, Формулы половинного аргумента и т.д.)
— по геометрии (Теорема косинусов, синусов; Конус; Длина окружности, площадь; Основные соотношения в треугольнике и т.д.)
Связанные страницы: