Формулы логарифмов 11 класс егэ по математике

Логарифмы

Предыдущую статью о показательных уравнениях мы начали с уравнения 2^x = 8. Там всё было ясно: x = 3.

А теперь рассмотрим уравнение 2^x = 7.

По графику функции y = 2^x мы видим, что это уравнение имеет корень, и притом единственный.

Ясно, что этот корень — не целое число (так как 2² = 4, 2³ = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.

Этот корень обозначается log₂7 (читается: «логарифм семи по основанию два»). Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log₂7 = 2,807354922057604107…

Итак, наше число log₂7 — это показатель степени, в которую надо возвести 2, чтобы получить 7.

Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).

Определение. Логарифм положительного числа b по основанию a (обозначается log_ab) — это показатель степени, в которую надо возвести a, чтобы получить b.

Иными словами,

Например:

  так как  ;

, так как  ;

  так как  ;

, так как  .

Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.

Логарифм с основанием e называется натуральным и обозначается ln.

Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log₂(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.

Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.

Основные формулы

По определению, log_ab — это показатель степени, в которую надо возвести число a, чтобы получить число b:

Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:

log_aa^x=x.

Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.

Логарифм произведения — это сумма логарифмов:

loga(bc) = logab + logac.

(2)

Логарифм частного — это разность логарифмов:

.

(3)

Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:

(4)

Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:

(5)

Формулы (4) и (5) вместе дают:

.

(6)

В частности, если m = n, мы получаем формулу:

.

(7)

Например, .

Наконец, важнейшая формула перехода к новому основанию:

.

(8)

В частности, если c = b, то log_bb = 1, и тогда:

.

(9)

Приведём несколько примеров из банка заданий.
1. (применили формулу (2) суммы логарифмов).

2. (применили основное логарифмическое тождество(1)).

3. (применили формулу (4)).

4. (применили формулу (9), перейдя к новому основанию 0,8).

5. (применили формулу (3) разности логарифмов).

Немного истории

Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?

Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.

Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?

Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.

В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.

Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.

Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).

А затем по таблице логарифмов найти само произведение чисел b и c.

Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.

Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.

18
Фев 2013

Категория: Справочные материалы

Логарифм. Определение. Свойства логарифмов

2013-02-18
2021-06-18



Логарифмы в заданиях ЕГЭ

Что такое логарифм?

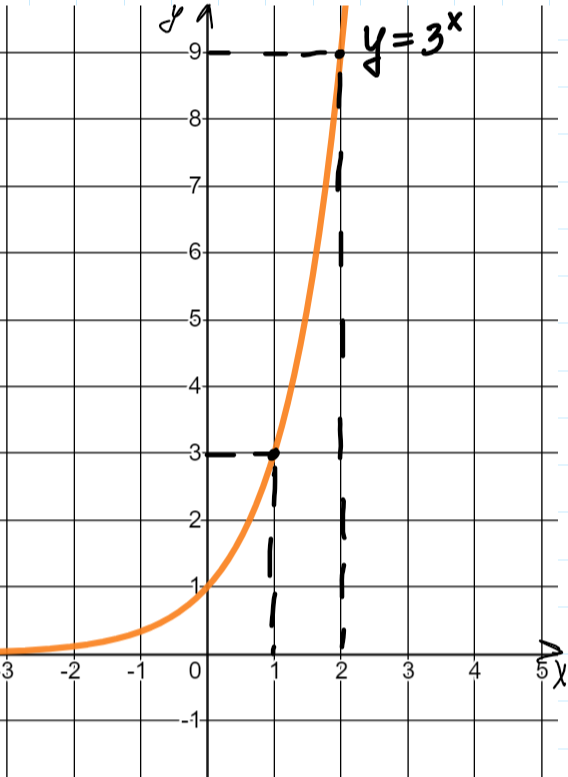
Нагляднее всего понять это с помощью графического решения уравнений. Начертим график

и с его помощью решим уравнения:

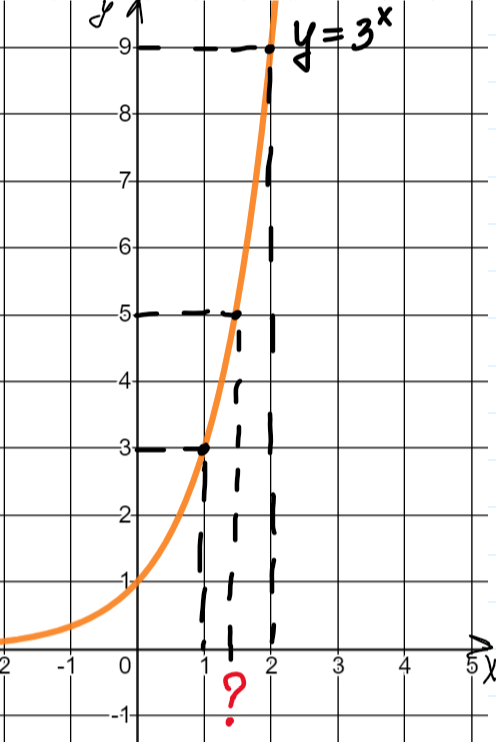
Отлично! А теперь решим уравнение

.

И в этом случае невозможно назвать точное значение, то есть мы понимаем, что корень больше одного и меньше двух, но более точных данных нет.

Вот такой корень и задается с помощью логарифма, а именно

(читается как «логарифм пяти по основанию три» или «логарифм по основанию три от пяти»).

Мы определили смысл — теперь перейдем к общему определению логарифма.

Логарифмом числа b по основанию a называют показатель степени с основанием a, равной b. То есть, попросту говоря, логарифм — это степень, в которую нужно возвести a для получения b. Однако у логарифма есть условия или ограничения, что основание а больше нуля и не равно единице, а также показатель b больше нуля.

Как решать примеры с логарифмами?

Рассмотрим пример, как решить логарифм:

Задаем вопрос: в какую степень нужно возвести 7, чтобы получить 49?

Ответ: во вторую степень. Значит,

.

Какие бывают виды логарифмов?

Логарифм по основанию 10 называется десятичным логарифмом и обозначается как

. Пример десятичного логарифма:

.

Логарифм по основанию e называется натуральным логарифмом и обозначается как

. Пример натурального логарифма:

.

Свойства и формулы логарифмов

1. Эта формула называется основным логарифмическим тождеством.

   Пример:

   .

2. Пример:

   .

3. Пример:

   .

4. Логарифм степени находится по формуле:

   .

   Видно, что показатель степени выносим перед логарифмом.

   Пример:

   .

5. Показатель степени основания также выносим перед логарифмом, но в виде обратного числа, то есть, например, вместо 5 будет

   .

   Пример:

   .

6. Если нужно перейти к другому основанию, то можно сделать это по формуле:

   . Свойство называется формулой перехода к новому основанию.

7. А частным случаем предыдущей формулы является формула, которая позволяет менять местами основание и аргумент логарифма:

   .

Конечно, это не все свойства логарифмов, а только самые главные. Комбинируя свойства выше, можно получать все новые и новые формулы для логарифмов. Например, соединив 4-ю и 5-ю формулы, получим

. Но запоминать ее нет смысла, важно знать лишь базовые свойства логарифмов.

Применение логарифмических свойств в примерах

Пример 1

Найдите значение выражения

, если

.

Если видите частное в показателе логарифма, то распишите по 3-й формуле:

.

Решение

У каждого логарифма в показателе стоит степень, значит, поможет 4-я формула:

.

Первый логарифм можно вычислить по определению. И обратите внимание на второй логарифм: у него в основании стоит а, а в условии задачи дан логарифм с основанием b, значит, нужно а как-то заменить на b. Возможно ли это? Конечно, 7-я формула в помощь!

.

Подставьте числовое значение из условия, и все готово:

.

Отличный пример! Мы использовали практически все свойства логарифмов. А теперь попрактикуйтесь еще, но помните, что задача с подвохом!

Пример 2

Вычислите:

.

Получился ответ 27? Если да, то поздравляю: вы попались на удочку самых популярных ошибок! Какое бы задание вам ни встретилось, действия с логарифмами нужно производить только по определениям и правилам. В примере вы видите деление двух логарифмов. А есть ли какая-то формула, в которой записано деление двух логарифмов?

Конечно, это формула перехода к новому основанию, которую мы привели в пункте 6 выше. Применим ее к этому случаю и вычислим логарифм по определению, задав вопрос: в какую степень нужно возвести основание, чтобы получился показатель?

.

И получается ответ 4, а не 27.

Практическое применение логарифмов

Помните, выше мы говорили, что логарифм объединяет задания на ЕГЭ, галактики и рога горных козлов? И если с баллами на ЕГЭ все понятно, то про галактики и рога — интереснее.

Все дело в том, что существует логарифмическая спираль, которая задается по формуле:

. По этой логарифмической спирали растут рога горных козлов, закручены многие галактики (и даже та, в которой мы живем), а также раковины некоторых морских животных, усики растений, ураганы, смерчи и многое другое.

Как видите, логарифмы имеют большое значение для нашей жизни — не только баллы на ЕГЭ!

Вопросы для самопроверки

Чтобы информация точно усвоилась, вспомните:

1. Что такое логарифм?

2. Какие ограничения есть у логарифма?

3. Какие логарифмические свойства вы знаете?

4. Какие бывают способы преобразования выражений с логарифмом?

5. В чем практическое применение логарифмов?

На курсах по математике в онлайн-школе Skysmart мы всегда показываем, зачем нужны математические правила и формулы в реальной жизни — ведь так учиться гораздо интереснее! И подтянуть знания перед ЕГЭ тоже поможем: приходите на бесплатный вводный урок и все увидите сами.

Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.

Теперь при помощи этой таблицы введем понятие логарифма.

Логарифм от числа 32 по основанию 2 ((log_{2}(32))) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:

$$ log_{2}(32)=5;$$

Аналогично, глядя в таблицу получим, что:

$$log_{2}(4)=2;$$
$$log_{2}(8)=3;$$
$$log_{2}(16)=4;$$
$$log_{2}(64)=6;$$
$$log_{2}(128)=7.$$

Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.

Теперь дадим определение логарифма в общем виде:

Логарифмом положительного числа (b) по основанию положительно числа (a) называется степень (c), в которую нужно возвести число (a), чтобы получить (b)

$$log_{a}(b)=c;$$
$$a^{c}=b.$$

Будьте внимательны! В первое время обычно путают, что такое основание и то, что стоит под логарифмом (аргумент). Логарифм — это всегда функция, зависящая от двух переменных. Чтобы их не путать, помните определение логарифма – это степень, в которую нужно возвести основание, чтобы получить аргумент.

Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:

$$log_{2}(5)=???$$

Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:

$$log_{2}(5)=2,32192809…$$

Или логарифм шести по основанию 4:

$$log_{4}(6)= 1.2924812…$$

На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!

Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм (log_{4}(6)). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6-ке:

$$ log_{4}(4) lt log_{4}(6) lt log_{4}(16);$$
$$ 1 lt log_{4}(6) lt 2. $$

Значит (log_{4}(6)) принадлежите промежутку от 1 до 2:

$$ log_{4}(6) in (1;2). $$

Как посчитать логарифм

Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма (log_{a}(b)) существует только при положительных значениях основания (a) и аргумента (b). И кроме этого на основание накладывается условие, что оно не должно быть равно (1).

$$ log_{a}(b) quad существует,;при quad a gt 0; ;b gt 0 ;a neq 1.$$

Почему так? Это следует из определения показательной функций. Показательная функция не может быть (0). А основание не равно (1), потому что тогда логарифм теряет смысл – ведь (1) в любой степени это будет (1).

При этих ограничениях логарифм существует.

В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.

Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.

$$log_{3}(frac{1}{3})=-1;$$

Так как (вспоминайте определение отрицательной степени)

$$3^{-1}=frac{1}{3};$$

Теперь давайте разберем общий алгоритм вычисления логарифмов:

• Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
• Разобраться в какую степень (x) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
• (x) и будет искомым значением логарифма.

Давайте разберем на примерах.

Пример 1. Посчитать логарифм (9) по основанию (3): (log_{3}(9))

• Сначала представим аргумент и основание в виде степени тройки:
  $$ 3=3^1, qquad 9=3^2;$$
• Теперь надо разобраться в какую степень (x) нужно возвести (3^1), чтобы получить (3^2)
  $$ (3^1)^x=3^2, $$
  $$ 3^{1*x}=3^2, $$
  $$ 1*x=2,$$
  $$ x=2.$$
• Вот мы и решили:
  $$log_{3}(9)=2.$$

Пример 2. Вычислить логарифм (frac{1}{125}) по основанию (5): (log_{5}(frac{1}{125}))

• Представим аргумент и основание в виде степени пятерки:
  $$ 5=5^1, qquad frac{1}{125}=frac{1}{5^3}=5^{-3};$$
• В какую степень (x) надо возвести (5^1), чтобы получить (5^{-3}):
  $$ (5^1)^x=5^{-3}, $$
  $$ 5^{1*x}=5^{-3},$$
  $$1*x=-3,$$
  $$x=-3.$$
• Получили ответ:
  $$ log_{5}(frac{1}{125})=-3.$$

Пример 3. Вычислить логарифм (4) по основанию (64): (log_{64}(4))

• Представим аргумент и основание в виде степени двойки:
  $$ 64=2^6, qquad 4=2^2;$$
• В какую степень (x) надо возвести (2^6), чтобы получить (2^{2}):
  $$ (2^6)^x=2^{2}, $$
  $$ 2^{6*x}=2^{2},$$
  $$6*x=2,$$
  $$x=frac{2}{6}=frac{1}{3}.$$
• Получили ответ:
  $$ log_{64}(4)=frac{1}{3}.$$

Пример 4. Вычислить логарифм (1) по основанию (8): (log_{8}(1))

• Представим аргумент и основание в виде степени двойки:
  $$ 8=2^3 qquad 1=2^0;$$
• В какую степень (x) надо возвести (2^3), чтобы получить (2^{0}):
  $$ (2^3)^x=2^{0}, $$
  $$ 2^{3*x}=2^{0},$$
  $$3*x=0,$$
  $$x=frac{0}{3}=0.$$
• Получили ответ:
  $$ log_{8}(1)=0.$$

Пример 5. Вычислить логарифм (15) по основанию (5): (log_{5}(15))

• Представим аргумент и основание в виде степени пятерки:
  $$ 5=5^1 qquad 15= ???;$$
  (15) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
  $$ log_{5}(15).$$

Внимание!

Как понять, что некоторое число (a) не будет являться степенью другого числа (b). Это довольно просто – нужно разложить (a) на простые множители.

$$16=2*2*2*2=2^4,$$

(16) разложили, как произведение четырех двоек, значит (16) будет степенью двойки.

$$ 48=6*8=3*2*2*2*2,$$

Разложив (48) на простые множители, видно, что у нас есть два множителя (2) и (3), значит (48) не будет степенью.

Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.

Десятичный логарифм

На самом деле, все просто. Десятичный логарифм – это любой обыкновенный логарифм, но с основанием 10. Обозначается — (lg(a)).

Пример 6

$$ log_{10}(100)= lg(100)=2;$$
$$log_{10}(1000)=lg(1000)=3;$$
$$log_{10}(10)=lg(10)=1.$$

Натуральный логарифм

Натуральным логарифмом называется логарифм по основанию (e). Обозначение — (ln(x)). Что такое (e)? Так обозначают экспоненту, число-константу, равную, примерно, (2,718281828459…). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием (e) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.

Пример 7

$$ log_{e}(e^2)=ln(e^2)=2;$$
$$ log_{e}(e)=ln(e)=1;$$
$$ log_{e}(e^5)=ln(e^5)=5.$$

Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.

У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.

Свойства логарифмов

$$1. ; log_{a}(1)=0;$$
$$2. ; log_{a}(a)=1;$$
$$3. ; log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$4. ; log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$5. ; log_{a}(b^m)= m*log_{a}(b);$$
$$6. ; log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
$$ 7. ; log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0; ; c gt 0; ; c neq 1; $$
$$ 8. ; log_{a}(b)=frac{1}{log_{b}(a)};$$
$$ 9. ; a^{ log_{a}(b)}=b.$$

Давайте разберем несколько примеров на свойства логарифмов.

Пример 8. Воспользоваться формулой (3). Логарифм от произведения – это сумма логарифмов.

$$log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$ log_{3}(12)=log_{3}(3*4)=log_{3}(3)+log_{3}(4)=1+log_{3}(4);$$
$$ log_{3}(2.7)+log_{3}(10)=log_{3}(2.7*10)=log_{3}(27)=3;$$

Пример 9. Воспользоваться формулой (4). Логарифм от частного – это разность логарифмов.

$$ log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$ log_{7}(98)-log_{7}(2)=log_{7}(frac{98}{2})=log_{7}(49)=2;$$

Пример 10. Формула (5,6). Свойства степени.

$$log_{a}(b^m)= m*log_{a}(b);$$
$$log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$

Логично, что будет выполняться и такое соотношение:

$$log_{a^m}(b^n)=frac{n}{m}* log_{a}(b);$$

И если (m=n), то:

$$log_{a^m}(b^m)=frac{m}{m}* log_{a}(b);=log_{a}(b)$$
$$log_{4}(9)=log_{2^2}(3^2)=log_{2}(3);$$

Пример 11. Формулы (7,8). Переход к другому основанию.

$$ log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0;c gt 0;c neq 1; $$
$$ log_{a}(b)=frac{1}{log_{b}(a)};$$
$$log_{4}(5)=frac{1}{log_{5}(4)};$$
$$log_{4}(5)=frac{log_{7}(5)}{log_{7}(4)};$$

Теория

1.	Основные свойства логарифмов
2.	Формулы перехода от одного основания логарифма к другому

Задания

1.	Логарифм произведения Сложность: лёгкое	2
2.	Логарифм частного Сложность: лёгкое	2
3.	Формула перехода от одного основания логарифма к другому основанию Сложность: лёгкое	2
4.	Сумма логарифмов, логарифм степени Сложность: лёгкое	3
5.	Основное логарифмическое тождество (логарифм степени) Сложность: среднее	4
6.	Свойства логарифмов (степени и произведения) Сложность: среднее	4
7.	Свойства логарифмов (степени и частного) Сложность: среднее	4
8.	Логарифм степени (произведение) Сложность: среднее	3
9.	Логарифм степени (частное) Сложность: среднее	5
10.	Свойства логарифмов (степень основания, основное логарифмическое тождество) Сложность: среднее	7
11.	Свойства логарифмов Сложность: сложное	7
12.	Свойства логарифмической функции Сложность: среднее	2
13.	Формула перехода к новому основанию (метод подстановки) Сложность: сложное	7
14.	Логарифм произведения (тригонометрическое выражение) Сложность: сложное	7
15.	Логарифм произведения Сложность: сложное	5

Тесты

1.

Тренировка по теме Базовые свойства логарифмов Сложность: лёгкое

15

Материалы для учителей

1.

Методическое описание