- Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Формулы для заданий ЕГЭ по информатике
Кодирование текстовой информации
I = n * i
- n — количество символов
- i — количество бит на 1 символ (кодировка)
Формула для нахождения количества цветов в используемой палитре
i = log2N
- N — количество цветов
- i — глубина цвета
Формула объема памяти для хранения растрового изображения
I = M * N * i
- I — объем памяти, требуемый для хранения изображения
- M — ширина изображения в пикселях
- N — высота изображения в пикселях
- i — глубина кодирования цвета или разрешение
Или
I = N * i битов
- N – количество пикселей (M * N)
- i – глубина кодирования цвета (разрядность кодирования)
Для указания объема выделенной памяти встречаются разные обозначения (V или I).
Формула объема звукового файла
I = β * ƒ * t * S
- I — объем
- β — глубина кодирования
- ƒ — частота дискретизации
- t — время
- S — количество каналов (S=1 для моно, S=2 для стерео, S=4 для квадро)
Формула объема переданной информации
I = V * t
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду и пр.)
- t — время передачи
Формула скорости передачи данных
V = I / t
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду и пр.)
- t — время передачи
Формулы преобразования
- 1 Мбайт = 220 байт = 223 бит,
- 1 Кбайт = 210 байт = 213 бит
- Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Шпаргалка ЕГЭ по информатике. Все необходимое
Скачать шпаргалку для подготовки к ЕГЭ по информатике. Содержимое:
— Логика
— Системы счисления
— Кодирование информации
— Программирование
— Теория игр
и другое
Похожие материалы
- 1
- 2
- 3
- 4
- 5
Оценка: 2.6 из 34
Комментарии
Всего комментариев: 0
1. Кодирование
текста
2.
Анализ таблицы истинности
4. Бд и файловая система
6. Алгоритмы
Сколько 1, 0, целых A<X<B, вычислить, перевести (-а) в 2сс
Свойства чисел:
1.числа вида 2k записываются в двоичной системе как единица и k нулей, например:16 = 24 = 100002 (числа,
являющиеся степенями 2,3.. ( в любой СС!!)
2. числа вида 2k-1 записываются в двоичной системе k единиц, например: 15 = 24-1 = 11112 (числа
, предшествующие степеням «2»- состоят из «1» и на разряд меньше (в 3 из 2, 4
из 3 , т.е n-1))
3. Двоичное число (другая n CC), оканчивающееся — на 0 – четное(кратно n), — на 1- нечетное (и любое отличное от нуля число в той СС
говорит о том, что число не кратно n).
Отрицательное число =
1) а-1 2) (а-1)из10 перводим в 2сс 3) первая 1
сохраняется, все остальные цифры переворачиваем 1-0,0-1
|
10сс |
2сс |
8 сс |
триады |
16сс |
тетрады |
|
0 |
0 |
0 |
000 |
0 |
0000 |
|
1 |
1 |
1 |
001 |
1 |
0001 |
|
2 |
10 |
2 |
010 |
2 |
0010 |
|
3 |
11 |
3 |
011 |
3 |
0011 |
|
4 |
100 |
4 |
100 |
4 |
0100 |
|
5 |
101 |
5 |
101 |
5 |
0101 |
|
6 |
110 |
6 |
110 |
6 |
0110 |
|
7 |
111 |
7 |
111 |
7 |
0111 |
|
8 |
1000 |
10 |
8 |
1000 |
|
|
9 |
1001 |
11 |
9 |
1001 |
|
|
10 |
1010 |
12 |
A |
1010 |
|
|
11 |
1011 |
13 |
B |
1011 |
|
|
12 |
1100 |
14 |
C |
1100 |
|
|
13 |
1101 |
15 |
D |
1101 |
|
|
14 |
1110 |
16 |
E |
1110 |
|
|
15 |
1111 |
17 |
F |
1111 |
|
|
16 |
10000 |
20 |
10 |
10000 |
|
0+0=0 |
0-0=0 |
0*0=0 |
|
0+1=1 |
1-0=1 |
0*1=0 |
|
1+0=1 |
1-1=0 |
1*0=0 |
|
1+1=10 |
10-1=1 |
1*1=1 |

Сопоставлять
значений переменных с функциями (начинать с «одиночных»)
1. Отрицание
(НЕ,¬ , Ā) меняет знаки: < на >=,> на<=.<= на
>, >= на <
2.
Логическое умножение (И, •, ˄, &)
3.
Логическое сложение (ИЛИ, +, ˅, |)
Порядок
выполнения операций: ( ), не, и, или, →,º ….
|
А |
не(А) |
А |
В |
А ˄ В |
А |
В |
А ˅ В |
А |
В |
А→В |
А |
В |
АºВ |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1)внимательно читать задание
2)файловая система:?-точно 1 знак, *-произвольное количество или
их отсутствие
Автомат(10 СС):
1)определяем СС
2)записываем правило a+b, c+d или другое
3)определяем порядок записи , ¯
4) определяем максимально возможное числов этой СС и
максимальные суммы(!!!помнить о правилах сложения в разных СС)
5) помним о разрядах числа (десятки, сотни, единицы)
Автомат(2СС): четное оканчивается 0, нечетное на 1.
Обработка искаженных сообщений, Калькулятор и др.
5. Декодирование (условие Фано)
Условие Фано: ни одно кодовое слово
не является началом другого кодового слова (дерево 0-1): минимальный код,
короткое слово, сумма кодовых слов, только для конкретного слова и др.
Алгоритм Хаффмана
(оптимальный префиксный код): для самого частого- самый короткий код. Самое
частое повторение обычно 1 бит(0),самые малые повторения обычно 2-3 бита
(умножаем и складываем все ветви)
9.
Кодирование информации (+передача)
7. Анализ диаграмм и таблица Excel
8. Анализ программ (цикл while)
Звук: I=n*i*f*t (n-кол-во дорожек, i-бит на отсчет, f-частота дискретизации ,t-время)
1)
запись близка 2) секунды-минуты
3)
перезаписывают один и тот же файл — пропорция
1кГц=1000Гц, моно-1, стерео-2, квадро -4, …
Графика: I=k*i, N=2i(k –кол-во пикселей (200dpi= 200ppi=200*200)
i -инф. вес 1 пикселя, N-количество цветов)
1)определить кол-во цветов
2)не может превышать <
, >=, > , <=
3) перезаписывают один и тот же файл — пропорция
4) сохраняют каждые t сек(мин)
Передача информации: Iбит=Vбит/сек*tсек , V =I/t, t=I/V
I – размер файла, V – скорость , t – время передачи.
1)сравнение
способов передачи А и Б и на сколько
Наименьшая
единица информации 1 бит
1
байт = 8 бит = 23бит
1Кбайт(килобайт)
= 1024байт = 210байт
1Мбайт(мегабайт)
= 1024Кбайт = 210Кбайт
1Гбайт(гигабайт) = 1024Мбайт = 210Мбайт
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
210 |
211 |
|
N |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
|
S передачи |
«Байт |
|
1 1 1 |
1 1 Кбайт/сек 1 Мбайт/сек |
!!!Важно в формулу подставлять значения в одинаковых единицах
измерения и переводить конечный результат в запрашиваемые в задаче единицы.
1)по формулам 2) по пропорции
1)геометрическая или арифметическая прогрессия
2)условие выполнения цикла (с предусловием)
1)вычисляем значения в ячейках по формулам какие можно
2) соотносим числовые величины и графические изображения
(подбираем число или формулу). Диапазон ячеек А1:D2 от первой ячейки до
последней. Весь круг соответствует сумме всех значений, по которым
строится диаграмма. Отдельные сектора пропорциональны доле одного значения в
общей сумм
В формулах * — умножение, / — деление, $ — абсолютная ссылка, при
копировании формулы значение не меняется
10. Перебор слов и СС
1)размещения(с повторениями, букву сколько угодно раз)Варианты =
2)перестановки (без повторов, букву 1 раз, буквы разные) Р=n!
2)перестановки (без повторов, букву 1 раз, есть одинаковые буквы
разные) Р=n!/n1! .n2!..
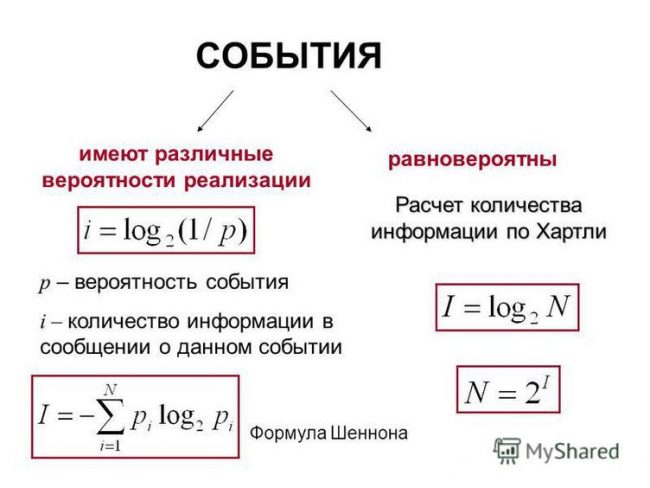
4) вероятности формула Шеннона.
5)Слова(определяем СС (= количество букв), переводим в ту СС, из
той в 10)
— На каком месте стоит слово +1
— Какое слово стоит под номером -1
3. Анализ информационной модели
15. Количество путей
Соотносим количество пересечений дорог и узлов вершин графа,
анализ начинаем с графа (вершин графа)
|
Город |
Откуда |
Кол-во путей |
|
А |
— |
1 |
|
Б |
А |
1 |
|
В |
АБ |
2 |
|
…… |
…. |
….. |
Потеря маршрутов, считая «вручную»
Траектория через А и
не через Б –внимательно!
22. Оператор ветвления
Строим дерево внимательно через те точки, которые указаны в
траектории
11.Рекурсия (функция возврата к самой себе)
14. Алгоритмы формальных исполнителей
1) Вызов функций F(n) или/и G(n) от предыдущих значений
2) Количество напечатанных
3) Сумма напечатанных
4) Какие выведет числа (!!!Важен порядок вызова (обращения к
рекурсии).
-если write
стоит в начале, то прямой последовательный обход.
— если write
стоит после какой-то первой функции, то выполняется вызов по этой ветке до
конца, по окончанию вызывается оставшаяся функция.
— если write
стоит после всех функций, аналогично предыдущему
Чертежник
Начал и вернулся туда же: (х,у)+…-…=(0,0)
Вернулся в другую точку: (х,у)+…-…=(х1,у1)
Повтори n
раз n*(3+2-4…)
Замена команды n*(а+2-4…)=0, n*(b+3-8….)=0
1)отдельно считаем смещение по x и по y;
2)внимательно читаем вопрос;
3)даём ответ на вопрос, поставленный в задаче.
Робот: клетка начала и конца
считается закрашенной, движение идет до упора и по условию.
Редактор: циклы считаем с НАЧАЛА!!!
17. Запросы интернета (Диаграммы Эйлера Венна)
23. Логические уравнения
19. Одномерные массивы
Знак
«&»-пересечение запросов (и) , а «|»-объединение запросов (или)
1) Обозначаем зоны запросов буквами a,b,c,d,e,f…..
2) !!! Два множества могут не пересекаться (просматриваем суммы
пересечений и объединений)
|
А ˄ В |
А ˅ В |
А→В |
АºВ |
А¹В |
|
1 и 1 |
1 и 1 |
1-1 |
1 и 1 |
0 и 1 |
|
0 и 1 |
0-0 |
0 и 0 |
1 и 0 |
|
|
1 и 0 |
0-1 |
1) замена переменных, если нужно
2) последовательное решение уравнений
Решение системы уравнений – это битовая цепочка (битовый вектор-
единичный объект)
3) уравнения–ограничения на битовый вектор (комбинации)
4) кол-во решений находиться по правилам комбинаторики (чаще
всего аn)
5) варианты комбинаций истинности и лжи для ˄,˅,→, º
Стратегия решения: трассировочная
таблица , узнать базовый алгоритм и проверить
а) алгоритм меняющий
элементы массива местами
б) массивы с индексами от 0
до 10 цикл for
в) цикл for или while в
нем ветвление (if)
г) двумерные
массивы(прямоугольная матрица A[i] , B[i]
Цикл for в цикле for
(выполняется первый внешний цикл, потом полностью выполняется внутренний цикл
for, далее 2 эл из 1, и все из
2го ) (прямоугольная матрица)
16. Уравнения в различных СС
26. Стратегия (теория игр)
13. Вычисление количества информации
21. Анализ программы с
подпрограммами
1)помнить,
что любое число в степени в соответвующей СС=
2)выражения
упрастить и определить СС, если сс 2,3,4,5,…..при вычитании 1 получается на
1 меньше чем СС.
3)
числа в конце переводим в нужную СС
4)
если произведение степени и числа, применяем правила арифменики в той СС
(арифметические операции выполняются в одной СС)
5) если
степень числа * на число, применяем арифметические правила той сс в которой
производиться *.
Важно!!!
Арифметика возможна только в одной и той же СС
Описывать стратегию для «выигравшего- выигрышную стратегию, для
проигравшего- все стратегии» (строим дерево игры)
1) камни (камни две кучи, 2 разных хода)
2) фишки (расстояние
3) карточки(таблички) с числами, убирать дубль, если нужно
укоротить, ставить дубль если нужно удлинить
4) слова (считаем количество букв в словах) Игрок 1- нечетные
ходы, Игрок 2- четные ходы
I=k*i, N=2i (N-алфавит, k–количество
символов в тексте, i–
инф. вес 1 символа:
КОИ-8(8 бит), ASCII(8 бит), Unicode (16
бит), др)
1) количество вариантов (кто прошел –это N из него находим i ( N=2i ), а I=k*i –это всего.
2) пароли и номера авто: доп. сведения + код+ пароль
!!!Внимательно читать условие (сведения могут быть в 2 коде или
другой СС)
1) Квадратичные
(биквадратные) уравнения:
Точки минимума =
,
=у(
или через F`(x)
Можно искать точки
(max, min), и
значения функций в точке (fmax, fmin). Оценивать
знаки , ¯ функции.
!!!Обязательно
проверять проверять значения на концах отрезков.
2) вызов функции k=10,64 и
т.п. min или max число
Если +1, то
интервал А £
х <В
Если ¯-1, то
интервал А < х £В
12. IP-адресация
20. Анализ алгоритма с циклами и ветвлениями
24. Поиск ошибки в программе
25. Обработка
массива
010=000000002 25510=111111112
маска-11111111.11111111.11111000.00000000 (1….потом 0)
1)мах количество 1 или 0 в маске
2)мах и min байт
маски
3) 2 байт маски, если 3 =0
4) сколько различных значений маски (сколько масок, варианты)
5)количество ПК в сети (2 в степени нулей маски )
6) номер ПК в сети (нули маски в проекции на ip-адрес)
7) два ip принадлежат
одной сети (однозначная маска для обоих)
Номер компьютера
Количество адресов в сети
1) Алгоритм Евклида (2 переменные и разность), НОД
прописан в условии, в условии смотреть какое х нужно вывести х>100, 150…
Выражаем L
через х, L кратно НОД, далее проверяем на числах.
Вычисление НОД(а,b)= НОД(а-b,b)= НОД(а,b—a)
Заменяем большее из двух чисел разностью большего и меньшего до
тех пор, пока они не станут равны. НОД(14,21)= НОД(14,7)= НОД(7,7)=7
Если разница велика и нужно определить количество шагов.
Заменяем большее остатком от деления на меньшее до тех пор, пока меньше не
станет равно нулю. НОД(21,28) (28mod21=7)= НОД(21,7) (21mod7=0)=НОД(0,7)=7
2) Обработка цифр в числе:
— на выводе отмечаем, какие числа выводит программа (указаны в
условии)
— ВАЖНО!!!определить СС в которой обрабатываются числа
x: = а div 10, x: = а div 2, x: = а div 3 , x: = а div 4 , x: = а div 5
ЗНАТЬ!!! числа входящие в конкретную СС (0- число четное!!!)
Перебор цифр в числе за счет цикла ( while x>0 ) пока оно не равно нулю.
— если определяют не просто число , а разрядное (трехзначное,
двузначное)- это дополнительное условие (первое двузначное-10n, трехзначное 100n и т.д конечная граница определяется переводом из 10 сс в нужную)
ЯЗЫК программирования Pascal не понимает другие СС, кроме 10!!
После решения задачи в какой-то СС , переводим полученное число
в 10СС
!!!Проверка на четность:
— в четных СС по последней цифре (0,2,4,6,8 СС)
— нечетных СС по сумме цифр в числе (1,3,5,7,9 СС)
Схема
решения задачи: прогнать задачу на требуемом числе или
на любом удобном Þ чаще всего можно сразу ответить на 1 и 3
вопрос задачи (найти ошибки) (прогнать и убедиться в правильности) Þ после
выполнить 2 задание задачи (найти число работающее правильно )
Решая
задачу делить ее на части:
1)
что выводит (writeln(…)) и
запрашивает readln(…))
2) проверять
инициализацию переменных s:=0, p:=1, k:=0
3)
проверяем условия циклов и условий (правила их работы) и сам алгоритм
Проверка
на степень: n=ak Þ , т.е if n=1.
Формулу для вычисления n-ого элемента арифметической прогрессии: аn=a1+d(n-1) формулу для вычисления суммы первых n членов арифметической прогрессии:,
где ai – i-ый
элемент последовательности,d – шаг (разность) последовательности
1) Организация ввода данных (уже есть)
2) Инициализация начальных значений некоторых переменных (требуется
задать!)
3)Обработка данных (требуется организовать!)
4) Вывод данных (требуется организовать!)
Обработка данных происходит в процессе циклической
обработки элементов ( может обрабатывается один, пара, тройка или
последовательность элементов, речь всегда идет о рядом стоящих элементах,
которые всегда можно обработать одним циклом) по некоторому комбинированному
условию, которое необходимо формализовать основе анализа условия задачи.
ВАЖНО!!! не писать программу полностью, а «дописать» её в рамках
уже организованного ввода, а также заданного количества переменных и их
типов: необходимо дописать инициализацию, организовать обработку и вывод.
Для проверки на кратность использовать —
a[i] mod
2 <> 0 (Кратность n)
18. Логические выражения
1) отрезки (преобразуем,
отделяем A (или Ā ) от отрезков, сумма должна
покрывать всю числовую прямую)
упростить А→В= Ā+В, А º В=А*В+Ā*, (см. табл задания№2)
2) неопределенный отрезок
(более чем 25 целых, т.е 26 чисел)преобразуем, пользуемся
распределительным законом)
Помнить два закона !А+В*С=(А+В)*(А+С)
и А*В+С=(А*В)+(А*С)
3) множества (отделяем
числа, отделяем А, делаем отрицание с числами и применяем закон де Моргана,
как с отрезками только на диаграммах Эйлера -Венна)
4) делители А=1,
остальное =0 (Ā=В, А= ) закон де Моргана
Если меду числами ˄-ищем
кратные, если ˅-делители
1. Если формула истинна (равна 1), и после упрощения A без
отрицания, то используется закон: Amin = ¬B
Если формула истинна (равна 1), и после
упрощения A с отрицанием, то используется закон:Amax =
B
2. Если формула ложна (равна 0), и после
упрощения A без отрицания, то используется закон: Amax =
¬B
Если формула ложна (равна 0), и 2. после
упрощения A с отрицанием, то используется закон: Amin =
B, где B — известная часть выражения
5)неравенства ( если А=1,
то остальное берется с отрицанием, если А=0 (отрицательно), то остальное не
меняем, оно положительно)
а)длина –это модуль от точки
до точки: (А..)→(….х ) ) ˄ ( (
….х) → (А..)) через
и
, если где-то парабола, то
модуль и отрезок значений параболы.
б) сколько существует
значений: кол-во чисел n+1
в) линейные неравенства
(графическим способом, как задача с параметром, определяем область и
пересечение графиков прямых линий, анализируем)
6) битовые операции
1) А→В= Ā+В
2) избавляемся от всех
отрицаний (закон де Моргана) и выстраиваем импликации
3) Упрощаем до выражений
следующего типа:
a) (Q•A) →P=1 , т.е Q+А=P
б) (Q•P) →А=1, т.е Q+ P = А
в) P→ (Q+A) =1, A→ (Q+P) =1,
г) (Q+Р) → (L+A) =1, т.е Q•А=A•L
(L•A) →(Q•Р) =1, т.е Q+А=A+L
д) побитовые операции равны числам
(переводим их в 2СС)
решаем как с делителями и отрезками А=1,
остальные =0, сначала находим маску х при =0 и варианты букв в маске х при ¹ 0) не решаем по общей схеме
4) применяем свойства 1)XP ˄XQ=XP or Q=P+Q
2) XP ˅ XQ=XP and Q=P•Q
Урок посвящен разбору задания 7 ЕГЭ по информатике
Содержание:
- Объяснение заданий 7 ЕГЭ по информатике
- Кодирование текстовой информации
- Кодирование графической информации
- Кодирование звуковой информации
- Определение скорости передачи информации
- Решение заданий 7 ЕГЭ по информатике
- Тема: Кодирование изображений
- Тема: Кодирование звука
- Тема: Кодирование видео
- Тема: Скорость передачи данных
7-е задание: «Кодирование графической и звуковой информации, объем и передача информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Умение определять объём памяти, необходимый для хранения графической и звуковой информации
До ЕГЭ 2021 года — это было задание № 9 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Если вычисления получаются слишком громоздкими, значит, Вы неправильно решаете задачу. Удобно выделить во всех множителях степени двойки, тогда умножение сведётся к сложению
показателей степеней, а деление – к вычитанию»
ФГБНУ «Федеральный институт педагогических измерений»
Кодирование текстовой информации
I = n * i
где:
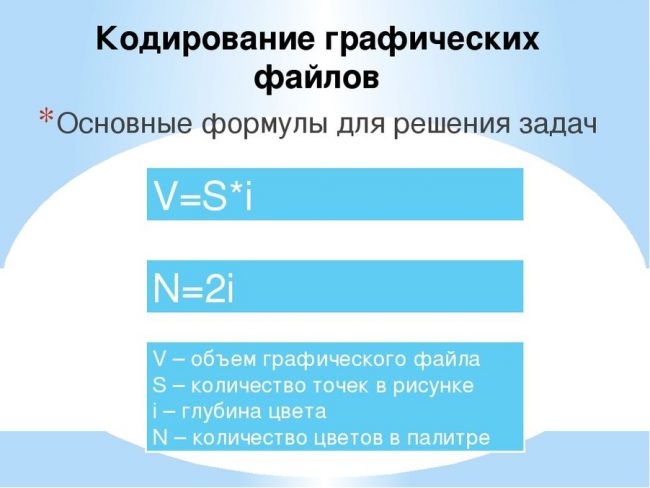
Кодирование графической информации
Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике данной темы.
- Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
- Разрешение – это количество пикселей на дюйм размера изображения.
- Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
- Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2i возможных вариантов, поэтому можно использовать не более 2i различных цветов.
- N — количество цветов
- i — глубина цвета
- В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> получаем 28 вариантов на каждый из трех цветов.
- R G B: 24 бита = 3 байта — режим True Color (истинный цвет)
- I — объем памяти, требуемый для хранения изображения
- M — ширина изображения в пикселях
- N — высота изображения в пикселях
- i — глубина кодирования цвета или разрешение
- где N – количество пикселей (M * N) и i – глубина кодирования цвета (разрядность кодирования)
- Следует также помнить формулы преобразования:
Формула для нахождения количества цветов в используемой палитре:
i = log2N
Найдем формулу объема памяти для хранения растрового изображения:
I = M * N * i
где:
Или можно формулу записать так:
I = N * i битов
* для указания объема выделенной памяти встречаются разные обозначения (V или I).
1 Мбайт = 220 байт = 223 бит,
1 Кбайт = 210 байт = 213 бит
Кодирование звуковой информации
Познакомимся с понятиями и формулами, необходимыми для решения заданий 7 ЕГЭ по информатике.
- Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.
- T – интервал дискретизации (измеряется в с)
- ƒ — частота дискретизации (измеряется в Гц, кГц)
- Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
- Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.
- Получим формулу объема звукового файла:
- I — объем
- β — глубина кодирования
- ƒ — частота дискретизации
- t — время
- S — количество каналов
Дискретизация, объяснение задания 7 ЕГЭ
* Изображение взято из презентации К. Полякова
Разрядность кодирования
* Изображение взято из презентации К. Полякова
Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования β бит требуется бит памяти:
I = β * ƒ * t * S
S для моно = 1, для стерео = 2, для квадро = 4
Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется:
✍ Решение:
I = 8000*16*128 = 16384000 бит
I = 8000*16*128/8 = 23 * 1000 * 24 * 27 / 23 = 214 / 23 =211 =
= 2048000 байт
Определение скорости передачи информации
- Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии связи(кабеля)
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду или подобных единицах)
- t — время передачи
Объем переданной информации I вычисляется по формуле:
I = V * t
* Вместо обозначения скорости V иногда используется q
* Вместо обозначения объема сообщения I иногда используется Q
Скорость передачи данных определяется по формуле:
V = I/t
и измеряется в бит/с
Егифка ©:
Решение заданий 7 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Тема: Кодирование изображений
7_1:
Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Типовые задания для тренировки
✍ Решение:
- Используем формулу нахождения объема:
- Подсчитаем каждый сомножитель в формуле, стараясь привести числа к степеням двойки:
- M x N:
160 * 160 = 20 * 2³ * 20 * 2³ = 400 * 26 = = 25 * 24 * 26
256 = 28 т.е. 8 бит на пиксель (из формулы кол-во цветов = 2i)
I = 25 * 24 * 26 * 23 = 25 * 213 - всего бит на всё изображение
(25 * 213) / 213 = 25 Кбайт
Результат: 25
Детальный разбор задания 7 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.2:
Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- где M * N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:
128 * 256 = 27 * 28 = 215
i = I / (M*N)
23 * 3 * 210 * 23: i = (23 * 3 * 210 * 23) / 215 = = 3 * 216 / 215 = 6 бит
26 = 64 вариантов цветов в цветовой палитре
Результат: 64
Смотрите видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.3:
После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- i можно найти, зная количество цветов в палитре:
где N — общее количество пикселей,
а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
до преобразования: i = 8 (28 = 256) после преобразования: i = 2 (22 = 4)
I = x * 8 I - 18 = x * 2
x = I / 8
I - 18 = I / 4
4I - I = 72
3I = 72
I = 24
Результат: 24
Подробный разбор 7 задания ЕГЭ смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.4:
Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- В такого рода задачах необходимо учесть, что уменьшение разрешения в 2 раза, подразумевает уменьшение в 2 раза пикселей отдельно по ширине и по высоте. Т.е. в целом N уменьшается в 4 раза!
- Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:
где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)
42 = N * i I = N / 4 * 4i
i = 42 / N
[ I= frac {N}{4} * 4* frac {42}{N} ]
I = 42
Результат: 42
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.5:
Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город Б?
Типовые задания для тренировки
✍ Решение:
- По формуле скорости передачи файла имеем:
- По формуле объема файла изображения имеем:
- Для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
- Изменим формулу получения объема файла для города Б:
- Для города А и Б заменим значения объема в формуле для получения скорости:
- Подставим значение скорости из формулы для города А в формулу для города Б:
- Выразим t:
где I — объем файла, а t — время
где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)
[ I= frac {2*N * i}{3} ]
Город А:
[ V= frac {N*i}{72} ]
Город Б:
[ 3*V= frac{frac {4*N*i}{3}}{t} ]
или:
[ t*3*V= frac {4*N*i}{3} ]
[ frac {t*3*N*i}{72}= frac {4*N*i}{3} ]
t = 4 * 72 / (3 * 3) = 32 секунды
Результат: 32
Другой способ решения смотрите в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
ЕГЭ по информатике задание 7.6:
Камера делает фотоснимки размером 1024 х 768 пикселей. На хранение одного кадра отводится 900 Кбайт.
Найдите максимально возможное количество цветов в палитре изображения.
Типовые задания для терировки
✍ Решение:
- Количество цветов зависит от глубины кодирования цвета, которая измеряется в битах. Для хранения кадра, т.е. общего количества пикселей выделено 900 Кбайт. Переведем в биты:
900 Кбайт = 22 * 225 * 210 * 23 = 225 * 215
1024 * 768 = 210 * 3 * 28
[ frac {225 * 2^{15}}{3 * 2^{18}} = frac {75}{8} approx 9 ]
9 бит на 1 пиксель
29 = 512
Результат: 512
Смотрите подробное решение на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование изображений:
7_8: Демоверсия ЕГЭ 2018 информатика:
Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится.
Какое максимальное количество цветов можно использовать в палитре?
✍ Решение:
- По формуле объема файла изображения имеем:
- Посмотрим, что из формулы нам уже дано:
I = N * i
где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
I = 320 Кбайт, N = 640 * 420 = 307200 = 75 * 212 всего пикселей, i - ?
количество цветов = 2i
320 Кбайт = 320 * 210 * 23 бит = 320 * 213 бит
[ i = frac {I}{N} = frac {320 * 2^{13}}{75 * 2^{12}} approx 8,5 бит ]
2i = 28 = 256
Результат: 256
Подробное решение данного 7 (9) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
7_21: : ЕГЭ по информатике задание 7.21:
Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт.
Определите количество цветов в палитре до оптимизации.
Типовые задания для тренировки
✍ Решение:
- По формуле объема файла изображения имеем:
- Так как по заданию имеем разрешение, выраженное в пикселях на дюйм, то фактически это означает:
- Формула количества цветов:
- Посмотрим, что из формулы нам уже дано до экономного варианта и при экономном варианте:
I = N * i
где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель).
I = значение ppi2 * N * i
количество цветов = 2i
Неэкономный вариант: I = 5 Мбайт = 5 * 223 бит, N - ?, i - ? 300 ppi Экономный вариант: I = 512 Кбайт = 29 * 213 бит = 222 бит, N - ?, i = 4 бит (24 = 16) 150 ppi
N = I / (i * 150*150 ppi) N = 222 / (4 * 22500)
I = N * 300*300 ppi * i 5 * 223 = (222 * 300 * 300 * i) / (22500 * 4);
i = (5 * 223 * 22500 * 4) / (222 * 300 * 300) = 9000 / 900 = 10 бит
210 = 1024
Результат: 1024
Тема: Кодирование звука
7_7:
На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт.
С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.
Типовые задания для тренировки
✍ Решение:
- По формуле объема звукового файла получим:
- Из задания имеем:
I = β * t * ƒ * S
I= 7500 Кбайт β= 32 бита t= 30 секунд S= 4 канала
[ ƒ = frac {I}{S*B*t} = frac {7500 * 2^{10} * 2^3 бит}{2^7 * 30}Гц = frac { 750 * 2^6}{1000}КГц = 2^4 = 16 ]
24 = 16 КГц
Результат: 16
Для более детального разбора предлагаем посмотреть видео решения данного 7 задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
ЕГЭ по информатике задание 7_9:
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.
Типовые задания для тренировки
✍ Решение:
- Для решения понадобится формула нахождения скорости передачи данных формулы:
- Вспомним также формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):
V = I/t
I = β * ƒ * t * s
где:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — кол-во каналов (если не указывается, то моно)
город Б: β - в 2 раза выше ƒ - в 3 раза меньше t - 15 секунд, пропускная способность (скорость V) - в 4 раза выше
город А: βБ / 2 ƒБ * 3 IБ / 2 VБ / 4 tБ / 2, tБ * 3, tБ * 4 - ?
t = t/2
t = t * 3
t = t * 4
[ t_А = frac {15}{2} * 3 * 4 ]
90 секунд
Результат: 90
Подробное решение смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
ЕГЭ по информатике задание 7.10:
Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.
Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:
I = β * ƒ * t * S
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов
1 состояние: S = 2 канала I = 30 Мбайт
2 состояние: S = 1 канал β = в 2 раза выше ƒ = в 1,5 раза ниже I = ?
I = I / 2
I = I * 2
I = I / 1,5
I = 30 Мбайт / 2 * 2 / 1,5 = 20 Мбайт
Результат: 20
Смотрите видеоразбор данной задачи:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звуковых файлов:
ЕГЭ по информатике задание 7_11:
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.
✍ Решение:
- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:
I = β * ƒ * t * S
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
А: t = 100 c.
Б: β = в 3 раза выше ƒ = в 4 раза ниже t = 15 c.
✎ 1 способ решения:
tA для преобразов. = 100 секунд * 3 / 4 = 75 секунд
75 / 15 = 5
Ответ: 5
✎ 2 способ решения:
А: tА = 100 c. VА = I / 100
Б: β = в 3 раза выше ƒ = в 4 раза ниже t = 15 c. IБ = (3 / 4) * I VБ = ((3 / 4) * I) / 15
[ frac {V_Б}{V_А} = frac {3/_4 * I}{15} * frac {100}{I} = frac {3/_4 * 100}{15} = frac {15}{3} = 5 ]
(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5
Результат: 5
Подробный видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
ЕГЭ по информатике задание 7_12:
Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится.
Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.
✍ Решение:
- Вспомним формулу объема звукового файла:
- Для простоты расчетов пока не будем брать во внимание количество каналов. Рассмотрим, какие данные у нас есть, и какие из них необходимо перевести в другие единицы измерения:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов
β = 32 бита ƒ = 32кГц = 32000Гц t = 2 мин = 120 с
(32 * 32000 * 120) / 223 = =( 25 * 27 * 250 * 120) / 223 = = (250*120) / 211 = = 30000 / 211 = = (24 * 1875) / 211 = = 1875 / 128 ~ 14,6
14,6 * 4 = 58,5
Результат: 60
Смотрите подробное решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
7_19: Государственный выпускной экзамен ГВЭ 2018 (информатика ГВЭ ФИПИ, задание 7):
Производится двухканальная (стерео) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 5 минут, её результаты записываются в файл, сжатие данных не производится.
Какая из приведённых ниже величин наиболее близка к размеру полученного файла?
1) 14 Мбайт
2) 28 Мбайт
3) 55 Мбайт
4) 110 Мбайт
✍ Решение:
- По формуле объема звукового файла имеем:
I — объем β — глубина кодирования = 32 бита ƒ — частота дискретизации = 48000 Гц t — время = 5 мин = 300 с S — количество каналов = 2
I = 48000 * 32 * 300 * 2
48000 | 2 24000 | 2 12000 | 2 6000 | 2 = 375 * 27 3000 | 2 1500 | 2 750 | 2 375 | 2 - уже не делится 187,5
300 | 2 = 75 * 22 150 | 2 75 | 2 - уже не делится 37,5
I = 375 * 75 * 215
I = 375 * 75 * 215 / 223 = 28125 / 28
210 = 1024 1024 * 2 2048 * 2 4096 * 2 8192 * 2 16384 * 2 32768
210 * 25 = 215 = 32768 210 * 24 = 214 = 16384
215 / 28 = 27 = 128 214 / 28 = 26 = 64
Результат: 4
Подробное решение ГВЭ задания 7 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование звука:
7_20:
Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится.
Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.
✍ Решение:
- По формуле объема звукового файла имеем:
I — объем β — глубина кодирования = 32 бита ƒ — частота дискретизации = 48000 Гц t — время = 5 мин = 300 с S — количество каналов = 2
ƒ = 4 кГЦ = 4 * 1000 Гц ~ 22 * 210 B = 64 бит = 26 / 223 Мбайт t = 1 мин = 60 c = 15 * 22 c S = 2
I = 26 * 22 * 210 * 15 * 22 * 21 / 223 = 15/4 ~ 3,75
Результат: 4
Видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Кодирование видео
7_22:
Камера снимает видео без звука с частотой 120 кадров в секунду, при этом изображения используют палитру, содержащую 224 = 16 777 216 цветов. При записи файла на сервер полученное видео преобразуют так, что частота кадров уменьшается до 20, а изображения преобразуют в формат, использующий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. 10 секунд преобразованного видео в среднем занимают 512 Кбайт.
Сколько Мбайт в среднем занимает 1 минута исходного видео?
Типовые задания для тренировки
✍ Решение:
- Посмотрим, как изменялись параметры файла до преобразования и после:
ДО: ƒ = 120, i = 24 бит ПОСЛЕ: ƒ = 20, i = 8 бит (28 = 256) t = 10 секунд I = 512 Кбайт = 29 Кбайт
за 10 секунд: I * 18 = 29 * 18 Кбайт = (29 * 18) . 210 Мбайт = 9 Мбайт
за 1 мин: 9 * 6 = 54 Мбайт
Результат: 54
Тема: Скорость передачи данных
ЕГЭ по информатике задание 7_13:
Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту.
Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
V = 128000 бит/с = 210 * 125 бит/с t = 1 мин = 60 с = 22 * 15 с 1 символ кодируется 16-ю битами всего символов - ?
Q = 210 * 125 * 22 * 15 = = 212 * 1875 бит на все символы
кол-во символов = 212 * 1875 / 16 = 212 * 1875 / 24 =
= 28 * 1875 = 480000
Результат: 480000
Разбор 7 задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_14:
У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 217 бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 216 бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных.
Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
Вася: V = 217 бит/с Петя: V = 216 бит/с Общий объем Q = 8 Мбайт
Q = 8Мбайт = 8 * 223 бит = 23 * 223 = 226 бит
t1 = 1024 Кбайт / 217 = 210 * 213 бит / 217 = = 210 / 24 = 64 с
t2 = 226 / 216 = 210 = 1024 c
t = t1 + t2 = 64 + 1024 = 1088
Результат: 1088
Подробный разбор смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_15:
Сколько секунд потребуется модему, передающему сообщения со скоростью 32000 бит/с, чтобы передать 16-цветное растровое изображение размером 800 x 600 пикселей, при условии, что в каждом байте закодировано максимально возможное число пикселей?
Типовые задания для тренировки
✍ Решение:
- Вспомним формулу скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
N — общее количество пикселей или разрешение, i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)
Q = 4 * 480000
t = 4 * 480000 / 32000 = 60 секунд
Результат: 60
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_16:
Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 9000 Мбайт данных, причем треть времени передача шла со скоростью 60 Мбит в секунду, а остальное время – со скоростью 90 Мбит в секунду?
✍ Решение:
- Формула скорости передачи данных:
* Вместо Q можно использовать обозначение I (для объема файла)
V - скорость Q - объем t - время
1 Мбайт = 8 Мбит
Q = 9000 Мбайт * 8 = 72000 Мбит
(60 * 1/3t) + (90 * 2/3t) = 72000
вынесем t за скобки, получим уравнение:
t * (20 + 60) = 72000
выразим t:
t = 72000 / 80 = 900 с = 15 мин
Результат: 15
Решение задания можно посмотреть и на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7.17:
Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
- средняя скорость передачи данных по каналу связи составляет 218 бит в секунду,
- объем сжатого архиватором документа равен 20% от исходного,
- время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
Типовые задания для тренировки
✍ Решение:
-
Рассмотрим способ А:
- Сначала найдем объем документа, зная, что он составляет 20% от исходного:
Q (объем) = 5 Мбайт * 0.2 = 1 Мбайт = 1 * 223 бит
V - скорость Q - объем t - время
t = Q / V + 7 + 1 = 8 + 223 / 218 = 8 + 25 = 40 c
Рассмотрим способ Б:
t = Q / V = 5 * 223 / 218 = 5 * 25 = 5 * 32 = 160 c
160 с - 40 с = 120 с
Результат: А120
Решение также можно посмотреть в видеоуроке:
📹 YouTube здесьздесь
Тема: Скорость передачи информации:
ЕГЭ по информатике задание 7_18:
Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:
А) сжать архиватором-1, передать архив по каналу связи, распаковать;
Б) сжать архиватором-2, передать архив по каналу связи, распаковать;
Какой способ быстрее и насколько, если
- средняя скорость передачи данных по каналу связи составляет 220 бит в секунду,
- объём документа, сжатого архиватором-1, равен 20% от исходного,
- на сжатие документа архиватором-1 требуется 15 секунд, на распаковку — 2 секунды,
- объём документа, сжатого архиватором-2, равен 10% от исходного,
- на сжатие документа архиватором-2 требуется 20 секунд, на распаковку — 4 секунды?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
✍ Решение:
-
Рассмотрим способ А:
- Сначала найдем объем документа, зная, что он составляет 20% от исходного:
Q (объем) = 20 Мбайт * 0.2 = 4 Мбайт = 22 * 223 бит = 225 бит
V - скорость Q - объем t - время
tA = 225 / 220 + 17 с = 25 + 17 = 49 с
Рассмотрим способ Б:
Q (объем) = 20 Мбайт * 0.1 = 2 Мбайт = 21 * 223 бит = 224 бит
tБ = 224 / 220 + 24 с = 24 + 24 = 40 с
49 - 40 = 9 с
Результат: Б9
Тема: Скорость передачи информации:
Решение 7 ЕГЭ по информатике, задание 7_19:
Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 1 минуту и 40 секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит 30 секунд. При этом на упаковку и распаковку данных всего ушло 10 секунд. Размер исходного документа 45 Мбайт.
Чему равен размер упакованного документа (в Мбайт)?
✍ Решение:
- Выпишем исходные данные для двух состояний документа, используя неизвестное x для искомого параметра — объема:
неупакованный:
I1 = 45 Мбайт t1 = 100 секунд (60 секунд + 40 секунд = 100)
упакованный:
I2 = x Мбайт t2 = 20 секунд (30 секунд - 10 секунд = 20)
45 = 100 х = 20
х = (45 * 20) / 100 = 9 Мбайт
Результат: 9
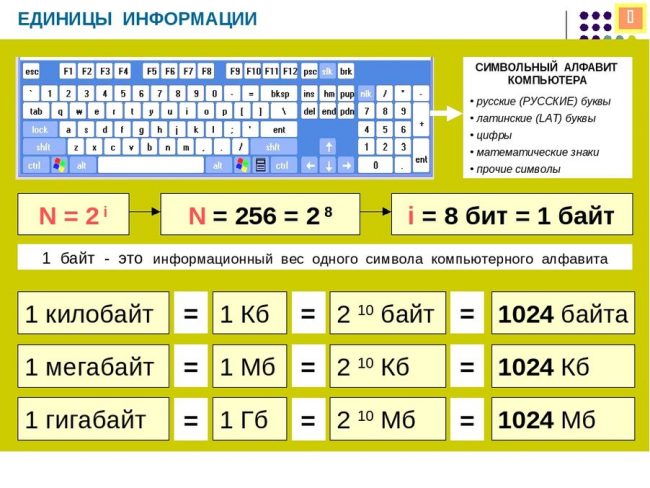
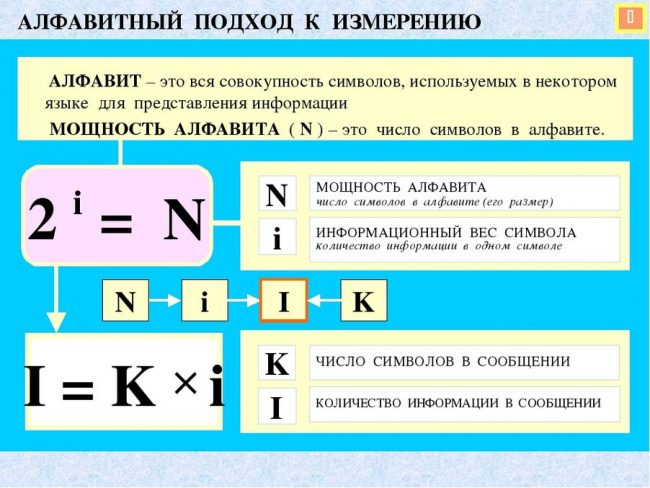
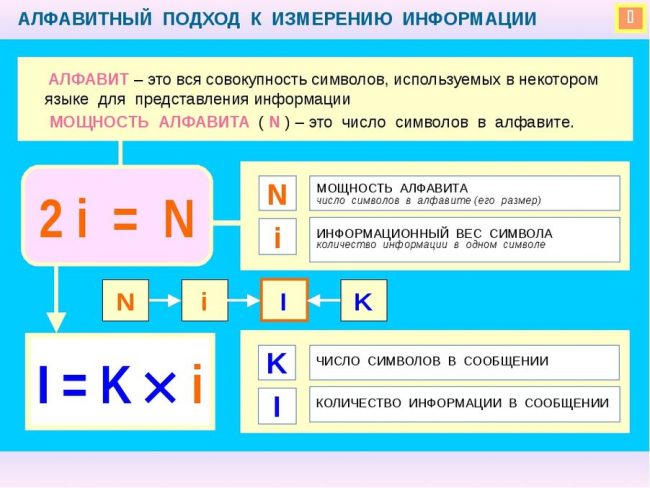
Формулы и Задачи (Информатика 10)
Формулы
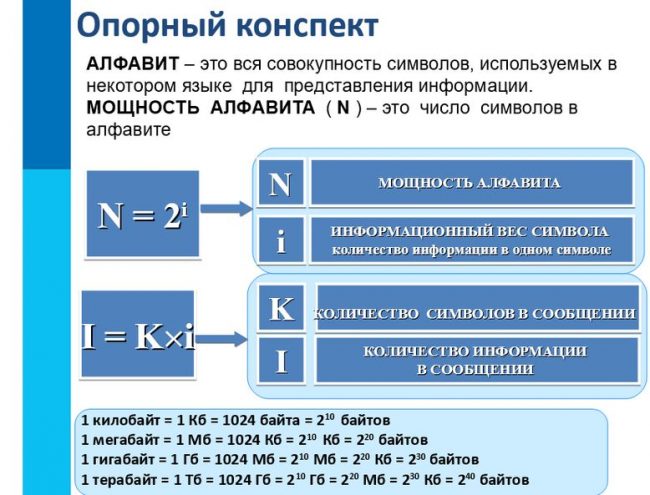
N = 2 i
N — мощность алфавита (количество знаков в алфавите)
i — информационный вес символа алфавита (количество информации в одном символе)
I = K * i
I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K — число символов в сообщении
i — информационный вес символа (количество информации в одном символе)
Q = N L
Q — количество разных сообщений
N — количество символов
L — длина сообщения
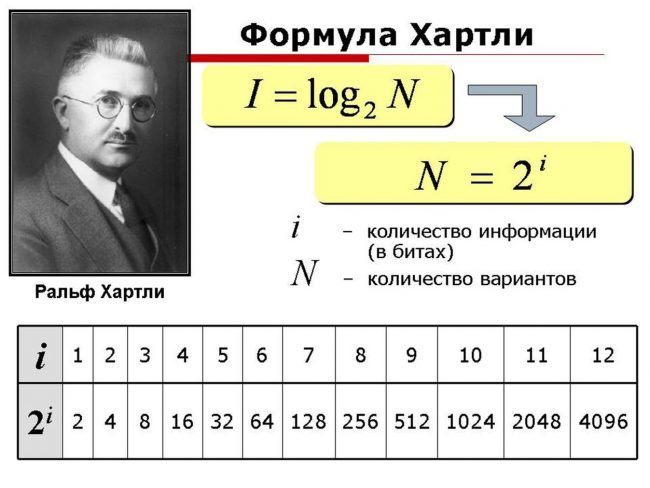
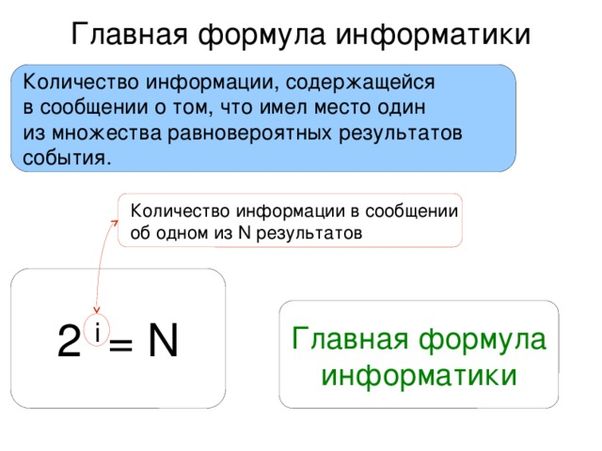
Формула Хартли:
I = log2N
I — количество информации, содержащееся в выбранном сообщении
N — количество сообщений
Римская система счисления
I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)
Перевод чисел из других систем счисления в десятичную систему счисления
Развернутая запись целого числа:
a 3a 2a 1a 0 = a 3 * p 3 + a 2 * p 2 + a 1 * p 1 + a 0 * p 0
Правило перевода числа из любой системы счисления в десятичную систему счисления — умножаем каждую цифру исходного числа на основание системы счисления в степени разряда , в котором находится эта цифра, а затем всё складываем.
Запись через схему Горнера:
p — основание системы счисления в котором представлено число.
Пример:
6 3 7 5 10 = 6 * 10 3 + 3 * 10 2 + 7 * 10 1 + 5 * 10 0
6 3 7 5 10 = (( 6 * 10 + 3 ) * 10 + 7 ) * 10 + 5
1 2 3 4 5 = 1 * 5 3 + 2 * 5 2 + 3 * 5 1 + 4 * 5 0 = 19410
1 2 3 4 5 = (( 1 * 5 + 2 ) * 5 + 3 ) * 5 + 4 = 19410
Развернутая запись дробного числа:
Запись через схему Горнера:
p — основание системы счисления в котором представлено число.
Пример:
0,6375 = 6 * 10 -1 + 3 * 10 -2 + 7 * 10 -3 + 5 * 10 -4
0,6375 = 10 -1 * (6 + 10 -1 * (3 + 10 -1 * (7 + 10 -1 * 5)))
0,1234 5 = 1 * 5 -1 + 2 * 5 -2 + 3 * 5 -3 + 4 * 5 -4
0,1234 5 = 5 -1 * (1 + 5 -1 * (2 + 5 -1 * (3 + 5 -1 * 4)))
Задачи
Алфавитный подход к измерению количества информации
Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.
- информационная ёмкость символа: 256 = 2 8 =>> i = 8 бит = 1 байт
- количество символов на странице:
32 * 64 = 2 5 * 2 6 = 2 11 - общее количество символов:
L = 10 * 2 11 - информационный объём сообщения:
I = L * i = 10 * 2 11 * 1 байт = 20 Кбайт
Системы счисления
Логические операции
Логической операцией называется выбор решения (действия), исходя из заданной ситуации, определяемой набором факторов (условий).
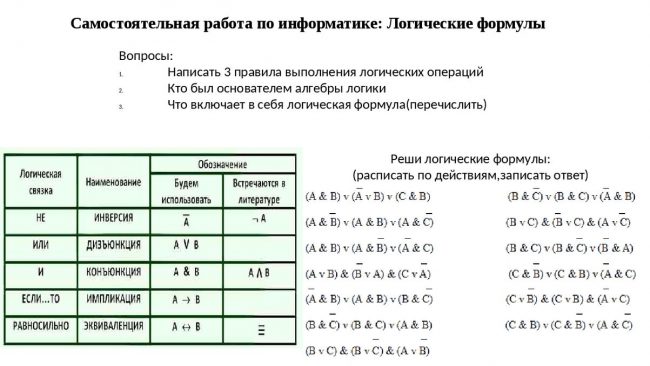
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.
Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.
Таблица истинности для операции НЕ имеет вид:
| A |  |
| 0 | 1 |
| 1 | 0 |
Действие, связанное с операцией НЕ можно записать следующим образом:
Логическая операция И ( конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия).
Таблица истинности для операции И имеет вид:
| A | B | X=A^B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Действие, связанное с операцией И можно записать следующим образом:
X = AB = A*B = A ^ B
Логическая операция ИЛИ ( дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.
Таблица истинности для операции ИЛИ имеет вид:
| A | B | X=A v B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Действие, связанное с операцией ИЛИ можно записать следующим образом:
Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.
Таблица истинности имеет вид:
| A | B | X=A B B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:
X = A 
Действие, связанное с операцией Импликации можно записать следующим образом:
Таблица истинности Импликации имеет вид:
| A | B | A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция тождество. Операция тождество определяет тождественность аргументов.
Таблица истинности для операции тождество имеет вид:
| A | B | A Ξ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Действие, связанное с операцией тождество можно записать следующим образом:
X = A 



Диаграммы Венна (круги Эйлера)
Поиск номера сети
Необходимо найти номер сети по IP-адресу 12.16.196.10 и маске 255.255.224.0.
Картинки формулы по информатике (43 фото)
Решение задач с формулами по информатике позволяет лучше понять устройство вычислительной техники. Понимание основ данной науки необходимо каждому человеку. Во многих формулах по информатике используются такие понятия как бит и байт. Они являются единицами измерения информации, которой оперирует компьютер. Предлагаем тут посмотреть красивые картинки про формулы по информатике.
Скорость передачи файла.
Число возможных вариантов.
Прикольная формула по информатике.
Глубина кодирования в бит.
Количество символов в тексте.
Картинка формулы по информатике.
Важное уравнение информационной науки.
Формулы по информатике в опорном конспекте.
Задача на кодирование текста.
Ученый Ральф Хартли.
Замечательная формула по информатике.
Самостоятельная работа на логику.
Красивая картинка формул по информатике.
Символы в одном сообщении.
Информационный вес символа.
Познавательный материал с формулами по информатике.
Сумма элементов в задаче.
Символьный алфавит компьютера.
Сложная формула по информатике.
Алфавитный подход к измерению.
Небольшие подсказки для экзамена.
Формулы по информатике на картинке.
Количество информации как степень.
Символы, используемые в некотором языке.
Главная формула информатики.
Простое задание с логарифмом.
Измерение информации в битах.
Красные рамки для формул по информатике.
Символы на темном фоне.
Вес символа алфавита.
Целые разряды числа в формуле по информатике.
Дано, решение, ответ.
Цветная картинка формулы по информатике.
Двоичное кодирование целых чисел.
Преобразуем логические выражения.
Разные события для формул по информатике.
Важная пометка в синей рамке.
Определения для обозначений.
Запоминаем формулу по информатике.
Количество возможных равновероятных альтернатив.
Формулы и уравнения по информатике
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬ A.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
источники:
http://proprikol.ru/kartinki/kartinki-formuly-po-informatike-43-foto.html
http://www.sites.google.com/site/uvarovaap/family-map/11-klass/osnovy-logiki-logiceskie-operacii-i-tablicy-istinnosti