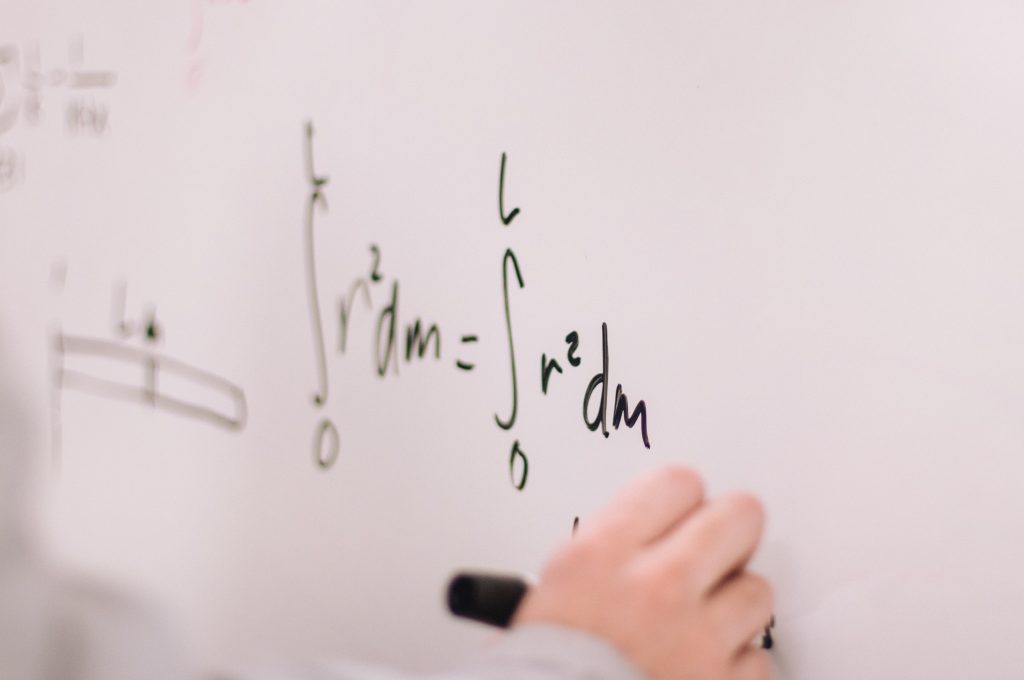Формулы обществознание егэ

Геометрия

• Треугольник
• Четырехугольники
• Окружность и круг
• Призма
• Пирамида
• Усеченная пирамида
• Цилиндр
• Конус
• Усеченный конус
• Сфера и шар

1. Формулы сокращённого умножения

Наверх

2. Модуль числа

Определение:

Основные свойства модуля:

Наверх

3. Степень с действительным показателем

Свойства степени с действительным показателем

Пусть Тогда верны следующие соотношения:

Наверх

4. Корень n-ой степени из числа

Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.

Основные свойства арифметического корня:

Наверх

5. Логарифмы

Определение логарифма:

Основное логарифмическое тождество:

Основные свойства логарифмов

Пусть Тогда верны следующие соотношения:

Наверх

6. Арифметическая прогрессия

Формула n-го члена арифметической прогрессии:

Характеристическое свойство арифметической прогрессии:

Сумма n первых членов арифметической прогрессии:

При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

7. Геометрическая прогрессия

Формула n-го члена геометрической прогрессии:

Характеристическое свойство геометрической прогрессии:

Сумма n первых членов геометрической прогрессии:

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

8. Бесконечно убывающая геометрическая прогрессия

Сумма бесконечно убывающей геометрической прогрессии:

Наверх

9. Основные формулы тригонометрии

Зависимость между тригонометрическими функциями одного аргумента:

Формулы сложения:

Формулы тригонометрических функций двойного аргумента:

Формулы понижения степени:

Формулы приведения

Все формулы приведения получаются из соответствующих формул сложения. Например:

Применение формул приведения укладывается в следующую схему:

— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;

— определяется знак приводимой функции;

— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или , то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид , то функция названия не меняет.

Например, получим формулу :

— — IV четверть;

— в IV четверти тангенс отрицательный;

— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,

Формулы преобразования суммы тригонометрических функций в произведение:

Формулы преобразования произведения тригонометрических функций в сумму:

Наверх

10. Производная и интеграл

Таблица производных некоторых элементарных функций

Правила дифференцирования:

1.

2.

3.

4.

5.

Уравнение касательной к графику функции в его точке :

Таблица первообразных для некоторых элементарных функций

Правила нахождения первообразных

Пусть ― первообразные для функций и соответственно, a, b, k ― постоянные, Тогда:

— ― первообразная для функции

— ― первообразная для функции

— ― первообразная для функции

— Формула Ньютона-Лейбница:

1. Треугольник

Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно; ― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно; ― длины высот AA₂, BB₂, CC₂ треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC; ― площадь треугольника ABC. Тогда имеют место следующие соотношения:

(теорема синусов);

(теорема косинусов);

Наверх
2. Четырёхугольники

Параллелограмм

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Ромбом называется параллелограмм, все стороны которого равны.

Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.

Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Площадь четырехугольника

Площадь параллелограмма равна произведению его основания на высоту.

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Наверх

3. Окружность и круг

Соотношения между элементами окружности и круга

Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга,  — длина дуги в градусов,  — длина дуги в радиан,  — площадь сектора, ограниченного дугой в n градусов,  — площадь сектора, ограниченного дугой в радиан. Тогда имеют место следующие соотношения:

Вписанный угол

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность, — прямой.

Вписанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Описанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.

Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны

Наверх

4. Призма

Пусть H ― высота призмы, AA₁ ― боковое ребро призмы,  ― периметр основания призмы,  ― площадь основания призмы,  ― площадь боковой поверхности призмы,  ― площадь полной поверхности призмы, V ― объем призмы,  ― периметр перпендикулярного сечения призмы,  ― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

Свойства параллелепипеда:

— противоположные грани параллелепипеда равны и параллельны;

— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;

— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Наверх

5. Пирамида

Пусть H ― высота пирамиды,  ― периметр основания пирамиды,  ― площадь основания пирамиды,  ― площадь боковой поверхности пирамиды,  ― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:

;

.

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то

Наверх

6. Усечённая пирамида

Пусть H ― высота усеченной пирамиды, и  ― периметры оснований усеченной пирамиды, и  ― площади оснований усеченной пирамиды,  ― площадь боковой поверхности усеченной пирамиды,  ― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.

Тогда имеют место следующие соотношения:

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то:

Наверх

7. Цилиндр

Пусть h ― высота цилиндра, r ― радиус цилиндра,  ― площадь боковой поверхности цилиндра,  ― площадь полной поверхности цилиндра, V ― объем цилиндра.

Тогда имеют место следующие соотношения:

Наверх

8. Конус

Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса,  ― площадь боковой поверхности конуса,  ― площадь полной поверхности конуса, V ― объем конуса.

Тогда имеют место следующие соотношения:

Наверх

9. Усечённый конус

Пусть h ― высота усеченного конуса, r и  ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,  ― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:

Наверх

10. Сфера и шар

Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы,  ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,  ― объем сегмента, высота которого равна h,  ― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:

Наверх

09.09.2012

Подборка шпаргалок по ОБЩЕСТВУ.

Дата обновления: 01.11.2022

Полный набор теоретического материала для подготовки к ЕГЭ. Таблицы, схемы, формулы, теория. Всё, что необходимо для самостоятельной работы по обществознанию.

• Тренировочные варианты ЕГЭ по обществознанию

Что содержите в себе сборник шпаргалок по обществознанию

• Шпаргалки с планами по обществознанию
• Термины по обществу
• Конспекты в схемах и таблицах
• Более 200 планов!

Для чтения шпаргалок необходимы бесплатные программы: WinDJView и Adobe Reader

СКАЧАТЬ

https://down.ctege.info/ege/obshee/shpory/obshestvo-ege-shpora.zip

Предварительный просмотр:

• Мне нравится 

 

1)  Учебное
пособие(учебник)

2)  Преподаватель

II.Алгоритм:

1)    1)Теория:
структура
и порядок действий для решения задачи.

2)    Практика:
метод- инструкция
для решения задачи.

III.Задача:

1)  Условие

2)  Вопрос

3)  Способ
решения

4)  Решение

5)  Ответ

6)  Контроль
и оценка

IV.Общество

1)  Экономика

2)  Политика

3)  Культура

4)  Социальная
структура

5)  Образ
жизни

6)  Тип
личности

V.Экономическая сфера:

1)    Технический
аспект

2)    Социальный
аспект

3)    Структурный
аспект

4)    Организационный
аспект

5)    Экономический
аспект(процесс)

6)    Аспект
собственности

VI.Социальная сфера:

1)Географический
аспект:

1)   
А)Территория

2)   
Б)Этнос

2)Демографический
аспект:

3)   
В)Пол,
возраст

4)   
Г)Семья,
брак

3)Культурологический
аспект:

5)   
Д)Образование

Е)Профессия
(страты)

VII.1.Политическая сфера как деятельность:

1)  Объект

2)  Субъект

3)  Деятельность

4)  Цель

5)  Средства

6)  Метод

VII.2.Политическая сфера как структура:

1)   Социологический
аспект

2)   Психологический
аспект

3)   Деятельностный
аспект

4)   Информационный
аспект

5)   Организационны
(ценностный)аспект

6)   Методологический
аспект

VII.3.Государство:

1)    Органы
власти

2)    Законы

3)    Устройство

4)    Форма
власти

5)    Право

6)    Политический
режим

VII.4.Партия

1)    Идеология

2)    Программа

3)    Социальная
основа

4)    Стратегия

5)    Тактика

6)    Организация

VII.5.Право:

1)  Юридический
источник

2)  Юридический
субъект

3)  Юридические
отношения

4)  Юридические
нормы

5)  Юридические
органы

6)  Юридические
санкции

VIII.1.Сфера культуры-1(как система):

1)    Наука

2)    Образование

3)    Право

4)    Мораль

5)    Искусство

6)    Религия

VIII.2.Сфера культуры-2(как формы культуры):

1)   Реальность 
(тема, идея)

2)   Сознание
(идеология, психология)

3)   Деятельность
(стиль, направление)

4)   Образ
–род (фабула, сюжет)

5)   Язык
–вид, изобразительные и выразительные средства

6)   Метод –
жанр, изобразительные и выразительные принципы

IX.Менеджмент:

1)   Информационно
-аналитический аспект

2)   Мотивационно-целевой
аспект

3)   Планово-прогностический
аспект

4)   Содержательно-
операционный аспект

5)   Контрольно-оценочный
аспект

6)   Регулятивно-коррекционный
аспект

X.Наука: предмет и метод:

1)Предмет

1)   
А)Факты

2)   
Б)Понятия

3)   
В)Картина
мира

2)Метод

4)   
Г)Связи

5)   
Д)Законы

Е)Принципы

XI.Структура конструктора:

Часть I

1)  Человек
и общество

2)  Общество
и культура

3)  Общество
и право

Часть II

4)  Экономическая
сфера общества

5)  Социальная
сфера общества

6)  Политическая
сфера общества

XII.Интегральный алгоритм изучения общества:

1)   
Факторы :

А)Отношения

Б)Сознание

В)Деятельность

2)   
Структура:

А)Объект

Б)Субъект

В)Деятельность

Г)Цель

Д)Средства

Е)Методы

3)   
Функции:

А)   Информационная-знания

Б)    Ценностно –ориентационная-ценности

В)   Деятельностно –коммуникативная-действия

4)Значение:

А)Отношения-1

Б)Сознание -1

В)Деятельность-1

     В данной статье
представлена теоретическая модель формул-алгоритмов изучения общества на
основе теории поэтапного формирования умственных действий П.Я. Гальперина
через конструирование ориентировочной основы действия в виде алгоритма.

     Философской основой
конструирования ориентировочной основы действия является теория познания
Г.Ф.В. Гегеля в виде формулы: тезис-антитезис-синтезис. В качестве примера
можно представить интегральный алгоритм изучения общества:

Интегральное понятие-время:

Тезис-прошлое-факторы(причины-необходимость,
предпосылки-возможность).

Антитезис-настоящее-структура(содержание
и форма деятельности).

Синтезис-будущее(значение-
новые причины и предпосылки).

    Конкретное применение
предложенного подхода будет показано в дальнейших публикациях автора.

СПИСОК ЛИТЕРАТУРЫ:

1.     Барабанов, В.В. ЕГЭ. Обществознание. Новый полный справочник
школьника для подготовки к ЕГЭ / В.В. Барабанов. — М.: АСТ, 2018. — 208 c.

2.     Баранов, П.А. ЕГЭ. Обществознание. Новый полный справочник для
подготовки к ЕГЭ / П.А. Баранов, А.В. Воронцов, С.С. Шевченко. — М.: АСТ,
2019. — 544 c.

3.     Домашек, Е.В. Обществознание в кармане: справочник для 7-11 кл /
Е.В. Домашек. — Рн/Д: Феникс, 2017. — 384 c.

4.     Кишенкова, О.В. ОГЭ. Обществознание. Универсальный справочник /
О.В. Кишенкова. — М.: Эксмо, 2018. — 320 c.

5.     Маркин, С.А. Обществознание. ОГЭ. Интенсивный курс подготовки с
разбором реальных тестовых заданий / С.А. Маркин. — М.: Омега-Л, 2018. — 94
c.

6.      Обществознание.
10
класс : учеб, для общеобразоват. организаций : базовый уровень / [Л. Н.
Боголюбов, Ю. И. Аверьянов, А. В. Белявский и др.]; под ред. Л. Н. Боголюбова
[и др.]. — 5-е изд., доп. — М. : Про­свещение, 2018. — 350 с.

7.    
Обществознание.
11
класс: учеб, для общеобразоват. организаций : базовый уровень / [Л. Н. Боголю­бов,
Н. И. Городецкая, Л. Ф. Иванова и др.] ; под ред. Л. Н. Боголюбова [и др.]. —
3-е изд. — М. : Просвеще­ние, 2017. — 335 с.

8.     Пазин, Р.В. Обществознание: человек и общество: 10-11 классы /
Р.В. Пазин. — РнД: Феникс, 2018. — 286 c.

9.     Рутковская, Е.Л. ЕГЭ 2019. Обществознание. Сборник заданий: 550
заданий с ответами / Е.Л. Рутковская. — М.: Эксмо, 2018. — 304 c.

10. Семке,
Н.Н. ЕГЭ. Обществознание. ЕГЭ. Экспресс-подготовка (в схемах и таблицах) /
Н.Н. Семке. — М.: Эксмо, 2018. — 159 c.

Формулы для егэ обществознание

Рубрика: Подготовка к обществознанию

Тут собираются материалы для подготовки к ЕГЭ обществознанию.

Добавляются только проверенные и качественные материалы.

Шпаргалки по обществознанию для ЕГЭ и ОГЭ 9-11 класс

Как сдать ЕГЭ по обществознанию на максимальный балл

Как сдать ЕГЭ по обществознанию на 100 баллов? … Продолжить чтение →

Как писать эссе по обществознанию, готовые сочинения

В данной статье вы узнаете, как написать эссе по обществознанию. Примеры прилагаются. … Продолжить чтение →

Примеры эссе по обществознанию (ЕГЭ)

Примеры эссе по обществознанию для ЕГЭ … Продолжить чтение →

Словарь терминов по обществознанию

Список терминов по обществознанию. Сортирован по алфавиту. В словаре около тысячи терминов. … Продолжить чтение →

Как сдать ЕГЭ по обществознанию на максимальный балл

Как сдать ЕГЭ по обществознанию на 100 баллов? … Продолжить чтение →

В данной статье вы узнаете, как написать эссе по обществознанию. Примеры прилагаются. … Продолжить чтение →

Словарь терминов по обществознанию.

5-ege. ru

23.03.2020 19:17:27

2020-03-23 19:17:27

Источники:

Https://5-ege. ru/ob/

Важные формулы для ЕГЭ по математике профильный уровень 2021 » /> » /> .keyword { color: red; } Формулы для егэ обществознание

Главные формулы для ЕГЭ по профильной математике

Главные формулы для ЕГЭ по профильной математике

Ученики, сдающие базовую математику, почти не тратят времени на подготовку к ней, ведь в экзамене нужно решить лишь задания, которые требуют самых основ. Тем же выпускникам, которые хотят поступать в технические вузы, предстоит готовиться не только к предметам по выбору, но и к профилю. В этой статье мы расскажем, какие формулы для ЕГЭ по математике (профильный уровень) сделают подготовку легче, а баллы на экзамене — выше.

Какие формулы необходимы для сдачи ЕГЭ по профильной математике?

Помимо очевидного, что для сдачи профиля нужно уметь складывать, вычитать и умножать, необходимы еще некоторые знания. Все это проходится в течение школы, но повторить или заполнить пробелы перед экзаменом нужно обязательно. Вот, что пригодится:

Формулы сокращенного умножения; Арифметическая и геометрическая прогрессии; Вероятность; Свойства степеней; Свойства логарифмов; Тригонометрия; Производные; Первообразные.

Список внушительный, но вполне реальный, чтобы его выучить. Для того, чтобы лишний раз не гуглить в интернете «формулы для ЕГЭ по математике профильный уровень», приложим их ниже. А начнем по порядку из списка выше.

Формулы сокращённого умножения

Первые в нашем списке – формулы сокращенного умножения – нужны для решения задания №9 из профильного уровня. Вам встретятся задачи на преобразование выражений, поэтому умение это делать будет вознаграждено баллами.

Вот то, что будет вашим спасательным кругом:

Есть те, которые знать не обязательно. Но чем большими знаниями вы будете обладать, тем легче вам будет на экзамене. Вот они:

Умея применять эти формулы для ЕГЭ по математике, профильный уровень вам уже будет решить легче. Но это далеко не все, что нужно знать, чтобы получить сто баллов за ЕГЭ.

Арифметическая и геометрическая прогрессии

Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:

Вероятность

Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:

Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.

Свойства степеней

Эти свойства нужно знать и для того, чтобы решить «базу», так что гуманитарии тоже могут обратить внимание на это:

Как вы видите, запоминать не очень много, зато формулы не самые простые. Но есть еще сложнее, и сейчас узнаем, какие они.

Свойства логарифмов

Формулы логарифмов лучше всего начать с их определения:

Теперь перейдем к более сложному:

Тригонометрия

Тригонометрические уравнения встречаются в задании №13. Для того, чтобы заработать баллы, нужно знать это:

Но это еще не все. Есть такая вещь, как основное тригонометрическое тождество. Вот оно:

Формулы двойного угла:

Формулы суммы и разности аргументов:

Преобразование суммы и разности в произведение:

Формулы половинного аргумента:

На этом с тригонометрией все.

Производные

Начнем с основных правил дифференцирования:

Производные элементарных функций:

Закончим эту статью первообразными.

Первообразные

Она выглядит так:

То, что работа предстоит колоссальная — и правда, и нет. Да, придется хорошо постараться, чтобы набрать высокие баллы, так как составители ЕГЭ все больше усложняют экзамен. С другой стороны, хотя бы часть формул, описанных выше, вы уже знаете. А значит, работы хоть на немного, но меньше. А это ли не счастье в такие тяжелые времена подготовки?

Арифметическая и геометрическая прогрессии

Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:

Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:

Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.

Тем не менее, придется применять знания, которые представлены ниже.

Umschool. net

19.06.2018 15:46:08

2018-06-19 15:46:08

Источники:

Https://umschool. net/journal/ege/glavnye-formuly-dlya-ege-po-profilnoj-matematike/

Формулы по математике для ЕГЭ » /> » /> .keyword { color: red; } Формулы для егэ обществознание

ЕГЭ по математике – формулы

ЕГЭ по математике – формулы

Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:

таблица квадратных чисел от 0 до 99; свойства арифметического квадратного корня; формулы сокращенного умножения; корни квадратного уравнения; свойства степени и логарифма; теорема Пифагора; формула расчета длины окружности и площади круга; расчет средней линии треугольника и трапеции; радиус вписанной и описанной окружности правильного треугольника; формулы расчета площади планиметрических фигур; вычисление поверхностей и объемов тел; основные тригонометрические функции и тождества; график линейной функции; геометрический смысл производной.

Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.

Основные формулы для профильного ЕГЭ

Выпускники, планирующие сдавать профиль, ставятся в более жесткие условия, чем те, кто выбрал базовый уровень. Учитывая то, что они видят перспективу своего дальнейшего обучения по направлениям, тесно или напрямую связанным с математикой, к их знаниям предъявляются повышенные требования. В частности, на официальные справочные материалы особенно рассчитывать не приходится. Все, что в них есть, это 5 тригонометрических тождеств.

Естественно, чтобы сдать профильную математику, для ЕГЭ потребуется запомнить намного больше формул. Выяснить, на какие темы нужно обратить внимание, можно по тому же алгоритму, что и для базы (из КЭС или, решая тренировочные задания).

Основываясь на данных, опубликованных на сайте ФИПИ, с большой долей вероятности потребуется знание следующих формул для сдачи ЕГЭ по профильной математике:

правила сокращенного умножения; арифметическая и геометрическая прогрессии; основы вероятностной теории; свойства степеней и логарифмов; азы тригонометрии (формулы двойного угла, суммы и разности аргументов; алгоритм преобразования разности и суммы в произведение; обратные функции); производная (правила дифференцирования, элементарнее функции и уравнение касательной); первообразная; двухмерная планиметрия; правила нахождения площадей геометрических фигур; трехмерная стереометрия.

Опытные учителя и репетиторы собрали все формулы по математике, которые приходилось использовать на ЕГЭ в последние три года:

Материалы для скачивания – в формате pdf.

Выученные назубок формулы к ЕГЭ по математике – это только часть пути к успешной сдаче, надо еще научиться правильно применять их. Хорошую практику даст решение сложных задач.

Аттестат государственного образца, программа ФГОС

Живые уроки с преподавателями и проверка домашних заданий

Естественно, чтобы сдать профильную математику, для ЕГЭ потребуется запомнить намного больше формул. Выяснить, на какие темы нужно обратить внимание, можно по тому же алгоритму, что и для базы (из КЭС или, решая тренировочные задания).

Материалы для скачивания в формате pdf.

Edunews. ru

26.08.2020 12:14:48

2020-08-26 12:14:48

Источники:

Https://edunews. ru/ege/podgotovka/formuly. html

ЕГЭ по обществознанию

Готовимся к ЕГЭ по обществознанию: справочный материал

Клышникова Любовь Ивановна

Учитель истории и обществознания

СОДЕРЖАНИЕ

1. Что изучает обществознание?

2. Общество.

3. Человек.

4. Познание.

5. Культура и духовная сфера.

6. Экономика.

7. Социальная сфера

8. Политика.

9. Право

Что изучает обществознание?

Объектом изучения обществознания является общество. Общество – очень сложная система, которое подчиняется различным законам. Естественно, нет одной науки, которая могла бы охватить все сторон общества, поэтому его изучают несколько наук. Каждая наука изучает какую-либо одну сторону развития общества: экономику, общественные связи, пути развития и другие.

Обществознание — обобщающее название наук, изучающих общество в целом и общественные процессы.

В каждой науке есть объект и субъект.

Объект науки — явление объективной реальности, которая изучает наука.

Субъект науки — Личность, группа лиц, познающая объект.

Науки разделяются на три группы.

Науки:

Точные науки	Естественные науки	Общественные (гуманитарные)
Математика, информатика, логика и другие	Химия, физика, биология, астрономия и другие	Философии, экономика, социология и другие

Общество изучают общественные (гуманитарные науки).

Главное отличие общественных наук от гуманитарных наук:

Отличие	Общественные науки	Гуманитарные науки
Главный объект изучения	Общество	Человек

Общественные (гуманитарные) науки, изучающие общество и человека:

археология, экономика, история, культурология, лингвистика, политология, психология, социология, право, этнография, философия, этика, эстетика.

Археология – наука, которая изучает прошлое по материальным источникам.

Экономика – наука о хозяйственной деятельности общества.

История – наука о прошлом человечества.

Культурология – наука, изучающая культуру общества.

Лингвистика – наука о языке.

Политология — наука о политике, общества, о взаимоотношения между людьми, обществом и государством.

Психология – наука о развития и функционирования психики человека.

Социология — наука о закономерностях становления и развития социальных систем, групп, личностей.

Право – совокупность законов и правил поведения в обществе.

Этнография – наука, изучающая быт, культуру народов и наций.

Философия — наука о всеобщих законах развития общества.

Этика – наука о морали.

Эстетика – наука о прекрасном.

Науки изучают общества в узком и широком смыслах.

Общество в узком смысле:

1. Все население Земли, совокупность всех народов.

2. Исторический этап развития человечества (феодальное общество, рабовладельческое общество).

3. Страна, государство (французское общество, российское общество).

4. Объединение людей с какой-либо целью (клуб любителей животных, общество солдатских

матерей).

5. Круг людей, объединенных общностью положения, происхождения, интересов (высшее общество).

6. Способы взаимодействия власти и населения страны (демократическое общество, тоталитарное общество)

Общество в широком смысле — обособившаяся от природы, но тесно связанная с ней часть материального мира, которая включает в себя способы взаимодействия людей и формы их объединения.

1. Общество.

Общественные науки: экономика, философия, социология, политология, этика (о морали), эстетика (о прекрасном).

Общество:

В узком смысле: Совокупность людей связанная общими интересами и целями.

В широком смысле: Обособившаяся от природы, но тесно связанная с ней часть материального мира, включающая все способы взаимодействия людей и формы их объединения.

Общество и природа взаимодействуют, влияют друг на друга. Экономическое взаимодействие – потребление природных богатств, экологическое – охрана природных богатств.

Ноосфера (В. Вернадский) – среда обитания (биосфера), управляемая человеческим разумом.

Общество – динамическая система.

Системные качества общества: целостность, динамичность, историчность, открытость, иерархичность.

В структуре общества 4 сферы (подсистемы):

1. Экономическая — материальной производство и производственные отношения.

2. Политическая — политика, государство, право, их отношения и функционирование, СМИ, армия.

3. Социальная – отношения между классами, группами, нациями и т.д.

4. Духовная – формы общественного сознания: религия, мораль, наука, искусство.

Сферы взаимодействуют и взаимосвязаны.

Общественные отношения – отношения и формы, возникающие в процессе жизнедеятельности между социальными группами, классами, нациями, а также внутри них.

Общественные отношения

Духовные Материальные

Важнейший компонент общества – социальный институт – исторически сложившаяся форма организации людей, на основе комплекса норм и статусов регулирующая их деятельность и удовлетворяющая фундаментальные человеческие потребности.

Социальные институты

: собственность, государство, политические партии, семья, церковь, трудовые организации, учреждения образования и воспитания, наука, СМИ и т.д. Типы обществ (по Дэниел Беллу, Элвин Тоффлер)

Доиндустриальное (традиционное, аграрное)	Индустриальное	Постиндустриальное, информационное
С/хозяйство, ремесло, община, религия, нет мобильности	Массовое производство, промышленность, товарно-денежные отношения, урбанизация, массовая культура индивидуальность, мобильность	Информация, сфера услуг, наука, индивидуализация производства

Типы обществ (по О. Тоффлеру)

Восточное (традиционное)	Западное (современное)
Религия, коллективное начало, традиции, авторитарная власть.	Индивидуальность, либерально-демократическая власть, инновации.

Социальное изменение – переход социальных систем, общностей, организаций из одного состояния в другое (природные, демографические, социальные, духовные изменения и т.д.).

Направленное развитие

прогресс стагнация регресс

Критерий прогресса – степень свободы, которую дает человеку общество для ее оптимального развития. Прогресс противоречив (и положительные, и отрицательные процессы)

Формы прогресса: революция и реформа. Эволюция – постепенное развитие.

Научно-технический прогресс (НТП) — качественное изменение производительных сил общества под воздействием научно-технической революции.

Научно-техническая революция (НТР) – скачок в развитии производительных сил общества на основе коренных сдвигов в системе научных знаний.

Исторический процесс – хронологическая последовательность событий, оказывающих влияние на развитие общества. Субъекты исторического процесса: личности, социальные группы, массы. Исторический факт – событие общественной жизни.

Цивилизация – совокупность материальных, духовных и нравственных средств, которыми обладает данное общество в данный исторический период.

Термин выдвинул Н. Данилевский, называл цивилизации культурно-историческими типами. Цивилизации различал по 4 признакам: экономическим, культурным, политическим, религиозным. Для характеристики цивилизаций выделяют также понятие менталитет.

Менталитет — образ мышления, мировосприятия, присущий определенной группе, индивиду

Две теории: теория стадиального развития (изучают развитие как единый процесс) и теория локальных цивилизаций (изучают большие исторически сложившиеся общности).

Подходы к изучению исторического процесса:

Формационный подход (К. Маркс)	Цивилизационный подход (А. Тойнби)	Культурологический подход (О. Шпенглер)
В основе переход от одной формации к другой. Общественно-экономические формации: первобытно-общинная, рабовладельческая, феодальная, капиталистическая, коммунистическая. В общественно-экономической формации есть два главных компонента — базис и надстройка. Базис — экономика общества, составляющими которой являются производительные силы и производственные отношения (способ производства материальных благ). Надстройка — государство, политические, общественные институты. К переходу от одной общественно-экономической формации к другой приводят изменения в экономическом базисе. Большую роль играет классовая борьба.	Цивилизации – устойчивые общности людей, объединенные духовными традициями, сходным образом жизни, географическими, историческими рамками. В основе – смена цивилизаций. Развитие всей истории строится по схеме «вызов — ответ». Каждая цивилизация в своей судьбе проходит четыре стадии: зарождение; рост; надлом; дезинтеграция, завершающаяся смертью и полным исчезновением цивилизации.	Центральное понятие данного подхода — культура. Культура — совокупность религии, традиций, материальной и духовной жизни. Культура зарождается, живет и умирает. Цивилизация в рамках культурологического подхода — высший уровень развития культуры, завершающий период развития культуры, предшествующий ее смерти.

Глобальные проблемы современности – комплекс общественных и природных противоречий, затрагивающий весь мир в целом. Являются показателем целостности и взаимосвязи современного мира, создают угрозу человечеству, требуют объединения усилий для решения.

Главные проблемы:

1. Экологическая: загрязнение, вымирание видов, «озоновые дыры» и т.д.

Термин «Экология» ввел Э. Геккель.

2. Демографическая;

3. Проблема безопасности и предотвращения мировой войны;

4. Проблема ресурсов;

5. Проблема «Север-Юг»: развивающиеся и высокоразвитые страны.

Глобализация – усиление интеграционных связей в различных сферах между государствами, организациями, общностями.

Международные организации: ООН (Организация Объединенных Наций); МАГАТЭ (Международное агентство по атомной энергии); ЮНЕСКО (ООН по вопросам образования, науки и культуры); ВОИС (Всемирная организация интеллектуальной собственности); ВТО (Всемирная торговая организация); НАТО (Организация Североатлантического договора); ОБСЕ (Организация по безопасности и сотрудничеству в Европе); Европейский Союз; ОПЕК (Организация стран-производителей и экспортеров нефти); СНГ (Содружество независимых государств); ШОС (Шанхайская организация сотрудничества) и другие.

2. Человек.

Человек	Индивид	Индивидуальность	Личность
Высшая ступень живых организмов на земле, субъект общественно- исторической деятельности и культуры	Единичный представитель человеческого рода	Неповторимые, самобытные черты и качества, присущие человеку (биологические, психологические, социальные)	Совокупность социально-значимых черт, характеризующих человека как члена данного общества, человек как субъект отношений и сознательной деятельности

Теории происхождения: религиозная, эволюционная (Ч.Дарвин), марксистская (труд сделал человека)

Биосоциальная проблема – проблема соотношения биологического и социального в человеке.

Человек	Животное
Изменяет, преобразует природу, не только физические, но и духовные, культурные потребности, обладает сознанием, речью, деятельность, целеполагание.	Приспосабливается к природе, существует инстинктами, изменяется по потребностям своего вида.

В момент рождения человек – индивид. Личностью становится в процессе социализации.

Социализация — процесс усвоения человеком социального опыта, форм поведения, приемлемых для данного общества.

Первичная социализация: агенты (родственники, учителя) и институты социализации (семья, школа).

Вторичная социализация: агенты (коллеги, преподаватели, должностные лица) и институты (ВУЗы, армия, церковь).

Десоциализация – процесс отхода от старых ценностей, норм, правил, ролей.

Ресоциализация – процесс обучения новым ценностям, нормам, правилам, ролям.

Свобода личности — способность творить себя и мир других людей, делать выбор, быть ответственным. «Свобода – познанная необходимость» — Г. Гегель.

Межличностные отношения – отношения между различными индивидами по различным основаниям.

Межличностные отношения

Официальные	Неофициальные
Регламентированы, обезличены, стандартизированы, ограничена возможность выбора.	Личностны, возможность выбора, не закреплены нормами.

Мировоззрение личности – совокупность принципов, взглядов, убеждений и установок на объективную реальность и место человека в нем.

Мировоззрение:

обыденное, религиозное, мифологическое, научное, философское, гуманистическое.

Деятельность – человеческая активность, направленная на изменение и преобразование окружающего мира и себя. Субъект — тот, кто осуществляет деятельность. Объект – то, на что деятельность направлена.

Структура деятельности:

Мотив——цель—— средства——-действия——результат.

Мотив – материальный или идеальный предмет, который побуждает к действию.

Цель – осознанный образ ожидаемого результата.

Виды деятельности:

1. По содержанию: труд, игра, общение, учеба.

Труд – вид человеческой деятельности, направленный на достижение практически полезного результата.

Общение- процесс взаимодействия людей, заключающийся в восприятии и понимании и в обмене информации ( коммуникации)

2. По направленности: духовная, практическая, творческая, управленческая.

Творчество – деятельность, порождающая нечто новое, никогда ранее не существовавшее.

Эвристика – наука, изучающая творческую деятельность.

Потребности человека – переживаемая или осознаваемая нужда в чем-либо.

Потребности:

биологические, социальные, идеальные.

Потребности по А. Маслоу.

1.Физиологические, 2.Экзистенциальные, 3.Социальные, 4.Престижные, 5. Духовные

Первичные, врожденные Вторичные, приобретенные

Потребности каждого уровня становятся насущными, когда удовлетворены предыдущие.

Интерес – осознанная потребность, которая характеризует отношение людей к предметам и явлениям, имеющих для них важное общественное развитие. Интересы являются побудителями к различным видам деятельности.

Способности – индивидуальные особенности человека, от которых зависит успешность различных видов деятельности.

Способности имеют биологическую основу.

Талант— совокупность способностей, которая позволяет получить продукт деятельности, отличающийся новизной и значимостью.

Гениальность – высшая ступень развития таланта, позволяющая осуществлять принципиальные сдвиги в той или иной сфере деятельности.

Гениальность — культурное явление человеческой природы.

«Сознательное» и «бессознательное» — это соотносительные понятия, выражающие особенности работы человеческой психики. Человек обдумывает ситуации и принимает решения. Такие действия называют осознанными. Однако часто человек поступает необдуманно, а иногда он сам не может понять, почему он так поступил. Бессознательные действия предполагают, что человек поступает по внутреннему побуждению, без всякого анализа ситуации, без выяснения возможных следствий. (З. Фрейд).

Бытие – что-либо сущее, существующее вообще (бытие изучает раздел философии онтология).

Формы бытия: материальное бытие, духовное бытие, человеческое бытие, социальное бытие.

Духовный мир человека (микрокосм) – сложная система внутреннего мира человека, элементами которого являются духовные потребности, мысли, чувства, мировоззрение, эмоции, ценности и т. д.

3. Познание.

Познание – процесс, направленный на получение знания.

Знание – объективная реальность, данная в сознании человека. Знания – результат познавательной деятельности.

Субъект познания – тот, кто познает. Объект познания – то, на что направлено познание.

Гносеология – наука о познании.

Гностицизм (гностики) – считают, мир познаваем (Платон, Сократ, К. Маркс, Г. Гегель).

Агностицизм (агностики) – мир познаваем в ограниченных пределах или непознаваем (И. Кант).

Типы познания: чувственное и рациональное.

Формы чувственного познания:

Ощущение – отражение отдельных свойств и качеств предметов и явлений, возникающих при воздействии на органы чувств.

Восприятие – целостный чувственный образ предмета, явления.

Представление – чувственный образ предмета или явления, возникающий при помощи памяти без непосредственного контакта с предметом.

Формы рационального познания:

Понятие – форма мышления, в которой фиксируются общие и существенные свойства предмета.

Суждение – форма мышления, в которой утверждается или отрицается что-либо.

Умозаключение – форма мышления, в которой из имеющихся суждений выводятся новые.

Две теории на типы познания:

1. Эмпиризм (эмпирики) – признают источником знаний чувственный опыт (Т. Гоббс, Д. Локк).

2. Рационализм (рационалисты) – знание может быть получено с помощью разума (Р.Декарт, И. Кант)

Интуиция – своеобразный тип познания вне процесса чувственного ознакомления и без обдумывания.

Черты: внезапность, необдуманность, скрытость механизма.

Цель познания – получение истины.

Истина – знание, соответствующее отраженной действительности. Истина объективна по содержанию и субъективна по форме.

Абсолютная истина – полное, исчерпывающее знание, не опровергаемое дальнейшим развитием науки.

Относительная истина – неполное, неточное знание, опровергаемое дальнейшим развитием науки.

Критерий истины – способ различения истинного и неистинного в совокупности знаний.

Главный критерий истины – практика.

Антиподы истины – ложь, дезинформация, заблуждение.

Ложь – преднамеренное возведение заведомо неправильных представлений в истину.

Дезинформация – передача ложного знания как истинного или истинного как ложного.

Заблуждение – непреднамеренное несоответствие суждений или понятий объекту.

Виды познания.

I.Ненаучное познание:

-Обыденное (житейское)

— Практическое (народная мудрость)

— Религиозное

-Мифологическое

— Художественное (средствами искусства).

II. Научное познание – познание, направленное на получение объективного знания. Цель – описание, объяснение, предсказание явлений действительности. Признаки: объективность, системность, обоснованность, достоверность, особый язык, необходимость специальных приспособлений и специалистов.

2 уровня научного познания: эмпирический и теоретический.

Эмпирический уровень:

Наблюдение — целенаправленное восприятие явлений объективной действительности.

Описание — фиксация средствами естественного или искусственного языка сведений об объекте.

Измерение — сравнение объекта по каким-либо сходным свойствам или сторонам.

Эксперимент — наблюдение в специально создаваемых и контролируемых условиях, что позволяет восстановить ход явления при повторении условий.

Теоретический уровень:

Гипотеза – предположения, выдвигаемые в ходе научного исследования.

Теория – система взаимосвязанных утверждений.

Закон – выводы о существенных, повторяющихся связях между явлениями.

Научные методы:

1. Всеобщие: диалектика (диалектический изучает явления в движении) и метафизика (метафизический изучает явления в покое).

2. Общенаучные: Анализ — это реальное или мысленное разделение объекта на составные части. Синтез — объединение составных частей в единое целое. Индукция — движение мысли от единичного к общему. Дедукция — восхождение процесса познания от общего к единичному. Аналогия (соответствие, сходство) — установление сходства в некоторых сторонах, свойствах и отношениях между нетождественными объектами.

3. Частнонаучные: анкетирование, экспертиза, интервьюирование, графический метод.

III. Социальное познание – познание, направленное на изучение природы социальных связей, социальных групп, социальной структуры общества.

Особенность – субъект и объект познания совпадают, получаемое знание всегда связано с интересами индивидов, субъективность выводов и оценок.

Цель: выявление исторических закономерностей развития общества, социальное прогнозирование.

Методы: контент-анализ (анализ статистических данных, документов), опрос, наблюдение, эксперемент.

IV.Самопознание – познание самого себя, самооценка, создание «Я-концепции» — образа Я.

Особенность – объектом является сам субъект.

Цель: познание своих физических, душевных, духовных возможностей, своего места среди других людей.

Самопознание совершается:

1. В анализе результатов собственной деятельности, своего поведения, взаимоотношений с другими.

2. Осознания отношения к себе других (качеств своей личности, черт характера), через мнения других

людей и соотнесения себя с другими.

3.Самонаблюдения своих состояний, переживаний, мыслей.

4. Культура и духовная сфера.

I. Культура (от лат. – «культура» — «возделывание, воспитание»)

Черты культуры: функциональность, качественность, ценность, нормативность, креативность (творческое начало).

В широком смысле культура – все виды преобразовательной деятельности человека и общества, а также ее результаты.

В общем смысле культура – совокупность достижений людей в материальной и духовной сферах.

Материальная культура – создается в процессе материального производства (здания, оборудование, орудия труда).

Духовная культура – включает в себя процесс духовного творчества и созданные духовные ценности в виде произведений искусства, научных открытий, религии.

Структура культуры:

форма – воплощение достижений культуры содержание – значение для личности и общества.

Функции культуры: познавательная, информативная, коммуникативная, нормативная, гуманистическая.

Виды культур: доминирующая (господствующая), элитарная (для избранных), массовая (для большинства, коммерческая, через СМИ), народная (на традициях, фольклор, анонимная), донорская (из которой заимствуют элементы), рецепиентная (которая заимствует элементы другой культуры), мертвая (устарело содержание).

Субкультура – культура социальных групп.

Контркультура – субкультура, которая враждебна доминирующей.

Термины:

Аккумуляция культуры – пополнение культуры новыми элементами, знаниями.

Культурная трансмиссия – передача культуры через обучение.

Культурная диффузия – взаимное проникновение культур.

Аккультурация культуры – процесс взаимовлияния двух или более культур.

Ассимиляция культуры – поглощение малой культуры со стороны более крупной.

Адаптация культуры – приспособление культур друг к другу.

II. Духовная сфера.

Структура духовной сферы:

1. Духовные потребности – нужда общества и человека в создании и освоении духовных ценностей. Духовные потребности не заданы биологически, от рождения. Формируются в процессе социализации.

2. Духовная деятельность (производство) – деятельность людей по созданию духовных ценностей.

Виды духовной деятельности:

1. Познавательная — научная, религиозная, художественная

2. Ценностно-ориентировочная — отношение к явлениям действительности

3. Прогностическая — предвидение и планирование изменений действительности

3. Духовные ценности (блага) – то, что создается в процессе духовного производства: произведения искусства, учения, научные открытия и т.д.

Виды духовного производства: религия, мораль, искусство, наука.

Религия.

Религия – форма общественного сознания и мировоззрение, основанное на вере в существование сверхъестественного начала.

Элементы: вера, учение, религиозная деятельность, религиозные институты.

Функции: мировоззренческая, компенсаторная, коммуникативная, регулятивная, воспитательная.

Религии:

Мировые: буддизм, христианство, ислам (большое число последователей, за пределы нации)

Национальные: конфуцианство (Китай), даосизм (Китай) иудаизм (Израиль), синтоизм (Япония), зороастризм (Иран).

Атеизм – отрицание существование бога

Конфессиональный – церковный, конфессия — вероисповедание

Мораль.

Мораль — форма общественного сознания, в которой находят отражение представления о добре и зле, справедливости и несправедливости и вид общественных отношений, совокупность норм поведения людей по отношению друг к другу.

Функции морали: регулятивная, воспитательная, коммуникативная, познавательная, мировоззренческая.

Исполнение норм морали санкционируется нормами духовного воздействия (оценка, одобрение, осуждение).

Искусство.

Искусство – форма общественного сознания и вид человеческой деятельности, которая представляет собой отражение окружающей действительности в художественных образах.

Искусство – ядро эстетической культуры.

Теории происхождения искусства: игровая (Г. Спенсер), трудовая (Г. Плеханов), биологизаторская (Ч. Дарвин), магическая.

Функции искусства: эстетическая, познавательная, творческая, очищающая, коммуникативная, воспитательная, компенсаторная, гедонистическая (функция наслаждения).

Виды искусства: литература, архитектура, музыка, кино, театр, живопись, графика, декоративно-прикладное, танец, скульптура, фотоискусство.

Черты искусства: является образным, наглядным; наличие специфических способов воспроизведения, огромная роль воображения, фантазии.

Наука.

Наука – сфера познавательной деятельности людей, система объективно-истинного знания о природной и социальной действительности, о человеке.

Элементы науки: научные знания, научная деятельность, научное самосознание.

Модели развития науки:

1. Постепенного развития

2. Через научные революции. Научная революция – процесс коренного, качественного изменения господствующей системы идей и теорий (парадигмы), которая служит эталоном мышления в конкретный исторический период.

Функции науки: познавательная, мировоззренческая, прогностическая.

Функции современной науки: производительная, социальная, культурно-мировоззренческая.

Классификация наук:

Естественные технические общественные (гуманитарные)

Образование.

Образование — целенаправленная познавательная деятельность по получению знаний, умений и навыков и их совершенствованию.

Самообразование – процесс получения знаний самостоятельно.

Функции образования: экономическая, социальная, культурная, сохранения и передача культурного достояния.

Образование в РФ:

дошкольное общее профессиональное дополнительное

Черты современного образования: интеграция областей знаний, развитие непрерывного образования, информатизация (компьютеризация), развитие дистанционного образования (через Интернет), гуманизация (внимание к личности), гуманитаризация (усиление внимания к общественным наукам, интернационализация (создание единой системы для разных стран).

5. Экономика.

Понятие экономика (Аристотель, А. Монкретьен) – «искусства ведения домашнего хозяйства».

Типы хозяйства: натуральное (производство не для продажи) и товарное (для продажи).

1. Экономика – сфера деятельности и отношений между людьми по производству, распределению. обмену и потреблению, в которой создаются богатства для удовлетворения разнообразных потребностей людей.

2. Экономика – наука, изучающая деятельность людей в процессе производства и обмена, способы рационального использования ограниченных ресурсов.

Разделы экономики: микроэкономика и макроэкономика.

Функции экономики:

Системообразующая, практическая, познавательная, оценочная.

Вопросы, на которые отвечает экономика: (П. Самуэльсон)

Что производить? Как производить? Для кого производить?

Элементы экономической деятельности:

1. Потребности (первичные и вторичные)»

2. Блага – средства удовлетворения потребностей (естественные и экономические, взаимозаменяемые и взаимодополняемые, потребительские и факторы производства)

3. Ресурсы – источники производства благ (характеристика — ограниченность, ценность, полезность)

4. Хозяйствующие субъекты: домохозяйства, предприятия, государство.

Экономическая система – способ организации хозяйственной жизни, представляющая совокупность упорядоченных взаимосвязей между производителями и потребителями.

Командно-административная система	Рыночная система	Традиционная система	Смешанная система
Государственное регулирование, государственная собственность, планирование	Свободное ценообразование, конкуренция, частная собственность, свободное предпринимательство, ограничение контроля государства, экономический цикл.	Традиционное ведение хозяйства, отсутствие технического прогресса, слабый производственный потенциал, преобладает общинная, государственная собственность	Сочетает черты рыночной, командно-административной, традиционной

Фазы экономического цикла: кризис———депрессия———оживление———подъем.

Факторы производства: капитал, земля, труд, предпринимательская деятельность, наука.

Экономический рост – количественное увеличение (интенсивный) и качественное совершенствование производства (экстенсивный).

Показатели: ВВП – совокупность стоимости конечных благ и услуг, созданных национальными предприятиями. ВНП — совокупность стоимости конечных благ и услуг, созданных национальными предприятиями внутри и за рубежом. Чистый национальный продукт – часть ВНП за вычетом амортизационных отчислений.

Типы собственности: государственная, общая, частная, корпоративная, кооперативная.

Реализация собственности – рента, доход, прибыль, процент, дивиденд.

Право собственности: 1. владения 2. пользования 3. распоряжения.

Приватизация – передача государственной собственности в частную собственность.

Национализация – частной собственности в государственную собственность.

Предпринимательство – хозяйственная деятельность, осуществляемая на свой страх и риск с целью получения прибыли. Функции – ресурсная, организационная, творчества.

Предпринимательство: коммерческое, финансовое, страховое, посредническое, венчурное (рисковое).

Мелкий бизнес (до 50 человек), средний (до 500), крупный (несколько тысяч).

Издержки производства – затраты, понесенные в процессе производства. Постоянные издержки – не зависит от объема производства, переменные издержки – зависят от объема производства.

Рынок – весь сложный механизм товаров и услуг в форме товаров и денег в рамках всего общественного воспроизводства.

Виды рынков: рынок товаров, рынок труда, фондовый рынок, рынок инвестиций, рынок средств производства, рынок иностранных валют, рынок информации.

Конкуренция – соперничество продавцов и покупателей на рынке за лучшие условия.

Рынок по типу конкуренции: 1. свободной (совершенный) конкуренции – все имеют равные права и возможности 2. несовершенной конкуренции: 1. монополия – контролируется одним продавцом. 2. олигополия – контролируется несколькими продавцами 3. монопсония – контролируется одним покупателем.

Искусственные монополии: картель (соглашение о целях), синдикат (теряют коммерческую самостоятельность), трест (все объединяют, акции взамен), концерн (различные отрасли).

Биржи: товарная, фондовые, биржи труда.

Рыночное саморегулирование (А. Смит).

Спрос – количество товара, который может быть куплен по определенной цене в определенный момент времени. Закон спроса: чем ниже цена, тем выше спрос. Предложение – количество товара, который производитель готов продать по определенной цене в определенный момент. Закон предложения: чем ниже цена, тем ниже предложение. Цена – выраженная в деньгах стоимость товара. Фактор спроса: ценовой и неценовой: реклама, мода, доходы, наличие взаимодополняемых и взаимозаменяемых товаров. Фактор предложения: ценовой и неценовой: изменение издержек (расходов), цена и наличие ресурсов, социальные и политические факторы. Цена равновесия – оптимальная цена для покупателей и продавцов в определенный момент времени на рынке.

Деньги – всеобщий товарный эквивалент, выражающий стоимость всех товаров т служащий посредником при их обмене. Обмен без денег – бартер.

Функции денег: 1.мера стоимости, 2.средство обращения, 3.средство накопления, 4.средство платежа. Инфляция – обесценивание денег. Стагфляция – обесценивание денег и сокращение производства.

Инфляция: умеренная, ползучая, галопирующая, гиперинфляция.

Банковская система: Центральный и коммерческие (частные и государственные).

Функции Центрального банка: 1. эмиссия – выпуск денег, 2. хранение резервов других банков, 3.кредитование, 4. контроль за банками, 5. проведение расчетов для правительства.

Государственный бюджет – основной финансовый план государства, имеющий силу закона.

Бюджет: 1. дефицитный, 2. профицитный, 3. сбалансированный.

Бюджет состоит: доход (налоги, займы) и расход (содержание госаппарата, военные расходы, социальная сфера, инвестиции, выплата долгов).

Налоги – обязательные платежи, взимаемые с юридических и физических лиц. Функции налогов: 1. фискальная (с их помощью формируются финансы), 2. регулирующая, 3. распределительная.

Налоги: прямые (на доходы, на прибыль, на имущество, на наследство) и косвенные (акциз, таможенный, налог на добавленную стоимость).

Налогообложение 1. прогрессивное (налог возрастает от облагаемой суммы), 2. регрессивный (налог снижается, когда возрастает сумма), 3. пропорциональный (налог не зависит от облагаемой суммы).

Безработица – положение в экономике, при котором часть способных и желающих трудиться по найму не могут найти работу по способностям.

Виды безработицы:

1. фрикционная – человек ушел с работы и ищет новую

2. структурная – связана со структурными преобразованиями производства

3. застойная (циклическая) – связана с экономическим кризисом.

4. скрытая – человек соглашается на неполный рабочую неделю или день.

Экономический кризис – нарушение в ходе развития рыночной экономики основных пропорций воспроизводства, проявляющийся в падении производства, сокращении капитальных вложений, росте безработицы, увеличении количества банкротств фирм, падении курса акций и других экономических потрясениях.

Две теории на роль государства в экономике: 1. Монетаризм (Д. Юм) – освобождение экономики от вмешательства государства 2. Кейнсианство (Д.Кейнс) — увеличение государственного регулирования. экономики.

6. Социальная сфера

Социология – наука о закономерностях, становлении, функционирования, развития общества и общественных отношений. (О.Конт).

Структура социальной сферы включает:

I. Социальные связи – зависимости социальных групп и людей друг от друга (бывают формальными и неформальными). Социальные связи:

1. Социальные контакты – неустойчивые связи, возникающие по конкретным поводам (например, пассажиры метро).

2. Социальные взаимодействия – устойчивые, регулярные связи, основанные на совместной деятельности (например, коллеги на работе).

3. Социальные взаимоотношения – сверхустойчивые, самовозобновляющие связи, носящие системный характер (например, друзья).

II. Социальные группы – сообщества индивидов, объединенные по какому-либо признаку. (Т. Гоббс).

Признаки:

численность: малые группы (отличаются прямым контактом и неформальным общением), средние, большие

демографический: по полу, возрасту, образование, состояние в браке

поселенческий критерий: горожане, жители деревни

конфессиональный: католики, православные, мусульмане

по этническому, по профессиональному и т. д.

III. Социальные общности – группы, способные к самовоспроизводству.

Этносоциальные общности: род (племя), народность, нация.

Род – объединение людей на основе кровнородственных связей, племя – объединение родов, народности – объединения людей на основе территориального и языкового признака, нация – большие группы людей, объединенных экономическим пространством, языком, культурой, традициями, национальным самосознанием.

IV. Социальный институт – см. главу Общество. Главный социальный институт – семья.

Функция семьи как социального института: детопроизводство. Семья также малая группа. Функции семьи: воспитательная, социализации, досуговая, создание чувства безопасности, хозяйственно-экономическая. Семья: матриархальная, патриархальная, партнерская. Нуклеарная семья – состоящая из 2 поколений.

V. Социальная культура – социальных норм и социальных ценностей, на основе которых формируются социальные отношения.

VI. Социальные ценности – цели, к которым стремятся люди в обществе. Базовые ценности – жизненно важные для общества (здоровье, благополучие, семья и т. д.)

VII. Социальные нормы – правила социального поведения.

Социальные нормы (бывают писаные и неписаные):

Нормы морали, этические нормы, нормы традиций и обычаев, религиозные нормы, политические нормы, правовые нормы.

Функции социальных норм: регулирующая, объединяющая, воспитательная.

Конформистское поведение – соответствующее принятым нормам.

Поведение, не соответствующее социальным нормам – отклоняющееся.

Отклоняющееся поведение:

Девиантное поведение – нарушение, не соответствующе нормам.

Девиация может быть положительной (герои) и отрицательной (наркоманы, убийцы)

Делинквентное поведение – совершение преступлений.

Соблюдение норм обеспечивается применением санкций – реакция общества на поведение индивида или группы. Функция санкций – социальный контроль.

Санкции:

Позитивные (поощрительные) и негативные (наказывающие)

Официальные и неофициальные.

Социальная стратификация

Социальная стратификация (дифференциация) – расслоение и иерархическая организация общества. (П. Сорокин).

Критерии дифференциации: доход (экономическая), объем власти (политическая), образование (род деятельности.), выделяют также престиж — оценка общества социальной значимости статуса личности. Престиж зависит от реальной полезности деятельности и системы ценностей общества.

Социальные слои:

Касты – строго замкнутые слои традиционных обществ.

Сословия – группы людей, различающиеся по правам и обязанностям.

Классы – социальные группы, выделяемые по способу их участия в общественном производстве и распределении, месту в общественном разделении труда.

Страты – неформальные группы, имеющие относительно равное социальное положение, критериями которого являются доход, доступ к политической власти, образование.

Статус

Статус – позиция в социальной структуре общества, связанная с другими позициями через систему прав и обязанностей.

Личный статус – положение, которое занимает индивид в малой группе

Социальный статус – положение личности в социальной группе.

Статусный набор – совокупность статусов одной личности.

Предписанный (прирожденный) статус: пол, возраст, национальность, родство

Приобретенный (достигнутый) статус: профессия, образование, должность, семейное положение, религия.

Социальная роль — некоторый образец поведения, признанный для людей определенного статуса.

Социальная мобильность

Социальная мобильность (П. Сорокин)– переход индивида или группы из одной позиции в иерархии социальной стратификации в другую.

Социальная мобильность: горизонтальная — внутри одного слоя и вертикальная – переход из одного слоя в другой. Вертикальная мобильность может быть нисходящей и восходящей.

Каналы социальной мобильности («социальные лифты») – образование, армия, школы, семья, собственность.

Маргинал – индивид, утративший свой прежний социальный статус, неспособный адаптироваться к новой социальной среде («на краю»).

Маргинальность – промежуточное положение индивида между социальными группами, связанные с его перемещениями в социальном пространстве.

Люмпены – люди, опустившиеся «на дно» общественной жизни.

Социальный конфликт.

Социальный конфликт (Г. Спенсер) – столкновение противоположных интересов, целей, взглядов, идеологий между индивидами, группами, классами в обществе.

Структура конфликта: конфликтная ситуация——инцидент——активные действия——завершение

Типы поведения в конфликте: приспособление, компромисс, сотрудничество, игнорирование, соперничество. Большинство ученых считают конфликт закономерным, прогрессивным явлением.

Типы конфликтов: внутренние, внешние, глобальные, локальные, экономические, политические, семейные, национальные.

Национальные конфликты связаны с обострением национального вопроса – о самоопределении народов и преодолении этнического неравенства, а также тенденциями в современном мире.

Две тенденции в современном мире:

1. Интернациональная – интеграция, сближение наций.

2. Национальная – дифференциация, стремление к независимости.

Социальная политика государства — целенаправленная деятельность государства по совершенствованию социальной сферы общества. Направления: 1.совершенствование социальной структуры общества, 2. регулирование взаимоотношений между различными слоями, 3. развитие человеческого потенциала (программы развития образования, пенсии, здравоохранение, экология).

Социальная политика: активная — непосредственное воздействие государства (бывает централизованная и децентрализованная) и пассивная — опосредована экономическими факторами

7. Политика.

Политика (Аристотель) – «искусство управления государством» — совокупность связей и социальных групп, которые характеризуются господством и подчинением.

Политика: 1. сфера жизнедеятельности 2. отношения между государствами, группами, нациями по поводу власти 3. деятельность государственных органов.

Функции политики:

1. определение целей и задач общества 2. согласование интересов групп 3. обеспечение стабильности 4. контроль за выполнением норм 5. распределение ресурсов.

Политика: микроуровень, макроуровень (уровень государства), мегауровень (между государствами).

Политическая система – совокупность элементов, в которых реализуется политическая власть.

Тип политической система определяет политико-правовой режим: демократическая, тоталитарная, авторитарная.

Элементы политической системы (сферы или подсистемы):

1. Институциональная: государство, партии, движения (институты)

2. Коммуникативная – совокупность отношений между группами по поводу власти

3. Нормативная – правила и нормы

4. Культурно-идеологическая – идеология, политическая культура, взгляды, эмоции.

Власть – возможность осуществлять свою волю, оказывать воздействие.

Структура власти:

1. Субъекты власти – государство, политические лидеры, партии

2. Объекты власти – индивиды, группы, массы

3. Основания власти — юридические, экономические, силовые, социальные, информационные

4. Ресурсы власти – принуждение, убеждение, право, традиции, страх, поощрение, мифы

5. Функции власти – господство, руководство, регуляция, контроль, управление, координация, организация, мобилизация.

Власть легальная – юридически законная власть, легитимная власть – та, что не навязывается силой, принимается народом добровольно.

Легитимность или господство власти (М. Вебер)

1. Традиционное господство – обусловлено традициями

2. Легальное господство – на признании юридических норм

3. Харизматическое господство – опирается на авторитет лидера.

Политическая власть подразделяется: государственная и общественная власть.

Теории происхождения государства:

1. Патриархальная теория — Аристотель 2. Религиозная теория – Фома Аквинский 3. Договорная теория – Д. Локк, Т. Гоббс 4. Органическая теория – Г. Спенсер 5. Классовая теория – К. Маркс

Государство – особая организация власти и управления, располагающая специальным аппаратом принуждения и способная придать своим велениям обязательную силу для всей страны.

Признаки государства –

1. Наличие особой публичной власти

2. Наличие специального аппарата управления

3. Территориальная организация

4. Налоги

5. Суверенитет власти

6. Монополия на правотворчество.

Функции государства – основные, социально значимые направления деятельности государства.

Функции:

1. По объекту: внутренние и внешние

2. По содержанию: политическая, экономическая, социальная, культурно-воспитательная, правовая, организаторская, экологическая.

3. По характеру воздействия: охранительные (обеспечение охраны общественных отношений) и регулятивные (развитие общественных отношений).

Форма государства – совокупность основных способов организации, устройства и осуществления государственной власти, выражающих его сущность.

Формы государства:

1. Форма правления – способ организации верховной власти.

Форма правления: 1. Монархия – власть сосредоточена в руках одного главы и передается по наследству. 2. Республика – власть осуществляется выборными органами, избираемыми на определенный срок. Монархия: 1. абсолютная, 2. парламентарная, 3. дуалистическая. Республика: 1. президентская, 2. парламентская, 3. смешанная.

2. Форма государственного устройства – способ национального и административно-территориального устройства. Формы: 1. унитарное государство, 2. федерация, 3. конфедерация.

3. Политико-правовой режим – совокупность политико-правовых средств и способов осуществления власти. Режим: 1. демократический, 2. антидемократический (1. авторитарный, 2тоталитарный, 3. военный).

Демократия – признание принципа равенства всех людей, активное участие народа в политической жизни.

Признаки демократии: 1. признание народа источником власти и суверенитета, 2. наличие прав и свобод, 3. плюрализм, 4. разделение властей (законодательная, исполнительная, судебная), 5. гласность. 6. выборность власти, 7. развитая система органов местного самоуправления.

Формы демократии: 1. прямая (непосредственная), 2 косвенная (представительная).

Институты прямой демократии: 1.выборы, 2. референдум (всенародное голосование).

Избирательная система (включает избирательное право, избирательный процесс и порядок отзыва депутатов) – порядок формирования выборных органов.

Избирательное право – принципы и условия участия граждан в выборах. Избирательное право: 1. активное (право избирать), 2. пассивное (право быть избранным). Признаки: 1. всеобщее, 2. равное, 3. гласное, 4. открытое. Определение результатов проходит по двум системам: 1. мажоритарная избирательная система – победившим считается кандидат, набравший большинство голосов. 2. пропорциональная избирательная система – голосование по партийным спискам и распределение мандатов между партиями строго пропорционально числу поданных голосов. Мандат – документ, удостоверяющий права депутата.

Гражданское общество (Г. Гегель) – это негосударственная часть общественно-политической жизни, огражденных от прямого вмешательства государства, равенство прав и свобод всех людей; Признаки гражданского общества: 1. наличие в обществе свободных владельцев средств производства; 2. развитость и разветвленность демократии; 3. правовая защищенность граждан; 4. определенный уровень гражданской культуры.

Правовое государство – государство, которое в своей деятельности подчиняется праву. Признаки правового государства: 1. верховенство закона, 2. соблюдение прав и свобод, 3. принцип разделения властей, 4. взаимная ответственность государства и граждан.

Политическая партия – институт политической системы, группа приверженцев тех или иных целей, объединяющийся для борьбы за власть. Признаки партии: 1. борьба за власть, 2. программа с целями и стратегией, 3. устав, 4. организационная структура, 5. наличие руководящих органов.

Виды партий: 1. По методам: революционные, реформаторские. 2. По характеру членства: кадровые, массовые. 3. По идеологии: консервативные, либеральные, социал-демократические, коммунистические. 4. По представительству во власти: правящие, оппозиционные. 5. По характеру действий: радикальные, реакционные, умеренные, экстремистские, консервативные.

Политическая культура (Г. Алмонд, С. Верба) – совокупность системы мнений, позиций, ценностей, господствующих в обществе или группе.

Виды политической культуры:

1. Патриархальная – ориентация граждан на местные ценности, 2. подданическая – пассивное отношение граждан в политической системе. 3. политическая культура участия (активистская) – активное участие граждан в политической жизни. Абсентеизм – неучастие, уклонение от политической жизни.

Политическая идеология – система идей. Виды идеологий:

1. Консерватизм – сохранение порядков. 2. либерализм – свобода индивидуальности, предпринимательства, права. 3. Социализм – справедливое устройство общества. 4. анархизм – устранение государства 5. национализм – превосходство нации 6. экстремизм – насильственные методы.

Конституции России – 1918 (первая), 1925, 1937, 1978, 1993 (12 декабря). Первая в мире – 1787 – Конституция США. 10 декабря 1948 – «Всеобщая декларация прав человека», 1966 – «Международный пакт о гражданских и политических правах» и «Международный пакт об экономических, социальных и культурных правах». 1959 – «Декларация прав ребенка», 1989 – «Ко

8. Право

Право

1. Система правил и норм поведения, установленная и охраняемая государством.

2. Возможность что-либо делать, осуществлять, иметь (право на труд, образование).

Признаки права (и нормы права): нормативность, обязательность, общий характер, формальная определенность.

Теории происхождения права: теория естественного права (Т. Гоббс), либеральной традиции (сначала право – потом государство), этатистской традиции (сначала государство – потом право), марксистская, социологическая. Этатизм – теория, утверждающая, что государство высший результат и цель общественного развития

Функции права – регулятивная, воспитательная, охранительная.

Правовая культура: правовые знания, отношение к праву, правоохранительная деятельность.

Отличия права и морали:

Право	Мораль
Письменная форма, устанавливается государством, юридическая ответственность	Устная форма, устанавливаются обществом, общественное порицание.
Сходства: регулируют поведение, имеют одни цели и задачи, создаются в процессе жизнедеятельности.

Источник (форма) права – специфические виды социальных явлений, которые формируют право и результат правотворчества государства. Источники (формы) права:

1. Правовой обычай – укоренившиеся в обществе в результате их повторения образцы поведения, превратившиеся в правила поведения.

2. Судебная практика.

3. Юридический (судебный) прецедент – юридическое решение, принятое ранее по конкретному юридическому делу и послужившее примером для последующих решений.

4. Нормативный договор – соглашение сторон, содержащее нормы права

5. Нормативно-правовой акт – акт правотворчества органов государственной власти, устанавливающий или отменяющий нормы права.

Нормативно-правовой акт: законы и подзаконные акты.

I. Законы – нормативно-правовые акты, принимаемые высшим законодательным органом государства (или референдумом), закрепляющие наиболее существенные социальные отношения. Бывают Федеральные Законы и Законы субъектов Федерации.

Законы подразделяются:

1. Конституционные законы (1. Конституции, 2. Законы, вносящие изменение в Конституцию.

3. Законы, предусмотренные Конституцией).

2. Обыкновенные законы – нормативно-правовые акты текущего законодательства. Они бывают текущие (действующие в течение определенного срока) и кодифицированные (своды законов – кодексы).

II. Подзаконные акты – нормативно-правовые акты, конкретизирующие положения законов. – указы, постановления, декреты.

Правовая система (семья) — объединение государств по признаку правового регулирования.

1. Романо-германская – главный источник — нормативно-правовой акт. (Россия).

2. Англо-саксонская – главный источник – юридический прецедент

3. Мусульманская – главный источник – правовой обычай.

Право разделяют на частное право – обслуживает частные интересы (семейное, гражданское) и публичное право (конституционное, уголовное).

Реализация права – воплощение права в жизнь. Формы реализации права:

1. Использование права – использование прав

2. Исполнение права – выполнение обязанностей

3. Соблюдение права – не нарушение права

4. Применение права – осуществляется с помощью должностных лиц.

Система права – совокупность взаимосвязанных между собой норм, институтов и отраслей права.

Элементы системы — 1. Правовая норма (норма права) – единица системы. 2. Институт права – небольшая группа прав, регулирующих один вид отношений. (Например, институт дарения в гражданском праве, институт брака в семейном праве). 3. Отрасль права – совокупность однородных правовых норм.

Норма права – основной элемент правовой системы, правило поведения, установленное и охраняемое государством.

Структура нормы права:

1. Гипотеза — часть нормы, указывающая на условия возникновения прав и обязанностей.

2. Диспозиция – часть нормы, указывающая содержание нормы

3. Санкция – часть нормы, указывающая на правовые последствия нарушения.

Виды норм права

1. По функциям: регулятивные (устанавливают права и обязанности) и охранительные (меры воздействия на нарушителей)

2. По отраслям: семейные, гражданские и т. д.

3. По содержания: 1. нормы обязывающие (что нужно делать) 2. нормы запрещающие (что нельзя делать), 3. нормы управомочивающие (что можно делать).

Отрасли права.

1. Конституционное (государственное) право – регулирует социальнозначимые общественные отношения, устройство государства.

2. Семейное право – регулирует вопросы брачно-семейных отношений, родство.

3. Гражданское право – регулирует имущественные и связанные с ними неимущественные отношения.

4. Административное право – регулирует общественные отношения в сфере управления, связано с деятельностью исполнительной власти.

5. Трудовое право – регулирует отношения между работником и работодателем

6. Уголовное право – регулирует отношения, связанные с совершением преступных деяний.

Правоотношения – виды общественных отношений, регулируемых нормами права.

Чтобы стать участниками правоотношений юридические и физические лица (субъекты общественных отношений) должны обладать правоспособностью и дееспособностью.

Правоспособность – способность субъектов правоотношений иметь юридические права и нести обязанности. Наступает с рождения и заканчивается смертью.

Дееспособность – способность субъектов правоотношений самостоятельно реализовывать права и обязанности. 1. Полная – с 18 лет. 2. Частичная – (в уголовном с 16лет, за некоторые преступления с 14 лет, в семейном с 16 лет, в гражданском – с 14 лет, в административном – с 16 лет) 3. Ограниченная – по суду.

Юридический факт – жизненные условия, в связи с которыми возникают правоотношения.

Юридические факты – 1. Правообразующие. 2. Правоизменяющие. 3. Правопрекращающие.

Юридические факты: 1. События (не зависят от воли людей), 2. Действия (зависят от воли людей).

Действия бывают правомерные и неправомерные (правонарушения).

Правонарушения – деяния, противоречащие предписаниям правовых норм, выражаются как в действии, так и бездействии.

Правонарушения делятся на проступки и преступления.

Проступки (деликты) и юридическая ответственность.

1. Административные (в сфере государственного и местного регулирования) – административная ответственность (предупреждение, штраф, лишение прав, конфискация предмета, исправительные работы, административный арест)

2. Дисциплинарные (в сфере служебных отношений) – дисциплинарная ответственность (замечание, выговор, увольнение), материальная ответственность (возмещение ущерба)

3. Гражданские (в сфере имущественных и неимущественных отношений) – гражданско-правовая ответственность.

Преступления – общественно-опасные противоправные деяния, причиняющие особый вред или угрозу. Наступает уголовная ответственность.

Признаки правонарушения: виновность, противоправность, общественная опасность.

Юридический состав правонарушения:

1.Объект правонарушения – на что направлено деяние. 2. Субъект правонарушения – кто совершил

3. Объективная сторона правонарушения – характеристика, включающая признаки противоправности, общественной опасности, общественно опасные последствия.

4. Субъективная сторона правонарушения — внутренняя характеристика правонарушения (мотив и цель).

5. Мотив правонарушения – осознанное побуждение к совершению деяния.

6. Цель правонарушения – мысленный результат, к которому