Все формулы по математике для 9 класса для успешной сдачи экзамена ОГЭ 2021, который пройдёт 23 и 24 мая 2022 года.
Формулы по математике 9 класс: сборник №1 | сборник №2| сборник №3
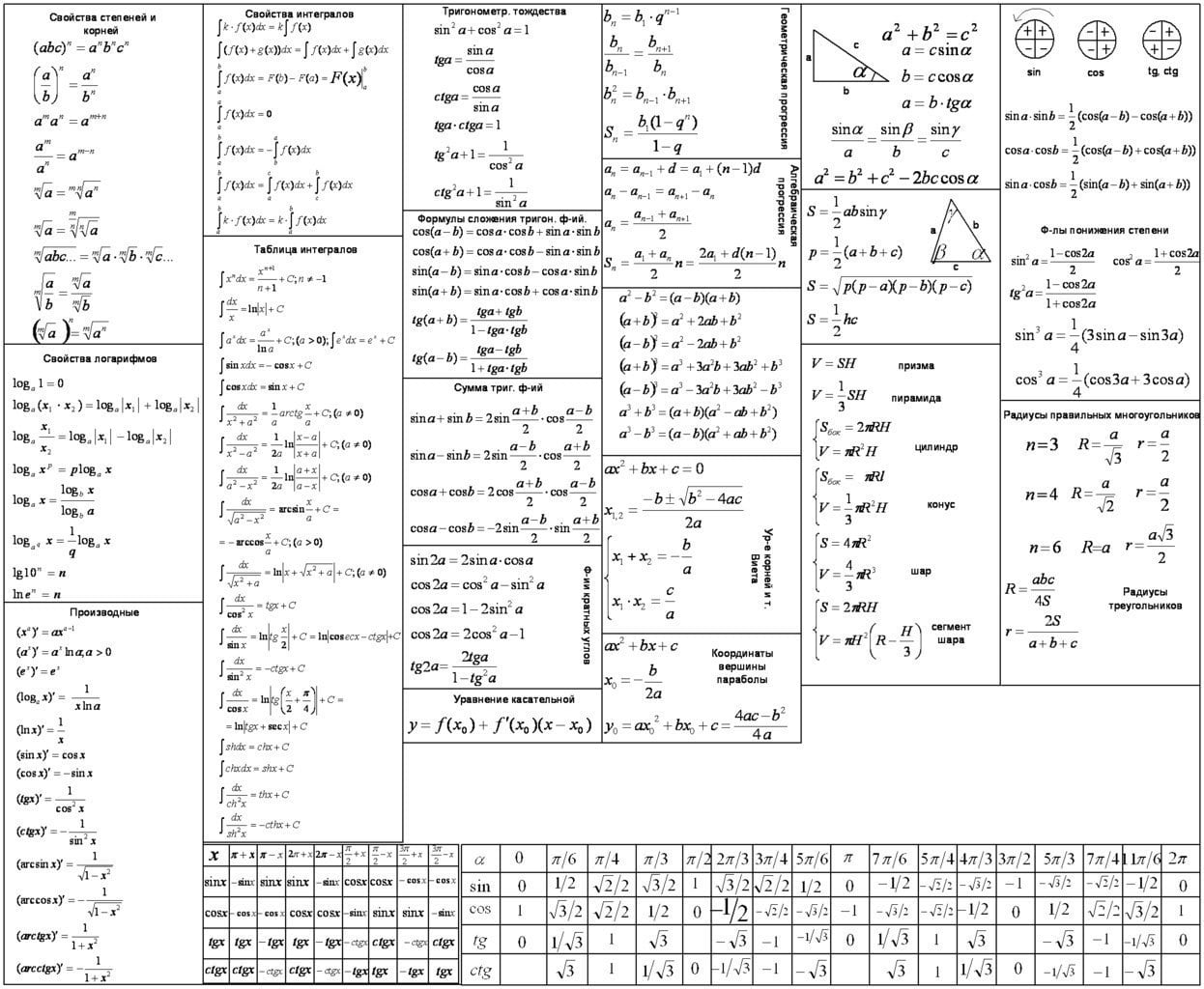
Смотреть сборник формул по математике 9 класс №1:
Смотреть сборник формул по математике 9 класс №2:
Смотреть сборник формул по математике 9 класс №3:
Тренировочные варианты ОГЭ по математике 9 класс:
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Справочные материалы ОГЭ 2022-2023 по математике
График экзаменов ЕГЭ по математике и физике в 2023 году (11 класс)
Экзамены ЕГЭ по математике и физике в 2023 году будут проводиться в следующие сроки.
График экзаменов ОГЭ по математике и физике в 2023 году (9 класс)
Экзамены ОГЭ по математике и физике в 2023 году будут проводиться в следующие сроки.
ОГЭ: Демоверсии, Спецификации, Кодификаторы по физике и математике
Демоверсии, Спецификации, Кодификаторы для ОГЭ в 2023 году по физике и математике
ЕГЭ: Демоверсии, Спецификации, Кодификаторы по физике и математике
Демоверсии, Спецификации, Кодификаторы для ЕГЭ в 2023 году по физике и математике
- ОГЭ по математике
Формулы по алгебре и геометрии приведены в демонстрационном в варианте ОГЭ по математике, опубликованном на официальном сайте ФИПИ.
Справочные материалы ОГЭ по математике выдаются вместе с вариантом. Ими можно воспользоваться при выполнении экзаменационной работы.
Справочные материалы ОГЭ по математике
Скачать файл pdf
Дополнительные материалы и оборудование (из файла спецификация к демоверсии ОГЭ по математике)
Перечень дополнительных материалов и оборудования, пользование которыми разрешено на ОГЭ, утвержден приказом Минобрнауки России.
Участникам разрешается использовать справочные материалы, содержащие основные формулы курса математики, выдаваемые вместе с работой.
Разрешается использовать линейку, угольник, иные шаблоны для построения геометрических фигур. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
Смотрите также:
Формулы, правила, свойства. Можно использовать для сдачи ЕГЭ и ОГЭ по математике.
Для начала шпаргалка в компактном виде:
Формулы сокращенного умножения
(а+b)2 = a2 + 2ab + b2
(а-b)2 = a2 – 2ab + b2
a2 – b2 = (a-b)(a+b)
a3 – b3 = (a-b)( a2 + ab + b2)
a3 + b3 = (a+b)( a2 – ab + b2)
(a + b)3 = a3 + 3a2b+ 3ab2+ b3
(a – b)3 = a3 – 3a2b+ 3ab2— b3
Свойства степеней
a0 = 1 (a≠0)
am/n = (a≥0, n ε N, m ε N)
a— r = 1/ a r (a>0, r ε Q)
a m · a n = a m + n
a m : a n = a m – n (a≠0)
(a m) n = a mn
(ab) n = a n b n
(a/b) n = a n/ b n
Первообразная
Если F’(x) = f(x), то F(x) – первообразная
для f(x)
Функция f(x) = Первообразная F(x)
k = kx + C
xn = xn+1/n+1 + C
1/x = ln |x| + C
ex = ex + C
ax = ax/ ln a + C
1/√x = 2√x + C
cos x = sin x + C
1/ sin2 x = – ctg x + C
1/ cos2 x = tg x + C
sin x = – cos x + C
1/ x2 = – 1/x
Геометрическая прогрессия
b n+1 = bn · q, где n ε N
q – знаменатель прогрессии
b n = b1 · q n – 1 – n-ый член прогрессии
Сумма n-ых членов
S n = (b n q – b 1 )/q-1
S n = b 1 (q n – 1 )/q-1
Модуль
|a| = a, если a≥0
-a, если a<0
Формулы cos и sin
sin (-x) = -sin x
cos (-x) = cos x
sin (x + π) = -sin x
cos (x + π) = -cos x
sin (x + 2πk) = sin x
cos (x + 2πk) = cos x
sin (x + π/2) = cos x
Объемы и поверхности тел
1. Призма, прямая или наклонная, параллелепипед V = S·h
2. Прямая призма SБОК = p·h, p – периметр или длина окружности
3. Параллелепипед прямоугольный
V = a·b·c; P = 2(a·b + b·c + c·a)
P – полная поверхность
4. Куб: V = a3 ; P = 6 a2
5. Пирамида, правильная и неправ.
S = 1/3 S·h; S – площадь основания
6. Пирамида правильная S =1/2 p·A
A – апофема правильной пирамиды
7. Цилиндр круговой V = S·h = πr2h
8. Цилиндр круговой: SБОК = 2 πrh
9. Конус круговой: V=1/3 Sh = 1/3 πr2h
10. Конус круговой: SБОК = 1/2 pL= πrL
Тригонометрические уравнения
sin x = 0, x = πn
sin x = 1, x = π/2 + 2 πn
sin x = -1, x = – π/2 + 2 πn
cos x = 0, x = π/2 + 2 πn
cos x = 1, x = 2πn
cos x = -1, x = π + 2 πn
Теоремы сложения
cos (x +y) = cosx ·cosy – sinx ·siny
cos (x -y) = cosx ·cosy + sinx ·siny
sin (x +y) = sinx ·cosy + cosx ·siny
sin (x -y) = sinx ·cosy – cosx ·siny
tg (x ±y) = tg x ± tg y/ 1 —+ tg x ·tg y
ctg (x ±y) = tg x —+ tg y/ 1± tg x ·tg y
sin x ± sin y = 2 cos (x±y/2)· cos (x—+y/2)
cos x ± cosy = -2 sin (x±y/2)· sin (x—+y/2)
1 + cos 2x = 2 cos2 x; cos2x = 1+cos2x/2
1 – cos 2x = 2 sin2 x; sin2x = 1- cos2x/2
6. Трапеция
a,b – основания; h – высота, c – средняя линия S = (a+b/2)·h = c·h
7. Квадрат
а – сторона, d – диагональ S = a2 = d2/2
8. Ромб
a – сторона, d1, d2 – диагонали, α – угол между ними S = d1d2/2 = a2sinα
9. Правильный шестиугольник
a – сторона S = (3√3/2)a2
10. Круг
S = (L/2) r = πr2 = πd2/4
11. Сектор
S = (πr2/360) α
Правила дифференцирования
( f (x) + g (x) )’ = f ’(x) + g’(x)
(k(f(x))’ = kf ’ (x)
(f(x) g(x))’ = f ’(x)·g(x) + f(x)·g’(x)
(f(x)/g(x))’=(f ’(x)·g(x) – f(x)·g’(x))/g2 (x)
(xn)’ = nx n-1
(tg x)’ = 1/ cos2 x
(ctg x)’ = – 1/ sin2 x
(f (kx + m))’ = kf ’(kx + m)
Уравнение касательной к графику функции
y = f ’(a) (x-a) + f(a)
Площадь S фигуры, ограниченной прямыми x=a, x=b
S = ∫( f(x) – g(x)) dx
Формула Ньютона-Лебница
∫ab f(x) dx = F(b) – F (a)
| t | π/4 | π/2 | 3π/4 | π |
| cos | √2/2 | 0 | -√2/2 | 1 |
| sin | √2/2 | 1 | √2/2 | 0 |
| t | 5π/4 | 3π/2 | 7π/4 | 2π |
| cos | -√2/2 | 0 | √2/2 | 1 |
| sin | -√2/2 | -1 | -√2/2 | 0 |
| t | 0 | π/6 | π/4 | π/3 |
| tg | 0 | √3/3 | 1 | √3 |
| ctg | — | √3 | 1 | √3/3 |
sin x = b x = (-1)n arcsin b + πn
https://5-ege.ru/shpargalki-po-matematike/
cos x = b x = ± arcos b + 2 πn
tg x = b x = arctg b + πn
ctg x = b x = arcctg b + πn
Теорема синусов: a/sin α = b/sin β = c/sin γ = 2R
Теорема косинусов: с2=a2+b2-2ab cos y
Неопределенные интегралы
∫ dx = x + C
∫ xn dx = (x n +1/n+1) + C
∫ dx/x2 = -1/x + C
∫ dx/√x = 2√x + C
∫ (kx+b) = 1/k F(kx + b)
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ dx/sin2 x = -ctg + C
∫ dx/cos2 x = tg + C
∫ x r dx = x r+1/r+1 + C
Логарифмы
1. loga a = 1
2. loga 1 = 0
3. loga (bn) = n loga b
4. log An b = 1/n loga b
5. loga b = log c b/ log c a
6. loga b = 1/ log b a
| Градус | 0 | 30 | 45 | 60 |
| sin | 0 | 1/2 | √2/2 | √3/2 |
| cos | 1 | √3/2 | √2/2 | 1/2 |
| tg | 0 | √3/3 | 1 | √3 |
| t | π/6 | π/3 | 2π/3 | 5π/6 |
| cos | √3/2 | 1/2 | -1/2 | -√3/2 |
| sin | 1/2 | √3/2 | √3/2 | 1/2 |
| 90 | 120 | 135 | 150 | 180 |
| 1 | √3/2 | √2/2 | 1/2 | 0 |
| 0 | -1/2 | -√2/2 | -√3/2 | -1 |
| — | -√3 | -1 | √3/3 | 0 |
| t | 7π/6 | 4π/3 | 5π/3 | 11π/6 |
| cos | -√3/2 | -1/2 | 1/2 | √3/2 |
| sin | -1/2 | -√3/2 | -√3/2 | -1/2 |
Формулы двойного аргумента
cos 2x = cos2x – sin2 x = 2 cos2 x -1 = 1 – 2 sin2 x = 1 – tg2 x/1 + tg2 x
sin 2x = 2 sin x · cos x = 2 tg x/ 1 + tg2 x
tg 2x = 2 tg x/ 1 – tg2 x
ctg 2x = ctg 2 x – 1/ 2 ctg x
sin 3x = 3 sin x – 4 sin3 x
cos 3x = 4 cos3 x – 3 cos x
tg 3x = 3 tg x – tg3 x / 1 – 3 tg2 x
sin s cos t = (sin (s+t) + sin (s+t))/2
sin s sin t = (cos (s-t) – cos (s+t))/2
cos s cos t = (cos (s+t) + cos (s-t))/2
Формулы дифференцирования
c’ = 0 ()’ = 1/ 2
x’ = 1 (sin x)’ = cos x
(kx + m)’ = k (cos x)’ = – sin x
(1/x)’ = – (1/x2) ( ln x)’ = 1/x
(ex)’ = ex; (xn)’ = nx n-1;(log a x)’=1/x ln a
Площади плоских фигур
1. Прямоугольный треугольник
S = 1/2 a·b (a, b – катеты)
2. Равнобедренный треугольник
S = (a/2)·√ b2 – a2/4
3. Равносторонний треугольник
S = (a2/4)·√3 (a – сторона)
4. Произвольный треугольник
a,b,c – стороны, a – основание, h – высота, A,B,C – углы, лежащие против сторон; p = (a+b+c)/2
S = 1/2 a·h = 1/2 a2b sin C =
a2sinB sinC/2 sin A= √p(p-a)(p-b)(p-c)
5. Параллелограмм
a,b – стороны, α – один из углов; h – высота S = a·h = a·b·sin α
cos (x + π/2) = -sin x
Формулы tg и ctg
tg x = sin x/ cos x; ctg x = cos x/sin x
tg(-x) = – tg x
ctg(-x) = – ctg x
tg (x + πk) = tg x
ctg (x + πk) = ctg x
tg (x ± π) = ± tg x
ctg (x ± π) = ± ctg x
tg (x + π/2) = – ctg x
ctg (x + π/2) = – tg x
sin2 x + cos2 x =1
tg x · ctg x = 1
1 + tg2 x = 1/ cos2 x
1 + ctg2 x = 1/ sin2 x
tg2 (x/2) = 1 – cos x/ 1 + cos x
cos2 (x/2) = 1 + cos x/ 2
sin2 (x/2) = 1 – cos x/ 2
11. Шар: V=4/3 πR3 = 1/6 πD3
P = 4 πR2 = πD2
12. Шаровой сегмент
V = πh2 (R-1/3h) = πh/6(h2 + 3r2)
SБОК = 2 πRh = π(r2 + h2); P= π(2r2 + h2)
13. Шаровой слой
V = 1/6 πh3 + 1/2 π(r2 + h2)· h;
SБОК = 2 π·R·h
14. Шаровой сектор:
V = 2/3 πR2 h’ где h’ – высота сегмента, содержащего в секторе
Формула корней квадратного уравнения
(a≥0, b≥0)
(a≥0)
ax2 + bx + c = 0 (a≠0)
Если D=0, то x = -b/2a (D = b2-4ac)
Если D>0, то x1,2 = -b± /2a
Теорема Виета
x1 + x2 = -b/a
x1 · x2 = c/a
Арифметическая прогрессия
a n+1 = a n + d, где n – натуральное число
d – разность прогрессии;
a n = a 1 + (n – 1)·d – формула n-го члена
Сумма n членов
S n = ((a 1 + a n )/2) · n
S n = ((2a 1 + (n-1)d)/2) · n
Радиус описанной окружности около многоугольника
R = a/ 2 sin 180/n
Радиус вписанной окружности
r = a/ 2 tg 180/n
Окружность
L = 2 πR S = πR2
Площадь конуса
S БОК = πRL
S КОН = πR(L+R)
Тангенс угла — отношение противолежащего катета к прилещащему. Котангенс – наоборот.
Скачать шпаргалки по математике
Скачать всё это в компактном виде: matematika-shpory.doc.
Рекомендуем: