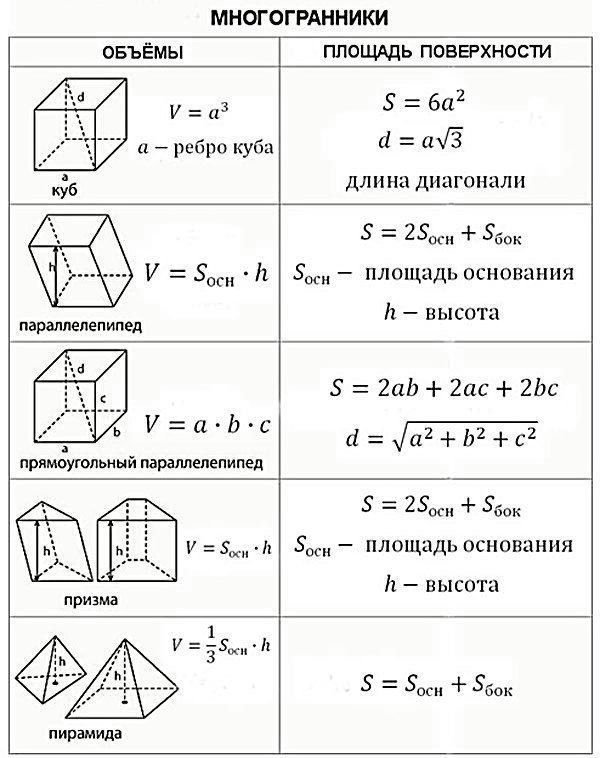
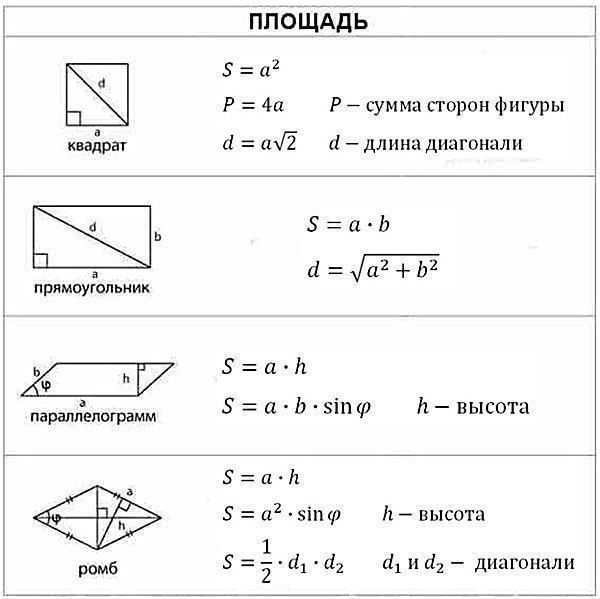
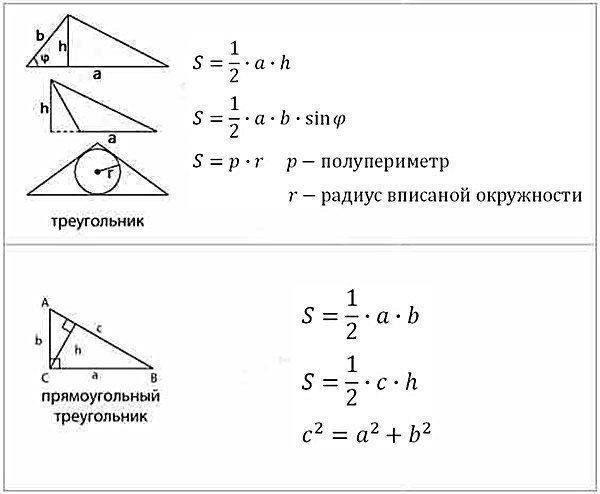
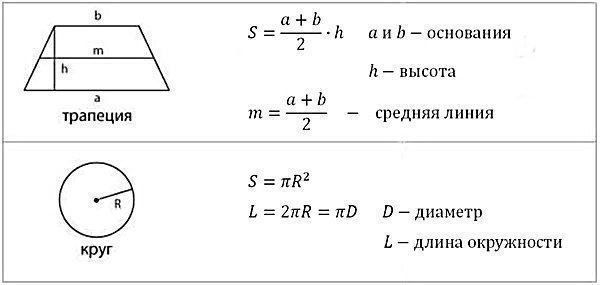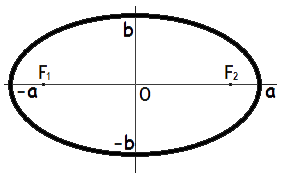Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.
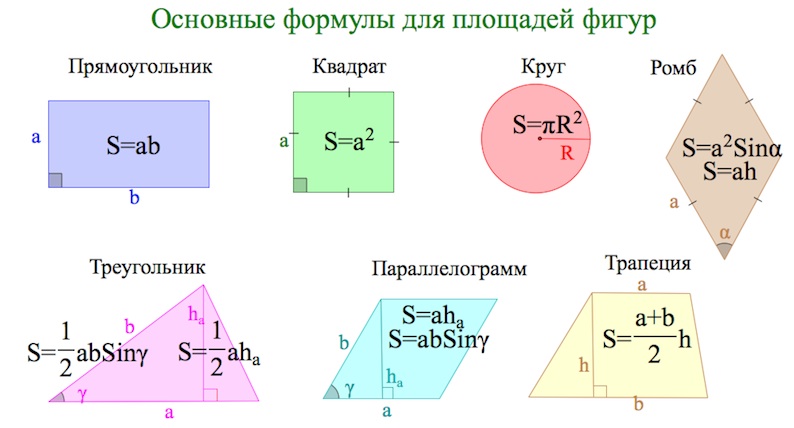
Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.
В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом.
17
Фев 2013
Категория: ПланиметрияСправочные материалы
Площади фигур
Елена Репина
2013-02-17
2014-02-10
Площади основных фигур. Набор формул
Эта таблица хороша для начального знакомства с темой “Площади фигур”.
Для более подготовленных учеников интересна будет расширенная таблица (!)
Автор: egeMax |
комментариев 12
| Метки: Площади, шпаргалки-таблицы
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Печать страницы
- Материалы для подготовки к ЕГЭ
-
- Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
- II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
- Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
- Свежие записи
- Архивы Архивы
Площади фигур. Основные формулы.
Площадь треугольника.
| Формула | Рисунок | Расшифровка формулы |
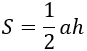 |
 |
а — основание, h — высота, проведенная к этому основанию. Формула применима для любого треугольника. |
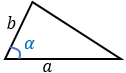 |
a, b — стороны, α — угол между этими сторонами. Формула применима для любого треугольника. |
|
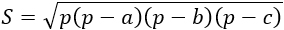 |
 |
a, b, с — стороны, р — полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
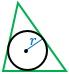 |
r — радиус вписанной в треугольник окружности, р — полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
|
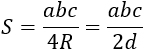 |
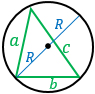 |
a, b, с — стороны, R — радиус описанной около треугольника окружности, d — диаметр описанной окружности. Формула применима для любого треугольника. |
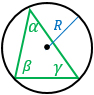 |
R — радиус описанной около треугольника окружности, α, β, γ — углы треугольника. Формула применима для любого треугольника. |
|
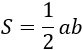 |
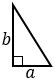 |
a, b — катеты. Формула применима для прямоугольного треугольника. |
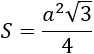 |
 |
a — сторона. Формула применима для равностороннего (правильного) треугольника. |
Площадь квадрата и прямоугольника.
Площадь параллелограмма и ромба.
| Формула | Рисунок | Расшифровка формулы |
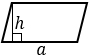 |
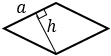
а — одна из сторон параллелограмма, h — высота, проведенная к этой стороне | |
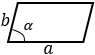 |
а, b — стороны параллелограмма, α — угол между этими сторонами | |
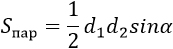 |
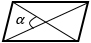 |
d1, d2 — диагонали, α — угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны) |
 |
а — сторона ромба, h — высота, проведенная к этой стороне | |
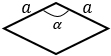 |
а — сторона ромба, α — угол между этими сторонами | |
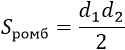 |
 |
d1, d2 — диагонали ромба |
Площадь трапеции.
| Формула | Рисунок | Расшифровка формулы |
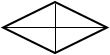
 |
а, b — основания трапеции, h — высота. Формула применима для любой* трапеции. |
|
|
m — средняя линия трапеции, h — высота. Формула применима для любой трапеции. |
||
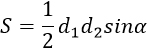 |
 |
d1, d2 — диагонали трапеции, α — угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны). Формула применима для любой трапеции. |
*Любая трапеция — это и равнобедренная, и прямоугольная, и тупоугольная, и произвольная 
Площадь круга и кругового сектора.
Площадь многоугольника.
| Формула | Рисунок | Расшифровка формулы |
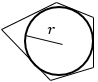 |
р — полупериметр (сумма всех сторон многоугольника, деланная на 2), r — радиус вписанной в этот многоугольник окружности. *Пятиугольник нарисован для примера. Формула работает как для правильного, так и для произвольного многоугольника, главное, чтобы в него можно было вписать окружность. |
Формулы площади геометрических фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
-
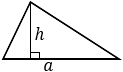
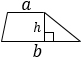
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,p = a + b + c — полупериметр треугольника. 2
Формулы площади квадрата
-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Формулы площади ромба
-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
Формулы площади трапеции
-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a — b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,p = a + b + c + d — полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)
Формулы площади круга
-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.
Формулы площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S — Площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам
Формула Герона
S = √
p
(
p — a
)(
p — b
)(
p — c
)
- Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними. - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
a, b, c
— длины сторон треугольника,
h
— высота треугольника,
γ
— угол между сторонами
a
и
b
,
r
— радиус вписанной окружности,
R — радиус описанной окружности,
|
p = |
a + b + c |
— полупериметр треугольника. |
| 2 |
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
a, b
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади параллелограмма по диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей, умноженному на синус угла между ними.
S = 1/2d1 · d2 · sin
γ
- Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон, умноженному на синус угла между ними.
где S — Площадь параллелограмма,
a, b
— длины сторон параллелограмма,
h
— длина высоты параллелограмма,
α
— угол между сторонами параллелограмма,
- γ — угол между диагоналями параллелограмма,
- d1, d2 — длины диагоналей параллелограмма.
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
Формулы площади ромба
где S — Площадь ромба,
a
— длина стороны ромба,
h
— длина высоты ромба,
α
— угол между сторонами ромба,
d
1,
d
2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
S = a
+
b
√( p — a
)(
p — b
)(
p — a — c
)(
p — a — d
)
4| a
—
b
|
- Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
где S — Площадь трапеции,a, b
— длины основ трапеции,
c, d
— длины боковых сторон трапеции,
p
=
a
+
b
+
c
+
d
— полупериметр трапеции. 2
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
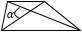
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):