Формулы по биологии егэ

Геометрия

• Треугольник
• Четырехугольники
• Окружность и круг
• Призма
• Пирамида
• Усеченная пирамида
• Цилиндр
• Конус
• Усеченный конус
• Сфера и шар

1. Формулы сокращённого умножения

Наверх

2. Модуль числа

Определение:

Основные свойства модуля:

Наверх

3. Степень с действительным показателем

Свойства степени с действительным показателем

Пусть Тогда верны следующие соотношения:

Наверх

4. Корень n-ой степени из числа

Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.

Основные свойства арифметического корня:

Наверх

5. Логарифмы

Определение логарифма:

Основное логарифмическое тождество:

Основные свойства логарифмов

Пусть Тогда верны следующие соотношения:

Наверх

6. Арифметическая прогрессия

Формула n-го члена арифметической прогрессии:

Характеристическое свойство арифметической прогрессии:

Сумма n первых членов арифметической прогрессии:

При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

7. Геометрическая прогрессия

Формула n-го члена геометрической прогрессии:

Характеристическое свойство геометрической прогрессии:

Сумма n первых членов геометрической прогрессии:

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

8. Бесконечно убывающая геометрическая прогрессия

Сумма бесконечно убывающей геометрической прогрессии:

Наверх

9. Основные формулы тригонометрии

Зависимость между тригонометрическими функциями одного аргумента:

Формулы сложения:

Формулы тригонометрических функций двойного аргумента:

Формулы понижения степени:

Формулы приведения

Все формулы приведения получаются из соответствующих формул сложения. Например:

Применение формул приведения укладывается в следующую схему:

— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;

— определяется знак приводимой функции;

— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или , то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид , то функция названия не меняет.

Например, получим формулу :

— — IV четверть;

— в IV четверти тангенс отрицательный;

— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,

Формулы преобразования суммы тригонометрических функций в произведение:

Формулы преобразования произведения тригонометрических функций в сумму:

Наверх

10. Производная и интеграл

Таблица производных некоторых элементарных функций

Правила дифференцирования:

1.

2.

3.

4.

5.

Уравнение касательной к графику функции в его точке :

Таблица первообразных для некоторых элементарных функций

Правила нахождения первообразных

Пусть ― первообразные для функций и соответственно, a, b, k ― постоянные, Тогда:

— ― первообразная для функции

— ― первообразная для функции

— ― первообразная для функции

— Формула Ньютона-Лейбница:

1. Треугольник

Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно; ― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно; ― длины высот AA₂, BB₂, CC₂ треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC; ― площадь треугольника ABC. Тогда имеют место следующие соотношения:

(теорема синусов);

(теорема косинусов);

Наверх
2. Четырёхугольники

Параллелограмм

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Ромбом называется параллелограмм, все стороны которого равны.

Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.

Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Площадь четырехугольника

Площадь параллелограмма равна произведению его основания на высоту.

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Наверх

3. Окружность и круг

Соотношения между элементами окружности и круга

Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга,  — длина дуги в градусов,  — длина дуги в радиан,  — площадь сектора, ограниченного дугой в n градусов,  — площадь сектора, ограниченного дугой в радиан. Тогда имеют место следующие соотношения:

Вписанный угол

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность, — прямой.

Вписанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Описанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.

Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны

Наверх

4. Призма

Пусть H ― высота призмы, AA₁ ― боковое ребро призмы,  ― периметр основания призмы,  ― площадь основания призмы,  ― площадь боковой поверхности призмы,  ― площадь полной поверхности призмы, V ― объем призмы,  ― периметр перпендикулярного сечения призмы,  ― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

Свойства параллелепипеда:

— противоположные грани параллелепипеда равны и параллельны;

— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;

— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Наверх

5. Пирамида

Пусть H ― высота пирамиды,  ― периметр основания пирамиды,  ― площадь основания пирамиды,  ― площадь боковой поверхности пирамиды,  ― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:

;

.

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то

Наверх

6. Усечённая пирамида

Пусть H ― высота усеченной пирамиды, и  ― периметры оснований усеченной пирамиды, и  ― площади оснований усеченной пирамиды,  ― площадь боковой поверхности усеченной пирамиды,  ― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.

Тогда имеют место следующие соотношения:

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то:

Наверх

7. Цилиндр

Пусть h ― высота цилиндра, r ― радиус цилиндра,  ― площадь боковой поверхности цилиндра,  ― площадь полной поверхности цилиндра, V ― объем цилиндра.

Тогда имеют место следующие соотношения:

Наверх

8. Конус

Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса,  ― площадь боковой поверхности конуса,  ― площадь полной поверхности конуса, V ― объем конуса.

Тогда имеют место следующие соотношения:

Наверх

9. Усечённый конус

Пусть h ― высота усеченного конуса, r и  ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,  ― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:

Наверх

10. Сфера и шар

Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы,  ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,  ― объем сегмента, высота которого равна h,  ― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:

Наверх

ЕГЭ по биологии

09.09.2012

Подборка шпаргалок по БИОЛОГИИ.

Обновлено: 01.11.2022

Полный набор теоретического материала для подготовки к ЕГЭ в 2023 году. Таблицы в кратком виде, схемы, теория по задания. Всё, что необходимо для самостоятельной работы. Эти шпаргалки помогут написать биологию на 100 баллов.

• Тренировочные варианты ЕГЭ по биологии

Подборка шпаргалок содержит

• Биология в схемах и таблицах
• Весь курс биологии в таблицах
• Шпаргалки по генетике, ДНК, митоз, мейоз и клеточная теория
• Теоретические конспекты по биологии
• Все термины по биологии
• Книжка-шпаргалка по биологии

Для чтения шпаргалок необходимы бесплатные программы: WinDJView и Adobe Reader

СКАЧАТЬ

https://down.ctege.info/ege/obshee/shpory/bio-ege-shpora.zip

Формулы цветков растений

16-Янв-2014 | Нет комментариев | Лолита Окольнова

Не часто, но все же встречается в вопросах ГИА и ЕГЭ по биологии тема, которая относится к ботанике, проходят ее в 7 или 8 классе, поэтому к моменту подготовки к экзаменам она успешно забывается…

Итак, рассмотрим строение цветков и соцветий и

Формулы цветков растений

Царство Растений принято делить на отделы, потом — на  классы (одно-и двудольные), далее — порядок (его часто пропускают) и затем уже  на семейства.

У растений класса двудольные количество лепестков в цветке кратно 4 или 5, у однодольных — 3 и околоцветник простой, либо совсем отсутствует.

Растения каждого из семейств имеют общие признаки. У цветковых растений основными признаками являются строение цветка и плода, тип соцветия, а также особенности внешнего и внутреннего строения вегетативных органов.

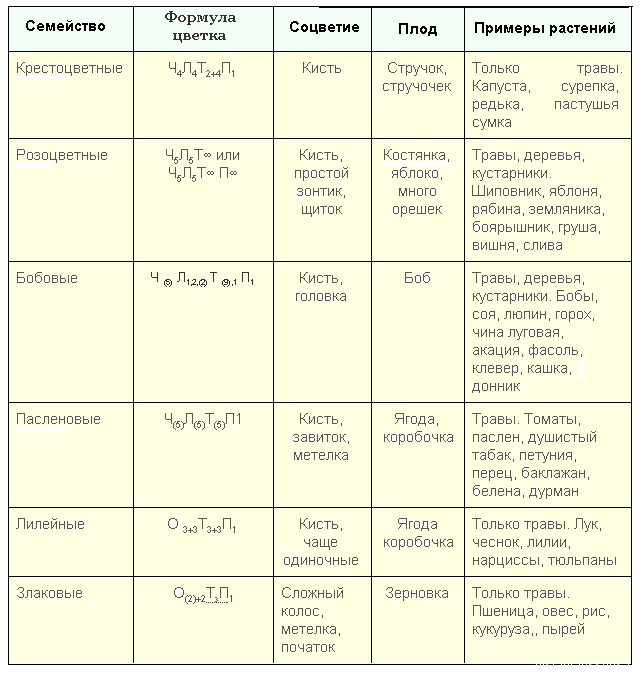
Соответственно, у каждого семейства цветковых есть своя формула.

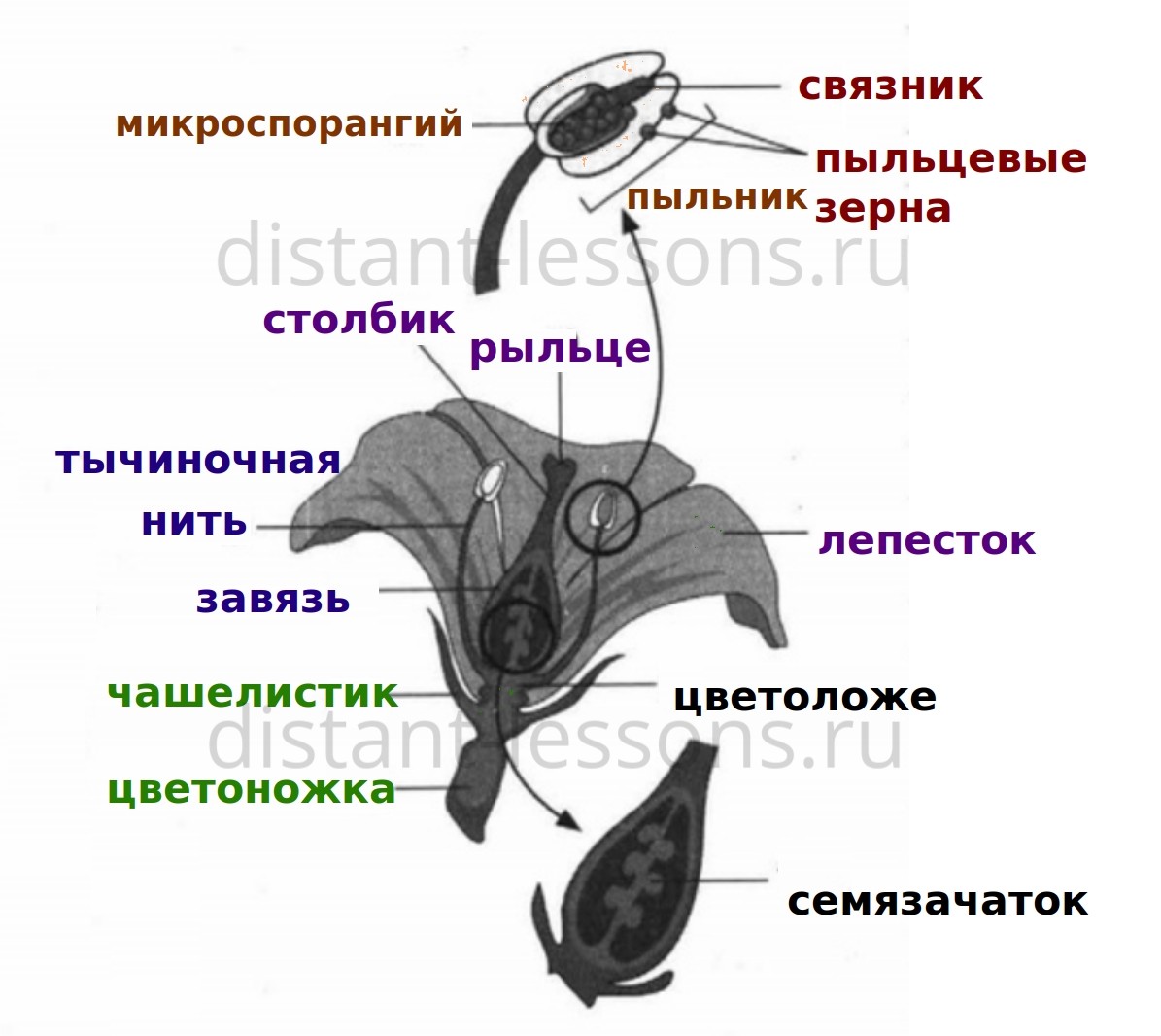
 Для начала давайте рассмотрим более детально строение цветка (при подготовке к ЕГЭ обычно цветок рассматривают только в контексте двойного оплодотворения).

 

Стеблевая часть:

• цветоножка
• цветоложе

 Околоцветник:

• чашелистики
• лепестки венчика

 Генеративная часть:

• пестик
• тычинки
• Завязь

Соцветие  — часть системы побегов покрытосеменного растения, несущая цветки и в связи с этим разнообразно видоизмененная. Соцветия обычно более или менее чётко отграничены от вегетативной части растения.

Биологический смысл возникновения соцветий — в возрастающей вероятности опыления цветков  ветроопыляемых , так и  насекомоопыляемых растений.

Закладываются соцветия внутри цветочных или смешанных почек.

 

 

Для построения формулы цветковых растений используют Околоцветник и Генеративную часть

1. В международной системе сначала указывают пол цветка (мужской, женский или двудомный), в школьном формате этот пункт зачастую пропускают;
2. обозначают симметрию (правильный или неправильный цветок) — этот пункт тоже пропускаем;
3. буквами указывают:

О — околоцветник

Ч — чашелистики;

Л — лепестки;

Т — тычинки;

П — пестики;

• числами указывают число элементов, если их больше 12, то ставят знак «бесконечность»;
• дополнительные обозначения:
  числа в скобках — сросшиеся элементы;
  знак «+» — круговое расположение элементов.

Примеры:

Формула цветка тюльпана *О3+3Т3+3П(3)

цветок правильный, околоцветник простой и состоит из шести листочков (причём они различаются), шести тычинок (тычинки также неодинаковые) и трёх сросшихся плодолистиков.

Формула цветка шиповника – *Ч5Л5Т∞П∞

цветок правильный, с 5 чашелистиками и 5 лепестками. Тычинок и пестиков много (более 12)

 
Еще можно добавить сюда Семейство Сложноцветные

Формула цветка: Л₍₅₎Т₍₅₎П₁
Соцветие – корзинка.
Плод – семянка.

Пример вопроса из теста ГИА:

Цветок одуванчика — это

1) головка
2) корзинка
3) цветок, имеющий 5 сросшихся тычинок и 5 сросшихся лепестков
4) цветок с  числом лепестков и тычинок больше 12

Ответ: т.к. одуванчик относится к семейству сложноцветных, то его формула Л (5)Т (5) — соответствует ответу 3)

Вопросы по формулам цветков растений встречаются на экзаменах редко, но стоит их выучить — на всякий случай

---

 

• примеры вопросов ОГЭ по строению цветка
• несколько ЕГЭ вопросов

Обсуждение: «Формулы цветков растений»

(Правила комментирования)

Основные термины генетики

Ген — это участок молекулы ДНК, несущий информацию о первичной структуре одного белка. Ген — это структурная и функциональная единица наследственности.

Аллельные гены (аллели) — разные варианты одного гена, кодирующие альтернативное проявление одного и того же признака. Альтернативные признаки — признаки, которые не могут быть в организме одновременно.

Гомозиготный организм — организм, не дающий расщепления по тем или иным признакам. Его аллельные гены одинаково влияют на развитие данного признака.

Гетерозиготный организм — организм, дающий расщепление по тем или иным признакам. Его аллельные гены по-разному влияют на развитие данного признака.

Доминантный ген отвечает за развитие признака, который проявляется у гетерозиготного организма.

Рецессивный ген отвечает за признак, развитие которого подавляется доминантным геном. Рецессивный признак проявляется у гомозиготного организма, содержащего два рецессивных гена.

Генотип — совокупность генов в диплоидном наборе организма. Совокупность генов в гаплоидном наборе хромосом называется геномом.

Фенотип — совокупность всех признаков организма.

Законы Г. Менделя

Первый закон Менделя — закон единообразия гибридов 

Этот закон выведен на основании результатов моногибридного скрещивания. Для опытов было взято два сорта гороха, отличающихся друг от друга одной парой признаков — цветом семян: один сорт имел желтую окраску, второй — зеленую. Скрещивающиеся растения были гомозиготными.

Для записи результатов скрещивания Менделем была предложена следующая схема:

 — желтая окраска семян
 — зеленая окраска семян

Формулировка закона: при скрещивании организмов, различающихся по одной паре альтернативных признаков, первое поколение единообразно по фенотипу и генотипу.

Второй закон Менделя — закон расщепления

Из семян, полученных при скрещивании гомозиготного растения с желтой окраской семян с растением с зеленой окраской семян, были выращены растения, и путем самоопыления было получено .

Формулировка закона: у потомства, полученного от скрещивания гибридов первого поколения, наблюдается расщепление по фенотипу в соотношении , а по генотипу — .

Третий закон Менделя — закон независимого наследования

Этот закон был выведен на основании данных, полученных при дигибридном скрещивании. Мендель рассматривал наследование двух пар признаков у гороха: окраски и формы семян.

В качестве родительских форм Мендель использовал гомозиготные по обоим парам признаков растения: один сорт имел желтые семена с гладкой кожицей, другой — зеленые и морщинистые.

 — желтая окраска семян,  — зеленая окраска семян,
 — гладкая форма,  — морщинистая форма.

Затем Мендель из семян  вырастил растения и путем самоопыления получил гибриды второго поколения.

В  произошло расщепление на  фенотипических класса в соотношении .  всех семян имели оба доминантных признака (желтые и гладкие),  — первый доминантный и второй рецессивный (желтые и морщинистые),  — первый рецессивный и второй доминантный (зеленые и гладкие),  — оба рецессивных признака (зеленые и морщинистые).

При анализе наследования каждой пары признаков получаются следующие результаты. В  частей желтых семян и  части зеленых семян, т.е. соотношение . Точно такое же соотношение будет и по второй паре признаков (форме семян).

Формулировка закона: при скрещивании организмов, отличающихся друг от друга двумя и более парами альтернативных признаков, гены и соответствующие им признаки наследуются независимо друг от друга и комбинируются во всевозможных сочетаниях.

Третий закон Менделя выполняется только в том случае, если гены находятся в разных парах гомологичных хромосом.

Закон (гипотеза) «чистоты» гамет

При анализе признаков гибридов первого и второго поколений Мендель установил, что рецессивный ген не исчезает и не смешивается с доминантным. В  проявляются оба гена, что возможно только в том случае, если гибриды  образуют два типа гамет: одни несут доминантный ген, другие — рецессивный. Это явление и получило название гипотезы чистоты гамет: каждая гамета несет только один ген из каждой аллельной пары. Гипотеза чистоты гамет была доказана после изучения процессов, происходящих в мейозе.

Гипотеза «чистоты» гамет — это цитологическая основа первого и второго законов Менделя. С ее помощью можно объяснить расщепление по фенотипу и генотипу.

Анализирующее скрещивание

Этот метод был предложен Менделем для выяснения генотипов организмов с доминантным признаком, имеющих одинаковый фенотип. Для этого их скрещивали с гомозиготными рецессивными формами.

Если в результате скрещивания все поколение оказывалось одинаковым и похожим на анализируемый организм, то можно было сделать вывод: исходный организм является гомозиготным по изучаемому признаку.

Если в результате скрещивания в поколении наблюдалось расщепление в соотношении , то исходный организм содержит гены в гетерозиготном состоянии.

Наследование групп крови (система АВ0)

Наследование групп крови в этой системе является примером множественного аллелизма (это существование у вида более двух аллелей одного гена). В человеческой популяции имеется три гена , кодирующие белки-антигены эритроцитов, которые определяют группы крови людей. В генотипе каждого человека содержится только два гена, определяющих его группу крови: первая группа ; вторая  и ; третья  и и четвертая .

Наследование признаков, сцепленных с полом

У большинства организмов пол определяется во время оплодотворения и зависит от набора хромосом. Такой способ называют хромосомным определением пола. У организмов с таким типом определения пола есть аутосомы и половые хромосомы —  и .

У млекопитающих (в т.ч. у человека) женский пол обладает набором половых хромосом , мужской пол — . Женский пол называют гомогаметным (образует один тип гамет); а мужской — гетерогаметным (образует два типа гамет). У птиц и бабочек гомогаметным полом являются самцы , а гетерогаметным — самки .

В ЕГЭ включены задачи только на признаки, сцепленные с -хромосомой. В основном они касаются двух признаков человека: свертываемость крови ( — норма;  — гемофилия), цветовое зрение ( — норма,  — дальтонизм). Гораздо реже встречаются задачи на наследование признаков, сцепленных с полом, у птиц.

У человека женский пол может быть гомозиготным или гетерозиготным по отношению к этим генам. Рассмотрим возможные генетические наборы у женщины на примере гемофилии (аналогичная картина наблюдается при дальтонизме):  — здорова;  — здорова, но является носительницей;  — больна. Мужской пол по этим генам является гомозиготным, т.к. -хромосома не имеет аллелей этих генов:  — здоров;  — болен. Поэтому чаще всего этими заболеваниями страдают мужчины, а женщины являются их носителями.

Типичные задания ЕГЭ по генетике

Определение числа типов гамет

Определение числа типов гамет проводится по формуле: , где  — число пар генов в гетерозиготном состоянии. Например, у организма с генотипом  генов в гетерозиготном состоянии нет, т.е. , следовательно, , и он образует один тип гамет . У организма с генотипом  одна пара генов в гетерозиготном состоянии , т.е. , следовательно, , и он образует два типа гамет. У организма с генотипом  три пары генов в гетерозиготном состоянии, т.е. , следовательно, , и он образует восемь типов гамет.

Задачи на моно- и дигибридное скрещивание

На моногибридное скрещивание

Задача: Скрестили белых кроликов с черными кроликами (черный цвет — доминантный признак). В белых и  черных. Определите генотипы родителей и потомства.

Решение: Поскольку в потомстве наблюдается расщепление по изучаемому признаку, следовательно, родитель с доминантным признаком гетерозиготен.

На дигибридное скрещивание

Доминантные гены известны

Задача: Скрестили томаты нормального роста с красными плодами с томатами-карликами с красными плодами. В  все растения были нормального роста;  — с красными плодами и  — с желтыми. Определите генотипы родителей и потомков, если известно, что у томатов красный цвет плодов доминирует над желтым, а нормальный рост — над карликовостью.

Решение: Обозначим доминантные и рецессивные гены:  — нормальный рост,  — карликовость;  — красные плоды,  — желтые плоды.

Проанализируем наследование каждого признака по отдельности. В  все потомки имеют нормальный рост, т.е. расщепления по этому признаку не наблюдается, поэтому исходные формы — гомозиготны. По цвету плодов наблюдается расщепление , поэтому исходные формы гетерозиготны.

Доминантные гены неизвестны

Задача: Скрестили два сорта флоксов: один имеет красные блюдцевидные цветки, второй — красные воронковидные цветки. В потомстве было получено  красных блюдцевидных,  красных воронковидных,  белых блюдцевидных и  белых воронковидных. Определите доминантные гены и генотипы родительских форм, а также их потомков.

Решение: Проанализируем расщепление по каждому признаку в отдельности. Среди потомков растения с красными цветами составляют , с белыми цветами — , т.е. . Поэтому  — красный цвет,  — белый цвет, а родительские формы — гетерозиготны по этому признаку (т.к. есть расщепление в потомстве).

По форме цветка также наблюдается расщепление: половина потомства имеет блюдцеобразные цветки, половина — воронковидные. На основании этих данных однозначно определить доминантный признак не представляется возможным. Поэтому примем, что  — блюдцевидные цветки,  — воронковидные цветки.

 — красные блюдцевидные цветки,
 — красные воронковидные цветки,
 — белые блюдцевидные цветки,
 — белые воронковидные цветки.

Решение задач на группы крови (система АВ0)

Задача: у матери вторая группа крови (она гетерозиготна), у отца — четвертая. Какие группы крови возможны у детей?

Решение:

Решение задач на наследование признаков, сцепленных с полом

Такие задачи вполне могут встретиться как в части А, так и в части С ЕГЭ.

Задача: носительница гемофилии вышла замуж за здорового мужчину. Какие могут родиться дети?

Решение:

Решение задач смешанного типа

Задача: Мужчина с карими глазами и  группой крови женился на женщине с карими глазами и  группой крови. У них родился голубоглазый ребенок с  группой крови. Определите генотипы всех лиц, указанных в задаче.

Решение: Карий цвет глаз доминирует над голубым, поэтому  — карие глаза,  — голубые глаза. У ребенка голубые глаза, поэтому его отец и мать гетерозиготны по этому признаку. Третья группа крови может иметь генотип  или , первая — только . Поскольку у ребенка первая группа крови, следовательно, он получил ген  и от отца, и от матери, поэтому у его отца генотип .

Задача: Мужчина дальтоник, правша (его мать была левшой) женат на женщине с нормальным зрением (ее отец и мать были полностью здоровы), левше. Какие могут родиться дети у этой пары?

Решение: У человека лучшее владение правой рукой доминирует над леворукостью, поэтому  — правша,  — левша. Генотип мужчины  (т.к. он получил ген  от матери-левши), а женщины — .

Мужчина-дальтоник имеет генотип , а его жена — , т.к. ее родители были полностью здоровы.

Задачи для самостоятельного решения

1. Определите число типов гамет у организма с генотипом .
2. Определите число типов гамет у организма с генотипом .
3. Определите число типов гамет у организма с генотипом .
4. Скрестили высокие растения с низкими растениями. В  — все растения среднего размера. Какое будет ?
5. Скрестили белого кролика с черным кроликом. В  все кролики черные. Какое будет ?
6. Скрестили двух кроликов с серой шерстью. В  с черной шерстью,  — с серой и с белой. Определите генотипы и объясните такое расщепление.
7. Скрестили черного безрогого быка с белой рогатой коровой. В  получили  черных безрогих, черных рогатых,  белых рогатых и  белых безрогих. Объясните это расщепление, если черный цвет и отсутствие рогов — доминантные признаки.
8. Скрестили дрозофил с красными глазами и нормальными крыльями с дрозофилами с белыми глазами и дефектными крыльями. В потомстве все мухи с красными глазами и дефектными крыльями. Какое будет потомство от скрещивания этих мух с обоими родителями?
9. Голубоглазый брюнет женился на кареглазой блондинке. Какие могут родиться дети, если оба родителя гетерозиготны?
10. Мужчина правша с положительным резус-фактором женился на женщине левше с отрицательным резусом. Какие могут родиться дети, если мужчина гетерозиготен только по второму признаку?
11. У матери и у отца  группа крови (оба родителя гетерозиготны). Какая группа крови возможна у детей?
12. У матери  группа крови, у ребенка —  группа. Какая группа крови невозможна для отца?
13. У отца первая группа крови, у матери — вторая. Какова вероятность рождения ребенка с первой группой крови?
14. Голубоглазая женщина с  группой крови (ее родители имели третью группу крови) вышла замуж за кареглазого мужчину со  группой крови (его отец имел голубые глаза и первую группу крови). Какие могут родиться дети?
15. Мужчина-гемофилик, правша (его мать была левшой) женился на женщине левше с нормальной кровью (ее отец и мать были здоровы). Какие могут родиться дети от этого брака?
16. Скрестили растения земляники с красными плодами и длинночерешковыми листьями с растениями земляники с белыми плодами и короткочерешковыми листьями. Какое может быть потомство, если красная окраска и короткочерешковые листья доминируют, при этом оба родительских растения гетерозиготны?
17. Мужчина с карими глазами и  группой крови женился на женщине с карими глазами и  группой крови. У них родился голубоглазый ребенок с  группой крови. Определите генотипы всех лиц, указанных в задаче.
18. Скрестили дыни с белыми овальными плодами с растениями, имевшими белые шаровидные плоды. В потомстве получены следующие растения:  с белыми овальными,  с белыми шаровидными,  с желтыми овальными и  с желтыми шаровидными плодами. Определите генотипы исходных растений и потомков, если у дыни белая окраска доминирует над желтой, овальная форма плода — над шаровидной.

Ответы

1.  типа гамет.
2.  типов гамет.
3.  типа гамет.
4.  высоких,  средних и  низких (неполное доминирование).
5.  черных и  белых.
6.  — черные,  — белые,  — серые. Неполное доминирование.
7. Бык: , корова — . Потомство:  (черные безрогие),  (черные рогатые), (белые рогатые),  (белые безрогие).
8.  — красные глаза,  — белые глаза;  — дефектные крылья,  — нормальные. Исходные формы —  и , потомство .
   Результаты скрещивания:
   а) 

   б) 

9.  — карие глаза,  — голубые;  — темные волосы,  — светлые. Отец , мать — .
10.  — правша,  — левша;  — положительный резус,  — отрицательный. Отец , мать — . Дети:  (правша, положительный резус) и  (правша, отрицательный резус).
11. Отец и мать — . У детей возможна третья группа крови (вероятность рождения — ) или первая группа крови (вероятность рождения — ).
12. Мать , ребенок ; от матери он получил ген , а от отца — . Для отца невозможны следующие группы крови: вторая , третья , первая , четвертая .
13. Ребенок с первой группой крови может родиться только в том случае, если его мать гетерозиготна. В этом случае вероятность рождения составляет .
14.  — карие глаза,  — голубые. Женщина , мужчина . Дети:  (карие глаза, четвертая группа),  (карие глаза, третья группа),  (голубые глаза, четвертая группа),  (голубые глаза, третья группа).
15.  — правша,  — левша. Мужчина , женщина . Дети  (здоровый мальчик, правша),  (здоровая девочка, носительница, правша),  (здоровый мальчик, левша),  (здоровая девочка, носительница, левша).
16.  — красные плоды,  — белые;  — короткочерешковые,  — длинночерешковые.
    Родители:  и . Потомство:  (красные плоды, короткочерешковые),  (красные плоды, длинночерешковые),  (белые плоды, короткочерешковые),  (белые плоды, длинночерешковые).
    Скрестили растения земляники с красными плодами и длинночерешковыми листьями с растениями земляники с белыми плодами и короткочерешковыми листьями. Какое может быть потомство, если красная окраска и короткочерешковые листья доминируют, при этом оба родительских растения гетерозиготны?
17.  — карие глаза,  — голубые. Женщина , мужчина . Ребенок: 
18.  — белая окраска,  — желтая;  — овальные плоды,  — круглые. Исходные растения:  и . Потомство:
     с белыми овальными плодами,
     с белыми шаровидными плодами,
     с желтыми овальными плодами,
     с желтыми шаровидными плодами.

По какой формуле определяют число фенотипов в потомстве при расщеплении?

Для определения используется формула 2ⁿ, в которой n — количество пар аллельных генов.

Если происходит моногибридное скрещивание, «родители», наделенные отличием в одной паре признаков (Мендель экспериментировал с горошинами желтыми и зелеными), во втором поколении дают два фенотипа (2¹). При дигибридном скрещивании они имеют различия по двум парам признаков и, соответственно, во втором поколении производят четыре фенотипа (2²).

Точно таким же образом подсчитывается количество фенотипов, получившихся во втором поколении методом тригибридного скрещивания — появится восемь фенотипов (2³).

По какой формуле определяют число различных видов гамет у гетерозигот?

Это число высчитывают также по формуле (2ⁿ). Однако n в этом случае — количество пар генов в гетерозиготном состоянии. На использовании этой формулы построены задачи в ЕГЭ по биологии и внутреннем экзамене МГУ.

По какой формуле определяют число генотипов в потомстве при расщеплении?

Здесь применяется формула 3ⁿ, где n — количество пар аллельных генов. Если скрещивание моногибридное, расщепление по генотипу в F₂ происходит в соотношении 1:2:1, то есть образуются три различающихся генотипа (3¹). 

При дигибридном скрещивании возникают 9 генотипов (3²), при тригибридном — 27 генотипов (3³). 

Хочешь сдать экзамен на отлично? Жми сюда — подготовка к ОГЭ по биологии онлайн