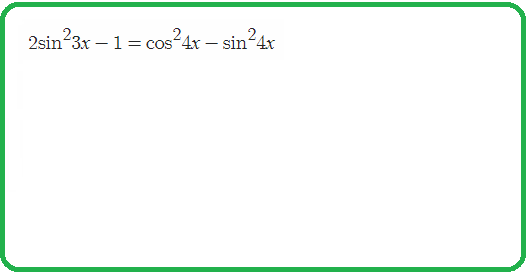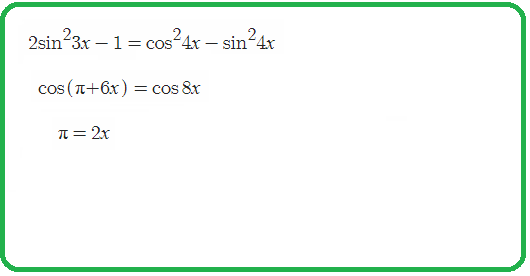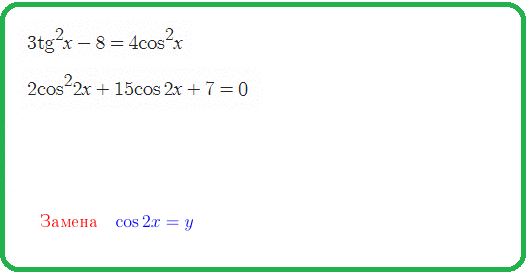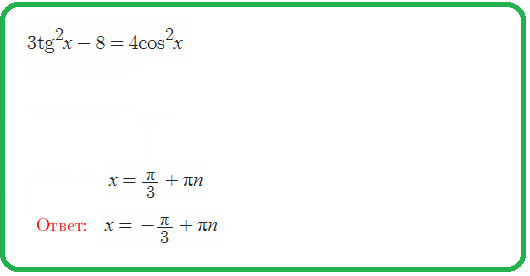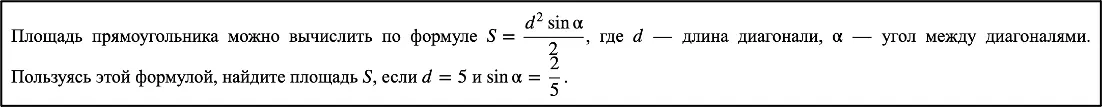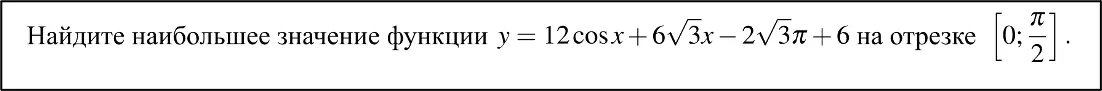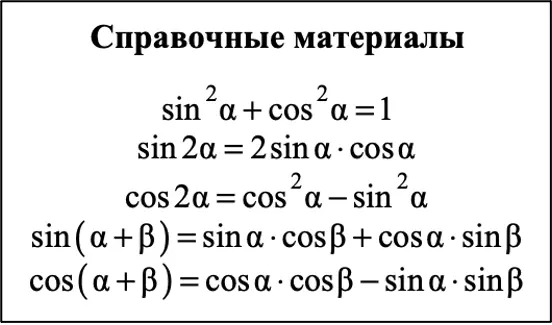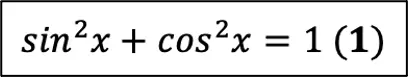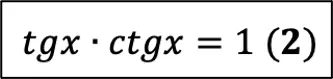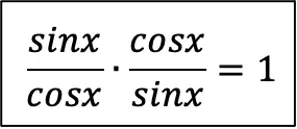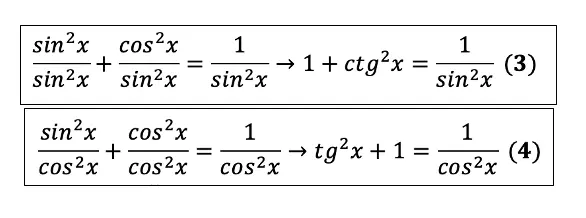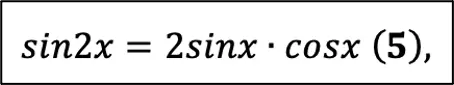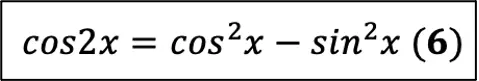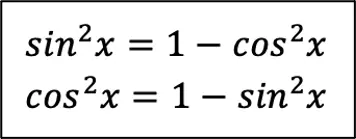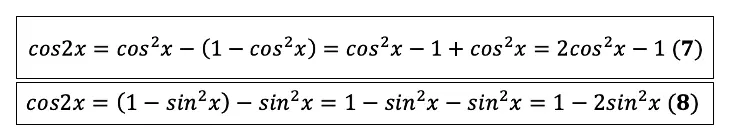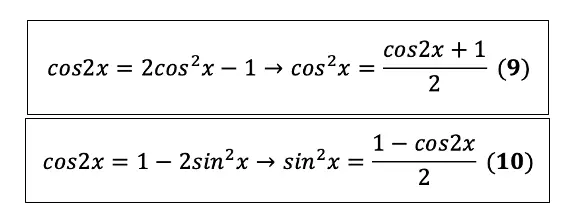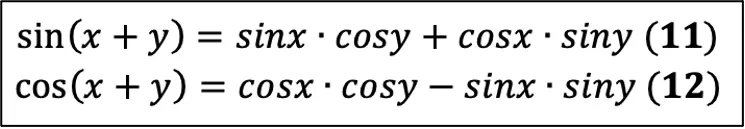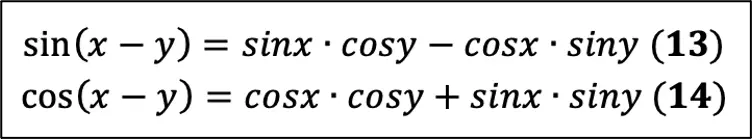Всего: 15 1–15
Добавить в вариант
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 28.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 386.
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 66.
В треугольнике АВС AB = BC = 10, AC = 12. Биссектриса угла ВАС пересекает сторону BC в точке D и описанную около треугольника окружность в точке P.
а) Докажите, что ∠ABP = ∠BDP.
б) Найдите отношение площадей треугольников ADB и BDP.
Источник: А. Ларин: Тренировочный вариант № 64.
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 376.
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 159.
а) Решите уравнение
б) Найдите все корни, принадлежащие промежутку
Источник: А. Ларин: Тренировочный вариант № 52.
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 106.
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 122.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 128.
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие промежутку
Источник: А. Ларин: Тренировочный вариант № 158.
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 400.
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 156.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 391.
Всего: 15 1–15
Примеры:
(sin^24α=)(frac{1-cos8α}{2})
(cos^2 15^°=)(frac{1+cos30^°}{2})(=)(frac{1+frac{sqrt{3}}{2}}{2})(=)(frac{2+sqrt{3}}{4})
(cosx=±)(sqrt{frac{1+cos2x}{2}})
(2 sin^2(x+frac{π}{4})=2cdotfrac{1-cos(2x+frac{π}{2})}{2}=1+sin2x)
Примеры решения задач из ЕГЭ на формулы половинного угла
Пример (ЕГЭ). Найдите значение выражения (sqrt{108} cos^2frac{23π}{12}-sqrt{27}).
Решение. (sqrt{108}cos^2frac{23π}{12}-sqrt{27}=sqrt{108})( frac{1+cosfrac{2cdot 23π}{12}}{2})(-sqrt{27}=sqrt{108})(frac{1+cosfrac{23π}{6}}{2})(-sqrt{27}=)…
(frac{23π}{6}=frac{24π-π}{6}=frac{24π}{6}-frac{π}{6}=4π-frac{π}{6}).

Попали в самое большое из трех стандартных значений косинуса: (frac{1}{2}), (frac{sqrt{2}}{2}), (frac{sqrt{3}}{2}). Значит (cosfrac{23π}{6}=frac{sqrt{3}}{2}).
…(=sqrt{108})(frac{1+frac{sqrt{3}}{2}}{2})(-sqrt{27}=sqrt{27cdot 4})(frac{1+frac{sqrt{3}}{2}}{2})(-sqrt{27}=2sqrt{27}cdot)(frac{1+frac{sqrt{3}}{2}}{2})(-sqrt{27}=sqrt{27}(1+frac{sqrt{3}}{2})-sqrt{27}=)
(=sqrt{27}+frac{sqrt{27cdot 3}}{2}-sqrt{27}=frac{sqrt{81}}{2}=frac{9}{2}=4,5).
Это решение не самое простое из всех возможных (наиболее легкое приведено в статье «формулы двойного угла»), но до него легче всего догадаться, если знаешь формулу половинного угла.
Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrt{32}-sqrt{128}sin^2frac{7π}{8}).
Решение:
|
(sqrt{32}-sqrt{128}sin^2frac{7π}{8}=) |
Сразу применим формулу половинного угла для (sin^2frac{7π}{8}). |
|
|
(=sqrt{32}-sqrt{128})(frac{1-cosfrac{7π}{4}}{2})(=) |
Вычислим косинус с помощью формулы приведения. Для этого сначала преобразуем (frac{7π}{4}): (frac{7π}{4}=frac{8π-π}{4}=frac{8π}{4}-frac{π}{4}=2π-frac{π}{4}) |
|
|
(=sqrt{32}-sqrt{128})(frac{1-cos(2π-frac{π}{4})}{2})(=) |
Теперь применим к косинусу формулу приведения:
|
|
|
(=sqrt{32}-sqrt{128})(frac{1-cosfrac{π}{4}}{2})(=) |
(cosfrac{π}{4}=frac{sqrt{2}}{2}). |
|
|
(=sqrt{32}-sqrt{128})(frac{1-frac{sqrt{2}}{2}}{2})(=) |
Домножим числитель и знаменатель дроби на (2), чтоб избавиться от «трехэтажности». |
|
|
(=sqrt{32}-sqrt{128})(frac{2-sqrt{2}}{4})(=) |
Игнорировать корни больше невозможно. Вынесем из (sqrt{128}) четверку, чтоб она сократилась со знаменателем: (sqrt{128}=sqrt{16cdot 8}=4sqrt{8}) |
|
|
(=sqrt{32}-4sqrt{8})(frac{2-sqrt{2}}{4})(=) |
Сократим четверки. |
|
|
(=sqrt{32}-sqrt{8}(2-sqrt{2})=) |
Раскроем скобки. |
|
|
(=sqrt{32}-2sqrt{8}+sqrt{16}=) |
Занесем (2) под корень и вычислим (sqrt{16}). |
|
|
(=sqrt{32}-sqrt{32}+4=4). |
Ответ: (4).
Смотрите также:
Формулы тригонометрии с примерами
Решение уравнений с помощью формул понижения степени
Метод понижения степени
Формулы понижения: $sin^2frac{a}{2}=frac{1-cos a}{2}$
$cos^2frac{a}{2}=frac{1+cos a}{2}$ $tg^2frac{a}{2}=frac{1-cos a}{1+cos a}$ $ctg^2frac{a}{2}=frac{1+cos a}{1-cos a}$
по другому, «формула половинного угла» : справа аргумент в 2 раза больше, чем слева, слева — половина правого.
Пример 1: Упростить: $sin^6left(x-frac{pi}{4}right)+cos^6left(frac{3pi}{4}+xright)$
- Решение: степень 6 синуса представим как куб от квадрата $left(sin^2left(x-frac{pi}{4}right)right)^3+left(cos^2left(frac{3pi}{4}+xright)right)^3$ , выражение
- готово для формул понижения степени . удвоив аргументы $left(frac{1-cos left(2left(x-frac{pi }{4}right)right)}{2}right)^3+left(frac{1+cos left(2left(frac{3pi }{4}+xright)right)}{2}right)^3$ ,
- упростим аргументы, выделим ПИ — добавки $left(frac{1-cosleft(2x-frac{pi}{2}right)}{2}right)^3+left(frac{1+cosleft(frac{3pi}{2}+2xright)}{2}right)^3$ , применим
- формулы приведения $cosleft(frac{3pi}{2}+aright)=sin a$ , $cosleft(x-frac{pi}{2}right)=sin a$ получим $left(frac{1-sinleft(2xright)}{2}right)^3+left(frac{1+sinleft(2xright)}{2}right)^3$ .
- вот и понизилась степень : вместо шестой получился куб. для получившейся суммы кубов применим
- формулы куба суммы/разности $left(apm bright)^3=a^3pm3a^2b+3ab^2pm b^3$ , получим громоздкое выражение
- $frac{1-3cdotsin2x+3cdotsin^22x-sin^32x}{8}+frac{1+3cdotsin2x+3cdotsin^22x+sin^32x}{8}$ , упростим его $frac{1+3cdotsin^22x}{4}$ , опять применим
- понижение квадрата синуса $frac{1+3cdotfrac{1-cos4x}{2}}{4}$ . окончательный Ответ: $frac{5-3cdotcos4x}{8}$ . Учетверение аргумента.
Пример 2: Решить уравнение $cos^23x+cos^24x+cos^25x+cos^26x=2$
- Решение: в уравнении несколько функций в квадратах. уберем квадраты за счет удвоения угла по формулам понижения:
- $frac{1+cos6x}{2}+frac{1+cos8x}{2}+frac{1+cos10x}{2}+frac{1+cos12x}{2}=2$ $Leftrightarrow$ теперь, квадратов нет. упростим, преобразуем
- $cos6x+cos8x+cos10x+cos12x=0$ $Leftrightarrow$ такое уравнение мы умеем решать …….
- разложим на множители, используя формулы превращения суммы в произведение. но пока переставим в более удобном порядке
- $cos6x+cos12x+cos8x+cos10x=0$ $Leftrightarrow$ $2cdotcosfrac{6x+12x}{2}cdotcosfrac{6x-12x}{2}+2cdotcosfrac{8x+10x}{2}cdotcosfrac{8x-10x}{2}=0$
- учтем формулу приведения $cosleft(-alpharight)=cosalpha$ $Leftrightarrow$ $2cdotcos9xcdotcos3x+2cdotcos9xcdotcos x=0$ , вынос за скобки
- $2cdotcos9xcdotleft(cos3x+cos xright)=0$ $Leftrightarrow$ еще раз превращение в произведение $2cdotcos9xcdotcos2xcdotcos x=0$
- » произведение = $0$ « $Rightarrow$ разбиваем на 3 уравнения $Leftrightarrow$ $cos9x=0$ $cos2x=0$ $cos x=0$
- далее, решение простейших. Ответы: $x_1=frac{pi}{18}+frac{picdot n}{9}$ $x_2=frac{pi}{4}+frac{picdot m}{2}$ $x_3=frac{pi}{2}+picdot k$
Пример 3: Решить уравнение $sin^6t+cos^6t=frac{5}{6}cdotleft(sin^4t+cos^4tright)$
- Решение: понизим высокие степени путем представления 6-ой степени как куб квадрата, формула $A^{2n}=left(A^2right)^n$ ,
- $left(sin^2tright)^3+left(cos^2tright)^3=frac{5}{6}cdotleft(left(sin^2tright)^2+left(cos^2tright)^2right)$ теперь, к квадратам применим формулы
- понижения степени $Leftrightarrow$ $left(frac{1-cos2t}{2}right)^3+left(frac{1+cos2t}{2}right)^3=frac{5}{6}cdotleft(left(frac{1-cos2t}{2}right)^2-left(frac{1+cos2t}{2}right)^2right)$ итоговые степени
- уменьшились, но аргументы удвоились $Leftrightarrow$ упростим $frac{left(1-cos2tright)^3}{8}+frac{left(1+cos2tright)^3}{8}=frac{5}{6}cdotleft(frac{left(1-cos2tright)^2}{4}+frac{left(1+cos2tright)^2}{4}right)$
- домножим обе части на $8$ $Leftrightarrow$ $left(1-cos2tright)^3+left(1+cos2tright)^3=frac{5}{3}cdotleft(left(1-cos2tright)^2+left(1+cos2tright)^2right)$ применим
- формулы сумм кубов $left(apm bright)^3=a^3pm3a^2b+3ab^2pm b^3$ , квадратов $left(apm bright)^2=a^2pm2ab+b^2$
- $1-3cdotcos2t+3cdotcos^22t-cos^32t+1+3cdotcos2t+3cdotcos^22t+cos^32t=$
- $=frac{5}{3}cdotleft(1-2cdotcos2t+cos^22t+1-2cdotcos2t+cos^22tright)$ соберем подобные слагаемые $Leftrightarrow$
- $2+6cdotcos^22t=frac{5}{3}cdotleft(2+2cdotcos^22tright)$ $Leftrightarrow$ сократим обе части на $2$ $1+3cdotcos^22t=frac{5}{3}cdotleft(1+cos^22tright)$,
- домножим на $3$ $Leftrightarrow$ $3+9cdotcos^22t=5+5cdotcos^22t$ , перенесём числа, выразим функцию $cos^22t=frac{1}{2}$ $Leftrightarrow$
- еще раз понизим степень $frac{1+cos4t}{2}=frac{1}{2}$ $Leftrightarrow$ выразим косинус $cos4t=0$ $Leftrightarrow$ $4t=frac{pi}{2}+picdot n$ $Leftrightarrow$ упростим,
- Ответы: $t=frac{pileft(1+4nright)}{8}$
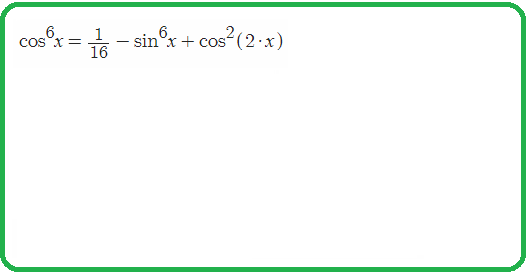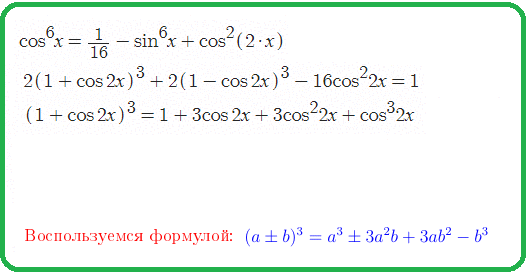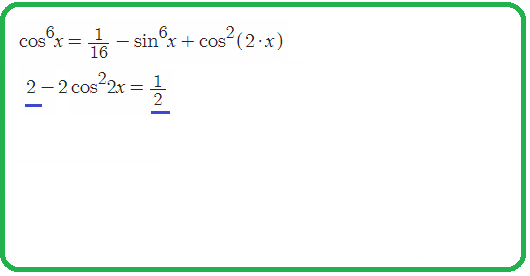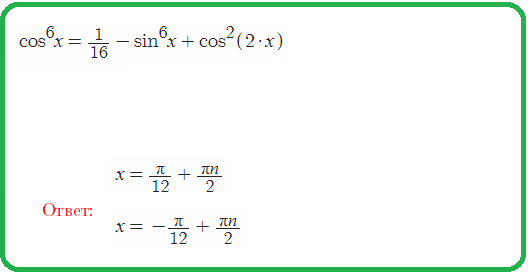
Классная Интерактивная Доска:
Упражнения:
Чуть больше 30% выпускников справляется с тригонометрией на ЕГЭ по математике. И неудивительно: для решения заданий из базы и профиля надо знать очень много формул, которые сложно освоить за 1-2 года. На самом деле, это миф! Чтобы решить задания по тригонометрии, нужно знать всего 5 формул — и просто уметь ими пользоваться.
Тригонометрия на ЕГЭ: основные проблемы темы
Чаще всего тригонометрию начинают изучать в 10 классе — но в некоторых школах оставляют до 11. В первом случае у учеников есть 2 года, чтобы освоить новую тему. А во втором, к сожалению, всего год. И это проблема. Дело в том, что в тригонометрии очень много формул, которые нужно знать, чтобы успешно решать задания. Если за 2 года их можно успеть выучить, то за год это будет сделать проблематично.
Ситуация осложняется ещё двумя факторами. Во-первых, в самой математике много формул, признаков, теорем и т.д. Во-вторых, кроме математики есть и другие экзамены, для которых нужно выучить большой объём информации.
Именно поэтому я всегда советую своим ученикам не учить формулы для тригонометрии на ЕГЭ, а выводить! Но об этом мы поговорим чуть позже, а сейчас давайте обсудим, почему тригонометрия так важна и где в ЕГЭ ее можно встретить.
Задания по тригонометрии в базе и профиле на ЕГЭ
Так как ЕГЭ по математике делится на базовый и профильный, а тригонометрия встречается в обоих, то давайте рассмотрим оба уровня экзамена.
Тригонометрия в базе
Что касается Базового уровня, то в нём всего 3 задания, в которых можно столкнуться с тригонометрией:
В № 7 в виде простейшего выражения
Как правило, для успешного решения таких заданий достаточно воспользоваться формулами из справочного материала.
В № 8 в виде формулы прикладной задачи
Стоит отметить, что в базовом ЕГЭ в прикладных задачах тригонометрия попадается редко, но нужно быть готовыми.
В № 15 как тригонометрия в геометрии
В справочном материале есть вся необходимая информация для успешного решения данного задания, а именно определение всех тригофункций в прямоугольном треугольнике.
Тригонометрия в профиле
Базовый уровень мы рассмотрели, теперь перейдём к профильному. Здесь уже больше вариантов, в которых можно встретиться с тригонометрией. Давайте посмотрим на Части 1 и 2.
В № 3 как тригонометрия в геометрии (Часть 1)
То же самое задание, как в базовом ЕГЭ, вот только в справочном материале уже нет необходимой информации.
В № 4 в виде выражения (Часть 1)
То же самое задание, как в базовом ЕГЭ.
В № 7 в виде формулы прикладной задачи (Часть 1)
То же самое задание, как в базовом ЕГЭ. Для успешного решения подойдут базовые навыки работы с тригонометрией.
В № 11 как часть функции (Часть 1)
Функцию нужно проанализировать для поиска наибольшего/наименьшего значения или точек максимума/минимума.
Если с Частью 1 профиля всё более-менее очевидно, то во второй части бывают сюрпризы, о которых ученики даже не подозревают. Да-да, тригонометрия на ЕГЭ умеет прятаться и в Части 2. Давайте посмотрим на эти задания.
В № 12 (Часть 2)
Тут сюрпризов нет. Это уравнение второй части, в котором ученики как раз ожидают увидеть тригонометрию, хотя она там бывает не всегда!
В № 13 — стереометрия (Часть 2)
Да, тригонометрия может встретиться здесь в виде теоремы синусов или теоремы косинусов, а ещё в виде формул в методе координат (для любителей решать этим методом).
В № 16 — планиметрия (Часть 2)
Здесь всё аналогично стереометрии: есть геометрические формулы, в которых прячется тригонометрия. Ведь, как я и сказала выше, в геометрии она тоже бывает!
5 формул тригонометрии: теория для ЕГЭ
А теперь предлагаю перейти к самому интересному — а именно к формулам. К сожалению, их действительно много. А ещё они похожи, и если их просто учить (или бездумно зубрить), то велик риск перепутать «+» с «–» или забыть какую-нибудь единичку.
Именно поэтому я рекомендую не учить формулы, а выводить. Это очень удобно тем более, что в профильном ЕГЭ по математике весь справочный материал состоит из 5-ти формул тригонометрии, из которых очень легко выводятся все остальные.
Но прежде чем я расскажу вам, как выводятся тригонометрические формулы, пообещайте, что обязательно отработаете все правила выведения! Для этого нужно будет регулярно выводить формулы по указанным ниже схемам.
Вот формулы, которые будут у вас в справочном материале:
Формула № 1 и как она пригодится в поиске котангенса и тангенса
Первая формула — основное тригонометрическое тождество (ОТТ):
Обычно ученики знают ее очень хорошо. Она связывает синус и косинус и помогает найти одну функцию через другую.
С этой формулой косвенно связана другая (ее нет в справочном материале), которая тоже легко дается школьникам:
Эту формулу очень легко запомнить, если знать, как можно расписать тангенс и котангенс через синус и косинус:
Эти 2 формулы связывают по отдельности синус с косинусом и тангенс с котангенсом. Но иногда требуется, чтобы были связаны все 4 функции, и здесь на помощь приходят следствия из ОТТ (как раз та самая формула № 1).
Чтобы вывести следствия нужно всего лишь разделить ОТТ на sin2 и cos2:
Теперь можно легко найти:
- котангенс, зная синус,
- или тангенс, зная косинус.
Формула № 2 и что из нее можно вывести
С тождествами разобрались, давайте перейдём к формулам двойного угла. Что касается синуса двойного угла (вторая формула в справочном материале):
Здесь всё просто, берёте и применяете формулу, если видите, что она нужна для задания.
Формула № 3 и что из нее можно вывести
А вот с косинусом двойного угла (третья формула в справочном материале) всё интереснее. Безусловно, косинус двойного угла:
в чистом виде встречается, и тогда вы делаете всё тоже самое, что с синусом. Но на самом деле есть ещё 2 формулы, которые очень просто вывести, используя ОТТ (формулу № 1). Для начала нужно выразить квадрат синуса и квадрат косинуса из ОТТ (Шаг 1):
А потом нужно подставить эти значения в формулу (6, или третья формула справочного материала) (Шаг 2):
Вот мы вывели ещё 2 формулы! А сейчас я покажу вам как практически ничего не делая получить ещё 2. Мы будем выводить формулы понижения степени из формул двойного угла. Смотрите, нужно всего лишь выразить одно из другого:
Формулы № 4 и 5 и что из них можно вывести
Давайте посмотрим на справочный материал, у нас там ещё целых 2 формулы, из которых мы получим конечно же ещё 2! Сейчас вообще ничего удивительного не будет. Вот формулы, которые уже даны:
Как вы заметили, они для суммы углов, а чтобы получить формулы для разности углов, нам нужно всего лишь поменять знаки в формуле на противоположные (разумеется, я говорю про «+» и «–»):
Вот так при помощи нехитрых преобразований из 5-ти формул справочного материала мы получили целых 14!
Все скриншоты взяты из открытого банка заданий ФИПИ или из демоверсий ЕГЭ по математике 2022.
Что еще пригодится вам для тригонометрии на ЕГЭ
Скажу по секрету, что это далеко не все формулы тригонометрии, которые существуют. Есть и другие:
- некоторые можно вывести из вышеуказанных,
- некоторые можно обобщить и вместо огромного количества формул использовать короткое правило.
Но мне кажется, что пока этого и так много!
Советую сначала хорошо отработать формулы, которые я перечислила в этой статье, и только потом браться за другие. Так вы не загрузите свою память и будете быстрее решать сложные задания по тригонометрии из ЕГЭ. Это, кстати, касается любой темы на экзамене по математике: а в ЕГЭ их очень много. Поэтому чтобы получить высокий балл, надо правильно и системно отработать их все.
Именно так я и строю подготовку к ЕГЭ по математике вместе со своими учениками: строгая система подготовки — ключ к успеху на экзамене. Сначала мы разбираем простые темы и задания и учимся решать их самыми удобными способами — почти на автомате. А после я добавляю более хитрые и сложные задания. В итоге ребята и имеют хорошую базу знаний по математике, и умеют решать самые разные типы задач. Так что если вы хотите по-настоящему знать математику, а не зазубривать формулы, приходите на мои уроки!
А чтобы отрабатывать выведение было не так скучно, держите моего котика, который любезно согласился позировать в позе котангенса:
Хотя, положа руку на сердце, я скажу тебе, что знание последней не так уж и обязательно (хотя желательно!), поскольку она легко выражается через тангенс.
Да и сам тангенс, по сути – тоже лишь тригонометрическое выражение, зависящее от синуса и косинуса.
Таким образом, у нас есть две основные тригонометрические функции – синус и косинус и две «второстепенные» – тангенс и котангенс.
Я не буду сейчас определять, что такое синус и косинус, ты и так это уже знаешь из предыдущих разделов. Я лишь скажу пару слов про важность этих понятий.
Итак, пара слов: первые зачатки тригонометрии возникли более 3 тысяч лет назад. Я думаю, что тебе очевидно, что тогда люди не занимались «формулами ради формул».
Так что тригонометрические функции имеют полезные практические свойства. Я не буду их перечислять. Если тебе интересно, ты всегда можешь найти море информации в интернете.
Если все, что я сказал выше, звучало для тебя древним эльфийским языком, то посмотри статью о тригонометрической окружности.
А сейчас я приведу тебе некоторые основные соотношения между тригонометрическими величинами, которые оказываются полезными при решении задач.
Уже получилось 7 формул! К сожалению, это еще далеко не предел. Совсем не предел.
Тем не менее последние 4 формулы есть ни что иное, как простое следствие первой. В самом деле, ты заметил, почему это так?
Формула 4 получается делением обеих частей формулы 1 на ( displaystyle co{{s}^{2}}alpha ) и применением формулы 2.
Формула 5 получается аналогично: разделим обе части формулы 1 на ( displaystyle si{{n}^{2}}alpha ) и вместо выражения ( displaystyle frac{co{{s}^{2}}alpha }{si{{n}^{2}}alpha }) запишем ( displaystyle ct{{g}^{2}}alpha ), исходя из определения 3.
Формулы 1 – 5 мы трактуем вполне однозначно. Чего нельзя сказать про формулы 6 и 7. В чем «фишка» формул 6 и 7?
Их особенность заключается в знаке ( displaystyle pm ), который стоит перед корнем.
Как это понимать? А понимать надо так: в некоторых случаях мы ставим плюс, а в некоторых – минус.
Теперь у тебя должен возникнуть вопрос: в каких-таких «некоторых случаях»? Туманность этой формулировки снимается следующим правилом:
Если в формуле
( displaystyle sin alpha =pm sqrt{1-co{{s}^{2}}alpha })
угол ( displaystyle alpha ) таков, что ( displaystyle text{sin} text{ }!!alpha!!text{ }<0), то ставим знак «минус», иначе – «плюс».
Если в формуле
( displaystyle cos alpha =pm sqrt{1-si{{n}^{2}}alpha })
угол ( displaystyle alpha ) таков, что ( displaystyle text{cos} text{ }!!alpha!!text{ }<0), то ставим знак «минус», иначе – «плюс».
Есть опять некий «запутанный» момент в правиле, не так ли? В чем осталось разобраться?
Осталось понять, как связан угол со знаком тригонометрической функции. Ответом на этот вопрос (если ты, конечно, забыл) служат следующие картинки:
Они подскажут тебе, какой нужно выбирать знак для той или иной функции, так что ты не допустишь досадной ошибки.
К тому же это избавит тебя от мучительных размышлений по поводу того «а зачем в этом примере нужен этот угол?!».
Решения:
1. Так как ( displaystyle cosalpha =pm sqrt{1-si{{n}^{2}}alpha }), то подставим сюда значение( displaystyle sinalpha =-frac{2sqrt{2}}{3}), тогда ( displaystyle cosalpha =pm sqrt{1-{{left( -frac{2sqrt{2}}{3} right)}^{2}}}=pm sqrt{1-frac{4cdot 2}{9}}=pm sqrt{1-frac{8}{9}}=)
( displaystyle=pm sqrt{frac{1}{9}}=pm frac{1}{3}.)
Теперь дело за малым: разобраться со знаком. Что нам для этого нужно? Знать, в какой четверти находится наш угол.
По условию задачи: ( displaystyle alpha in left( frac{3pi }{2};2pi right)). Смотри на картинку. Какая это четверть? Четвертая.
Каков знак косинуса в четвертой четверти? На картинке стоит знак «плюс», значит косинус в четвертой четверти положительный.
Тогда нам остается выбрать знак «плюс» перед ( displaystyle frac{1}{3}). ( displaystyle text{cos} text{ }!!alpha!!text{ }=frac{1}{3}), тогда ( displaystyle 3cosalpha =3cdot frac{1}{3}=1).
Ответ: ( displaystyle 1).
Ну вот видишь, ничего сложного. Абсолютно ничего. Нужно лишь запомнить знаки синуса, косинуса и тангенса (котангенса) по четвертям. Ну а как это делать автоматически описано в статье, посвященной тригонометрической окружности.
Давай разберем оставшиеся примеры.
2. Так как ( displaystyle sin alpha =pm sqrt{1-co{{s}^{2}}alpha }), то все, что нам нужно – это подставить ( displaystyle cosalpha =frac{2sqrt{6}}{5}) в нашу формулу. Что мы с тобой и сделаем:
( displaystyle sinalpha =pm sqrt{1-{{left( frac{2sqrt{6}}{5} right)}^{2}}}=pm sqrt{1-left( frac{4cdot 6}{25} right)}=pm sqrt{frac{1}{25}}=pm frac{1}{5}).
Опять нужно определиться со знаком. Смотрим на рисунок. Четверть – снова четвертая. Знак синуса четвертой четверти – отрицательный. Ставим знак «минус». ( displaystyle sinalpha =-frac{1}{5}), тогда ( displaystyle 5sinalpha =-5cdot frac{1}{5}=-1).
Ответ: ( displaystyle -1).
3. Ничего нового. Скорее для закрепления. Снова подставляем в формулу ( displaystyle cos alpha =pm sqrt{1-si{{n}^{2}}alpha }) значение ( displaystyle sinalpha =frac{2sqrt{6}}{5}):
( displaystyle cosalpha =pm sqrt{1-{{left( frac{2sqrt{6}}{5} right)}^{2}}}=pm sqrt{1-left( frac{4cdot 6}{25} right)}=pm sqrt{frac{1}{25}}=pm frac{1}{5}).
Смотрим на знак косинуса при ( displaystyle alpha in left( frac{pi }{2};pi right)). Какая это четверть? Вторая. Косинус второй четверти отрицательный. Тогда выбираем знак «минус».
Ответ: ( displaystyle -0,2).
4. Здесь перед нами стоит задачка чуть сложнее. Однако, не стоит огорчаться. Давай вспомним, что такое тангенс. Это ведь отношение синуса к косинусу. Синус нам уже дан.
Давай вначале найдем косинус. Как это сделать, ты уже знаешь. ( displaystyle cosalpha =pm sqrt{1-{{left( -frac{5}{sqrt{26}} right)}^{2}}}=pm sqrt{1-frac{25}{26}}=pm sqrt{frac{1}{26}}=pm frac{1}{sqrt{26}}).
Так как ( displaystyle alpha in left( pi ;frac{3pi }{2} right)) (это угол в третьей четверти, а косинус в третьей четверти имеет знак «минус»), то ( displaystyle cosalpha =-frac{1}{sqrt{26}}).
Теперь все, что нам осталось, это воспользоваться определением тангенса:
( displaystyle tgalpha =frac{sinalpha }{cosalpha }=frac{-frac{5}{sqrt{26}}}{-frac{1}{sqrt{26}}}=5.)
Ответ: ( displaystyle 5).
Уф, выдохнули! Ну вот мы с тобой решили некоторые (довольно типичные и распространенные) примеры. Ты спросишь: «И что, это все?». Я отвечу, что, увы нет. Это далеко не все.
Далее нам потребуются более сложные формулы тригонометрии.
Разбор 3 примеров
1. Доказать тождество: ( displaystyle frac{3-4cos2alpha +cos4alpha }{3+4cos2alpha +cos4alpha }=t{{g}^{4}}alpha )
С виду тождество угрожающе! Но разберёмся по порядку. Формулы понижения степени, конечно, если их прочитать задом наперёд повышают степень!
И вообще, приглядись внимательно: первые две формулы есть ничто иное, как косинус двойного угла, записанный в несколько странной форме!
Вот и распишем по правилам:
( displaystyle begin{array}{l}frac{3-4cos2alpha +cos4alpha }{3+4cos2alpha +cos4alpha }=frac{3-4cos2alpha +left( 2{cos^{2}}2alpha -1 right)}{3+4cos2alpha +left( 2{cos^{2}}2alpha -1 right)}=\=frac{2-4cos2alpha +2{cos^{2}}2alpha }{2+4cos2alpha +2{cos^{2}}2alpha }=frac{1-2cos2alpha +{cos^{2}}2alpha }{1+2cos2alpha +{cos^{2}}2alpha }end{array})
Тебе ничего по форме не напоминают числитель и знаменатель дроби? Приглядись внимательно, здесь «зарыта» хорошо известная тебе формула. Увидел её? Это же квадрат разности и квадрат суммы! (Подробнее об этом читай в статье о формулах сокращенного умножения)
( displaystyle frac{1-2cos2alpha +{cos^{2}}2alpha }{1+2cos2alpha +{cos^{2}}2alpha }=frac{{{left( 1-cos2alpha right)}^{2}}}{{{left( 1+cos2alpha right)}^{2}}}={{left( frac{1-cos2alpha }{1+cos2alpha } right)}^{2}})
А выражение в скобках есть ничто иное, как ( displaystyle t{{g}^{2}}alpha ), окончательно получим:
( displaystyle {{left( frac{1-cos2alpha }{1+cos2alpha } right)}^{2}}={{left( t{{g}^{2}}alpha right)}^{2}}=t{{g}^{4}}alpha )
Тождество доказано!
Следующий пример очень схож с предыдущим, постарайся решить его самостоятельно.
2. Доказать тождество: ( displaystyle frac{1+sin2alpha +cos2alpha }{1+sin2alpha -cos2alpha }=ctgalpha )
Решение (хотя может и отличаться от твоего):
Опять «повысим степень» у косинуса: ( displaystyle cos2alpha =2{cos^{2}}alpha -1)
( displaystyle frac{1+sin2alpha +cos2alpha }{1+sin2alpha -cos2alpha }=frac{1+sin2alpha +2{cos^{2}}alpha -1}{1+sin2alpha -2{cos^{2}}alpha +1}=frac{sin2alpha +2{cos^{2}}alpha }{2+sin2alpha -2{cos^{2}}alpha })
Надо сокращать дальше! Что делать? Ясно, что надо избавляться от двойных углов у синуса. Действуем по формуле синуса двойного угла и сокращаем двойки:
( displaystyle frac{sin2alpha +2{cos^{2}}alpha }{2+sin2alpha -2{cos^{2}}alpha }=frac{2sin{alpha} cos{alpha} +2{cos^{2}}alpha }{2+2sin{alpha} cos{alpha}-2{cos^{2}}alpha }=frac{sinalpha cosalpha +{cos^{2}}alpha }{1+sinalpha cos{alpha}-{cos^{2}}alpha })
Числитель раскладывается на множители. Знаменатель –пока нет. До тех пор, пока мы не применим основное тригонометрическое тождество:
( displaystyle 1-{cos^{2}}alpha ={sin^{2}}alpha )
( displaystyle frac{sinalpha cosalpha +{cos^{2}}alpha }{1+sinalpha cosalpha -{cos^{2}}alpha }=frac{sinalpha cosalpha +{cos^{2}}alpha }{{sin^{2}}alpha +sinalpha cosalpha }=frac{cosalpha left( sinalpha +cosalpha right)}{sinalpha left( sinalpha +cosalpha right)}=ctgalpha )
Вот ещё один пример, но не такой простой.
3. Доказать, что если ( displaystyle 0<alpha <frac{pi }{2}), то ( displaystyle sqrt{1+sinalpha }-sqrt{1-sinalpha }=2sinfrac{alpha }{2})
Зачем нам дан угол? Наверное, чтобы оценить выражения: синус ( displaystyle alpha )будет положительным, ( displaystyle sinfrac{alpha }{2}>0,~1+sinalpha >1,~0<1-sinalpha <1)
Тогда и левая, и правая части тождества больше нуля. Это даёт мне право без задней мысли возвести их в квадрат:
( displaystyle {{left( sqrt{1+sinalpha }-sqrt{1-sinalpha } right)}^{2}}=4{sin^{2}}frac{alpha }{2}) – вот такое тождество нам нужно теперь доказать.
Раскроем скобки в левой части по формуле квадрата разности!
( displaystyle begin{array}{l}{{left( sqrt{1+sin alpha }-sqrt{1-sin alpha } right)}^{2}}=1+sin alpha -2sqrt{1+sin alpha }cdot sqrt{1-sin alpha }+1-\-sin alpha =2-2sqrt{1+sin alpha }cdot sqrt{1-sin alpha }=2left( 1-sqrt{1+sin alpha }cdot sqrt{1-sin alpha } right)=\2left( 1-sqrt{1+{{sin }^{2}}alpha } right)=2left( 1-sqrt{{cos^{2}}}alpha right)end{array})
Я не сомневаюсь в твоей грамотности и поэтому даже не упоминаю про использованные мною формулы в выкладках.
Теперь надо бы убрать корень из косинуса. Но мы знаем, что просто так это делать нельзя, ибо ( displaystyle sqrt{{{a}^{2}}}=left| a right|).
В то же время вспоминаем про четверть: наш угол лежит в первой четверти, тогда косинус имеет знак «плюс» и мы просто убираем корень:
( displaystyle 2left( 1-sqrt{{cos^{2}}}alpha right)=2left( 1-cosalpha right))
Тогда нам надо доказать, что
( displaystyle 2left( 1-cosalpha right)=4{sin^{2}}frac{alpha }{2})
( displaystyle left( 1-cosalpha right)=2{sin^{2}}frac{alpha }{2})
Справа применим формулу понижения степени:
( displaystyle {sin^{2}}frac{alpha }{2}=frac{1-cosalpha }{2}), тогда ( displaystyle 2{sin^{2}}frac{alpha }{2}=1-cosalpha )
Тождество доказано!
Конечно, можно привести ещё массу примеров, где применяются формулы понижения степени, ты их и сам без труда отыщешь.
Теперь вторая (и заключительная в этом обзоре) группа формул – формулы преобразования произведения в сумму и суммы в произведение.
Решение 5 примеров
1. Доказать тождество: ( displaystyle frac{sinalpha +sin3alpha }{cosalpha +cos3alpha }=tg2alpha )
Давай не будем долго думать, а, как говорится, пойдём в лобовую атаку: в числителе и знаменателе перейдём от суммы к произведению:
( displaystyle begin{array}{l}~frac{sinalpha+sin3alpha}{cosalpha+cos3alpha}=frac{2sinfrac{alpha+3alpha}{2}cosfrac{alpha-3alpha}{2}}{2cosfrac{alpha+3alpha}{2}cosfrac{alpha-3alpha}{2}}=frac{2cdot sin2alphacdot cosleft( -alpha right)}{2cdot cos2alphacdot cosleft( -alpha right)}=\=frac{sin2alpha}{cos2alpha}=tg2alphaend{array})
И минуты не прошло, а пример уже решён!
Теперь попробуй сам.
2. Доказать тождество: ( displaystyle frac{sin2alpha +sin4alpha }{cos2alpha -cos4alpha }=ctgalpha )
Решение – опять лобовая атака:
( displaystyle begin{array}{l}frac{sin2alpha+sin4alpha}{cos2alpha-cos4alpha}=frac{2sinfrac{2alpha+4alpha}{2}cosfrac{2alpha-4alpha}{2}}{-2sinfrac{2alpha+4alpha}{2}sinfrac{2alpha-4alpha}{2}}=frac{2sin3alphacdot cosleft( -alpha right)}{-2sin3alphacdot sinleft( -alpha right)}=frac{cosleft( -alpha right)}{-sinleft( -alpha right)}end{array})
Так как синус – функция нечётная, а косинус – чётная, то:
( displaystyle frac{cosleft( -alpha right)}{-sinleft( -alpha right)}=frac{cosalpha }{-left( -sinalpha right)}=frac{cosalpha }{sinalpha }=ctgalpha )
Этот пример чуть похитрее, будь внимателен!
3. Доказать тождество: ( displaystyle frac{sin2alpha +sin5alpha -sin3alpha }{cosalpha +1-2{sin^{2}}2alpha }=2sinalpha )
Я не хочу трогать синус двойного угла. Уж больно он удобно раскладывается на множители, чего не скажешь о синусе тройного и тем более пятикратного угла.
Поэтому я сверну в произведение последние 2 слагаемых в числителе:
( displaystyle begin{array}{l}frac{sin2alpha +sin5alpha -sin3alpha }{cosalpha +1-2{sin^{2}}2alpha }=frac{sin2alpha +2sinfrac{5alpha -3alpha }{2}cosfrac{5alpha +3alpha }{2}}{cosalpha +1-2{sin^{2}}2alpha }=\=frac{2sinalpha cosalpha +2sinalpha cos4alpha }{cosalpha +1-2{sin^{2}}2alpha }=frac{2sinalpha left( cosalpha +cos4alpha right)}{cosalpha +1-2{sin^{2}}2alpha }end{array})
Конечно, теперь можно было бы и свернуть числитель ещё раз, но я пойду иным путём. В знаменателе у меня тоже спрятана формула, вот она:
( displaystyle 1-2{sin^{2}}2alpha ).
Что это за формула? Это косинус двойного угла!
( displaystyle 1-2{sin^{2}}2alpha =cosleft( 2cdot 2alpha right)=cos4alpha )
( displaystyle frac{2sinalpha left( cosalpha +cos4alpha right)}{cosalpha +1-2{sin^{2}}2alpha }=frac{2sinalpha left( cosalpha +cos4alpha right)}{cosalpha +cos4alpha }=2sinalpha )
Тождество доказано!
Теперь попробуй решить вот этот пример для закрепления пройденного материала.
4. Доказать тождество: ( displaystyle {cos^{4}}alpha -{sin^{4}}alpha +sin2alpha =sqrt{2}cosleft( 2alpha -frac{pi }{4} right))
Проверяем!
( displaystyle begin{array}{l}{cos^{4}}alpha -{sin^{4}}alpha +sin2alpha =left( {cos^{2}}alpha -{sin^{2}}alpha right)left( {cos^{2}}alpha +{sin^{2}}alpha right)+sin2alpha =\=cos2alpha +sin2alpha end{array})
C другой стороны:
( displaystyle begin{array}{l}sqrt{2}cos left( 2alpha-frac{pi }{4} right)=sqrt{2}left( cos{2alpha}cos{frac{pi }{4}}+sin{2alpha}sin{frac{pi }{4}} right)=\=sqrt{2}left( frac{sqrt{2}}{2}cos2alpha+frac{sqrt{2}}{2}sin2alpha right)=sqrt{2}cdot frac{sqrt{2}}{2}left( cos2alpha+sin2alpha right)=\=cos2alpha+sin2alphaend{array})
Тождество доказано!
На этом примере я буду закругляться потихоньку.
Сразу оговорюсь: не переживай и не волнуйся, если у тебя что-то сразу не выходит. Тригонометрия – сложная и очень обширная тема. Здесь все зависит не только от знания формул, но и от мастерства и смекалки. На их выработку тебе понадобится время и усердие.
Более того, скажу тебе вот что: изначально я хотел вставить другой пример в качестве заключительного. Однако на его решение мне понадобилось около 20 минут, причём я использовал ещё более сложную методику его решения. Так что не только ты сталкиваешься с трудностями при решении примеров, трудности бывают у всех!
Все-таки я приведу здесь этот трудный пример, вдруг да и получится у тебя решить его, может, я что-то упустил. Вот он:
5. Упростить: ( displaystyle frac{1+sinalpha -cos2alpha -sin3alpha }{2{sin^{2}}alpha +sinalpha -1})
А вот какой у меня получился в итоге ответ: ( displaystyle 2sinalpha.)
Дерзай!
В следующей части статьи я рассмотрю его решение, но прибегну к ещё более изощрённой технике нежели та, что рассматривалась здесь! Удачи!
Формулы понижения 3-й степени
- ( displaystyle si{{n}^{3}}alpha =frac{3sinalpha -sin3alpha }{4})
- ( displaystyle co{{s}^{3}}a=frac{3cosa+cos3a}{4})
Из данных формул можно вывести формулы тройного угла.
Формулы тройного угла
- ( displaystyle sin3alpha =3sinalpha -4si{{n}^{3}}alpha )
- ( displaystyle cos3a=4co{{s}^{3}}a-3cosa)
- ( displaystyle tg3alpha =frac{3tgalpha -t{{g}^{3}}alpha }{1-3t{{g}^{2}}alpha })
- ( displaystyle ctg3alpha =frac{3ctgalpha -ct{{g}^{3}}alpha }{1-3ct{{g}^{2}}alpha })
Ты мне можешь задать резонный вопрос: как часто эти формулы используются? Я отвечу: постарайся избегать прибегать к ним. Они нужны на тот случай, когда ничего другого уже не можешь придумать.
В частности, они могут быть полезными при решении сложных уравнений, которые встречаются во вступительных экзаменах на математические специальности.
Однако уравнениям у нас будет посвящена отдельная статья, так что здесь я рассмотрю случаи, когда данные формулы позволяют упрощать тригонометрические выражения.
Пример 1
Упростить: ( displaystyle A=frac{1}{3}co{{s}^{3}}alpha cdot sin3alpha +frac{1}{3}si{{n}^{3}}alpha cdot cos3alpha )
Решение:
Подставим вместо ( displaystyle sin3alpha ) и ( displaystyle cos3alpha ) их представления согласно формулам тройного угла, тогда:
( displaystyle begin{array}{l}A=frac{1}{3}co{{s}^{3}}alpha left( 3sinalpha -4si{{n}^{3}}alpha right)+frac{1}{3}si{{n}^{3}}alpha left( 4co{{s}^{3}}alpha -3cosalpha right)=\=co{{s}^{3}}alpha cdot sinalpha -frac{4}{3}co{{s}^{3}}alpha cdot si{{n}^{3}}alpha +frac{4}{3}co{{s}^{3}}alpha cdot si{{n}^{3}}alpha -si{{n}^{3}}alpha cdot cosalpha =\=co{{s}^{3}}alpha cdot sinalpha -si{{n}^{3}}alpha cdot cosalpha end{array})
Теперь вынесем в оставшемся выражении общий множитель за скобки:
( displaystyle co{{s}^{3}}alpha cdot sinalpha -si{{n}^{3}}alpha cdot cosalpha =sinalpha cdot cosalpha left( co{{s}^{2}}alpha -si{{n}^{2}}alpha right))
По формулам двойного угла: ( displaystyle sinalpha cdot cosalpha =frac{1}{2}sin2alpha ), ( displaystyle co{{s}^{2}}alpha -si{{n}^{2}}alpha =cos2alpha ):
( displaystyle sinalpha cdot cosalpha left( co{{s}^{2}}alpha -si{{n}^{2}}alpha right)=frac{1}{2}sin2alpha cdot cos2alpha )
Ну а здесь снова спрятан синус двойного угла:
( displaystyle frac{1}{2}sin2alpha cdot cos2alpha =frac{1}{4}sin4alpha )
Ответ: ( displaystyle A=frac{1}{4}sin4alpha )
Следующий пример попробуй решить самостоятельно. Не уверен, что в нем обязательно использовать формулу тройного угла, но можно сделать и с ее помощью.
Пример 2
Упростить: ( displaystyle frac{1+sinalpha -cos^2{alpha}-cos2alpha -sin3alpha }{2si{{n}^{2}}alpha +sinalpha -1})
Решение:
Моя цель – свести числитель дроби к выражению, зависящему только от синусов одиночного угла. Для этого я преобразую
( displaystyle cos^2 {alpha} =1-si{{n}^{2}}alpha )
( displaystyle cos2alpha =1-2si{{n}^{2}}alpha )
( displaystyle sin3alpha =3sinalpha -4si{{n}^{3}}alpha )
Имеем:
( displaystyle begin{array}{l}frac{1+sinalpha -cos2alpha -sin3alpha }{2si{{n}^{2}}alpha +sinalpha -1}=frac{1+sinalpha -left( 1-si{{n}^{2}}alpha right) -left( 1-2si{{n}^{2}}alpha right)-left( 3sinalpha -4si{{n}^{3}}alpha right)}{2si{{n}^{2}}alpha +sinalpha -1}=\=frac{4si{{n}^{3}}alpha +3si{{n}^{2}}alpha -2sinalpha -1}{2si{{n}^{2}}alpha +sinalpha -1}end{array})
Казалось бы, стало еще хуже. Но это так кажется. Давай для удобства вычислений заменим ( displaystyle sinalpha =t), тогда мне надо упростить дробь
( displaystyle frac{4{{t}^{3}}+3{{t}^{2}}-2t-1}{2{{t}^{2}}+t-1})
Нижнее выражение разложим на множители:
( displaystyle 2{{t}^{2}}+t-1=left( t+1 right)left( 2t-1 right))
С верхним фокус сложнее. Мы не умеем с тобой решать кубические уравнения. Но мы хорошо играем в «угадайку».
Угадай-ка один корень уравнения ( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1=0). Угадал? Я угадал ( displaystyle -1).
Тогда по теореме Безу (которую ты, быть может, знаешь, а если не знаешь, то без проблем отыщешь сам) выражение ( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1) делится без остатка на ( displaystyle t+1)
Разделим столбиком ( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1) на ( displaystyle t+1). Я получу:
( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1=left( t+1 right)left( 4{{t}^{2}}-t-1 right))
В свою очередь ( displaystyle 4{{t}^{2}}-t-1=4left( t-frac{1}{2} right)left( t+frac{1}{4} right))
Окончательно получим:
( displaystyle begin{array}{l}frac{4{{t}^{3}}+3{{t}^{2}}-2t-1}{2{{t}^{2}}+t-1}=frac{4left( t+1 right)left( t-frac{1}{2} right)left( t+frac{1}{4} right)}{left( t+1 right)left( 2t-1 right)}=frac{left( t+1 right)left( 2t-1 right)left( 2t+0,5 right)}{left( t+1 right)left( 2t-1 right)}=\=2t+0,5end{array})
Тогда исходное выражение можно упростить до: ( displaystyle 2sinx+0,5)
В завершение я приведу тебе пример одного уравнения, которое было предложено на психологический (???!!!) факультет одного из ВУЗов в 1990 году. Такие задачи называются задачи-гробы (никакая смекалка без знания конкретной формулы не позволит их решить):
Решить уравнение: ( displaystyle sqrt{3}co{{s}^{3}}x-3co{{s}^{2}}x-3sqrt{3}cosx+1=0)
Не сделав вот такую странную замену: ( displaystyle cosx=tgalpha ) решить его очень сложно. А с такой заменой у нас получится вот что:
( displaystyle sqrt{3}t{{g}^{3}}alpha -3t{{g}^{2}}alpha -3sqrt{3}tgalpha +1=0)
( displaystyle sqrt{3}t{{g}^{3}}alpha -3sqrt{3}tgalpha =3t{{g}^{2}}alpha -1)
( displaystyle sqrt{3}(t{{g}^{3}}alpha -3tgalpha )=3t{{g}^{2}}alpha -1)
( displaystyle -sqrt{3}left( 3tgalpha -t{{g}^{3}}alpha right)=-left( 1-3t{{g}^{2}}alpha right))
( displaystyle frac{left( 3tgalpha -t{{g}^{3}}alpha right)}{left( 1-3t{{g}^{2}}alpha right)}=frac{1}{sqrt{3}})
А вот ради чего весь этот сыр-бор: ( displaystyle frac{left( 3tgalpha -t{{g}^{3}}alpha right)}{left( 1-3t{{g}^{2}}alpha right)}=tg3alpha )
( displaystyle tg3alpha =frac{1}{sqrt{3}})
Это уравнение уже несказанно легче решается. Скоро мы вместе в этом убедимся. Но тут проблема в обратной замене… Тем не менее, эта задача почти нерешаема без знания формулы тангенса тройного угла. Вот так вот.
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 9. Тригонометрическая окружность, табличные значения
На этом уроке мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии. М
ы увидим, что она – основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.
Мы поймем, как “работает” окружность – а значит, поймём тригонометрию в целом.
ЕГЭ 13б. Тригонометрическая окружность
Тригонометрическая окружность – это очень простой и эффективный инструмент для решения любой тригонометрической задачи. На этом уроке вы узнаете как пользоваться тригонометрической окружностью для решения пункта “б” из задачи №13 профильного ЕГЭ.
Пункт “б” задачи №13 ЕГЭ 2020 В 2020 году на ЕГЭ в пункте “б” необходимо было указать корни тригонометрического уравнения принадлежащие отрезку.
Вообще-то решать пункт “б” можно двумя способами: – отметить корни уравнения на единичной окружности (способ разобранный в этом видео); – через двойное неравенство.
И вы должны знать, что второй способ чуть дольше, чем первый, но зато вы сможете проще описать все ваши рассуждения и вам будет сложнее ошибиться.
И еще один плюс второго способа – его проще оформить, так, чтобы к вам не придрались на ЕГЭ.
Мы считаем второй способ (через двойное неравенство) более предпочтительным на ЕГЭ по математике, но теме не менее для глубокого понимания темы (что может выручить на ЕГЭ) необходимо разобраться и с первым способом