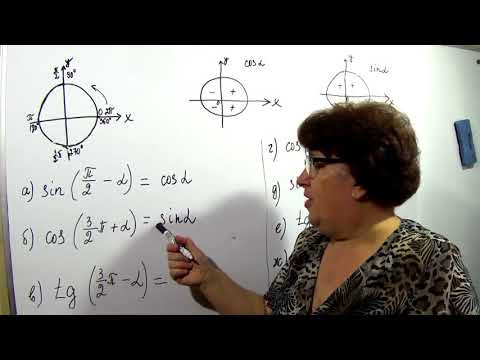Формулы приведения егэ видео - Помощь в подготовке к экзаменам и поступлению

Формулы приведения

Применять формулы приведения — легко! Их не надо зубрить наизусть. И не надо тащить на экзамен шпаргалки, рискуя спалиться. Надо всего лишь запомнить два правила, о которых вы узнаете, посмотрев этот ролик. Это так просто, что даже лошадка поймет! Посмотри и передай друзьям.

Часто в задачах встречаются выражения вида $displaystyle cos (x+frac{3 pi }{2}),$ $displaystyle sin(frac{ pi }{2}-x),$ $displaystyle tg(x+frac{ pi }{2}),$ а также или — то есть такие, где к аргументу прибавляется нечетное число, умноженное на $displaystyle frac{ pi }{2},$ или целое число, умноженное на pi . Они упрощаются с помощью формул приведения.

Запомните: формулы приведения, от слова «привести». К привидениям, то есть к призракам и прочим глюкам, эти формулы отношения не имеют : -)

Эти формулы называются так потому, что с их помощью можно привести выражения к более простым.

Например,

$displaystyle cos(x+frac{3 pi }{2})=sin x,$

$displaystyle sin(frac{ pi }{2}-x)=cos x,$

$displaystyle tg(x+frac{ pi }{2})=-ctg x,$

Зубрить наизусть формулы приведения не нужно. Достаточно знать правило, состоящее из двух пунктов.

1) Если в тригонометрической формуле к аргументу прибавляется (или вычитается из него) $displaystyle frac{ pi }{2},;frac{3 pi }{2},;frac{7 pi }{2}$ — в общем, угол, лежащий на вертикальной оси, — функция меняется на кофункцию. Синус меняется на косинус, косинус на синус, тангенс на котангенс и наоборот.

Если же мы прибавляем или вычитаем — в общем, то, что лежит на горизонтальной оси, — функция на кофункцию не меняется.

Это легко запомнить. Если прибавляемый угол лежит на вертикальной оси — вертикально киваем головой, говорим: «Да, да, меняется функция на кофункцию». Если прибавляемый угол лежит на горизонтальной оси — горизонтально мотаем головой, говорим: «Нет, нет, не меняется функция на кофункцию».

Это первая часть правила. Теперь вторая.

2) Знак получившегося выражения такой же, каким будет знак тригонометрической функции в левой его части, при условии, что аргумент мы берем из первой четверти.

Упростим, например, выражение $displaystyle {cos left(x+frac{ pi }{2}right)}.$ Функция меняется на кофункцию — и в результате получится синус. Взяв x из первой четверти и прибавив к нему $displaystyle frac{ pi }{2},$ попадем во вторую четверть. Во второй четверти косинус отрицателен. Значит, получится -sin x.

Посмотрим, как формулы приведения применяются в задачах ЕГЭ по математике.

1. Найдите значение выражения: $displaystyle frac{11{cos 28^circ }}{{sin 62^circ }}.$

$displaystyle frac{11{cos 28^circ }}{{sin 62^circ }}=displaystyle frac{11{cos left(90^circ -62^circ right)}}{{sin 62^circ }}=displaystyle frac{11{sin 62^circ }}{{sin 62^circ }}=11.$

Ответ: 11.

2. Вычислите:

Ответ: 4.

3. Вычислите: $displaystyle frac{12}{{sin left(-displaystyle frac{25 pi }{4}right){cos left(displaystyle frac{23 pi }{4}right)}}}.$

$displaystyle frac{12}{{sin left(-displaystyle frac{25 pi }{4}right){cos left(displaystyle frac{23 pi }{4}right)}}}=displaystyle frac{12}{-{sin left(6 pi +displaystyle frac{ pi }{4}right)cdot {cos left(6 pi -displaystyle frac{ pi }{4}right)}}}=-displaystyle frac{12}{{sin displaystyle frac{ pi }{4}cdot {cos displaystyle frac{ pi }{4}}}}=$

$=-displaystyle frac{12}{displaystyle frac{sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}}=-24.$

Мы упростили выражения в скобках.

$displaystyle frac{23 pi }{4}=displaystyle frac{24 pi }{4}-displaystyle frac{ pi }{4}=6 pi -displaystyle frac{ pi }{4}.$

$displaystyle frac{25 pi }{4}=6 pi +displaystyle frac{ pi }{4}.$

Ответ: — 24.

4. Найдите значение выражения: $displaystyle frac{2{sin 152^circ }}{{cos 76^circ cdot {cos 14^circ }}}.$

$displaystyle frac{2{sin 152^circ }}{{cos 76^circ cdot {cos 14^circ }}}=displaystyle frac{4{sin 76^circ cdot {cos 76^circ }}}{{cos 76^circ cdot {cos 14^circ }}}=displaystyle frac{4{sin 76^circ }}{{cos 14^circ }}=displaystyle frac{4{sin left(90^circ -14^circ right)}}{{cos 14^circ }}=$

$=displaystyle frac{4{cos 14^circ }}{{cos 14^circ }}=4 .$

Ответ: 4.

5. Упростите выражение: $displaystyle frac{3cos left( pi - beta right)+{sin left(displaystyle frac{ pi }{2}+ beta right)}}{{cos left( beta +3 pi right)}}.$

$displaystyle frac{3{cos left( pi - beta right)+{sin left(displaystyle frac{ pi }{2}+ beta right)}}}{{cos left( beta +3 pi right)}}=displaystyle frac{-3{cos beta +{cos beta }}}{-{cos beta }}=displaystyle frac{-2{cos beta }}{-{cos beta }}=2 .$

Ответ: 2.

6. Найдите значение выражения: $displaystyle frac{3{cos left(-3pi -beta right) }+3{sin left(displaystyle frac{pi }{2}+beta right) }}{5{cos left(beta +3pi right) }}.$

Решение:

Используя формулы приведения, получим

$displaystyle frac{3{cos left(-3pi -beta right) }+3{sin left(displaystyle frac{pi }{2}+beta right) }}{5{cos left(beta +3pi right) }}=displaystyle frac{-3{cos beta +{cos beta } }}{-5{cos beta }}=$

$=displaystyle frac{-2{cos beta }}{-5{cos beta }}=0,4.$

Ответ: 0,4.

7. Найдите значение выражения: cos $left(-225{}^circ right).$

Решение:

cos cos $left(180{}^circ +45{}^circ right)=-12sqrt{2}cdot$ cos $45{}^circ =-12sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=-12.$

Снова формула приведения.

Ответ: -12.

8. Найдите значение выражения: $displaystyle frac{35{cos 11{}^circ }}{{sin 79{}^circ }}+7.$

Решение:

$displaystyle frac{35{cos 11{}^circ }}{{sin 79{}^circ }}+7=displaystyle frac{35{cos 11{}^circ }}{{sin left(90{}^circ -11{}^circ right) }}+7=$

$=displaystyle frac{35{cos 11{}^circ }}{{cos 11{}^circ }}+7=35+7=42.$

Мы применили одну из формул приведения.

Ответ: 42.

9. Найдите значение выражения: $displaystyle frac{38}{{{sin}^2 51{}^circ }+3+{{sin}^2 141{}^circ }}.$

Решение:

Воспользуемся формулами приведения:

$displaystyle frac{38}{{{sin}^2 51{}^circ +3+{{sin}^2 141{}^circ } }}=displaystyle frac{38}{{{sin}^2 51{}^circ +4+{{sin}^2 left(90{}^circ +51{}^circ right) } }}=$

$=displaystyle frac{38}{{{cos}^2 51+3+{{sin}^2 51 } }}=displaystyle frac{38}{4}=9,5.$

Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.

Ответ: 9,5.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Формулы приведения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник

Главная
Школа Пифагора ЕГЭ по математике
ФОРМУЛЫ ПРИВЕДЕНИЯ (ТРИГОНОМЕТРИЯ ЕГЭ МАТЕМАТИКА ПРОФИЛЬ)

ФОРМУЛЫ ПРИВЕДЕНИЯ (ТРИГОНОМЕТРИЯ ЕГЭ МАТЕМАТИКА ПРОФИЛЬ)

Просмотров: 1 300

Если вам понравилось бесплатно смотреть видео формулы приведения (тригонометрия егэ математика профиль) онлайн которое загрузил Школа Пифагора ЕГЭ по математике 16 декабря 2020 длительностью 00 ч 34 мин 04 сек в хорошем качестве, то расскажите об этом видео своим друзьям, ведь его посмотрели 1 300 раз.

please dont.

1 месяц назад

обычно в формулах приведения я полагаюсь на подругу, для меня всегда было магией как она это всё решала(а ещё лупасила меня по башке потому что «ТУТ МИНУС ТУПАС». пока есть свободное время, решила глянуть как же это всё преобразовывать, считать, вычислять. спасибо большое🙌🙌

Мурад

3 месяца назад

фух.. получилось решить все 10 заданий с домашки. спасибо

Krus-krus Gaming

3 месяца назад

Спасибо тебе большое за этот ролик! МЕНЯ ОСЕНИЛО после того как я его посмотрел

Саша Сотнам

4 месяца назад

ЗАЧЕТ, Я ТО (П/3+3) НЕ МОГ РЕШИТЬ,ДУМАЛ Ф/А ПРИВЕДЕНИЯ

Алёна Кроткова

6 месяцев назад

Спасибо Вам большое! Очень понятный разбор

Merfo

9 месяцев назад

За 3 дня до ЕГЭ разобрал формулу приведения, Пифагор очень просто объяснил. А я все время просто расписывал триг. функцию как сумму произведений, потому что у меня алгоритм в голове не укладывался и я решил не забивать себе голову.

Вискас

9 месяцев назад

Спасибо

jambuli antidze

9 месяцев назад

Respect

Дима

10 месяцев назад

Спасибо, наконец-то понял как это делать

Виктор 47

10 месяцев назад

Спасибо

k1m0n34

10 месяцев назад

что такое пи на 2?

Арина Агаева

10 месяцев назад

Сколько-то раз по 2П можно просто убирать и не смотреть на знак? А в остальных случаях смотреть, правильно? Единственный непонятный момент

Альберт

11 месяцев назад

Добрый день, а если в скобках будет например Sin(a-8П)? Мы добавим 8П у нас что получится?

luft

11 месяцев назад

Спасибо огромное за объяснение. В школе понимаю, но дома нужно еще закрепить, чтоб наверняка и твои объяснения для этого подходят ни чуть не хуже, чем объяснения учителя.

Источник

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены