Формулы приведения на егэ по математике

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 172    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 172    1–20 | 21–40 | 41–60 | 61–80 …

Как вы, наверное, уже обратили внимание, формулы приведения разработаны для углов, представленных в одном из следующих видов: (frac{pi}{2}+a), (frac{pi}{2}-a), (π+a), (π-a), (frac{3pi}{2}+a), (frac{3pi}{2}-a), (2π+a) и (2π-a). Аналогично их можно использовать для углов представленных в градусах: (90^°+a), (90^°-a), (180^°+a), (180^°-a), (270^°+a), (270^°-a), (180^°+a), (180^°-a).
К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.

Содержание:

• Как быстро получить любую формулу приведения
• Как определить знак перед конечной функцией (плюс или минус)?
• Менять ли функцию на кофункцию или оставить прежней?
• Примеры из ЕГЭ с формулами приведения
• Как доказать формулу приведения

Как быстро получить любую формулу приведения

Для начала обратите внимание, что все формулы имеют похожий вид:

Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.

Функция:                Кофункция:
(sin⁡) (a)          (→)            (cos⁡) (a)
(cos⁡) (a)          (→)             (sin⁡) (a)
(tg⁡) (a)            (→)            (ctg) (a)
(ctg⁡) (a)          (→)             (tg) (a)

Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс
или котангенс, он либо останется синусом, либо превратиться в косинус. А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее. 

Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
— как определить знак перед конечной функцией (плюс или минус)?
— как определить меняется ли функция на кофункцию или нет?

Как определить знак перед конечной функцией (плюс или минус)?

Например, выводим формулу приведения для (⁡cos⁡(frac{3pi}{2}-a) =….) С исходной функцией понятно – косинус, а исходная четверть?

Для того, чтобы ответить на этот вопрос, представим, что (a) – угол от (0) до (frac{pi}{2}), т.е. лежит в пределах (0°…90^°) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол (frac{3pi}{2}-a)?
Чтобы ответить на вопрос, надо от точки, обозначающей (frac{3pi}{2}), повернуть в отрицательную сторону на угол (a).

В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: (cos(frac{3pi}{2}-a)=-…)

Менять ли функцию на кофункцию или оставить прежней?

Здесь правило еще проще:

То есть, при аргументах исходной функции (frac{pi}{2}+a), (frac{pi}{2}-a), (frac{3pi}{2}+a) или (frac{pi}{2}-a), мы должны поменять функцию, а при аргументах (π+a), (π-a), (2π+a) или (2π-a) — нет. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:

Точки, обозначающие (frac{pi}{2}) ((90^°)) и (frac{3pi}{2}) ((270^°)), расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да».

Точки же, обозначающие (π) ((180^°)) и (2π) ((360^°)), расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».

 

Эти «да» и «нет» — и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше (cos⁡(frac{3π}{2}-a)=…) косинус будет меняться на синус. В конечном итоге получаем, (cos⁡(frac{3π}{2}-a)=-sin⁡) (a). Это и есть верная формула приведения.

Примеры из ЕГЭ с формулами приведения:

Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{18 cos {⁡{41}^°} }{sin⁡ {{49}^°}})

Решение:

(frac{18 cos {{⁡41}^°} }{sin⁡{{49}^°}}=)	Углы ({41}^°) и ({49}^°) нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако использовав формулы привидения, мы легко найдем правильный ответ. Прежде всего, обратите внимание на один важный момент: (49^°=90^°-41^°). Поэтому мы можем заменить (49^°) на (90^°-41^°).
(=frac{18 cos {⁡41^° }}{sin⁡ {({90}^°-{41}^°)}}=)	Теперь применим к синусу формулу приведения: (90^°-41^°) – это первая четверть, синус в ней положителен. Значит, знак будет плюс; (90^°)- находится на «вертикали» — функция меняется на кофункцию. (sin⁡{(90^°-41^°)}=cos⁡ 41^° )
(=frac{18 cos {⁡41^° }}{cos⁡ {{41}^°}}=)	В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
(= 18)	Записываем ответ

Ответ:  (18).

Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{5,tg⁡,163^°}{tg⁡,17^°})

Решение:

(frac{5, tg⁡,163^°}{tg⁡,17^°}=)		Опять замечаем интересное «совпадение»: (163^°=180^°-17^°). Поэтому можно заменить (163^°) на (180^°-17^°).
(=frac{5,tg⁡,(180^°-17^°)}{tg⁡,17^°}=)		Воспользуемся формулой приведения: ((180^°-17^°)) – это вторая четверть, тангенс в ней отрицателен. Значит, знак будет минус; (180^°) — находится на «горизонтали» — функция остается прежней. Значит, (tg⁡,(180^°-17^°)=-tg⁡,17^°).
(=-frac{5,tg⁡,17^°}{tg⁡,17^°})(=-5)

Ответ:  (-5).

Пример. (Задание из ЕГЭ) Найдите значение выражения (-19,tg,101^°cdot tg,191^°)

Решение:

(-19,tg,101^°cdot tg ,91^°=)		(101^°=90^°+11^°); (191^°=180^°+11^°).
(=-19,tg,(90^°+11^° )cdot tg, (180^°+11^° )=)		Применим формулы приведения: ((90^°+11^°)) – это вторая четверть, тангенс в ней отрицателен. Значит, знак будет минус; (90^°)- находится на «вертикали» — функция меняется. Значит, (tg⁡,(90^°+11^°)=-ctg⁡,11^°). ((180^°+11^°)) – это третья четверть, тангенс в ней положителен. Значит, знак будет плюс; (180^°) — находится на «горизонтали» — функция остается прежней. Значит, (tg⁡,(180^°+11^°)=tg⁡,11^°).
(=19,ctg,11^°cdot tg,11^°=)		Вот тут можно применить одну из формул связи.
(=19).

Ответ:  (19).

Пример. (Задание из ЕГЭ) Вычислить: (frac{-12}{sin^2⁡{131}^° + sin^2⁡{221}^°}).

Решение:

(frac{-12}{sin^2⁡{131}^° + sin^2⁡{221}^°})		(131^°=90^°+41^°); (221^°=180^°+41^°).
(frac{-12}{sin^2⁡(90^°+41^°)+ sin^2⁡(180^°+41^°)})		(sin^2⁡(90^°+41^°):) ((90^°+41^°)) – (90^°) на вертикали, синус меняется на косинус; Знак синуса не важен, так как он все равно в квадрате. (sin^2⁡(180^°+41^° ):) ((180^°+41^°)) – (180^°) на горизонтальной оси, синус остается синусом.
(frac{-12}{cos^2⁡{41^°} + sin^2⁡{41^°}})		Очевидно, что в знаменателе можно применить основное тригонометрическое тождество.
(=frac{-12}{1}=-12).

Ответ:  (-12).

Пример. (Задание из ЕГЭ) Найдите (26, cos⁡(frac{3π}{2}+α)), если (cos⁡α=frac{12}{13}) и (α∈(frac{3π}{2};2π)).

Решение:

Очевидно, что к исходному выражению можно применить формулу приведения (26,cos⁡(frac{3π}{2}+α)=26,sin⁡α). Задача свелась к нахождению синуса по косинусу, много похожих заданий было разобрано в статье «формулы связи».

(sin^2⁡α+cos^2⁡α=1)
(sin^2⁡α+(frac{12}{13})^2=1)
(sin^2⁡α+frac{144}{169}=1)
(sin^2⁡α=1-frac{144}{169})
(sin^2⁡α=frac{169-144}{169})
(sin^2⁡α=frac{25}{169})
(sin⁡,α=±frac{5}{13})

С учетом того, что (α∈(frac{3π}{2};2π)), то есть в четвертой четверти, (sin,⁡α=-frac{5}{13}).

(26,cos⁡(frac{3π}{2}+α)=26,sin⁡α=26cdot (-frac{5}{13})=-frac{26cdot 5}{13}=-2cdot 5=-10).

Ответ:  (-10).

Ну и последний пример – с очень важным выводом после него.

Пример. (Задание из ЕГЭ) Вычислить, чему равен (ctg(-a-frac{7π}{2})), если (tg⁡,a=2).

Решение:

(ctg(-a-frac{7π}{2})=)		Прежде чем применять формулу приведения, приведем аргумент функции к стандартному (одному из указанных в начале статьи). Давайте поменяем местами слагаемые аргумента, сохраняя знаки – для того, чтобы a стояла после «точки привязки».
(= ctg(-frac{7π}{2}-a) =)		Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента.
(= ctg(-(frac{7π}{2}+a)) =)		Теперь вспомним о том, что котангенс – функция нечетная, то есть (ctg,(-t)=- ctg,t). Преобразовываем наше выражение.
(=- ctg(frac{7π}{2}+a) =)		Теперь преобразуем (frac{7π}{2}) следующим образом: (frac{7π}{2}=frac{4π+3π}{2}=2π+frac{3π}{2}).
(=- ctg(2π+frac{3π}{2}+a) =)		Но ведь (2π) – это просто полный оборот по кругу, он не оказывает никакого влияния на значение функции: (ctg,(2π+x)=ctg(x)). Так что, его можно просто отбросить.
(=- ctg(frac{3π}{2}+a) =)		Вот теперь применяем формулу приведения. ((frac{3π}{2}+a)) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем (ctg(frac{3π}{2}+a)=-tg,a).
(= — (- tg,a) = tg,a = 2)		Готов ответ.

Ответ:  (2).

Важное замечание! На самом деле преобразовывать функцию по формулам приведения можно было сразу после получения (ctg(-frac{7π}{2}-a)), не делая все последующие преобразования.
Действительно:
((-frac{7π}{2}-a)) – это первая четверть, там котангенс положителен.
«Точка привязки» — вертикальная, то есть функцию меняем.
Таким образом, можно сразу получить, что (ctg,(-frac{7π}{2}-a)=tg,a).

Вывод:

Но обратите внимание – они никогда не могут быть (-frac{π}{3}),(frac{5π}{6}),(frac{17π}{4}) и т.д. – потому что эти точки не лежат на пересечении с осями. Давайте, вместе выясним почему это так.

Как доказать формулу приведения, или почему «точки привязки» обязательно должны быть точками пересечения с осями

Возьмем какую-либо формулу приведения – например, вот эту (sin⁡(frac{π}{2}+a)=cos⁡a) – и попробуем получить из левой части правую.
Что у нас слева? Синус суммы аргументов.
У нас на этот случай есть формула: (sin⁡(x+y)=sin⁡x cos⁡y+sin⁡y cos⁡x)
Применим ее: (sin⁡(frac{π}{2}+a)=sin⁡frac{π}{2}cos⁡a+sin⁡a cos⁡frac{π}{2})
Мы знаем, что (sin⁡frac{π}{2}=1, а cos⁡frac{π}{2}=0). Таким образом имеем окончательную цепочку преобразований:

(sin⁡(frac{π}{2}+a)=sin⁡frac{π}{2}cos⁡a+sin⁡a cos⁡frac{π}{2}=1·cos⁡a+sin⁡a·0=cos⁡a)

Получилось!

Попробуем еще. Возьмем вот эту формулу: (cos⁡(π-a)=-cos⁡a)
Преобразовываем с помощью формулы разности в косинусе:

(cos⁡(π-a)=cos⁡π cos⁡a+sin⁡a sin⁡π=-1·cos⁡a+sin⁡a·0=-cos⁡a)

Опять всё верно.

Ну и еще одну: (cos⁡(frac{3π}{2}+a)=sin⁡a)
Преобразовываем с помощью формулы суммы в косинусе:

(cos⁡(frac{3π}{2}+a)=cos⁡frac{3π}{2}cos⁡a-sin⁡a sin⁡frac{3π}{2}=0·cos⁡a-sin⁡a·(-1)=sin⁡a)

Сошлось.

А теперь присмотритесь к преобразованиям. Замечаете что-нибудь общее?
Да, всё верно — во всех случаях у нас одна из функций превращается в (1) или (-1), а вторая в (0). И именно благодаря этому — итоговое выражение становится проще!

А теперь давайте попробуем взять в качестве «точки привязки» не точку пересечения с осями, а какую-нибудь другую, например, (frac{π}{3}):

(cos⁡(frac{π}{3}-a)=cos⁡frac{π}{3}cos⁡a+sin⁡a sin⁡frac{π}{3}=frac{1}{2}·cos⁡a+sin⁡a·frac{sqrt{3}}{2}=)(frac{cos⁡a+sqrt{3}sin⁡a}{2})

Мда… Что-то такое себе упрощение получилось…

Понимаете теперь?

«Точки привязки» должны быть точками пересечения с осями, потому что только в этом случае получаются более простые выражения. Так происходит потому, что в точках пересечения круга с осями всегда одна из функций (синус или косинус) равна нулю, а вторая плюс или минус единице. Для всех остальных точек – это не работает.

Смотрите также:
Формулы тригонометрии с примерами
Как доказать тригонометрическое тождество?

Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.

Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.

$1$ радиан $={180}/{π}≈57$ градусов

$1$ градус $={π}/{180}$ радиан

Значения тригонометрических функций некоторых углов

$α$	$ 0$	${π}/{6}$	${π}/{4}$	${π}/{3}$	${π}/{2}$	$π$
$sinα$	$ 0$	$ {1}/{2}$	$ {√2}/{2}$	$ {√3}/{2}$	$ 1$	$ 0$
$cosα$	$ 1$	$ {√3}/{2}$	$ {√2}/{2}$	$ {1}/{2}$	$ 0$	$ -1$
$tgα$	$ 0$	$ {√3}/{3}$	$ 1$	$ √3$	$ -$	$ 0$
$ctgα$	$ -$	$ √3$	$ 1$	$ {√3}/{3}$	$ 0$	$ -$

Периоды повтора значений тригонометрических функций

Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$

Знаки тригонометрических функций по четвертям

Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.

Чтобы правильно раскрыть формулы приведения необходимо помнить, что:

1. если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ (${π}/{2}$ и ${3π}/{2}$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
2. чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.

Четность тригонометрических функций

Косинус четная функция: $cos(-t)=cos t$

Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$

Тригонометрические тождества

Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса

$sinα=±√{1-cos^2α}$

$cosα=±√{1-sin^2α}$

1. $tgα·ctgα=1$
2. $1+tg^2α={1}/{cos^2α}$
3. $1+ctg^2α={1}/{sin^2α}$

04
Авг 2013

Категория: Справочные материалы

Формулы приведения

2013-08-04
2021-06-18

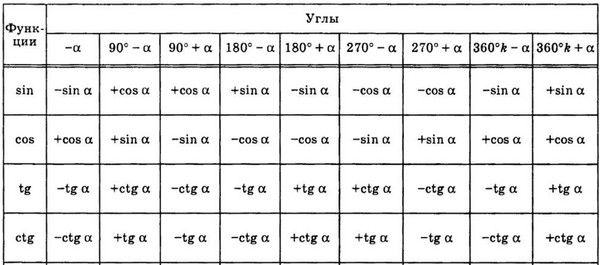
Стоит ли учить формулы приведения?

Вы в состоянии выучить вот такую таблицу?

А без приведения сложных аргументов тригонометрических функций к аргументам первой четверти на ЕГЭ по математике никуда.

Но нет необходимости учить эту таблицу!

Нужно просто потратить немного времени и понять алгоритм применения формул приведения.

Не будем терять время! Поехали!

Зачем вообще формулы приведения?

Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций  к аргументам  I четверти.

Вот, например, типичное задание из ЕГЭ по математике:

Вычислите или

Давайте разбираться. А к примерам вернемся чуть позже.

Если хотите докапаться до самой сути, то –> + показать

---

Мнемоническое правило для формул приведения 

1. Задаем себе вопрос: «Меняется ли название функции на кофункцию?» + показать

2. Ставим справа, на выходе, тот знак, какой несет в себе левая, исходная, часть.

Данное правило еще  называется «лошадиным».

Примеры 

При выполнении заданий нам понадобятся основные значения тригонометрических функций

Пример 1. Вычислить . + показать

---

Пример 2. Вычислить  + показать

---

Пример 3. Упростить + показать

Автор: egeMax |

комментариев 7

• Мне нравится