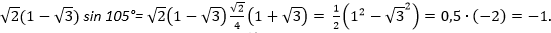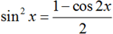Формулы приведения теория егэ

Формулы приведения

Применять формулы приведения — легко! Их не надо зубрить наизусть. И не надо тащить на экзамен шпаргалки, рискуя спалиться. Надо всего лишь запомнить два правила, о которых вы узнаете, посмотрев этот ролик. Это так просто, что даже лошадка поймет! Посмотри и передай друзьям.

Часто в задачах встречаются выражения вида   а также или — то есть такие, где к аргументу прибавляется нечетное число, умноженное на или целое число, умноженное на Они упрощаются с помощью формул приведения.

Запомните: формулы приведения, от слова «привести». К привидениям, то есть к призракам и прочим глюкам, эти формулы отношения не имеют : -)

Эти формулы называются так потому, что с их помощью можно привести выражения к более простым.

Например, 

Зубрить наизусть формулы приведения не нужно. Достаточно знать правило, состоящее из двух пунктов.

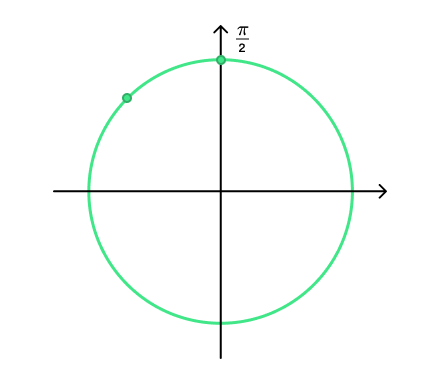
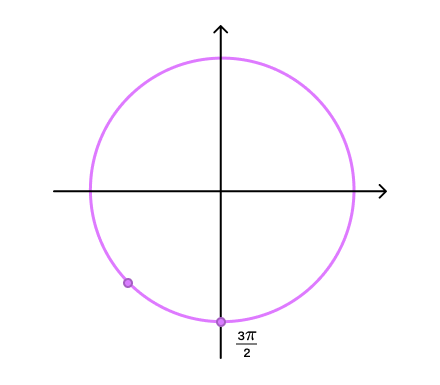
1) Если в тригонометрической формуле к аргументу прибавляется (или вычитается из него) — в общем, угол, лежащий на вертикальной оси, — функция меняется на кофункцию. Синус меняется на косинус, косинус на синус, тангенс на котангенс и наоборот.

Если же мы прибавляем или вычитаем — в общем, то, что лежит на горизонтальной оси, — функция на кофункцию не меняется.

Это легко запомнить. Если прибавляемый угол лежит на вертикальной оси — вертикально киваем головой, говорим: «Да, да, меняется функция на кофункцию». Если прибавляемый угол лежит на горизонтальной оси — горизонтально мотаем головой, говорим: «Нет, нет, не меняется функция на кофункцию».

Это первая часть правила. Теперь вторая.

2) Знак получившегося выражения такой же, каким будет знак тригонометрической функции в левой его части, при условии, что аргумент мы берем из первой четверти.

Упростим, например, выражение Функция меняется на кофункцию — и в результате получится синус. Взяв x из первой четверти и прибавив к нему попадем во вторую четверть. Во второй четверти косинус отрицателен. Значит, получится

Посмотрим, как формулы приведения применяются в задачах ЕГЭ по математике.

1. Найдите значение выражения:

Ответ: 11.

2. Вычислите:

Ответ: 4.

3. Вычислите:

Мы упростили выражения в скобках.

Ответ: — 24.

4. Найдите значение выражения:

Ответ: 4.

5. Упростите выражение:

Ответ: 2.

6. Найдите значение выражения:

Решение:

Используя формулы приведения, получим

Ответ: 0,4.

7. Найдите значение выражения: cos

Решение:

cos cos cos

Снова формула приведения.

Ответ: -12.

8. Найдите значение выражения:

Решение:

Мы применили одну из формул приведения.

Ответ: 42.

9. Найдите значение выражения:

Решение:

Воспользуемся формулами приведения:

Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.

Ответ: 9,5.

Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.

Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.

$1$ радиан $={180}/{π}≈57$ градусов

$1$ градус $={π}/{180}$ радиан

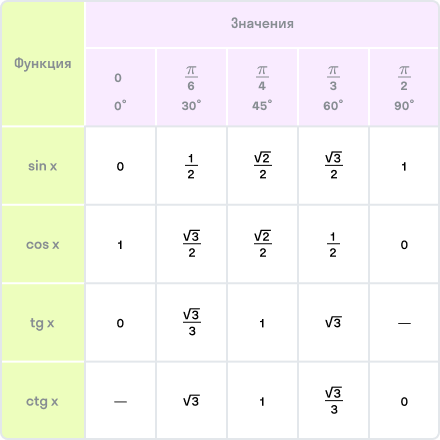
Значения тригонометрических функций некоторых углов

$α$	$ 0$	${π}/{6}$	${π}/{4}$	${π}/{3}$	${π}/{2}$	$π$
$sinα$	$ 0$	$ {1}/{2}$	$ {√2}/{2}$	$ {√3}/{2}$	$ 1$	$ 0$
$cosα$	$ 1$	$ {√3}/{2}$	$ {√2}/{2}$	$ {1}/{2}$	$ 0$	$ -1$
$tgα$	$ 0$	$ {√3}/{3}$	$ 1$	$ √3$	$ -$	$ 0$
$ctgα$	$ -$	$ √3$	$ 1$	$ {√3}/{3}$	$ 0$	$ -$

Периоды повтора значений тригонометрических функций

Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$

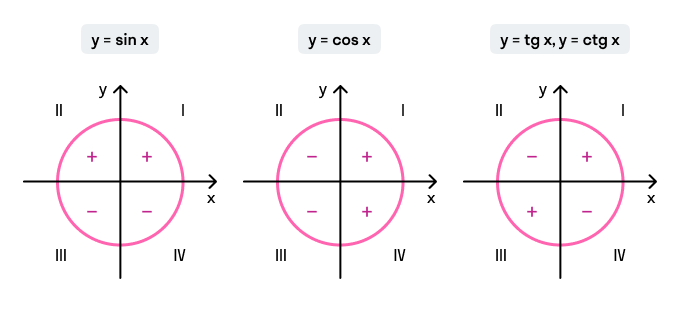
Знаки тригонометрических функций по четвертям

Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.

Чтобы правильно раскрыть формулы приведения необходимо помнить, что:

1. если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ (${π}/{2}$ и ${3π}/{2}$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
2. чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.

Четность тригонометрических функций

Косинус четная функция: $cos(-t)=cos t$

Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$

Тригонометрические тождества

Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса

$sinα=±√{1-cos^2α}$

$cosα=±√{1-sin^2α}$

1. $tgα·ctgα=1$
2. $1+tg^2α={1}/{cos^2α}$
3. $1+ctg^2α={1}/{sin^2α}$

Вы наверняка помните значения тригонометрических функций основных аргументов:

Но что делать, если в задаче просят вычислить

? В этом и других случаях, когда из огромного аргумента нам нужно получить аргумент в пределе от 0 до 90 градусов, работают формулы приведения.

Всего формул приведения тридцать две штуки, но прежде чем мы перейдем к формулам, давайте договоримся, что точку тригонометрической окружности, отвечающую углу

, где n — целое число, мы будем называть опорной точкой.

Список формул приведения

Формулы приведения c опорной точкой

(случай n = 1):

• ;

• ;

• ;

• ;

• ;

• ;

• ;

• .

Формулы приведения c опорной точкой

(случай n = 2):

• ;

• ;

• ;

• ;

• ;

• ;

• ;

• .

Формулы приведения c опорной точкой

(случай n = 3):

• ;

• ;

• ;

• ;

• ;

• ;

• ;

• .

Формулы приведения c опорной точкой

(случай n = 4):

• ;

• ;

• ;

• ;

• ;

• ;

• ;

• .

Доказательство формул

Чтобы убедиться, что формулы рабочие, рассмотрим примеры доказательств нескольких из них.

Для этого нам нужно будет вспомнить формулы сложения для синуса и косинуса:

• ;

• .

Формула приведения с синусом

Разберем первый пример формулы приведения с синусом:

. Нужно доказать, что левая часть равна правой.

По формуле синуса суммы представим левую часть выражения:

Вычислим

и

в получившемся выражении:

Таким образом,

, что и требовалось доказать.

Формула приведения с косинусом

Рассмотрим также пример формулы приведения с косинусом и докажем ее:

Аналогично распишем левую часть по формуле косинуса суммы:

Вычислим

и

Следовательно,

, что и требовалось доказать.

Формула приведения с тангенсом

Чтобы доказать формулу приведения с тангенсом, нужно вспомнить, что тангенс — это отношение синуса к косинусу. Тогда для доказательства нужно лишь дважды использовать формулы сложения — попробуйте сами на формуле

и сравните с примером.

При желании таким образом вы сможете доказать справедливость всех формул.

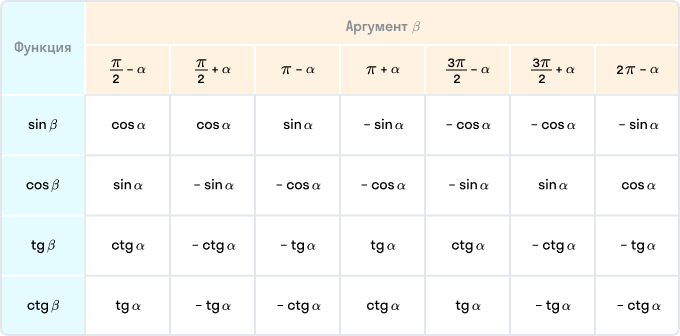
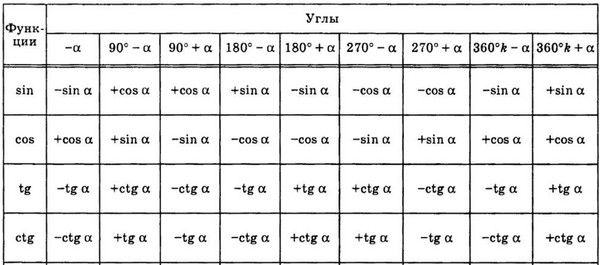
Таблица формул приведения

Нередко можно встретить такой вариант оформления формул приведения — в виде таблицы.

Для того чтобы воспользоваться этой таблицей, выберите строку с нужной функцией и столбец с необходимым аргументом — на их пересечении вы узнаете ответ.

Например, нужно упростить

.

говорит нам о том, что нужно выбрать первую строку,

указывает на шестую колонку. На их пересечении нашли ответ:

. Значит,

Маленькую распечатанную таблицу формул приведения тригонометрических функций удобно иметь в пенале на случай неожиданных контрольных.

Как запомнить формулы приведения

Одно дело — воспользоваться формулами, а совсем другое — выучить их. Знать наизусть все формулы приведения или всю таблицу — дело нелегкое и, к счастью, абсолютно ненужное.

Поэтому познакомимся с мнемоническим алгоритмом:

1. Представьте аргумент в виде

   , где n — целое число, а

   — острый угол, то есть принадлежит отрезку

2. Изобразите (на листе или мысленно) на единичной окружности данный угол.

3. С помощью окружности определите знак исходной функции. Полученная функция в правой части будет иметь такой же знак.

   Напоминаю знаки тригонометрических функций во всех четвертях тригонометрической окружности:

   

4. Если в аргументе у опорной точки

   n — нечетное число, то исходную функцию замените на кофункцию, то есть на противоположную функцию (синус меняется на косинус, тангенс — на котангенс, и наоборот).

   Если в аргументе у опорной точки

   n — четное число, то функция не меняется.

Вот с этим пунктом изменения или сохранения функции возникает постоянная путаница. А запомнить поможет «правило лошадки».

Таким образом, формулы приведения — это тригонометрические тождества вида

Задание 1

Найдите значение выражения

Вы видите, что каждое слагаемое выражения — это формула приведения тригонометрической функции. Упростим их по отдельности.

1. Сначала нужно представить аргумент в виде

   , где n — целое число, а

   — острый угол. Здесь этот шаг уже выполнен, поэтому пропускаем его.

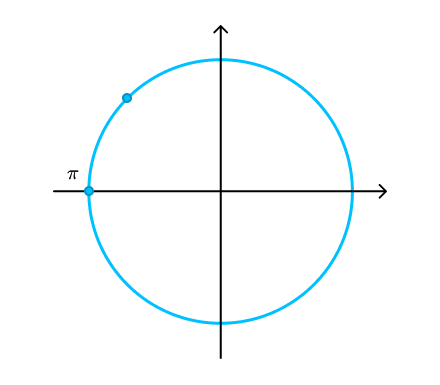
2. Далее изображаем данный угол на тригонометрической окружности:

   

3. Определяем знак исходной функции, то есть синуса. Синус этого угла принимает положительные значения.

4. В конце определяем, меняется ли функция. В этом нам поможет «правило лошадки»: опорная точка

   лежит на горизонтальной оси, значит, функция не меняется на кофункцию, то есть синус не меняется на косинус.

Значит,

.

Приведем аналогичные рассуждения для всех слагаемых в выражении.

1. Аргумент уже представлен в виде

   , где n — целое число, а

   — острый угол.

   

2. Косинус во второй четверти тригонометрической окружности принимает отрицательные значения.

3. Опорная точка

   лежит на вертикальной оси — это случай, когда косинус меняется на синус.

Значит,

.

1. Аргумент уже представлен в виде

   , где n — целое число, а

   — острый угол.

   

2. Косинус в третьей четверти тригонометрической окружности принимает отрицательные значения.

3. Опорная точка

   лежит на вертикальной оси — это случай, когда косинус меняется на синус.

Значит,

.

А теперь запишем преобразованные выражения в наше исходное и упростим:

Обратите внимание, к какому простому виду удалось привести это сложное, на первый взгляд, выражение.

Задание 2

До этого момента мы говорили о формулах приведения тригонометрических функций углов, выраженных в радианах. Однако мы понимаем, что градусы и радианы — это разные способы представления одних и тех же углов или аргументов, поэтому тригонометрические формулы приведения работают и для выражений с градусами.

Разберем на примере: найдите значение выражения

.

В этом случае важно заметить, что

, а значит, одну из функций, например

, можно представить в виде

, то есть в виде, необходимом для использования формулы приведения.

Так как первый шаг выполнен, то продолжаем идти по алгоритму.

Косинус в первой четверти тригонометрической окружности принимает положительные значения.

Опорная точка

лежит на вертикальной оси, поэтому косинус меняется на синус.

Значит,

Запишем преобразованные выражения в наше исходное и упростим:

Формулы приведения в тригонометрии занимают второе место по важности и частоте использования после основного тригонометрического тождества, так что осваивайте теоретические материалы, практикуйтесь на задачках, а за другими полезными формулами и самыми хитрыми заданиями приходите на онлайн-курсы математики для детей в Skysmart.

04
Авг 2013

Категория: Справочные материалы

Формулы приведения

2013-08-04
2021-06-18

Стоит ли учить формулы приведения?

Вы в состоянии выучить вот такую таблицу?

А без приведения сложных аргументов тригонометрических функций к аргументам первой четверти на ЕГЭ по математике никуда.

Но нет необходимости учить эту таблицу!

Нужно просто потратить немного времени и понять алгоритм применения формул приведения.

Не будем терять время! Поехали!

Зачем вообще формулы приведения?

Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций  к аргументам  I четверти.

Вот, например, типичное задание из ЕГЭ по математике:

Вычислите или

Давайте разбираться. А к примерам вернемся чуть позже.

Если хотите докапаться до самой сути, то –> + показать

---

Мнемоническое правило для формул приведения 

1. Задаем себе вопрос: «Меняется ли название функции на кофункцию?» + показать

2. Ставим справа, на выходе, тот знак, какой несет в себе левая, исходная, часть.

Данное правило еще  называется «лошадиным».

Примеры 

При выполнении заданий нам понадобятся основные значения тригонометрических функций

Пример 1. Вычислить . + показать

---

Пример 2. Вычислить  + показать

---

Пример 3. Упростить + показать

Автор: egeMax |

комментариев 7

$$ctg(pi-alpha)=-ctg(alpha);$$

Давайте вместо угла (alpha) возьмем какой-нибудь реальный угол. Суть от этого не изменится. Чтобы усложнить задачу, я не буду рисовать рисунок. Нарисуйте окружность сами и по пунктам сделайте пример.

Пример 7
$$cos(3pi+frac{pi}{6})=?;$$

• Угол ((3pi+frac{pi}{6})) лежит в третьей четверти. Действительно, (3pi=2pi+pi) можно представить как полный круг плюс еще половина;
• В третьей четверти косинус отрицательный. Знак минус;
• (3pi) лежит на горизонтальной оси в точке (C). Значит косинус не меняется на синус;

$$cos(3pi+frac{pi}{6})=-cos(frac{pi}{6})=-frac{sqrt{3}}{2};$$

До этого мы рассматривали примеры, когда угол (alpha) был острым. А что, если он больше (90^o)?

В этом случае нам придется сделать из него острый угол. Рассмотрим пример:

Пример 8
$$tg(frac{pi}{2}-frac{5pi}{6})=?;$$
Угол (frac{5pi}{6}) — тупой угол. Для того, чтобы воспользоваться формулой приведения, можно представить:
$$frac{5pi}{6}=pi-frac{pi}{6};$$
Подставим в исходный пример
$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{2}-pi+frac{pi}{6})=tg(frac{pi}{6}-frac{pi}{2});$$
Угол (frac{pi}{6}) острый и теперь можно воспользоваться правилом лошади.

• ((frac{pi}{6}-frac{pi}{2})) лежит в четвертой четверти. Отмечаем (frac{pi}{6}) и по часовой стрелке вычитаем из него (frac{pi}{2});
• В четвертой четверти тангенс отрицательный;
• (frac{pi}{2}) лежит на вертикальной оси, тангенс меняется на котангенс;

$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{6}-frac{pi}{2})=-ctg(frac{pi}{6})=-sqrt{3};$$

У любопытного читателя может возникнуть вопрос: а почему данный алгоритм называется правилом лошади? При чем тут, казалось бы, лошадь?

Лошадь, действительно, не при чем. Но дело в том, что когда вы определяете в третьем пункте, меняется ли наша тригонометрическая функция на противоположную или нет, то в случае, если дополнительный угол к (alpha) лежит на вертикальной оси, мы как бы смотрим вверх-вниз, киваем головой, как лошадь, говоря себе: «Да, меняем». Или если угол лежит на горизонтальной оси, то мы киваем влево вправо вдоль горизонтальной оси, как бы говоря: «Нет, не меняем». Такое вот странное название у правила.

Как вы, наверное, уже обратили внимание, формулы приведения разработаны для углов, представленных в одном из следующих видов: (frac{pi}{2}+a), (frac{pi}{2}-a), (π+a), (π-a), (frac{3pi}{2}+a), (frac{3pi}{2}-a), (2π+a) и (2π-a). Аналогично их можно использовать для углов представленных в градусах: (90^°+a), (90^°-a), (180^°+a), (180^°-a), (270^°+a), (270^°-a), (180^°+a), (180^°-a).
К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.

Содержание:

• Как быстро получить любую формулу приведения
• Как определить знак перед конечной функцией (плюс или минус)?
• Менять ли функцию на кофункцию или оставить прежней?
• Примеры из ЕГЭ с формулами приведения
• Как доказать формулу приведения

Как быстро получить любую формулу приведения

Для начала обратите внимание, что все формулы имеют похожий вид:

Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.

Функция:                Кофункция:
(sin⁡) (a)          (→)            (cos⁡) (a)
(cos⁡) (a)          (→)             (sin⁡) (a)
(tg⁡) (a)            (→)            (ctg) (a)
(ctg⁡) (a)          (→)             (tg) (a)

Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс
или котангенс, он либо останется синусом, либо превратиться в косинус. А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее. 

Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
— как определить знак перед конечной функцией (плюс или минус)?
— как определить меняется ли функция на кофункцию или нет?

Как определить знак перед конечной функцией (плюс или минус)?

Например, выводим формулу приведения для (⁡cos⁡(frac{3pi}{2}-a) =….) С исходной функцией понятно – косинус, а исходная четверть?

Для того, чтобы ответить на этот вопрос, представим, что (a) – угол от (0) до (frac{pi}{2}), т.е. лежит в пределах (0°…90^°) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол (frac{3pi}{2}-a)?
Чтобы ответить на вопрос, надо от точки, обозначающей (frac{3pi}{2}), повернуть в отрицательную сторону на угол (a).

В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: (cos(frac{3pi}{2}-a)=-…)

Менять ли функцию на кофункцию или оставить прежней?

Здесь правило еще проще:

То есть, при аргументах исходной функции (frac{pi}{2}+a), (frac{pi}{2}-a), (frac{3pi}{2}+a) или (frac{pi}{2}-a), мы должны поменять функцию, а при аргументах (π+a), (π-a), (2π+a) или (2π-a) — нет. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:

Точки, обозначающие (frac{pi}{2}) ((90^°)) и (frac{3pi}{2}) ((270^°)), расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да».

Точки же, обозначающие (π) ((180^°)) и (2π) ((360^°)), расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».

 

Эти «да» и «нет» — и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше (cos⁡(frac{3π}{2}-a)=…) косинус будет меняться на синус. В конечном итоге получаем, (cos⁡(frac{3π}{2}-a)=-sin⁡) (a). Это и есть верная формула приведения.

Примеры из ЕГЭ с формулами приведения:

Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{18 cos {⁡{41}^°} }{sin⁡ {{49}^°}})

Решение:

(frac{18 cos {{⁡41}^°} }{sin⁡{{49}^°}}=)	Углы ({41}^°) и ({49}^°) нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако использовав формулы привидения, мы легко найдем правильный ответ. Прежде всего, обратите внимание на один важный момент: (49^°=90^°-41^°). Поэтому мы можем заменить (49^°) на (90^°-41^°).
(=frac{18 cos {⁡41^° }}{sin⁡ {({90}^°-{41}^°)}}=)	Теперь применим к синусу формулу приведения: (90^°-41^°) – это первая четверть, синус в ней положителен. Значит, знак будет плюс; (90^°)- находится на «вертикали» — функция меняется на кофункцию. (sin⁡{(90^°-41^°)}=cos⁡ 41^° )
(=frac{18 cos {⁡41^° }}{cos⁡ {{41}^°}}=)	В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
(= 18)	Записываем ответ

Ответ:  (18).

Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{5,tg⁡,163^°}{tg⁡,17^°})

Решение:

(frac{5, tg⁡,163^°}{tg⁡,17^°}=)		Опять замечаем интересное «совпадение»: (163^°=180^°-17^°). Поэтому можно заменить (163^°) на (180^°-17^°).
(=frac{5,tg⁡,(180^°-17^°)}{tg⁡,17^°}=)		Воспользуемся формулой приведения: ((180^°-17^°)) – это вторая четверть, тангенс в ней отрицателен. Значит, знак будет минус; (180^°) — находится на «горизонтали» — функция остается прежней. Значит, (tg⁡,(180^°-17^°)=-tg⁡,17^°).
(=-frac{5,tg⁡,17^°}{tg⁡,17^°})(=-5)

Ответ:  (-5).

Пример. (Задание из ЕГЭ) Найдите значение выражения (-19,tg,101^°cdot tg,191^°)

Решение:

(-19,tg,101^°cdot tg ,91^°=)		(101^°=90^°+11^°); (191^°=180^°+11^°).
(=-19,tg,(90^°+11^° )cdot tg, (180^°+11^° )=)		Применим формулы приведения: ((90^°+11^°)) – это вторая четверть, тангенс в ней отрицателен. Значит, знак будет минус; (90^°)- находится на «вертикали» — функция меняется. Значит, (tg⁡,(90^°+11^°)=-ctg⁡,11^°). ((180^°+11^°)) – это третья четверть, тангенс в ней положителен. Значит, знак будет плюс; (180^°) — находится на «горизонтали» — функция остается прежней. Значит, (tg⁡,(180^°+11^°)=tg⁡,11^°).
(=19,ctg,11^°cdot tg,11^°=)		Вот тут можно применить одну из формул связи.
(=19).

Ответ:  (19).

Пример. (Задание из ЕГЭ) Вычислить: (frac{-12}{sin^2⁡{131}^° + sin^2⁡{221}^°}).

Решение:

(frac{-12}{sin^2⁡{131}^° + sin^2⁡{221}^°})		(131^°=90^°+41^°); (221^°=180^°+41^°).
(frac{-12}{sin^2⁡(90^°+41^°)+ sin^2⁡(180^°+41^°)})		(sin^2⁡(90^°+41^°):) ((90^°+41^°)) – (90^°) на вертикали, синус меняется на косинус; Знак синуса не важен, так как он все равно в квадрате. (sin^2⁡(180^°+41^° ):) ((180^°+41^°)) – (180^°) на горизонтальной оси, синус остается синусом.
(frac{-12}{cos^2⁡{41^°} + sin^2⁡{41^°}})		Очевидно, что в знаменателе можно применить основное тригонометрическое тождество.
(=frac{-12}{1}=-12).

Ответ:  (-12).

Пример. (Задание из ЕГЭ) Найдите (26, cos⁡(frac{3π}{2}+α)), если (cos⁡α=frac{12}{13}) и (α∈(frac{3π}{2};2π)).

Решение:

Очевидно, что к исходному выражению можно применить формулу приведения (26,cos⁡(frac{3π}{2}+α)=26,sin⁡α). Задача свелась к нахождению синуса по косинусу, много похожих заданий было разобрано в статье «формулы связи».

(sin^2⁡α+cos^2⁡α=1)
(sin^2⁡α+(frac{12}{13})^2=1)
(sin^2⁡α+frac{144}{169}=1)
(sin^2⁡α=1-frac{144}{169})
(sin^2⁡α=frac{169-144}{169})
(sin^2⁡α=frac{25}{169})
(sin⁡,α=±frac{5}{13})

С учетом того, что (α∈(frac{3π}{2};2π)), то есть в четвертой четверти, (sin,⁡α=-frac{5}{13}).

(26,cos⁡(frac{3π}{2}+α)=26,sin⁡α=26cdot (-frac{5}{13})=-frac{26cdot 5}{13}=-2cdot 5=-10).

Ответ:  (-10).

Ну и последний пример – с очень важным выводом после него.

Пример. (Задание из ЕГЭ) Вычислить, чему равен (ctg(-a-frac{7π}{2})), если (tg⁡,a=2).

Решение:

(ctg(-a-frac{7π}{2})=)		Прежде чем применять формулу приведения, приведем аргумент функции к стандартному (одному из указанных в начале статьи). Давайте поменяем местами слагаемые аргумента, сохраняя знаки – для того, чтобы a стояла после «точки привязки».
(= ctg(-frac{7π}{2}-a) =)		Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента.
(= ctg(-(frac{7π}{2}+a)) =)		Теперь вспомним о том, что котангенс – функция нечетная, то есть (ctg,(-t)=- ctg,t). Преобразовываем наше выражение.
(=- ctg(frac{7π}{2}+a) =)		Теперь преобразуем (frac{7π}{2}) следующим образом: (frac{7π}{2}=frac{4π+3π}{2}=2π+frac{3π}{2}).
(=- ctg(2π+frac{3π}{2}+a) =)		Но ведь (2π) – это просто полный оборот по кругу, он не оказывает никакого влияния на значение функции: (ctg,(2π+x)=ctg(x)). Так что, его можно просто отбросить.
(=- ctg(frac{3π}{2}+a) =)		Вот теперь применяем формулу приведения. ((frac{3π}{2}+a)) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем (ctg(frac{3π}{2}+a)=-tg,a).
(= — (- tg,a) = tg,a = 2)		Готов ответ.

Ответ:  (2).

Важное замечание! На самом деле преобразовывать функцию по формулам приведения можно было сразу после получения (ctg(-frac{7π}{2}-a)), не делая все последующие преобразования.
Действительно:
((-frac{7π}{2}-a)) – это первая четверть, там котангенс положителен.
«Точка привязки» — вертикальная, то есть функцию меняем.
Таким образом, можно сразу получить, что (ctg,(-frac{7π}{2}-a)=tg,a).

Вывод:

Но обратите внимание – они никогда не могут быть (-frac{π}{3}),(frac{5π}{6}),(frac{17π}{4}) и т.д. – потому что эти точки не лежат на пересечении с осями. Давайте, вместе выясним почему это так.

Как доказать формулу приведения, или почему «точки привязки» обязательно должны быть точками пересечения с осями

Возьмем какую-либо формулу приведения – например, вот эту (sin⁡(frac{π}{2}+a)=cos⁡a) – и попробуем получить из левой части правую.
Что у нас слева? Синус суммы аргументов.
У нас на этот случай есть формула: (sin⁡(x+y)=sin⁡x cos⁡y+sin⁡y cos⁡x)
Применим ее: (sin⁡(frac{π}{2}+a)=sin⁡frac{π}{2}cos⁡a+sin⁡a cos⁡frac{π}{2})
Мы знаем, что (sin⁡frac{π}{2}=1, а cos⁡frac{π}{2}=0). Таким образом имеем окончательную цепочку преобразований:

(sin⁡(frac{π}{2}+a)=sin⁡frac{π}{2}cos⁡a+sin⁡a cos⁡frac{π}{2}=1·cos⁡a+sin⁡a·0=cos⁡a)

Получилось!

Попробуем еще. Возьмем вот эту формулу: (cos⁡(π-a)=-cos⁡a)
Преобразовываем с помощью формулы разности в косинусе:

(cos⁡(π-a)=cos⁡π cos⁡a+sin⁡a sin⁡π=-1·cos⁡a+sin⁡a·0=-cos⁡a)

Опять всё верно.

Ну и еще одну: (cos⁡(frac{3π}{2}+a)=sin⁡a)
Преобразовываем с помощью формулы суммы в косинусе:

(cos⁡(frac{3π}{2}+a)=cos⁡frac{3π}{2}cos⁡a-sin⁡a sin⁡frac{3π}{2}=0·cos⁡a-sin⁡a·(-1)=sin⁡a)

Сошлось.

А теперь присмотритесь к преобразованиям. Замечаете что-нибудь общее?
Да, всё верно — во всех случаях у нас одна из функций превращается в (1) или (-1), а вторая в (0). И именно благодаря этому — итоговое выражение становится проще!

А теперь давайте попробуем взять в качестве «точки привязки» не точку пересечения с осями, а какую-нибудь другую, например, (frac{π}{3}):

(cos⁡(frac{π}{3}-a)=cos⁡frac{π}{3}cos⁡a+sin⁡a sin⁡frac{π}{3}=frac{1}{2}·cos⁡a+sin⁡a·frac{sqrt{3}}{2}=)(frac{cos⁡a+sqrt{3}sin⁡a}{2})

Мда… Что-то такое себе упрощение получилось…

Понимаете теперь?

«Точки привязки» должны быть точками пересечения с осями, потому что только в этом случае получаются более простые выражения. Так происходит потому, что в точках пересечения круга с осями всегда одна из функций (синус или косинус) равна нулю, а вторая плюс или минус единице. Для всех остальных точек – это не работает.

Смотрите также:
Формулы тригонометрии с примерами
Как доказать тригонометрическое тождество?

Основные тригонометрические формулы

Пример. Найти значение выражения:

Решение. Применяем основное тригонометрическое тождество в виде:

Пример. Найти значение выражения:

Решение. Из основного тригонометрического тождества следует:

Подставим в выражение:

Тригонометрические формулы суммы и разности двух углов

Пример. Вычислить

Решение.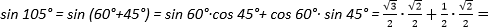

Пример. .

Решение.

Тригонометрические формулы двойного угла

Пример. Найдите 2cos2α, если sinα = — 0,7.

Решение. Используем формулу косинуса двойного угла: cos2α = 1 – 2sin²α.

Получаем: 2cos2α = 2·(1 – 2sin²α) = 2·(1-2·(-0,7)²) = 2·(1-2·0,49) = 0,04.

Пример. Найдите значение выражения

Решение. Применяем формулу sin2α = 2sinα·cosα:

Формулы понижения степени

Пример. Найти значение выражения $ 3sin^{2}4x $, если $ cos8x=0,5 $

Решение. Используем формулу понижения степени:

Применительно к углам 4x и 8x она будет выглядеть так:

Находим значение выражения:

Тригонометрические формулы произведения

Пример. Вычислить sin 20°·sin 40°, считать, что cos20° = 0,9

Решение. Заметим, что

Формулы суммы и разности тригонометрических функций

Формулы приведения

Формул приведения много, а точнее 32. И все формулы надо знать. К счастью существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения.

Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет.

1. В левой части формулы аргумент представляет собой сумму или разность одного из «основных координатных углов»: $ frac {pi}{2}, pi, frac {3pi}{2}, 2pi $ и острого угла $ alpha $, а в правой части аргумент $ alpha $

2. В правой части знак перед функцией либо «плюс», либо «минус».

Мнемоническое правило

Достаточно задать себе два вопроса:

1. Меняется ли функция на кофункцию?

Ответ: Если в формуле присутствуют углы $ frac {pi}{2} $ или $ frac {3pi}{2} $ — это углы вертикальной оси, киваем головой по вертикали и сами себе отвечаем: «Да», если же присутствуют углы горизонтальной оси π или 2π, то киваем головой по горизонтали и получаем ответ: «Нет».

2. Какой знак надо поставить в правой части формулы?

Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.

Например, sin $ ( frac {3 pi}{2} + alpha ) $.

1) «Меняется функция или нет?»

$ frac {3pi}{2} $ — угол вертикальной оси, киваем головой по вертикали: «Да, меняется». Значит, в правой части будет cosα.

2) «Знак?»

Угол $ ( frac {3 pi}{2} + alpha ) $ попадает в IV четверть. Синус в IV четверти имеет знак «минус». Значит, в правой части ставим знак «минус».

Итак, получили формулу, sin $ ( frac {3 pi}{2} + alpha ) = –cosα. $

Пример. Найдите значение выражения

Решение. Используем формулу приведения:

Пример. Найдите значение выражения 5tg17⁰ · tg107⁰.

Решение. Используем формулу приведения:

5tg17⁰ · tg107⁰ = 5tg17⁰·tg(90⁰ + 17⁰) = 5tg17⁰·(−ctg17⁰) = −5(tg17⁰·ctg17⁰) = −5·1 = −5.

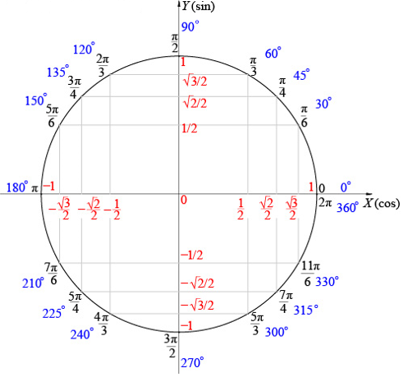
Тригонометрический круг

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Он заменяет десяток таблиц.

Сколько полезного на этом рисунке!

1. Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан.

2. Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси x, а значение синуса — на оси y.

3. И синус, и косинус принимают значения от –1 до 1.

Тригонометрический круг:

1. Значение тангенса угла α тоже легко найти — поделив sinα на cosα. А чтобы найти котангенс — наоборот, косинус делим на синус.

2. Знаки синуса, косинуса, тангенса и котангенса.

3. Синус — функция нечётная, косинус — чётная.

4. Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен 2π.

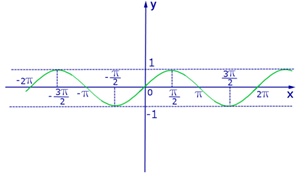
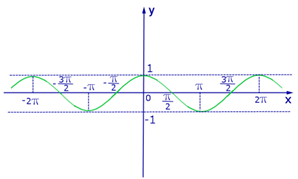
Графики тригонометрических функций

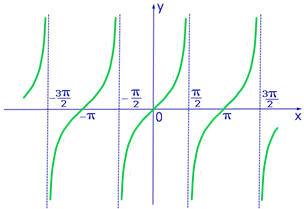
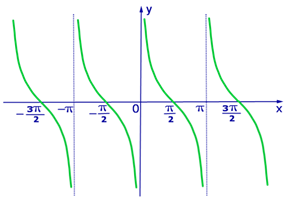
На рисунках приведены графики тригонометрических функций: y = sinx, y = cosx, y = tgx, y = ctgx.

1. График функции y = sinx

2. График функции y = cosx

3. График функции y = tgx

4. График функции y = ctgx