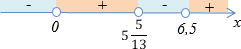
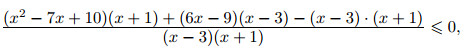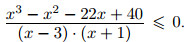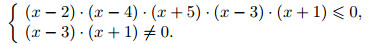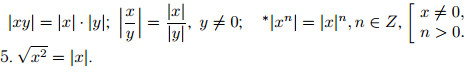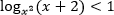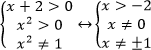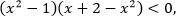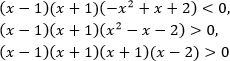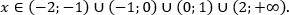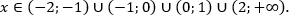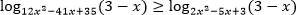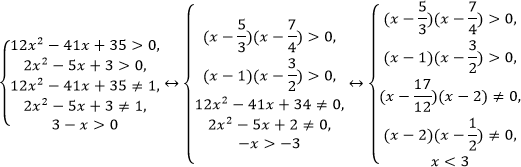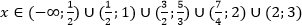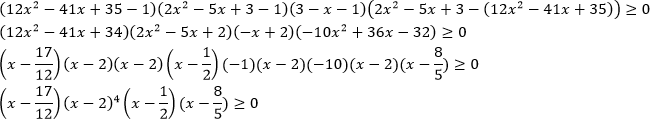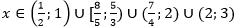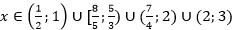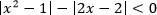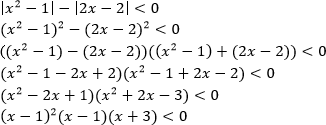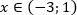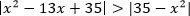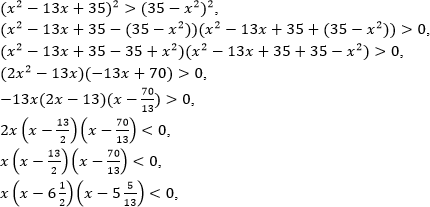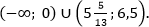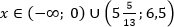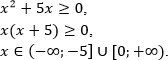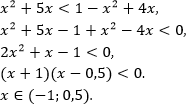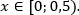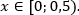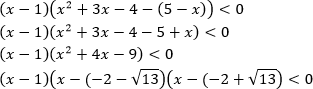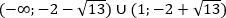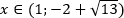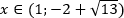Формулы рационализации для егэ по математике профиль 2022 - Помощь в подготовке к экзаменам и поступлению

урок 10. Математика ЕГЭ

Метод рационализации

Метод рационализации (равносильности) необходим для успешной сдачи ЕГЭ по профильной математике. В экзаменационных вариантах попадаются неравенства, которые удобнее и быстрее всего решать именно методом рационализации. Довольно часто можно обойтись и без него, но тогда количество вычислений в решении увеличивается в несколько раз, что повышает вероятность ошибки.

Прежде чем приступить к его изучению нужно обязательно знать следующие темы:

Свойства степеней и показательных функции
Свойства логарифмов
Решение показательных уравнений и показательных неравенств
Решение логарифмических уравнений и логарифмических неравенств
Метод замены переменной
Метод интервалов

Когда применяется метод рационализации?

Рационализация удобна, когда перед вами неравенство смешанного типа, то есть когда невозможно сделать замену переменной. Например:
$$ frac{2^{2x+1}-96*0,5^{2x+3}+2}{x+1} le 0$$
В числителе (x) стоит в степени показательной функции, а в знаменателе (x) сам по себе. Тут невозможно сделать замену так, чтобы ушли все (x). Как же такое решать? Перед вами большая дробь, которая сравнивается с нулем. Очевидно, дробь будет меньше нуля только тогда, когда числитель и знаменатель будут иметь противоположные знаки. Теперь можно рассмотреть две системы.

Первая:
$$ begin{cases}
2^{2x+1}-96*0,5^{2x+3}+2 ge 0, \
x+1 < 0.
end{cases}$$
И вторая такая же, только с противоположными знаками неравенства:
$$ begin{cases}
2^{2x+1}-96*0,5^{2x+3}+2 le 0, \
x+1 > 0.
end{cases}$$

Вторые неравенства в системах имеют строгий знак неравенства, так как это условия, накладываемые на знаменатель.

Согласитесь, решать две такие системы не очень приятное занятие. Хотя тут это вполне реально. Но что, если неравенства в системах будут значительно сложнее, или множителей будет не два, а больше. Тогда ваше решение будет очень громоздким. И вот тут на помощь приходит метод рационализации, или его еще называют методом равносильности. Он позволяет сократить вычисления в несколько раз.

Чуть ниже мы решим этот пример.

Второй случай, когда целесообразно применять метод рационализации, это когда в основании логарифмической или показательной функции лежит переменное основание. Показательных функций это касается в меньшей степени, а вот в логарифмах встречается часто. Например:

Пример 1
$$log_{5-x}(x+3) le 0$$
В основании логарифма стоит ((5-x)). Любое неравенство начинается с ОДЗ. Для того, чтобы правильно его записать, вспомним ограничения, накладываемые на любой логарифм (log_{a}b):
$$ begin{cases}
b > 0, \
a > 0, \
aneq 1.
end{cases}$$
Тогда в нашем примере ОДЗ будет выглядеть так:
$$ begin{cases}
x+3 > 0, \
5-x > 0, \
5-xneq 1.
end{cases}$$
$$ begin{cases}
x > -3, \
x< 5, \
xneq 4.
end{cases}$$
В итоге ОДЗ: (xin(-3;4)cup(4;5).)

Значит, во-первых, переменное основание дает нам дополнительные условия в ОДЗ, про которые ни в коем случае нельзя забывать!

А во-вторых, классические логарифмические неравенства решаются при помощи приведения левой и правой части неравенства к одинаковому основанию и вычеркиванию логарифма. Не будем отступать от традиций, воспользовавшись формулой представления любого числа или даже целого выражения, зависящего от (x), в виде логарифма с нужным нам основанием (b=log_{a}(a^b)):
$$log_{5-x}(x+3) le log_{5-x}(5-x)^0$$

В зависимости от (x) основание логарифмов может быть как больше единицы, так и меньше единицы. При решении логарифмических или показательных неравенств мы всегда смотрим на основание: если оно больше единицы, то знак неравенства сохраняется, а если от нуля до единицы, то обязательно нужно поменять знак неравенства на противоположный.

Проблема в том, что, так как основание переменное, оно может быть абсолютно любым в зависимости от (x). А следовательно, мы не знаем, менять нам знак неравенства или нет.

Здесь можно, конечно, рассмотреть опять две системы, когда основание больше единицы, и когда меньше на ОДЗ:
Либо
$$ begin{cases}
x+3 le (5-x)^0, \
5-x > 1.
end{cases}$$
$$ begin{cases}
x+3 le 1, \
5-x > 1.
end{cases}$$
$$ begin{cases}
x le -2, \
x < 4.
end{cases}$$
Решением этой системы будет (xle-2). А с учетом ОДЗ: (xin(-3;-2]).

Либо вторая система
$$ begin{cases}
x+3 ge (5-x)^0, \
0 lt 5-x lt 1.
end{cases}
$$
$$ begin{cases}
x+3 ge 1, \
0 lt 5-x lt 1.
end{cases}
$$
$$ begin{cases}
x ge -2, \
4 lt x lt 5.
end{cases}$$
Решением второй системы будет (xin(4;5).) C учетом ОДЗ: (xin(4;5).)

Так как обе системы нас устраивают, то решением исходного примера будет объединение решений эти двух систем на ОДЗ.
Ответ:(xin(-3;-2]cup(4;5).)

Даже в таком легком примере пришлось решать две системы плюс еще система с ОДЗ — не очень приятно. Здесь, опять же, выручает метод рационализации.

Метод рационализации в логарифмических неравенствах

Перед тем, как приступить к изучению, немного поговорим про равносильные преобразования. Им не уделяют достаточно внимания в школе, кажется, что это очевидная штука. Но это очень важно.

Итак, равносильные преобразования — это преобразования, при которых не меняются корни уравнения или неравенства. Например, перенос слагаемого в неравенстве слева направо от знака неравенства — это ни что иное, как равносильное преобразование. Ведь если перенести слагаемое, не забыв при этом поменять перед ним знак, то корни неравенства или уравнения останутся теми же самыми — они не изменятся, их не станет больше и даже меньше их не будет. Корни уравнения после преобразования будут один в один, как до преобразования.

Вам, возможно, кажется, что я говорю очевидные вещи. Но равносильные преобразования бывают гораздо сложнее. Например, в методе рационализации мы как раз будем делать равносильные преобразования.

Рассмотрим применение метода рационализации для начала на простом примере:

Пример 2
$$log_{x}(2x+5)>1;$$

ОДЗ: (x>0, quad xneq1.)

Приводим к одному основанию:
$$log_{x}(2x+5)>log_{x}(x); qquad (*)$$

Оказывается, вместо решения логарифмического неравенства с переменным основанием, я могу решить равносильное ему обыкновенное неравенство на ОДЗ, и корни будут абсолютно такие же:
$$(x-1)((2x+5)-x)>0; qquad (**)$$
$$(x-1)(x+5)>0;$$

Давайте попробуем разобраться, почему корни получившегося неравенства будут совпадать на ОДЗ с корнями исходного логарифмического неравенства.

Действительно, если основание логарифмов больше единицы — (x > 1), то знак неравенства (*) должен сохраниться или, другими словами, ((2х+5)) должно быть больше (x).

А если основание от нуля до единицы — (0 lt х lt 1), то знак неравенства меняется на противоположный и ((х+5)) должно быть меньше (х). (Смотри (*)).

Именно эти два условия и описывает неравенство (**). Посмотрите на него внимательно. Для того, чтобы неравенство было верно, необходимо, чтобы произведение двух скобок было больше нуля. Это возможно в двух случаях: если скобки обе положительные, и если обе отрицательные.

Первая скобка положительна при (x>1), тогда, чтобы неравенство (**) было верным, необходимо выполнение условия (2x+5>x). Один в один случай, когда основания логарифмов больше 1.

И наоборот, если первая скобка отрицательна на ОДЗ при (0 lt x lt 1), то вторая скобка тоже должна быть отрицательной, чтобы выполнялось неравенство (**), то есть (2x+5 lt x). Случай, когда основания логарифмов меньше единицы, но больше нуля.

В случае, если у нас неравенство (**) со знаком меньше, а не больше, как в примере выше, рассуждения будут точно такими же, только произведение двух множителей (скобок) будет меньше нуля, при условии, что они разных знаков: первый множитель отрицательный, второй положительный и наоборот!

Дорешаем пример (**) при помощи метода интервалов:

C учетом ОДЗ получим:
Ответ: (xin(1;+infty)).

Метод рационализации для логарифмов в общем виде

Общая схема метода рационализации выглядит так:

Пусть есть некоторое логарифмическое неравенство с одинаковыми, но зависящим от (х) основаниями:
$$log_{a(x)}(f(x))>log_{a(x)}(g(x));$$
Тогда вместо него можно решить равносильное неравенство на ОДЗ:
$$ begin{cases}
(a(x)-1)(f(x)-g(x))>0, \
f(x)>0, \
g(x)>0, \
a(x)>0, \
a(x)neq1.
end{cases}$$

Если знак меньше:
$$log_{a(x)}(f(x))<log_{a(x)}(g(x));$$
$$ begin{cases}
(a(x)-1)(f(x)-g(x))<0, \
f(x)>0, \
g(x)>0, \
a(x)>0, \
a(x)neq1.
end{cases}$$

Обратите внимание, что все преобразования в методе рационализации делаются на ОДЗ. Не забудьте про него, иначе все пойдет не по плану!

Разберем несколько примеров применения метода рационализации в логарифмических неравенствах без полного решения. Просто посмотрим, как делаются равносильные преобразования, дорешивать до конца не будем.

Пример 3

$$log_{x-4}(x^2-1)>1;$$
Представим в виде, чтобы слева и справа стоял логарифм с основанием (х-4):
$$log_{x-4}(x^2-1)>log_{x-4}(x-4);$$
Равносильное преобразование:
$$ begin{cases}
(x-4-1)(x^2-1—(x-4))>0, \
x^2-1>0, \
x-4>0, \
x-4neq1.
end{cases}$$
$$ begin{cases}
(x-5)(x^2-x+3))>0, \
x^2-1>0, \
x-4>0, \
x-4neq1.
end{cases}$$

Далее решаем получившуюся систему неравенств. В качестве тренировки, сделайте это сами.

Пример 4

$$log_{frac{25-x^2}{16}}left(frac{24+2x-x^2}{14}right)>1.$$
Выглядит страшно, но на самом деле все не так сложно. Первым делом представим единицу справа в виде логарифма с таким же основанием:
$$log_{frac{25-x^2}{16}}left(frac{24+2x-x^2}{14}right)>log_{frac{25-x^2}{16}}left(frac{25-x^2}{16}right).$$
Теперь воспользуемся рационализацией:
$$ begin{cases}
left(frac{25-x^2}{16}-1right)left(frac{24+2x-x^2}{14}-frac{25-x^2}{16}right)>0, \
frac{24+2x-x^2}{14}>0, \
frac{25-x^2}{16}>0, \
frac{25-x^2}{16}neq1.
end{cases}$$
В скобках в первом неравенстве все внимательно приводим к общему знаменателю и решаем методом интервалов.

Общий случай метода рационализации

Бывают логарифмические неравенства в виде произведения или частного различных множителей. В таких примерах обойтись без рационализации сложно. Разберем на примере:

Пример 5
$$ x*log_{x+3}(7-2x) ge 0 $$
Неравенство представляет из себя произведение двух функций-множителей (f(x)=х) и (g(x)=log_{x+3}(7-2x)). Тогда наше неравенство можно переписать в виде:
$$f(x)*g(x) ge 0;$$
Очевидно, что произведение двух множителей будет больше нуля, когда либо оба множителя одновременно положительны, либо когда оба одновременно отрицательны. Но решать две системы слишком долго, а что, если у нас множителей больше?

Было бы здорово решить наше неравенство методом интервалов, но, к сожалению, метод интервалов применим только для линейных множителей (без всяких логарифмов, показательных функций, степеней и др.).

И здесь нам на помощь приходит метод рационализации, он позволяет представить (g(x)=log_{x+3}(7-2x)) в виде произведения линейных множителей, знаки которого полностью совпадают со знаками логарифма. То есть это произведение будет положительно (отрицательно) при тех же самых (x), при которых положительна (отрицательна) наша функция (g(x)=log_{x+3}(7-2x)).

В самом общем виде знак любого логарифма (log_{q(x)}(p(x))) абсолютно совпадает при тех же самых (x) со знаком выражения ((q(x)-1)(p(x)-1)) при (p(x)>0), (q(x)>0), (q(x)neq1):

$$ log_{q(x)}(p(x)) ge 0 Rightarrow
begin{cases}
(q(x)-1)(p(x)-1)ge 0, \
p(x)>0, \
q(x)>0, \
q(x)neq1.
end{cases} qquad (***)$$

В нашем примере №5 логарифм можно заменить вот так:

$$ log_{x+3}(7-2x) ge 0 Rightarrow begin{cases}
(x+3-1)(7-2x-1) ge 0, \
7-2x>0, \
x+3>0, \
x+3neq1.
end{cases}; $$

Действительно, логарифм будет больше-равен нуля:
если основание логарифма (x+3 > 1), а аргумент (7-2x ge 1);
если основание логарифма (0

Обратите внимание, что неравенство ((x+3-1)(7-2x-1) ge 0 ) будет выполняться точно при таких же (x) на ОДЗ логарифма.

Аналогично логарифм (g(x)=log_{x+3}(7-2x)) будет меньше нуля при тех же самых (x), при которых выполняется неравенство ((x+3-1)(7-2x-1) le 0 ) на ОДЗ.

Возвращаясь к исходному примеру 5:
$$ x*log_{x+3}(7-2x) ge 0 $$
Согласно формулам выше (***) логарифм в этом неравенстве можно заменить на «приличное» выражение на ОДЗ:

$$ begin{cases}
x*(x+3-1)(7-2x-1) ge 0, \
7-2x>0, \
x+3>0, \
x+3neq1.
end{cases}; $$

$$ begin{cases}
x*(x+2)(6-2x) ge 0, \
x<3,5, \
x>-3, \
xneq-2.
end{cases}; $$

$$ begin{cases}
x*(x+2)(6-2x) ge 0, \
x in (-3;-2) cup (-2;3,5).
end{cases}; $$

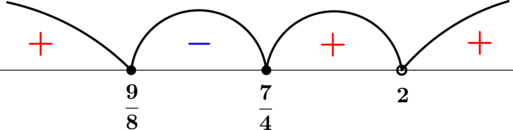
Решаем методом интервалов (зеленым показано решение первого неравенства, красным отмечены решения остальных условий в системе, а фиолетовой штриховкой отмечено итоговое решение системы) :

Ответ: ( x in (-3;-2) cup [0;3].)

Рассмотрим еще более сложный пример на рационализацию:

Пример 6
$$ (x-1)*log_{x+3}(x+2)*log_{3}((x+3)^2) le 0;$$

Первым делом найдем ОДЗ:
$$ begin{cases}
x+2>0, \
x+3>0, \
x+3 neq 1, \
(x+3)^2>0.
end{cases}; $$

В итоге ОДЗ получается (xin(-2;+infty);)
Теперь перейдем к решению самого примера. Тут сразу произведение трех множителей!
Но ничего страшного, применим метод рационализации для обоих логарифмов:

Логарифм (log_{x+3}(x+2)) совпадает со знаком выражения ((x+3-1)(x+2-1)).
А логарифм (log_{3}((x+3)^2)) совпадает со знаком ((3-1)((x+3)^2-1)).

Подставим получившееся преобразование в исходное неравенство:
$$ (x-1)*(x+3-1)(x+2-1)*(3-1)((x+3)^2-1) le 0;$$
Упростим выражения в скобках
$$ (x-1)*(x+2)(x+1)*2*(x+2)(x+4) le 0;$$
$$2 (x-1)*(x+2)^2*(x+1)*(x+4) le 0;$$

Решим методом интервалов с учетом ОДЗ:

Метод рационализации в показательных неравенствах

Рационализация бывает удобна не только в логарифмических неравенствах, а также в показательных. Принцип остается тем же самым, в общем виде он выглядит так:

$$a(x)^{f(x)} ge a(x)^{g(x)} Rightarrow
begin{cases}
(a(x)-1)(f(x)-g(x)) ge 0, \
a(x)>0.
end{cases} qquad (*)$$

(f(x)), (g(x)) — некоторые функции зависящие от (x);
(а(x)) — положительное основание показательной функции, в сложных примерах оно тоже может зависеть от (x).

Посмотрим, как это работает на простом примере из обыкновенных показательных неравенств:

Пример 7
$$5^{2x-3}ge5^{x+4}$$
Пример совершенно элементарный, и мы обычно решаем такие без всякой рационализации. Но он удобен для того, чтобы продемонстрировать, как работает метод. Надеюсь, вы помните, что метод рационализации сводится к равносильным преобразованиям. То есть мы заменяем исходное неравенство на другое попроще, без показательных функций, но имеющее абсолютно такие же корни, что и исходное. Сделаем это, воспользовавшись общим видом (*):
$$(5-1)((2x-3)-(x+4))ge0; qquad (**) $$
Пусть обилие скобок вас не смущает, я их поставил специально, чтобы выделить функции, стоящие в степенях. Можно легко преобразовать:
$$ 4*(2x-3-x-4)ge0;$$
$$4*(x-7)ge 0;$$
$$xge7.$$
Мы решили неравенство. Можно просто запомнить формулу, но лучше понять, почему работает (*).

Чтобы во всем разобраться, нужно вспомнить, как решаются показательные неравенства. Первым делом приводим к одинаковому основанию: у нас в примере №7 слева и справа основание 5, поэтому с этим все хорошо. Дальше мы смотрим, больше ли основание единицы, если да, то просто вычеркиваем основание, сохраняем знак неравенства и сравниваем степени. А если меньше, то не забываем поменять знак неравенства на противоположный.

В нашем примере основание (5>1) поэтому решение всего неравенства сводится к решению (2x-3 ge x+4). Обратите внимание на (**): оно представляет из себя произведение двух скобок ((5-1)) и (((2x-3)-(x+4))), а произведение будет больше нуля когда? Когда множители либо оба положительны, либо оба отрицательны.

Так как очевидно ((5-1)>0), то второй множитель (((2x-3)-(x+4))) тоже должен быть больше нуля, чтобы все неравенство было верным. Или другими словами, должно выполняться: (2x-3 ge x+4), что то же самое, если бы мы решали без всякой рационализации.
Можно вообще все показательные неравенства решать рационализацией. Она дает вам право не обращать внимания на основание (больше или меньше единицы). Посмотрим еще простой пример:

Пример 8
$$left(frac{1}{2}right)^{x+2}geleft(frac{1}{2}right)^{-2x-4};$$
Сразу по формуле (*) применим метод рационализации:
$$ (frac{1}{2}-1)((x+2)-(-2x-4))ge0;$$
Опять две скобки, но в этот раз первая скобка будет отрицательная (frac{1}{2}-1<0), а значит, для того, чтобы все произведение было больше равно нуля, вторая скобка ((x+2)-(-2x-4)) тоже должна быть меньше равна нуля. Или другими словами должно выполняться (x+2le-2x-4).

Это все эквивалентно обычному методу решения показательных неравенств с избавлением от основания. Здесь основания слева и справа одинаковые и меньше единицы, значит вычеркиваем их и меняем знак неравенства: (x+2le-2x-4). В методе рационализации у нас тоже все свелось к точно такому же неравенству.

Примеры №7 и 8 обычно не решают методом рационализации. Давайте разберем пример, в котором рационализация сильно упрощает решение:

Пример 9
$$ (x+2)^{3-7x} ge (x+2)^{6-5x}$$
Обратите внимание, что здесь уже появляется ОДЗ, так как показательная функция определена только для положительного основания.
ОДЗ:
$$x+2>0;$$
$$x>-2;$$
Следим, чтобы основание показательной функции было одинаково слева и справа. У нас все так. Вот только теперь мы не знаем, основание больше единицы или меньше, ведь при различных значениях (x) может быть и так, и так. Можно, конечно, рассмотреть два случая: когда основание больше единицы и когда меньше. Но придется решать две системы, а это долго. Воспользуемся методом рационализации по формуле (*), аналогично, как мы делали примеры №7 и 8:
$$(x+2-1)((3-7x)-(6-5x))ge0;$$
Раскроем скобки внутри скобок и приведем подобные слагаемые.
$$(x+1)(-2x-3)ge0;$$
Решим неравенство методом интервалов:

Получаем, что (xin[-frac{3}{2};-1]). Проверяем, чтобы все удовлетворяло ОДЗ. У нас весь промежуток подходит.
Ответ:(xin[-frac{3}{2};-1]).

Теперь разберем более общий случай применения метода рационализации. Дело в том, что часто встречаются смешанные неравенства, и в них кроме показательной функции бывают логарифмические, тригонометрические, линейные и т.д. В общем, намешана вся школьная программа. В таких случаях нам тоже может помочь рационализация.

Общее правило рационализации

Оказывается, любое выражение типа
$$a^{f(x)}-a^{g(x)}$$
будет иметь абсолютно такой же знак, что и выражение
$$(a-1)(f(x)-g(x)). qquad (***)$$
Это означает, что вместо неравенства (a^{f(x)}-a^{g(x)}>0) можно решить неравенство ((a-1)(f(x)-g(x))>0). Корни у этих неравенств будут абсолютно одинаковые. Со знаком меньше аналогично.

Пример 10
$$(x+1)*(5^x-5^{2x-4})le0;$$
Кроме показательных функций (5^x), у нас еще есть линейный множитель ((x+1)). Замену тут не сделать. Попробуем применить метод рационализации.

Выражение (5^x-5^{2x-4}) полностью совпадает по знаку с выражением ((5-1)(x-(2x-4))).
Попробуем разобраться почему. Будет немного запутанно, но стоит разобраться.

Действительно, так как основание у нас одинаковое и больше единицы, то если степень у (5^x) будет больше степени у (5^{2x-4}), то есть (x>2x-4), то (5^x>5^{2x-4}) и все выражение (5^x-5^{2x-4}>0). Вспомните свойства показательной функции: если основание больше единицы, то показательная функция будет возрастающей (с увеличением степени растет вся функция).
Поэтому (5^x-5^{2x-4}) будет положительно тогда, когда
$$x>2x-4 Rightarrow x-(2x-4)>0 Rightarrow (5-1)(x-(2x-4))>0. $$
И (5^x-5^{2x-4}) будет отрицательно тогда, когда
$$ x<2x-4 Rightarrow x-(2x-4)<0 Rightarrow (5-1)(x-(2x-4))<0 $$
А скобка ((5-1)) в данном случае ни на что не влияет, она всегда положительна.

А если бы выражение было такое: (left(frac{1}{5}right)^x-left(frac{1}{5}right)^{2x+7}). То согласно (***) его можно заменить на ((frac{1}{5}-1)(x-(2x+7))). Произведение двух множителей, где первая скобка ((frac{1}{5}-1)) всегда отрицательна. И опять при одних и тех же (x) у них будут одинаковые знаки.

Только в этот раз основание (frac{1}{5}) у показательных функций меньше единицы. А значит показательная функция будет убывающей (с увеличением степени сама функция падает). Значит (left(frac{1}{5}right)^x-left(frac{1}{5}right)^{2x+7}>0) будет больше нуля тогда, когда
$$x<2x+7 Rightarrow x-(2x+7)<0 Rightarrow (frac{1}{5}-1)(x-(2x+7))>0. $$
И наоборот:
$$left(frac{1}{5}right)^x-left(frac{1}{5}right)^{2x+7}<0 Rightarrow (frac{1}{5}-1)(x-(2x+7)<0.$$

И еще раз вернемся к нашему примеру №10
$$(x+1)*(5^x-5^{2x-4})le0;$$
Вторую скобку заменим согласно нашим рассуждениям по формуле (***):
$$(x+1)(5-1)(x-(2x-4))le0;$$
Приведем подобные
$$4*(x+1)(-x+4)le0;$$
И решим методом интервалов получившееся простейшее неравенство:
Ответ: (xin(-infty;-1]cup[4;+infty).)

Рассмотрим пример посложнее.

Пример 11
$$frac{(2^{x+1}-4^{x-3})*(x-2)}{7^{2x}-1}ge0;$$
Постараемся по максимуму привести к одинаковым основаниям. Выпишем для удобства отдельно:
$$4^{x-3}=left(2^{2}right) ^{x-3}=2^{2*(x-3)};$$
$$1=7^0;$$
Подставим в исходное неравенство:
$$frac{(2^{x+1}-2^{2(x-3)})*(x-2)}{7^{2x}-7^0}ge0;$$
Теперь воспользуемся формулой (***):
$$2^{x+1}-2^{2(x-3)} Rightarrow (2-1)((x+1)-2(x-3))=1*(-x+7)=7-x;$$
$$7^{2x}-7^0 Rightarrow (7-1)(2x-0)=6*2x=12x;$$
И подставим:
$$frac{(7-x)*(x-2)}{12x}ge0;$$
Наше страшное исходное неравенство при помощи формул рационализации превратилось в обыкновенное неравенство из 8-го класса, которое решается методом интервалов.

Ответ: (xin(-infty;0)cup[2;7].)

Пример 12
$$ frac{2^{2x+1}-96*0,5^{2x+3}+2}{x+1} le 0$$
Рассмотрим пример, про который мы говорили в самом начале статьи. Выпишем отдельно числитель и постараемся разложить его на множители. Для этого выпишем и приведем показательные функции к одинаковому основанию:
$$0,5^{2x+3}=2^{-1*(2x+3)}=frac{1}{2^{2x+3}}=frac{1}{2^2*2^{2x+1}}=frac{1}{4*2^{2x+1}};$$
Подставим в числитель исходного неравенства:
$$ 2^{2x+1}-96*frac{1}{4*2^{2x+1}}+2$$
Теперь у нас есть одинаковые показательные функции — (2^{2x+1}). Сделаем замену, пусть (t=2^{2x+1}:)
$$ t-96*frac{1}{4*t}+2;$$
Приводим к общему знаменателю:
$$ frac{4t^2+8t-96}{4*t};$$
Разложим квадратный многочлен на множители через дискриминант:
$$ frac{4(t+6)(t-4)}{4*t};$$
И сделаем обратную замену, напоминаю, что (t=2^{2x+1}:)
$$ frac{4(2^{2x+1}+6)(2^{2x+1}-4)}{4*2^{2x+1}};$$
Это мы разложили числитель исходного неравенства на множители, подставим наше разложение в неравенство:
$$frac{4(2^{2x+1}+6)(2^{2x+1}-4)}{4*2^{2x+1}*(x+1)} le 0;$$
Тут важно отметить один факт, что показательная функция по определению всегда положительна. А для нас это означает, что множители (2^{2x+1}+6>0) и (2^{2x+1}>0), а значит их можно просто вычеркнуть, так как они абсолютно не влияют на знак всего выражения:
$$frac{(2^{2x+1}-4)}{(x+1)} le 0;$$
А теперь воспользуемся методом рационализации:
$$2^{2x+1}-4=2^{2x+1}-2^2 Rightarrow (2-1)(2x+1-2)=2x-1; $$
Подставим рационализацию в неравенство:
$$frac{2x-1}{x+1} le 0;$$
Ну вот мы свели исходное неравенство к простейшему, которое легко решается методом интервалов.
Ответ: (xin(-1;frac{1}{2}];)

Формулы метода рационализации

Для логарифмов

$$log_{a(x)}(f(x))>log_{a(x)}(g(x)) Rightarrow log_{a(x)}(f(x))-log_{a(x)}(g(x))>0;$$

Вместо этих неравенств можно решить равносильную им систему на ОДЗ:
$$ begin{cases}
(a(x)-1)(f(x)-g(x))>0, \
f(x)>0, \
g(x)>0, \
a(x)>0, \
a(x)neq1.
end{cases}$$

Если знак неравенства меньше:
$$log_{a(x)}(f(x))<log_{a(x)}(g(x)) Rightarrow log_{a(x)}(f(x))-log_{a(x)}(g(x))<0; $$
$$ begin{cases}
(a(x)-1)(f(x)-g(x))<0, \
f(x)>0, \
g(x)>0, \
a(x)>0, \
a(x)neq1.
end{cases}$$

Любой логарифм совпадает по знаку с системой:

$$ log_{q(x)}(p(x)) ge 0 Rightarrow
begin{cases}
(q(x)-1)(p(x)-1)ge 0, \
p(x)>0, \
q(x)>0, \
q(x)neq1.
end{cases}
$$

В показательных неравенствах принцип очень похож:

$$a(x)^{f(x)} — a(x)^{g(x)} Rightarrow begin{cases}
(a(x)-1)(f(x)-g(x));, \
a(x)>0.
end{cases}$$

Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.

Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.

Урок по теме логарифмы и их свойства. Разбираемся, что такое логарифм и какие у него свойства. Научимся считать выражения, содержащие логарифмы. И рассмотри несколько возможных заданий №4 из ЕГЭ по профильной математике.

Разбираем, как вычислить степень с рациональным (дробным) показателем. Свойства степени с рациональным показателем. Примеры решения задания №9 из ЕГЭ по математике профильного уровня.

Что такое корень n-й степени. Познакомимся со свойствами коня n-й степени и методами оценки значения корня. Разберем какая у него областью определения.

В уроке разбираем, что такое арифметический квадратный корень и знакомимся с основными его свойствами. Выносим множитель из под знака корня. Избавляемся от иррациональности

Знакомимся с понятием степени с натуральным показателем и ее свойствами. Разбор преобразования сложные степенных выражений на примерах.

Цикл уроков про степени и логарифмы и их свойства. Учимся решать показательные и логарифмические уравнения и неравенства. Задания №9 и №15 ЕГЭ по профильной математике.

Индивидуальные занятия с репетитором для учеников 6-11 классов. Для каждого ученика я составляю индивидуальную программу обучения. Стараюсь заинтересовать ребенка предметом, чтобы он с удовольствием занимался математикой и физикой.

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Неравенства, решаемые методом рационализации

(blacktriangleright) Метод рационализации для показательной функции.
Если левая часть неравенства представлена в виде произведения некоторых множителей, а справа стоит ноль, то множители вида (a^{f(x)}-a^{g(x)}) можно заменить на произведение двух скобок: ((a-1)(f(x)-g(x))).

Пример.
Неравенство ((3^x-1)(0,25^x-16)(5x^2-9x-2)leqslant0) равносильно
неравенству ((3^x-3^0)(0,25^x-0,25^{-2})(5x^2-9x-2)leqslant 0),
которое в свою очередь по методу рационализации можно переписать в виде [(3-1)(x-0)(0,25-1)(x-(-2))(5x+1)(x-2)leqslant0]

(blacktriangleright) Метод рационализации для логарифмической функции.
Так как у логарифмов уже появляются ограничения на ОДЗ, то данный метод работает только при выполнении условий ОДЗ для логарифмов! Следовательно, последовательность решения подобных неравенств такая:

1) находим ОДЗ неравенства;

2) решаем неравенство, как будто ОДЗ выполнено;

3) пересекаем полученный ответ с ОДЗ и получаем итоговый ответ.

Суть метода рационализации:
1) если левая часть неравенства представлена в виде произведения некоторых множителей, а справа стоит ноль, то множители вида ((log_{a}f(x)-log_{a}g(x))) можно заменить на произведение двух скобок: ((a-1)(f(x)-g(x))) (при условии выполнения ОДЗ!).
2) если левая часть неравенства представлена в виде произведения некоторых множителей, а справа стоит ноль, то множители вида (log_{a}f(x)) можно заменить на произведение двух скобок: ((a-1)(f(x)-1)) (при условии выполнения ОДЗ!).

Пример.
Неравенство ((3+x-2x^2)log_{x+2}{(3x+5)}geqslant 0) с помощью метода рационализации можно переписать в виде: [begin{cases}
(3+x-2x^2)(x+2-1)(3x+5-1)geqslant 0\
x+2>0qquad qquad text{(ОДЗ)}\
x+2ne 1qquad qquad text{(ОДЗ)}\
3x+5>0 qquad qquad text{(ОДЗ)}end{cases}]

Задание
1

#1595

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
log_{x + 1} (x — 1)geqslant 0
end{aligned}]

ОДЗ: [begin{cases}
x + 1 > 0\
x + 1neq 1\
x — 1 > 0
end{cases}
qquadLeftrightarrowqquad
x > 1,.]

По методу рационализации: на ОДЗ

[begin{aligned}
log_{x + 1} (x — 1)geqslant 0qquadLeftrightarrowqquad (x + 1 — 1)cdot (x — 1 — 1)geqslant 0qquadLeftrightarrowqquad xcdot (x — 2)geqslant 0,.
end{aligned}]

Так как на ОДЗ (x > 1 > 0), то на ОДЗ последнее неравенство равносильно неравенству [x — 2geqslant 0qquadLeftrightarrowqquad x geqslant 2] C учётом ОДЗ в итоге: (xin[2; +infty).)

Ответ:

([2; +infty))

Задание
2

#1596

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
log_{x^2} (x^2 + 1) > 0
end{aligned}]

ОДЗ: [begin{cases}
x^2 > 0\
x^2 neq 1\
x^2 + 1 > 0
end{cases}
qquadLeftrightarrowqquad
begin{cases}
x neq 0\
x neq pm 1,.
end{cases}]

По методу рационализации: на ОДЗ

[begin{aligned}
log_{x^2} (x^2 + 1) > 0qquadLeftrightarrowqquad (x^2 — 1)cdot (x^2 + 1 — 1) > 0qquadLeftrightarrowqquad (x^2 — 1)cdot x^2 > 0,.
end{aligned}]

Так как на ОДЗ (x^2 > 0), то на ОДЗ последнее неравенство равносильно неравенству [x^2 — 1 > 0qquadLeftrightarrowqquad x in(-infty; -1)cup(1; +infty),.] C учётом ОДЗ в итоге: (xin(-infty; -1)cup(1; +infty).)

Ответ:

((-infty; -1)cup(1; +infty))

Задание
3

#3144

Уровень задания: Равен ЕГЭ

Решите неравенство [(x^2+3x-10)cdot log_{0,5}(x^2-1)cdot
log_{(x^2-1)}(x+2)leqslant 0]

Выпишем ОДЗ неравенства: [begin{cases}
x^2-1>0\
x^2-1ne 1\
x+2>0 end{cases} quadLeftrightarrowquad xin
(-2;-sqrt2)cup(-sqrt2;-1)cup(1;sqrt2)cup(sqrt2;+infty).] Решим неравенство на ОДЗ. Заметим, что по формуле (log_abcdot
log_bc=log_ac) неравенство можно переписать в виде: [(x^2+3x-10)cdot log_{0,5}(x+2)leqslant 0] По методу рационализации данное неравенство равносильно: [(x^2+3x-10)cdot (0,5-1)(x+2-1)leqslant 0 quadLeftrightarrowquad
(x+5)(x-2)(x+1)geqslant 0] Решим полученное неравенство методом интервалов и получим ответ: [xin [-5;-1]cup [2;+infty)] Пересечем ответ с ОДЗ и получим окончательный ответ [xin (-2;-sqrt2)cup(-sqrt2;-1)cup[2;+infty)]

Ответ:

((-2;-sqrt2)cup(-sqrt2;-1)cup[2;+infty))

Задание
4

#1623

Уровень задания: Равен ЕГЭ

Решите неравенство

[begin{aligned}
log_{(x — 2)} (x + 3) geqslant dfrac{1}{log_{x^{2}} (x — 2)}
end{aligned}]

ОДЗ: [begin{cases}
x — 2 > 0\
x — 2neq 1\
x + 3 > 0\
x^2 > 0\
x^{2} neq 1
end{cases}
qquadLeftrightarrowqquad
begin{cases}
x > 2\
xneq 3
end{cases}]

На ОДЗ:
исходное неравенство равносильно неравенству

[begin{aligned}
&log_{(x — 2)} (x + 3) geqslant log_{(x — 2)}x^{2}qquadLeftrightarrowqquad log_{(x — 2)} (x + 3) — log_{(x — 2)}x^{2}geqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad log_{(x — 2)} dfrac{(x + 3)}{x^2}geqslant 0,.
end{aligned}]

По методу рационализации: на ОДЗ

[begin{aligned}
&log_{(x — 2)} dfrac{(x + 3)}{x^2}geqslant 0 quadLeftrightarrowquad (x — 2 — 1)left(dfrac{x + 3}{x^2} — 1right)geqslant 0quadLeftrightarrow\
&Leftrightarrowquad (x — 3)cdotdfrac{x + 3 — x^2}{x^2}geqslant 0quadLeftrightarrowquad (x — 3)cdotdfrac{x^2 — x — 3}{x^2}leqslant 0
end{aligned}]

По методу интервалов на ОДЗ

Таким образом, с учётом ОДЗ исходное неравенство верно при [xinleft[dfrac{1+sqrt{13}}{2}; 3right).]

Ответ:

(left[0,5+0,5sqrt{13}; 3right))

Задание
5

#1598

Уровень задания: Равен ЕГЭ

Решите неравенство

[begin{aligned}
log_{(x + 1)} 2 geqslant dfrac{1}{log_{x} (x + 1)}
end{aligned}]

ОДЗ: [begin{cases}
x + 1 > 0\
x + 1neq 1\
x > 0\
xneq 1
end{cases}
qquadLeftrightarrowqquad
begin{cases}
x > 0\
xneq 1
end{cases}]

На ОДЗ:
исходное неравенство равносильно неравенству

[begin{aligned}
&log_{(x + 1)} 2 geqslant log_{(x + 1)} xqquadLeftrightarrowqquad log_{(x + 1)} 2 — log_{(x + 1)} xgeqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad log_{(x + 1)} dfrac{2}{x}geqslant 0,.
end{aligned}]

По методу рационализации: на ОДЗ

[begin{aligned}
&log_{(x + 1)} dfrac{2}{x}geqslant 0 qquadLeftrightarrowqquad (x + 1 — 1)left(dfrac{2}{x} — 1right)geqslant 0qquadLeftrightarrowqquad xcdotdfrac{2 — x}{x}geqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad 2 — xgeqslant 0qquadLeftrightarrowqquad xleqslant 2
end{aligned}]

Таким образом, с учётом ОДЗ исходное неравенство верно при [xin(0; 1)cup(1; 2].]

Ответ:

((0; 1)cup(1; 2])

Задание
6

#1602

Уровень задания: Равен ЕГЭ

Решите неравенство [log_{8-4x}(16x^2 — 8x + 1) leqslant 2.]

ОДЗ:

[begin{cases}
8 — 4x > 0\
8 — 4x neq 1\
16x^2 — 8x + 1 > 0
end{cases}
qquadLeftrightarrowqquad x in left(-infty; dfrac{1}{4}right) cup left(dfrac{1}{4}; dfrac{7}{4}right) cup left(dfrac{7}{4}; 2right).]

[log_{8-4x}(16x^2 — 8x + 1) — log_{8-4x}(8-4x)^2leqslant 0quadLeftrightarrowquad log_{8-4x}dfrac{16x^2 — 8x + 1}{(8 — 4x)^2}leqslant 0.] По методу рационализации это неравенство на ОДЗ равносильно:

[begin{aligned}
&(8 — 4x — 1)left(dfrac{16x^2 — 8x + 1}{(8 — 4x)^2} — 1right)leqslant 0 qquadLeftrightarrow\
&Leftrightarrowqquad (7 — 4x)cdotdfrac{16x^2 — 8x + 1 — (64 — 64x + 16x^2)}{(8 — 4x)^2}leqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad dfrac{(7 — 4x)(56x — 63)}{(8 — 4x)^2}leqslant 0quadLeftrightarrowquaddfrac{(4x — 7)(8x — 9)}{(4x — 8)^2}geqslant 0
end{aligned}]

По методу интервалов:

откуда (x inleft(-infty; dfrac{9}{8}right]cupleft[dfrac{7}{4}; 2right)cup(2; +infty)).
Пересечем ответ с ОДЗ: (x inleft(-infty; dfrac{1}{4}right)cupleft(dfrac{1}{4}; dfrac{9}{8}right]cupleft(dfrac{7}{4}; 2right)).
Окончательный ответ [x inleft(-infty; dfrac{1}{4}right)cupleft(dfrac{1}{4}; dfrac{9}{8}right]cupleft(dfrac{7}{4}; 2right),.]

Ответ:

(left(-infty; dfrac{1}{4}right)cupleft(dfrac{1}{4}; dfrac{9}{8}right]cupleft(dfrac{7}{4}; 2right))

Задание
7

#2645

Уровень задания: Равен ЕГЭ

Решите неравенство [{large{left(4^{x^2-x-6}-1right)cdot
log_{0,25}left(4^{x^2+2x+2}-3right)leqslant 0}}]

(Задача от подписчиков)

Найдем ОДЗ: [4^{x^2+2x+2}-3>0quadLeftrightarrowquad 4^{x^2+2x+2}>4^{log_43}quadLeftrightarrowquad
x^2+2x+1+1>log_43quadLeftrightarrowquad (x+1)^2>log_43-1.]

Заметим, что (log_43<log_44=1), следовательно, число (log_43-1<0). Т.к. квадрат любого выражения всегда неотрицателен, то неравенство ((x+1)^2>log_43-1) выполнено при всех (x).
Следовательно, ОДЗ: (xin mathbb{R}).

Перейдем к неравенству: [{large{left(4^{x^2-x-6}-4^0right)cdot
log_{0,25}left(4^{x^2+2x+2}-3right)leqslant 0}}] Преобразуем его по методу рационализации: [begin{aligned} &(4-1)(x^2-x-6-0)cdot
(0,25-1)left(4^{x^2+2x+2}-3-1right)leqslant 0
quadLeftrightarrow\[2ex] Leftrightarrowquad &3(x^2-x-6)cdot
(-0,75)left(4^{x^2+2x+2}-4^1right)leqslant
0quadLeftrightarrow\[2ex]
Leftrightarrowquad &(x^2-x-6)cdot (4-1)(x^2+2x+2-1)geqslant
0quadLeftrightarrow\[2ex]Leftrightarrowquad &(x+2)(x-3)cdot (x+1)^2geqslant
0end{aligned}] Решая данное неравенство методом интервалов, получим ответ: [xin (-infty;-2]cup{-1}cup[3;+infty).]

Ответ:

((-infty;-2]cup{-1}cup[3;+infty))

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Неравенства. Метод замены множителя (метод рационализации)

Полезный прием для решения сложных неравенств на ЕГЭ по математике – метод рационализации неравенства. Другое название — метод замены множителя. Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках о таком не написано.

Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные показательные или логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству.

Давайте для начала вспомним, что такое равносильные уравнения (или неравенства). В школьной программе этот важный вопрос почти не обсуждается. Поэтому запишем определение.

Равносильными называются уравнения, множества решений которых совпадают.

Заметим, что внешне уравнения могут быть и не похожи друг на друга.

Например, уравнения (x − 3)² = 0 и x − 3 = 0 равносильны. Число 3 является единственным решением и того, и другого.

Уравнения $x^{2}=-1$ и также равносильны. Оба они не имеют решений. Другими словами, множество решений каждого из них – пусто.

Уравнения и $2x-1=(x-2)^{2}$ не являются равносильными. Решением первого уравнения является только x = 5. Решения второго – два числа: x = 5 и x = 1. Получается, что возведение обеих частей уравнения в квадрат в общем случае приводит к уравнению, неравносильному исходному.

Аналогичное определение – для неравенств.

Равносильными называются неравенства, множества решений которых совпадают.

Например, неравенства и $frac{x-1}{x-3}>0$ равносильны – ведь множества их решений совпадают. В этом легко убедиться с помощью метода интервалов.

Неравенства $log_{2}x>log_{2}5$ и x> 5 также равносильны при x> 0 . Заметим, что внешне эти неравенства не похожи – одно из них логарифмическое, другое алгебраическое.

Другими словами, при x > 0 неравенства $log_{2}x-log_{2}5>0$ и x-5>0 имеют одинаковые решения. Если какое-либо число x > 0 является решением одного из них, то оно будет и решением второго.

А это значит, что при любом x > 0 выражение $log_{2}x-log_{2}5$ будет иметь такой же знак, как и выражение x − 5. Следовательно, если в какое-либо сложное неравенство входит в качестве множителя выражение $log_{2}x-log_{2}5$ , то при выполнении условия x > 0 его можно заменить на более простое x − 5 и получить неравенство, равносильное исходному.

Вот ключевой момент. На этом и основан метод рационализации – замены множителей, содержащих сложные логарифмические или показательные выражения, на более простые алгебраические множители.

Например, выражение вида $log_{a}f-log_{a}g$ , где f и g – функции от x, a – число, можно заменить на более простое (f − g) (a − 1) – конечно, при условии, что f(x) > 0 и g(x) > 0. Доказательство легко провести самостоятельно.

А сейчас – самое главное: волшебная таблица, позволяющая заменять сложные логарифмические (или показательные) множители в неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот увидите, она выручит вас на ЕГЭ по математике:

Сложный множитель	На что заменить
log_h f − log_h g	(h − 1) (f − g)
log_h f − 1	(h − 1) (f − h)
log_h f	(h − 1) (f − 1)
h^f − h^g	(h − 1) (f − g)
h^f − 1	(h − 1) · f
f^h − g^h	(f − g) · h
f, g — функции от x. h — функция или число.

Конечно же, все выражения, которые содержат логарифмы, существуют при f, g, h > 0 и h ≠ 1.

Когда на ЕГЭ по математике вы применяете метод рационализации (замены множителя), – обязательно поясните, что вы им воспользовались. И не забудьте доказать соответствующую формулу. Иначе можно потерять балл.

Обратите внимание, что мы говорим о замене множителя в неравенствах вида Знак здесь может быть любой: >, ≥, ≤. Правая часть обязательно должна быть равна нулю. И заменяем мы именно множитель (а не слагаемое, например). Иначе ничего не получится.

Перейдем к практике – к решению задач из вариантов ЕГЭ по математике Профильного уровня.

1. $log_{2-x}(x+2)cdot log_{x+3}(3-x)leq 0$ .

ОДЗ неравенства: .

Применим метод рационализации. В соответствии с нашей таблицей, множитель $log_{2-x}(x+2)$ заменим на (2 − x − 1)(x + 2 − 1). Множитель вида $log_{x+3}(3-x)$ заменим на (x + 3 − 1)(3 − x − 1). Таким образом, от логарифмического неравенства мы перешли к рациональному:

(1 − x) (x + 1) (x + 2) (2 − x) ≤ 0.

Решим его методом интервалов:

Ответ: .

2. $frac{10^{x}}{2cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}leq frac{(15cdot 3^{x})^{x}}{9cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}.$

Начнем с ОДЗ.

$left{begin{matrix} xneq 0;\ x>-2;\ xneq -1. end{matrix}right.$

Заметим, что выражение $log^{2}_{2}(x+1)^{2}$ положительно при x ∈ ОДЗ. Умножим обе части неравенства на это выражение.
Упростим числитель правой части неравенства:

$(15cdot 3^{x})^{x}=5^{x}cdot 3^{x}cdot 3^{x^{2}}=5^{x}cdot 3^{x^{2}+x}$
Поделим обе части неравенства на 5^x > 0:

$frac{2^{x}}{2log_{3}(x+2)}leq frac{3^{x^{2}+x}}{9log_{3}(x+2)}: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{x^{2}+x-2}}{log_{3}(x+2)}leq 0: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Неравенство уже намного проще, чем исходное. Но основания степеней разные! Чтобы применить метод рационализации, нам придется представить 2^{x − 1} в виде степени с основанием 3.

$2^{x-1}=3^{log_{3}2^{x-1}}=3^{(x-1)log_{3}2}.$ Неравенство примет вид:

$frac{3^{(x-1)log_{3}2}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Воспользуемся методом замены множителя. Множитель вида h^f −h^g можно заменить на (h − 1) (f − g). Да и логарифм в знаменателе можно заменить на выражение x + 1.

$frac{(x-1)(x-(log_{3}2-2))}{x+1}geq 0.$ Оценим $log_{3}2-2$ . Это необходимо сделать, чтобы правильно расставить точки на числовой прямой.

$log_{3}1<log_{3}2<log_{3}3;$ $0<log_{3}2<1$ $-2<log_{3}2-2<-1$ Ответ:

3. $frac{10^{log_{2}x}}{2x^{2}(x+1)}leq frac{(15cdot 3^{log_{2}x})^{log_{2}x}}{9x^{2}(x+1)}$ .

Постараемся упростить это неравенство. Область допустимых значений

$left{begin{matrix} x>0;\ x+1neq 0. end{matrix}right.$ Отсюда следует, что x > 0. Это хорошо, потому что при данных значениях x выражение x + 1 строго положительно, следовательно, мы можем умножить на него обе части неравенства. Да и на x² тоже можно умножить обе части неравенства, и тогда оно станет проще:

$frac{10^{log_{2}x}}{2}leq frac{15^{log_{2}x}cdot 3^{log^{2}_{2}x}}{9}$ Преобразуем числители выражений в левой и правой части и сделаем замену log₂x = t:

$frac{2^{t}cdot 5^{t}}{2}leq frac{3^{t}cdot 5^{t}cdot 3^{t^{2}}}{9}$ Теперь обе части неравенства можно сократить на 5^t > 0:

$2^{t-1}leq 3^{t^{2}+t-2};$
$2^{t-1}-3^{(t+2)(t-1)}leq 0.$

Поскольку $2=3^{log_{3}2}$ , выражение 2^t−1 можно записать как 3^{(t−1)·log₃2}:

$3^{(t-1)cdot log_{3}2}leq 3^{(t+2)(t-1)};$ $(t-1)cdot log_{3}2leq (t-1)(t+2);$ $(t-1)cdot log_{3}2-(t-1)(t+2)leq 0.$ $(t-1)(log_{3}2-t-2)leq 0;$ $(t-1)(t-(log_{3}2-2))leq 0.$ Заметим, что log₃2 − 2 < 0.

Мы получили квадратичное неравенство относительно t. Решим его:

Итак, t ≥ 1 или t ≤ log₃2 − 2.

Вернемся к переменной x:

$: \ log_{2}xgeq 1\ xgeq 2;$ или $: \ log_{2}xleq log_{3}2-2;\ 0<xleq 2^{log_{3}2-2}.$

Ответ: $x in (0;2^{log_3 2-2}]cup[2;+infty).$

4. Еще одна задача из той же серии:

$frac{14^{log_{2}(4x)}}{7cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}geq frac{(4cdot 2^{log_{2}(4x)})^{log_{2}(4x)}}{4cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}.$ Запишем ОДЗ:

$left{begin{matrix} x>0;\ 32xneq 1;\ 0,25xneq 1. end{matrix}right.$

$xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};4 right )cup left (4;+infty right ) .$

Умножим обе части неравенства на $log^{2}_{2}32x>0$ . Постараемся упростить числители выражений в левой и правой части:

$frac{7^{log_{2}(4x)}cdot 2^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{4^{log_{2}(4x)}cdot 2^{(log_{2}(4x))^{2}}}{4cdot log_{2}(0,25x)}$
Поделим обе части неравенства на $2^{log_{2}(4x)}>0.$

$frac{7^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{2^{(log_{2}(4x))^{2}+log_{2}(4x)}}{4cdot log_{2}(0,25x)};$

$frac{7^{log_{2}(4x)-1}-2^{left ((log_{2}(4x))^{2}+log_{2}(4x)-2 right )}}{ log_{2}(0,25x)} geq 0$
Хорошо бы сделать замену. Пусть log₂(4x) = t. Тогда:

$log_{2}x=t-2;$

$log_{2}(0,25x)=log_{2}left ( frac{1}{4} right )+log_{2}x=log_{2}x-2=t-4.$ Неравенство примет вид:

$frac{7^{t-1}-2^{t^{2}+t-2}}{t-4}geq 0.$
Мы уже знаем, как представить число 7 в виде степени числа 2: $7=2^{log_{2}7}.$

$frac{2^{(t-1)cdot log_{2}7}-2^{(t-1)(t+2)}}{t-4}geq 0.$ Применим метод рационализации:

$frac{(t-1)cdot log_{2}7-(t-1)(t+2)}{t-4}geq 0;$

$frac{(t-1) (log_{2}7-t-2)}{t-4}geq 0;$

Оценим $log_{2}7-2:$

4 < 7 < 8;

$log_{2}4<log_{2}7<log_{2}8;$

$2<log_{2}7<3$

$0<log_{2}7-2<1$

$tleq log_{2}7-2\ , \ log_{2}(4x)leq log_{2}7-2;\ , \ log_{2}(4x)leq log_{2}frac{7}{4};\ , \ 0<xleq frac{7}{16};$ или $1leq t<4;\ , \ 1leq log_{2}(4x)<4;\ , \ log_{2}2leq log_{2}(4x)<log_{2}16;\ , \ frac{1}{2}leq x<4;$

Ответ: $xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};frac{7}{16} right ]cup left [ frac{1}{2};4 right ).$

5. Еще одна задача-страшилка из того же сборника:

$frac{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( log_{(2x^{2}+10x+15)}(x^{2}+2x) right )}{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( x^{2}+10x+26 right )}geq 0.$ Начнем с ОДЗ. Условий будет много – все выражения под логарифмами должны быть положительны, все основания логарифмов положительны и не равны единице, и еще знаменатель не равен нулю

$left{begin{matrix} (x-1)^{2}-1neq 0;\ x(x+2)>0;\ xneq -5. end{matrix}right.$

Применим в левой части неравенства формулу перехода к другому основанию:

$frac{log_{c}b}{log_{c}a}=log_{a}b;$

$log_{x^{2}+10x+26}left ( log_{2x^{2}+10x+15} left ( x^{2}+2x right )right )geq 0.$

Последовательно применим метод замены множителя, то есть метод рационализации.

Напомним, что множитель log_h f можно заменить на (h-1)( f-1), а множитель (log_h f — 1) — на (h — 1)( f — h):

$(x^{2}+10x+25)(log_{2x^{2}+10x+15}(x^{2}+2x)-1)geq 0;$

Поскольку $(x+5)^{2}>0$ при x ∈ ОДЗ, а $2x^{2}+10x+14>0$ при всех x, получим:

С учетом ОДЗ:

Ответ: x ∈ (-5; -3].

Посмотрим, чем поможет метод замены множителя в решении сложного показательного неравенства.

6. Решите неравенство: $displaystyle frac{{rm 2}cdot {{rm 3}}^{{rm 2x+1}}{rm -}{{rm 6}}^{{rm x}}{rm -}{{rm 4}}^{{rm x+1}}{rm -}{rm 9}}{{{rm 9}}^{{rm x}}{rm -}{rm 3}}le {rm 3.}$

$displaystyle frac{{rm 2}cdot {{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 6}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}{rm -}{rm 3}cdot {{rm 3}}^{{rm 2x}}{rm -}{rm 9+9}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

$displaystyle frac{{{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 3}}^{{rm x}}cdot {{rm 2}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

Числитель дроби в левой части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим обе части неравенства на ${{rm 2}}^{{rm 2}{rm x}}{rm textgreater 0.}$

Получим:

$displaystyle newline frac{3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4}{3^{2x}-3}leq 0;$

$displaystyle newline , newline 3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4=0;$

$displaystyle newline , newline frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Разложим числитель на множители.

Сделаем замену:

$displaystyle newline left ( frac{3}{2} right )^x=t; , ,3t^2-t-4=0;$

$displaystyle newline , newline t=frac{1pm 7}{6}; , t_1=-1; , t_2=frac{4}{3};$

$displaystyle newline , newline 3t^2-t-4=3left ( t+1 right )left ( t-frac{4}{3} right ).$

Вернемся к неравенству:

$displaystyle frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Поскольку $displaystyle {left(frac{3}{2}right)}^x textgreater 0$ , поделим обе части неравенства на $displaystyle {left(frac{3}{2}right)}^x+1 textgreater 0.$

$displaystyle frac{{left(frac{3}{2}right)}^x-frac{4}{3}}{3^{2x}-3}le 0.$

Применяя метод рационализации, множитель вида h^f-h^g заменяем на

Получим: $displaystyle newline frac{left ( frac{3}{2} -1right )left ( x-log_{frac{3}{2}}frac{4}{3} right )}{left ( 3-1 right )left ( 2x-1 right )} leq 0;$

$displaystyle newline , newline frac{x-log_{frac{3}{2}}frac{4}{3}}{x-frac{1}{2}}leq 0.$

Остается решить неравенство методом интервалов. Но как сравнить $displaystyle frac{1}{2}$ и ${{log}_{frac{3}{2}} frac{4}{3} }$ ?

Что больше? Давайте представим $displaystyle frac{1}{2}$ как логарифм с основанием $displaystyle frac{3}{2}:$

$displaystyle frac{1}{2}={{log}_{frac{3}{2}} {left(frac{3}{2}right)}^{frac{1}{2}} }={{log}_{frac{3}{2}} sqrt{frac{3}{2}} };$

$displaystyle frac{4}{3} vee sqrt{frac{3}{2}};$

$displaystyle frac{16}{9} vee frac{3}{2};$

Значит, $displaystyle {{log}_{frac{3}{2}} frac{4}{3} } textgreater frac{1}{2}.$

Ответ: $displaystyle xin left(frac{1}{2}; {{log}_{frac{3}{2}} frac{4}{3} }right].$

7. Теперь логарифмическое неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и область его допустимых значений мы записываем в одну систему. И решаем ее.

Решите неравенство: $displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2.$

$displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2 textless = textgreater left{ begin{array}{c}3-x textgreater 0 \3-xne 1 \displaystyle frac{x+4}{{left(x-3right)}^2} textgreater 0 \displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }+2ge 0 end{array}right. .$

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что ${left(a-bright)}^2={left(b-aright)}^2 .$

Используем также условия

$left{ begin{array}{c}x textless 3 \xne 2 \x+4 textgreater 0 \{log}_{3-x}left(x+4right)-{log}_{3-x}{left(3-xright)}^2+2ge 0 end{array}right. textless = textgreater left{ begin{array}{c}x textless 3 \xne 2 \x textgreater -4 \{log}_{3-x}left(x+4right)ge 0 end{array}right. .$

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, ${{log}_a {left(bleft(xright)right)}^2=2{{log}_a left|bleft(xright)right| } }.$

Поскольку $3-x textgreater 0, { log}_{3-x}{left(3-xright)}^2=2{{log}_{3-x} left|3-xright|= }2{{log}_{3-x} left(3-xright)=2. }$

Согласно методу замены множителя, выражение ${log}_{3-x}left(x+4right)$ заменим на

Получим систему:

$left{ begin{array}{c}xne 2 \-4 textless x textless 3 \left(2-xright)left(x+3right)ge 0 end{array}right. .$

Решить ее легко.

Ответ:

8. А теперь неравенство с ловушкой. Мы надеемся, что вы помните — нельзя извлекать корень из неравенства.

Решите неравенство: $displaystyle {{lg}^2 frac{{left(x+2right)}^2left(x+5right)}{5} textless {lg}^2frac{x+5}{20} }.$

Извлекать корень из неравенства нельзя! Можно перенести все в левую часть неравенства и разложить на множители как разность квадратов:

$displaystyle left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}-lgfrac{x+5}{20} right )left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}+lgfrac{x+5}{20} right ) textless 0.$

Применим формулы разности и суммы логарифмов, следя за областью допустимых значений. Все выражения под логарифмами в исходном неравенстве должны быть положительны.

$left{ begin{array}{c}displaystyle lgfrac{{left(x+2right)}^2left(x+5right)cdot 20}{5cdot left(x+5right)}cdot {lg left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}right) } textless 0 \displaystyle {left(x+2right)}^2left(x+5right) textgreater 0 \x+5 textgreater 0 end{array}right. .$

Посмотрим на второе и третье неравенства системы. Поскольку х+5 положительно, то и выражение (x+2)^2 должно быть положительно.

Заметим, что решения неравенства — это все числа, кроме x= - 2.

Получим:

$left{ begin{array}{c}displaystyle lgleft ( 4cdotleft ( x+2 right )^2 right ) cdot lg left ( frac{left ( x+2 right )^2 cdot left ( x+5 right )^2}{100} right ) textless 0\x textgreater -5 \xne -2 end{array}right..$

По методу рационализации, каждый из множителей вида ${{log}_h f }$ заменяем на

$newline left{ begin{array}{c}displaystyle left(10-1right)cdot left(4{left(x+2right)}^2-1right)cdot left(10-1right)left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}-1right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+4-1right)left(2x+4+1right)left(left(x+2right)left(x+5right)-10right)left(left(x+2right)left(x+5right)+10right) textless 0 \x textgreater -5 \xne -2 end{array}right.newlinetextless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right)cdot left(x^2+7x+20right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right) textless 0 \x textgreater -5 \xne -2 end{array}right. .$

Просто равносильные преобразования. Выражение положительно всегда — так как в уравнении дискриминант отрицателен. Осталось применить метод интервалов.

Ответ: $displaystyle xin left(-5;-frac{5}{2}right)cup left(-frac{3}{2};0right).$

Больше неравенств: Задание 15 Профильного ЕГЭ по математике

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Неравенства. Метод замены множителя (метод рационализации)» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

4 октября 2017

В закладки

Обсудить

Жалоба

Памятка по использованию метода рационализации при решении логарифмических неравенств, показательных неравенств, иррациональных неравенств и неравенств с модулем.

Рекомендована при подготовке к ЕГЭ при решении задачи №15 способом, отличным от традиционного.
Приводится схема традиционного способа для решения логарифмического неравенства и стандартные ошибки в использовании нового.

met-r.docx

Источник

Метод рационализации

Разбор сложных заданий в тг-канале:

Рациональные неравенства
Рациональным называется всякое неравенство, сводящееся к неравенству вида

где P(x), Q(x) — некоторые многочлены.

Поскольку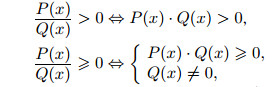

то для решения рациональных неравенств удобно применять метод интервалов.

Пример. Решите неравенство

Решение.

Числитель последней дроби разложим на множители. Подбором находим, что x = 2 является корнем многочлена
x³ − x² − 22x + 40; разделив данный многочлен (уголком или по схеме Горнера) на x − 2, получаем
x³ − x² − 22 x + 40 = (x − 2)·(x2 + x − 20) = (x − 2)·(x − 4)·(x + 5). Значит, исходное неравенство равносильно системе

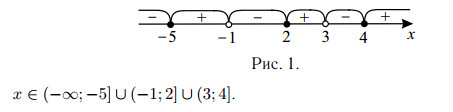
Решая первое неравенство этой системы методом интервалов (см. рис. 1)
и выкалывая точки $x = −1, x = 3$, получаем ответ

Определение модуля числа

2. Геометрически |x| есть расстояние от точки x числовой оси до начала отсчёта — точки O.
3. |x − a| есть расстояние между точками x и a числовой оси.

4. Модуль произведения, частного и степени.

Источник

Метод рационализации — это процедура, позволяющая в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов).

Позволяет перейти от выражения f к выражению g, сохранив все решения.

Метод рационализации для логарифмических неравенств

Здесь мы сравниваем значения относительно друг друга и допускаем случай, когда одно значение больше, а другое меньше и наоборот. Один из способов сравнения двух величин – это вычесть из одного другое. Если разность будет больше нуля, значит, первое число было больше. В первой скобке мы вычитаем из основания единицу. Это значит, что мы сравниваем основание с 1. Во второй скобке мы из одного под логарифмического выражения вычитаем другое, т.е. снова сравниваем их.

Пример. Решите неравенство

Решение.

ОДЗ:

Преобразуем неравенство

Воспользуемся методом рационализации:

Нам нужно найти такие х, при которых левое выражение меньше правого. В записанном неравенстве, если основание больше единицы, первая скобка будет положительна, и если первое подлогарифмическое выражение будет меньше второго, то их разность будет меньше 0, т.е. вторая скобка будет меньше нуля и это как раз те решения, что нужны нам по условию. Если же основание будет меньше единицы, первая скобка будет отрицательна, что изменит общий знак неравенства. Так же мы действовали, когда писали равносильный переход в виде двух случаев для логарифмического неравенства.

С учетом ОДЗ получаем решение неравенства:

Ответ:

Из рассмотренного метода рационализации вытекают следствия:

Пример. Решите неравенство:

Решение.

ОДЗ:

Применим метод рационализации:

С учетом ОДЗ:

Ответ:

Метод рационализации для неравенств с модулем

При сравнении двух чисел по модулю нас не интересует знак числа, поэтому можем от знака избавиться при помощи чётной степени. избавит нас от знака. При дальнейшей работе с полученным неравенством выполнять возведение в квадрат не обязательно, лучше применить формулу разности квадратов.

Пример. Решите неравенство

Решение. Воспользуемся методом рационализации:

Решением неравенства является интервал (-3;1)

Ответ:

Пример. Решите неравенство

Решение. Воспользуемся равносильным переходом:

Решением неравенства является промежуток

Ответ:

Метод рационализации для иррациональных неравенств

Пример. Решите неравенство .

Решение.

ОДЗ (находим ОДЗ для меньшего из выражений, ОДЗ для большего выражения выполнится автоматически):

Воспользуемся методом рационализации:

С учетом ОДЗ получаем окончательное решение неравенства:

Ответ:

Метод рационализации для показательных неравенств

Для показательно-степенных неравенств действуют те же правила, что и для логарифма. При основании, большем 1, знак неравенства мы можем сохранить, при основании меньше единицы, знак неравенства должен измениться при переходе к степеням. Тогда мы можем записать это, как произведение двух скобок, в первой мы будем сравнивать основание с единицей, а во второй – значения показателей степеней.

Пример. Решите неравенство

ОДЗ:

Воспользуемся методом рационализации:

Видим, что решением является промежуток:

С учетом ОДЗ:

Ответ:

Сведем все рассмотренные равносильные преобразования в таблицу

Источник

Метод рационализации это весьма мощная процедура, позволяющая в определённых случаях упростить неравенство и свести его к рациональному неравенству

Скачать:

Предварительный просмотр:

Метод рационализации это весьма мощная процедура, позволяющая в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов).Предположим, что имеется монотонно возрастающая функция f(x). Пусть числа a и b принадлежат области определения данной функции. Тогда справедливы следующие утверждения.

1.Неравенство f(a)> f(b)эквивалентно неравенству a > b;

иными словами, неравенство f(a)−f(b)>0 эквивалентно неравенству a−b >0.

2.Аналогично, неравенство f(a)−f(b)<0 эквивалентно неравенству a−b <0

Как работает эта идея применительно к решению неравенств? Пусть, например, имеется

Неравенство f(х)−f(a)/g(x)−g(b)>0, где f(x)и g(x) монотонно возрастающие функции. Тогда разность f(x)−f(a) можно заменить разностью x−a (того же знака), а разность g(x)−g(b)можно заменить разностью x−b(тогоже знака). Получим рациональное неравенство x−a/x−b>0 решаемое методом интервалов.

По теме: методические разработки, презентации и конспекты

Решение неравенств методом рационализации

Решение неравенств — важный раздел в математике. Успешное изучение математики невозможно без умения решать разнообразные неравенства, поэтому я решила рассмотреть один из способов решения …

Мне нравится

Источник