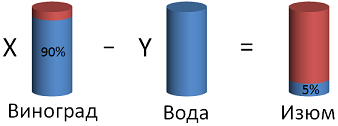Задачи ЕГЭ на сплавы, смеси, растворы.
Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.
. В сосуд, содержащий
литров
-процентного водного раствора некоторого вещества, добавили
литров воды. Сколько процентов составляет концентрация получившегося раствора?
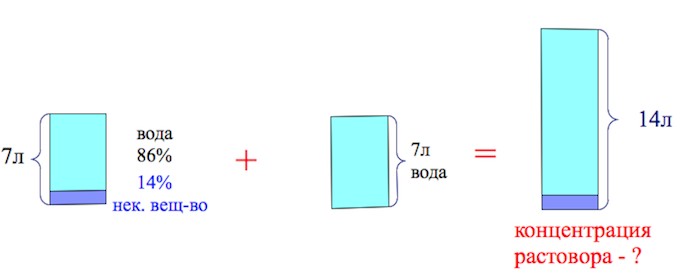
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .
Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
.
. Смешали некоторое количество
-процентного раствора некоторого вещества с таким же количеством
-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна . Масса второго — тоже
. В результате получили раствор массой
. Рисуем картинку.
Получаем:
Ответ: .
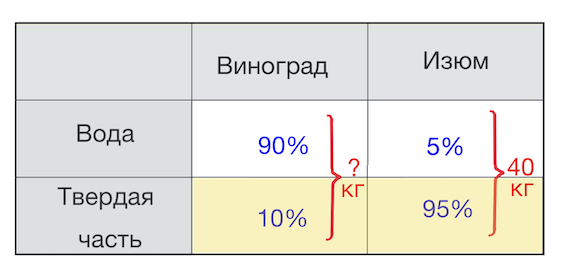
. Виноград содержит
влаги, а изюм —
. Сколько килограммов винограда требуется для получения
килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось воды, значит, «сухого вещества» было
. В изюме
воды и
«сухого вещества». Пусть из
кг винограда получилось
кг изюма. Тогда
от
от
Составим уравнение:
и найдем .
Ответ: .
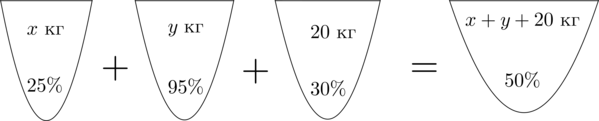
. Имеется два сплава. Первый сплав содержит
никеля, второй —
никеля. Из этих двух сплавов получили третий сплав массой
кг, содержащий
никеля. На сколько килограммов масса первого сплава меньше массы второго?
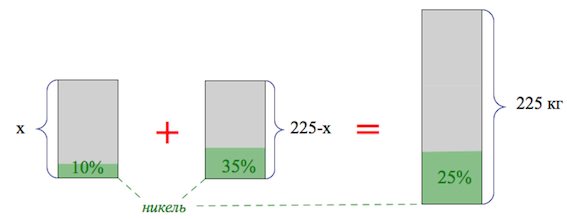
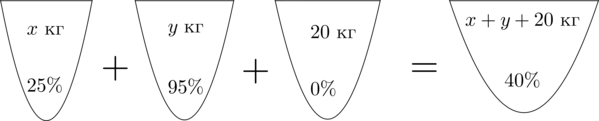
Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .
Запишем простую систему уравнений:
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что .
Ответ: .
. Смешав
-процентный и
-процентный растворы кислоты и добавив
кг чистой воды, получили
-процентный раствор кислоты. Если бы вместо
кг воды добавили
кг
-процентного раствора той же кислоты, то получили бы
-процентный раствор кислоты. Сколько килограммов
-процентного раствора использовали для получения смеси?
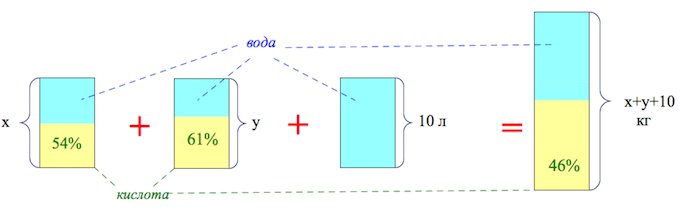
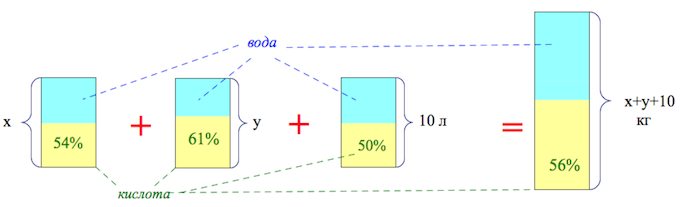
Пусть масса первого раствора , масса второго равна
. Масса получившегося раствора равна
. Запишем два уравнения, для количества кислоты.
Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
Ответ: .
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на сплавы, смеси, растворы.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Задачи на смеси и сплавы – подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах “Дроби, и действия с дробями”и “Проценты”.
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы – на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты – в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической” задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Всего: 101 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 12% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 1
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: ЕГЭ — 2016. Основная волна по математике 06.06.2016. Вариант 437. Юг
Имеется два сплава. Первый сплав содержит 5% меди, второй — 40% меди. Масса первого сплава больше массы второго на 50 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 2
Имеется два сплава. Первый сплав содержит 40% меди, второй — 25% меди. Масса первого сплава больше массы второго на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего
сплава. Ответ дайте в килограммах.
Источник: ЕГЭ по математике 27.03.2020. Досрочная волна. Вариант 1
Имеется два сплава. Первый сплав содержит 45% меди, второй — 20% меди. Масса первого сплава больше массы второго на 30 кг. Из этих двух сплавов получили третий сплав, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: ЕГЭ по математике 27.03.2020. Досрочная волна. Вариант 2
Имеется два сплава. Первый сплав содержит 35% меди, второй — 5% меди. Масса первого сплава больше массы второго на 80 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: ЕГЭ по математике 28.03.2022. Досрочная волна. Москва. Вариант 1
Имеется два сплава. Первый сплав содержит 5% меди, второй — 12% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй − 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 1.
Имеется два сплава. Первый содержит 15% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 4
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Смешав 11-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 11-процентного раствора использовали для получения смеси?
Всего: 101 1–20 | 21–40 | 41–60 | 61–80 …
Задачи на сплавы и смеси и проценты егэ математика
Задачи на смеси и сплавы очень простые.
Нужно уметь определять Концентрацию вещества – это легко, это просто процент…
И понимать Алгоритм решения – он тоже очень простой.
Ничего зубрить не нужно!
Задачи на смеси и сплавы — коротко о главном
Задачи на смеси и сплавы бывают двух видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси. В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.
Концентрация вещества – это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.
Масса раствора равна сумме масс всех составляющих.
При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов.
Масса растворенного вещества при смешивании двух растворов суммируется.
Алгоритм решения задач на смеси и сплавы:
Определить, какое вещество влияет на концентрацию раствора (главное вещество). Следить за весом главного вещества при добавлении других веществ в раствор. Исходя из данных об изменениях состояния главного вещества — сделать выводы.
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – Это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к Сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется В процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac>=fraccdot 100), но ведь ( displaystyle frac) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Решение задач на смеси и сплавы
Задачи на смеси и сплавы бывают Двух основных видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить Массу и концентрацию этого вещества в новой смеси. В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, кАкой стала концентрация вещества.
Строго говоря, подход к решению от этого не меняется.
Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.
Давай попробуем решить несколько задачек. Попробуй решить каждую самостоятельно, а если не получится – посмотри в решение.
Задача №1
В ( displaystyle 5%) раствор кислоты массой ( displaystyle 3,8) кг добавили ( displaystyle 1,2) кг чистой воды. Чему стала равна концентрация раствора (в процентах)?
Решение
- Для начала вычислим, сколько кислоты содержится в ( displaystyle 5%) растворе. Из ( displaystyle 3,8) кг ( displaystyle 5%) — это кислота, а значит в растворе ( displaystyle 0,05cdot 3,8=0,19 кг) кислоты Далее определим массу нового раствора. Как мы уже знаем – масса раствора равна массе его составляющих, т. е. ( displaystyle 3,8) кг + ( displaystyle 1,2) кг = ( displaystyle 5) кг Поскольку в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось – ( displaystyle 0,19) кг. Таким образом, концентрация кислоты стала равна ( displaystyle frac=0,038) Теперь выразим концентрацию в процентах — ( displaystyle 0,038cdot 100%=3,8%)
Ответ: ( displaystyle 3,8).
Теперь давай попробуем решить задачу посложнее.
Задача №2
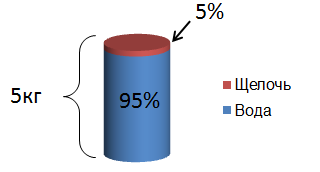
Смешали ( displaystyle 3) кг ( displaystyle 5%)-го водного раствора щелочи и ( displaystyle 7) кг ( displaystyle 15%)-го. Какова концентрация вновь полученного раствора? Ответ дайте в процентах.
Решение
Давай попробуем визуализировать ситуацию. ( displaystyle 3) кг ( displaystyle 5%) водного раствора. Значит воды в этом растворе ( displaystyle 95%).
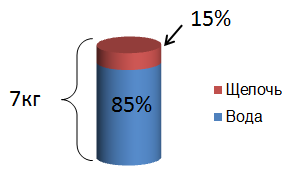
А теперь второй раствор:
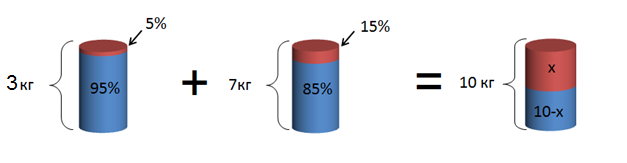
После смешивания, вновь получившийся раствор будет весить ( displaystyle 3) кг + ( displaystyle 7) кг = ( displaystyle 10) кг. Обозначим количество щелочи в новом растворе за ( displaystyle x), а количество воды – ( displaystyle (10-x)):
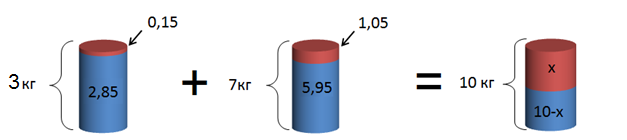
Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе – ( displaystyle 0,05cdot 3=0,15) кг щелочи и ( displaystyle 3-0,15=2,85) кг воды, во втором — ( displaystyle 0,15cdot 7=1,05) кг щелочи и ( displaystyle 7-1,05=5,95) кг воды:
Из картинки видно, что количество щелочи в новом растворе равно сумме весов кислоты в старых растворах: ( displaystyle x=0,15+1,05=1,2) кг кислоты.
Теперь, зная количество щелочи в новом растворе и зная его массу, мы можем легко определить концентрацию:
Поскольку ответ просят дать в процентах – умножим на ( displaystyle 100%) —( displaystyle 0,12cdot 100%=12%).
Ответ: ( displaystyle 12).
Эту визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.
Задача №3
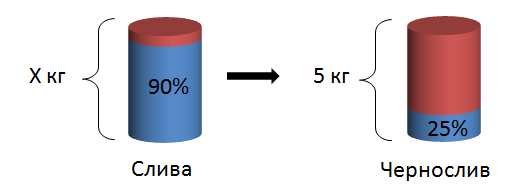
Чернослив содержит ( displaystyle 25%) влаги. Его получают из сливы, содержащей ( displaystyle 90%) влаги, путем сушки. Сколько нужно килограмм сливы, для получения ( displaystyle 5) кг чернослива?
Решение:
Давай попробуем нарисовать.
Количество сухого (красного на рисунке) вещества не изменилось. Просто испарилась вода! Изменилась лишь пропорция сухого вещества. Давай попробуем найти его вес. Поскольку сухого вещества в черносливе – ( displaystyle 100%-25%=75%), то масса сухого вещества составит – ( displaystyle 0,75cdot 5 кг = 3,75 кг). Нам нужно взять такое количество сливы, чтобы в нем было ( displaystyle 3,75) кг сухого вещества. Обозначим вес необходимого количества сливы за ( displaystyle x). По условию мы знаем, что сухого вещества в сливе — ( displaystyle 100%-90%=10%), т. е. ( displaystyle 0,1cdot x кг), а нам нужно ( displaystyle 3,75) кг. Получается, что ( displaystyle begin0,1x=3,75\x=37,5end). Для получения ( displaystyle 5) кг чернослива, нам нужно взять ( displaystyle 37,5) кг сливы.
Ответ: ( displaystyle 37,5).
Задача №4
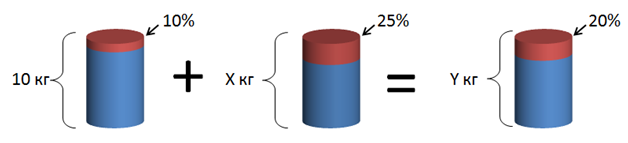
Имеются два сплава серебра с медью. В первом содержится ( displaystyle 10%) серебра, во втором – ( displaystyle 25%). Сколько килограмм второго сплава нужно добавить к ( displaystyle 10)кг первого, чтобы получить сплав с ( displaystyle 20%) содержанием серебра?
Решение:
Обозначим за ( displaystyle x) искомый вес второго сплава, а за ( displaystyle y) – массу получившегося сплава. Масса серебра в первом сплаве –( displaystyle 10%cdot 10 кг=0,1cdot 10 кг=1 кг), во втором–( displaystyle 25%cdot x=0,25x), в новом сплаве –( displaystyle 20%cdot y=0,2y). Теперь у нас есть система уравнений, решив которую найдем искомый ( displaystyle x): ( displaystyle begin left< begin10+x=y\1+0,25x=0,2yend right. , rightarrow left< begin10+x=y\1+0,25y=0,2(10+x)end right.rightarrow \rightarrow left< begin10+x=y\1+0,25x=2+0,2xend right.rightarrow left< begin10+x=y\0,250,2x=2-1end right.\rightarrow left< begin10+x=y\0,05x=1end right. ,,,,rightarrow left< beginy=30\x=20end right.end) Получается, добавив в ( displaystyle 10) килограммов ( displaystyle 10%) сплава, ( displaystyle 20) килограммов ( displaystyle 25%) сплава — мы получим ( displaystyle 30) килограммов ( displaystyle 20%) сплава.
Ответ: ( displaystyle 20).
Подведем промежуточные итоги
Если ты заметил, во всех задачах мы сначала определяли, Какое вещество влияет на концентрацию, назовем его «главным».
Дальше следили за абсолютной величиной этого главного вещества (в килограммах, литрах). Если в раствор (сплав) что-то доливали, добавляли, то, в зависимости от состава «добавки», вес «главного» вещества либо изменялся, либо нет.
Важно определить, что произошло с «главным» веществом, а дальше решение становится совсем простым.
5 задач на самостоятельную работу (с ответами)
А теперь попробуй решить несколько задач самостоятельно, и проверь ответы:
А теперь попробуй решить несколько задач самостоятельно, и проверь ответы:
- Имеются два сплава с содержанием цинка 15% и 22%. Какова будет концентрация цинка, если сплавить 90 кг первого и 50 кг второго. Сколько миллилитров 55% раствора уксуса нужно добавить к 500 миллилитрам 1% раствора, чтобы получить 5%раствор уксуса? Смешали некоторое количество 12% раствора вещества с таким же количеством 22% раствора этого же вещества. Какова концентрация (в процентах) вещества в новом растворе? В сосуд, содержащий 8 литров 14% раствора кислоты, добавили 12 литров воды. Сколько процентов кислоты содержится в новом растворе? Сколько килограмм 17% сплава меди нужно добавить к 5 килограммам 10% сплава меди, чтобы получить 12%сплав?
Ответы:
Задача №10
В ( displaystyle 10%) раствор кислоты массой ( displaystyle 3) кг добавили ( displaystyle 1,8) кг чистой воды. Чему стала равна концентрация раствора (в процентах)?
- Вычисляем массу кислоты. Для этого запишем, что такое концентрация: ( displaystyle fraccdot 100%=10%text< >Rightarrow text< >frac=0,1text< >Rightarrow text< >M=0,1cdot M=0,1cdot 3=0,3) кг. Впредь проценты всегда будем сразу записывать в виде десятичной дроби: ( displaystyle 1%=0,01). Вычисляем массу нового раствора: ( displaystyle 3+1,8=4,8) кг. Новая концентрация: ( displaystyle frac=0,0625=6,25%).
Задача №11
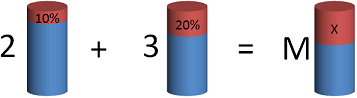
Смешали два раствора: ( displaystyle 2) кг ( displaystyle 10%)-ного и ( displaystyle 3) кг ( displaystyle 20%)-ного. Какова концентрация полученного раствора?
Решение:
Визуализируем ситуацию: схематично изобразим емкости с растворами, около них подпишем массу раствора, а внутри – содержание кислоты:
Теперь составляем два уравнения: первое – это сложение емкостей целиком, то есть: ( displaystyle 2+3=M) – масса нового раствора.
Второе – складываем только кислоту. В первом сосуде ее ( displaystyle 0,1cdot 2) кг, а во втором ( displaystyle 0,2cdot 3) кг. Значит, ( displaystyle 0,1cdot 2+0,2cdot 3=Mcdot x) – масса кислоты в новом растворе.
( displaystyle left. beginM=2+3=text\Mcdot x=0,1cdot 2+0,2cdot 3=0,8text< кг >end right|Rightarrow text< >X=frac=0,16=16%).
Ответ: ( displaystyle 16%).
Эту визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.
Задача №12
Изюм содержит ( displaystyle 5%) влаги. Его получают из винограда, содержащего ( displaystyle 90%) влаги. Сколько потребуется винограда, чтобы получить ( displaystyle 3) кг изюма?
Решение:
Получаем систему: ( displaystyle left< beginx-y=3\0,9x-y=0,05cdot 3end right.)
В первом уравнении вычитаем то, что написано снаружи «сосудов», а во втором – то, что внутри.
Итак, решаем систему и получаем: ( displaystyle 0,1x=3-0,15text< >Rightarrow text< >X=28,5) кг.
Ответ: ( displaystyle 28,5).
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на Растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать Сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем Математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают Вклады, научимся решать и, главное, правильно Оформлять решение таких задач.
Задание 8 № 99567
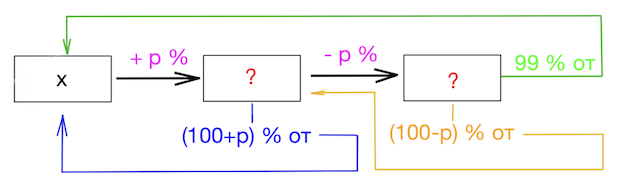
Если величину дважды увеличить на процентов, получим
Если величину дважды уменьшить на процентов, получим
Нам нужно взять такое количество сливы, чтобы в нем было displaystyle 3,75 кг сухого вещества.
Youclever. org
08.02.2019 1:56:44
2019-02-08 01:56:44
Задачи на сплавы и смеси и проценты егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 8 № 99565
В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на а в 2010 году на по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
В 2009 году число жителей стало человек, а в 2010 году число жителей стало человек.
Задание 8 № 99566
В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Обозначим первоначальную стоимость акций за 1. Пусть в понедельник акции компании подорожали на и их стоимость стала составлять Во вторник акции подешевели на и их стоимость стала составлять В результате они стали стоить на дешевле, чем при открытии торгов в понедельник, то есть 0,96. Таким образом,
Задание 8 № 99567
Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять таких же рубашек дороже куртки?
Стоимость четырех рубашек составляет 92% стоимости куртки. Значит, стоимость одной рубашки составляет 23% стоимости куртки. Поэтому стоимость пяти рубашек составляет 115% стоимости куртки. Это превышает стоимость куртки на 15%.
Задание 8 № 99568
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Условие «если бы зарплата отца увеличилась вдвое, доход семьи вырос бы на 67%» означает, что зарплата отца составляет 67% дохода семьи. Условие «если бы стипендия дочери уменьшилась втрое, доход семьи сократился бы на 4%», означает, что 2/3 стипендии составляют 4% дохода семьи, то есть вся стипендия дочери составляет 6% дохода семьи. Таким образом, доход матери составляет дохода семьи.
. Четыре рубашки дешевле куртки на. На сколько процентов пять рубашек дороже куртки?
И еще одна очевидность:
Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки.
Ege. sdamgia. ru
23.08.2020 23:51:09
2020-08-23 23:51:09
Задачи на проценты из вариантов ЕГЭ по математике
Смотри также видео «Текстовые задачи на ЕГЭ по математике».
Текстовая задача — это не только задача на движение и работу. Есть еще задания на проценты, на растворы, сплавы и смеси, на движение по окружности и нахождение средней скорости. О них мы и расскажем.
Начнем с задач на проценты. Если эта тема сложна для тебя — посмотри материал простейшие текстовые задачи. В частности, в нем мы сформулировали важное правило: за мы принимаем ту величину, с которой сравниваем.
Мы также вывели полезные формулы:
Если величину увеличить на процентов, получим.
Если величину уменьшить на процентов, получим.
Если величину увеличить на процентов, а затем уменьшить на, получим.
Если величину дважды увеличить на процентов, получим
Если величину дважды уменьшить на процентов, получим
Воспользуемся ими для решения задач.
. В году в городском квартале проживало человек. В году, в результате строительства новых домов, число жителей выросло на, а в году — на по сравнению с годом. Сколько человек стало проживать в квартале в году?
По условию, в году число жителей выросло на, то есть стало равно человек.
А в году число жителей выросло на, теперь уже по сравнению с годом. Получаем, что в году в квартале стало проживать жителей.
Следующая задача предлагалась на пробном ЕГЭ по математике в декабре года. Она проста, но справились с ней немногие.
. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
На первый взгляд кажется, что в условии ошибка и цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но не будем спешить. Пусть при открытии торгов в понедельник акции стоили рублей. К вечеру понедельника они подорожали на и стали стоить. Теперь уже эта величина принимается за, и к вечеру вторника акции подешевели на по сравнению этой величиной. Соберем данные в таблицу:
| В понедельник утром | В понедельник вечером | Во вторник вечером |
| Стоимость акций |
По условию, акции в итоге подешевели на.
Поделим обе части уравнения на (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения.
По смыслу задачи, величина положительна.
Получаем, что.
. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за рублей.
Эта задача тоже решается по одной из формул, приведенных в начале статьи. Холодильник стоил рублей. Его цена два раза уменьшилась на, и теперь она равна
. Четыре рубашки дешевле куртки на. На сколько процентов пять рубашек дороже куртки?
Пусть стоимость рубашки равна, стоимость куртки. Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет от цены куртки, то есть.
Стоимость одной рубашки — в раза меньше:
А стоимость пяти рубашек:
Получили, что пять рубашек на дороже куртки.
. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на. Сколько процентов от общего дохода семьи составляет зарплата жены?
Нарисуем таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась. ») назовем «ситуация » и «ситуация ».
| Муж | Жена | Дочь | Общий доход |
| В реальности | |||
| Ситуация | |||
| Ситуация |
Осталось записать систему уравнений.
Но что же мы видим? Два уравнения и три неизвестных! Мы не сможем найти, и по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму. Получим:
Это значит, что зарплата мужа составляет от общего дохода семьи.
Во втором уравнении мы тоже вычтем из обеих частей выражение, упростим и получим, что
Значит, стипендия дочки составляет от общего дохода семьи. Тогда зарплата жены составляет общего дохода.
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Эту визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege-study. ru
13.07.2019 18:54:04
2019-07-13 18:54:04
Источники:
Https://youclever. org/book/zadachi-na-smesi-i-splavy-1/
Https://ege. sdamgia. ru/test? theme=88
Https://ege-study. ru/ru/ege/materialy/matematika/zadachi-ege-na-procenti/
В14 егэ по математике. Текстовые задачи на сплавы, растворы | Подготовка к ЕГЭ по математике » /> » /> .keyword { color: red; } Задачи на сплавы и смеси и проценты егэ математика
08. Задачи на смеси и сплавы и т. п
08. Задачи на смеси и сплавы и т. п.
Задача 1. В сосуд, содержащий литров — процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
После того, как в сосуд долили литров воды, жидкости стало л, а некоторого вещества – по-прежнему л.
Пусть – процентная доля некоторого вещества в получившемся растворе.
Задача 2. Смешали некоторое количество — процентного раствора некоторого вещества с таким же количеством — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть – вес первого раствора. В нем некоторого вещества.
Второго раствора по весу взяли столько же, – . В нем того же некоторого вещества.
Тогда в смешанном растворе будет то есть по весу некоторого вещества.
Пусть концентрация получившегося раствора – %, тогда
Задача 3. Имеется два сплава. Первый сплав содержит % никеля, второй — % никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть кг – масса первого сплава. Тогда согласно условию кг – масса второго сплава.
В первом сплаве кг никеля, во втором – кг никеля.
В новом сплаве кг никеля.
Значит, масса второго сплава – кг, что на кг больше массы первого сплава.
Задача 4. Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
Пусть вес первого расвора литров. В нем согласно условию л кислоты.
Пусть вес второго раствора литров. В нем согласно условию л кислоты.
При смешивании двух растворов и добавлении 10 л воды, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Рассмотрим второй случай.
При смешивании двух растворов и добавлении л %-го раствора кислоты, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Итак, нам предстоит решить систему уравнений:
Вычитая строки, получаем:
Задача 5. Имеются два сосуда. Первый содержит кг, а второй — кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Пусть % – концентрация кислоты в первом растворе, % – концентрация кислоты во втором растворе.
Пусть вес каждого смешиваемого раствора – кг.
Итак, нам предстоит работать с системой уравнений:
Складывая уравнения системы, получаем:
Тогда в первом растворе содержится кг кислоты.
Задача 6. Виноград содержит % влаги, а изюм — %. Сколько килограммов винограда требуется для получения килограммов изюма?
Обратите внимание! Что очень важно понимать для решения данной задачи?
«Твердая часть винограда» = «твердая часть изюма»!
Начнем с изюма.
Твердая часть винограда (изюма) составляет % веса изюма, то есть
Итак, в изюме массой кг, также как и в винограде, из которого он получен, твердая часть – кг.
Переходим к винограду.
Пусть кг – вес винограда. Твердая часть в винограде занимает % веса, поэтому
Итак, необходимо взять кг винограда (чтобы получить 40 кг изюма) .
Задача 7. В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на %, а в 2010 году — на % по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
В 2009 году число жителей составляет % от числа жителей в 2008 году, то есть их столько:
В 2010 году число жителей составляет % от числа жителей в 2009 году, то есть их столько:
Итак, количество жителей в 2010 году есть
Задача 8. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за рублей.
Пусть цена холодильника ежегодно уменьшаетя на процентов.
Тогда через год после выставления на продажу он будет стоить
Еще через год цена на холодильник будет такой:
А поскольку холодильник через два года был продан за рублей, то составим уравнение:
Задача 9. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
1) Пусть в понедельник акции компании подорожали на %, а до повышения цены стоимость акций обозначим за.
Итак, в понедельник цена акций будет составлять % по отношению к стоимости акций до повышения.
Поэтому новая цена акций на понедельник:
2) Вторник. Цена акций будет составлять % по отношению к стоимости акций в понедельник.
Поэтому новая цена акций на вторник:
3) Что мы имеем? На открытие торгов в понедельнки стоимость акций – , во вторник стоимость акций – при этом последняя стоимость акций составляет % от стоимости на открытие торгов. Составим уравнение:
Откуда получаем, что %.
Задача 10. Шесть рубашек дешевле куртки на %. На сколько процентов девять рубашек дороже куртки? Видео *
Согласно условию цена рубашек составляет % по отношению к цене куртки.
А значит, рубашка составляет % по отношению к цене куртки.
Стало быть, рубашек составляют % по отношению к цене куртки.
То есть рубашек дороже куртки на %.
Задача 11. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на %. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на %. Сколько процентов от общего дохода семьи составляет зарплата жены?
Пусть зарплата мужа – рублей, жены – , стипендия дочери – .
Тогда общий доход семьи –
Если бы зарплата мужа увеличилась вдвое, то есть стала бы, то общий доход семьи увеличился бы на рублей.
То есть, согласно условию, рублей составляет % от общего дохода семьи (до повышения зарплаты мужа).
Если бы стипендия дочери уменьшилась вдвое, то есть стала бы, то общий доход семьи уменьшился бы на рублей, что соответствует, согласно условию, % от первоначального общего дохода семьи. Значит, стипендия дочери () составляет % от дохода семьи.
Выясним, наконец, сколько процентов от общего дохода семьи составляет зарплата жены:
Задача 12. Дима, Андрей, Гриша и Коля учредили компанию с уставным капиталом рублей. Дима внес % уставного капитала, Андрей — рублей, Гриша — уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли рублей причитается Коле? Ответ дайте в рублях.
Найдем процент уставного капитала Андрея:
А так как проценты уставного капитала Димы и Гриши % и % соответственно, то уставной процент Коли – %.
А значит, от прибыли в рублей он получит рублей.
Задача 13. Клиент А. сделал вклад в банке в размере рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Пусть банковский процент –
Тогда через год клиент А. будет иметь на счету рублей.
Еще через год клиент А. будет иметь на счету рублей.
Клиент В. через год после открытия вклада будет иметь на счету рублей.
Поскольку клиент А. получил на рубля больше клиента Б., составим уравнение:
Помогите другим пользователям — будьте первым, кто поделится своим мнением об этой презентации.
Задачи на смеси и сплавы и т. п.
Задача 1. В сосуд, содержащий литров — процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
После того, как в сосуд долили литров воды, жидкости стало л, а некоторого вещества – по-прежнему л.
Пусть – процентная доля некоторого вещества в получившемся растворе.
Задача 2. Смешали некоторое количество — процентного раствора некоторого вещества с таким же количеством — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть – вес первого раствора. В нем некоторого вещества.
Второго раствора по весу взяли столько же, – . В нем того же некоторого вещества.
Тогда в смешанном растворе будет то есть по весу некоторого вещества.
Пусть концентрация получившегося раствора – %, тогда
Задача 3. Имеется два сплава. Первый сплав содержит % никеля, второй — % никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть кг – масса первого сплава. Тогда согласно условию кг – масса второго сплава.
В первом сплаве кг никеля, во втором – кг никеля.
В новом сплаве кг никеля.
Значит, масса второго сплава – кг, что на кг больше массы первого сплава.
Задача 4. Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
Пусть вес первого расвора литров. В нем согласно условию л кислоты.
Пусть вес второго раствора литров. В нем согласно условию л кислоты.
При смешивании двух растворов и добавлении 10 л воды, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Рассмотрим второй случай.
При смешивании двух растворов и добавлении л %-го раствора кислоты, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Итак, нам предстоит решить систему уравнений:
Вычитая строки, получаем:
Задача 5. Имеются два сосуда. Первый содержит кг, а второй — кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Пусть % – концентрация кислоты в первом растворе, % – концентрация кислоты во втором растворе.
Пусть вес каждого смешиваемого раствора – кг.
Итак, нам предстоит работать с системой уравнений:
Складывая уравнения системы, получаем:
Тогда в первом растворе содержится кг кислоты.
Задача 6. Виноград содержит % влаги, а изюм — %. Сколько килограммов винограда требуется для получения килограммов изюма?
Обратите внимание! Что очень важно понимать для решения данной задачи?
«Твердая часть винограда» = «твердая часть изюма»!
Начнем с изюма.
Твердая часть винограда (изюма) составляет % веса изюма, то есть
Итак, в изюме массой кг, также как и в винограде, из которого он получен, твердая часть – кг.
Переходим к винограду.
Пусть кг – вес винограда. Твердая часть в винограде занимает % веса, поэтому
Итак, необходимо взять кг винограда (чтобы получить 40 кг изюма) .
Задача 7. В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на %, а в 2010 году — на % по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
В 2009 году число жителей составляет % от числа жителей в 2008 году, то есть их столько:
В 2010 году число жителей составляет % от числа жителей в 2009 году, то есть их столько:
Итак, количество жителей в 2010 году есть
Задача 8. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за рублей.
Пусть цена холодильника ежегодно уменьшаетя на процентов.
Тогда через год после выставления на продажу он будет стоить
Еще через год цена на холодильник будет такой:
А поскольку холодильник через два года был продан за рублей, то составим уравнение:
Задача 9. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
1) Пусть в понедельник акции компании подорожали на %, а до повышения цены стоимость акций обозначим за.
Итак, в понедельник цена акций будет составлять % по отношению к стоимости акций до повышения.
Поэтому новая цена акций на понедельник:
2) Вторник. Цена акций будет составлять % по отношению к стоимости акций в понедельник.
Поэтому новая цена акций на вторник:
3) Что мы имеем? На открытие торгов в понедельнки стоимость акций – , во вторник стоимость акций – при этом последняя стоимость акций составляет % от стоимости на открытие торгов. Составим уравнение:
Откуда получаем, что %.
Задача 10. Шесть рубашек дешевле куртки на %. На сколько процентов девять рубашек дороже куртки? Видео *
Согласно условию цена рубашек составляет % по отношению к цене куртки.
А значит, рубашка составляет % по отношению к цене куртки.
Стало быть, рубашек составляют % по отношению к цене куртки.
То есть рубашек дороже куртки на %.
Задача 11. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на %. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на %. Сколько процентов от общего дохода семьи составляет зарплата жены?
Пусть зарплата мужа – рублей, жены – , стипендия дочери – .
Тогда общий доход семьи –
Если бы зарплата мужа увеличилась вдвое, то есть стала бы, то общий доход семьи увеличился бы на рублей.
То есть, согласно условию, рублей составляет % от общего дохода семьи (до повышения зарплаты мужа).
Если бы стипендия дочери уменьшилась вдвое, то есть стала бы, то общий доход семьи уменьшился бы на рублей, что соответствует, согласно условию, % от первоначального общего дохода семьи. Значит, стипендия дочери () составляет % от дохода семьи.
Выясним, наконец, сколько процентов от общего дохода семьи составляет зарплата жены:
Задача 12. Дима, Андрей, Гриша и Коля учредили компанию с уставным капиталом рублей. Дима внес % уставного капитала, Андрей — рублей, Гриша — уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли рублей причитается Коле? Ответ дайте в рублях.
Найдем процент уставного капитала Андрея:
А так как проценты уставного капитала Димы и Гриши % и % соответственно, то уставной процент Коли – %.
А значит, от прибыли в рублей он получит рублей.
Задача 13. Клиент А. сделал вклад в банке в размере рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Пусть банковский процент –
Тогда через год клиент А. будет иметь на счету рублей.
Еще через год клиент А. будет иметь на счету рублей.
Клиент В. через год после открытия вклада будет иметь на счету рублей.
Поскольку клиент А. получил на рубля больше клиента Б., составим уравнение:
Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20 процентный раствор кислоты? Решение Объем чистой кислоты в растворе не меняется, процентное содержание кислоты в растворе уменьшится в 3 раза (60:20=3) Объем раствора увеличится в 3раза:2·3=6(л) 6 – 2 = 4 (л) воды нужно добавить Ответ: 4 л.
Аннотация к презентации
12 2,4 5 Ответ 5.
Egemaximum. ru
18.07.2018 17:03:39
2018-07-18 17:03:39
Задачи на проценты, сплавы и смеси
Занимайся дополнительно с куратором, чтобы получить на экзамене максимальные баллы!
- Онлайн-занятие по 60 минут 1 раз в неделю Еженедельное д/з Проверка д/з и тестов Ежемесячное тестирование в формате реального экзамена Поддержка и ответы на вопросы 24/7
До 31 мая 2022 года
В 2018-2019 учебном году у тебя есть возможность заниматься лично с создателими курса в общих чатах!
Чаты в ВК строго до 8 человек, где ты общаешься с единомышленниками, которые сдают тот же предмет, что и ты.
Но самое главное — всю твою работу курирует лучшие преподаватели центра “Годограф”. Все вопросы от первого до последнего номера ЕГЭ или ОГЭ будут разобраны максимально подробно.
Куратор будет проверять 2 часть ЕГЭ/ОГЭ, которую платформа проверить не может. В итоге, у тебя есть все шансы написать экзамен на максимальный балл!
90% упустят возможность, считая что сейчас нет времени на прохождение курса. Но разве есть дело важнее, чем поступление в институт?
То есть, согласно условию, рублей составляет % от общего дохода семьи (до повышения зарплаты мужа).
1) Пусть в понедельник акции компании подорожали на %, а до повышения цены стоимость акций обозначим за.
Содержание
Через год после открытия вклада будет иметь на счету рублей.
80-ballov. ru
26.04.2019 4:00:52
2019-04-26 04:00:52
Презентация на тему «Задачи на смеси и сплавы-подготовка к ЕГЭ»
Помогите другим пользователям — будьте первым, кто поделится своим мнением об этой презентации.
Аннотация к презентации
Скачать презентацию (0.39 Мб). Тема: «Задачи на смеси и сплавы-подготовка к ЕГЭ». Предмет: математика. 15 слайдов. Добавлена в 2017 году. Средняя оценка: 4.0 балла из 5.
Содержание
ЗАДАЧИ НА СМЕСИ И СПЛАВЫ В 13 МКОУ «Зыряновская СОШ» Заринский район Алтайский край Учитель математики Степина Татьяна Сергеевна золото серебро 2 3 ЕГЭ
Слайд 2
Способы решения задач на смеси и сплавы Арифметический Применение уравнения Применение систем уравнений 10% никель
Слайд 3
В сосуд, содержащий 5 литров 12 процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? Ответ: 5% Решение I способ = + 5 л. 7 л. 12 % 0 % 0,6л 0,6л. 12 л. II способ Ответ: 5% III способ Объем раствора увеличился в 2,4 раза (было 5 л., стало 12 л. 12:5 = 2,4), содержание вещества не изменилось, поэтому процентная концентрация получившегося раствора уменьшилась в 2,4 раза. 12:2,4=5(%) Ответ: 5%
Слайд 4
Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20 процентный раствор кислоты? Решение Объем чистой кислоты в растворе не меняется, процентное содержание кислоты в растворе уменьшится в 3 раза (60:20=3) Объем раствора увеличится в 3раза:2·3=6(л) 6 – 2 = 4 (л) воды нужно добавить Ответ: 4 л.
Слайд 5
Смешали 4 литра 15 процентного водного раствора с 6 литрами 25 процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Решение Ответ: 4 л. + = 6л. 4л. 15% 25% 0,6л. 1,5л. 2,1л. 10л.
Слайд 6
Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг. Решение? Было Стало 400кг. 18% 20% 80% 328кг. 328кг. 72кг. Вода Цемент Вода Цемент
Слайд 7
Решение Сколько надо взять 5 процентного и 25 процентного раствора кислоты, чтобы получить 4 л 10 процентного раствора кислоты? 5% 10% + = 25% х л 0,25 · (4 — х) л – кислоты во втором растворе 4 л (4-х) л 0,4л (1-0,2х)л 0,05х 0,25(4-х)л 0,05 х ( л )– кислоты в первом растворе 0,1 · 4 = 0,4 л – кислоты в полученном растворе 0,05+0,25(4-х)=(1- 0,2х) л – кислоты в полученном растворе Получим уравнение 1 — 2х = 0,4 х = 3 3л – надо взять 5процентного раствора 4 – 3 = 1(л) – 25 процентного Ответ: 1л; 3л.
Слайд 8
Решение В сосуд емкостью 6л налито 4л 70% раствора серной кислоты. Во второй сосуд той же емкости налито 3л 90% раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нем получился 74% раствор серной кислоты? Найдите все допустимые значения процентного содержания раствора серной кислоты в 6л раствора в первом сосуде. + = 4л 3л хл 90% 74% 70% кислоты в I сосуде 2,8л 0,9хл кислоты нужно перелить кислоты вновом растворе (2,8+0,9х)л (4+х)л 0,74(4+х)л кислоты вновом растворе Получим уравнение 70% 2,8л 90% 1,8л 4л 2л 6л Допустимые значения процентного содержания Из второго сосуда в первый можно перелить максимальное количество раствора кислоты 2л + = кислоты в 2 литрах кислоты в 1 сосуде 4,6л Ответ: 1л;
Слайд 9
Ответ: 9 кг. + _ _ медь медь медь 10% 40% 30% х кг. (х+3) кг. (х+(х+3)) кг. 0,4(х+3)кг 0,3(2х+3)кг Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. 0,1х кг Решение Масса меди в первом сплаве 0,1х(кг) Во втором – 0,4(х+3)(кг) В третьем – 0,3(2х+3)(кг) Получим уравнение
Слайд 10
Имеется два сплава золота и серебра: в одном массы этих металлов находятся в отношении 2:3, а в другом – в отношении 3:7. Сколько килограммов нужно взять от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро находились бы в отношении 5:11? Решение + _ _ (8 – х)кг 8кг х кг Ответ:1 кг. и 7 кг. золото серебро 5 11 золото серебро 2 3 золото серебро 3 7 золото серебро 2 3 золото серебро 3 7 — от 2 сплава — от 1 сплава Получим уравнение 3/10(8-х) кг 2/5 х кг Масса золота в новом сплаве Масса золота в первом куске 2,5 кг Масса золота во втором куске
Слайд 11
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Решение + _ _ 200 кг х кг Масса никеля в первом сплаве 0,1х кг Масса никеля во втором сплаве 0,3у кг. Ответ: на 100 кг. у кг 30% никель 25% никель 0,3у кг Масса никеля в новом сплаве 200·0,25=50 (кг). 50кг 10% никель 0,1х кг 50 кг — масса первого сплава. 150 кг — масса второго сплава. 150 – 50 = 100 (кг)
Слайд 12
При смешивании 30 процентного раствора серной кислоты с 10 процентным раствором серной кислоты получилось 400 г 15 процентного раствора. Сколько граммов 30 процентного раствора было взято? + = х г 15% 30% 10% Решение 400г. у г кислоты впервом растворе 0,3х г кислоты во втором растворе кислоты вновом растворе 0,1у г 60 г Ответ: 100 г. 100 г – 30% раствора было взято.
Слайд 13
Решение Имеются два слитка сплава серебра и олова. Первый слиток содержит 360г серебра и 40г олова, а второй слиток – 450г серебра и 150г олова. От каждого слитка взяли по куску, сплавили их и получили 200г сплава, в котором оказалось 81% серебра. Определите массу (в граммах) куска, взятого от второго слитка. 200 г серебро олово 81% х г у г + _ _ 400г 600г серебро олово серебро олово 450 г 150 г серебро олово серебро олово 360 г 40 г Ответ:120 г. серебра вновом сплаве 162 г серебра в первом слитке 75% серебра во втором слитке 90% 0,9х(г) серебра в первом куске 0,9х(г) — 0,75у(г) серебра во втором куске 0,75у(г)- 90% 75%
Слайд 14
Первый раствор содержит 40% кислоты, а второй — 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 процентного раствора, то получился бы 70 процентный раствор. Сколько литров 60 процентного раствора кислоты было первоначально? Решение 60% 0% 20% = + + 5 л 40% х л у л (х+у+5) л 0,4х (л) — кислоты в первом растворе 0,4х л 0,6у (л) — кислоты во втором растворе 0,6у л 0,2(х+у+5) (л) — кислоты в новом растворе 0,2(х+у+5) л 70% 80% 4 л 0,7(х+у+5) л кислоты в 5 литрах 0,7(х+у+5) (л) — кислоты в новом растворе Ответ: 2 л
Слайд 15
Откуда получаем, что %.
Аннотация к презентации
Скачать презентацию (0.39 Мб). Тема: «Задачи на смеси и сплавы-подготовка к ЕГЭ». Предмет: математика. 15 слайдов. Добавлена в 2017 году. Средняя оценка: 4.0 балла из 5.
ЗАДАЧИ НА СМЕСИ И СПЛАВЫ В 13 МКОУ «Зыряновская СОШ» Заринский район Алтайский край Учитель математики Степина Татьяна Сергеевна золото серебро 2 3 ЕГЭ
Слайд 2
Способы решения задач на смеси и сплавы Арифметический Применение уравнения Применение систем уравнений 10% никель
Слайд 3
В сосуд, содержащий 5 литров 12 процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? Ответ: 5% Решение I способ = + 5 л. 7 л. 12 % 0 % 0,6л 0,6л. 12 л. II способ Ответ: 5% III способ Объем раствора увеличился в 2,4 раза (было 5 л., стало 12 л. 12:5 = 2,4), содержание вещества не изменилось, поэтому процентная концентрация получившегося раствора уменьшилась в 2,4 раза. 12:2,4=5(%) Ответ: 5%
Слайд 4
Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20 процентный раствор кислоты? Решение Объем чистой кислоты в растворе не меняется, процентное содержание кислоты в растворе уменьшится в 3 раза (60:20=3) Объем раствора увеличится в 3раза:2·3=6(л) 6 – 2 = 4 (л) воды нужно добавить Ответ: 4 л.
Слайд 5
Смешали 4 литра 15 процентного водного раствора с 6 литрами 25 процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Решение Ответ: 4 л. + = 6л. 4л. 15% 25% 0,6л. 1,5л. 2,1л. 10л.
Слайд 6
Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг. Решение? Было Стало 400кг. 18% 20% 80% 328кг. 328кг. 72кг. Вода Цемент Вода Цемент
Слайд 7
Решение Сколько надо взять 5 процентного и 25 процентного раствора кислоты, чтобы получить 4 л 10 процентного раствора кислоты? 5% 10% + = 25% х л 0,25 · (4 — х) л – кислоты во втором растворе 4 л (4-х) л 0,4л (1-0,2х)л 0,05х 0,25(4-х)л 0,05 х ( л )– кислоты в первом растворе 0,1 · 4 = 0,4 л – кислоты в полученном растворе 0,05+0,25(4-х)=(1- 0,2х) л – кислоты в полученном растворе Получим уравнение 1 — 2х = 0,4 х = 3 3л – надо взять 5процентного раствора 4 – 3 = 1(л) – 25 процентного Ответ: 1л; 3л.
Слайд 8
Решение В сосуд емкостью 6л налито 4л 70% раствора серной кислоты. Во второй сосуд той же емкости налито 3л 90% раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нем получился 74% раствор серной кислоты? Найдите все допустимые значения процентного содержания раствора серной кислоты в 6л раствора в первом сосуде. + = 4л 3л хл 90% 74% 70% кислоты в I сосуде 2,8л 0,9хл кислоты нужно перелить кислоты вновом растворе (2,8+0,9х)л (4+х)л 0,74(4+х)л кислоты вновом растворе Получим уравнение 70% 2,8л 90% 1,8л 4л 2л 6л Допустимые значения процентного содержания Из второго сосуда в первый можно перелить максимальное количество раствора кислоты 2л + = кислоты в 2 литрах кислоты в 1 сосуде 4,6л Ответ: 1л;
Слайд 9
Ответ: 9 кг. + _ _ медь медь медь 10% 40% 30% х кг. (х+3) кг. (х+(х+3)) кг. 0,4(х+3)кг 0,3(2х+3)кг Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. 0,1х кг Решение Масса меди в первом сплаве 0,1х(кг) Во втором – 0,4(х+3)(кг) В третьем – 0,3(2х+3)(кг) Получим уравнение
Слайд 10
Имеется два сплава золота и серебра: в одном массы этих металлов находятся в отношении 2:3, а в другом – в отношении 3:7. Сколько килограммов нужно взять от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро находились бы в отношении 5:11? Решение + _ _ (8 – х)кг 8кг х кг Ответ:1 кг. и 7 кг. золото серебро 5 11 золото серебро 2 3 золото серебро 3 7 золото серебро 2 3 золото серебро 3 7 — от 2 сплава — от 1 сплава Получим уравнение 3/10(8-х) кг 2/5 х кг Масса золота в новом сплаве Масса золота в первом куске 2,5 кг Масса золота во втором куске
Слайд 11
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Решение + _ _ 200 кг х кг Масса никеля в первом сплаве 0,1х кг Масса никеля во втором сплаве 0,3у кг. Ответ: на 100 кг. у кг 30% никель 25% никель 0,3у кг Масса никеля в новом сплаве 200·0,25=50 (кг). 50кг 10% никель 0,1х кг 50 кг — масса первого сплава. 150 кг — масса второго сплава. 150 – 50 = 100 (кг)
Слайд 12
При смешивании 30 процентного раствора серной кислоты с 10 процентным раствором серной кислоты получилось 400 г 15 процентного раствора. Сколько граммов 30 процентного раствора было взято? + = х г 15% 30% 10% Решение 400г. у г кислоты впервом растворе 0,3х г кислоты во втором растворе кислоты вновом растворе 0,1у г 60 г Ответ: 100 г. 100 г – 30% раствора было взято.
Слайд 13
Решение Имеются два слитка сплава серебра и олова. Первый слиток содержит 360г серебра и 40г олова, а второй слиток – 450г серебра и 150г олова. От каждого слитка взяли по куску, сплавили их и получили 200г сплава, в котором оказалось 81% серебра. Определите массу (в граммах) куска, взятого от второго слитка. 200 г серебро олово 81% х г у г + _ _ 400г 600г серебро олово серебро олово 450 г 150 г серебро олово серебро олово 360 г 40 г Ответ:120 г. серебра вновом сплаве 162 г серебра в первом слитке 75% серебра во втором слитке 90% 0,9х(г) серебра в первом куске 0,9х(г) — 0,75у(г) серебра во втором куске 0,75у(г)- 90% 75%
Слайд 14
Первый раствор содержит 40% кислоты, а второй — 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 процентного раствора, то получился бы 70 процентный раствор. Сколько литров 60 процентного раствора кислоты было первоначально? Решение 60% 0% 20% = + + 5 л 40% х л у л (х+у+5) л 0,4х (л) — кислоты в первом растворе 0,4х л 0,6у (л) — кислоты во втором растворе 0,6у л 0,2(х+у+5) (л) — кислоты в новом растворе 0,2(х+у+5) л 70% 80% 4 л 0,7(х+у+5) л кислоты в 5 литрах 0,7(х+у+5) (л) — кислоты в новом растворе Ответ: 2 л
Слайд 15
Пусть кг – вес винограда. Твердая часть в винограде занимает % веса, поэтому
Какая сумма от прибыли рублей причитается Коле.
Pptcloud. ru
22.07.2017 0:29:32
2017-07-22 00:29:32
Источники:
Https://egemaximum. ru/13-zadachi-na-smesi-i-splavy/
Https://80-ballov. ru/video_page/zadanie-11-tekstovye-zadachi-teorija-zadachi-chast-1/
Https://pptcloud. ru/matematika/zadachi-na-smesi-i-splavy
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задачи на сплавы и смеси и проценты егэ математика
Задачи на сплавы и смеси и проценты егэ математика
Задачи на смеси и сплавы
Материал по алгебре (9 класс) по теме
В данном уроке рассмотрены основные методы решения задач на смеси и сплавы. Рассмотрены задачи из сборника для подготовки к ГИА, могут быть использованы для подготовки к ЕГЭ.
Скачать:
ВложениеРазмер
| zadachi_na_smesi_i_splavy. nellya. doc | 220.5 КБ |
Предварительный просмотр:
«Решение текстовых задач на смеси и сплавы».
Создание условий для систематизации, обобщения и углубления знаний учащихся при решении текстовых задач.
Повышение практической направленности предмета через решение практических задач.
Формирование математической грамотности учащихся.
Развитие навыков логического, творческого мышления, сообразительности и наблюдательности.
1. Сотая часть числа называется …(процент)
Устная разминка:
Соотнести проценты и соответствующие им дроби: 5% — 0,05; 17% — 0,17; 123% — 1,23; 0,3% — 0,003; 25% — 0,25
2. Частное двух чисел называют …(отношение)
3. Верное равенство двух отношений называют …(пропорция)
4. В химии определение этого понятия звучало бы так: гомогенная смесь, образованная не менее чем двумя компонентами … (раствор) . Один из которых называется растворителем, а другой растворимым веществом.
5. Отношение массы растворимого вещества к массе раствора называют массовой долей вещества в растворе или …(концентрация)
Итак, ребята, сегодня на уроке мы с вами рассмотрим задачи, решение которых связано с понятиями «концентрация», «процентное содержание». В условиях таких задач речь идет, чаще всего, о сплавлении каких-либо металлов, растворении друг в друге различных веществ или переливании жидкостей, состоящих из нескольких компонентов. Эти задачи входят в различные сборники заданий по подготовке к итоговой аттестации по математике за курс основной школы и включаются в варианты ЕГЭ.
Долей (концентрацией, процентным содержанием) α основного вещества в смеси будем называть отношение массы основного вещества m в смеси к общей массе смеси M:
Эта величина может быть выражена либо в долях единицы, либо в процентах. В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы, рисунки, таблицы. Современные психологи утверждают, что решение одной задачи несколькими способами часто бывает более полезным, чем решение одним способом нескольких задач.
Поэтому мы с вами рассмотрим несколько способов решения задач на смеси и сплавы.
I. Рассмотрим решения задач с применением таблицы.
Таблица для решения задач имеет вид.
Наименование веществ, растворов, смесей, сплавов
% содержание вещества (доля содержания вещества)
Масса раствора (смеси, сплава)
Задача №1 Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Наименование веществ, растворов, смесей, сплавов
% содержание меди (доля содержания вещества)
Масса раствора (смеси, сплава)
Сумма масс меди в двух первых сплавах (то есть в первых двух строчках) равна массе меди в полученном сплаве (третья строка таблицы):
Решив это уравнение, получаем х=140 . При этом значении х выражение
200 – х=60. Это означает, что первого сплава надо взять 140г, а второго 60г.
II. Рассмотрим решение этой же задачи с помощью следующей модели. Изобразим каждый из растворов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Для того, чтобы показать, что происходит смешивание веществ поставим знак «+» между первым и вторым прямоугольниками, а знак «=» между вторым и третьим прямоугольниками показывает, что третий раствор получен в результате смешивания первых двух. Полученная схема имеет следующий вид:
Рассм атр иваемый в задаче процесс можно представить в виде следующей модели — схемы:
Пусть х г – масса первого сплава. Тогда, (200- х )г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:
Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):
Решив это уравнение, получаем х=140 . При этом значении х выражение 200- х=60. Это означает, что первого сплава надо взять140г, а второго-60г.
III. Старинный способ решения задач на смеси, сплавы и растворы. Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого.
Ввиду большой простоты предложенный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо, как в предыдущей задаче, рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ.
Задача №2 (смешивание двух веществ, предлагалась на экзамене в 2006 году). Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?
Задача №3 (8.21 Сборник для подготовки к ГИА под ред. Л. В.Кузнецовой) Влажность свежих грибов 90%, а сухих 15%. Сколько сухих грибов получится из 1,7 кг свежих?
Задача №4. Имеется склянка 20%-го раствора кислоты и склянка 40%-го раствора кислоты. Смешали 200 г раствора из первой склянки и 300 г из второй. Определите массу кислоты и её концентрацию.
Задача №5 . Имеется два раствора поваренной соли разной концентрации. Если слить вместе 100г первого раствора и 200 г второго, то получится 50% раствор. Если слить 300 г первого раствора и 200 г второго, то получится 42% раствор. Определить концентрации первого и второго растворов.
Задача №6 (для самостоятельного решения) (Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе, 8.22). Сколько граммов воды нужно добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20%?
. В сосуд, содержащий литров — процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
Задачи на смеси и сплавы
Материал по алгебре (9 класс) по теме
В данном уроке рассмотрены основные методы решения задач на смеси и сплавы. Рассмотрены задачи из сборника для подготовки к ГИА, могут быть использованы для подготовки к ЕГЭ.
ВложениеРазмер
| zadachi_na_smesi_i_splavy. nellya. doc | 220.5 КБ |
Составим уравнение:
И найдем.
Это означает, что первого сплава надо взять 140г, а второго 60г.
Nsportal. ru
10.03.2018 4:47:18
2018-03-10 04:47:18
Задачи на сплавы и смеси и проценты егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 8 № 99572
Смешали некоторое количество 15%-го раствора некоторого вещества с таким же количеством 19%-го раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Процентная концентрация раствора (массовая доля) равна Пусть масса получившегося раствора Таким образом, концентрация полученного раствора равна:
Формирование математической грамотности учащихся.
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Для сплавов и смесей действуем аналогично.
Math-ege. sdamgia. ru
09.08.2019 14:18:46
2019-08-09 14:18:46
Задачи ЕГЭ на сплавы, смеси, растворы.
Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.
. В сосуд, содержащий литров — процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим.
Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
. Смешали некоторое количество — процентного раствора некоторого вещества с таким же количеством — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть масса первого раствора равна. Масса второго — тоже. В результате получили раствор массой. Рисуем картинку.
. Виноград содержит влаги, а изюм — . Сколько килограммов винограда требуется для получения килограммов изюма?
Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось воды, значит, «сухого вещества» было. В изюме воды и «сухого вещества». Пусть из кг винограда получилось кг изюма. Тогда
Составим уравнение:
И найдем.
. Имеется два сплава. Первый сплав содержит никеля, второй — никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой.
Запишем простую систему уравнений:
Первое уравнение — масса получившегося сплава, второе — масса никеля.
Решая, получим, что.
. Смешав — процентный и — процентный растворы кислоты и добавив кг чистой воды, получили — процентный раствор кислоты. Если бы вместо кг воды добавили кг — процентного раствора той же кислоты, то получили бы — процентный раствор кислоты. Сколько килограммов — процентного раствора использовали для получения смеси?
Пусть масса первого раствора, масса второго равна. Масса получившегося раствора равна. Запишем два уравнения, для количества кислоты.
Решаем получившуюся систему. Сразу умножим обе части уравнений на, поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.
5. Отношение массы растворимого вещества к массе раствора называют массовой долей вещества в растворе или …(концентрация)
Задача №3 (8.21 Сборник для подготовки к ГИА под ред. Л. В.Кузнецовой) Влажность свежих грибов 90%, а сухих 15%. Сколько сухих грибов получится из 1,7 кг свежих?
В изюме воды и сухого вещества.
Ege-study. ru
16.12.2018 15:44:31
2018-12-16 15:44:31
Источники:
Https://nsportal. ru/shkola/algebra/library/2012/02/07/zadachi-na-smesi-i-splavy
Https://math-ege. sdamgia. ru/problem? id=99572
Https://ege-study. ru/zadachi-ege-na-splavy-smesi-rastvory/
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 — x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 — x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 — x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 — x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
$а_1$ — первый член арифметической прогрессии
$d$ — разность между последующим и текущим членом прогрессии
$d=a_{n+1}-a_n$
$a_n$ — член арифметической прогрессии, стоящий на $n$-ом месте
$n$ — номер места для членов арифметической прогрессии
$S_n$ — сумма первых n членов арифметической прогрессии
Формула для нахождения $n$-ого члена прогрессии:
$a_n=a_1+d(n-1)$
Формула суммы первых n членов арифметической прогрессии:
$S_n={(a_1+a_n)·n}/{2}$
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
$b_1$ — первый член геометрической прогрессии
$q$ — знаменатель геометрической прогрессии, показывает во сколько раз последующее число больше предыдущего.
$q={b_{n+1}}/{b_n}$
$b_n$ — $n$-ый член геометрической прогрессии
$S_n$ — сумма первых $n$ членов геометрической прогрессии
Формула, для нахождения $n$-ого члена прогрессии:
$b_n=b_1·q^{n-1}$
Формула суммы первых $n$ членов арифметической прогрессии:
$S_n={b_1·(q^n-1)}/{q-1},q≠1$
В задачах на прогрессии важно:
- Определить тип прогрессии
- Верно сопоставить приведенные величины с их обозначением в формулах, записать дано.
- Подставить известные данные в формулу и вывести неизвестную величину.
Пример:
Предприниматель Петров получил в $2000$ году прибыль в размере $5000$ рублей. Каждый следующий год его прибыль увеличивалась на $300%$ по сравнению с предыдущим годом. Сколько рублей заработал Петров за 2003 год?
Решение:
Для начала посчитаем увеличение прибыли: так как она увеличивалась на $300%$, то $100%+300%=400%$. $400%$ — это то же самое, что увеличение прибыли в $4$ раза.
Данная задача на геометрическую прогрессию, так как прибыль увеличивалась В четыре раза по сравнению с предыдущим годом.
Запишем дано: $b_1=5000$ — первая прибыль
$q=4$ — величина, показывающая, во сколько раз увеличивалась прибыль каждый год
$n=4$, так как с $2000$ по $2003$ прошло $4$ года (т.к. 2000 — 1й год, 2001 — 2й, 2002 — 3й, 2003 -4й)
$b_4-?$ — количество заработанных денег в четвертый год от начала прибыли
Запишем формулу для нахождения $n$-ого члена прогрессии:
$b_n=b_1·q^{n-1}$
Подставим известные величины из дано и найдем $b_4$:
$b_4=5000·4^3=320000$
Ответ: $320000$
Задачи на смеси и сплавы.
В задачах на растворы и сплавы для удобства решения можно делать схему, для каждого раствора в схеме необходимо записать две величины:
- Массу или объем, в зависимости от условия задачи;
- Процентное содержание чистого вещества в растворе.
Потом, если мы смешиваем составы, для смешанного вещества тоже записываем:
- Массу или объем полученной смеси – она равна сумме масс или объемов изначальных растворов.
- Процентное содержание чистого вещества в полученной смеси.
Далее составляем уравнение, для этого надо процентное содержание чистого вещества умножить на массу своего раствора, сложить получившиеся величины каждого раствора и все это приравнять к полученной величине смеси.
$m_{1 раствора}·%_{1 вещества}+m_{2 раствора}·%_{2 вещества}=m_{смеси}·%_{смеси}$
Пример:
Смешали $2$ кг $15%$-ного водного раствора некоторого вещества с $8$ кг $10%$-ного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
Пусть $х%$ — концентрация получившегося раствора.
Составим к задаче схему.
| $1$ раствор
Масса — $2$кг Процентное содержание вещества — $15%$ |
$2$ раствор
Масса — $8$кг Процентное содержание вещества — $10%$ |
| Смесь растворов
Масса – $2$кг$+8$кг$=10$кг Процентное содержание вещества — $х%$ |
Составим уравнение:
$15%·2+10%·8=х%·10$ Уберем в уравнении знак процента, чтобы он не мешал при расчетах
$15·2+10·8=10·х$
$30+80=10х$
$10х=110$
$х=11%$ — концентрация получившегося раствора.
Ответ: $11$