Формулы тригонометрии для егэ профиль распечатать

Самые необходимые тригонометрические формулы

Для того чтобы сдать ЕГЭ по математике, вам понадобится около 20 формул тригонометрии. Это не много. Но их надо знать наизусть!

Вот таблица, в которой собраны основные тригонометрические формулы. Здесь все самое необходимое. Их легко выучить и применять.

Эти формулы применяются и в заданиях 1 части ЕГЭ по математике, и в заданиях 2 части.

Эта полезная табличка – только одна из многих страниц Справочника Анны Малковой для подготовки к ЕГЭ. Скачай Справочник бесплатно здесь.

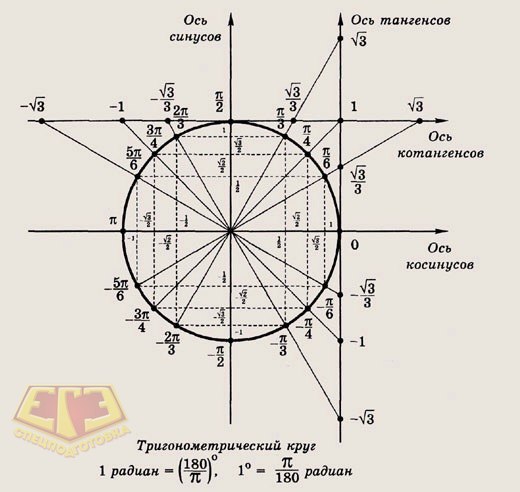
Кроме того, надо знать определения синуса, косинуса и тангенса, а также значения этих функций для основных углов.

Первые 3 блока формул из нашей таблицы часто встречаются в заданиях 1 части ЕГЭ и в задаче из второй части, где надо решить тригонометрическое уравнение.

В первую очередь это основное тригонометрическое тождество:

sin ${}^2 alpha +$ cos ${}^2 alpha =1.$

Это формулы, которые показывают, как выразить тангенс через косинус и котангенс через синус угла.

tg ${}^2alpha +1=displaystyle frac{1}{{{cos}^2 alpha }};$

1 + ctg ${}^2alpha =displaystyle frac{1}{{{sin}^2 alpha }}.$

Формулы синуса и косинуса двойного угла, формулы синуса суммы, косинуса разности, – все это надо знать, чтобы без ошибок решать тригонометрические уравнения.

А вот формулы суммы синусов и косинусов, а также преобразование произведения в сумму могут пригодиться при решении задач с параметрами.

Где же могут встретиться формулы из двух последних блоков, внизу таблицы?

Формулы понижения степени могут присутствовать и в тригонометрических уравнениях, и в «параметрах». И даже в задачах с физическим содержанием из 1 части ЕГЭ, если там вдруг попадется тригонометрия.

А универсальная тригонометрическая замена, когда мы выражаем синус и косинус угла альфа через тангенс половинного угла? А формулы синуса и косинуса тройных углов? Где же они применяются? Оказывается, они помогают решать задачи по геометрии из 2 части ЕГЭ. Так что их тоже стоит знать, если хотите сдать на высокий балл.

Обратите внимание, что в этой таблице нет формул приведения. О них мы рассказываем в отдельной статье нашего сайта.

Как же выучить тригонометрические формулы?

1. Учите формулы сразу. Не рассказывайте себе сказки о том, что в последнюю ночь перед ЕГЭ все выучите. Каждый день – один блок, то есть три-четыре формулы из нашей таблицы.

2. Тренируйтесь. Выучить иностранный язык проще всего тому, кто вынужден постоянно на нем говорить. Так и здесь. Для тренировки можно из классического задачника Сканави выбрать 20-50 заданий на преобразование тригонометрических выражений и доказательство тождеств.

3. Универсальный способ: ежедневно, садясь за уроки, берите чистый листок и выписывайте наизусть все тригонометрические формулы, какие помните. Когда всё готово — сверяете. И к экзамену вы будете помнить всё.

4. Еще один отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются легко и быстро!

5. И конечно, решаем задания ЕГЭ на применение этих формул. Начнем с задач 1 части, преобразование тригонометрических выражений.

Задача 1.

Найдите tg alpha , если cos $alpha =displaystyle frac{sqrt{10}}{10}$ и $alpha in left(displaystyle frac{3pi }{2};2pi right).$

Решение:

Воспользуемся формулой:

tg ${}^2x+1=displaystyle frac{1}{{cos}^2x} Rightarrow$ tg x $=pm sqrt{displaystyle frac{1}{{cos}^2x}-1}.$

Какой знак будет у тангенса, «плюс» или «минус»?

В условии дано, что $alpha in left(displaystyle frac{3pi }{2};2pi right)$ , то есть это угол из четвертой четверти, значит tgx

tgx $=-sqrt{displaystyle frac{100}{10}-1}=-3.$

Ответ: -3.

Задача 2.

Найдите $displaystyle frac{10{sin 6alpha }}{3{cos 3alpha }},$ если sin

Решение:

Воспользуемся формулой синуса двойного угла: sin2 alpha = 2sin alpha cos alpha :

$displaystyle frac{10{sin 6alpha }}{3{sin 3alpha }}=displaystyle frac{10cdot 2{sin 3alpha }{cos 3alpha }}{3{sin 3alpha }}=displaystyle frac{20cdot {cos 3alpha }}{3}=displaystyle frac{20cdot 0,6}{3}=4.$

Ответ: 4.

Задача 3.

Найдите 24cos если sin

Решение:

Воспользуемся формулой косинуса двойного угла: cos 2 alpha = 1 — 2sin ${}^2$ alpha :

24cos2 alpha = 24(1 — 2sin ${}^2 alpha )=24left(1-2{left(-0,2right)}^2right)=$

Ответ: 22,08.

Задача 4.

Найдите $displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }},$ если tg alpha =3.

Решение:

Вынесем косинус альфа за скобки в числителе и знаменателе:

$displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }}=displaystyle frac{{cos alpha }left(3-4tgalpha right)}{{cos alpha }left(2tgalpha -5right)}=displaystyle frac{3-4cdot 3}{2cdot 3-5}=displaystyle frac{-9}{1}=-9.$

Ответ: -9.

Задача 5.

Найдите значение выражения: $displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ }cdot {sin 41{}^circ }}.$

Решение:

Воспользуемся формулой синуса двойного угла:

sin2 alpha = 2sin alpha cos alpha ; тогда sin alpha cos alpha = $displaystyle frac{1}{2}{sin 2alpha } .$

$displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 49{}^circ }cdot {cos 49{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 41{}^circ }}{{sin 41{}^circ }}=10.$

Ответ: 10.

Задача 6.

Найдите значение выражения: sqrt{3} cos ${}^2 displaystyle frac{5pi }{12}-sqrt{3}$ sin ${}^2 displaystyle frac{5pi }{12} .$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos alpha = cos ${}^2$ alpha — sin ${}^2$ alpha.

$sqrt{3}{{cos}^2 displaystyle frac{5pi }{12} }-sqrt{3}{{sin}^2 displaystyle frac{5pi }{12}=sqrt{3}left({{cos}^2 displaystyle frac{5pi }{12} }-{{sin}^2 displaystyle frac{5pi }{12} }right) }=$

cos $displaystyle frac{5pi }{6}=sqrt{3}cdot left(-displaystyle frac{sqrt{3}}{2}right)=-1,5.$

Ответ: -1,5.

Задача 7.

Найдите значение выражения: $-50tg 9{}^circ cdot$ tg $81{}^circ +31.$

Решение:

Используя формулы приведения, получим: tg $81{}^circ$ = tg $left(90{}^circ -9{}^circ right)$ = ctg $9{}^circ.$

Пользуемся также тем, что тангенс и котангенс угла альфа — взаимно обратные величины,

Получим:

-50tg $9{}^circ cdot$ ctg $9{}^circ +31=-50+31 = - 19.$

Ответ: -19.

Задача 8.

Найдите значение выражения: sin ${}^2 displaystyle frac{21pi }{8}.$

Решение:

sin ${}^2 displaystyle frac{21pi }{8}=6sqrt{2}-12sqrt{2}$ sin ${}^2 displaystyle frac{21pi }{8}=6sqrt{2}cdot left(1-2{}^2 displaystyle frac{21pi }{8} right)=$

cos $(2cdot displaystyle frac{21pi }{8})=6sqrt{2}$ cos $displaystyle frac{21pi }{4}=6sqrt{2}$ cos $displaystyle frac{5pi }{4}=6sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=6.$

Мы вынесли за скобки множитель и применили формулу косинуса двойного угла, выразив его через квадрат синуса угла.

Ответ: 6.

Задача 9.

Найдите значение выражения: 5sin $displaystyle frac{11pi }{12}cdot$ cos $displaystyle frac{11pi }{12}.$

Решение:

Воспользуемся формулой синуса двойного угла: sin alpha = 2sin alpha cos alpha . Также применим одну из формул приведения: sin = -sin alpha .

5sin $displaystyle frac{11pi }{12}$ cos $displaystyle frac{11pi }{12}=displaystyle frac{5}{2}cdot$ sin $displaystyle frac{11pi }{6}=displaystyle frac{5}{2}cdot$ sin $left(2pi -displaystyle frac{pi }{6}right)=-displaystyle frac{5}{2}cdot$ sin $displaystyle frac{pi }{6}=-displaystyle frac{5}{2}cdot displaystyle frac{1}{2}=-1,25.$

Ответ: -1,25.

Задача 10.

Найдите значение выражения: $2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}}.$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2 alpha = 1 — 2 ${sin}^2 alpha.$

$2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}= }2sqrt{3}(1-2{{sin}^2 displaystyle frac{7pi }{12})= }$

cos $displaystyle frac{7pi }{6}=2sqrt{3}cdot$ cos $left(pi +displaystyle frac{pi }{6}right)=-2sqrt{3}cdot$ cos $displaystyle frac{pi }{6}=-2sqrt{3}cdot displaystyle frac{sqrt{3}}{2}=-3.$

Ответ: -3.

Задача 11.

Найдите значение выражения: $sqrt{108}{{cos}^2 displaystyle frac{pi }{12} }-sqrt{27}.$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2 alpha = ${cos}^2 alpha -sin{}^2 alpha = 2cos{}^2 alpha -1.$

cos ${}^2 displaystyle frac{pi }{12}-sqrt{27}=6sqrt{3}$ cos ${}^2 displaystyle frac{pi }{12}-3sqrt{3}=3sqrt{3}left(2{{cos}^2 displaystyle frac{pi }{12} }-1right)=3sqrt{3}cdot$ cos $displaystyle frac{pi }{6}=$

$=3sqrt{3}cdot displaystyle frac{sqrt{3}}{2} =4,5.$

Ответ: 4,5.

Задача 12.

Найдите значение выражения: $-displaystyle frac{6{sin 374{}^circ }}{{sin 14{}^circ }}.$

$displaystyle frac{-6{sin 374{}^circ }}{{sin 14{}^circ }}=displaystyle frac{-6{sin 14{}^circ }}{{sin 14{}^circ }}=-6.$

Мы воспользовались периодичностью функции синус: sinsin alpha . В нашей задаче 374 = 360 + 14.

Ответ: — 6.

Задача 13.

Найдите значение выражения: $7sqrt{2}{sin displaystyle frac{15pi }{8}cdot {cos displaystyle frac{15pi }{8} } }.$

Решение:

Воспользуемся формулой синуса двойного угла: sin2 alpha = 2sin alpha cos alpha.

sin $displaystyle frac{15pi }{8}cdot$ cos $displaystyle frac{15pi }{8}=displaystyle frac{7sqrt{2}}{2}cdot$ sin $displaystyle frac{15pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot$ sin $left(4pi -displaystyle frac{pi }{4}right)=displaystyle frac{7sqrt{2}}{2}cdot$ sin $displaystyle frac{pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=3,5.$

Ответ: 3,5.

Заметим, что если в задаче нам встретилось произведение синуса альфа на косинус альфа, то, скорее всего, нужно будет применять формулу синуса двойного угла.

Задача 14.

Найдите tg alpha , если cos alpha $=-displaystyle frac{5sqrt{41}}{41}$ и $alpha in left(pi ;displaystyle frac{3pi }{2}right).$

Решение:

Вспомним основное тригонометрическое тождество: ${{cos}^2 alpha }+ {{sin}^2 alpha }=1.$ Выразим из этой формулы синус альфа:

sin alpha $=pm sqrt{1-{{cos}^2 alpha }}.$

Какой же знак выбрать, «плюс» или «минус»?

Угол альфа в третьей четверти, значит, его синус отрицателен.

sin alpha $=-sqrt{1-{left(-displaystyle frac{5sqrt{41}}{41}right)}^2}=-sqrt{1-displaystyle frac{25}{41}}=-sqrt{displaystyle frac{16}{41}}=-displaystyle frac{4}{sqrt{41}}.$

tg $alpha =displaystyle frac{{sin alpha }}{{cos alpha }}=left(-displaystyle frac{5sqrt{41}}{41}right):left(-displaystyle frac{4}{sqrt{41}}right)=displaystyle frac{5}{4}=1,25.$

Ответ: 1,25.

Задача 15.

Найдите sin alpha , если cos alpha $=-displaystyle frac{sqrt{19}}{10}$ и $alpha in left(displaystyle frac{pi }{2};pi right).$

Решение:

Как и в предыдущей задаче, выразим синус альфа из основного тригонометрического тождества:

sin $alpha =pm sqrt{1-{{cos}^2 alpha }}.$

Дан угол альфа, принадлежащий второй четверти, значит, его синус положителен.

sin $alpha =sqrt{1-{left(displaystyle frac{sqrt{19}}{10}right)}^2}=sqrt{displaystyle frac{81}{100}}=0,9.$

Ответ: 0,9.

Задача 16.

Найдите tg alpha , если sin alpha $=-displaystyle frac{4sqrt{41}}{41}$ и $alpha in left(pi ;displaystyle frac{3pi }{2}right).$

Решение:

Аналогично предыдущим задачам, выразим косинус альфа из основного тригонометрического тождества:

cos alpha $=pm sqrt{1-{{sin}^2 alpha }}.$

Угол альфа в третьей четверти, значит, его косинус отрицателен.

cos alpha $=-sqrt{1-displaystyle frac{16}{41}}=-sqrt{displaystyle frac{25}{41}}=-displaystyle frac{5}{sqrt{41}}$ , тогда tg $alpha =displaystyle frac{{sin alpha }}{{cos alpha }}=-displaystyle frac{4}{sqrt{41}}div left(-displaystyle frac{5}{sqrt{41}}right)=displaystyle frac{4}{5}=0,8.$

Ответ: 0,8.

Задача 17.

Найдите значение выражения: — 42tg $34{}^circ cdot$ tg $56{}^circ +6.$

Решение:

-42tg $34{}^circ cdot$ tg ${56}^circ =$ -42tg $34{}^circ cdot$ tg $left(90{}^circ -34{}^circ right)=$ -42tg $34{}^circ cdot$ ctg $34{}^circ =-42.$

Мы применили формулу приведения, а также то, что тангенс и котангенс угла альфа — взаимно обратные величины, и их произведение равно единице.

Ответ: -42.

Задача 18.

Найдите значение выражения: $displaystyle frac{24}{{{sin}^2 127{}^circ }}+4+$ sin ${}^2 217{}^circ .$

Решение:

Воспользуемся формулами приведения:

$displaystyle frac{24}{{{sin}^2 127+4+sin{}^2 217}}=displaystyle frac{24}{{{sin}^2 left(90{}^circ +37{}^circ right)+4+{{sin}^2 left(180{}^circ +37{}^circ right) } }}=$

$=displaystyle frac{24}{{{cos}^2 37{}^circ +4+{{sin}^2 37{}^circ } }}=displaystyle frac{24}{5}=4,8.$

Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.

Ответ: 4,8.

Задача 19.

Найдите значение выражения: $displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }cdot {sin 22{}^circ }}.$

Решение:

Так как $68{}^circ +22{}^circ =90{}^circ ,$ то заменим ${sin 68{}^circ }$ на ${cos 22 }^circ$ по формуле приведения и воспользуемся формулой синуса двойного угла:

sin2 alpha = 2sin alpha cos alpha.

$displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }{sin 22{}^circ }}=displaystyle frac{2{sin 136{}^circ }}{{cos 22{}^circ }{sin 22{}^circ }}=displaystyle frac{4{sin left(180{}^circ -44{}^circ right) }}{{sin 44{}^circ }}=$

$=displaystyle frac{4{sin 44{}^circ }}{{sin 44{}^circ }}=4.$

Ответ: 4.

Задача 20.

Найдите значение выражения: $displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}.$

Решение:

Воспользуемся формулой косинуса двойного угла:

${cos 2alpha ={{cos}^2 alpha }-{{sin}^2 alpha } }.$

$displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}=displaystyle frac{-21{cos 132{}^circ }}{{cos 132{}^circ }}=-21.$

Ответ: -21.

Задача 21.

Найдите значение выражения: $sqrt{2}{sin displaystyle frac{7pi }{8}cdot {cos displaystyle frac{7pi }{8}} }.$

Решение:

Воспользуемся формулой синуса двойного угла:

$sqrt{2}{sin displaystyle frac{7pi }{8} }cdot {cos displaystyle frac{7pi }{8}=displaystyle frac{sqrt{2}}{2}{sin displaystyle frac{7pi }{4} } }=displaystyle frac{sqrt{2}}{2}{sin left(2pi -displaystyle frac{pi }{4}right) }=-displaystyle frac{sqrt{2}}{2}sin displaystyle frac{pi }{4}=$

$= -displaystyle frac{sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=-0,25.$

Ответ: -0,25.

Задача 22.

Найдите значение выражения: $3sqrt{2}{{cos}^2 displaystyle frac{9pi }{8} }-3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }.$

Решение:

$3sqrt{2}{cos}^2 displaystyle frac{9pi }{8} -3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }=3sqrt{2}left({{cos}^2 displaystyle frac{9pi }{8} }-{{sin}^2 displaystyle frac{9pi }{8} }right)=3sqrt{2}{cos displaystyle frac{9pi }{4} }=$

$=3sqrt{2}cos left(2pi +displaystyle frac{pi }{4}right)=3sqrt{2}cos displaystyle frac{pi }{4}=3sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=3.$

И здесь тоже была формула косинуса двойного угла, но только в другой форме.

Ответ: 3.

Задача 23.

Найдите значение выражения: $26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{3} }.$

Решение:

$26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{4} }=26sqrt{2}cdot displaystyle frac{sqrt{2}}{2}cdot left(-displaystyle frac{1}{2}right)=-13.$

А здесь мы просто вычислили косинус и синус табличного угла $displaystyle frac{pi }{4}.$

Ответ: -13.

Задача 24.

Найдите значение выражения: $18sqrt{2}tgdisplaystyle frac{pi }{4}{sin displaystyle frac{pi }{4} }.$

Решение:

$18sqrt{2}cdot tgdisplaystyle frac{pi }{4}{cdot sin displaystyle frac{pi }{4}= }18sqrt{2}cdot 1cdot displaystyle frac{sqrt{2}}{2}=18.$

Это задача на вычисление тригонометрических функций для табличного угла $displaystyle frac{pi }{4}.$ Если этот угол выразить в градусах, то он равен 45 градусов.

Ответ: 18.

Задача 25.

Найдите значение выражения: $displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}.$

Решение:

Используя формулы приведения, получим:

$displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}=displaystyle frac{2{cos beta }+3{cos beta }}{-2{cos beta }}=$

$=-displaystyle frac{5{cos beta }}{2{cos beta }}=-2,5.$

Лайфхак: если вам сложно запомнить формулы приведения, вы можете вместо них использовать формулы косинуса разности и синуса суммы.

Ответ: -2,5.

Посмотрим, как формулы тригонометрии применяются при решении уравнений.

Задача 26.

Решите уравнение: ${{sin}^2 left(displaystyle frac{pi }{4}-xright) }={{sin}^2 left(displaystyle frac{pi }{4}+xright) }.$

Решение:

Воспользуемся формулой понижения степени: sin ${}^2 x=displaystyle frac{1-{cos 2x }}{2}.$

$displaystyle frac{1-{cos left(displaystyle frac{pi }{2}-2xright) }}{2}=displaystyle frac{1-{cos left(displaystyle frac{pi }{2}+2xright) }}{2}Leftrightarrow {cos left(displaystyle frac{pi }{2}-2xright) }={cos left(displaystyle frac{pi }{2}+2xright)Leftrightarrow }$

$Leftrightarrow {cos 2x=-{cos 2xLeftrightarrow 2 } }{cos 2x=0 }Leftrightarrow 2x=displaystyle frac{pi }{2}+pi kLeftrightarrow x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.$

Ответ: $x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.$

Задача 27.

Решите уравнение: ${{cos}^2 3x }+{{cos}^2 4x }+{{cos}^2 5x }=displaystyle frac{3}{2}.$

Решение:

Воспользуемся формулой понижения степени: ${{cos}^2 x }=displaystyle frac{1+{cos 2x }}{2}.$

${cos}^2 3x+{cos}^2 4x+{cos}^2 5x=displaystyle frac{3}{2}Leftrightarrow displaystyle frac{1+{cos 6x }}{2}+$

$+displaystyle frac{1+{cos 8x }}{2}+displaystyle frac{1+{cos 10x }}{2}=displaystyle frac{3}{2}.$

Умножим обе части на два:

Воспользуемся формулой суммы косинусов: cos alpha + cos beta = 2cos $displaystyle frac{alpha +beta }{2}$ cos $displaystyle frac{alpha -beta }{2};$

cos6x + cos10x = 2cos8x cos2x.

Уравнение примет вид:

2cos8x cos2x + cos8x =0.

Вынесем общий множитель за скобки. Теперь произведение двух множителей равно нулю, а с этим мы умеем работать.

${cos 8xleft(2{cos 2x+1 }right)=0Leftrightarrow left[ begin{array}{c}{cos 8x=0 } \{cos 2x=-displaystyle frac{1}{2} } end{array}Leftrightarrow left[ begin{array}{c}8x=displaystyle frac{pi }{2}+pi k \2x=pm displaystyle frac{2pi }{3}+2pi k;kin Z end{array}right.right. }Leftrightarrow left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .$

Ответ: $left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .$

Все о решении тригонометрических уравнений здесь.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Самые необходимые тригонометрические формулы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Опубликовано 04.12.2014 — 11:35 — Лобышева Ирина Сергеевна

каждый год выпускаю классы и имею подборку тригонометрических формул используемых в обеих частях ЕГЭ, которыми хочу поделиться с Вами.

Скачать:

Вложение	Размер
trigonometriya.docx	1.28 МБ

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Разработка урока алгебры в 10 классе по теме «Формулы тригонометрии»

Данный урок является обобщающим по теме «Тригонометрические формулы»…

Формулы тригонометрии

Обобщающий урок по теме в 10 классе по учебнику А.Г. Мордкович…

Основные формулы по тригонометрии

Приведены основные формулы по тригонометрии для 10 класса….

Тригонометрия. Сборник формул

Тригонометрия. Сборник формул…

Основные формулы тригонометрии

Основные формулы тригонометрии, которые необходимы при подготовке к ЕГЭ по математике…

Формулы тригонометрии

В презентации содержится материал о различных формулах по тригонометрии. Содержание презентации можно использовать как…

Тригонометрия учебник с формулами

Учебник по тригонометрии включает теоретический материал с формулами…

Мне нравится

Источник

11 декабря 2020

В закладки

Обсудить

Жалоба

Шпаргалка по тригонометрии

Основные тригонометрические тождества и формулы.

shpargalka_po_trigonometrii.pdf

Содержание

Основные тригонометрические тождества.
Формулы приведения.
Формулы периодических углов.
Формулы суммы и разности углов.
Формулы двойного угла.
Формулы половинного угла (формулы понижения степени).
Формулы произведения тригонометрических функций.
Формулы суммы и разности тригонометрических функций.
Универсальная тригонометрическая подстановка (УТП).
Обратные тригонометрические функции (аркфункции).
Простые тригонометрические уравнения.

Источник

Алгебра — ЕГЭ Тригонометрия — ЕГЭ Геометрия — ЕГЭ Стереометрия — ЕГЭ Алгебра — ОГЭ Геометрия — ОГЭ

Самые необходимые тригонометрические формулы

Как же выучить тригонометрические формулы?

Скачать:

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Разработка урока алгебры в 10 классе по теме «Формулы тригонометрии»

Формулы тригонометрии

Основные формулы по тригонометрии

Тригонометрия. Сборник формул

Основные формулы тригонометрии

Формулы тригонометрии

Тригонометрия учебник с формулами

Шпаргалка по тригонометрии

Формулы по тригонометрии

Шпаргалка по тригонометрическим формулам

Таблица формул тригонометрии

Единичный круг — тригонометрия