Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д6 B9 № 902
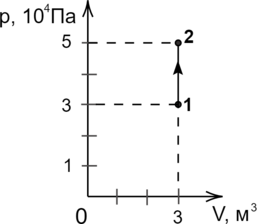
В цилиндрическом сосуде под поршнем находится идеальный газ, давление которого Па и температура 300 K. Как надо изменить объем газа, не меняя его температуры, чтобы давление увеличилось до
?
1) увеличить в 2 раза
2) увеличить в 4 раза
3) уменьшить в 2 раза
4) уменьшить в 4 раза
2
Задания Д6 B9 № 904
В воздушном насосе перекрыли выходное отверстие и быстро сжали воздух в цилиндре насоса. Какой процесс происходит с воздухом в цилиндре насоса?
1) изобарный
2) изохорный
3) изотермический
4) адиабатный
3
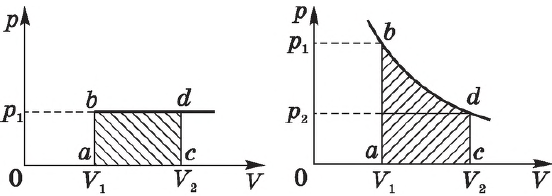
Задания Д6 B9 № 908
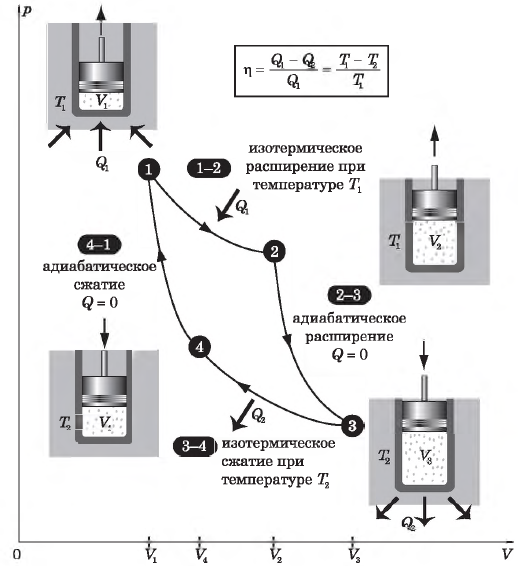
На рисунке представлены графики процессов, проводимых с постоянным количеством идеального газа.
Какой из изопроцессов изображает график 1?
1) адиабатный
2) изотермический
3) изобарный
4) изохорный
4
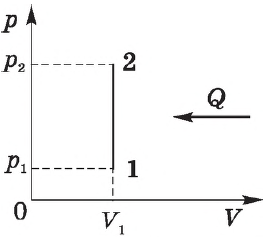
Задания Д6 B9 № 909
На рисунке показан цикл, осуществляемый с идеальным газом.
Изобарному нагреванию соответствует участок
1) AB
2) BC
3) CD
4) DA
5
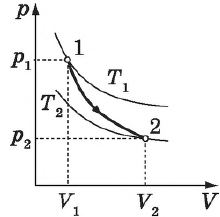
Задания Д6 B9 № 911
Идеальный газ сначала нагревался при постоянном давлении, потом его давление уменьшалось при постоянном объеме, затем при постоянной температуре объем газа уменьшился до первоначального значения. Какой из графиков на рисунке в координатных осях V—Т соответствует этим изменениям состояния газа?
1) 1
2) 2
3) 3
4) 4
Пройти тестирование по этим заданиям
Изопроцессы
-
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
-
Изотермический процесс
-
Графики изотермического процесса
-
Изобарный процесс
-
Графики изобарного процесса
-
Изохорный процесс
-
Графики изохорного процесса
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
к оглавлению ▴
Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором —
. Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса и молярная масса
предполагаются неизменными.
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
(1)
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
(2)
Данное утверждение называется законом Бойля — Мариотта.
Записав закон Бойля — Мариотта в виде
(3)
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
к оглавлению ▴
Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
• -диаграмма: ось абсцисс
, ось ординат
;
• -диаграмма: ось абсцисс
, ось ординат
;
• -диаграмма: ось абсцисс
, ось ординат
.
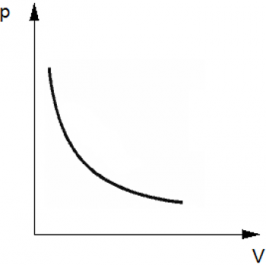
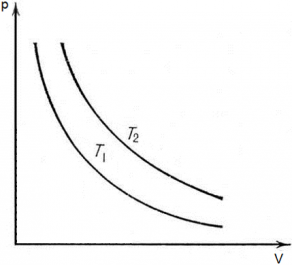
График изотермического процесса называется изотермой.
Изотерма на -диаграмме — это график обратно пропорциональной зависимости
.
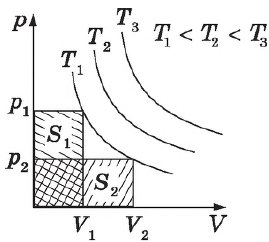
Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1.
Рис. 1. Изотерма на -диаграмме
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме.
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2). Первый процесс идёт при температуре , второй — при температуре
.
Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление
, на второй —
. Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит,
.
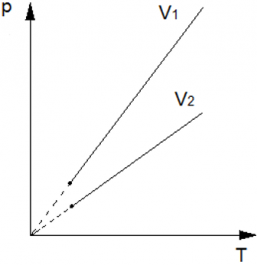
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):
Рис. 3. Изотермы на и
-диаграммах
к оглавлению ▴
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня
, то давление газа всё время постоянно и равно
где — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны
и
.
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
(4)
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
(5)
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:
(6)
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
к оглавлению ▴
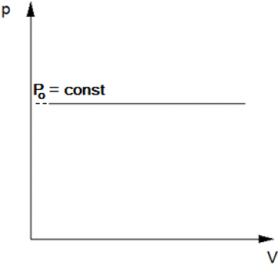
Графики изобарного процесса
График изобарного процесса называется изобарой. На -диаграмме изобара
является прямой линией (рис. 4):
Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
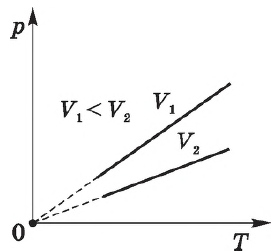
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на —диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и
(рис. 5):
Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что
. Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):
Рис. 6. Изобары на и
-диаграммах
к оглавлению ▴
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами
и
. Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
(7)
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
(8)
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:
(9)
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
к оглавлению ▴
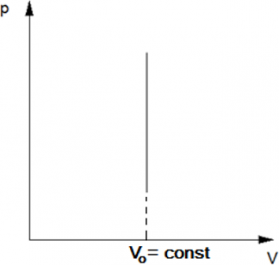
Графики изохорного процесса
График изохорного процесса называется изохорой. На -диаграмме изохора
является прямой линией (рис. 7):
Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
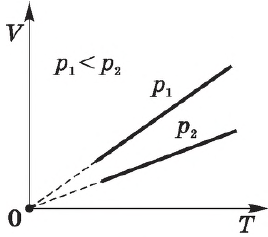
Далее, чем больше объём, тем ниже идёт изохора на —диаграмме (рис. 8):
Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что
. Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть,
.
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):
Рис. 9. Изохоры на и
-диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Изопроцессы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Изопроцессы в газах
Изопроцессами называются процессы, протекающие при неизменном значении одного из параметров: давления ($р$), объема ($V$), температуры ($Т$).
В идеальном газе эти процессы подчиняются газовым законам.
Газовыми законами называются количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра.
Закон Бойля-Мариотта
Закон Бойля-Мариотта — один из основных газовых законов, он описывает изотермические процессы в газе.
Процесс изменения состояния термодинамической системы при постоянной температуре называется изотермическим.
Закон гласит:
Для данной массы произведение давления газа на его объем постоянно, если температура газа не меняется.
$pV=const$ при $T=const$
Этот закон был экспериментально открыт английским ученым Р. Бойлем в 1662 г., в 1676 г. его сформулировал также французский ученый Э. Мариотт.
Закон строго выполняется только для идеальных газов. Для реальных газов он выполняется достаточно хорошо при небольших давлениях и высоких температурах. Так, при давлении $100$ атм. и температуре $0°$С отклонение измеренного значения $рV$ от расчетного составляет $7%$. Закон Бойля-Мариотта, как и другие газовые законы, является следствием уравнения состояния идеального газа.
Графики зависимости $p(V)$ при $T=const$ ($p={const}/{V}$) называются изотермами и представляют собой равносторонние гиперболы (площади $S_1=S_2$). Чем выше температура, тем выше лежит соответствующая ей изотерма.
Закон Шарля
Давление $p$ данной массы газа при постоянном объеме пропорционально температуре.
$p=constT$ при $T=const$
Закон был открыт французским физиком Ж. Шарлем в 1787 году.
Процесс изменения состояния термодинамической системы при постоянном объеме называется изохорным (от греч. hora — пространство).
Закон Шарля, как и другие газовые законы, является следствием уравнения состояния идеального газа:
${p}/{T}=const$ при $V=const$
Согласно ${p}/{T}=const$ при $V=const$, давление газа линейно зависит от температуры при постоянном объеме. Эта зависимость изображается прямой, которая называется изохорой. С ростом объема газа при постоянной температуре давление его, согласно закону Бойля—Мариотта, падает. Поэтому изохора, соответствующая большему объему, лежит ниже изохоры, соответствующей меньшему объему.
В соответствии с ${p}/{T}=const$ при $V=const$, все изохоры начинаются в точке $Т=0$ (давление идеального газа при абсолютном нуле равно нулю).
Изохорный процесс используется в газовых термометрах постоянного объема.
Закон Гей-Люссака
При постоянном давлении $р$ объем $V$ идеального газа меняется линейно с температурой.
То есть
$V=V_0(1+αt)$
где $V_0$ — начальный объем, $t$ — разность начальной и конечной температур. Коэффициент теплового расширения идеальных газов $α=({1}/{273.15})K^{-1}$ одинаков для всех газов.
Процесс изменения состояния термодинамической системы при постоянном давлении называется изобарным (от греч. baros — вес, тяжесть).
Закон открыт французским ученым Ж. Гей-Люссаком в 1802 г. и независимо от него Дж. Дальтоном в 1801 г.
Закон Гей-Люссака, как и другие газовые законы, является следствием уравнения состояния идеального газа. Это становится очевидным, если в $V=V_0(1+αt)$ заменить $t$ абсолютной температурой $T=t+273.15$, а коэффициент расширения $α$ — его численным значением ${1}/{273.15}$:
$V=V_0{T}/{273.15}$
или
${V}/{T}=const$ при $p=const$
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
Согласно ${V}/{T}=const$ при $p=const$, объем газа линейно зависит от температуры при постоянном давлении:
$V=constT$
Эта зависимость графически изображается прямой, которая называется изобарой.
Различным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре, согласно закону Бойля—Мариотта, уменьшается, поэтому изобара, соответствующая более высокому давлению $р_2$, лежит ниже изобары, соответствующей более низкому давлению $р_1$.
В области низких температур все изобары идеального газа сходятся в точке $Т=0$, но это не означает, что объем реального газа действительно обращается в нуль. При низких температурах все газы обращаются в жидкости, а к жидкостям уравнение состояния не применимо.
Насыщенные и ненасыщенные пары
Насыщенный пар
При испарении одновременно с переходом молекул из жидкости в пар происходит и обратный процесс. Беспорядочно двигаясь над поверхностью жидкости, часть молекул, покинувших ее, снова возвращается в жидкость.
Если испарение происходит в закрытом сосуде, то сначала число молекул, вылетевших из жидкости, будет больше числа молекул, возвратившихся обратно в жидкость. Поэтому плотность пара в сосуде будет постепенно увеличиваться. С увеличением плотности пара увеличивается и число молекул, возвращающихся в жидкость. Довольно скоро число молекул, вылетающих из жидкости, станет равным числу молекул пара, возвращающихся обратно в жидкость. С этого момента число молекул пара над жидкостью будет постоянным. Для воды при комнатной температуре это число приблизительно равно $10^{22}$ молекул за $1с$ на $1см^2$ площади поверхности. Наступает так называемое динамическое равновесие между паром и жидкостью.
Пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным паром.
Это означает, что в данном объеме при данной температуре не может находиться большее количество пара.
При динамическом равновесии масса жидкости в закрытом сосуде не изменяется, хотя жидкость продолжает испаряться. Точно так же не изменяется и масса насыщенного пара над этой жидкостью, хотя пар продолжает конденсироваться.
Давление насыщенного пара. При сжатии насыщенного пара, температура которого поддерживается постоянной, равновесие сначала начнет нарушаться: плотность пара возрастет, и вследствие этого из газа в жидкость будет переходить больше молекул, чем из жидкости в газ; продолжаться это будет до тех пор, пока концентрация пара в новом объеме не станет прежней, соответствующей концентрации насыщенного пара при данной температуре (и равновесие восстановится). Объясняется это тем, что число молекул, покидающих жидкость за единицу времени, зависит только от температуры.
Итак, концентрация молекул насыщенного пара при постоянной температуре не зависит от его объема.
Поскольку давление газа пропорционально концентрации его молекул, то и давление насыщенного пара не зависит от занимаемого им объема. Давление $р_0$, при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара.
При сжатии насыщенного пара большая его часть переходит в жидкое состояние. Жидкость занимает меньший объем, чем пар той же массы. В результате объем пара при неизменной его плотности уменьшается.
Зависимость давления насыщенного пара от температуры. Для идеального газа справедлива линейная зависимость давления от температуры при постоянном объеме. Применительно к насыщенному пару с давлением $р_0$ эта зависимость выражается равенством:
$p_0=nkT$
Так как давление насыщенного пара не зависит от объема, то, следовательно, оно зависит только от температуры.
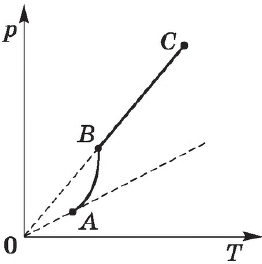
Экспериментально определенная зависимость $Р_0(Т)$ отличается от зависимости $p_0=nkT$ для идеального газа. С увеличением температуры давление насыщенного пара растет быстрее, чем давление идеального газа (участок кривой $АВ$). Это становится особенно очевидным, если провести изохору через точку $А$ (пунктирная прямая). Происходит это потому, что при нагревании жидкости часть ее превращается в пар, и плотность пара растет.
Поэтому, согласно формуле $p_0=nkT$, давление насыщенного пара растет не только в результате повышения температуры жидкости, но и вследствие увеличения концентрации молекул (плотности) пара. Главное различие в поведении идеального газа и насыщенного пара заключается в изменении массы пара при изменении температуры при неизменном объеме (в закрытом сосуде) или при изменении объема при постоянной температуре. С идеальным газом ничего подобного происходить не может (МКТ идеального газа не предусматривает фазового перехода газа в жидкость).
После испарения всей жидкости поведение пара будет соответствовать поведению идеального газа (участок $ВС$ кривой).
Ненасыщенный пар
Если в пространстве, содержащем пары какой-либо жидкости, может происходить дальнейшее испарение этой жидкости, то пар, находящийся в этом пространстве, является ненасыщенным.
Пар, не находящийся в состоянии равновесия со своей жидкостью, называется ненасыщенным.
Ненасыщенный пар можно простым сжатием превратить в жидкость. Как только это превращение началось, пар, находящийся в равновесии с жидкостью, становится насыщенным.
Влажность воздуха
Влажность воздуха — это содержание в воздухе водяного пара.
Окружающий нас атмосферный воздух вследствие непрерывного испарения воды с поверхности океанов, морей, водоемов, влажной почвы и растений всегда содержит в себе водяные пары. Чем больше водяных паров находится в определенном объеме воздуха, тем ближе пар к состоянию насыщения. С другой стороны, чем выше температура воздуха, тем большее количество водяных паров требуется для его насыщения.
В зависимости от количества водяных паров, находящихся при данной температуре в атмосфере, воздух бывает различной степени влажности.
Количественная оценка влажности
Для того чтобы количественно оценить влажность воздуха, пользуются, в частности, понятиями абсолютной и относительной влажности.
Абсолютная влажность — это количество граммов водяного пара, содержащееся в $1м^3$ воздуха при данных условиях, т. е. это плотность водяного пара $р$, выраженная в г/$м^3$.
Относительная влажность воздуха $φ$ — это отношение абсолютной влажности воздуха $р$ к плотности $р_0$ насыщенного пара при той же температуре.
Относительную влажность выражают в процентах:
$φ=({p}/{p_0})·100%$
Концентрация пара связана с давлением ($p_0=nkT$), поэтому относительную влажность можно определить как процентное отношение парциального давления $р$ пара в воздухе к давлению $р_0$ насыщенного пара при той же температуре:
$φ=({p}/{p_0})·100%$
Под парциальным давлением понимают давление водяного пара, которое он производил бы, если бы все другие газы в атмосферном воздухе отсутствовали.
Если влажный воздух охлаждать, то при некоторой температуре находящийся в нем пар можно довести до насыщения. При дальнейшем охлаждении водяной пар начнет конденсироваться в виде росы.
Точка росы
Точка росы — это температура, до которой должен охладиться воздух, чтобы находящийся в нем водяной пар достиг состояния насыщения при постоянном давлении и данной влажности воздуха. При достижении точки росы в воздухе или на предметах, с которыми он соприкасается, начинается конденсация водяного пара. Точка росы может быть вычислена по значениям температуры и влажности воздуха или определена непосредственно конденсационным гигрометром. При относительной влажности воздуха $φ = 100%$ точка росы совпадает с температурой воздуха. При $φ < 100%$ точка росы всегда ниже температуры воздуха. Так, при температуре воздуха $15°$С и относительной влажности $(%) 100, 80, 60, 40$ точка росы оказывается равной $15.0; 11.6; 7.3; 1.5°$С.
Изменение агрегатных состояний вещества: испарение и конденсация, кипение жидкости
Агрегатные состояния вещества (от лат. aggrego — присоединяю) — это состояния одного и того же вещества в различных интервалах (промежутках) температур и давлений.
Агрегатными состояниями принято считать газообразное, жидкое и твердое.
Самыми простыми примерами существования одного и того же вещества в этих трех агрегатных состояниях, которые наблюдаются в повседневной жизни, являются лед, вода и водяной пар. Невидимый водяной пар всегда присутствует и в окружающем нас воздухе. Вода существует в интервале температур от $0°$С до $100°$С, лед — при температуре ниже $0°$С. При температуре выше $100°$С и нормальном атмосферном давлении молекулы воды существуют только в газообразном состоянии — в виде водяного пара. Вода, лед и водяной пар — это одно и то же вещество с химической формулой $Н_2O$.
Многие вещества в обыденной жизни мы наблюдаем только в одном из агрегатных состояний. Так, кислород в окружающем нас воздухе представляет собой газ. Но при температуре $-193°$С он превращается в жидкость. Охладив эту жидкость до $-219°$С, мы получим твердый кислород. И наоборот, железо в обычных условиях твердое. Однако при температуре $1535°$С железо плавится и превращается в жидкость. Над расплавленным железом будет находиться газ — пар из атомов железа.
Различные агрегатные состояния существуют у каждого вещества. Отличаются эти вещества не молекулами, а тем, как эти молекулы расположены и как движутся. Расположение молекул воды в трех агрегатных состояниях показано на рисунке.
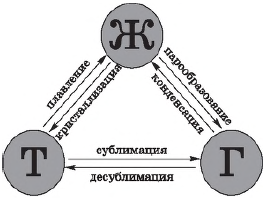
Переход из одного агрегатного состояния в другое. При определенных условиях вещества могут переходить из одного агрегатного состояния в другое. Все возможные при этом превращения отображены на рисунке.
Всего различают шесть процессов, при которых происходят агрегатные превращения вещества.
Переход вещества из твердого (кристаллического) состояния в жидкое называется плавлением, обратный процесс называется кристаллизацией, или отвердеванием. Пример плавления — таяние льда, обратный процесс происходит при замерзании воды.
Переход вещества из жидкого состояния в газообразное называется парообразованием, обратный процесс называется конденсацией. Пример парообразования — испарение воды, обратный процесс можно наблюдать при выпадении росы.
Переход вещества из твердого состояния сразу в газообразное (минуя жидкое) называется сублимацией, или возгонкой, обратный процесс называется десублимацией. Например, графит можно нагреть до тысячи, двух тысяч и даже трех тысяч градусов и, тем не менее, в жидкость он не превратится: он будет сублимироваться, т. е. из твердого состояния сразу переходить в газообразное. Непосредственно в газообразное состояние (минуя жидкое) переходит и так называемый сухой лед (твердый оксид углерода $СO_2$), который можно увидеть в контейнерах для транспортировки мороженого. Все запахи, которыми обладают твердые тела (например, нафталин), также обусловлены возгонкой: вылетая из твердого тела, молекулы образуют над ним газ (или пар), обладающий запахом.
Примером десублимации является образование на окнах зимой узоров из кристалликов льда. Эти красивые узоры образуются при десублимации водяного пара, находящегося в воздухе.
Переходы вещества из одного агрегатного состояния в другое играют важную роль не только в природе, но и в технике. Так, воду, превращенную в пар, можно использовать в паровых турбинах на электростанциях. Из расплавленных металлов на заводах получают различные сплавы: сталь, чугун, латунь и т. д. Для понимания этих процессов надо знать, что происходит с веществом при изменении его агрегатного состояния и при каких условиях это изменение возможно.
Испарение
Испарение — это переход вещества из жидкого состояния в газообразное (пар), происходящее со свободной поверхности жидкости.
Сублимацию, или возгонку, т. е. переход вещества из твердого состояния в газообразное, также называют испарением.
Из повседневных наблюдений известно, что количество любой жидкости (бензина, эфира, воды), находящейся в открытом сосуде, постепенно уменьшается. Жидкость не исчезает бесследно — она превращается в пар. Испарение — это один из видов парообразования. Другой вид — это кипение.
Механизм испарения. Как происходит испарение? Молекулы любой жидкости находятся в непрерывном и беспорядочном движении, причем чем выше температура жидкости, тем больше кинетическая энергия молекул. Среднее значение кинетической энергии имеет определенную величину. Но у каждой молекулы кинетическая энергия может быть как больше, так и меньше средней. Если вблизи поверхности окажется молекула с кинетической энергией, достаточной для преодоления сил межмолекулярного притяжения, она вылетит из жидкости. То же самое повторится с другой быстрой молекулой, со второй, третьей и т. д. Вылетая наружу, эти молекулы образуют над жидкостью пар. Образование этого пара и есть испарение.
Поглощение энергии при испарении. Поскольку при испарении из жидкости вылетают более быстрые молекулы, средняя кинетическая энергия оставшихся в жидкости молекул становится все меньше и меньше. Это значит, что внутренняя энергия испаряющейся жидкости уменьшается. Поэтому если нет притока энергии к жидкости извне, температура испаряющейся жидкости понижается, жидкость охлаждается (именно поэтому, в частности, человеку в мокрой одежде холоднее, чем в сухой, особенно при ветре).
Однако при испарении воды, налитой в стакан, мы не замечаем понижения ее температуры. Чем это объяснить? Дело в том, что испарение в данном случае происходит медленно, и температура воды поддерживается постоянной за счет теплообмена с окружающим воздухом, из которого в жидкость поступает необходимое количество теплоты. Значит, чтобы испарение жидкости происходило без изменения ее температуры, жидкости необходимо сообщать энергию.
Количество теплоты, которое необходимо сообщить жидкости для образования единицы массы пара при постоянной температуре, называется теплотой парообразования.
Скорость испарения жидкости. В отличие от кипения испарение происходит при любой температуре, однако с повышением температуры жидкости скорость испарения возрастает. Чем выше температура жидкости, тем больше быстро движущихся молекул имеет достаточную кинетическую энергию, чтобы преодолеть силы притяжения соседних частиц и вылететь за пределы жидкости, и тем быстрее идет испарение.
Скорость испарения зависит от рода жидкости. Быстро испаряются летучие жидкости, у которых силы межмолекулярного взаимодействия малы (например, эфир, спирт, бензин). Если капнуть такой жидкостью на руку, мы ощутим холод. Испаряясь с поверхности руки, такая жидкость будет охлаждаться и отбирать у нее некоторое количество теплоты.
Скорость испарения жидкости зависит от площади ее свободной поверхности. Это объясняется тем, что жидкость испаряется с поверхности, и чем больше площадь свободной поверхности жидкости, тем большее количество молекул одновременно вылетает в воздух.
В открытом сосуде масса жидкости вследствие испарения постепенно уменьшается. Это связано с тем, что большинство молекул пара рассеивается в воздухе, не возвращаясь в жидкость (в отличие от того, что происходит в закрытом сосуде). Но небольшая часть их возвращается в жидкость, замедляя тем самым испарение. Поэтому при ветре, который уносит молекулы пара, испарение жидкости происходит быстрее.
Применение в технике. Испарение играет важную роль в энергетике, холодильной технике, в процессах сушки, испарительного охлаждения. Например, в космической технике быстроиспаряющимися веществами покрывают спускаемые аппараты. При прохождении через атмосферу планеты корпус аппарата в результате трения нагревается, и покрывающее его вещество начинает испаряться. Испаряясь, оно охлаждает космический аппарат, спасая его тем самым от перегрева.
Конденсация
Конденсация (от лат. condensatio — уплотнение, сгущение) — переход вещества из газообразного состояния (пара) в жидкое или твердое состояние.
Известно, что при наличии ветра жидкость испаряется быстрее. Почему? Дело в том, что одновременно с испарением с поверхности жидкости идет и конденсация. Конденсация происходит из-за того, что часть молекул пара, беспорядочно перемещаясь над жидкостью, снова возвращается в нее. Ветер же выносит вылетевшие из жидкости молекулы и не дает им возвращаться.
Конденсация может происходить и тогда, когда пар не соприкасается с жидкостью. Именно конденсацией объясняется, например, образование облаков: молекулы водяного пара, поднимающиеся над землей, в более холодных слоях атмосферы группируются в мельчайшие капельки воды, скопления которых и представляют собой облака. Следствием конденсации водяного пара в атмосфере являются также дождь и роса.
При испарении жидкость охлаждается и, став более холодной, чем окружающая среда, начинает поглощать ее энергию. При конденсации же, наоборот, происходит выделение некоторого количества теплоты в окружающую среду, и ее температура несколько повышается. Количество теплоты, выделяющееся при конденсации единицы массы, равно теплоте испарения.
Кипение жидкости
Кипение — это интенсивный переход жидкости в пар, происходящий с образованием пузырьков пара по всему объему жидкости при определенной температуре.
В отличие от испарения, которое происходит при любой температуре жидкости, другой вид парообразования — кипение — возможен лишь при совершенно определенной (при данном давлении) температуре — температуре кипения.
При нагревании воды в открытом стеклянном сосуде можно увидеть, что по мере увеличения температуры стенки и дно сосуда покрываются мелкими пузырьками. Они образуются в результате расширения мельчайших пузырьков воздуха, которые существуют в углублениях и микротрещинах не полностью смачиваемых стенок сосуда.
Пары жидкости, которые находятся внутри пузырьков, являются насыщенными. С ростом температуры давление насыщенных паров возрастает, и пузырьки увеличиваются в размерах. С увеличением объема пузырьков растет и действующая на них выталкивающая (архимедова) сила. Под действием этой силы наиболее крупные пузырьки отрываются от стенок сосуда и поднимаются вверх. Если верхние слои воды еще не успели нагреться до $100°$С, то в такой (более холодной) воде часть водяного пара внутри пузырьков конденсируется и уходит в воду; пузырьки при этом сокращаются в размерах, и сила тяжести заставляет их снова опускаться вниз. Здесь они опять увеличиваются и вновь начинают всплывать вверх. Попеременное увеличение и уменьшение пузырьков внутри воды сопровождается возникновением в ней характерных звуковых волн: закипающая вода шумит.
Когда вся вода прогреется до $100°$С, поднявшиеся вверх пузырьки уже не сокращаются в размерах, а лопаются на поверхности воды, выбрасывая пар наружу. Возникает характерное булькание — вода кипит.
Кипение начинается после того, как давление насыщенного пара внутри пузырьков сравнивается с давлением в окружающей жидкости.
Во время кипения температура жидкости и пара над ней не меняется. Она сохраняется неизменной до тех пор, пока вся жидкость не выкипит. Это происходит потому, что вся подводимая к жидкости энергия уходит на превращение ее в пар.
Температура, при которой кипит жидкость, называется температурой кипения.
Температура кипения зависит от давления, оказываемого на свободную поверхность жидкости. Это объясняется зависимостью давления насыщенного пара от температуры. Пузырек пара растет, пока давление насыщенного пара внутри него немного превосходит давление в жидкости, которое складывается из внешнего давления и гидростатического давления столба жидкости.
Чем больше внешнее давление, тем больше температура кипения.
Всем известно, что вода кипит при температуре $100°$С. Но не следует забывать, что это справедливо лишь при нормальном атмосферном давлении (примерно $101$ кПа). При увеличении давления температура кипения воды возрастает. Так, например, в кастрюлях-скороварках пищу варят под давлением около $200$ кПа. Температура кипения воды при этом достигает $120°$С. В воде такой температуры процесс варки происходит значительно быстрее, чем в обычном кипятке. Этим и объясняется название «скороварка».
И наоборот, уменьшая внешнее давление, мы тем самым понижаем температуру кипения. Например, в горных районах (на высоте $3$ км, где давление составляет $70$ кПа) вода кипит при температуре $90°$С. Поэтому жителям этих районов, использующим такой кипяток, требуется значительно больше времени для приготовления пищи, чем жителям равнин. А сварить в этом кипятке, например, куриное яйцо вообще невозможно, так как при температуре ниже $100°$С белок не сворачивается.
У каждой жидкости своя температура кипения, которая зависит от давления насыщенного пара. Чем выше давление насыщенного пара, тем ниже температура кипения соответствующей жидкости, т. к. при меньших температурах давление насыщенного пара становится равным атмосферному. Например, при температуре кипения $100°$С давление насыщенных паров воды равно $101 325$ Па ($760$ мм рт. ст.), а паров ртути — всего лишь $117$ Па ($0.88$ мм рт. ст.). Кипит ртуть при $357°$С при нормальном давлении.
Изменение агрегатных состояний вещества: плавление и кристаллизация
Переход вещества из твердого кристаллического состояния в жидкое называется плавлением.
Чтобы расплавить твердое кристаллическое тело, его нужно нагреть до определенной температуры, т. е. подвести тепло.
Температура, при которой вещество плавится, называется температурой плавления вещества.
Обратный процесс — переход из жидкого состояния в твердое — происходит при понижении температуры, т. е. тепло отводится.
Переход вещества из жидкого состояния в твердое называется отвердеванием, или кристаллизацией.
Температура, при которой вещество кристаллизуется, называется температурой кристаллизации.
Опыт показывает, что любое вещество кристаллизуется и плавится при одной и той же температуре.
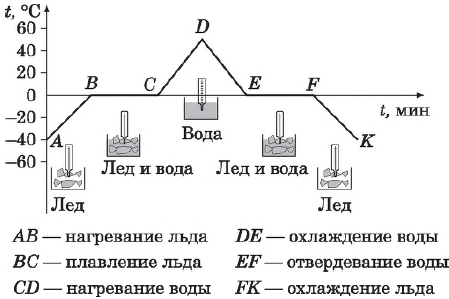
На рисунке представлен график зависимости температуры кристаллического тела (льда) от времени нагревания (от точки $А$ до точки $D$) и времени охлаждения (от точки $D$ до точки $К$). На нем по горизонтальной оси отложено время, а по вертикальной — температура.
Из графика видно, что наблюдение за процессом началось с момента, когда температура льда была $-40°$С, или, как принято говорить, температура в начальный момент времени ($t_{нач} =-40°$С (точка $А$ на графике). При дальнейшем нагревании температура льда растет (на графике это участок $АВ$). Увеличение температуры происходит до $0°$С — температуры плавления льда. При $0°$С лед начинает плавиться, а его температура перестает расти. В течение всего времени плавления (т. е. пока весь лед не расплавится) температура льда не меняется, хотя горелка продолжает гореть и тепло, следовательно, подводится. Процессу плавления соответствует горизонтальный участок графика $ВС$. Только после того как весь лед расплавится и превратится в воду, температура снова начинает подниматься (участок $CD$). После того, как температура воды достигнет $+40°$С, горелку гасят и воду начинают охлаждать, т. е. тепло отводят (для этого можно сосуд с водой поместить в другой, больший сосуд со льдом). Температура воды начинает снижаться (участок $DE$). При достижении температуры $0°$С температура воды перестает снижаться, несмотря на то, что тепло по-прежнему отводится. Это идет процесс кристаллизации воды — образования льда (горизонтальный участок $ЕF$). Пока вся вода не превратится в лед, температура не изменится. Лишь после этого начинает уменьшаться температура льда (участок $FK$).
Вид рассмотренного графика объясняется следующим образом. На участке $АВ$ благодаря подводимому теплу средняя кинетическая энергия молекул льда увеличивается, и температура его повышается. На участке $ВС$ вся энергия, получаемая содержимым колбы, тратится на разрушение кристаллической решетки льда: упорядоченное пространственное расположение его молекул сменяется неупорядоченным, меняется расстояние между молекулами, т. е. происходит перестройка молекул таким образом, что вещество становится жидким. Средняя кинетическая энергия молекул при этом не меняется, поэтому неизменной остается и температура. Дальнейшее увеличение температуры расплавленного льда-воды (на участке $СD$) означает увеличение кинетической энергии молекул воды вследствие подводимого горелкой тепла.
При охлаждении воды (участок $DЕ$) часть энергии у нее отбирается, молекулы воды движутся с меньшими скоростями, их средняя кинетическая энергия падает — температура уменьшается, вода охлаждается. При $0С$ (горизонтальный участок $ЕF$) молекулы начинают выстраиваться в определенном порядке, образуя кристаллическую решетку. Пока этот процесс не завершится, температура вещества не изменится, несмотря на отводимое тепло, а это означает, что при отвердевании жидкость (вода) выделяет энергию. Это как раз та энергия, которую поглотил лед, превращаясь в жидкость (участок $ВС$). Внутренняя энергия у жидкости больше, чем у твердого тела. При плавлении (и кристаллизации) внутренняя энергия тела меняется скачком.
Металлы, плавящиеся при температуре выше $1650°$С, называют тугоплавкими (титан, хром, молибден и др.). Самая высокая температура плавления среди них у вольфрама — около $3400°$С. Тугоплавкие металлы и их соединения используют в качестве жаропрочных материалов в самолетостроении, ракетостроении и космической технике, атомной энергетике.
Подчеркнем еще раз, что при плавлении вещество поглощает энергию. При кристаллизации оно, наоборот, отдает ее в окружающую среду. Получая определенное количество теплоты, выделяющееся при кристаллизации, среда нагревается. Это хорошо известно многим птицам. Недаром их можно заметить зимой в морозную погоду сидящими на льду, который покрывает реки и озера. Из-за выделения энергии при образовании льда воздух над ним оказывается на несколько градусов теплее, чем в лесу на деревьях, и птицы этим пользуются.
Плавление аморфных веществ
Наличие определенной точки плавления — это важный признак кристаллических веществ. Именно по этому признаку их можно легко отличить от аморфных тел, которые также относят к твердым телам. К ним, в частности, относятся стекла, очень вязкие смолы, пластмассы.
Аморфные вещества (в отличие от кристаллических) не имеют определенной температуры плавления — они не плавятся, а размягчаются. При нагревании кусок стекла, например, сначала становится из твердого мягким, его легко можно гнуть или растягивать; при более высокой температуре кусок начинает менять свою форму под действием собственной тяжести. По мере нагревания густая вязкая масса принимает форму того сосуда, в котором лежит. Эта масса сначала густая, как мед, затем — как сметана и наконец становится почти такой же маловязкой жидкостью, как вода. Однако указать определенную температуру перехода твердого тела в жидкое здесь невозможно, поскольку ее нет.
Причины этого лежат в коренном отличии строения аморфных тел от строения кристаллических. Атомы в аморфных телах расположены беспорядочно. Аморфные тела по своему строению напоминают жидкости. Уже в твердом стекле атомы расположены беспорядочно. Значит, повышение температуры стекла лишь увеличивает размах колебаний его молекул, дает им постепенно все большую и большую свободу перемещения. Поэтому стекло размягчается постепенно и не обнаруживает резкого перехода «твердое—жидкое», характерного для перехода от расположения молекул в строгом порядке к беспорядочному.
Преобразование энергии в фазовых переходах
Рассмотренные в предыдущих параграфах изменения агрегатных состояний вещества относятся к фазовым превращениям. По определению Д. У. Гиббса (основателя термодинамики), фазой называется любое вещество, которое может быть удалено из системы соприкасающихся веществ чисто механическим способом. Здесь под системой веществ понимают вещество одного химического состава, части которого отличаются физическими свойствами (например, плотностью).
Так, смесь воды и льда — это две фазы одного и того же вещества с химической формулой $Н_2O$. Аналогично любое твердое тело в процессе плавления распадается на две фазы — твердую и жидкую. Туман (капли жидкости в смеси с воздухом) является двухфазной системой. Вода, лед и водяной пар над ними — пример трехфазной системы. А вот раствор одного вещества в другом представляет собой одну фазу, поскольку составные части такого раствора не могут быть отделены друг от друга механическим способом. Таким образом, вещество в разных агрегатных состояниях представляет собой разные фазы вещества. Часто так и говорят: такое-то вещество в твердой фазе, в жидкой фазе. Однако различными фазами вещества не обязательно являются его агрегатные состояния. Иногда это могут быть различные структуры одного и того же кристаллического соединения, например, графит и алмаз.
Переход вещества из одного фазового состояния в другое называется фазовым переходом (или фазовым превращением). Таким образом, испарение и конденсация, кипение, возгонка и сублимация, плавление и кристаллизация, рассмотренные выше, — все это примеры фазовых переходов.
Если фазовый переход проходит при определенной температуре (температуре фазового перехода) и сопровождается выделением или поглощением тепла, он называется фазовым переходом первого рода. Процессы превращения вещества из твердого в жидкое состояние и обратно (плавление и затвердевание), как и из жидкого в газообразное и обратно (кипение и конденсация) относятся к фазовому переходу первого рода.
Температурой фазового перехода здесь являются температура плавления и температура кипения. При этом происходит скачкообразное изменение плотности вещества.
Что происходит с внутренней энергией в процессе фазового перехода первого рода? Напомним, что внутреннюю энергию тела составляют кинетическая энергия всех его молекул и потенциальная энергия их взаимодействия. Минимальное значение потенциальной энергии взаимодействия частиц, $U_{min}$ представляет собой энергию связи молекул вещества. Эту энергию необходимо передать системе для того, чтобы связь эту разорвать, или как говорят преодолеть потенциальную яму. Относительным вкладом этих двух составляющих внутренней энергии тела и определяется фазовое состояние и фазовые превращения вещества. Когда $Е_k << |U_{min}|$, частицы находятся в связанном состоянии. Для разных фаз характерны следующие соотношения между ними: $Е_k << |U_{min}|$ — твердое тело; $Е_k ~ |U_{min}|$ — жидкость; $Е_k >> |U_{min}|$ — газ.
Как уже было показано, в процессе плавления кинетическая энергия движения молекул не меняется, так как температура системы неизменна, а подводимое тепло идет на разрушение кристаллической решетки твердого тела, т. е. на увеличение потенциальной энергии молекул и разрыва связей между ними, что приводит к превращению твердого тела в жидкость. В жидкостях средняя кинетическая энергия молекул меньше абсолютного значения средней потенциальной энергии (и внутренняя энергия в целом отрицательна, хотя ее абсолютное значение незначительно отличается от нуля).
При затвердевании , кинетическая энергия жидкости в результате контакта с окружающей средой (теплообмен) уменьшается до величины, при которой расстояния между молекулами становятся достаточными для образования устойчивых связей (образования кристаллических зародышей). Потенциальная энергия молекул в узлах образующейся кристаллической решетки уменьшается, а избыток кинетической энергии выделяется в виде тепла при неизменной температуре. Внутренняя энергия вещества в твердой фазе определяется главным образом взаимодействием молекул и зависит от их расположения: $Е_k << |U_{min}|$.
Аналогично, при кипении, подводимое тепло идет на увеличение потенциальной энергии молекул жидкости, т.е. на совершение работы по удалению молекул на расстояния при которых силы притяжения не в состоянии удерживать молекулы вблизи своих соседей и жидкость переходит в газ.
Таким образом, при фазовых переходах первого рода происходят скачкообразные изменения величины и состава внутренней энергии вещества:
- внутренняя энергия вещества в твердой фазе для температуры, при которой могут существовать одновременно и другие фазы, имеет наименьшее значение, а в газообразной фазе — наибольшее;
- в то же время в твердой фазе средняя потенциальная энергия взаимодействия (по абсолютной величине) во много раз больше средней кинетической энергии, в жидкости они сравнимы по величине, но средняя потенциальная энергия (по абсолютной величине) по-прежнему остается больше средней кинетической энергии молекул, а в газе абсолютное значение средней потенциальной энергии взаимодействия молекул во много раз меньше средней кинетической энергии молекул.
Тепловое движение атомов и молекул вещества
В соответствии с молекулярно-кинетической теорией, молекулы и атомы, из которых состоит вещество, совершают безостановочное хаотическое движение.
Хаотическое, или беспорядочное движение молекул называют тепловым движением. При таком движении атомы и молекулы постоянно и беспорядочно меняют скорость и направление своего движения, интенсивность которого зависит от температуры тела.
Если нехаотическое, скажем, механическое движение можно описывать с помощью формул, например, скорость равномерно ускоренной точки можно найти с помощью формулы $υ=υ_0+at$, то при хаотическом движении нельзя предугадать величину скорости и направление движения отдельной молекулы в любой момент времени. Поэтому в молекулярной физике и термодинамике оперируют средней скоростью молекул, которая зависит от температуры тела.
Атомы и молекулы, находясь в постоянном движении, обладают определенной кинетической энергией. Эта энергия связана с так называемой тепловой энергией, запасенной в теле. Кроме того, атомы и молекулы постоянно взаимодействуют между собой, то есть обладают также и потенциальной энергией, которую называют энергией межмолекулярного взаимодействия.
Тепловое движение частиц вещества обуславливает такие явления, как теплопередача, броуновское движение, диффузия, которые послужили обоснованием молекулярно-кинетической теории вещества.
Взаимодействие частиц вещества
Третье положение МКТ о взаимодействии молекул является очевидным. Достаточно вспомнить, сколько усилий требуется, чтобы сломать, скажем, деревянную палку.
Твердые тела и жидкости не распадаются на отдельные молекулы, несмотря на то, что их молекулы разделены промежутками и находятся в непрерывном беспорядочном движении.
Более того, твердое тело, например, трудно растянуть или сжать. Чем же объяснить, что молекулы в телах не только удерживаются друг около друга, но и в некоторых случаях промежутки между ними трудно увеличить?
Дело в том, что молекулы взаимодействуют друг с другом, и природа этого взаимодействия — электрическая. Молекула состоит из заряженных частиц — электронов и ядер. Заряженные частицы одной молекулы при соответствующих расстояниях взаимодействуют (притягиваются или отталкиваются) с заряженными частицами других молекул.
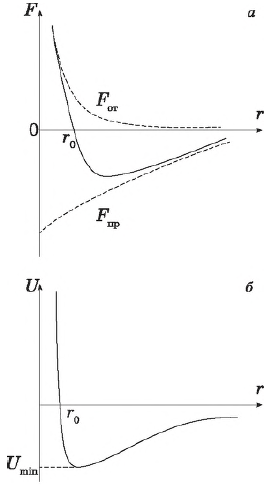
Так, между ядрами атомов одной молекулы и электронами другой существуют силы притяжения, а между электронами соседних молекул, как и между их ядрами — силы отталкивания. Зависимость сил $F_r$ и потенциальной энергии $U$ межмолекулярного взаимодействия от расстояния $r$ изображена на рисунке. Сила взаимодействия складывается из сил притяжения и сил отталкивания. Силы притяжения в физике принято считать отрицательными, силы отталкивания — положительными.
На расстояниях, превышающих $2-3$ диаметра молекул, результирующая сила взаимодействия определяется силами притяжения. Вклад последних по мере уменьшения растояния между молекулами сначала растет, затем убывает. Силы взаимодействия обращаются в нуль, когда расстояние между молекулами становится равным сумме радиусов молекул.
Энергия взаимодействия в этой точке становится минимальной — $U_{min}$. На таком расстоянии система (в данном случае молекула) находится в устойчивом состоянии, поскольку обладает наименьшим значением потенциальной энергии, или, как говорят, находится «в потенциальной яме».
Дальнейшее уменьшение расстояния приводит к перекрыванию электронных оболочек, что вызывает быстрое нарастание сил отталкивания.
Броуновское движение. Диффузия
Диффузия, растворимость и броуновское движение могут быть объяснены только на основе представления о молекулярном строении веществ и являются убедительными обоснованиями первого и второго положений молекулярно-кинетической теории.
Броуновское движение (брауновское движение) — беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды.
Впервые такое движение исследовал и описал в 1827 г. английский ботаник Р. Браун при изучении под микроскопом взвешенной в воде цветочной пыльцы. Он обнаружил, что частички пыльцы находятся в непрерывном беспорядочном движении, как бы исполняя дикий фантастический танец. Он писал: «Это движение, как я убежден, обусловлено не потоками жидкости, не постепенным ее испарением, а принадлежит самим частицам».
Наблюдаемые (броуновские) частицы размером $~1$ мкм и менее совершают неупорядоченные независимые движения, описывая сложные зигзагообразные траектории.
Подобный опыт можно проделать, пользуясь краской или тушью, предварительно растертой до таких мельчайших крупинок, которые видны лишь в микроскоп. Можно увидеть, что крупинки краски непрерывно движутся. Самые мелкие из них беспорядочно перемещаются с одного места в другое, более крупные лишь беспорядочно колеблются.
Броуновское движение можно наблюдать и в газе. Например, в воздухе его совершают взвешенные там частицы пыли или дыма.
Броуновское движение никогда не прекращается! В капле воды (если не давать ей высохнуть) движение крупинок можно наблюдать в течение многих дней, месяцев, лет. Оно не прекращается ни летом, ни зимой, ни днем, ни ночью. В кусках кварца, пролежавших в земле тысячи лет, попадаются иногда капельки воды, замурованные в минерале. В этих капельках тоже наблюдали броуновское движение плавающих в воде частиц.
Интенсивность броуновского движения увеличивается с повышением температуры, уменьшением вязкости среды, уменьшением размера частиц. Оно не зависит от химической природы частиц и времени наблюдения.
Броуновское движение служит доказательством существования еще более мелких частиц — молекул жидкости, невидимых даже в самые сильные оптические микроскопы.
Броуновское движение объясняется тем, что благодаря случайной неодинаковости количества ударов молекул жидкости о частицу с разных направлений возникает равнодействующая сила определенного направления. Поскольку подобные флуктуации (флуктуация — случайное отклонение физической величины от ее среднего значения) очень кратковременны, то в следующий миг направление равнодействующей меняется и, следовательно, изменится направление перемещения частицы. Отсюда наблюдающаяся хаотичность броуновского движения, которая отражает хаотичность молекулярного движения.
Открытие броуновского движения имело большое значение для изучения строения вещества. Оно показало, что тела действительно состоят из отдельных частиц — молекул — и что молекулы находятся в непрерывном беспорядочном движении.
Полная теория броуновского движения была разработана Эйнштейном и Смолуховским в 1905— 1906 гг. и экспериментально подтверждена Ж. Перреном. Выводы теории показали, что среднее значение квадрата смещения броуновской частицы за определенный промежуток времени пропорционально этому промежутку времени, температуре и постоянной Больцмана.
Эксперименты Ж. Перрена, в которых он определял положение одной определенной частицы через каждые 30с, подтвердили выводы теории. Перрен проводил также опыты по проверке зависимости концентрации молекул газа от высоты и барометрической формулы — зависимости атмосферного давления от высоты. Он предположил, что броуновские частицы, являясь своего рода большими молекулами, должны подчиняться тем же законам, что и молекулы атмосферы, а, следовательно, их концентрация с высотой должна падать. Его эксперименты полностью подтвердили теорию. Они позволили ему определить постоянную Авогадро, значение которой совпало с уже известным.
Таким образом, броуновское движение является самым ярким подтверждением теплового движения молекул — одного из положений молекулярно-кинетической теории.
Диффузия
Явление, при котором происходит взаимное проникновение молекул одного вещества между молекулами другого, называется диффузией.
Явление это объясняется свойством молекул находиться в беспрерывном движении.
Подтверждением движения молекул газа является всем известное распространение запаха какого- либо пахучего вещества, внесенного в комнату.
В жидкостях наблюдать взаимное проникновение одного вещества в другое можно, если в крепкий раствор медного купороса осторожно добавить воду. Вначале резкая граница между темноголубым медным купоросом и бесцветной водой со временем исчезает. Механизм проникновения молекул следующий. Сначала вследствие движения отдельные молекулы воды и медного купороса, находящиеся около границы между ними, обмениваются местами. Молекулы медного купороса попадают в нижний слой воды, а молекулы воды — в верхний слой медного купороса. Граница между жидкостями из-за этого расплывается. Проникнув в слой «чужой» жидкости, молекулы начинают обмениваться местами с ее частицами, находящимся во все более глубоких слоях. Граница между жидкостями становится все более расплывчатой. Благодаря беспрерывному и беспорядочному движению молекул этот процесс, в конце концов, приводит к тому, что вся жидкость становится однородной.
В твердых телах также наблюдается диффузия. Так, в одном из опытов гладко отшлифованные пластины свинца и золота положили друг на друга и сжали грузом. Через пять лет золото и свинец проникли друг в друга на $1$ мм.
Скорость диффузии зависит от агрегатного состояния вещества и температуры тела. В газах, где расстояние между молекулами очень велико по сравнению с их размерами и движение молекул хаотично, скорость диффузии наибольшая. В жидкостях она меньше, так как и расстояние между молекулами меньше, и движение молекул чуть более упорядочено. В твердых телах, где наблюдается строгий порядок в расположении атомов (или молекул), а сами они совершают лишь небольшие колебательные движения около своих мест, скорость диффузии наименьшая.
Скорость протекания диффузии увеличивается с ростом температуры.
Модель идеального газа в МКТ
Идеальный газ — это теоретическая модель газа, в которой пренебрегают размерами и взаимодействиями частиц газа и учитывают лишь их упругие столкновения.
Другими словами, предполагается, что внутренняя энергия идеального газа определяется лишь кинетической энергией его частиц (т. е. потенциальной энергией взаимодействия молекул пренебрегают).
Модель идеального газа была предложена в 1847 г. Дж. Герапатом. На основе этой модели были теоретически выведены газовые законы (закон Бойля—Мариотта, закон Гей-Люссака, закон Шарля, закон Авогадро), которые ранее были установлены экспериментально. Модель идеального газа была положена в основу молекулярно-кинетической теории газа.
Основными законами идеального газа являются уравнение состояния и закон Авогадро, в которых впервые были связаны макрохарактеристики газа (давление, температура, масса) с массой молекулы (уравнение Менделеева-Клапейрона, или уравнение состояния идеального газа).
В современной физике ее используют также для описания ансамблей любых слабовзаимодействующих частиц. Модель идеального газа справедлива для реальных классических газов при достаточно высоких температурах и разрежениях, когда среднее расстояние между молекулами много больше размеров самих молекул. В этом случае силами притяжения можно пренебречь. Силы же отталкивания проявляются лишь при столкновении друг с другом в течение ничтожно малых интервалов времени.
В простейшей модели газа молекулы рассматриваются как очень маленькие твердые шарики, обладающие массой. Движение отдельных молекул подчиняется законам механики Ньютона. Конечно, не все процессы в разреженных газах можно объяснить с помощью такой модели, однако давление газа вычислить с ее помощью можно.
Основное уравнение МКТ (давление газа)
Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.
Вывод основного уравнения МКТ основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.
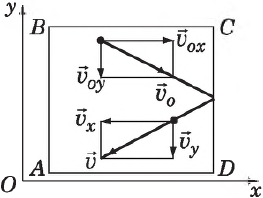
Определим давление газа на стенку площадью $S$ сосуда $ABCD$.
Каждая молекула массой $m_0$, отскакивая от стенки после упругого соударения со стенкой, передает ей импульс $2m_{0}υ_x$, где $υ_x$ — проекция скорости молекулы $υ↖{→}$ на ось $О_х$, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен $2m_{0}υ_{x}Z$, где $Z$ — число таких столкновений (за $1$ с) всех молекул. Очевидно, что $Z=n={N}/{V}$, где $n$ — концентрация молекул в единице объема; $N$ — число всех молекул. Число $Z$ пропорционально также скорости молекул $υ_x$ и площади стенки $S:Z∼nυ_{x}S$. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости $υ_x$, только половина движется в сторону стенки $CD$ вторая половина — в сторону $АВ$ (т. е. в обратную). Поэтому $Z={1}/{2}nυ_{x}S$, а полный импульс, переданный стенке за $1$ с, равен $2m_{0}nυ_x^{2}S$. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе $F={∆(mυ)}/{∆t}$, то $F=m_{0}nυ_x^{2}S$. В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить: $F↖{-}={m_{0}nυ_x^{2}S}↖{-}$.
Сила эта зависит, таким образом, от среднего квадрата скорости ${υ_x^{2}}↖{-}$.
Поскольку вследствие хаотичности движения все направления равноправны, то
${υ_x^{2}}↖{-}={υ_y^{2}}↖{-}={υ_z^{2}}↖{-}$
С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:
$υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$
Усредняя это выражение по всем молекулам и учитывая $υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$, получим:
${υ^2}↖{-}={υ_x^{2}}↖{-}+{υ_y^{2}}↖{-}+{υ_z^{2}}↖{-}=3{υ_x^{2}}↖{-}$
Отсюда:
${υ_x^{2}}↖{-}={1}/{3}{υ_^2}↖{-}$
С учетом последней формулы $F↖{-}={1}/{3}m_{0}n{υ^2}↖{-}$
Следовательно, давление на стенку сосуда равно:
$p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$
Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в МКТ.
Уравнение $p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$ позволяет получить связь между давлением и средней кинетической энергией молекул ${E_k}↖{-}={m_{0}{υ^2}↖{-}}/{2}:$
$p={2}/{3}n{E_k}↖{-}$
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа — понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).
Абсолютная температура
Согласно основному уравнению МКТ, давление $р$ прямо пропорционально средней кинетической энергии $E↖{-}$ поступательного движения молекул:
$p={2}/{3}n{E}↖{-}$
где $n$ — объемная концентрация молекул. Заменив в $p={2}/{3}n{E}↖{-}$ $n$ отношением числа молекул $N$ к объему газа $V(n={N}/{V})$, получим:
${pV}/{N}={2}/{3}{E}↖{-}$
В состоянии теплового равновесия при постоянном объеме средняя кинетическая энергия данной массы газа должна иметь вполне определенное значение, как и температура. Согласно формуле ${pV}/{N}={2}/{3}{E}↖{-}$, это означает, что отношение ${pV}/{N}$ для данной температуры должно быть одним и тем же для любых идеальных газов. То, что это действительно так, было подтверждено экспериментально для разных газов, находящихся в условиях теплового равновесия при постоянном объеме (измерялось давление).
Таким образом, величина $Θ={pV}/{N}$, которую, в отличие от микропараметра ${E}↖{-}$, легко измерить, является вполне однозначной характеристикой теплового состояния газа, как и температура. Измеряется $Θ$ (как и энергия) в джоулях. Зависит она только от температуры и может рассматриваться как естественная мера температуры. Однако в силу укоренившейся привычки измерять температуру в градусах был введен коэффициент пропорциональности $k$ между температурой $Θ$, выраженной в энергетических единицах, и температурой $Т$, выраженной в градусах:
$Θ=kT$
или
${pV}/{N}=kT$
Температура $Т$, определяемая равенством $Θ=kT$, называется абсолютной температурой.
Значения температуры, определенной по формуле ${pV}/{N}={2}/{3}{E}↖{-}$, всегда положительны в силу положительности $Θ={pV}/{N}$ (ни давление, ни объем, ни число частиц отрицательными быть не могут). Поэтому минимальным значением температуры является нуль. Температура может равняться нулю, если давление либо объем равны нулю. Из принятого определения температуры следует, что нулем температуры является температура, при которой прекращается хаотическое движение молекул. Она называется абсолютным нулем температуры.
Температура, как и давление, определяется средней кинетической энергией молекул идеального газа. Поэтому температура, как и давление, является статистической величиной (статистической называется величина, имеющая смысл только для систем, содержащих очень большое число частиц). Нельзя говорить о температуре одной или нескольких молекул.
Абсолютную шкалу температур ввел английский ученый У. Кельвин в 1850 г. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Единица абсолютной температуры является одной из семи основных единиц СИ и измеряется в кельвинах (обозначается буквой $К$).
Связь между температурами, измеренными по шкалам Цельсия $t$ и Кельвина $Т$, описывается формулой:
$T(K)=t(°C)+273.15K$
Абсолютный нуль равен $-273.15°$С. Как правило, при расчетах пользуются округленным значением абсолютного нуля ($-273°$С).
Коэффициент пропорциональности к в формуле $Θ=kT$ называется постоянной Больцмана в честь Л. Больцмана — одного из основателей молекулярно-кинетической теории газа. Этот коэффициент составляет $k=1.38^{-23}$ Дж/К.
Постоянная Больцмана связывает температуру $Θ$ в энергетических единицах с температурой $Т$ в кельвинах. Это одна из наиболее важных постоянных в молекулярно-кинетической теории.
Температура как мера кинетической энергии
Из основного уравнения молекулярно-кинетической теории, записанного в форме $p={2}/{3}{E}↖{-}$
${pv}/{N}={2}/{3}{E}↖{-}$
и определения абсолютной температуры согласно ${pV}/{N}=kt$
${pv}/{N}=kT$
получим:
$E↖{-}={3}/{2}kT$
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Из полученного результата однозначно следует, что абсолютная температура есть мера средней кинетической энергии движения молекул.
Соотношение между температурой и кинетической энергией справедливо не только для разреженных газов (идеальных газов), но также для любых тел, подчиняющихся законам механики Ньютона. Оно справедливо и для жидкостей, и для твердых тел, атомы которых колеблются около положения равновесия.
Уравнение $р = nkТ$
Из формулы $p={2}/{3}n{E_k}↖{-}$ может быть получена зависимость давления газа от абсолютной температуры $Т$ и концентрации его молекул, если воспользоваться выражением для средней кинетической энергии:
$p=nkT$
где $k$ — постоянная Больцмана.
Из формулы $p=nkT$ очевидно, что при одинаковых давлениях и температурах концентрация молекул у всех газов одинакова.
Отсюда следует известный закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Средняя скорость теплового движения молекул может быть также выражена через абсолютную температуру, если в формуле $E↖{-}={3}/{2}kT$ заменить $E↖{-}$ на ${m_{0}{υ^2}↖{-}}/{2}$:
${m_{0}{υ^2}↖{-}}/{2}={3}/{2}kT→{υ^2}↖{-}=3{kT}/{m_0}$
Квадратный корень из этой величины называется средней квадратичной скоростью:
$υ↖{-}=√{{3kT}/{m_0}}$
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
Уравнение состояния идеального газа — это зависимость между параметрами идеального газа — давлением $р$, объемом $V$ и абсолютной температурой $Т$, определяющими его состояние:
$pV=BT$
где $В$ зависит от массы газа $m$ и его молекулярной массы $М$. В таком виде уравнения впервые получено в 1834 г. французским ученым Б. П. Э. Клапейроном и называется уравнением Клапейрона.
В 1874 г. Д. И. Менделеев вывел уравнение состояния для одного моля идеального газа: $pV=RT$, где $R$ — универсальная газовая постоянная. Если молярная масса газа $М$, то
$pV={m}/{M}RT$
Уравнение состояния в форме $pV={m}/{M}RT$ называется уравнением Клапейрона-Менделеева. Оно объединяет газовые законы Гей-Люссака, Бойля—Мариотта, Авогадро, Шарля.
Уравнение состояния $pV={m}/{M}RT$ может быть получено из зависимости давления от температуры $p=nkT$, если в нее подставить концентрацию молекул $n$ из выражения
$n={N}/{V}={1}/{V}·{m}/{M}N_A$
где $N_А$ — постоянная Авогадро, $N$ — число молекул в теле.
В результате получим:
$pV={m}/{M}kN_{A}T$
где $kN_A=R$ — универсальная газовая постоянная, равная $8.31$ Дж/моль$·$К; $k$ — постоянная Больцмана, равная $1.38·10^{-23}$ Дж/К. Заменив в $pV={m}/{M}kN_{A}T$ $kN_A$ на $R$, получаем уравнение состояния в виде $pV={m}/{M}RT$. Отношение уравнений $pV={m}/{M}RT$ или $pV=BT$ при двух наборах параметров $p_1,V_1,T_1$ и $p_2,V_2,T_2$ дает:
${p_1V_1}/{T_1}={p_2V_2}/{T_2}=const$
Внутренняя энергия идеального одноатомного газа
Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул. Для ее вычисления нужно умножить среднюю кинетическую энергию одного атома $E↖{-}={3}/{2}kT$ на число атомов $N={m}/{M}N_A$.
Учитывая, что $kN_A=R$, получим значение внутренней энергии идеального газа:
$U={3}/{2}·{m}/{M}RT$
Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.
Если воспользоваться уравнением Клапейрона-Менделеева, то выражение для внутренней энергии идеального газа можно представить в виде:
$U={3}/{2}pV$
Следует отметить, что, согласно выражению для средней кинетической энергии одного атома $(E↖{-}={3}/{2}kT)$ и в силу хаотичности движения, на каждое из трех возможных направлении движения или каждую степень свободы по оси $X,Y$ и $Z$ приходится одинаковая энергия ${kT}/{2}$.
Число степеней свободы — это число возможных независимых направлений движения молекулы.
Газ, каждая молекула которого состоит из двух атомов, называется двухатомным. Каждый атом может двигаться по трем направлениям, поэтому общее число возможных направлений движения — $6$. За счет связи между молекулами число степеней свободы уменьшается на одну, поэтому число степеней свободы для двухатомной молекулы равно пяти.
Средняя кинетическая энергия двухатомной молекулы равна ${5}/{2}kT$. Соответственно внутренняя энергия идеального двухатомного газа равна:
$U={5}/{2}·{m}/{M}RT={5}/{2}pV$
Формулы для внутренней энергии идеального газа можно обобщить:
$U={i}/{2}·{m}/{M}RT={i}/{2}pV$
где $i$ — число степеней свободы молекул газа ($i = 3$ для одноатомного и $i=5$ для двухатомного газа).
Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объема, т. к. потенциальная энергия равна нулю (объем определяет среднее расстояние между молекулами).
Для реальных газов потенциальная энергия не равна нулю. Поэтому внутренняя энергия в термодинамике в общем случае однозначно определяется параметрами, характеризующими состояние этих тел: объемом ($V$) и температурой ($Т$).
Закон Дальтона
Закон Дальтона для смеси идеальных газов гласит: давление смеси газов равно сумме парциальных давлений ее компонент.
Парциальным давлением какого-либо газа — компонента газовой смеси называется давление, которое оказывал бы этот газ, если бы он один занимал весь объем, занимаемый смесью.
Для доказательства закона Дальтона перепишем уравнение $p=nkT$ в виде:
$pV=NkT$
Рассмотрим сосуд объемом $V$, в котором имеется смесь нереагирующих химически газов, находящихся в состоянии теплового равновесия. Уравнение состояния для такой смеси имеет вид:
$pV=(N_{1}+N_{2}+N_{3}+…)kT$
где $N_{1},N_{2},N_{3}…$ — числа компонент смеси.
Очевидно, что
$N_{1},N_{2},N_{3}+…=N$
где $N$ — общее число молекул в сосуде.
Давление смеси газа получим, поделив обе части $pV=(N_{1}+N_{2}+N_{3}+…)kT$ на объем $V$:
$p={N_1}/{V}kT+{N_2}/{V}kT+{N_3}/{V}kT+…$
Слагаемые этой суммы представляют собой давления каждой из компонент смеси, занимающей объем $V$, т. е. являются парциальными давлениями компонент смеси $р_1 р_2, р_3, …$ что и утверждает закон Дальтона:
$p=р_1+р_2+р_3+…$
То, что каждая группа молекул оказывает давление, не зависящее от давления, оказываемого другими группами, обусловлено отсутствием взаимодействия между молекулами. Последнее реально выполняется только для газов при невысоких давлениях, которые приближаются к идеальному газу.
Термодинамика
Термодинамика — наука о наиболее общих тепловых свойствах макроскопических тел.
В термодинамике не вводятся упрощенные модели изучаемых явлений, поэтому выводы термодинамики имеют универсальный характер.
В частности, в термодинамике не учитывается молекулярное строение тел.
Термодинамика возникла при изучении оптимальных условий использования теплоты для совершения работы.
Основные понятия термодинамики:
- макроскопическая система — система, состоящая из большого числа частиц, причем чем большее число частиц входит в термодинамическую систему, тем точнее описание свойств системы;
- замкнутая система — это система, изолированная от любых внешних воздействий;
- телом в термодинамике называют макроскопическую систему, заключенную в определенный объем;
- равновесное состояние — это состояние, в которое приходит термодинамическая система при неизменных внешних условиях. В равновесном состоянии в системе отсутствуют потоки энергии, импульса, массы и т. д.;
- параметры состояния (термодинамические параметры) — это физические величины, характеризующие равновесное состояние термодинамической системы. К ним относятся в первую очередь температура, объем и давление. В равновесном состоянии параметры состояния не зависят от времени;
- связь между параметрами равновесных термодинамических систем определяется уравнением состояния;
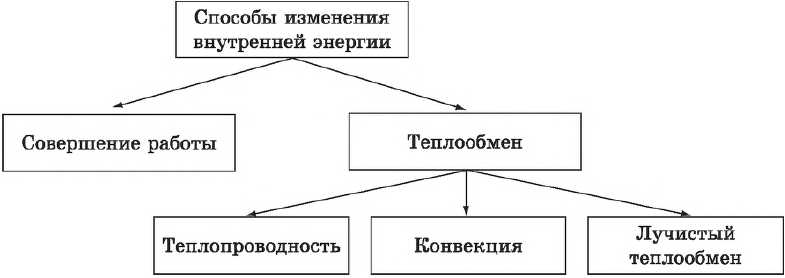
- процессом в термодинамике называется изменение состояния тела со временем. Важными характеристиками процесса являются поглощенное телом количество теплоты $Q$, совершенная над ним работа $А$.
Главное содержание термодинамики состоит в двух ее началах (законах) — первом и втором; первое распространяет закон сохранения энергии на тепловые явления, второе же указывает направление возможных энергетических превращений в природе.
Как уже было сказано, термодинамика не учитывает молекулярное строение вещества при изучении тепловых свойств макроскопических тел и в этом смысле является макроскопической теорией.
Тепловое равновесие и температура
Температура— физическая величина, характеризующая тепловое состояние тел.
В окружающем нас мире происходят различные явления, связанные с нагреванием и охлаждением тел. Их называют тепловыми явлениями. Так, при нагревании холодная вода сначала становится теплой, а затем горячей; вынутая из пламени металлическая деталь постепенно охлаждается и т. д. Степень нагретости тела, или его тепловое состояние, мы обозначаем словами «теплый», «холодный», «горячий». Для количественной оценки этого состояния и служит температура.
Температура — один из макроскопических параметров системы. В физике тела, состоящие из очень большого числа атомов или молекул, называют макроскопическими. Размеры макроскопических тел во много раз превышают размеры атомов. Все окружающие тела — от стола или газа в воздушном шарике до песчинки — макроскопические тела.
Величины, характеризующие состояние макроскопических тел без учета их молекулярного строения, называют макроскопическими параметрами. К ним относятся объем, давление, температура, концентрация частиц, масса, плотность, намагниченность и т. д. Температура — один из важнейших макроскопических параметров системы (газа в частности).
Температура — характеристика теплового равновесия системы.
Известно, что для определения температуры среды следует поместить в эту среду термометр и подождать до тех пор, пока температура термометра не перестанет изменяться, приняв значение, равное температуре окружающей среды. Другими словами, необходимо некоторое время для установления между средой и термометром теплового равновесия.
Тепловым, или термодинамическим, равновесием называют такое состояние, при котором все макроскопические параметры сколь угодно долго остаются неизменными. Это означает, что не меняются объем и давление в системе, не происходят фазовые превращения, не меняется температура.
Однако микроскопические процессы при тепловом равновесии не прекращаются: скорости молекул меняются, они перемещаются, сталкиваются.
Любое макроскопическое тело или группа макроскопических тел — термодинамическая система — может находиться в различных состояниях теплового равновесия. В каждом из этих состояний температура имеет свое вполне определенное значение. Другие величины могут иметь разные (но постоянные) значения. Например, давление сжатого газа в баллоне будет отличаться от давления в помещении и при температурном равновесии всей системы тел в этом помещении.
Температура характеризует состояние теплового равновесия макроскопической системы: во всех частях системы, находящихся в состоянии теплового равновесия, температура имеет одно и то же значение (это единственный макроскопический параметр, обладающий таким свойством).
Если два тела имеют одинаковую температуру, между ними не происходит теплообмен, если разную — теплообмен происходит, причем тепло передается от более нагретого тела к менее нагретому до полного выравнивания температур.
Измерение температуры основано на зависимости какой-либо физической величины (например, объема) от температуры. Эта зависимость и используется в температурной шкале термометра — прибора, служащего для измерения температуры.
Действие термометра основано на тепловом расширении вещества. При нагревании столбик используемого в термометре вещества (например, ртути или спирта) увеличивается, при охлаждении — уменьшается. Использующиеся в быту термометры позволяют выразить температуру вещества в градусах Цельсия ($°С$).
А. Цельсий (1701—1744) — шведский ученый, предложивший использовать стоградусную шкалу температур. В температурной шкале Цельсия за нуль (с середины XVIII в.) принимается температура тающего льда, а за $100$ градусов — температура кипения воды при нормальном атмосферном давлении.
Поскольку различные жидкости расширяются с повышением температуры по-разному, то температурные шкалы в термометрах с разными жидкостями различны.
Поэтому в физике используют идеальную газовую шкалу температур, основанную на зависимости объема (при постоянном давлении) или давления (при постоянном объеме) газа от температуры.
Внутренняя энергия
Внутреннюю энергию тела составляют кинетическая энергия всех его молекул и потенциальная энергия их взаимодействия.
Внутренняя энергия входит в баланс энергетических превращений в природе. После открытия внутренней энергии был сформулирован закон сохранения и превращения энергии. Рассмотрим взаимное превращение механической и внутренней энергий. Пусть на свинцовой плите лежит свинцовый шар. Поднимем его вверх и отпустим. Когда мы подняли шар, то сообщили ему потенциальную энергию. При падении шара она уменьшается, т. к. шар опускается все ниже и ниже. Но с увеличением скорости постепенно увеличивается кинетическая энергия шара. Происходит превращение потенциальной энергии шара в кинетическую. Но вот шар ударился о свинцовую плиту и остановился. И кинетическая, и потенциальная энергии его относительно плиты стали равными нулю. Рассматривая шар и плиту после удара, мы увидим, что их состояние изменилось: шар немного сплющился, и на плите образовалась небольшая вмятина; измерив же их температуру, мы обнаружим, что они нагрелись.
Нагрев означает увеличение средней кинетической энергии молекул тела. При деформации изменяется взаимное расположение частиц тела, поэтому изменяется и их потенциальная энергия. Таким образом, можно утверждать, что в результате удара шара о плиту происходит превращение механической энергии, которой обладал в начале опыта шар, во внутреннюю энергию тела.
Нетрудно наблюдать и обратный переход внутренней энергии в механическую.
Например, если взять толстостенный стеклянный сосуд и накачать в него воздух через отверстие в пробке, то спустя какое-то время пробка из сосуда вылетит. В этот момент в сосуде образуется туман. Появление тумана означает, что воздух в сосуде стал холоднее и, следовательно, его внутренняя энергия уменьшилась. Объясняется это тем, что находившийся в сосуде сжатый воздух, выталкивая пробку (т. е. расширяясь), совершил работу за счет уменьшения своей внутренней энергии. Кинетическая энергия пробки увеличилась за счет внутренней энергии сжатого воздуха.
Таким образом, одним из способов изменения внутренней энергии тела является работа, совершаемая молекулами тела (или другими телами) над данным телом. Способом изменения внутренней энергии без совершения работы является теплопередача.
Теплообмен
Теплообмен — это самопроизвольный (т. е. совершаемый без принуждения) процесс передачи теплоты, происходящий между телами с разной температурой.
Можно сказать, что теплообмен — один из способов изменения внутренней энергии тела. Различают три вида теплопередачи: теплопроводность, конвекцию и лучистый теплообмен.
К одному из способов теплообмена относится также и теплопередача. Теплопередача — это теплообмен между двумя теплоносителями через разделяющую их твердую стенку или через поверхность раздела между ними. Теплопередача включает в себя теплоотдачу от более горячей жидкости или газа к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной жидкой или газообразной среде.
Теплопроводность
Теплопроводность — это один из видов переноса тепла, при котором происходит непосредственная передача энергии от частиц (молекул, атомов) более нагретой части тела к частицам его менее нагретой части.
Рассмотрим ряд опытов с нагревом твердого тела, жидкости и газа.
Закрепим в штативе толстую медную проволоку, а к проволоке прикрепим воском или пластилином несколько гвоздиков. При нагревании свободного конца проволоки в пламени спиртовки воск плавится, и гвоздики постепенно отпадают от проволоки. Причем сначала отпадают те, что находятся ближе к пламени, затем по очереди все остальные. Объясняется это следующим образом. Сначала увеличивается скорость движения тех частиц металла, которые находятся ближе к пламени. Температура проволоки в этом месте повышается. При взаимодействии этих частиц с соседними скорость последних также увеличивается, в результате чего повышается температура следующей части проволоки. Затем увеличивается скорость движения следующих частиц и т. д., пока не прогреется вся проволока.
Следует помнить, что при теплопроводности само вещество не перемещается вдоль тела, переносится лишь энергия.
Рассмотрим теперь теплопроводность жидкостей. Возьмем пробирку с водой. Положим в нее кусочек льда и станем нагревать верхнюю часть пробирки. Вода у поверхности скоро закипит. Лед же на дне пробирки за это время почти не растает. Значит, у жидкостей теплопроводность невелика, за исключением ртути и жидких металлов.
Это объясняется тем, что в жидкостях молекулы расположены на больших расстояниях друг от друга, чем в твердых телах.
Исследуем теплопроводность газов. Сухую пробирку наденем на палец и нагреем в пламени спиртовки донышко. Палец при этом долго не чувствует тепла.
Это связано с тем, что расстояние между молекулами газа еще больше, чем у жидкостей и твердых тел. Следовательно, теплопроводность газов еще меньше.
Итак, теплопроводность различных веществ различна.
Наибольшей теплопроводностью обладают металлы, особенно серебро и медь. Если теплопроводность различных веществ сравнивать с теплопроводностью меди, то окажется, что у железа она меньше примерно в $5$ раз, у воды — в $658$ раз, у пористого кирпича — в $848$ раз, у свежевыпавшего снега — почти в $4000$ раз, у ваты, древесных опилок и овечьей шерсти — почти в $10 000$ раз, а у воздуха она меньше примерно в $20 000$ раз. Плохой теплопроводностью обладают также волосы, перья, бумага, пробка и другие пористые тела. Это связано с тем, что между волокнами этих веществ содержится воздух. Самой низкой теплопроводностью обладает вакуум (освобожденное от воздуха пространство). Объясняется это тем, что теплопроводность — это перенос энергии от одной части тела к другой, который происходит при взаимодействии молекул или других частиц. В пространстве, где нет частиц, теплопроводность осуществляться не может.
Если возникает необходимость предохранить тело от охлаждения или нагревания, то применяют вещества с малой теплопроводностью. Так, ручки для кастрюль, сковородок изготавливают из пластмассы. Дома строят из бревен или кирпича, обладающих плохой теплопроводностью, а значит, предохраняют помещения от охлаждения. На применении вакуума в качестве теплоизоляционного «материала» основано устройство термоса, или сосуда Дьюара, который был изобретен в 1892 г. английским ученым Джеймсом Дьюаром.
Конвекция. Конвективный теплообмен
Конвекция (от лат. convectio — доставка) — это перенос массы в результате перемещения газа или жидкости.
Существуют различные виды конвекции. Мы рассмотрим свободную и вынужденную конвекции.
Свободная конвекция в газе или жидкости возникает тогда, когда имеются небольшие области, в которых плотность отличается от плотности основной окружающей их массы вещества. Тогда в условиях земного тяготения под действием силы Архимеда эти области начинают перемещаться. Примером свободной конвекции является всем известное движение воздуха в помещении, в котором топится печь, имеется радиатор или другой источник тепла.
Поясним сказанное на примерах.
Поместив руку над горячей плитой или горящей электрической лампочкой, можно почувствовать, что над ними поднимаются теплые струи воздуха. Небольшая бумажная вертушка, поставленная над пламенем свечи или электрической лампочкой, под действием поднимающегося нагретого воздуха начинает вращаться.
Это явление можно объяснить таким образом. Часть воздуха, которая соприкасается с теплой лампой, нагревается, расширяется и становится менее плотной, чем окружающий ее более холодный воздух. Под действием архимедовой (выталкивающей) силы эта более теплая часть воздуха начинает подниматься вверх. Ее место заполняет холодный воздух. Через некоторое время, прогревшись, этот слой воздуха также поднимается вверх, уступая место следующей порции воздуха, и т. д. Это и есть конвекция. В результате перемещения более теплых слоев воздуха происходит перенос тепла (т. е. энергии), или конвективный теплообмен.
Точно так же переносится энергия и при нагревании жидкости. Нагретые слои жидкости, менее плотные и поэтому более легкие, вытесняются вверх более тяжелыми, холодными слоями. Холодные слои жидкости, опустившись вниз, в свою очередь, нагреваются от источника тепла и вновь вытесняются менее нагретой жидкостью. Благодаря такому движению жидкость равномерно прогревается. Это становится наглядным, если на дно колбы с водой бросить несколько кристалликов марганцовокислого калия, который окрашивает воду в фиолетовый цвет.
Вынужденная конвекция вызывается внешним механическим воздействием на среду. Примерами ее являются обычное перемешивание жидкости ложечкой, движение воздуха в комнате под действием вентилятора, течение жидкости в трубе под действием гидронасоса и т. д. Физические процессы, происходящие при вынужденной конвекции, связанной с движением тел с большими скоростями в атмосфере, моделируются в аэродинамических трубах, где воспроизводится обтекание неподвижных моделей потоком воздуха.
Таким образом, конвективный теплообмен может осуществляться в газообразной и жидкой среде при условии, что имеется разность температур между частями этой среды. Для осуществления эффективного конвективного теплообмена в земных условиях в жидкостях и газах их следует прогревать снизу. Если их прогревать сверху, конвекция не происходит, ведь теплые слои и так находятся сверху и опуститься ниже холодных, более тяжелых, они не могут.
В отсутствие силы тяжести (в ракете, спутнике, межпланетном корабле) конвекция наблюдаться не будет. Следовательно, пользоваться там, например, спичками и газовыми горелками нельзя: продукты сгорания затушат пламя.
Конвекция в твердых телах происходить не может, поскольку частицы в них колеблются около определенной точки, удерживаемые сильным взаимным притяжением. В связи с этим при нагревании твердых тел потоки вещества в них образовываться не могут. Энергия в твердых телах передается теплопроводностью.
Лучистый теплообмен
Лучистый теплообмен — это теплообмен, при котором энергия переносится различными лучами.
Это могут быть солнечные лучи, а также лучи, испускаемые нагретыми телами, находящимися вокруг нас.
Так, например, сидя около костра, мы чувствуем, как тепло передается от огня нашему телу. Однако причиной такой теплопередачи не может быть ни теплопроводность (которая у воздуха, находящегося между пламенем и телом, очень мала), ни конвекция (так как конвекционные потоки всегда направлены вверх). Здесь имеет место третий вид теплообмена — лучистый теплообмен.
Возьмем небольшую, закопченную с одной стороны, колбу. Через пробку в нее вставим изогнутую под прямым углом стеклянную трубку. В эту трубку, имеющую узкий канал, введем подкрашенную жидкость. Укрепив на трубке шкалу, получим прибор — термоскоп. Этот прибор позволяет обнаружить даже незначительное нагревание воздуха в закопченной колбе.
Если к темной поверхности термоскопа поднести кусок металла, нагретый до высокой температуры, то столбик жидкости переместится вправо. Очевидно, воздух в колбе нагрелся и расширился.
Быстрое нагревание воздуха в термоскопе можно объяснить лишь передачей ему энергии от нагретого тела. Как и в случае с костром, энергия здесь передалась не теплопроводностью и не конвективным теплообменом. Энергия в данном случае передалась с помощью невидимых лучей, испускаемых нагретым телом. Эти лучи называют тепловым излучением.
Лучистый теплообмен может происходить в полном вакууме. Этим он отличается от других видов теплообмена.
Излучают энергию все тела: и сильно нагретые, и слабо, например, тело человека, печь, электрическая лампочка. Но чем выше температура тела, тем сильнее его тепловое излучение. Излученная энергия, достигнув других тел, частично поглощается ими, а частично отражается. При поглощении энергия теплового излучения превращается во внутреннюю энергию тел, и они нагреваются.
Светлые и темные поверхности поглощают энергию по-разному. Так, если в опыте с термоскопом повернуть колбу к нагретому телу сначала закопченной, а затем светлой стороной, то столбик жидкости в первом случае переместится на большее расстояние, чем во втором. Из этого следует, что тела с темной поверхностью лучше поглощают энергию (и, следовательно, сильнее нагреваются), чем тела со светлой или зеркальной поверхностью.
Тела с темной поверхностью не только лучше поглощают, но и лучше излучают энергию.
Способность по-разному поглощать энергию излучения находит широкое применение в технике. Например, воздушные шары и крылья самолетов часто красят серебристой краской, чтобы они меньше нагревались солнечными лучами.
Если же нужно использовать солнечную энергию (например, для нагревания некоторых приборов, установленных на искусственных спутниках), то эти устройства окрашивают в темный цвет.
Количество теплоты. Удельная теплоемкость вещества
Количеством теплоты называют количественную меру изменения внутренней энергии тела при теплообмене.
Количество теплоты — это энергия, которую тело отдает при теплообмене (без совершения работы). Количество теплоты, как и энергия, измеряется в джоулях (Дж).
Удельная теплоемкость вещества
Теплоемкость — это количество теплоты, поглощаемой телом при нагревании на $1$ градус.
Теплоемкость тела обозначается заглавной латинской буквой С.
От чего зависит теплоемкость тела? Прежде всего, от его массы. Ясно, что для нагрева, например, $1$ килограмма воды потребуется больше тепла, чем для нагрева $200$ граммов.
А от рода вещества? Проделаем опыт. Возьмем два одинаковых сосуда и, налив в один из них воду массой $400$ г, а в другой — растительное масло массой $400$ г, начнем их нагревать с помощью одинаковых горелок. Наблюдая за показаниями термометров, мы увидим, что масло нагревается быстрее. Чтобы нагреть воду и масло до одной и той же температуры, воду следует нагревать дольше. Но чем дольше мы нагреваем воду, тем большее количество теплоты она получает от горелки.
Таким образом, для нагревания одной и той же массы разных веществ до одинаковой температуры требуется разное количество теплоты. Количество теплоты, необходимое для нагревания тела и, следовательно, его теплоемкость зависят от рода вещества, из которого состоит это тело.
Так, например, чтобы увеличить на $1°$С температуру воды массой $1$ кг, требуется количество теплоты, равное $4200$ Дж, а для нагревания на $1°$С такой же массы подсолнечного масла необходимо количество теплоты, равное $1700$ Дж.
Физическая величина, показывающая, какое количество теплоты требуется для нагревания $1$ кг вещества на $1°$С, называется удельной теплоемкостью этого вещества.
У каждого вещества своя удельная теплоемкость, которая обозначается латинской буквой $с$ и измеряется в джоулях на килограмм-градус (Дж/(кг$·°$С)).
Удельная теплоемкость одного и того же вещества в разных агрегатных состояниях (твердом, жидком и газообразном) различна. Например, удельная теплоемкость воды равна $4200$ Дж/(кг$·°$С), а удельная теплоемкость льда $2100$ Дж/(кг$·°$С); алюминий в твердом состоянии имеет удельную теплоемкость, равную $920$ Дж/(кг$·°$С), а в жидком — $1080$ Дж/(кг$·°$С).
Заметим, что вода имеет очень большую удельную теплоемкость. Поэтому вода в морях и океанах, нагреваясь летом, поглощает из воздуха большое количество тепла. Благодаря этому в тех местах, которые расположены вблизи больших водоемов, лето не бывает таким жарким, как в местах, удаленных от воды.
Расчет количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении
Из вышеизложенного ясно, что количество теплоты, необходимое для нагревания тела, зависит от рода вещества, из которого состоит тело (т. е. его удельной теплоемкости), и от массы тела. Ясно также, что количество теплоты зависит от того, на сколько градусов мы собираемся увеличить температуру тела.
Итак, чтобы определить количество теплоты, необходимое для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость тела умножить на его массу и на разность между его конечной и начальной температурами:
$Q=cm(t_2-t_1)$
где $Q$ — количество теплоты, $c$ — удельная теплоемкость, $m$ — масса тела, $t_1$ — начальная температура, $t_2$ — конечная температура.
При нагревании тела $t_2 > t_1$ и, следовательно, $Q > 0$. При охлаждении тела $t_2 < t_1$ и, следовательно, $Q < 0$.
В случае, если известна теплоемкость всего тела $С, Q$ определяется по формуле
$Q=C(t_2-t_1)$
Удельная теплота парообразования, плавления, сгорания
Теплота парообразования (теплота испарения) — количество теплоты, которое необходимо сообщить веществу (при постоянном давлении и постоянной температуре) для полного превращения жидкого вещества в пар.
Теплота парообразования равна количеству теплоты, выделяющемуся при конденсации пара в жидкость.
Превращение жидкости в пар при постоянной температуре не ведет к увеличению кинетической энергии молекул, но сопровождается увеличением их потенциальной энергии, т. к. расстояние между молекулами существенно увеличивается.
Удельная теплота парообразования и конденсации. Опытами установлено, что для полного обращения в пар $1$ кг воды (при температуре кипения) необходимо затратить $2.3$ МДж энергии. Для обращения в пар других жидкостей требуется иное количество теплоты. Например, для спирта оно составляет $0.9$ МДж.
Физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить жидкость массой $1$ кг в пар без изменения температуры, называется удельной теплотой парообразования.
Удельную теплоту парообразования обозначают буквой $r$ и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты, необходимое для парообразования (или выделяющееся при конденсации). Чтобы вычислить количество теплоты $Q$, необходимое для превращения в пар жидкости любой массы, взятой при температуре кипения, нужно удельную теплоту парообразования $r$ умножить на массу $m$:
$Q=rm$
При конденсации пара происходит выделение такого же количества теплоты:
$Q=-rm$
Удельная теплота плавления
Теплота плавления — это количество теплоты, которое необходимо сообщить веществу при постоянном давлении и постоянной температуре, равной температуре плавления, чтобы полностью перевести его из твердого кристаллического состояния в жидкое.
Теплота плавления равна тому количеству теплоты, которое выделяется при кристаллизации вещества из жидкого состояния.
При плавлении вся подводимая к веществу теплота идет на увеличение потенциальной энергии его молекул. Кинетическая энергия не меняется, поскольку плавление идет при постоянной температуре.
Изучая на опыте плавление различных веществ одной и той же массы, можно заметить, что для превращения их в жидкость требуется разное количество теплоты. Например, для того чтобы расплавить один килограмм льда, нужно затратить $332$ Дж энергии, а для того чтобы расплавить $1$ кг свинца — $25$ кДж.
Физическая величина, показывающая, какое количество теплоты необходимо сообщить кристаллическому телу массой $1$ кг, чтобы при температуре плавления полностью перевести его в жидкое состояние, называется удельной теплотой плавления.
Удельную теплоту плавления измеряют в джоулях на килограмм (Дж/кг) и обозначают греческой буквой $λ$ (лямбда).
Удельная теплота кристаллизации равна удельной теплоте плавления, поскольку при кристаллизации выделяется такое же количество теплоты, какое поглощается при плавлении. Так, например, при замерзании воды массой $1$ кг выделяются те же $332$ Дж энергии, которые нужны для превращения такой же массы льда в воду.
Чтобы найти количество теплоты, необходимое для плавления кристаллического тела произвольной массы, или теплоту плавления, надо удельную теплоту плавления этого тела умножить на его массу:
$Q=λm$
Количество теплоты, выделяемое телом, считается отрицательным. Поэтому при расчете количества теплоты, выделяющегося при кристаллизации вещества массой $m$, следует пользоваться той же формулой, но со знаком «минус»:
$-Q=λm$
Удельная теплота сгорания
Теплота сгорания (или теплотворная способность, калорийность) — это количество теплоты, выделяющейся при полном сгорании топлива.
Для нагревания тел часто используют энергию, выделяющуюся при сгорании топлива. Обычное топливо (уголь, нефть, бензин) содержит углерод. При горении атомы углерода соединяются с атомами кислорода, содержащегося в воздухе, в результате чего образуются молекулы углекислого газа. Кинетическая энергия этих молекул оказывается большей, чем у исходных частиц. Увеличение кинетической энергии молекул в процессе горения называют выделением энергии. Энергия, выделяющаяся при полном сгорании топлива, и есть теплота сгорания этого топлива.
Теплота сгорания топлива зависит от вида топлива и его массы. Чем больше масса топлива, тем больше количество теплоты, выделяющейся при его полном сгорании.
Физическая величина, показывающая, какое количество теплоты выделяется при полном сгорании топлива массой $1$ кг, называется удельной теплотой сгорания топлива.
Удельную теплоту сгорания обозначают буквой $q$ и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты $Q$, выделяющееся при сгорании $m$ кг топлива, определяют по формуле:
$Q=qm$
Чтобы найти количество теплоты, выделяющееся при полном сгорании топлива произвольной массы, нужно удельную теплоту сгорания этого топлива умножить на его массу.
Работа в термодинамике
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
Рассмотрим работу газа при изобарическом расширении.
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V < 0$, поскольку $∆h < 0$.
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q < 0$ и $∆U < 0$, внутренняя энергия уменьшается.
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q < 0$ и $А’ < 0$. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой $р(V)$.
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А < 0$.
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T < 0,$
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
Второй закон термодинамики. Необратимость
Необратимый процесс
Необратимым называется физический процесс, который может самопроизвольно протекать только в одном определенном направлении.
В обратном направлении такие процессы могут протекать только как одно из звеньев более сложного процесса.
Необратимыми являются практически все процессы, происходящие в природе. Это связано с тем, что в любом реальном процессе часть энергии рассеивается за счет излучения, трения и т. д. Например, тепло, как известно, всегда переходит от более горячего тела к более холодному — это наиболее типичный пример необратимого процесса (хотя обратный переход не противоречит закону сохранения энергии).
Также висящий на легкой нити шарик (маятник) никогда самопроизвольно не увеличит амплитуду своих колебаний, наоборот, приведенный однажды в движение посторонней силой он обязательно в конце концов остановится в результате сопротивления воздуха и трения нити о подвес. Таким образом, сообщенная маятнику механическая энергия переходит во внутреннюю энергию хаотического движения молекул (воздуха, материала подвеса).
Математически необратимость механических процессов выражается в том, что уравнение движения макроскопических тел изменяется с изменением знака времени: они не инвариантны при замене $t$ на $-t$. При этом ускорение и силы, зависящие от расстояний, не изменяют свои знаки. Знак при замене $t$ на $-t$ меняется у скорости $(υ={∆s}/{∆t})$.Соответственно знак меняет сила, зависящая от скорости, — сила трения. Именно поэтому при совершении работы силами трения кинетическая энергия тела необратимо переходит во внутреннюю.
На направленность процессов в природе указывает второй закон термодинамики.
Второй закон термодинамики
Второй закон термодинамики — один из основных законов термодинамики, устанавливающий необратимость реальных термодинамических процессов.
Второй закон термодинамики был сформулирован как закон природы Н. Л. С. Карно в 1824 г., затем У. Томсоном (Кельвином) в 1841 г. и Р. Клаузиусом в 1850 г. Формулировки закона различны, но эквивалентны.
Немецкий ученый Р. Клаузиус формулировал закон так: невозможно перевести теплоту от более холодной системы к более горячей при отсутствии других одновременных изменений в обеих системах или окружающих телах. Это означает, что теплота не может самопроизвольно переходить от более холодного тела к более горячему (принцип Клаузиуса).
Согласно формулировке Томсона процесс, при котором работа переходит в тепло без каких-либо иных изменений состояния системы, необратим, т. е. невозможно преобразовать в работу все тепло, взятое от тела, не производя никаких других изменений состояния системы (принцип Томсона).
Принцип действия тепловых двигателей
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.
Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η < 1$.
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 — T_2=0$ двигатель не может работать.
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2 < Т_1$. В процессе ($3-4$) газ изотермически сжимается, передавая холодильнику количество теплоты $Q_2$:
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.
Уравнение теплового баланса
В замкнутой (изолированной от внешних тел) термодинамической системе изменение внутренней энергии какого-либо тела системы $∆U_i$ не может приводить к изменению внутренней энергии всей системы. Следовательно,
$∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$
Если внутри системы не совершается работа никакими телами, то, согласно первому закону термодинамики, изменение внутренней энергии любого тела происходит только за счет обмена теплом с другими телами этой системы: $∆U_i=Q_i$. Учитывая ($∆U_1+∆U_2+∆U_3+…+∆U_n=∑↙{i}↖{n}∆U_i=0$), получим:
$Q_1+Q_2+Q_3+…+Q_n=∑↙{i}↖{n}Q_i=0$
Это уравнение называется уравнением теплового баланса. Здесь $Q_i$ — количество теплоты, полученное или отданное $i$-м телом. Любое из количеств теплоты $Q_i$ может означать теплоту, выделяемую или поглощаемую при плавлении какого-либо тела, сгорании топлива, испарении или конденсации пара, если такие процессы происходят с различными телами системы, и будут определятся соответствующими соотношениями.
Уравнение теплового баланса является математическим выражением закона сохранения энергии при теплообмене.
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) — формула, устанавливающая зависимость между давлением, объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
pV = 
p — давление [Па],
V — объём [м3],
R — универсальная газовая постоянная 8,31 [Дж/моль∙К],
T — абсолютная температура [K].
Количество вещества — физическая величина, характеризующая количество атомов или молекул, содержащихся веществе. Единица измерения количества вещества —моль.
υ = 
υ ― количество вещества [моль],
m — масса [кг],
M — молярная масса [кг/моль].
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными.
Изохорический процесс — термодинамический процесс, который происходит при постоянном объёме. Следовательно, объем V не изменяется, и значение давления прямолинейно зависит от температуры.
Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма, например, в запаянном сосуде.
Изобарический процесс — термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа. Следовательно, давление р не изменяется, и значение объёма прямолинейно зависит от температуры.
Простейшим примером изобарического процесса может служить нагревание воды в открытом сосуде.
Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре. Следовательно, температура Т не меняется, и значение давления обратно пропорционально объёму(гипербола).
p = 

График имеет вид гиперболы, поскольку давление обратно пропорционально объему при постоянной температуре.
Рассмотрим две изотермы с одинаковой массой, но разной температурой на pV диаграмме (T1 < T2).
Изотерма с температурой Т2 будет располагаться на диаграмме pV выше, чем изотерма с температурой Т1, как следствие закона pV = vRT. Так как при большем значение температуры значение коэффициента перед V в уравнении p = 
Теперь рассмотрим две изохоры одной массы, но разного объёма (V2 > V1) на pT диаграмме. Изохора с V1 будет выше V2, аналогично, как следствие закона pV = vRT. Так как при большем значении объема, коэффициент при Т будет меньше 
Изопроцессы в МКТ — это процессы, протекающие в газах с каким-нибудь неизменным параметром. Рассмотрим, как решаются некоторые задачи, представленные в графиках, при наличии неизменных параметров.

Приступаем. Фраза «постоянная масса газа» означает, что мы имеем задачу с изопроцессом. Смотрим.
1-2: Температура не меняется (изотерма), но при этом увеличивается объем. В изотермическом процессе увеличение объема ведет к уменьшению давления и наоборот. Давление обратно пропорционально объему. Следовательно, в точке 2 давление ниже, чем в точке.
2-3: Не меняется объем (изохора), но при этом температура уменьшается. А в изохорном процессе давление прямо пропорционально температуре. То есть, в нашем случае — уменьшается.Давление в точке 3 будет меньше, чем в точке 2.
Ответ: Наибольшее давление будет в точке 1.
Задача 2: Зависимость объема идеального газа от температуры показана на V-P диаграмме. Масса газа постоянна. Выберите два верных утверждения о процессе, происходящем с газом:
- Давление газа максимально в состоянии D.
- При переходе из состояния D в состояние А средняя квадратичная скорость молекул увеличивается.
- При переходе из состояния В в состояние С плотность газа возрастает.
- Давление газа в состоянии С больше, чем в состоянии А
- При переходе из состояния В в состояние С средняя кинетическая энергия молекул возрастает
Процесс, изображенный на диаграмме (окружность), конечно же не является изопроцессом в чистом виде. Но у нас есть газ постоянной массы, а следовательно, мы можем воспользоваться графиками изобар для сравнения давления в заданных точках диаграммы. Температуру и объем можно сравнить на диаграмме по осям. Изобары здесь уже нарисованы. Это красная, синяя и коричневая прямые, то есть в этих осях на каждой изохоре какое-то свое, но постоянное даление. Для сравнения давления в точках можно провести изотерму или изохору. Я провела изохору.
Максимальное давление соответствует точке D. Первое утверждение верно.
При рассмотрении уравнения состояния идеального газа было определено, что давление прямо пропорционально температуре и средней квадратичной скорости движения молекул
р ∼ Т ∼ v²
Максимальная скорость соответствует максимальному давлению, значит в точке А она , скорость, меньше, чем в точке В. Второе утверждение неверно
Теперь плотность. Плотность — это масса единицы объема. Масса у нас постоянная, а объем в точке С больше, чем в точке В. Значит, плотность будет меньше. Третье утверждение неверно.
В точках А и С давление одинаковое, т.к. они лежат на изобаре. Четвертое утверждение неверное.
При переходе из В в С давление увеличивается, следовательно, увеличивается средняя квадратичная скорость, а значит, увеличивается средняя кинетическая энергия. Пятое утверждение верное.
Ответ: 1 и 5

Рассмотрим уравнение Менделеева-Клайперона:
PV = νRT
где P — давление (Па); V — объем газа (м 3); ν — количество вещества (моли); R — газовая постоянная; T — температура (абсолютная).
В нашем случае постоянными будут объем V , газовая постоянная R и молярная масса μ.
Преобразуем уравнение Менделеева-Клайперона:
Перенесем постоянные величины в одну сторону, а переменные — в другую:
Получается, что масса будет наибольшей при наибольшем отношении , а это отношение будет наибольшим в точке А, посмотрите на график.
Ответ: В точке А
Еще больше разобранных задач по МКТ здесь!
Качественный разбор изопроцессов в ЕГЭ
Изопроцесс (изо – с греч. «постоянный», «ровный») – процесс, при котором постоянен один из параметров (P, V, T) и масса m.
Во первых. Нужно осознать, что любой процесс – это последовательное изменение состояний.
Для описания состояний идеального газа вводятся параметры:
P – давление [Па]
V – объем [м3]
T – температура [К]
Во вторых. Исследовать изопроцессы удобнее по двум формулам:
1. Уравнение Менделеева-Клапейрона (уравнение состояния газа):
где
— количество вещества [моль];
— универсальная газовая постоянная [м2 кг с-2 К-1 Моль-1]
2. Первое начало термодинамики:
где
Q — количество теплоты переданное газу [Дж];
— изменение внутренней энергии газа [Дж];
— работа, совершенная самим газом [Дж].
Теперь две эти формулы просто будем подстраивать под наши процессы. Обращаю внимание, запомнить и разбирать нужно только их!
Итак изопроцессы:
1. Изотермический процесс(термо – это температура, изо — постоянная) Т=const
По первой формуле:
Поскольку масса не меняется, как было сказано выше, то в правой части уравнения все величины постоянные (const):
По этой формуле очень легко построить графики можно интуитивно:
1) График P от V. Строим так, чтобы PV=const. Если давление P уменьшается, то для того чтобы PV=const, объем V должен увеличиваться и наоборот.
2) График P от Т. Поскольку Т=const, при изменении давления температура остается одна и та же, то есть прямая линия параллельная Р.
3) График V от Т. Поскольку Т=const, при изменении объема температура остается одна и та же, то есть прямая линия параллельная V.
По второй формуле:
Так как здесь Т=const, поэтому T1=T2, и
Формула приобретает вид:
Вывод. Все переданное газу количество теплоты идет на совершение самим газом работы.
По аналогии остальные процессы:
2. Изохорный процесс (хора – это объем, изо — постоянный) V=const
По первой формуле:
Перенесем константы в правую часть, а изменяющиеся параметры в левую, получим:
Графики:
Здесь второй график приобретает вид линии, проходящей через начало координат. Почему? Потому, что формулу можно, для удобства, записать в виде P=T*const — это есть уравнение прямой, проходящей через начало отсчета.
По второй формуле:
Поскольку V=const, поэтому V1=V2, и
Формула приобретает вид:
Вывод. Все количество теплоты, переданное газу, идет на увеличение его внутренней энергии.
3. Изобарный процесс (бара – это давление, изо — постоянное) P=const
По первой формуле:
Перенесем константы в правую часть, а изменяющиеся параметры в левую, получим:
По второй формуле:
Поскольку P=const, поэтому P1=P2, и ничего не обнуляется! Формула приобретает вид:
Вывод. Количество теплоты, переданное газу, идет на увеличение его внутренней энергии и совершения им самим работы.
Еще один процесс, который не относится к изо-, но знать нужно:
4. Адиабатный процесс
Процесс без теплообмена с окружающей средой (Q=0) (например взрыв).
По первой формуле:
По второй формуле:
Т.к. Q=0 формула приобретает вид:
Вывод. Уменьшение внутренней энергии газа идет за счет совершения самим газом работы.
*Спасибо, что дочитали до конца, пишите вопросы в комментарии.
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Газовые законы
1 моль гелия изохорно нагревают на 154 К, при этом давление газа увеличивается в 2,1 раза. До какой температуры нагрели газ? Ответ дайте в кельвинах.
Процесс изохорный, т.е. объём не меняется. Запишем закон Шарля: [hspace{ 5 mm} dfrac{p_1}{T_1}=dfrac{p_2}{T_2} hspace{ 5 mm} (1)] Изменение температуры есть разница конечной и начальной температуры газа: [hspace{ 5 mm} Delta T = T_2 — T_1 hspace{3 mm} Rightarrow hspace{3 mm} T_1 = T_2 — Delta T hspace{ 5 mm} (2)] По условию давление газа увеличивается в 2,1 раза: [hspace{ 5 mm}p_2 = 2,1 p_1hspace{ 5 mm} (3)] Подставим (2), (3) в (1) и выразим температуру, до которой нагрели газ: [dfrac{p_1}{T_2 — Delta T}=dfrac{2,1 p_1}{T_2}] [T_2 = dfrac{2,1 p_1 Delta T}{2,1p_1 — p_1} = dfrac{2,1 Delta T}{1,1} = dfrac{2,1 cdot 154text{ K}}{1,1} = 294 text{ K}]
Ответ: 294
Воздух при температуре 27(^{circ})C и давлении 202,65 кПа занимает объём 0,3 м(^3). Газ изобарно нагрели, причём объём газа увеличился до 0,5 м(^3). Найдите конечную температуру воздуха. Ответ дайте в кельвинах.
Т.к. процесс изобарный ((p=const)), используем закон Гей – Люссака: [dfrac{V_1}{T_1}=dfrac{V_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_2=dfrac{T_1 cdot V_2}{V_1}] Переведём (T_1) в кельвины: 27(^{circ})С + 273 = 300 К. [T_2=dfrac{300 text{ К} cdot 0,5 text{ м$^3$}}{0,3text{ м$^3$}}=500 text{ К}]
Ответ: 500
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 1 равна 56(^{circ})C. Какова температура аргона в состоянии 2? Ответ дайте в кельвинах.
Из графика видно, что процесс 1–2 — изобарный ((p=const)). Воспользуемся законом Гей – Люссака: [dfrac{V_1}{T_1}=dfrac{V_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_2=dfrac{T_1 cdot V_2}{V_1}] Переведём (T_1) в кельвины: 56(^{circ})С + 273 = 329 К. [T_2=dfrac{329text{ К} cdot 14text{ м$^3$}}{7text{ м$^3$}} = 658 text{ К}]
Ответ: 658
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 2 равна 212(^{circ})C. Какова температура аргона в состоянии 1? Ответ дайте в кельвинах.
Из графика видно, что процесс 1–2 — изохорный ((V=const)). Воспользуемся законом Шарля: [dfrac{p_1}{T_1}=dfrac{p_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_1=dfrac{p_1 cdot T_2}{p_2}] Переведём (T_2) в кельвины: 212(^{circ})С + 273 = 485 К. [T_1=dfrac{3cdot 10^4 text{ Па} cdot 485text{ К}}{5 cdot 10^4text{ Па}} = 291 text{ К}]
Ответ: 291
Давление газа при температуре 306 К равно 159 кПа. Газ нагрели до температуры (T_2), при этом объём газа не изменился. После нагревания давление газа стало равно 212 кПа. Найдите, до какой температуры (T_2) нагрели газ. Ответ дайте в кельвинах.
По условию процесс изохорный ((V=const)).
Согласно закону Шарля: [dfrac{p_1}{T_1} = dfrac{p_2}{T_2}hspace{3 mm}Rightarrowhspace{3 mm} T_2 = dfrac{T_1 p_2}{p_1}] [T_2 = dfrac{306 text{ K} cdot 212 cdot 10^3 text{ Па}}{159 cdot 10^3 text{ Па}} = 408 text{ K}]
Ответ: 408
Газ занимает объём 0,03 м(^3) при температуре 418 К. Какой объём займёт этот же газ, если его температура понизится до 209 К? Давление и масса газа не меняются. Ответ дайте в м(^3).
По условию процесс изобарный ((p=const)). По закону Гей – Люссака: [dfrac{V_1}{T_1} = dfrac{V_2}{T_2}hspace{3 mm}Rightarrowhspace{3 mm} V_2 = dfrac{V_1T_2}{T_1}] [V_2 = dfrac{0,03 text{ м$^3$} cdot 209 text{ К}}{418 text{ К}} = 0,015 text{ м$^3$}]
Ответ: 0,015
На рисунке представлен график зависимости давления от температуры газа. Объём газа в состоянии 2 равен 6 л. Какой объём занимает газ в состоянии 1? Масса газа не меняется. Ответ дайте в м(^3).
По графику видно, что процесс 1–2 — изотермический ((T=const)). По закону Бойля – Мариотта: [p_1V_1 = p_2V_2hspace{3 mm}Rightarrowhspace{3 mm} V_1 = dfrac{p_2V_2}{p_1}] Переведём объём газа в м(^3): (; 
Ответ: 0,03

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ