Зарубежные тесты
Представленные ниже материалы для подготовки к вступительным экзаменам по математике в зарубежные школы и варианты международных экзаменов по математике прошлых лет Вы можете использовать для самостоятельной подготовки.
Если же Вы решите воспользоваться помощью профессионального преподавателя, то буду рад Вас видеть на своих занятиях математикой на английском языке для подготовки к поступлению в зарубежную школу или к любым международным экзаменам по математике, в т.ч. к A-Level, International Baccalaureate, GCSE, IGCSE, GRE, SAT, SSAT, ISEE и GMAT.
Меня зовут Евгений, я магистр британского университета University of Wales Swansea, кандидат технических наук и доцент МГТУ им. Н.Э. Баумана с опытом преподавания более 19 лет. Специализируюсь на подготовке к зарубежным экзаменам по математике.
В 2011-2012 учебном году я стал победителем конкурса “Лучший преподаватель МГТУ им. Н.Э. Баумана”. Экзаменатор Международного Бакалавриата (International Baccalaureate Examiner) 2016, 2017, 2018, 2019 г. Эксперт ЕГЭ по математике 2011, 2013, 2014, 2015, 2016, 2017, 2018, 2019 г. Выпускник МГТУ им. Н.Э. Баумана по специальности “Прикладная математика”.
Я буду рад ответить на все Ваши вопросы – позвоните мне напрямую по телефону 8-905-741-62-46 или напишите на email info@mathconsult.ru
За годы работы у меня образовалась целая библиотека иностранных учебников и скопилось около 1000 вступительных тестов различных уровней в более чем 120 британских школ (часть тестов ограниченного доступа). Кроме этого, есть масса вариантов экзаменов A-Level, GCSE и IB по математике прошлых лет (past papers). Так что задачами я Вас обеспечу 🙂
В том числе, и нестандартными задачами, примеры которых размещены в моей группе Занимательные задачи по математике на английском в сети ВКонтакте.
Мои ученики получают фундаментальные знания по предмету и успешно сдают вступительные тесты экзамены по математике на английском языке в топовые британские школы на различные программы от Year 7 (11+) до 6th form (16+). Кроме того, многие мои студенты успешно сдали различные международные экзамены по математике и поступили в желанные для них учебные заведения. У меня более 80 рекомендательных писем, некоторые из них находятся здесь.
- Типовые варианты вступительных экзаменов по математике в частные школы Великобритании
- Материалы для подготовки к экзамену International Baccalaureate Diploma Programme по математике
- Типовые варианты экзамена SAT / SAT practice test from the College Board
- Варианты экзамена A-Level / A-Level maths past papers Edexcel, OCR, AQA
- Варианты экзамена GCSE / GCSE maths past papers
- Варианты экзамена IGCSE / IGCSE maths past papers
Типовые варианты вступительных экзаменов по математике в частные школы Великобритании
Вступительные экзамены по математике на программу 11+
- Kent College. 11+ mathematics sample paper
- The Perse Upper School. Year 7 entrance exams. Maths
- Sevenoaks School. Entrance examination sample paper mathematics. Year 7 (11+ entry)
- Magdalen College School Oxford. 11+/pre test entrance examination. Year 7 (11+ entry)
- St Paul’s School. Junior scholarship examination. Year 7 (11+ entry)
Вступительные экзамены по математике на программу 12+
- Oundle School. Entrance Examination to the Second Form Mathematics. Year 8 (12+ entry)
- St Swithun’s. Mathematics Past paper. Year 8 (12+ entry)
- St Albans School. 12+ Mathematics Specimen. Year 8 (12+ entry)
Вступительные экзамены по математике на программу 13+
- Eton College. King’s Scholarship examination. Maths A. (13+ entry)
- Eton College. King’s Scholarship examination. Maths B. (13+ entry)
- Sevenoaks School. Entrance examination sample paper mathematics. Year 9 (13+ entry)
- Westminster School Challenge. Mental Test. Year 9 (13+ entry)
- Westminster School. The Challenge. Mathematics II. Year 9 (13+ entry)
- Westminster School. The Challenge. Mathematics III. Year 9 (13+ entry)
- Mill Hill School. Sample Maths Paper. Year 9 (13+ entry)
- The Perse School Entrance Examination Specimen Paper. 13+ Mathematics. Year 9 (13+ entry)
- Bromsgrove school. Entrance examination paper. Mathematics. Year 9 (13+ entry)
Вступительные экзамены по математике на программу 14+
- St Edward’s School Oxford. Past math paper. Entrance exam. Year 10 (14+ entry)
- The King’s School, Canterbury. Mathematics Entrance Examinations. Year 10 (14+ entry)
- St Swithun’s. Mathematics Past paper. Year 10 (14+ entry)
- Oundle School. Entrance Examination to the Fourth Form Mathematics. Year 10 (14+ entry)
Вступительные экзамены по математике на программу 16+
- Dulwich College. Specimen examination paper mathematics. Upper school entrance examination. Year 12 (16+ entry)
- Downe House. 16+ entrance paper mathematics. Year 12 (16+ entry)
- St Edward’s School Oxford. Past maths paper. Lower Sixth Form entrance assessment. Year 12 (16+ entry)
- Wellington College. 16+ entrance examination. Mathematical skills paper. Year 12 (16+ entry)
- Wellington College. 16+ entrance examination. Mathematics. Year 12 (16+ entry)
Материалы для подготовки к экзамену International Baccalaureate Diploma Programme по математике
- Mathematics: applications and interpretation guide SL / HL. First assessment 2021
- Mathematics: analysis and approaches guide SL / HL. First assessment 2021
- Mathematics: applications and interpretation subject brief SL / HL. First assessment 2021
- Mathematics: analysis and approaches subject brief SL / HL. First assessment 2021
В моей копилке есть все варианты экзаменов IB HL / IB SL / IB Studies по математике за последние 22 года. Предоставлю их вам на своих занятиях, так как по правилам International Baccalaureate Organization размещать IB math past papers на сторонних сайтах запрещено.
Типовые варианты экзамена SAT / SAT practice test from the College Board
- New SAT Practice Test, 2016
- Getting Ready for the SAT. Effective september 2013
- SAT practice test 2012-2013
- SAT practice test 2009-2010
Варианты экзамена A-Level / A-Level maths past papers
Pearson Edexcel GCE. May 2018.
- Pearson Edexcel GCE. Core Mathematics C1. May 2018
- Pearson Edexcel GCE. Core Mathematics C2. May 2018
- Pearson Edexcel GCE. Core Mathematics C3. May 2018
- Pearson Edexcel GCE. Core Mathematics C4. May 2018
- Pearson Edexcel GCE. Further Pure Mathematics FP1. May 2018
- Pearson Edexcel GCE. Further Pure Mathematics FP2. May 2018
- Pearson Edexcel GCE. Mechanics M1. May 2018
- Pearson Edexcel GCE. Mechanics M2. May 2018
- Pearson Edexcel GCE. Statistics S1. May 2018
- Pearson Edexcel GCE. Statistics S2. May 2018
- Pearson Edexcel GCE. Decision Mathematics D1. May 2018
- Pearson Edexcel GCE. Decision Mathematics D2. May 2018
A-Level Edexcel past papers. January 2013
- Edexcel GCE. Core Mathematics C1. 14 January 2013
- Edexcel GCE. Core Mathematics C2. 14 January 2013
- Edexcel GCE. Core Mathematics C3. 25 January 2013
- Edexcel GCE. Core Mathematics C4. 28 January 2013
- Edexcel GCE. Further Pure Mathematics FP1. 28 January 2013
- Edexcel GCE. Mechanics M1. 23 January 2013
- Edexcel GCE. Statistics S1. 18 January 2013
- Edexcel GCE. Decision Mathematics D1. 23 January 2013
A-Level OCR past papers. June 2010
- OCR A-Level. Core Mathematics 1, 24 May 2010
- OCR A-Level. Core Mathematics 2, 27 May 2010
- OCR A-Level. Core Mathematics 3, 9 June 2010
- OCR A-Level. Core Mathematics 4, 11 June 2010
A-Level AQA past papers. January 2007
- AQA A-Level. Mathematics Unit Pure Core 1, 10 January 2007
- AQA A-Level. Mathematics Unit Pure Core 2, 10 January 2007
- AQA A-Level. Mathematics Unit Pure Core 3, 18 January 2007
- AQA A-Level. Mathematics Unit Pure Core 4, 25 January 2007
- AQA A-Level. Mathematics Unit Further Pure 1, 26 January 2007
- AQA A-Level. Mathematics Unit Further Pure 2, 1 February 2007
- AQA A-Level. Mathematics Unit Further Pure 3, 26 January 2007
- AQA A-Level. Mathematics Unit Further Pure 4, 31 January 2007
Варианты экзамена GCSE / GCSE maths past papers
Pearson Edexcel Level 1/Level 2 GCSE (9–1). November 2018
- Pearson Edexcel GCSE. Paper 1. Foundation Tier. November 2018
- Pearson Edexcel GCSE. Paper 1. Higher Tier. November 2018
- Pearson Edexcel GCSE. Paper 2. Foundation Tier. November 2018
- Pearson Edexcel GCSE. Paper 2. Higher Tier. November 2018
- Pearson Edexcel GCSE. Paper 3. Foundation Tier. November 2018
- Pearson Edexcel GCSE. Paper 3. Higher Tier. November 2018
GCSE Edexcel past papers. June 2011
- Edexcel GCSE. Mathematics (Linear). Paper 1. 6 June 2011
- Edexcel GCSE. Mathematics (Linear). Paper 2. 10 June 2011
- Edexcel GCSE. Mathematics (Linear). Paper 3. 6 June 2011
- Edexcel GCSE. Mathematics (Linear). Paper 4. 10 June 2011
GCSE OCR past papers. January 2009
- OCR GCSE. Mathematics Syllabus A. Paper 1 (Foundation Tier). 9 January 2009
- OCR GCSE. Mathematics Syllabus A. Paper 2 (Foundation Tier). 14 January 2009
- OCR GCSE. Mathematics Syllabus A. Paper 3 (Higher Tier) 9 January 2009
- OCR GCSE. Mathematics Syllabus A. Paper 4 (Higher Tier). 14 January 2009
Варианты экзамена IGCSE / IGCSE maths past papers
Pearson Edexcel International GCSE. January 2019
- Pearson Edexcel IGCSE. Level 1/2. Paper 1F. Foundation Tier. January 2019
- Pearson Edexcel IGCSE. Level 1/2. Paper 1H. Higher Tier. January 2019
- Pearson Edexcel IGCSE. Level 1/2. Unit 2F. January 2019
- Pearson Edexcel IGCSE. Level 1/2. Unit 2H. January 2019
Cambridge IGCSE May/June 2018
- Cambridge international mathematics. Paper 1 (Core). May/June 2018
- Cambridge international mathematics. Paper 2 (Extended). May/June 2018
- Cambridge international mathematics. Paper 3 (Core). May/June 2018
- Cambridge international mathematics. Paper 4 (Extended). May/June 2018
- Cambridge international mathematics. Paper 5 (Core). May/June 2018
- Cambridge international mathematics. Paper 6 (Extended). May/June 2018
Edexcel IGCSE June 2011
- Edexcel IGCSE. Mathematics A. Paper 1F. 6 June 2011
- Edexcel IGCSE. Mathematics A. Paper 2F. 10 June 2011
- Edexcel IGCSE. Mathematics A. Paper 3H. 6 June 2011
- Edexcel IGCSE. Mathematics A. Paper 4H. 10 June 2011
Записаться на занятия математикой на английском языке для поступления в зарубежную школу или для подготовки к международным экзаменам и задать мне любые интересующие Вас вопросы можно по телефону 8-905-741-62-46 или email info@mathconsult.ru .
Contents
- What papers are in a maths GCSE?
- What is the difference between GCSE maths foundation and higher?
- How many papers are in Maths GCSE?
- Where to find maths GCSE past papers?
- Maths GCSE past paper for AQA
- Maths GCSE past paper for Eduqas
- Maths GCSE past paper for Edexcel
- Maths GCSE past paper for OCR
- Maths GCSE past paper for WJEC
- Maths GCSE past paper for CCEA
Your GCSE maths exam is fast approaching and you’ve found out that practicing with GCSE maths past papers is one of the most effective ways to reach the highest grade.
In 2021 6% of students in England achieved grade 9 in their mathematics GCSE. With our top tips and links to GCSE maths past papers, there’s no reason why you can’t aim for the highest maths GCSE grades possible too.
What papers are in a maths GCSE?
Different exam boards have different papers, and they can vary quite drastically so it’s important that you understand exactly which papers you’ll be taking on the exam day.
The best way to find out is to ask your maths teacher which exam board you are studying for, they will probably say either AQA, Eduqas, Edexcel, OCR, WJEC or CCEA.
Exam boards also offer a ‘foundation’ paper or a ‘higher’ paper so be sure that you know which paper you’ll be taking. You’ll also be taking a mix of calculator and non-calculator papers.
What is the difference between GCSE maths foundation and higher?
Foundation tier GCSE maths paper:
- Less content to learn
- The maximum possible grade is 5
Higher tier GCSE maths paper:
- More content to cover which is harder
- The maximum possible grade is 9
The tier that you take for your maths GCSE will influence your further studies so it’s a decision that your teacher should guide based on their understanding of your abilities.
How many papers are in Maths GCSE?
This depends on the exam board that has written your maths GCSE exam. Once you know your exam board, you can find out how many papers you’ll need to take.
For the Eduqas exam board, you will need to take two GCSE maths GCSE papers. This is true whether you are studying for the foundation tier or higher tier exam.
For OCR, Edexcel, and AQA whether studying foundation or higher maths GCSE, you will need to take three Maths GCSE papers, two are with a calculator, and one is a non-calculator.
Within each tier of maths GCSE paper for WJEC there are two maths GCSE papers. For one paper a calculator is allowed and for the other paper, you are not allowed a calculator.
WJEC is unlike the other exam boards as there are three tiers of difficulty rather than the usual foundation and higher tiers, these tiers are:
1. Foundation
2. Intermediate
3. Higher
Make sure that you are practicing for the right tier!
For CCEA GCSE Maths, whether you are studying for the foundation tier or higher tier, you will need to take six maths GCSE papers. Four of the papers is with a calculator, and two papers are without a calculator.
Let’s summarise how many papers are in your maths GCSE below:
|
Exam board |
Number of maths GCSE papers |
|
AQA |
3 |
|
Eduqas |
2 |
|
Edexcel |
3 |
|
OCR |
3 |
|
WJEC |
2 |
|
CCEA |
6 |
Where to find maths GCSE past papers?
The best place to find GCSE maths past papers is on the official website of your exam board for your maths GCSE exam. Exam boards post online their previous years’ GCSE past papers for every subject online for free. Even more helpful is that exam boards provide the marking scheme too. So you have all of the resources available to practice GCSE maths past papers under exam conditions and to mark them afterward too.
Maths GCSE past paper for AQA
Find your tier below and click to download the past paper:
- 2020 Foundation Tier, non-calculator
- 2020 Foundation Tier, calculator (1)
- 2020 Foundation Tier, calculator (2)
- 2020 Higher Tier, non-calculator
- 2020 Higher Tier, calculator (1)
- 2020 Higher Tier, calculator (2)
- 2019 Foundation Tier, non-calculator
- 2019 Foundation Tier, calculator (1)
- 2019 Foundation Tier, calculator (2)
- 2019 Higher Tier, non-calculator
- 2019 Higher Tier, calculator (1)
- 2019 Higher Tier, calculator (2)
- 2018 Foundation Tier, non-calculator
- 2018 Foundation Tier, calculator (1)
- 2018 Foundation Tier, calculator (2)
- 2018 Higher Tier, non-calculator
- 2018 Higher Tier, calculator (1)
- 2018 Higher Tier, calculator (2)
Maths GCSE past paper for Eduqas
Find your tier below and click to download the past paper:
- 2020 Foundation Tier, non-calculator
- 2020 Foundation Tier, calculator
- 2020 Higher Tier, non-calculator
- 2020 Higher Tier, calculator
- 2019 Foundation Tier, non-calculator
- 2019 Foundation Tier, calculator
- 2019 Higher Tier, non-calculator
- 2019 Higher Tier, calculator
- 2018 Foundation Tier, non-calculator
- 2018 Foundation Tier, calculator
- 2018 Higher Tier, non-calculator
- 2018 Higher Tier, calculator
Maths GCSE past paper for Edexcel
Find your tier below and click to download the past paper:
- 2020 Foundation Tier, non-calculator
- 2020 Foundation Tier, calculator (1)
- 2020 Foundation Tier, calculator (2)
- 2020 Higher Tier, non-calculator
- 2020 Higher Tier, calculator (1)
- 2020 Higher Tier, calculator (2)
- 2019 Foundation Tier, non-calculator
- 2019 Foundation Tier, calculator (1)
- 2019 Foundation Tier, calculator (2)
- 2019 Higher Tier, non-calculator
- 2019 Higher Tier, calculator (1)
- 2019 Higher Tier, calculator (2)
- 2018 Foundation Tier, non-calculator
- 2018 Foundation Tier, calculator (1)
- 2018 Foundation Tier, calculator (2)
- 2018 Higher Tier, non-calculator
- 2018 Higher Tier, calculator (1)
- 2018 Higher Tier, calculator (2)
Maths GCSE past paper for OCR
Find your tier below and click to download the past paper:
- 2020 Foundation Tier, non-calculator
- 2020 Foundation Tier, calculator (1)
- 2020 Foundation Tier, calculator (2)
- 2020 Higher Tier, non-calculator
- 2020 Higher Tier, calculator (1)
- 2020 Higher Tier, calculator (2)
- 2019 Foundation Tier, non-calculator
- 2019 Foundation Tier, calculator (1)
- 2019 Foundation Tier, calculator (2)
- 2019 Higher Tier, non-calculator
- 2019 Higher Tier, calculator (1)
- 2019 Higher Tier, calculator (2)
- 2018 Foundation Tier, non-calculator
- 2018 Foundation Tier, calculator (1)
- 2018 Foundation Tier, calculator (2)
- 2018 Higher Tier, non-calculator
- 2018 Higher Tier, calculator (1)
- 2018 Higher Tier, calculator (2)
Maths GCSE past paper for WJEC
Find your tier below for the WJEC GCSE mathematics papers and click to download the past paper:
- 2020 Foundation Tier, non-calculator
- 2020 Foundation Tier, calculator
- 2020 Intermediate Tier, non-calculator
- 2020 Intermediate Tier, calculator
- 2020 Higher Tier, non-calculator
- 2020 Higher Tier, calculator
- 2019 Foundation Tier, non-calculator
- 2019 Foundation Tier, calculator
- 2019 Intermediate Tier, non-calculator
- 2019 Intermediate Tier, calculator
- 2019 Higher Tier, non-calculator
- 2019 Higher Tier, calculator
- 2018 Foundation Tier, non-calculator
- 2018 Foundation Tier, calculator
- 2018 Intermediate Tier, non-calculator
- 2018 Intermediate Tier, calculator
- 2018 Higher Tier, non-calculator
- 2018 Higher Tier, calculator
Maths GCSE past paper for CCEA
Whether you are taking the foundation or higher tier maths GCSE, you will need to take six papers. Before 2019 there were four papers and the modules had different names too.
Since 2019 the Foundation modules are: M1, M2, M5 and M6
Higher modules are: M3, M4, M7 and M8
Find your tier below and click to download the past paper:
- 2020 Foundation Tier, M1, calculator
- 2020 Foundation Tier, M2, calculator
- 2020 Foundation Tier, M5, non-calculator
- 2020 Foundation Tier, M5 (2), calculator
- 2020 Foundation Tier, M6, non-calculator
- 2020 Foundation Tier, M6 (2), calculator
- 2020 Higher Tier, M3, calculator
- 2020 Higher Tier, M4, calculator
- 2020 Higher Tier, M7, non-calculator
- 2020 Higher Tier, M7 (2), calculator
- 2020 Higher Tier, M8, non-calculator
- 2020 Higher Tier, M8 (2), calculator
- 2019 Foundation Tier, M1, calculator
- 2019 Foundation Tier, M2, calculator
- 2019 Foundation Tier, M5, non-calculator
- 2019 Foundation Tier, M5 (2), calculator
- 2019 Foundation Tier, M6, non-calculator
- 2019 Foundation Tier, M6 (2), calculator
- 2019 Higher Tier, M3, calculator
- 2019 Higher Tier, M4, calculator
- 2019 Higher Tier, M7, non-calculator
- 2019 Higher Tier, M7 (2), calculator
- 2019 Higher Tier, M8, non-calculator
- 2019 Higher Tier, M8 (2), calculator
For further support with your maths GCSE, book a free trial lesson with a GoStudent tutor who can help you to reach your full potential in maths.
P1B
GCSE, Russian
21 revision cards
Colours
GCSE, Russian
20 flashcards
Search again
Resource type:
-
Flashcards (8)
Small question and answer cards, perfect for testing your memory.
-
Past papers (3,858)
Real past papers and mark schemes to help you prepare for exams.
-
Crosswords (6)
Take a break with revision themed crosswords.
-
Quizsearches (6)
A wordsearch that requires you to answer revision questions first.
-
Revision cards (5)
Small cards (A5) useful for revising key topics and facts.
-
Quizzes (4)
Timed multiple choice quizzes for checking your revision.
-
Mindmaps (2)
A series of connected nodes useful for charting relationships within a topic.
-
Revision notes (1)
In-depth revision and class notes on subjects and topics.
-
Shared resources (1)
Class notes, video lessons, slideshows and podcasts shared by our members.
Click on the relevant GCSE subject below to go straight to the quizzes
GCSE quizzes written by teachers for years 10 and 11 of the curriculum. Say goodbye to monotonous worksheets and say hello to faster and more effective revision.
The General Certificate of Education suite of exams are perhaps the most important set of tests a student will take.
For an in-depth look at GCSE have a read of our GCSE Explained article.
Many exams will follow if students decide to pursue A-Levels and a university degree, but these are the first large set of exams students face, knowing their future depends on it.
Our What Does Secondary School Entail? will take you through the Secondary School journey. For more specific details about the National Curriculum at Secondary School, take a look at our Subjects at Secondary School page.
Phew. Let’s just take a breather shall we? It’s getting a little hot in here.
You already know that this stage of your education is extremely important. You also know that good grades won’t just fall out of the sky (if only they did). It takes work to land those high grades on that fateful piece of results paper, but that doesn’t mean revision has to be laborious. Often, where students go wrong is they subject themselves to revision that doesn’t engage them, and it can produce underwhelming results. Long revision sessions can amount to not very much at all, if it’s not the correct revision.
The English Baccalaureate (EBacc)
If your child is studying the EBacc and you want to know what it entails, have a read of our What is the English Baccalaureate? page.
GCSE Revision Boredom
When revising, boredom can happen in an instant. Before you know it, what should have been a revision session has turned into a TV show marathon… now what?
When it comes to revision, it’s natural for minds to wander. There’s so much information to retain and so many distractions at hand. The problem of boredom is an important one and one that has to be listened to. If students aren’t engaged, they won’t learn. So, how can focus be brought to this type of revision? How can students find something engaging while still learning the core curriculum? We’re glad you asked.
Exam revision is notoriously difficult to get into, especially at GCSE level. Get some tips in our What is the Best Way to Revise for GCSE Exams? article.
How Education Quizzes Works
Here at Education Quizzes, we provide engaging and relevant material for students, in order to help them revise key subjects. We have quizzes on English, maths, science and more, ready and waiting for students to dive into. Each quiz has ten questions, with helpful feedback after each one. In adddition, most of the quizzes have a handy link at the bottom to the relevant BBC Bitesize page. It’s a revision dream! We keep students on their toes and students stay focussed.
«It’s a quick way to find out where there are gaps in your knowledge and improve on them.» — Jenny, Parent Reviewer
Don’t Banish the Screens
With our quizzes on hand to help, students can turn screen time into revision time, and lose themselves in revision that actually engages them. The great thing is, revision doesn’t have to be a solo event. Gone are the days when students have to read textbook after textbook in a silent room — students can come together to help each other revise in a way that won’t leave them bored or unstimulated.
Short, Sweet but Seriously Clever
By keep our quizzes short, but packed with information, revision sessions can be more focussed, without being boring. We give students the chance to engage with material, rather than just read page after page, only to skip back a few paragraphs because nothing has sunk in…
Our revision quizzes are written by teachers and concentrate on the essential knowledge students need for exam success. Access the entire suite of quizzes for just £9.99 per month or £49.99 per year. When you consider how much some pay for tutors, and that we cover most subject areas, there really is little to deliberate!
GCSE maths questions have always been a popular part of the online lessons and maths revision resources that Third Space Learning has developed for secondary schools. Here we provide 25 of these to give students and teachers a flavour of the full range of question types you’ll need to be familiar with.
All the exam questions have been inspired by real life questions that have appeared in past papers for the AQA, OCR and Edexcel GCSE. Many of the questions are written in a diagnostic quiz format with several multiple choice options that have been designed to highlight key misconceptions and all questions come with answers.
To accompany the blog there is also a free downloadable worksheet of all 25 GCSE maths questions and answers. Third Space Learning also offers a wide range of GCSE maths worksheets and GCSE maths past papers.
Varied challenge level
GCSE papers need to be accessible to students with a wide range of abilities. This enables the exam boards to produce a distribution of results in order to calculate appropriate GCSE grade boundaries. Therefore, every exam paper will have questions which can present challenges to students.
Elements that can increase the difficulty of the question include:
- the language in the question,
- presenting a topic in an unfamiliar context,
- limited structure and guidance,
- interleaving of skills.
In the following GCSE exam questions, you will find questions for a range of key GCSE maths topics from Grade 9 to foundation. The level of difficulty for each GCSE maths question has been determined by:
- the complexity of the question,
- common errors students are likely to make on a question,
- how many students are likely to be able to access the question,
- my own experience preparing students for GCSE maths exams for many years.
Grade 8 and Grade 9 style GCSE maths questions
These GCSE questions require a secure set of mathematical skills and accuracy in applying them. The questions may look simple in their presentation, but they require key skills to be carefully selected and applied. These are skills very often revisited as an introduction to an A Level maths course.
1. Factorising maths question
(a) Factorise d^{2} – e^{2}
(b) Hence, or otherwise, simplify fully
(x^{2} + 8)^{2} – (x^{2} – 4)^{2}
Which is the correct answer?
A) (x + 8)(x – 4)
B) x^{2} + 12
C) x^{2} + 4
D) 24x^{2} + 48
Calculator
Show answer
Answers
(a) (d+e)(d-e)
(1 mark)
(b) D) 24x^{2} + 48
(3 marks)
Answer explanation
For b) students may not use the difference of two squares as they did in part a) and proceed to try and expand then simplify the brackets. While this is a correct method, it is a longer process and is therefore subject to potential errors. In order to spot the more efficient method of the difference of two squares, students first have to recognise part b) is in the same form as part a) and that it can be rewritten in the form (x2 + 8 − x2 + 4)(x2 + 8 + x2 − 4).
Next, the algebra needs to be simplified with extra care needed to ensure that the negative and positive signs are correct. Finally, the student needs to decide how to present the fully simplified answer.
For more GCSE maths questions take a look at our free Factorising lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
2. Surds maths question
Show that frac{2sqrt{14}}{sqrt{5}}-frac{sqrt{7}}{sqrt{10}} can be written in the form frac{asqrt{b}}{10}
Where a and b are integers.
Which is the correct answer?
A) frac{3sqrt{7}}{10}
B) frac{3sqrt{70}}{10}
C) frac{2sqrt{7}}{10}
D) frac{sqrt{7}}{sqrt{10}}
Non-calculator
Show answer
Answer
B) frac{3sqrt{70}}{10}
(3 marks)
Answer explanation
This question requires confidence with subtracting fractions and manipulating surds. There are various methods to completing this question, but the easiest way is to multiply the numerator and denominator of the first fraction by √2 so that both fractions have a common denominator of √10. This can present difficulties as the numerator could be multiplied by 2 rather than √2. Students then need to recognise that once both fractions have common denominators, they can simply subtract the surds on the numerator.
Finally, they need to rationalise the denominator by multiplying the numerator and denominator by √10 and simplifying.
For more GCSE maths questions take a look at our free Surds lesson and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
3. Algebraic fractions maths question
2-frac{x+2}{x-3}-frac{2 x-5}{x+3} can be written as a single fraction in the form frac{ax^{2}+b x+c}{x^{2}-9}
Where a and b are integers.
Work out the value of a and the value of b and c .
Calculator
Show answer
Answer
=frac{2(x-3)(x+3)-(x+2)(x+3)-(2 x-5)(x-3)}{(x+3)(x-3)}
(1 mark)
=frac{2left(x^2-9right)-left(x^2+5 x+6right)-left(2 x^2-6 x-5 x+15right)}{x^2-9}
=frac{2 x^2-18-x^2-5 x-6-2 x^2+11 x-15}{x^2-9}
(1 mark)
=frac{-x^2+6 x-39}{x^2-9}
(1 mark)
a=-1, b=6, c=-39
(1 mark)
Answer explanation
Students need to be confident with a variety of skills including order of operations, subtracting fractions and integers, expanding brackets and simplifying. There are a variety of mistakes that can be made when expanding brackets and simplifying the fractions. It is important to consider the effect of negative signs when subtracting brackets.
For more GCSE maths questions take a look at our free Algebraic fractions lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.

Set of 25 Printable GCSE Maths Questions
Try these challenging GCSE maths questions with your students in class. They all include answers on a separate page and are organised by difficulty!
Hard GCSE maths questions
The following GCSE maths questions have been selected to highlight the more unusual way they are presented. This can lead to assumptions being made about the question, which may lead to an incorrect approach.
4. Quadratic graphs maths questions
The diagram shows part of the graph y = x^{2} – 3x + 4 .
(a) By drawing a suitable line, use your graph to find estimates for the solutions of x^{2} – 2x -1 = 0 .
P is a point of the graph y = x^{2} – 3x + 4 where x = 4 .
(b) Calculate an estimate for the gradient of the graph at the point P .
Show answer
Answers
(a) x = 2.4, -0.4
(2 marks)
(b) Answers around 4
(3 marks)
Answer explanation
Students may try to solve the equation by attempting to factorise or use the quadratic formula. However, as the question states, to use the graph, students need to compare the equation of the graph with the equation given in a) and identify what has changed. They need to identify that the x value has decreased by 1 and the constant value has increased by 5. Therefore, they need to accurately plot the line y = − x + 5 on the graph. Finally, they need to remember that the two solutions are found at the two intersection points.
Part b) is a more challenging question as they need to find appropriate points either side of the point P to calculate the gradient.
For more GCSE maths questions take a look at our free Quadratic graphs lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
5. Nth term maths question
The n th of a sequence is given by an^{2} + bn where a and b are integers.
The 3rd term of the sequence is 3 .
The 6th term of the sequence is 42 .
Find the 5th term of the sequence.
Which is the correct answer?
A) 29
B) 5
C) 25
D) 18
Show answer
Answer explanation
Students need to construct the two equations by substituting n = 3 and n = 6 in an2 + bn in order to produce a pair of simultaneous equations which can then be solved. After calculating the values of a and b, students need to remember to finish the question by substituting ‘5’ into the nth term.
For more GCSE maths questions take a look at our free Nth term lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
6. Algebraic fractions maths question
Solve frac{4x+1}{4}-frac{2x+1}{3}=frac{1-x}{6}
Which is the correct answer?
A) x = 0.5
B) x = -0.5
C) x = – 5
D) x = 12
Calculator
Show answer
Answer
A) x = 0.5
(4 marks)
Answer explanation
Fractions can present difficulties for both higher and foundation students. As this question gives two fractions subtracting to give a third, students may attempt to find a common denominator for all three fractions in the first step. When subtracting the fractions, students must take care to insert brackets and/or multiply every term. E.g. if 4x + 1 is multiplied by 3, this should be 3(4x + 1) or 12x + 3.
A common mistake would be to not multiply the term that is outside the bracket by every term inside the bracket.
For more GCSE maths questions take a look at our free Algebraic fractions lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
GCSE higher maths questions
These GCSE maths questions appear on the higher tier paper and draw on a range of skills. They often lack structure and hints, and require the student to confidently work out what is required to work out the solution.
7. Venn diagram maths question
60 people were asked if they spoke French, German or Italian.
Of these people,
- 21 speak French
- 1 speaks French, German and Italian
- 4 speak French and Italian but not German
- 7 speak German and Italian
- 18 do not speak any of the languages
- All 11 people who speak German speak at least one other language.
Two of the 60 people are chosen at random. Work out the probability that they both only speak French.
Which is the correct answer?
A) frac{12}{60}
B) frac{13}{295}
C) frac{1}{25}
D) frac{11}{295}
Calculator
Show answer
Answer
D) frac{11}{295}
(5 marks)
Answer explanation
Students need to recognise that this question requires a 3-way Venn diagram as it could easily be mistaken for a two-way table question. Extracting the correct meaning from the language used in the question can present a challenge in order to place the numbers correctly in the diagram or calculate missing values.
To answer the final question, they need to correctly identify the probability that the person speaks only French and multiply these probabilities.
For more GCSE maths questions take a look at our free Venn diagram lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
8. Quadratic equations maths question
In the diagram, the square and the trapezium share a common side length of x cm.
The area of the square is equal to the area of the trapezium.
Work out the value of x .
Which is the correct answer?
A) 12 cm
B) 6 cm
C) 64 cm
D) 8 cm
Calculator
Show answer
Answer
A) 12 cm
(6 marks)
Answer explanation
Students often find forming equations difficult. After recognising that they need to form a quadratic equation, they need to apply the formula for the area of a trapezium (one which students often struggle to recall). Once they have successfully constructed the correct equation, they then need to rearrange it to make the equation equal to 0 and then factorise.
A common mistake that is made when students see terms on each side of the equals sign, is that they attempt to solve as though it is a linear equation. Once the equations have been correctly solved, they need to interpret their solutions by only selecting the positive result. This is because it is impossible to have a negative distance for a side length.
For more GCSE maths questions take a look at our free Quadratic equations lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
9. Area of a circle maths question
A square with sides of length x mm, is inside a circle.
Each vertex of the square is on the circumference of the circle.
The area of the circle is 64 mm ^{2} .
Work out the value of x .
Give your answer correct to 3 significant figures.
Which is the correct answer?
A) 4.51 mm
B) 20.35 mm
C) 6.38 mm
D) 40.74 mm
Calculator
Show answer
Answer
C) 6.38 mm
(4 marks)
Answer explanation
The first challenge with this question is the absence of a diagram. Students need to interpret the question correctly and create their own diagram. Students need to recall the formula for area of a circle and rearrange it to calculate the radius, which is also the distance from the centre of the square to one of its vertices.
Students are required to know that the diagonal lines within a square are perpendicular and therefore need to apply Pythagoras’ theorem to calculate the side length of the square. Finally, it is important they correctly round their answer to 3 significant figures.
For more GCSE maths questions take a look at our free Area of a circle lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
10. Rearranging formulae maths question
Make b the subject of the formula c=frac{25(a-3b)}{b}
Which is the correct answer?
A) b=frac{cb-25a}{3}
B) b=frac{25a}{c+75}
C) b=frac{a}{c+75}
D) b=frac{c b-25 a}{-75}
Calculator
Show answer
Answer
B) b=frac{25a}{c+75}
(3 marks)
Answer explanation
A rearranging question where the subject appears twice will be accessible to more able students. However, this question has some unfamiliar elements compared to the usual rearranging questions which require factorising, due to the placing of the brackets and b appearing on its own as the denominator.
For more GCSE maths questions take a look at our free Rearranging formulae lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
11. Tree diagrams maths question
David has two spinners, spinner A and spinner B.
Each spinner can only land on blue or green.
The probability that spinner A will land on blue is 0.25.
The probability that spinner B will land on green is 0.8.
The probability tree diagram shows this information.
David spins spinner A and spinner B together.
He does this a number of times.
The number of times both spinners land on blue is 40.
Work out an estimate for the numbers of times both spinners land on green.
Which is the correct answer?
A) 800
B) 64
C) 128
D) 480
Calculator
Show answer
Answer explanation
Tree diagram questions can be straightforward for students to identify what to do, but this question has a twist as students need to understand the calculation within a tree diagram in order to work backwards and calculate how many times the spinner was spun. Relative frequency is disguised in this question rather than a typical part a) complete the tree diagram part b) calculate the probability.
For more GCSE maths questions take a look at our free Tree diagrams lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
12. Circle theorems maths question
W , X , Y and Z are four points on the circumference of a circle.
WCY and XCZ are straight lines.
Prove that triangle CWX and triangle CYZ are similar.
You must give reasons for each stage of your working.
Calculator
Show answer
Answer
Angle WXC = Angle CYZ because angles in the same segment are equal.
Angle XWC = Angle CZY because angles in the same segment are equal.
Angle WCX = Angle ZCY because vertically opposite angles are equal.
(We only need two of these angles as we can calculate the third by using the fact that angles in a triangle add to 180 degrees.)
(3 marks)
Answer explanation
Students need to identify the word ‘similar’ and understand its significance in this question. Students often struggle with ‘prove’ type questions and it is common for them to be unsure how to set out their working. Ensuring students are confident with angle notation and how to recall the circle theorems are essential.
Modelling how this style of question should be set out using very logical steps with angle and reasons side by side can be beneficial.
For more GCSE maths questions take a look at our free Circle theorems lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
13. Direct and inverse proportion maths question
y is inversely proportional to t^{2}
When t = 3 , y = 4 .
t is directly proportional to x^{2}
When x = 2 , t = 8 .
Find a formula for y in terms of x .
Give your answer in its simplest form.
Which is the correct answer?
A) y=frac{9}{x^{2}}
B) y=frac{9}{x^{4}}
C) y=frac{18}{x^{2}}
D) y=frac{18}{x^{4}}
Non-calculator
Show answer
Answer
B) y=frac{9}{x^{4}}
(5 marks)
Answer explanation
Students must be confident with finding the value of the constant for each equation and apply the powers. They need to recognise how to substitute the second equation into the first, taking care to make it ‘t =’ and not ‘y =’, then simplify the fraction.
For more GCSE maths questions take a look at our free Direct and inverse proportion lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
14. Standard form maths question
Use the formula F=frac{s}{sqrt{tm}} to find the value of F when
s = 6.2 × 10^{9}
t = 4.3 × 10^{8}
m = 3.6 × 10^{-3}
Give your answer in standard form, correct to 2 significant figures.
Which is the correct answer?
A) 5.0 × 10^{6}
B) 4.9 × 10^{2}
C) 4.0 × 10^{4}
D) 4.9 × 10^{4}
Calculator
Show answer
Answer
A) 5.0 × 10^{6}
(3 marks)
Answer explanation
This is a calculator paper question, so if students are confident with efficient use of their scientific calculator and correctly insert brackets where they are needed, they can enter the calculation to work it out. However, this is often subject to errors and if they work through the calculation in stages, they need to consider the order of operations and understand the effect of square rooting on the powers.
For more GCSE maths questions take a look at our free Standard form lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
15. Histograms maths question
The histogram shows information about the weights of some letters handled by a delivery company in one week.
Sam says:
“There are more letters weighing between 20 g and 60 g than letters weighing between 60 g and 100 g.”
Is Sam correct?
Show how you decide.
Calculator
Show answer
Answer
Sam is wrong.
Number of letters between 20 g and 60 g = 20 × 17.5 + 20 × 30 = 950
Number of letters between 60 g and 100 g = 30 × 20 + 10 × 40 = 1000
(4 marks)
Answer explanation
Students need to understand that the height of the bars is frequency density. Therefore, they need to calculate the area of the bars to calculate the frequencies and then compare the values. Once frequency has been calculated, these sorts of questions can then relate to other frequency-related question types, such as averages from a frequency table and cumulative frequency.
For more GCSE maths questions take a look at our free Histograms lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
16. Straight line graphs maths question
A straight line graph goes through points
( a , b ) and ( c , d ), where
a + 3 = c
b + 6 = d
Find the gradient of the line.
Which is the correct answer?
A) 2
B) 3
C) 6
D) ½
Non-calculator
Show answer
Answer explanation
Students need to know how to calculate the gradient between two coordinate points and then correctly identify the x and y coordinates. This question can easily become overly complicated, but with some simple rearranging to find d – b = 6 and c – a = 3, it is possible to calculate the gradient in a few steps. With four unknowns, students could easily become confused and think that the gradient is given as a formula.
However, it may also be that students can guess the answer to this question. Other question types could involve calculating the midpoint of two coordinates, or working out the equation of the straight line that passes through them, or is parallel or perpendicular to them.
For more GCSE maths questions take a look at our free Straight line graphs lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
Grade 4 and Grade 5 style GCSE maths questions
The following GCSE maths questions are all questions that appear on both the higher and foundation paper, so are targeted at Grade 4 and Grade 5 students. Questions that solely appear on the foundation paper have not been selected as they tend to have simpler underlying structures or provide structure.
Read more: Question Level Analysis Of Edexcel Maths Past Papers (Foundation)
17. Pythagoras’ theorem maths question
This rectangular frame is made from 5 straight pieces of wood.
The weight of the wood is 2.5 kg per metre.
Work out the total weight of the metal in the frame.
Which is the correct answer?
A) 5 kg
B) 17.5 kg
C) 19 kg
D) 47.5 kg
Non-calculator
Show answer
Answer
D) 47.5 kg
(5 marks)
Answer explanation
The numbers and calculations required for this question are straightforward. However, as it is a non-calculator paper, it presents some extra challenges. Students must identify that use of Pythagoras’ theorem is required, which can be unexpected on a non-calculator paper, despite the use of Pythagorean triples here. This question uses multiple skills including Pythagoras’ theorem, perimeter and multiplying decimals.
For more GCSE maths questions take a look at our free Pythagoras theorem lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
18. Parallel lines maths question
The equation of the line L_{1} is y = 5x – 1 .
The equation of the line L_{2} is 5y – 25x + 4 = 0 .
Show that these two lines are parallel.
Non-calculator
Show answer
Answer
Rearrange L_{2} to make y the subject.
begin{aligned}
5 y-25 x+4 &=0 \
5 y &=25 x-4 \
y &=5x-frac{4}{5}
end{aligned}
L_{1} and L _{2} have the same gradient so they are parallel.
(2 marks)
Answer explanation
Students may make a mistake in thinking that the x coefficient always indicates the gradient and when given two equations, if these coefficients are equal, then the lines are parallel. In this question, the fact that the first equation has ‘5x’ term and the second has ‘5y’ term could be mistaken as an indication that the two lines have the same gradient.
The second equation requires rearranging and dividing the whole equation by 5, which presents a fraction for the y-intercept value.
For more GCSE maths questions take a look at our free Parallel lines lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
19. Lowest common multiple and highest common factor maths questions
(a) Find the lowest common multiple (LCM) of
30 and 54.
Which is the correct answer?
A) 270
B) 1620
C) 6
D) 540
(b) Write down the highest common factor (HCF) of
A and B .
A = 2^{2} × 3^{2} × 5
B = 2^{2} × 3 × 5^{2}
Which is the correct answer?
A) 60
B) 54000
C) 900
D) 120
Calculator
Show answer
Answers
(a) A) 270
(2 marks)
(b) A) 60
(1 mark)
Answer explanation
Students will often try to list multiples of each number until they find a common multiple. This can be a laborious process and is therefore subject to arithmetic errors. The most efficient method is to write each number as a product of its prime factors.
For more GCSE maths questions take a look at our free Lowest common multiple and Highest common factor lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
20. Venn diagrams maths question
This diagram represents students in a year group who study Geography (G) or History (H).
How many students study both Geography and History?
Which is the correct answer?
A) Not enough information to tell
B) All of them
C) None of them
D) Half of them
Non-calculator
Show answer
Answer
C) None of them
(1 mark)
Answer explanation
This style of question can be unfamiliar to students as Venn diagrams are almost always presented as overlapping circles. Students may not recognise this as a Venn diagram, and therefore may be unlikely to identify that the sets are independent of each other and share no data.
For more GCSE maths questions take a look at our free Venn diagrams lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
21. Solving equations maths question
sqrt{3^{2}+4^{2}}=^{3}sqrt{125b^{3}}
Work out the value of b .
Which is the correct answer?
A) 1
B) 5
C) 2
D) 25
Non-calculator
Show answer
Answer explanation
Students need to be confident using square numbers, cube numbers and how to correctly apply square and cube roots. The question can appear to be challenging upon first inspection, but once the powers and roots have been simplified, it is an easy question to solve.
For more GCSE maths questions take a look at our free Solving equations lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
22. Trigonometry maths question
XYZ is a right-angled triangle.
XZ = 15 cm.
Angle Z = 90° .
Size of angle ZYX : size of angle YXZ = 3:2 .
Work out the length of XY .
Give your answer correct to 3 significant figures.
Which is the correct answer?
A) 18.5 cm
B) 12.1 cm
C) 14.5 cm
D) 25.5 cm
Calculator
Show answer
Answer
A) 18.5 cm
(4 marks)
Answer explanation
With the absence of angles YXZ and XYZ on the diagram, students need to firstly identify this as a trigonometry question and calculate the missing angles using the ratio. This then allows them to decide which trigonometric function to use. Finally, students need to correctly round their answer to 3 significant figures.
Higher graded questions on trigonometry can include using the Sine Rule, the Cosine Rule and calculating the area of any triangle using the formula ½abSinC.
For more GCSE maths questions take a look at our free Trigonometry lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
23. Order of operations (BIDMAS) maths question
Sam is using these numbers to make a new number.
He can only use brackets, +, −, ×, ÷ once.
He cannot use any number more than once.
He cannot use powers.
He cannot put numbers together
e.g. he cannot use ‘147’.
What is the biggest number he can make?
Show how he can make this number.
Which is the correct answer?
A) 144
B) 132
C) 336
D) 51
Calculator
Show answer
Answer explanation
There are multiple aspects to this question that need to be interpreted. and it requires a good understanding of the order of operations and place value. This must then be communicated clearly to obtain full marks. It could be assumed that multiplying all the numbers will find the largest result but the presence of the number ‘1’ is what alters this and requires the application of the order of operations.
For more GCSE maths questions take a look at our free Order of operations (BIDMAS) lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
24. Formulae maths question
A puma is running with a velocity of 2 m/s.
It then accelerates at 3 m/s ^{2} for 5 seconds.
Use the formula
v = u + at
to work out the final velocity of the puma.
Which is the correct answer?
A) 13 m/s
B) 17 m/s
C) 11 m/s
D) 10 m/s
Show answer
Answer
B) 17 m/s
(2 marks)
Answer explanation
The first challenge is that students have to identify the values of u, a and t from the information, and this requires an understanding of the formula and velocity. Compound measures such as speed and density are often covered at foundation GCSE, but rarely expressed as acceleration and velocity.
For more GCSE maths questions take a look at our free Formulae lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
See also: GCSE maths formulas
25. Density maths question
The density of orange juice is 1.02 grams per cm ^{3} .
The density of fruit syrup is 1.5 grams per cm ^{3} .
The density of lemonade is 0.95 grams per cm ^{3} .
30 cm ^{3} of orange juice is mixed with 20 cm ^{3} of fruit syrup and 150 cm ^{3} of lemonade to make a drink.
Work out the density of the drink.
Give your answer correct to 2 decimal places.
Which is the correct answer?
A) 3.47 g/cm ^{3}
B) 203.1 g/cm ^{3}
C) 1.02 g/cm ^{3}
D) 0.98 g/cm ^{3}
Calculator
Show answer
Answer
C) 1.02 g/cm ^{3}
(4 marks)
Answer explanation
At a glance, this looks simple as students may think that they just need to total the densities of each part. However, they need to work out the mass of each part in order to calculate the total mass and total volume of the drink before calculating the total density. It is important to set out the calculations clearly.
Organising the information as a two-way table is an effective way of simplifying the problem. Students need to correctly round their solution to 2 decimal places.
For more GCSE maths questions take a look at our free Density lessons and for more personalised support schools can plug gaps with our targeted one-to-one interventions.
What topics are in maths GCSE?
The GCSE maths topics are:
• Number including fractions, decimals and percentages
• Algebra including equations, nth term etc.
• Geometry and measure including trigonometry
• Ratio and proportion including exchange rates
• Probability including frequency
• Statistics including pie chart
Is GCSE maths difficult?
No, GCSE maths is not difficult if you are sitting the right exam and you have prepared. There are two GCSE exams – the foundation paper and the higher paper. The higher paper is more difficult. GCSE maths papers need to be accessible to students with a wide range of abilities. Therefore, every exam paper will have questions that can present difficulties to students.
The main elements that can increase the difficulty of a question include:
• The language of the question
• Presenting a topic in an unfamiliar context
• Limited structure and guidance
• Interleaving of skills
To help overcome initial difficulties, it is useful to be aware of these different elements when you first approach a GCSE question. Try to overlook your first concerns and identify the question they are asking you.
How do you answer GCSE maths questions?
To answer a GCSE maths question the first thing you need to do is read the question properly. It is so important to take your time and really make sure you understand the intention behind the question. It is easy to get caught up in the language of the question and lose sight of what it is actually asking! So, take your time, and make sure you understand what the question is asking before putting the maths into practice.
How can I practice GCSE maths?
A great way to practice GCSE maths is by using a range of different resources, such as practice questions, summary worksheets and quick quizzes. You want to find resources that are both engaging and effective, getting you to familiarise yourself with the material and layout of a GCSE Maths question. Third Space Learning has a growing resource library of GCSE Maths lessons and GCSE maths revision support created by maths experts to help prepare for maths GCSE. Take a look, see what works for you and get practising!
Conclusion
To summarise, students need to be secure with some essential skills in order to access the sorts of GCSE maths questions that have been included above. Focus on these to start with:
| Higher | Foundation |
| – Surds – Fraction operations – Factorising – Rounding to significant figures |
– Recall formulae – Solving equations – Substitution – Square and cube numbers and roots – Rounding to decimal places and significant figures |
Read more:
- How We Developed Our GCSE Maths Revision Programme
- GCSE Intervention Strategies
- How To Revise For GCSE
- Exam Techniques
Do you have students who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 130,000 primary and secondary students become more confident, able mathematicians. Find out more about our GCSE Maths tuition or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
- /
- /
- /
- /
GCSE — первая аттестация в британской школе. Подготовка к экзаменам занимает 2 года и влияет на дальнейшую судьбу школьника. Недавно GCSE претерпел изменения, усложнился, поэтому мы составили гид по тому, как сдать экзамен, какие задания ждут школьника и где пройти подготовку.
Общие изменения в GCSE
В связи с реформой британского образования GCSE претерпел изменения как в программе обучения, так и в самих экзаменах. Впервые «по-новому» GCSE сдавали в 2017 году. Мы выделили 6 ключевых изменений — обратите внимание: Уменьшится количество вопросов, где можно ответить односложно или отметить правильный ответ в тесте, им на смену придет больше вопросов в формате эссе. Сами задания по сути станут сложнее: с более содержательными текстами в английской литературе и рядом новых тем по математике. Среди выбранных предметов на GCSE нужно будет взять хотя бы две естественнонаучные дисциплины. Уход от модульной системы и промежуточных оценок: теперь обучение по всем выбранным предметам длится 2 года, в конце которых сдаются экзамены GCSE. Буквенные оценки вытеснит 9-балльная система. Пересдать GCSE можно будет в ноябре, но только английский язык и математику.
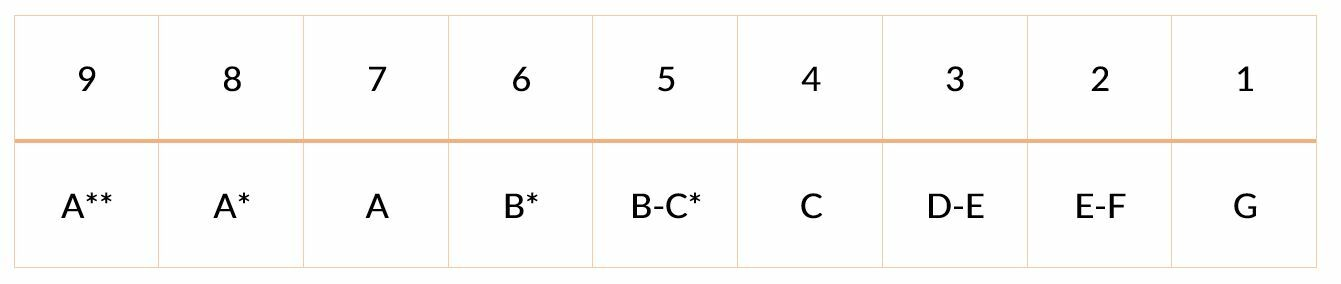
Таблица системы оценок GCSE: как соотнести 9-балльную шкалу с буквенной
Какие задания GCSE/IGCSE предполагаются по основным предметам
С точки зрения заданий оба формата (GCSE и IGCSE) схожи, задания могут отличаться лишь количеством времени на секцию или иной группировкой модулей.
English language (Английский язык)
Экзамен по английскому проходит в письменной и в устной форме. Письменная часть предполагает выполнение заданий в два этапа: Paper 1и Paper 2. Каждый этап предполагает чтение отрывка текста, ответы на вопросы по прочитанному и написание эссе. Всего в рамках экзамена нужно будет написать два эссе, оценка за которые — 50% успеха. Помимо знания грамматики, лексики и умения понять прочитанное важно продемонстрировать и навыки письма, а также умение увидеть и объяснить позицию автора. Тексты в заданиях как художественные, так и нон-фикшн. Устная часть по английскому проходит в виде презентации на заданную тему, ответов на вопросы экзаменатора и оценивается отдельно от письменной.
English literature (Английская литература)
Экзамен по литературе состоит из двух частей: Paper 1 и Paper 2. Задания касаются понимания содержания и построения текстов в прозе и поэзии. Например, школьнику нужно будет ответить на вопросы по диалогу из «Ромео и Джульетты» Шекспира, объяснить смысл повести «О мышах и людях» Стейнбека, провести анализ стихотворения и сравнить его с другим из антологии, не имея перед глазами текста. Стоит ли говорить, что для сдачи экзамена стоит, как минимум, прочесть всю рекомендованную литературу, научиться соотносить произведение с эпохой, судьбой писателя и грамотно выражать мысли в ответах-эссе.
Mathematics (Математика)
На экзамене по математике нужно будет выбрать уровень, который вы будете сдавать. Те, кто планирует дальше изучать гуманитарные дисциплины, останавливаются на базовом уровне, а «технари» выбирают усложненный. Общие темы для проверки знаний: алгебра, включая логарифмы, тригонометрия, базовая статистика и теория вероятностей. Задания делятся на те, где нужен короткий ответ и те, где требуется решение. С первой частью задач (Paper 1) нужно будет справиться без калькулятора, в двух оставшихся (Paper 2 и Paper 3) калькулятором можно пользоваться.
Biology (Биология)
Экзамен по биологии разделен на 2 равнозначные секции. Он проверяет, как школьник умеет работать с диаграммами, графиками, статистикой, фотографиями. Для решения некоторых задач потребуется калькулятор. Основные темы: клетки и простейшие, физиология растений и животных, генетика и анатомия, экология и экосистемы, медицина.
Chemistry (Химия)
Согласно исследованиям BBC в 2019 году, чтобы сдать GCSE по химии на высший балл, английские школьники должны были решить от 80% всех задач. Поэтому рекомендуем уделить подготовке максимум внимания. Задания классически представлены в двух секциях. Темы посвящены основам неорганической химии: вещества и их состояния, химические реакции, выделение металлов, группы элементов в периодической таблице, скорость реакции и изменения энергии.
Physics (Физика)
Задания по физике представлены как в виде коротких вопросов, так и в виде задач с развернутым решением. Вопросы разделены на 2 равные секции. Среди главных тем: движение и силы, сохранение энергии, волны, радиоактивность, астрономия, электричество, электромагнитная индукция. По данным BBC, чтобы получить высший балл GCSE по физике в 2019 году, британские школьники давали 77% правильных ответов и более. Рекомендуем подготовиться основательно.
History (История)
Задания по истории делятся на 3 секции с разным весом в итоговой оценке. Самая значимая — Paper 2: на нее приходится 40% баллов за экзамен. Здесь нужно будет ответить на вопросы, выбрав два исторических периода из предложенных. Например, «Холодную войну 1941−1991» и «Елизаветинскую Англию 1558−1588». Первая часть (Paper 1) посвящена вопросам о британском обществе в разные периоды, а третья (Paper 3) — мировой истории XX века. За каждую из этих частей получите 30% баллов.
Business (Бизнес)
Задания GCSE по бизнесу — одни из самых прикладных. Первая секция проверяет знания школьника о создании малого бизнеса: бизнес-идея, ее реализация и что может ей помешать. Вторая секция посвящена росту и развитию бизнеса, принятию решений: финансовых, маркетинговых, кадровых. Секции оцениваются поровну.
Когда и где сдавать экзамены?
Экзамены GCSE проходят очно и сдать их можно в Москве, в российско-британской школе «Алгоритм» на Лубянке. Наша школа аккредитована британской экзаменационной комиссией Pearson Edexcel, мы гарантируем соблюдение протокола проведения экзамена GCSE, поэтому в нашей школе сдают экзамен и наши ученики, и внешние кандидаты.
Сдача экзаменов возможна трижды в год:
- в ноябре
- в январе
- в мае-июне (основная сессия)
Для допуска к сессии нужно зарегистрироваться за 2 месяца до экзаменов. Для этого обратитесь в наш экзаменационный отдел — сориентируем по процессу и ответим на все вопросы.
Как подготовиться к экзаменам?
А вот подготовку к экзаменам стоит начинать за 1−2 года до сдачи экзаменов. Лучший вариант — пройти обучение по программе GCSE по выбранным предметам в нашей школе «Алгоритм». Изучите предметы на английском, углубитесь в нужные темы, разберетесь со структурой экзаменов и системой баллов.
Наши выпускники набирают максимально возможные баллы по GCSE, заканчивают у нас старшую школу, A-level, и по итогам поступают в ТОП-20 британских и европейских вузов.
GCSE считается первой аттестационной системой в любых школах Великобритании. При подготовке к подобным экзаменам уходит много сил и времени. По времени вам необходимо для отличной подготовки потратить порядка 2 лет, прежде чем вы сможете сдать все испытания и сдать дипломную работу (по другому она называется выпускная квалификационная работа). Экзамен сможет сильно повлиять на вашу дальнейшую судьбу, вплоть до нахождения лучшего места работы.
При этом у системы GCSE имеются определенные изменения, которые перекочевали в новую систему. Работа над подготовкой немного усложнилась, именно потому в этой статье вы узнаете о том, какие из заданий будут ждать школьников, и каким образом проходит подготовка и самое главное, где можно сделать это.
В связи с тем, какие реформы пришли в систему британского образования, притерпелись и изменения как в обучение, так и в сам прием экзаменов. Самые первые студенты, сдающие по новой системе, были 2017 года выпуска. Всего можно выделить 6 основных отличий, на которые вы можете обратить внимание:
- Сокращения количества вопросов, где имеется право выбрать правильный вариант ответа (один или несколько). На смену будут иметься вопросы, где надо писать краткий ответ.
- Задание, используемые для экзамена станут сложнее. Будут использоваться наиболее содержательные тексты, где уровень воды и других непригодных для текста элементов низок.
- Среди выбранных на выбор предметов, хотя бы два должны будут иметь естественнонаучные направления.
- Переходы из систем модульной и промежуточной оценки. В нынешнее время обучение по выбранным предметам будет длиться два года, после которых будут сдавать специальные экзамены GCSE.
- Буквенные оценки будут вытеснены 9-балльной системой.
- Пересдача GCSE, которая происходит в ноябре, выполняется только по таким предметам как английский язык и математика.
Таблица с системами оценивания GCSE: каким образом стоит соотносить 9-балльную шкалу
Изучение каких предметов подразумевает программа GCSE
В этой великобританской системе углубленное изучают дисциплины в количестве от пяти до десяти штук. Всегда имеет важное значение изучение английского языка с математикой. Иногда потребуется осваивать науки, информационную технологию, английскую литературу.
Превосходство GCSE составляет то, что многие предметы ученику можно выбрать самому. В этом ему помогают преподаватели, консультанты из университета, родители. Часто происходят изменения в списке с дисциплинами, которые выбирает школа. Могут предложить физику, химию, биологию, географию, изучение иностранных языков, например, итальянского, китайского, японского, а также прикладных предметов бизнеса, бухгалтерского учета, высшей математики и так далее.
Возникли сложности?
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Какие задания необходимо выполнять по общеобразовательным предметам в экзаменах GCSE и iGCSE?
Если говорить про оба этих формата экзаменов, то все задания будут схожими. Отличия будут касаться лишь в незначительных моментах: количество времени на секцию, а также другого рода группировка модулей.
- Английский язык (English language). Экзамен по английскому языку происходит как письменно, так и устно. Первая часть предполагает выполнения определенного уровня сложности заданий в пару этапов. Любой из этих этапов может предполагать чтение отрывка текста, а также ответы на определенные вопросы по написанному авторами тексту и написания конкретного эссе. Всего в момент написания текста вы должны будете представить два эссе, которые занимают по общему оцениванию примерно половину от общего количества. Кроме проверки знаний, связанных с грамматикой надо показав собственные навыки письма на английском, а также умение думать и что более важно объяснять и улавливать позицию авторов. Тексты заданий могут быть как художественного характера, так и нон-фикшн. Устный вариант экзамена при сдаче английского языка проходит в формате презентации, ответов на поставленные вопросы, которые подготовил экзаменатор. Оценки устного и письменного экзамена оцениваются отдельно.
- Английская литература (English literature). Экзамен данного вида состоит из двух частей. Основное направление заданий – понимание содержания и построения текстов в прозах или поэзии. К примеру, школьнику требуется ответить на поставленные вопросы по диалогам, которые могут разворачиваться в пьесе «Ромео и Джульетта» Шекспира, провести необходимые анализирования стихотворений, а также сравнить его с совершенно другими из антологии работами, не имея перед глазами сами текста произведений. Такой экзамен может стать настоящим испытанием для тех людей, которые мало читают. Поэтому перед сдачей экзамена необходимо прочесть как минимум большую часть рекомендованной литературы, уметь соотносить произведение с той или иной эпохой, судьбой писателей художественной или другого типа литературы, а также грамотно выражать собственные мысли в ответах-эссе.
- Математика (Mathematics). Экзамены по математике имеют определенные уровни, на которые вам следует сдавать. Те люди, которые планируют в дальнейшем изучать дисциплины гуманитарной направленности можно без проблем брать базовый уровень, а вот если вы «технарь», то имеет смысл выбирать усложненный вариант. В качестве основных предметов для проверки знаний являются алгебра, знание тригонометрии, логарифмов, базовая статистика, а также теория вероятности чисел. Задания будут поделены на те, которые требуют коротких ответов и длинных решений. Причем первая часть выполняется без применения приборов вычисления, а вот в двух оставшихся калькулятором можно будет воспользоваться.
- Биология (Biology). В Великобритании сдают этот экзамен в два этапа. С его помощью можно проверить насколько хорошо экзаменуемый умеет работать с диаграммами, графическими или другими источниками информации, в том числе статистикой и изображениями. Чтобы решить некоторые из предложенных задач, следует применить калькулятор, так как вычислять придется достаточно много. Основные тем для экзаменуемого будет клетки, простейшие организмы, физиология как растений, так и животных, генетика и анатомическое строение существ, экология и экосистема, а также медицина.
- Химия (Chemistry). Если учитывать исследования ВВС, то с 2019 года чтобы хорошо сдать экзамен GCSE по химии на более высокий балл, школьники из Великобритании должны решить порядка 80% от всех имеющихся задач. Таким образом, вы должны уделить подготовке экзамену гораздо большое внимание. Задания в стандартном варианте представлены как две самостоятельные части. Суммируя, вы сможете получить общий итог. Темы, используемые на экзамене посвящены неорганической химии: вещества и их исходное состояние, химические реакции, а также выделение тех или иных металлов, группы химических элементов из периодической таблицы Менделеева, изображенных в периодической таблице, скорость реакции, а также изменения энергетической ценности.
- Физика (Physics). Все задания, используемые на экзамене, представляются в двух видах: как коротких, так и длинных вопросов с развернутым ответом. Вопросы поделены на 2 одинаковые по объему секции. Среди основных тем можно выделить движение и силы, сохранения энергии, волны, уровень радиоактивности, астрономия, электромагнетизм, в том числе индукция электромагнитного типа, а также ЭМИ (электромагнитные импульсы) и электричество в целом. Если судить по данным BBC, то для получения высокого балла по экзамену GCSE, то британским школьникам нужно было дать порядка 75% правильных ответов и более (по состоянию на 2019 год). К такому экзамену, как и ко всем остальным следует подготавливаться основательно.
- История (History). Задания, связанные с историей, можно разделить на 3 части, которые имеют разный вес для итогового балла. Наиболее продуктивным считается вторая часть, так как с её помощью вы сможете набрать более 40% баллов. В этой части необходимо будет выбрать любые исторические периоды в количестве двух штук из предложенных. Остальные части оцениваются равностепенно по количеству баллов – по 30% на каждую часть. Самая первая часть посвящается вопросам о британском обществе в те или иные периоды. В последней — история мира в 20 веках.
- Бизнес (Business). Наиболее прикладным экзаменом считается экзамен по бизнесу на GCSE. Основная секция будет проверять знания учащегося о том, как создать малый бизнес: формирование бизнес-идеи, ее реализация, а также факторы, мешающие этому процессу. Другая секция будет посвящена росту, а также процессам по развитию бизнеса, принятию решений, как в финансовой части, так и в маркетинге и кадровой перестановке. Обе секции будут оценены по 50% от общего количества баллов.
Как оцениваются экзамены по системе GCSE и iGCSE?
Самое главное при обучении по такой системе, знать каким образом они оцениваются. Ниже вы сможете увидеть, как оцениваются экзамены в буквенных обозначения — не забывайте, что сейчас британцы переходят по системе 9-балльной системе, о которой написано выше.
Система оценивания в GCSE
Когда кончается курс, ученикам нужно выполнить сдачу экзаменов, чтобы получить сертификат, подтверждающий среднее образование. Финальное испытание имеет формат в виде теста, который предусмотрен для каждого изученного предмета.
- Ученикам дается отметка А* до G. А считается самым высоким баллом. G является низким баллом. Оценка U ставится тем, кто не справился с экзаменом. Отметки бывают двух групп. Группа от А* до С подразумевает получение высокой отметки.
- Группа от D до G содержит низкие оценки. Математика предлагает применение шкалы из трех уровней. Если получают оценку из группы А* – С, учеников считают продвинутым. Группа от B до T дает оценки средним ученикам. В группе от D до G находятся оценки базового уровня.
Уровней оценивания в iGCSE
Уровни сложностей называются tires. Детям иногда приходится сдавать экзамен, который имеет высокую сложность и обозначается как Higher tire. После его сдачи дают оценку из группы от А* до D.
Когда сдают экзамены, имеющие низкую сложность, которая называется Foundation, тогда ему ставят оценку из группы С-G.
- Бывает, при сдаче экзамена, имеющего высокую сложность, получена оценка не D, а Е.
- Или при сдаче экзамена, имеющего высокую сложность, никак не удается получить оценку D или дети сдавшие экзамены, имеющие низкую сложность, не набирают баллы, надлежащие для оценки G, в этом случае ему ставят U. Потом считают, что экзамен им не сдан.
Когда изучением предмета занимаются в пределах одного уровня, ученики получают за него разные отметки.
Какой особенностью характеризуется классическая программа GCSE
На итоговую оценку оказывает влияние состояние качества, с которой будет потом выполнена курсовая или в будущем дипломная работа. Финальную оценку IGCSE складывают, учитывая результаты, полученные на экзаменах. При этом высший балл это A, но, не А*.
Чтобы поступить на подготовительную программу до того, как стать студентом университета, нужно иметь оценку не меньше, чем C по пяти предметам.
Что должны учесть иностранные абитуриенты?
Чтобы пройти курс двухлетней английской программы GCSE, ученику должно исполниться четырнадцать лет. Чтобы стать учеником годичного курса, One Year, необходимо иметь пятнадцать лет. Требуется наличие табеля с успеваемостью, которая была в период последних 2-3 лет учёбы. Также требуют сдачи экзамена по английскому языку с прохождением тестов по нескольким дисциплинам.
Перечень с предметами и проходными баллами определяет школа. Имеется наличие одной закономерности. Чтобы стать учеником годичной программы, необходимо по английскому языку иметь самый высокий уровень знаний в сравнении с курсами, которые проходят два года.
Возникли сложности?
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Как подготовиться для GCSE?
Использование комплексного подхода подразумевает успешную подготовку и поступление на GCSE. Уже с семи лет изучают углубленно английский язык. Хорошую базу знаний вы сможете получить в том случае, если будете проходить специальные языковые курсы. Все существующие занятиями в этом случае проходит с участием специально обученного репетитора. Также хорошие знания могут быть получены частыми поездками за рубеж, чтением специальной литературы и просмотром кино на английском языке. Не помешает пройти летние программы в школе Британии. С их помощью дается более полное изучение языка, можно познакомиться с новыми друзьями, узнать лучше образовательную систему, культуру в стране.
До того, как поступать, надо подготовиться к вступительным экзаменам, чтобы стать студентом британской обучающей схемы. Для этого рекомендуют прохождение специальных курсов. Чаще всего подготовительная программа состоит из занятий, где используются британские учебные пособия, тесты для тренировок, репетиция при собеседовании и адаптации к великобританской образовательной системе. Чтобы пройти качественную подготовку, следует проводить комплексные занятия, которые позволяют выполнить множество важных задач одним разом экономя время. При подготовке к экзамену такого рода время является определяющим моментом, который следует учитывать.
Продвижение в образовании на другую ступень
Кто хочет учиться, используя программу A-level для получения полного среднего образования, довольно часто в качестве обязательного требования считают оценку из группы от A* до C, когда сдают пять дисциплин GCSE вместе с математикой и английским языком. Дети должны сами выбрать предметы, изучением которых они будут заниматься по программе A-level. Оценку им нужно получить не меньше, чем С. Когда сдаются экзамены для зачисления в высшее учебное заведение, приёмной комиссии приходиться учитывать, какая оценка GCSE есть после сдачи экзамена по предмету английский язык и математика, не учитывая оценок, полученных во время прохождения курса A-level, IB, Foundation. Оценки GCSE за математику с английским языком нужно иметь не ниже, чем С. Если у ученика есть низкая оценка за эти предметы в курсе GCSE, требуется пересдача экзаменов GCSE этих предметов через некоторый промежуток времени.
Выполнение курсовых работ
При изучении некоторых дисциплин обязательно требуют выполнить курсовую работу. Количество баллов, полученных во время сдачи, часто составляет от 10 до 100% оценки при экзамене, когда сдают этот предмет. Число баллов, которые получены при сдаче курсовой работы в творческом предмете нередко могут составить значительный процент от полной оценки за предмет.
Выполняя курсовую работу, можно получить несколько дополнительных баллов. Но, учащиеся нередко воспринимают это как дополнительную нагрузку.
Чтобы дети не списывали, когда пишут курсовую работу, нередко за процессом наблюдают педагоги.
Подведение итогов
Как вы можете понять, система GCSE является одной из самых сложных, но при этом лучшим. Британское образование всегда считалась самым лучшим в мире, именно поэтому готовится к экзаменам у них надо намного лучше, чем в России.