Сейчас существует множество бесплатных инструментов, которые позволяют подготовиться к ЕГЭ и увеличить балл на 40% с минимальными временными затратами.
Наиболее эффективными являются подписки на видеокурсы. Попробовать можно с
компанией Twostu
,
тем более здесь это ничего не стоит.
Источники информации
Переходить на темную сторону в поисках ответов ЕГЭ по математике совсем необязательно. Стопроцентно легальные и абсолютно правильные ответы на все вопросы КИМов ЕГЭ профильного и базового уровней есть только в одном месте – в демоверсии на сайте ФИПИ. Конечно, единственный вариант даст всего лишь примерное представление о том, что будет на самом экзамене и как решать самые сложные задания, но это уже хотя бы что-то.
Чтобы получить доступ к ответам на ЕГЭ по математике не нужно даже проходить процедуру регистрации. Достаточно выполнить несколько простых действий:
- Установить на компьютере программное обеспечение для распаковки zip-архивов.
- Перейти на главную страницу официального сайта ФИПИ.
- В разделе меню «ЕГЭ и ГВЭ-11» выбрать вкладку «Демоверсии, спецификации и кодификаторы».
- Пройти по ссылке «Математика», выбрать нужный уровень.
- Скачать и распаковать архив.
В папке будет целый пул сопроводительных материалов, но ответы содержатся в конце демоверсии. Для сравнения можно ознакомиться еще и с вариантами предыдущих лет – они выложены, начиная с 2007 года. Структура ЕГЭ по математике не меняется только с 2016 года, так что слишком глубоко копать не стоит, ради интереса, разве что.
Зачем это делать? Хотя бы для того, чтобы иметь четкое представление, соответствует ли подлинным заданиям экзамена все то, что предлагается в Интернете и многочисленных печатных сборниках для подготовки в качестве заданий с ответами по ЕГЭ по математике.
Структура демоверсий
В базовой версии на одной позиция представлены две-три разновидности вопросов, которые могут попасться на ЕГЭ.
Ответы даны на все варианты, но в самом конце демоверсии.
Так что есть возможность прорешать официальный вариант КИМа.
В демоверсии КИМа усложненного профильного ЕГЭ по математике ответы представлены по-другому, так как задания с 13 по 19 требуют развернутых обоснований полученных результатов. Итоги, которые должны получиться после вычислений или выбора варианта в первых 12 вопросах, тоже сгруппированы в таблицу.
Ход решения и ответы самых трудных заданий изложены более обстоятельно.
Что дальше
Теперь, если в интернете попался сайт с тренировочными заданиями и ответами ЕГЭ по математике, как две капли воды похожими на официальные прототипы, смело можно браться за их решение.
Сайту с таким вариантом можно доверять.
Конечно же, актуальные для текущего года версии КИМов ЕГЭ по математике, тем более ответы к ним, – тайна за семью печатями вплоть до начала экзамена. Но, решая десятки, а возможно, и сотни вариантов заданий, скажем, на все виды неравенств, волей-неволей придется повторить все формулы, которые могут понадобиться для вычислений. Тогда одна измененная цифра или переставленные местами слова в условии задачи не собьют с толку на экзамене, и решение придет, если и не само собой, то без мучительных терзаний и лишней потери времени.
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
Ответы на ЕГЭ по профильной и базовой математике для 11 классов — один из самых популярных поисковых запросов в мае 2022 года. Многие школьники активно ищут в Сети готовые решения, варианты задач и тестов.
К ЕГЭ для 11 классов в 2022 году юноши и девушки готовятся по-разному. Кто-то активно решает задачи и проходит тесты по базовой и профильной математике, а кто-то ищет в интернете готовые решения, стремясь обезопасить себя и подстелить соломки.
На многочисленные запросы по поиску готовых решений к ЕГЭ по математике для 11 классов в интернете уже находятся подходящие варианты. В сообществах в социальных сетях, в группах, а также в Telegram можно найти множество объявлений, в которых их авторы обещают предоставить гарантированные реальные варианты тестов по предметам и решений к ним. В большинстве случаев такие услуги предоставляются не бесплатно: ученикам 11 классов предлагают перевести ту или иную сумму, чтобы открыть онлайн доступ к якобы правильным ответам к тестам за 2022 год.
Стоит ли верить таким обещаниям и насколько это реально — получить варианты правильных ответов к ЕГЭ по математике за 2022 год? В Роспотребнадзоре утверждают: речь идет о мошенничестве, так как материалы, имеющие отношение к единому государственному экзамену для 11 классов, не могут утечь в интернет. Решения, конкретные задачи, тесты и даже варианты, которые будут отправлены в тот или иной регион РФ, — информация, которая остается строго засекреченной вплоть до начала ЕГЭ.
В разные города и области страны тесты и варианты отправляются в виде шифра. Любые утечки, как подчеркивают в Роспотребнадзоре, исключены.
Так что авторы объявлений о продаже доступов к готовым решениям к единому государственному экзамену по математике — не более чем мошенники. Ученики 11 классов, которые всерьез верят таким предложениям, рискуют потерять свои деньги. Прецеденты есть: школьники переводят деньги, ожидая получить решения и ответы к ЕГЭ по различным предметам, затем сайт, на котором они нашли соответствующее объявление, перестает существовать. Регулярно по таким случаям проводятся проверки, которые приносят результат.
Ученикам 11 классов в 2022 году можно посоветовать использовать время перед ЕГЭ с пользой — на подготовку, решение задач и прохождение тестов, а не на онлайн поиски готовых экзаменационных материалов, которые в любом случае не принесут ожидаемого результата.
Резервные даты сдачи ЕГЭ по профильной и базовой математике 24 июня, 2 июля и 20 сентября 2022
В 2022 году для выпускников 11 классов предусмотрены резервные сдачи ЕГЭ по математике базового и профильного уровней — 24 июня и 2 июля. Кроме того, осенью предусмотрен еще один резервный день для ЕГЭ по математике базового уровня — 20 сентября.
#Новости#Экзамен#Выпускники#ЕГЭ 2023#Ольга Земскова#Общество
Реальные варианты ЕГЭ по математике
Дорогие друзья! На этой странице вы можете найти варианты реальных КИМ ЕГЭ по математике (база и профиль). На сайте размещены только ссылки на варианты КИМ ЕГЭ и их решения. Здесь вы можете сказать тренировочный и реальный вариант ЕГЭ по математике (профиль и база) 2022 и 2023 гг с ответами и решениями. Если материалы вам пригодились, можете финансово поддержать работу сайта через форму ниже:
2022-2023 учебный год
| Реальный вариант ЕГЭ по математике-2023 | ||
| Скачать вариант (профиль) | Решение и ответы | 02.06.2023 |
| Досрочные варианты ЕГЭ по математике-2023 | ||
| Скачать вариант 1 (профиль) | Решение и ответы | 28.03.2023 |
| Открытый вариант досрочного ЕГЭ по математике-2023 | ||
| Скачать вариант (профиль) |
Решение и ответы | 28.03.2023 |
| Скачать вариант (база) | Решение и ответы | 28.03.2023 |
| Демонстрационный вариант ЕГЭ по математике-2023 | ||
| Вариант (профиль) | Спецификация | Кодификатор |
| Вариант (база) | Спецификация | |
| Тренировочные работы Статград в формате ЕГЭ по математике-2023 | ||
| Тренировочная работа №1
Профиль База |
Ответы и решения | 28 сентября 2021 г. |
| Тренировочная работа №2
Профиль База |
Ответы и решения | 15 декабря 2021 г. |
| Тренировочная работа №3
Профиль База |
Ответы и решения (профиль) | 27 января 2022 г. |
| Тренировочная работа №4
Профиль База |
||
| Тренировочная работа №5
Профиль База |
Ответы и решения | 28 апреля 2022 г. |
2021-2022 учебный год
| Реальный вариант ЕГЭ по математике-2022 | ||
| Скачать вариант (профиль) Дальний Восток | Решение и ответы | 02.06.2022 |
| Досрочные варианты ЕГЭ по математике-2022 | ||
| Скачать вариант 1 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 2 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 3 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 4 (профиль) | Решение и ответы | 28.03.2022 |
| Открытый вариант досрочного ЕГЭ по математике-2022 | ||
| Скачать вариант (профиль) |
Решение и ответы | 28.03.2022 |
| Скачать вариант (база) | Решение и ответы | 28.03.2022 |
| Демонстрационный вариант ЕГЭ по математике-2022 | ||
| Вариант (профиль) | Спецификация | Кодификатор |
| Вариант (база) | Спецификация | |
| Перспективный вариант демо-версии КИМ ЕГЭ по математике-2022 |
||
| Вариант | Спецификация | |
| Тренировочные работы Статград в формате ЕГЭ по математике-2022 | ||
| Тренировочная работа №1 (профиль)
Тренировочная работа №1 (база) |
Ответы и решения | 28 сентября 2021 г. |
| Тренировочная работа №2 (профиль) Варианты 1 и 2Варианты 3 и 4 |
Ответы и решения | 15 декабря 2021 г. |
| Тренировочная работа №3 (профиль)
Тренировочная работа №3 (база) |
Ответы и решения (профиль) | 27 января 2022 г. |
| Тренировочная работа №4 | ||
| Тренировочная работа №5 (база)
Тренировочная работа №5, варианты 1 и 2 (профиль) Тренировочная работа №5, варианты 3 и 4 (профиль) |
Ответы и решения | 28 апреля 2022 г. |
2020-2021 учебный год
| Реальные варианты КИМ ЕГЭ по математике | ||
| Основная волна ЕГЭ по математике-2021 | ||
| Вариант 1 | Ответы и решения | |
| Открытый вариант ЕГЭ по математике-2021 от ФИПИ | ||
| Вариант (профиль) | Ответы и решения | |
| Демонстрационный вариант ЕГЭ по математике-2021 (проект) | ||
| Вариант Ответы | Кодификатор | Спецификация |
|
Тренировочные варианты ЕГЭ по математике-2021 |
||
| Вариант 1
Вариант 2 |
Вариант 1 — ответы и решения
Вариант 2 — ответы, критерии |
Admin
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
-
Главная
-
ЕГЭ
-
ЕГЭ 2022
-
Реальные варианты ЕГЭ 2022
- 29.03.2022
Дата обновления: 07.06.2022
СОХРАНИ СТРАНИЦУ С ЗАКЛАДКИ!
Общая страница, на которой мы будем собирать все реальные варианты, которые будут появляться по ЕГЭ в 2022 году. Все варианты будут публиковаться после проведения экзамена.
- 02.04.2022 — Варианты досрочного ЕГЭ 2022 по всем предметам
- 01.05.2022 — Опубликованы открытые варианты по всем предметам
- 26.05.2022 — Началась основная волна ЕГЭ 2022 (см ссылки ниже)
- 07.06.2022 — Обновлены задания по тем предметам, которые прошли — история, физика, русский, математика
Реальные варианты 2022 ПО ПРЕДМЕТАМ (по алфавиту)
- Английский язык
- Биология от 07.04.2022
- География от 26.05.2022
- История от 06.06.2022
- Литература от 26.05.2022
- Математика профильная обновлено от 06.06.2022
- Математика базовая — обновлено 05.06.2022
- Обществознание от 07.04.2022
- Русский язык от 30.05.2022, 31.05.2022
- Физика от 06.06.2022
- Химия от 26.05.2022
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
Решение заданий и ответы вариантов Дальнего Востока Москвы и других регионов реального ЕГЭ от 2 июня 2022 года по математике (профильный уровень). Основная волна КИМ, ДВ, МСК Дальневосточный, Владивосток, профиль.

Задание 1.
Найдите корень уравнения sqrt{22-3x}=2.
ИЛИ
Найдите корень уравнения 7−6−х = 343.
Задание 2.
В чемпионате по гимнастике участвуют 70 спортсменок: 14 из Сербии, 23 из Хорватии, остальные из Словении. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Сербии.
ИЛИ
В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 6 из Черногории, 7 из Сербии, 8 из Хорватии и 9 из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Словении.
ИЛИ
В сборнике билетов по химии всего 60 билетов, в 3 из них встречаются вопрос по теме «Белки». Найдите вероятность того что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Белки».
ИЛИ
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 7 спортсменов из Германии и 9 спортсменов из США. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать спортсмен из Германии.
Задание 3.
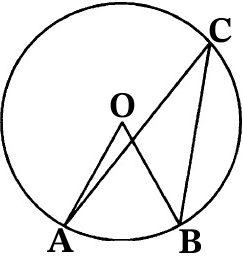
Отрезки АС и ВD – диаметры окружности с центром О. Угол АОD равен 108°. Найдите вписанный угол АСВ. Ответ дайте в градусах.
ИЛИ
Найдите центральный угол АОВ, если он на 67 градусов больше острого вписанного угла АСВ, опирающегося на ту же дугу. Ответ дайте в градусах.
ИЛИ
Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.
Задание 4.
Найдите значение выражения sqrt{2}sinfrac{7pi}{8}cosfrac{7pi}{8}.
ИЛИ
Найдите значение выражения frac{10sin38°}{sin19°cdot sin71°}.
ИЛИ
Найдите значение выражения frac{7sin154°}{cos77°cdot cos13°}.
Задание 5.
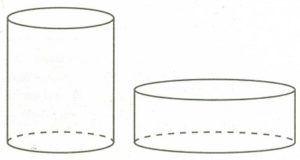
Объем первого цилиндра равен 6 кубических метров. У второго цилиндра высота в 2 раза меньше, а радиус основания – в 3 раза больше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
ИЛИ
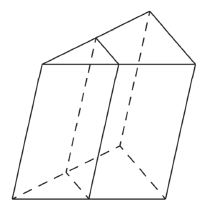
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
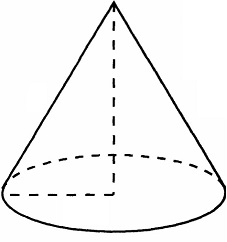
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 12 раз, а радиус основания не изменится?
Задание 6.
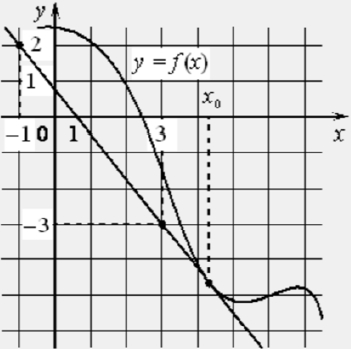
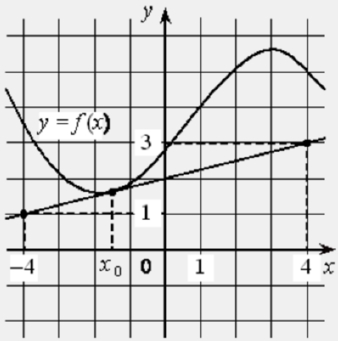
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
ИЛИ
На рисунке изображены график функции 𝑦 = 𝑓(𝑥) и касательная к нему в точке с абсциссой 𝑥0. Найдите значение производной функции 𝑓(𝑥) в точке 𝑥0.
Задание 7.
В ходе распада радиоактивного изотопа его масса уменьшается по закону , где m0 – начальная масса изотопа, t – время, прошедшее от начального момента, Т – период полураспада. В начальный момент времени масса изотопа 20 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
ИЛИ
Водолазный колокол, содержащий v = 2 моль воздуха при давлении p1 = 2,4 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2 в атмосферах. Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле ‚ где α = 13,5 Дж/моль·К – постоянная, Т = 300 К – температура воздуха. Найдите, какое давление p2 будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 16200 Дж. Ответ дайте в атмосферах.
ИЛИ
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением а = 6500 км/ч2. Скорость v (в км/ч) вычисляется по формуле ‚ где l – пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 130 км/ч.
Задание 8.
Теплоход проходит по течению реки до пункта назначения 216 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 23 часа после отплытия из него.
ИЛИ
От пристани A к пристани B, расстояние между которыми равно 176 км, отправился с постоянной скоростью первый теплоход, а через 5 часов после этого следом за ним, со скоростью на 5 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым. Ответ дайте в км/ч.
ИЛИ
Катер в 8:40 вышел из пункта А в пункт В, расположенный в 48 км от А. Пробыв 40 минут в пункте В, катер отправился назад и вернулся в пункт А в 16:20 того же дня. Найдите собственную скорость катера (в км/ч), если известно, что скорость течения реки 2 км/ч.
Задание 9.
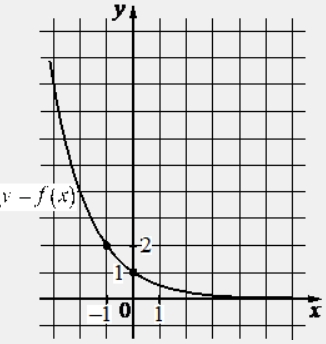
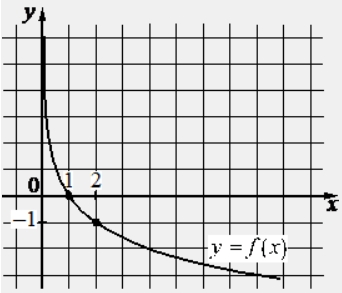
На рисунке изображён график функции вида f(x) = ax. Найдите значение f(–4).
ИЛИ
На рисунке изображён график функции вида f(x) = loga x. Найдите значение f(8).
ИЛИ
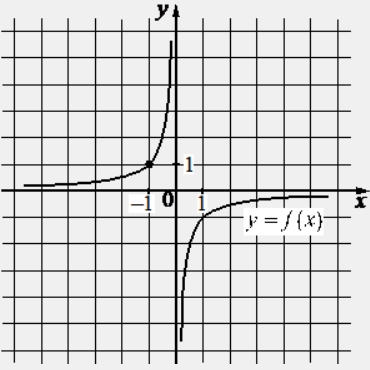
На рисунке изображён график функции вида f(x)=frac{k}{x}. Найдите значение f(10).
Задание 10.
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последние 2 промахнулся. Результат округлите до сотых.
ИЛИ
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
ИЛИ
Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».
ИЛИ
Помещение освещается фонарем с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
ИЛИ
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Задание 11.
Найдите точку минимума функции y = x3 – 16x2 + 64x + 17.
ИЛИ
Найдите наименьшее значение функции
y=11+frac{7sqrt{3}}{18}pi-frac{7sqrt{3}}{3}x-frac{14sqrt{3}}{3}cosx
на отрезке [0;frac{pi}{2}].
ИЛИ
Найдите точку минимума функции y = x2 – 28x + 96lnx – 5.
Задание 12.
а) Решите уравнение 2cos2x – 3sin(–x) – 3 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].
ИЛИ
а) Решите уравнение sin2x – 2sin(–x) – cos(–x) – 1 = 0.
б) Найдите все корни уравнения, принадлежащие отрезку [2pi;frac{7pi}{2}].
ИЛИ
а) Решите уравнение 5^{2log_{2}^{2}(sinx)}=frac{5}{5^{log_{2}(sinx)}}.
б) Найдите все корни уравнения, принадлежащие отрезку [pi;frac{5pi}{2}].
Задание 13.
Точка M – середина бокового ребра SC правильной четырёхугольной пирамиды SABCD, точка N лежит на стороне основания BC. Плоскость α проходит через точки M и N параллельно боковому ребру SA.
а) α пересекает ребро SD в точке L. Докажите, что BN : NC = DL : LS.
б) Пусть BN : NC = 1 : 2. Найдите отношение объёмов многогранников, на которые плоскость α разбивает пирамиду.
ИЛИ
В кубе ABCDA1B1C1D1 отмечены середины M и N отрезков AB и AD соответственно.
а) Докажите, что прямые B1N и CM перпендикулярны.
б) Найдите расстояние между этими прямыми, если B1N = 3√5.
ИЛИ
В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N – середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD = 10, BC = 8, SO = 8, а прямая SO перпендикулярна прямой AD.
ИЛИ
В прямоугольном параллелепипеде ABCDA1B1C1D1 на диагонали BD1 отмечена точка N так, что BN:ND1 = 1:2. Точка O – середина отрезка CB1.
а) Докажите, что прямая NO проходит через точку A.
б) Найдите объём параллелепипеда ABCDA1B1C1D1, если длина отрезка NO равна расстоянию между прямыми BD1 и CB1 и равна √2.
Задание 14.
Решите неравенство frac{6}{5^{x}–125}le frac{1}{5^{x}–25}.
ИЛИ
Решите неравенство 5^{x}+frac{125}{5^{x}–126}ge 0.
Задание 15.
В июле 2026 года планируется взять кредит на три года в размере 900 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равными;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 1482,3 тыс. рублей. Сколько рублей составит платёж 2029 года?
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 800 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равны;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита равна 971,8 тыс. рублей. Сколько рублей составит платёж в 2027 году?
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 800 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равными;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что платёж в 2029 году составит 833,8 тыс. рублей. Сколько рублей составит платёж в 2027 году?
ИЛИ
В июле 2026 года планируется взять кредит в размере 880 тыс. руб.
Условия возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь необходимо выплатить часть долга;
– в июле 2027, 2028 и 2029 годов долг остается равным 880 тыс. руб.
– суммы выплат 2030 и 2031 годов равны;
– к июлю 2031 года долг будет выплачен полностью.
Найдите разницу между первым и последним платежами.
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 700 тысяч рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– платёж в 2027 и 2028 годах должен быть по 400 тыс. рублей;
– к июлю 2029 года долг должен быть выплачен полностью.
Найдите сумму всех платежей после полного погашения кредита.
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 900 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равными;
– к июлю 2029 года долг должен быть выплачен полностью.
Найдите сумму всех платежей после полного погашения кредита, если известно, что платёж в 2029 году равен 1027,2 тыс. рублей?
ИЛИ
В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы:
– каждый январь долг будет возрастать на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть по 300 тыс. рублей;
– к июлю 2029 года долг должен быть выплачен полностью.
Какую сумму планируется взять в кредит, если известно, что платёж в 2029 году равен 860,6 тыс. рублей?
ИЛИ
В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть по 500 тыс. рублей;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита равна 1235,2 тыс. рублей. Какую сумму планируется взять в кредит?
Задание 16.
Биссектриса ВВ1 и высота СС1 треугольника АВС пересекают описанную окружность в точках М и N. Известно, что угол ВСА = 85° и угол ABC равен 40°.
а) Докажите, что CN = ВМ.
б) Пусть МN и ВС пересекаются в точке D. Найти площадь треугольника ВDN, если его высота BH равна 7.
ИЛИ
На стороне BC параллелограмма ABCD отмечена точка М такая, что треугольник АМС – равнобедренный, так, что AM = MC.
а) Докажите, что центр окружности, вписанной в треугольник АMD лежит на диагонали параллелограмма. б) Найдите радиус окружности, вписанной в треугольник АMD, если известно, что AB = 7, BC = 21, а ∠DAB = 60°.
ИЛИ
В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE = CE.
а) Докажите, что AL·BC = AB·AC.
б) Найдите EL, если AC = 8, тангенс ∠BCA = frac{1}{2}.
ИЛИ
На стороне острого угла с вершиной A отмечена точка B. Из точки B на биссектрису и другую сторону угла опущены перпендикуляры BC и BD соответственно.
а) Докажите, что AC2 + CB2 = AD2 + DB2 .
б) Прямые AC и BD пересекаются в точке T найдите отношение AT:TC, если cos∠ABC = frac{3}{8}.
Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение
х2 – 2х – 6а + а2 = |6х – 2а|
имеет 2 различных решения.
ИЛИ
Найдите все значения a, при каждом из которых уравнение
|х2 + а2 – 7x – 5a| = х + а
имеет 4 различных решения.
ИЛИ
Найдите все значения a, при каждом из которых уравнение
a2 – 4x2 + 8|x| – 4 = 0
имеет ровно два различных корня.
ИЛИ
Найдите все значения a, при каждом из которых уравнение
– 2x2 + 9|x| + a2 – 6a + ax – 3x = 0
имеет меньше 4 различных решения.
Задание 18.
С натуральным трёхзначным числом проводят следующую операцию: из числа вычитают его сумму цифр, и полученный результат делят на 3.
а) Может ли результатом выполнения операции быть число 300?
б) Может ли результатом выполнения операции быть число 151?
в) Сколько различных результатов можно получить, если применить данную операцию для всех трёхзначных чисел от 100 до 600?
ИЛИ
С натуральным трёхзначным числом производят следующую операцию: к нему прибавляют цифру десятков, умноженную на 10, а затем к получившейся сумме прибавляют 3.
а) Могло ли в результате такой операции получиться число 224?
б) Могло ли в результате такой операции получиться число 314?
в) Найдите наибольшее отношение получившегося числа к исходному.
ИЛИ
Есть четыре коробки: в первой коробке 101 камень, во второй – 102, в третьей – 103, а в четвёртой коробке камней нет. За один ход берут по одному камню из любых трёх коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 97 камней, во второй – 102, в третье – 103, а в четвёртой – 4?
б) Могло ли в четвёртой коробке оказаться 306 камней?
в) Какое наибольшее число камней могло оказаться в первой коробке?
ИЛИ
По кругу расставлено N различных натуральных чисел, каждое из которых не превосходит 305. Сумма любых четырёх идущих подряд чисел делится на 4, а сумма любых трёх идущих подряд чисел нечётна.
а) Может ли N быть равным 160?
б) Может ли N быть равным 89?
в) Найдите наибольшее значение N.
ИЛИ
По кругу расставлено N различных натуральных чисел, каждое из которых не превосходит 400. Сумма любых четырёх идущих подряд чисел делится на 3, а сумма любых трёх идущих подряд не делится на 3.
а) Может ли N быть равным 360?
б) Может ли N быть равным 149?
в) Найдите наибольшее значение N.
ИЛИ
На доске написано N различных натуральных чисел, каждое из которых не превосходит 99. Для любых двух написанных на доске чисел a и b, таких, что a < b, ни одно из написанных чисел не делится на b − a, и ни одно из написанных чисел не является делителем числа b − a.
а) Могли ли на доске быть написаны какие-то два числа из чисел 18, 19 и 20?
б) Среди написанных на доске чисел есть 17. Может ли N быть равно 25?
в) Найдите наибольшее значение N.
Источники заданий варианта: беседы vk.com и telegram, Школа Пифагора, Ягубов РФ.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.1 / 5. Количество оценок: 29
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.