Гидростатика формулы егэ

СТАТИКА И ГИДРОСТАТИКА
Теория и формулы (кратко)

Статика — раздел механики, изучаю­щий условия равновесия тел.

Условия рав­новесия  тела:

а) Поступательно движущееся тело на­ходится в состоянии равновесия (покоится или движется прямолинейно и равномерно),    если 

б) Вращающееся    тело,   имеющее   непо­движную ось вращения, находится в покое или равномерно вращается, если         М₁ + М₂ + М₃ + … + M_N = 0,  где М — момент силы —  произведение силы на её плечо.

---

Виды равновесия.

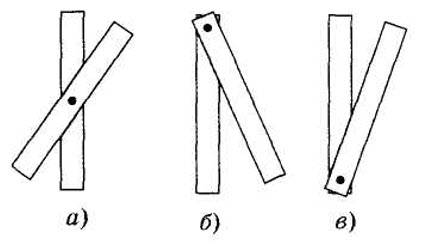
1. Виды равновесия тела с закрепленной осью вращения:

а) если ось проходит через центр масс, то тело находится в безразличном равновесии при любом положении тела (а);

б) ось выше точки центра тяжести — ус­тойчивое равновесие (б);

в) ось ниже точки центра тяжести — неус­тойчивое равновесие( в).

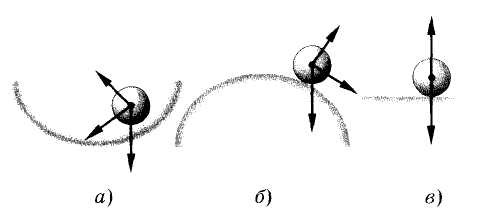
1. Виды равновесия тела, имеющего точ­ку опоры:

а) если равнодействующая всех сил направлена к положению равновесия, то тело нахо­дится в устойчивом положении (рис. а);

б)    если равнодействующая всех сил направлена от положения равновесия, то тело находится в неустойчивом  равновесии (рис. б);

в)    если Σ  = 0, — равновесие безразличное (рис. в).

1. Виды равновесия тела, имеющего пло­щадь опоры.

Если вертикаль, проведенная через центр тяжести тела, пересекает площадь его опоры, то равновесие тела устойчивое. Если не пересекает, то тело падает, — равновесие не­устойчивое.

Простые механизмы и блоки

Простые механизмы — приспособления, которые служат для преобразования силы. К ним относятся:  рычаг (блок, ворот) и наклонная плоскость (клин, винт). Они применяются для получения выигрыша в силе.

F₂/F₁ – выигрыш в силе.      F₁l₁=F₂l₂ — условие равновесия рычага для двух сил.

Золотое правило механики: все простые механизмы, не дают выигрыша в работе — во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.

Гидростатика.

Давление — скалярная физическая величина, равная отношению модуля силы, действующей перпендикулярно поверхности, к площади её поверхности.   

Гидростатическое давление — давление, обусловленное весом столба жидкости. Манометр — прибор для измерения давления в жидкости или газа. 

p = ρ_жgh   — давление на произвольной глубине несжимаемой жидкости            

F = pS = ρ_жghS_дна  — сила давления на дно сосуда         

---

 На одном и том же уровне давление одинаково во всех направлениях.

Давление р на произвольной глубине h сжимаемой поршнем жидкости определяется давлением поршня и давлением столба жидкости           р = р_порш. + ρ_жgh

---

---

 Атмосферное давление – давление, которое производит воздушная оболочка Земли.

Опыт Торричелли (1634 г.) свидетельствует: атмосферное  давление  равно давлению столба ртути в трубке.

Нормальное атмосферное давление:  1 атм = 760 мм.рт.ст. = 1 01325 Па ≈ 10⁵ Па (при 0ºС);     1 мм.рт.ст.=133,3 Па

Оно может изменяться от места к месту и во времени (циклоны и антициклоны) и убывает с увеличением высоты над уровнем моря (на каждые 12 м подъёма  оно уменьшается на 1 мм. рт. ст.).

Барометры — приборы для измерения атмосферного давления. Существуют 1) жидкостный;  2) барометр — анероид (металлический).

Закон Паскаля (1653 г.) —  жидкости и газы передают производимое на них давление во все стороны одинаково. 

 Сообщающимися называются сосуды, соединённые между собой каналом с жидкостью.

---

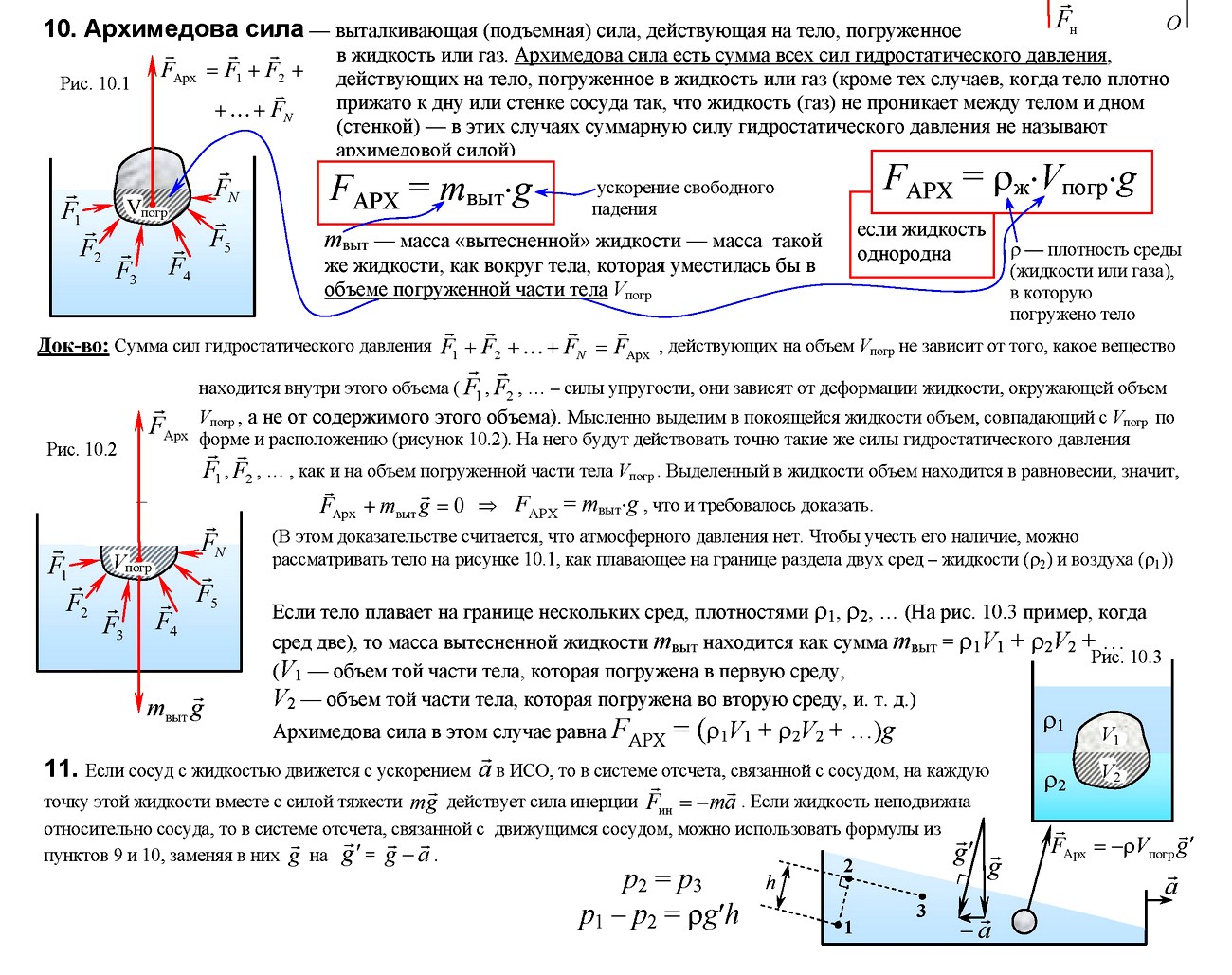
Закон Архимеда: на тело, погруженное в покоящуюся жидкость (или газ), действует выталкивающая сила, направленная  вертикально верх и равная весу жидкости, вытесненной телом.

F_A =ρ_жgV_пчт                        F_A = Р_ж,выт.= m_ж,выт g,

F_A = Р_воз — Р_жид.    V_пчт – объём погруженной части тела.    ρ_ж — плотность жидкости или газа.

Условие плавания тел:

а) F_A > mg, ρ_т > ρ_ж — тело всплывает;  

б) F_A < mg, ρ_т < ρ_ж — тело тонет;      

в) F_A = mg, ρ_т = ρ_ж — тело находится в равновесии на любой глубине.  

Условие плавания тела на поверхности  F_A = mg

Если тело будет плавать частично погрузившись в жидкость, то ρ_ж/ρ_т=V_т/V_пчт

На этом основано применение ареометра- прибора для определения плотности жидкости.

---

Конспект урока «Статика и гидростатика. Теория и формулы для ЕГЭ» + шпаргалка.

Еще конспекты для 10-11 классов:

Оглавление:

• Основные теоретические сведения
  • Давление. Закон Паскаля. Гидростатическое давление
  • Сообщающиеся сосуды
  • Гидравлический пресс
  • Закон Архимеда. Вес тела в жидкости
  • Плавание тел

Основные теоретические сведения

Давление. Закон Паскаля. Гидростатическое давление

К оглавлению…

Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, перемещаясь друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы. На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил в гидростатике вводится новая физическая величина – давление.

Давление определяется как отношение модуля силы F, действующей перпендикулярно поверхности, к площади S этой поверхности:

Если же сила направлена под некоторым углом к перпендикуляру к площадке, то создаваемое этой силой давление находится по формуле:

В системе СИ давление измеряется в паскалях (Па): 1 Па = 1 Н/м2. Часто используются внесистемные единицы: нормальное атмосферное давление (атм) и давление одного миллиметра ртутного столба (мм.рт.ст.):

1 атм = 101325 Па = 760 мм.рт.ст.

Закон Паскаля: давление, оказываемое на жидкость (или, к слову, газ), передается в любую точку этой жидкости без изменений и во всех направлениях.

Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости над той точкой в которой измеряется давление. Гидростатическое давление столба жидкости рассчитывается по формуле:

Обратите внимание, что оказываемое давление никоим образом не зависит от формы сосуда, а зависит только от рода жидкости (т.е. её плотности) и от высоты столба этой жидкости. Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда.

Итак, если в задаче по гидростатике идет речь о давлении столба жидкости на боковую грань в некоторой конкретной точке, то такое давление находится по предыдущей формуле, где h – расстояние от этой точки до поверхности жидкости. Но иногда в задачах по гидростатике необходимо рассчитать среднее давление на всю боковую поверхность сосуда. В таком случае применим формулу:

В этом случае, h – это общая высота столба жидкости в сосуде.

Если жидкость находится в цилиндре под поршнем, то действуя на поршень некоторой внешней силой F, можно создавать в жидкости дополнительное давление p₀ = F/S, где: S – площадь поршня. Таким образом, полное давление в жидкости на глубине h можно записать в виде:

Если поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению. Если мы погружаемся в воду, то давление на некоторой глубине тоже будет состоять из двух давлений – давления атмосферы и давления столба воды (которое определяется глубиной погружения).

Сообщающиеся сосуды

К оглавлению…

Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне. задачи на сообщающиеся сосуды очень распространены в гидростатике.

Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Дело в том, что в сообщающихся сосудах должно устанавливаться одинаковое давление на одной и той же высоте во всех частях сосуда. Но если жидкости различные, то и высота столбов этих жидкостей должна быть различной, чтобы создать одинаковое давление. Поэтому, разнородные жидкости в сообщающихся сосудах могут и не устанавливаться на одном уровне.

Алгоритм решения задач по гидростатике на сообщающиеся сосуды:

1. Сделать рисунок.
2. Выбрать горизонтальный уровень, ниже которого во всех сосудах находится одинаковая жидкость. Если такого уровня нет, то, естественно, за нулевой уровень выбираем дно сосудов.
3. Записать давления относительно этого уровня во всех сосудах и приравнять.
4. При необходимости использовать свойство несжимаемости жидкости (объем жидкости, вытекающей из одного сосуда, равен объему жидкости, втекающей в другой сосуд).
5. Решить математически полученную систему уравнений.

Гидравлический пресс

К оглавлению…

Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление p (согласно закону Паскаля). Если поршни имеют разные площади S₁ и S₂, то на них со стороны жидкости действуют разные силы F₁ = pS₁ и F₂ = pS₂. Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом, для гидравлического пресса имеем формулу:

Это соотношение вытекает из равенства давлений и выполняется только в идеальном гидравлическом прессе, т.е. таком в котором нет трения. Если S₂ >> S₁, то и F₂ >> F₁. Устройства в которых выполняются эти условия называют гидравлическими прессами (машинами, домкратами). Они позволяют получить значительный выигрыш в силе. Если поршень в узком цилиндре переместить вниз под действием внешней силы F₁ на расстояние h₁, то поршень в широком цилиндре переместится на расстояние h₂, которое может быть найдено из соотношения:

Данное соотношение вытекает из равенства объемов и выполняется в любом гидравлическом прессе. Это выражение получается потому, что при перемещении поршня перемещаются одинаковые объемы жидкости, то есть сколько жидкости ушло из одного цилиндра столько же пришло во второй, или V₁ = V₂. Таким образом, выигрыш в силе обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:

Последняя формула вытекает из равенства работ и выполняется только для идеальных машин, в которых не действуют силы трения. Таким образом, в гидравлическом прессе всё происходит в полном соответствии с «золотым правилом механики»: во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии. При этом ни одна машина не может дать выигрыша в работе.

Так как гидравлический пресс является механизмом, то его работу можно характеризовать КПД (коэффициентом полезного действия). КПД гидравлического пресса в задачах по гидростатике рассчитывается по следующей формуле:

где: А_пол = F₂h₂ – полезная работа (работа по подъему груза), А_затр = F₁h₁ – затраченная работа. В большинстве задач КПД гидравлического пресса принимают за 100%. КПД рассчитывается в том случае, если речь идет о неидеальном гидравлическом прессе.

Еще раз подчеркнем, что для неидеального гидравлического пресса выполняется только соотношение, вытекающее из равенства объемов вытесненной жидкости, а также для таких прессов рассчитывается КПД. Остальные соотношения из этого раздела выполняются только для идеального гидравлического пресса.

Закон Архимеда. Вес тела в жидкости

К оглавлению…

Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:

где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости.

Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.

При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg, а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:

Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρ_т больше плотности жидкости (или газа) ρ (или по–другому mg > F_A), тело будет опускаться на дно. Если же ρ_т < ρ (или по–другому mg < F_A), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.

Плавание тел

К оглавлению…

Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:

где: V_погр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел.

Статика жидкостей и газов.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: давление жидкости, закон Паскаля, закон Архимеда, условия плавания тел.

В гидро- и аэростатике рассматриваются два вопроса: 1) равновесие жидкостей и газов под действием приложенных к ним сил; 2) равновесие твёрдых тел в жидкостях и газах.

Многие из обсуждаемых далее фактов относятся равным образом как к жидкостям, так и к газам. В таких случаях мы будем называть жидкость и газ средой.

При сжатии среды в ней возникают силы упругости, называемые силами давления. Силы давления действуют между соприкасающимися слоями среды, на погружённые в среду твёрдые тела, а также на дно и стенки сосуда.

Сила давления среды обладает двумя характерными свойствами.

1. Сила давления действует перпендикулярно поверхности выделенного элемента среды или твёрдого тела. Это объясняется текучестью среды: силы упругости не возникают в ней при относительном сдвиге слоёв, поэтому отсутствуют силы упругости, касательные к поверхности.

2. Cила давления равномерно распределена по той поверхности, на которую она действует.

Естественной величиной, возникающей в процессе изучения сил давления среды, является давление.

Пусть на поверхность площади действует сила , которая перпендикулярна поверхности и равномерно распределена по ней. Давлением называется величина

.

Единицей измерения давления служит паскаль (Па). 1 Па — это давление, производимое силой 1 Н на поверхность площадью 1 м .

Полезно помнить приближённое значение нормального атмосферного давления: Па.

к оглавлению ▴

Гидростатическое давление.

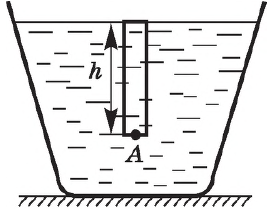
Гидростатическим называется давление неподвижной жидкости, вызванное силой тяжести. Найдём формулу для гидростатического давления столба жидкости.

Предположим, что в сосуд с площадью дна налита жидкость до высоты (рис. 1). Плотность жидкости равна

Рис. 1. Гидростатическое давление

Объём жидкости равен , поэтому масса жидкости . Сила давления жидкости на дно сосуда — это вес жидкости. Так как жидкость неподвижна, её вес равен силе тяжести:

.

Разделив силу на площадь , получим давление жидкости:

.

Это и есть формула гидростатического давления.

Так, на глубине 10 м вода оказывает давление Па, примерно равное атмосферному. Можно сказать, что атмосферное давление приблизительно равно 10 м водного столба.

Для практики столь большая высота столба жидкости неудобна, и реальные жидкостные манометры — ртутные. Посмотрим, какую высоту должен иметь столб ртути ( кг/м), чтобы создать аналогичное давление:

м = 750 мм.

Вот почему для измерения атмосферного давления широко используется миллиметр ртутного столба (мм рт. ст.).

к оглавлению ▴

Закон Паскаля.

Если поставить гвоздь вертикально и ударить по нему молотком, то гвоздь передаст действие молотка по вертикали, но не вбок. Твёрдые тела из-за наличия кристаллической решётки передают производимое на них давление только в направлении действия силы.

Жидкости и газы (напомним, что мы называем их средами) ведут себя иначе. В средах справедлив закон Паскаля.

Закон Паскаля. Давление, оказываемое на жидкость или газ, передаётся в любую точку этой среды без изменения по всем направлениям.

(В частности, на площадку, помещённую внутри жидкости на фиксированной глубине, действует одна и та же сила давления, как эту площадку ни поворачивай.)

Например, ныряльщик на глубине испытывает давление . Почему? Согласно закону Паскаля вода передаёт давление атмосферы без изменения на глубину , где оно прибавляется к гидростатическому давлению водяного столба .

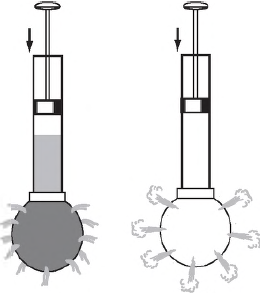
Отличной иллюстрацией закона Паскаля служит опыт с шаром Паскаля. Это шар с множеством отверстий, соединённый с цилиндрическим сосудом (рис. 2)

Рис. 2. Шар Паскаля

Если налить в сосуд воду и двинуть поршень, то вода брызнет из всех отверстий. Это как раз и означает, что вода передаёт внешнее давление по всем направлениям.

То же самое наблюдается и для газа: если сосуд наполнить дымом, то при движении поршня струйки дыма пойдут опять-таки из всех отверстий сразу. Стало быть, газ также передаёт давление по всем направлениям.

Вы ежедневно пользуетесь законом Паскаля, когда выдавливаете зубную пасту из тюбика. А именно, вы сжимаете тюбик в поперечном направлении, а паста двигается перпендикулярно вашему усилию — в продольном направлении. Почему? Ваше давление передаётся внутри тюбика по всем направлениям, в частности — в сторону отверстия тюбика. Туда-то паста и выходит.

к оглавлению ▴

Гидравлический пресс.

Гидравлический пресс — это устройство, дающее выигрыш в силе. То есть, прикладывая сравнительно небольшую силу в одном месте устройства, оказывается возможным получить значительно большее усилие в другом его месте.

Гидравлический пресс изображён на рис. 3. Он состоит из двух сообщающихся сосудов, имеющих разную площадь поперечного сечения и закрытых поршнями. В сосудах между поршнями находится жидкость.

Рис. 3. Гидравлический пресс

Принцип действия гидравлического пресса очень прост и основан на законе Паскаля.

Пусть — площадь малого поршня, — площадь большого поршня. Надавим на малый
поршень с силой . Тогда под малым поршнем в жидкости возникнет давление:

.

Согласно закону Паскаля это давление будет передано без изменения по всем направлениям в любую точку жидкости, в частности — под большой поршень. Следовательно, на большой поршень со стороны жидкости будет действовать сила:

.

Полученное соотношение можно переписать и так:

.

Мы видим, что больше во столько раз, во сколько больше . Например, если площадь большого поршня в 100 раз превышает площадь малого поршня, то усилие на большом поршне окажется в 100 раз больше усилия на малом поршне. Вот каким образом гидравлический пресс даёт выигрыш в силе.

к оглавлению ▴

Закон Архимеда.

Мы знаем, что дерево в воде не тонет. Следовательно, сила тяжести уравновешивается какой-то другой силой, действующей на кусок дерева со стороны воды вертикально вверх. Эта сила называется
выталкивающей или архимедовой силой. Она действует на всякое тело, погружённое в жидкость или газ.

Выясним причину возникновения архимедовой силы. Рассмотрим цилиндр площадью поперечного сечения и высотой , погружённый в жидкость плотности . Основания цилиндра горизонтальны. Верхнее основание находится на глубине , нижнее — на глубине (рис. 4).

На боковую поверхность цилиндра действуют силы давления, которые приводят лишь к сжатию цилиндра. Эти силы можно не принимать во внимание.

На уровне верхнего основания цилиндра давление жидкости равно . На верхнее основание действует сила давления , направленная вертикально вниз.

На уровне нижнего основания цилиндра давление жидкости равно . На нижнее основание действует сила давления , направленная вертикально вверх (закон Паскаля!).

Так как , то , и поэтому возникает равнодействующая сил давления, направленная вверх. Это и есть архимедова сила . Имеем:

.

Но произведение равно объёму цилиндра . Получаем окончательно:

. (1)

Это и есть формула для архимедовой силы. Возникает архимедова сила вследствие того, что давление жидкости на нижнее основание цилиндра больше, чем на верхнее.

Формулу (1) можно интерпретировать следующим образом. Произведение — это масса
жидкости , объём которой равен . Но тогда , где — вес жидкости, взятой в объёме . Поэтому наряду с (1) имеем:

. (2)

Иными словами, архимедова сила, действующая на цилиндр, равна весу жидкости, объём которой совпадает с объёмом цилиндра.

Формулы (1) и (2) справедливы и в общем случае, когда погружённое в жидкость или газ тело объёма имеет любую форму, а не только форму цилиндра (конечно, в случае газа — это плотность газа). Поясним, почему так получается.

Выделим мысленно в среде некоторый объём произвольной формы. Этот объём находится в равновесии: не тонет и не всплывает. Следовательно, сила тяжести, действующая на среду, находящуюся внутри выделенного нами объёма, уравновешена силами давления на поверхность нашего объёма со стороны остальной среды — ведь на нижние элементы поверхности приходится большее давление, чем на верхние.

Иными словами, равнодействующая сил гидростатического давления на поверхность выделенного объёма — архимедова сила — направлена вертикально вверх и равна весу среды в этом объёме.

Сила тяжести, действующая на наш объём, приложена к его центру тяжести. Значит, и архимедова сила должна быть приложена к центру тяжести выделенного объёма. В противном случае сила тяжести и архимедова сила образуют пару сил, которая вызовет вращение нашего объёма (а он находится в равновесии).

А теперь заменим выделенный объём среды твёрдым телом того же объёма и той же самой формы. Ясно, что силы давления среды на поверхность тела не изменятся, так как неизменной осталась конфигурация среды, окружающей тело. Поэтому архимедова сила попрежнему будет направлена вертикально вверх и равна весу среды, взятой в объёме . Точкой приложения архимедовой силы будет центр тяжести тела.

Закон Архимеда. На погружённое в жидкость или газ тело действует выталкивающая сила, направленная вертикально вверх и равная весу среды, объём которой равен объёму тела.

Таким образом, архимедова сила всегда находится по формуле (1). Заметим, что в эту формулу не входят ни плотность тела, ни какие-либо его геометрические характеристики — при фиксированном объёме величина архимедовой силы не зависит от вещества и формы тела.

До сих пор мы рассматривали случай полного погружения тела. Чему равна архимедова сила при частичном погружении? На ту часть тела, которая находится над поверхностью жидкости, никакая выталкивающая сила не действует. Если эту часть мысленно срезать, то величина архимедовой силы не изменится. Но тогда мы получим целиком погружённое тело, объём которого равен объёму погружённой части исходного тела.

Значит, на частично погружённое в жидкость тело действует выталкивающая сила, равная весу жидкости, объём которой равен объёму погружённой части тела. Формула (1) справедлива и в этом случае, только объём всего тела нужно заменить на объём погружённой части погр:

погр.

Архимед обнаружил, что целиком погружённое в воду тело вытесняет объём воды, равный собственному объёму. Тот же факт имеет место для других жидкостей и газов. Поэтому можно сказать, что на всякое тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом среды.

к оглавлению ▴

Плавание тел.

Рассмотрим тело плотности и жидкость плотности . Допустим, что тело полностью погрузили в жидкость и отпустили.

С этого момента на тело действуют лишь сила тяжести и архимедова сила . Если объём тела равен , то

.

Имеются три возможности дальнейшего движения тела.

1. Сила тяжести больше архимедовой силы: , или . В этом случае тело тонет.

2. Сила тяжести равна архимедовой силе: , или . В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.

3. Сила тяжести меньше архимедовой силы: , или . В этом случае тело всплывает, достигая поверхности жидкости. При дальнейшем всплытии начнёт уменьшаться объём погружённой части тела, а вместе с ним и архимедова сила. В какой-то момент архимедова сила сравняется с силой тяжести (положение равновесия). Тело по инерции всплывёт дальше, остановится, снова начнёт погружаться. . . Возникнут затухающие колебания, после которых тело останется плавать в положении равновесия (), частично погрузившись в жидкость.

Таким образом, условие плавания тела можно записать в виде неравенства: .

Закон Паскаля

Гидростатика (от греч. hydor — вода и statos — стоящий) — один из подразделов механики, изучающий равновесие жидкости, а также равновесие твердых тел, частично или полностью погруженных в жидкость.

Закон Паскаля — основной закон гидростатики, согласно которому давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях.

Этот закон был открыт французским ученым Б. Паскалем в 1653 г. и опубликован в 1663 г.

Чтобы убедиться в справедливости закона Паскаля, достаточно проделать простой опыт. Присоединим к трубке с поршнем полый шар со множеством маленьких отверстий. Наполнив шар водой, нажмем на поршень, чтобы увеличить в нем давление. Вода начнет выливаться, но не только через то отверстие, которое находится на линии действия прилагаемой нами силы, а и через все остальные тоже. Причем напор воды, обусловленный внешним давлением, во всех появившихся струйках будет одинаковым.

Аналогичный результат мы получим в том случае, если вместо воды будем использовать дым. Таким образом, закон Паскаля справедлив не только для жидкостей, но и для газов.

Жидкости и газы передают оказываемое на них давление по всем направлениям одинаково.

Передача давления жидкостями и газами во всех направлениях одновременно объясняется достаточно высокой подвижностью частиц, из которых они состоят.

Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление)

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то давление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидростатическим.

Получим формулу для расчета гидростатического давления жидкости на произвольной глубине $h$ (в окрестности точки А на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления $р$ в основании этого столба на площадь его сечения $S$:

$F=pS;$

2) как вес того же столба жидкости, т. е. произведение массы $m$ жидкости на ускорение свободного падения:

$F=mg$

Масса жидкости может быть выражена через ее плотность $р$ и объем $V$:

$m=pV,$

а объем — через высоту столба и площадь его поперечного сечения:

$V=Sh$

Подставляя в формулу $F=mg$ значение массы из $m=pV$ и объема из $V=Sh$, получим:

$F=pVg=pShg$

Приравнивая выражения $F=pS$ и $F=pVg=pShg$ для силы давления, получим:

$pS=pShg$

Разделив обе части последнего равенства на площадь $S$, найдем давление жидкости на глубине $h$:

$p=phg$

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе давление на стенки сосуда, а также давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

С учетом атмосферного давления $р_0$, формула для давления покоящейся в ИСО жидкости на глубине $h$ запишется следующим образом:

$p=p_0+pgh$

Гидростатический парадокс

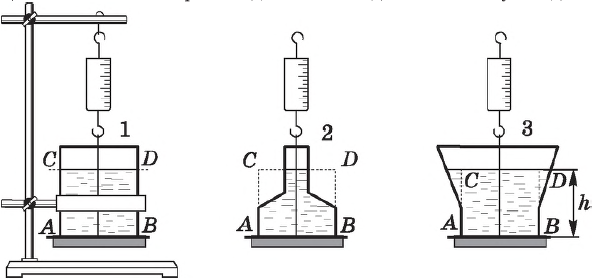
Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужающихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: $p=pgh$ (формула гидростатического давления). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосудов, одна и та же. Она равна весу вертикального столба $АВСD$ жидкости: $P=pghS$, здесь $S$ — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способностью жидкости передавать давление одинаково во всех направлениях.

Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное давление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давление. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Закон Архимеда

Закон Архимеда — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.

Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.

Ниже приведены выводы, следующие из закона Архимеда.

Действие жидкости и газа на погруженное в них тело

Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?

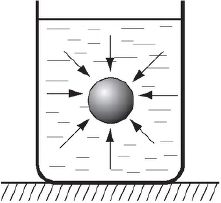
На тело, погруженное в воду, со всех сторон действуют силы давления воды. В каждой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростатическое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих на тело сверху.

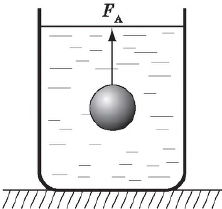
Если заменить все силы давления, приложенные к погруженному в воду телу, одной (результирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке она обозначена как $F_A$.

Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глубинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.

Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном пространстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.

Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).

Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен $Р_0$, то его вес в воздухе равен:

$P{возд}=P_0-F’A,$

где $F’A$ — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что $P{возд}=P_0=mg$.

Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе $P{возд}=P_0$, то вес тела в жидкости равен $Р{жидк}= Р_0 — F_A$. Здесь $F_A$ — архимедова сила, действующая в жидкости. Отсюда следует, что

$F_A=P_0-P{жидк}$

Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.

Другими словами, учитывая формулу $F_A=P_0-P_{жидк}$, можно сказать:

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.

Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем право это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила $F_A$ будет уравновешена действующей вниз силой тяжести $m_{ж}g$ (где $m_{ж}$ — масса жидкости в объеме данного тела):

$F_{a}=m_{ж}g$

Но сила тяжести $m_{ж}g$ равна весу вытесненной жидкости $Р_ж$, Таким образом,

$F_A=P_ж$

Учитывая, что масса жидкости равна произведению ее плотности $р_ж$ на объем, формулу $F_{A}=m_{ж}g$ можно записать в виде:

$F_A=p_{ж}V_{ж}g$

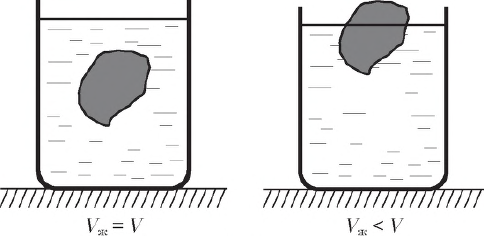
где $V_ж$ — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погружена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом $V$ всего тела; если же тело погружено в жидкость частично, то объем $V_ж$ вытесненной жидкости меньше объема $V$ тела.

Формула $F_{A}=m_{ж}g$ справедлива и для архимедовой силы, действующей в газе. Только в этом случае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.

С учетом вышеизложенного закон Архимеда можно сформулировать так:

На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или газа), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).

Статика и гидростатика (теория)

Статика — раздел механики, изучаю­щий условия равновесия тел.

Условия рав­новесиятела:

а) Поступательно движущееся тело на­ходится в состоянии равновесия (покоится или движется прямолинейно и равномерно),если ,( = 0).

б) Вращающеесятело,имеющее непо­движную ось вращения, находится в покое или равномерно вращается, еслиМ2 + М3 + … + MN = 0,где

М — момент силы — произведение силы на её плечо.

М = Fl = Frsinα, где

l- плечо силы — кратчайшее рас­стояние от оси

вращения до линиидействия силы.r- расстояние от

оси вращения до точки приложения силы;α — угол

между r и F.[М] = Н·м.

М >0, если F,М <0, если F(условно)

Центр масс системы.

l1l2

m1 m2

В большинстве случаев центр тяжести сов­падает с центром масс (например, когда раз­меры тела много меньше радиуса Земли) — воображаемая точка тела при опоре на которую тело находится в равновесии.

Виды равновесия.

1. Виды равновесия тела с закрепленной осью вращения:

а) если ось проходит через центр масс, то тело

находится в безразличном равновесии при любом

положении тела ( а);

б) ось выше точки центра тяжести — ус­тойчивое равновесие (б);

в) ось ниже точки центра тяжести — неус­тойчивое равновесие( в).

2. Виды равновесия тела, имеющего точ­ку опоры:

а) если равнодействующая всех сил направлена

к положению равновесия, то тело нахо­дится в

устойчивом положении (рис. а);

б)если равнодействующая всех сил направлена

от положения равновесия, то тело находится в

неустойчивомравновесии (рис. б);

в)если Σ = 0, — равновесие безразличное (рис. в).

3. Виды равновесия тела, имеющего пло­щадь опоры.

Если вертикаль, проведенная через центр тяжести тела, пересекает

площадь его опоры, то равновесие тела устойчивое. Если не

пересекает, то тело падает, — равновесие не­устойчивое.

Простые механизмы — приспособления, которые служат для преобразования силы. К ним относятся:рычаг (блок, ворот) и наклонная плоскость (клин, винт). Они применяются для получения выигрыша в силе.

F2/F1 – выигрыш в силе

Bl1Ol2AF1l1=F2l2 — условие равновесия рычага для двух сил.

т.е.

Блоки.

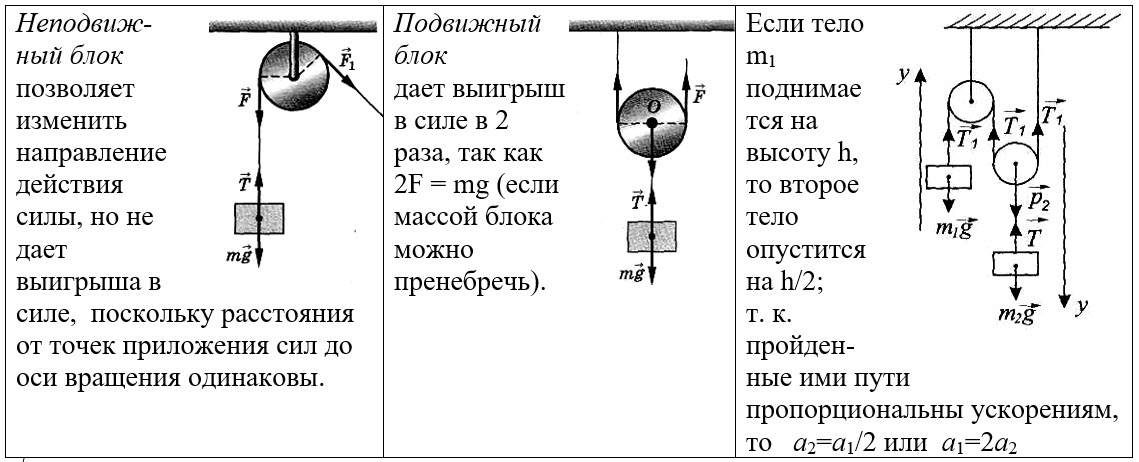
Неподвижный блок позволяет изменить направлениедействия силы, но не дает выигрыша в силе,поскольку расстояния от точек приложения сил дооси вращения одинаковы.

Подвижный блок

дает вы­игрыш в силе в 2 раза, так как 2F = mg (ес­ли массой блока можнопренебречь).

Если тело m1 поднимается на высоту h, то второе тело опустится на h/2;т. к. пройденные ими пути пропорциональны ускорениям, тоa2=a1/2 илиa1=2a2

Золотое правило механики: все простые механизмы, не дают выигрыша в работе — во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.

Гидростатика.

Давление — скалярная физическая величина, равная отношению модуля силы, действующей перпендикулярно поверхности, к площади её поверхности.[р] = 1 Па =1

Гидростатическое давление — давление, обусловленное весом столба жидкости. Манометр — прибор для измерения давления в жидкости или газа.

p = ρжgh— давление на произвольной глубине несжимаемой жидкости

F = pS = ρжghSдна— сила давления на дно сосуда

—среднее давление жидкости на боковую стенку высотой h

F = pS = ρжghSстен -сила давления жидкости на стенку сосуда

На одном и том же уровне давление одинаково во всех направлениях.

Давление р на произвольной глубине h сжимаемой поршнем жидкости определяется давлением поршня и давлением столба жидкости р = рρжgh

Атмосферное давление – давление, которое производит воздушная оболочка Земли.

Опыт Торричелли (1634 г.) свидетельствует: атмосферное давление равно давлению столба ртути в трубке.

Нормальное атмосферное давление:1атм = 760 мм.рт.ст. =1 01325 Па ≈ 10

1мм.рт.ст.=133,3 Па

Оно может изменяться от места к месту и во времени (циклоны и антициклоны) и убывает с увеличением высоты над уровнем моря (на каждые 12 м подъёмаоно уменьшается на 1мм. рт. ст.).

Барометры — приборы для измерения атмосферного давления.

1) жидкостный;2) барометр — анероид (металлический).

Закон Паскаля (1653 г.) —жидкости и газы передают производимое на них давление во все стороны одинаково.

Сообщающимися называются сосуды, соединённые между собой каналом с жидкостью.

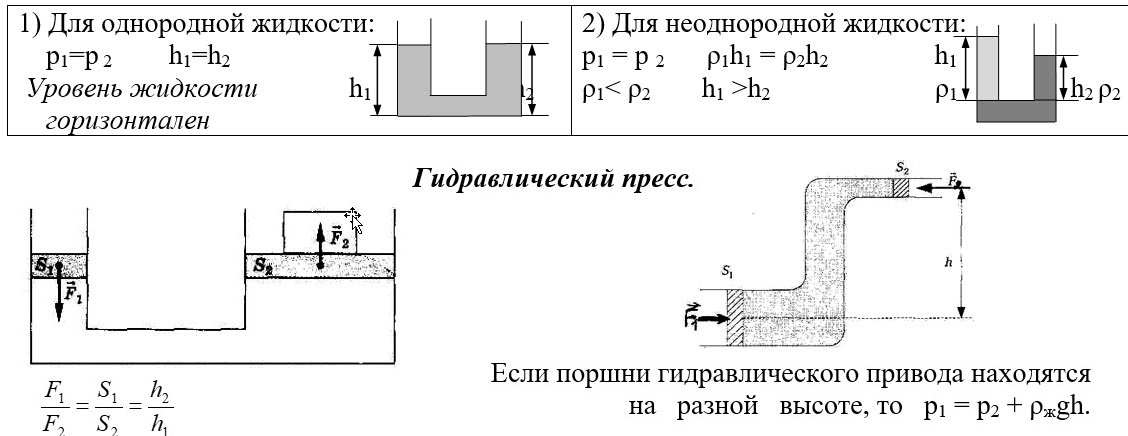
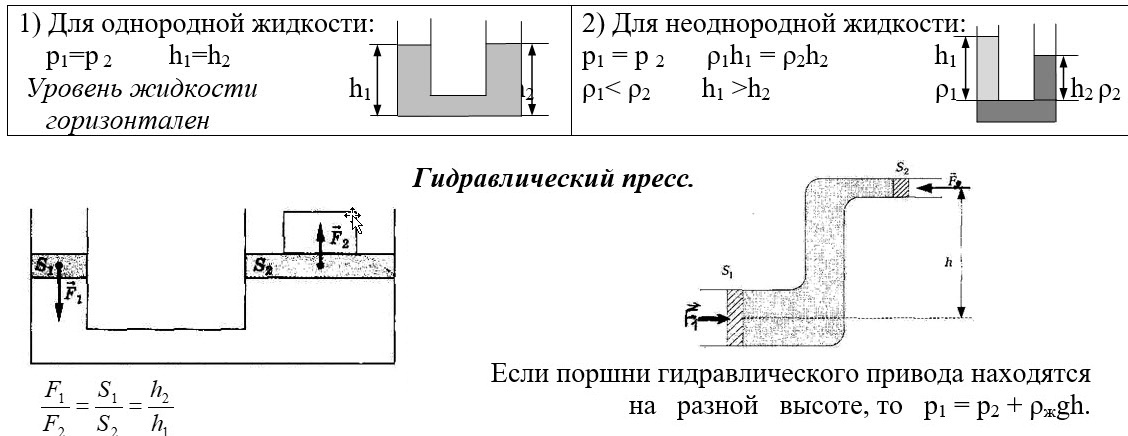
1) Для однородной жидкости:

р 2 h1=h2

Уровень жидкостиh1h2

горизонтален

2) Для неоднородной жидкости:

р2ρ1h1 = ρ2h2 h1

ρ1< ρ h1 >h2 ρ1h2 ρ2

Гидравлический пресс.

Если поршни гидравлического привода находятся

наразнойвысоте, тор2 + ρжgh.

Закон Архимеда: на тело, погруженное в покоящуюся жидкость (или газ), действует выталкивающая сила, направленная вертикально верх и равная весу жидкости, вытесненной телом.

F =ρжgVпчтFA = Рж,выт.= mж,выт g,FA

F = Рвоз — Ржид.Vпчт – объём погруженной части тела.

ρFA

Условие плавания тел:mg

а) F > mg, ρт > ρж — тело всплывает; FA

б) F < mg, ρт < ρж — тело тонет;mgFA=0

в) F = mg, ρт = ρж — тело находится в равновесии

на любой глубине.mg mg

Условие плавания тела на поверхностиF = mg

Если тело будет плавать частично погрузившись в жидкость, то ρт=Vт/Vпчт

На этом основано применение ареометра- прибора для определения плотности жидкости.

Далее вы найдете различные задания по теме «Статика и гидростатика»