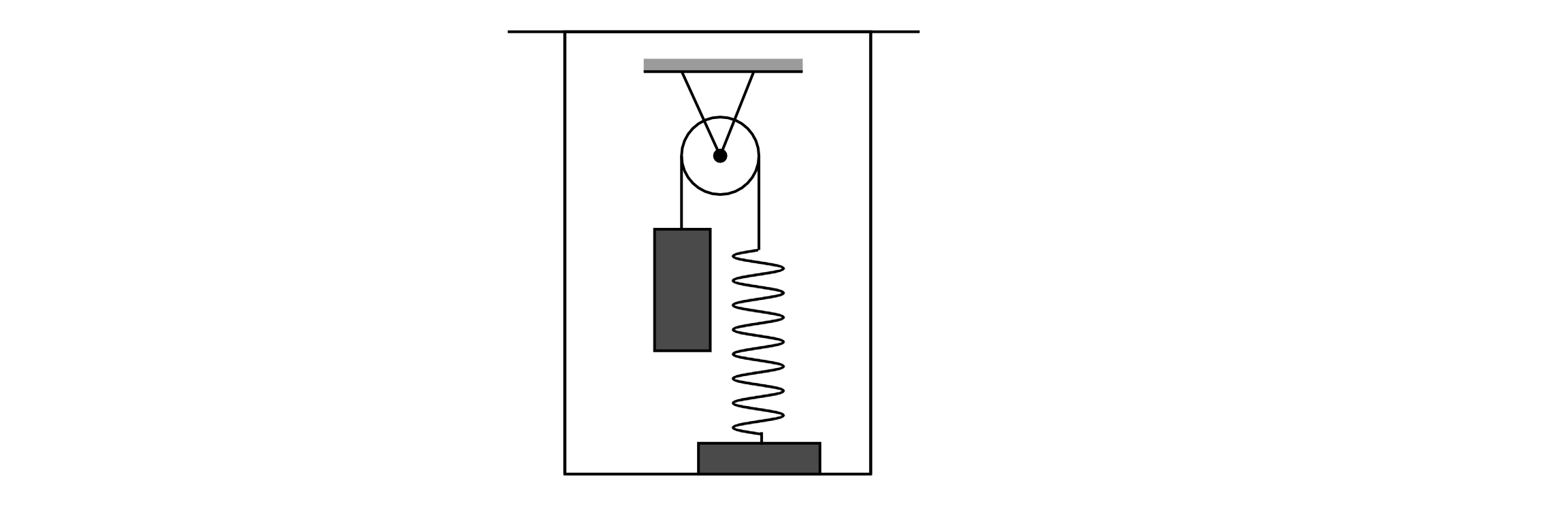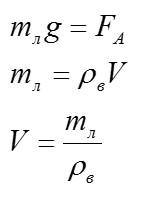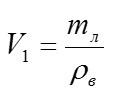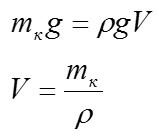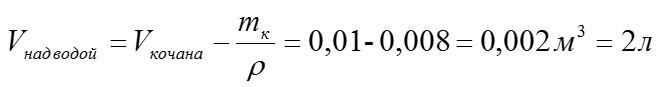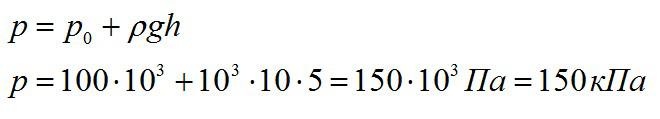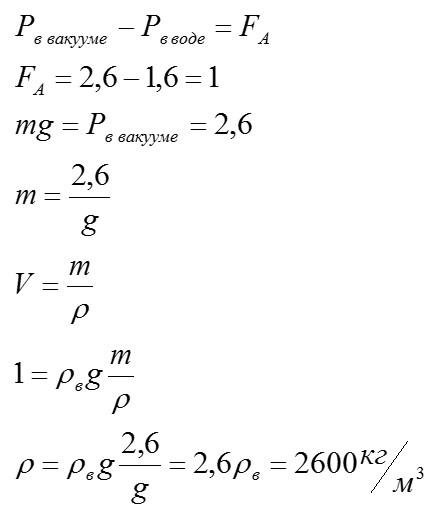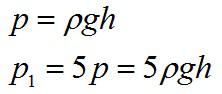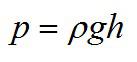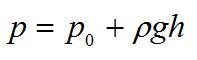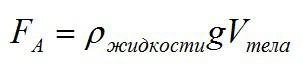Гидростатика задания егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На графике показана зависимость модуля силы Архимеда F_Арх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ответ приведите в килограммах на кубический метр. Ускорение свободного падения принять равным 10 м/с².

В четыре сосуда, вертикальные сечения которых показаны на рисунке, налита вода. Одна клеточка на рисунке соответствует 10 см.

В одном из этих сосудов гидростатическое давление на дно максимально. Чему оно равно? (Ответ дайте в паскалях.) Ускорение свободного падения принять равным 10 м/с².

Кубик из пробки с ребром 10 см опускают в воду. Каково отношение объёма кубика, находящегося над водой, к объёму кубика, находящегося под водой? Плотность пробки 0,25 г/см³.

Пустой цилиндрический стеклянный стакан плавает в воде, погрузившись на половину своей высоты. Дно стакана при плавании горизонтально, плотность стекла 2500 кг/м³. Чему равно отношение внутреннего объёма стакана к его наружному объёму? Ответ представьте в виде десятичной дроби, округлив до десятых долей.

Пройти тестирование по этим заданиям

Источник

Тема 30.

Механика (Расчетная задача высокого уровня сложности+обоснование)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

механика (расчетная задача высокого уровня сложности+обоснование)

30.01Кинематика

30.02Динамика

30.03Законы сохранения в механике

30.04Статика

30.05Гидростатика

30.06Механические колебания

Решаем задачи

Показать ответ и решение

Обоснование
1. Выберем систему отсчета, неподвижно связанную с Землей, и будем считать эту систему отсчета
инерциальной (ИСО).
2. Стержень будем считать твердым телом с осью вращения, проходящей перпендикулярно плоскости
рисунка через точку A. Условия равновесия твердого тела – равенство нулю суммы моментов сил,
приложенных к телу, относительно этой оси и равенство нулю суммы сил, приложенных к
телу.
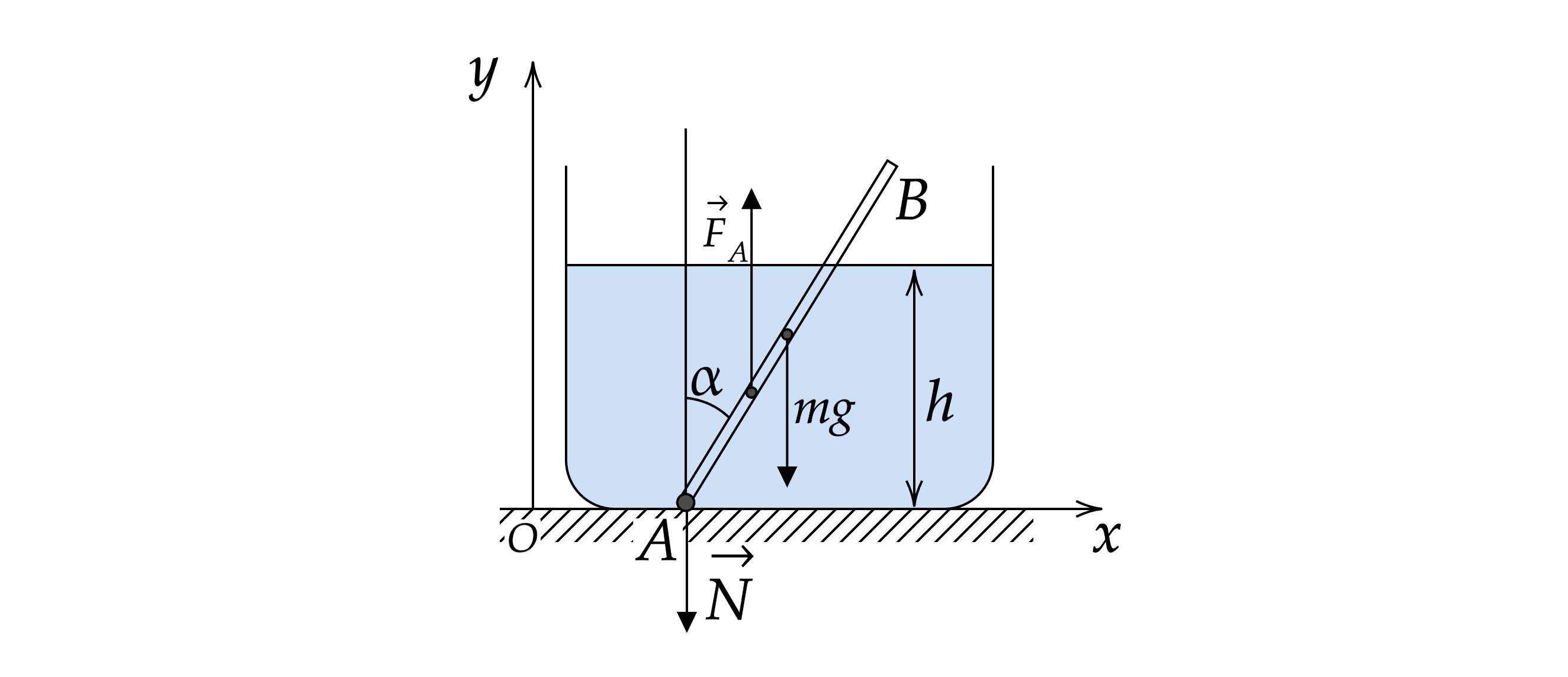
3. На стержень действует три силы: сила тяжести m ⃗g , сила Архимеда ⃗FA и сила реакции шарнира
. Силы m⃗g и ⃗FA направлены вертикально, поэтому из пункта 2 следует, что и сила направлена
вертикально.
4. Силы и связаны третьим законом Ньютона: , поэтому сила тоже направлена по
вертикали.

Решение
Рисунок с изображением сил сделан в обосновании. Сила m ⃗g приложена к центру стержня, а сила F⃗
A
приложена к центру погруженной части.

Пусть длина стержня . Найдем силу Архимеда, действующую на стержень. Стержень погружен в
жидкость на --h--S
cos α , то есть

h
F А = ρ0g -----S
cosα

Запишем правило моментов, относительно оси, проходящей перпендикулярно рисунку через
точку . С учетом того, что момент силы находится произведением силы на плечо этой
силы.

Масса стержня равна

Тогда

l h h
ρ сlSg ⋅--= ρ0g-----S ⋅-------.
2 cosα 2 cosα

Выразим :

∘ ---
l = --h-- ρ0-
cosα ρс

Запишем второй закон Ньютона:

где – ускорение тела.
Спроецируем второй закон Ньютона на вертикальную ось, с учётом, что стержень покоится:

Тогда

---
h h h ∘ ρ0
N = ρ0gS -----− ρ сlSg = ρ0gS ----- − ρ с----- ---Sg
cosα cos α cosα ρ с

Или

∘ -----------------------
--h-- √----- − 4 2 0,2-м- 3 3 3
N = gS cosα (ρ0− ρ0 ρс) = 10 Н/ кг⋅0,25⋅10 м cos30∘ (1000 кг/м − 1000 кг/м ⋅ 600 кг/ м ) ≈ 0,01 Н.

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тело будет рассматривать моделью абсолютно твердого тела (форма и размеры
неизменны).

3. Сказано, что движение тела описывается совокупностью поступательного и вращательного
движения.

4. Сказаны условия равновесия тела относительно поступательного и вращательного
движения.

5. Сказано использование третьего закона Ньютона.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записана формула моменты силы, записано
правило моментов. Записан третий закон Ньютона, записана формула силы Архимеда. Записана
формула для нахождения объёма и массы спицы. Указано, что сила Архимеда приложена к центру
погруженной части).

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Наружный объём бутылки будет складываться из внутреннего объёма бутылки и объёма стекла
M
---
ρ .

V0 = V + M--.
ρ

Запишем второй закон Ньютона:

где – сила Архимеда, – ускорение бутылки.
Сила Архимеда равна:

Условие плавания бутылки, полностью погруженной в воду, то есть объёмом , будет при условии
a = 0 .

Отсюда находим, что бутылка утонет, если в нее налить воды массой

( )
( ) 3 3
m > ρвV − M 1 − ρв- = 1000 кг/ м3 ⋅ 0,5 ⋅ 10 −3 м3 − 0,2 кг 1 −--10--кг/м---- = 0,38 кг
ρ 2,5 ⋅ 103 кг/м3

В сосуде (см. рис.) находится система тел, состоящая из блока с перекинутой через него нитью, к
концам которой привязаны тело объемом и пружина жесткостью . Нижний конец пружины
прикреплен ко дну сосуда. На какую величину изменится сила натяжения нити, действующая на
пружину, если эту систему целиком погрузить в жидкость плотностью ? Считать, что трение в
оси блока отсутствует. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.

Сборник задач «1000 задач»

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Описываем тело моделью абсолютно твёрдого тела (форма и размеры тела неизменны). Можно
применить второй закон Ньютона относительно ИСО для решения задачи.

3. На тело, погруженное в жидкость, действует сила Архимеда, приложенная к центру масс
погруженной части и направленная вертикально вверх

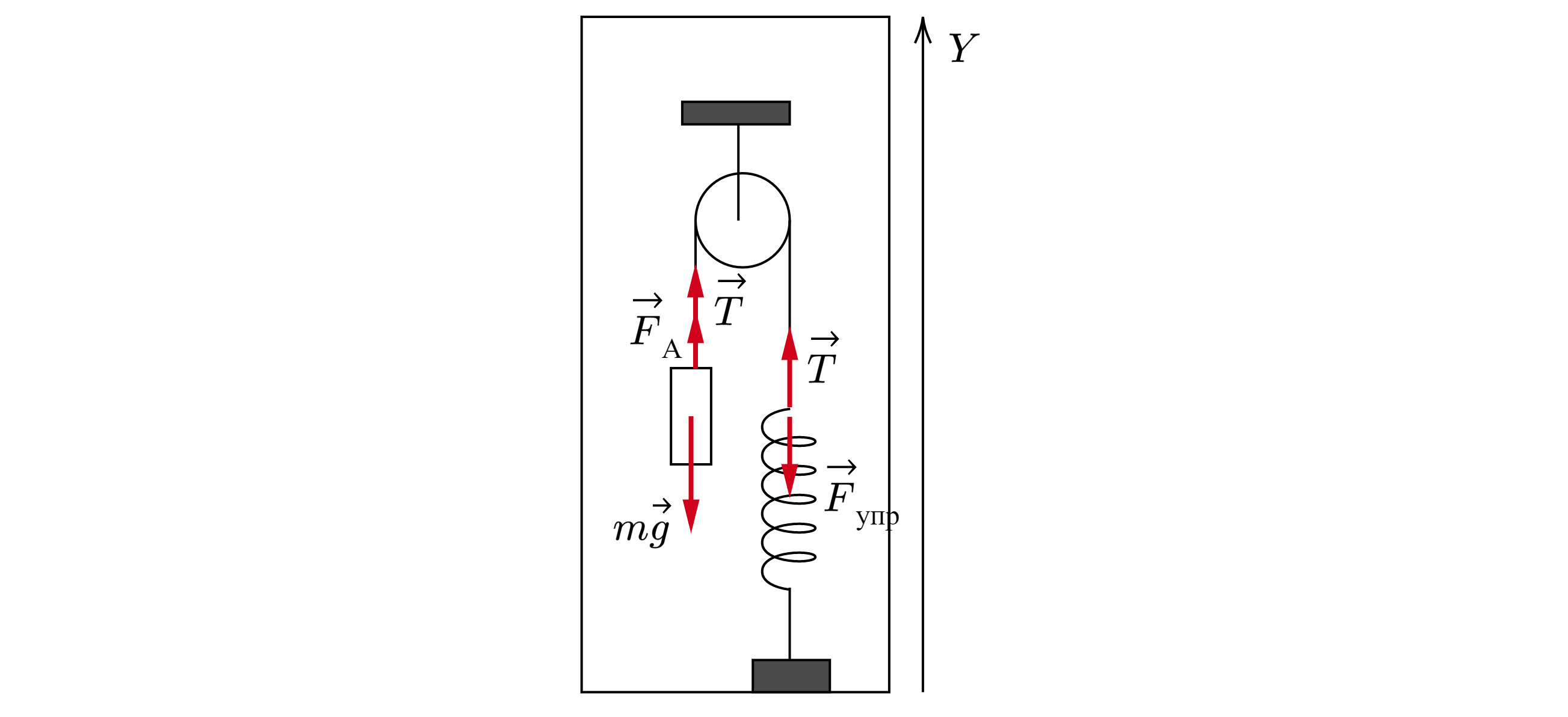
Решение

До погружения системы в жидкость, по второму закону Ньютона

где – сила натяжения нити до погружения системы в жидкость, – ускорение
системы.
Так как система неподвижна, то a1 = 0 . Проецируя второй закон Ньютона на ось

T1 = mg

После погружения системы в жидкость на тело начинает действовать сила Архимеда, поэтому по
второму закону Ньютона:

⃗ ⃗
T2 + m ⃗g + FA = m ⃗a2,

где – сила натяжения нити после погружения системы в жидкость, – сила Архимеда, –
ускорение системы.
Так как система неподвижна, то a1 = 0 . Проецируя второй закон Ньютона на ось

Сила Архимеда находится по формуле:

тогда сила натяжения нити изменится на величину:

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тела будем рассматривать моделью абсолютно твёрдого тела.

3. Обоснована применимость второго закона Ньютона для решения задачи.

4. Указано, что на тело, погруженное в жидкость действует сила Архимеда, приложенная к центру
погруженного объёма.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: сделаны рисунки с расстановкой всех сил
действующих на тела системы, второй закон Ньютона для тела в векторной форме и в проекции на
координатную ось, закон Архимеда).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Описываем спицу моделью твердого тела (форма и размеры тела неизменны, расстояние между
любыми двумя точками тела остаётся неизменным).

3. Движение твердого тела можно описать совокупностью движений — поступательного и
вращательного. Поэтому для равновесия твердого тела в ИСО необходимо два условия. Одно для
поступательного движения, другое — для вращательного движения.

4. Сумма всех приложенных к твёрдому телу внешних сил равна нулю (условие равновесия твёрдого
тела относительно поступательного движения). Также применимо правило моментов (условие
равновесия твёрдого тела относительно вращательного движения).

5. Сила давления на дно сосуда связана с силой реакции опоры по третьему закону Ньютона. Так
как поверхность гладкая, то трение отсутствует и на спицу действует сила реакции опоры со стороны
дна сосуда направленная перпендикулярно поверхности.

Решение

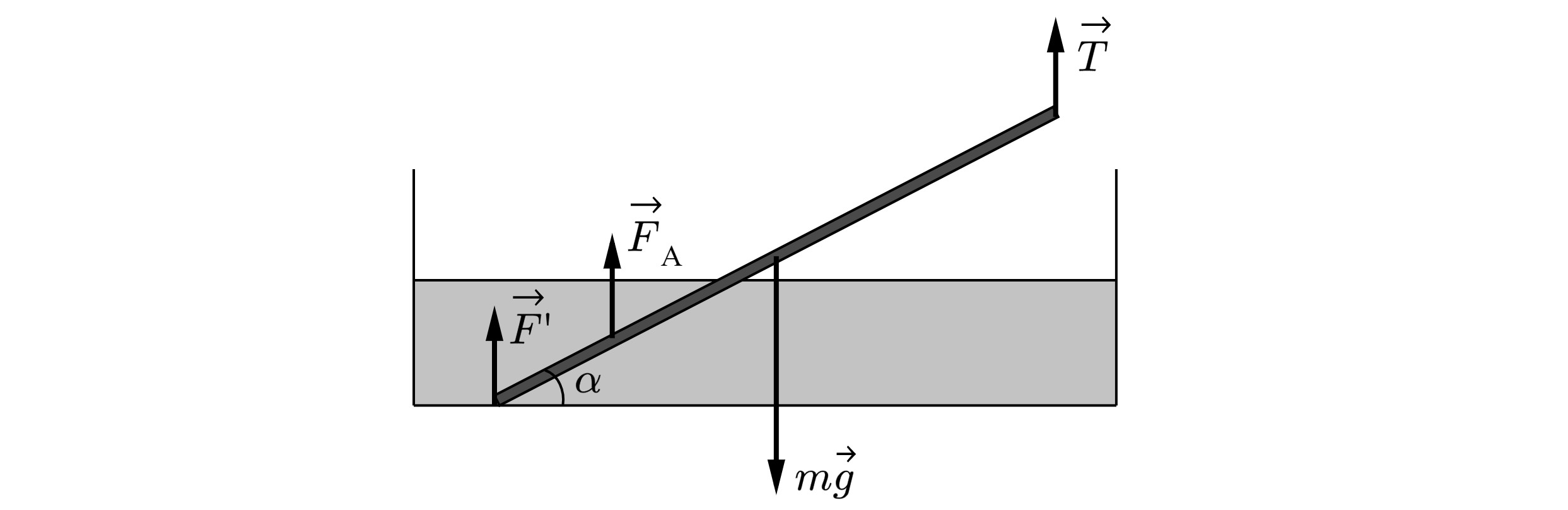
Сделаем рисунок с изображением сил, действующих на спицу

Здесь m ⃗g – сила тяжести, – сила натяжения нити, ⃗FA – архимедова сила, – сила реакции
дна сосуда. Приложение сил: сила тяжести приложена к центру спицы, архимедова сила – к центру
погруженной в воду ее части, сила реакции дна – в месте касания спицы дна, сила натяжения нити – в
месте крепления нити к спице.

Найдем массу спицы

также найдем модуль силы Архимеда

где – объём погруженной части спицы.
Уравнение моментов относительно точки подвеса спицы имеет вид:

( )
F ′L cosα + Slρ g L − l- cos α = SL ρ g L-cosα
в 2 a 2

Учитывая, что по третьему закону Ньютона ′
F = F , находим ответ

( ( ) ) ( 3 ( ) )
F = Lρa-− 1 − -l- lρв gS = 0,25-м-⋅ 2700-кг/м-− 1 − ---0,1---- ⋅ 0,1 м ⋅ 1000 кг/м3 ⋅10 Н/ кг⋅0,1⋅10−4 м2 ≈ 0,026 Н
2 2L 2 2 ⋅ 0,25 м

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тело будет рассматривать моделью абсолютно твердого тела (форма и размеры
неизменны).

3. Сказано, что движение тела описывается совокупностью поступательного и вращательного
движения.

4. Сказаны условия равновесия тела относительно поступательного и вращательного
движения.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

1. На подводную часть действует сила Архимеда, равная:

где
V п – объём погруженной части.
При этом на весь кусок действует сила тяжести

А
весь объём куска льда

M
V0 = ---.
ρ

По
второму закону Ньютона:

Так
как лёд находится в равновесии, то a = 0 и

M--
Fт = FA ⇔ M g = ρ0gV п ⇒ V п = ρ0.

Искомая величина равна

2.
Объем надводной части уменьшился в два раза, следовательно половина льда растаяла, при этом
температура воды в равновесии не изменилась. Запишем уравнение теплового баланса:

5
cm (t − t ) = 0,5M λ ⇒ m = 0,-5M-λ--= 0,5-⋅ 0,45-кг-⋅ 3,36-⋅ 10-Дж/-к-г = 0,6 кг
1 0 c(t1 − t0) 4200 Д ж/ (кг⋅∘C)(30∘C − 0∘C )

Показать ответ и решение

Давление на поршень определяется формулой:

F-
P = S ,

где
– сила, – площадь поршня.
Тогда давление у верхнего поршня

F
P2 = -2. (1)
S2

Давление жидкости на уровне нижнего (первого) поршня

P1 = F1. (2)
S1

При
этом на нижний поршень действует столб жидкости , при этом разность давлений равняется
гидростатическому давлению ρgh

Из
(1) – (3)

F1 F2 1, 76 кН 3,3 кН
---− --- -------2-− ------2-
h = S1----S2-= -110-см---3-220-см-2-= 1 м
ρg 1000 кг/м ⋅ 10 м/ с

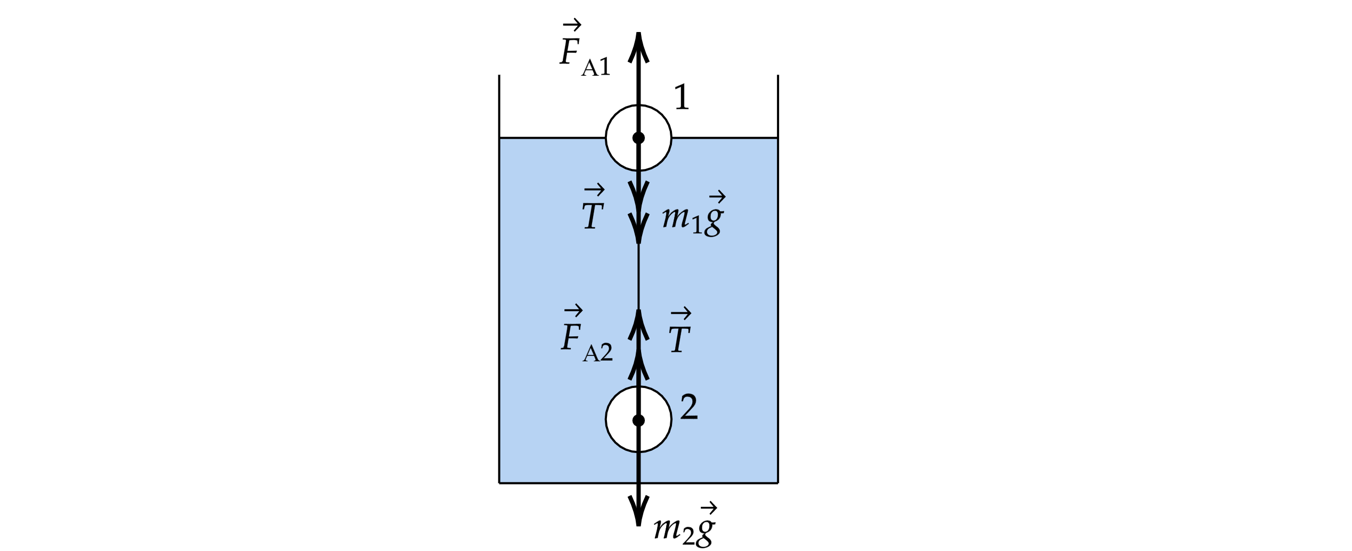
Определить натяжение нити, связывающей два плавающих в воде шара объёмом каждый,
если верхний плавает, наполовину погрузившись в воду, а нижний шар в = 3 тяжелее верхнего.
Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей. Второй закон Ньютона будем
записывать относительно ИСО

2. Описываем тело моделью абсолютно твердого тела (форма и размер тела неизменны).

Решение

Расставим все силы. Запишем второй закон Ньютона для каждого из шаров,

с учетом равновесия

(
{ V-
m1g − ρ0g 2 + T = 0
(
m2g − ρ0gV − T = 0

где m
1 и m
2 – масса верхнего и нижнего шара, ρ
0 – плотность воды, – сила натяжения
нити.
Сложим два уравнения с учетом условия

3 3
4m1g = -ρ0gV ⇒ m1 = -ρ0V
2 8

Подставим во второе уравнение массу шарика

9ρ gV − ρ gV − T = 0
8 0 0

Откуда сила натяжения нити

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тело будем рассматривать моделью абсолютно твердого тела.

3. Объяснена возможность применения второго закона Ньютона.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Шар, до половины погруженный в воду, лежит на дне сосуда и оказывает на него давление с силой,
равной 1/3 действующей на него силы тяжести. Найти плотность материала шара. Какие законы Вы
используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Описываем тело моделью абсолютно твёдрого тела (форма и размеры тела неизменны).

Решение

По третьему закону Ньютона, шари давит на дно с силой, равной силе давления дна на шар, то есть
силе реакции опоры .

Сила давления на дно будет равна разности силы тяжести и силы Архимеда, действующих на
шар

V
N = mg − ρ0g --,
2

где – сила давления на дно, – масса шарика, – плотность воды, – объем шарика. С
учётом условия получим, что:

1-
N = 3 mg

Масса шарика же равна

где – плотность материала, из которого сделан шар. Подставим (2) и (3) в (1) и получим

1 V
-ρgV = ρgV − ρ0g --
3 2

Откуда плотность тела

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тела будем рассматривать абсолютно твёдрого тела.

3. Обоснована применимость законов Ньютона для решения задачи.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

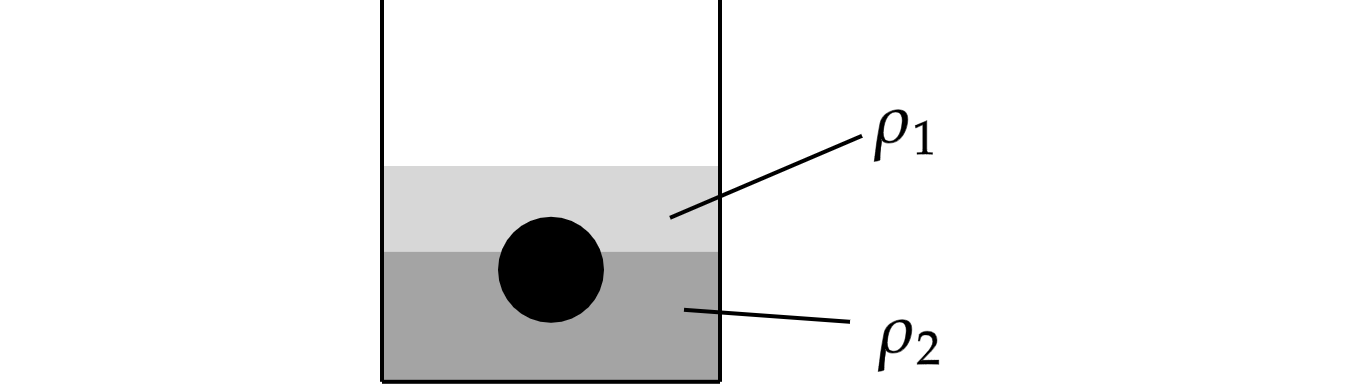
На границе раздела двух жидкостей плотностями и плавает шарик.
Какая должна быть плотность шарика , чтобы над границей раздела жидкостей находилось 25%
объема шарика. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Второй закон Ньютона будем записывать относительно ИСО.

Решение

Так как шарик неподвижен, то из второго закона Ньютона сила Архимеда должна уравновешивать
силу тяжести.

где и – объемы шарика, находящиеся над и под границей раздела жидкостей.
Так как по условию над границей раздела двух жидкостей должно находится 25 % объема,
то

---V1--- 1- ---V2--- 1- 3-
V + V = 4 ⇒ V + V = 1 − 4 = 4 (2)
1 2 1 2

Разделим (1) на и получим

С учетом (2) уравнение (3) можно переписать в виде

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Объяснена возможность применения второго закона Ньютона.

3. Указано, что на тело, погруженное в жидкость действует сила Архимеда, приложенная к центру
погруженного объёма.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон Архимеда, условие плавания тел
(или второй закон Ньютона в векторной форме и в проекции на вертикальную ось), формула
плотности вещества).

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Описываем тела моделью абсолютно твердого тела, так как тела имеют постояннуые размеры и
форму.

Решение

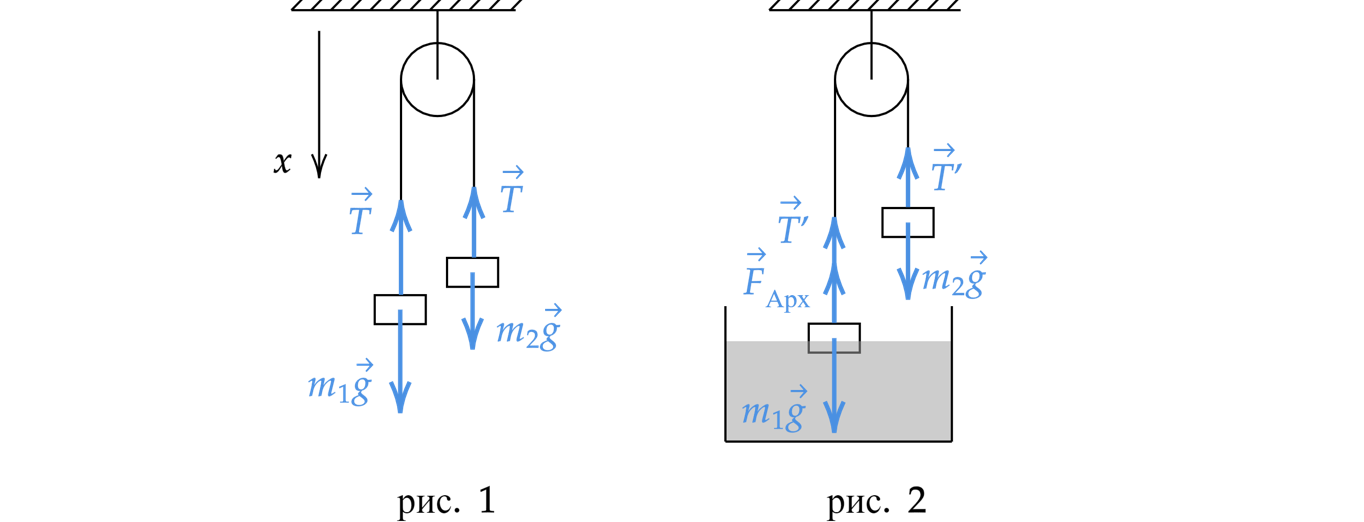
1. Сделаем рисунки с расставлением всех сил

2. Так как нить нерастяжима и невесома, то сила натяжения нить повсюду одинакова. Кроме того,
из кинематической связи имеем, что ускорение первого груза совпадает с ускорением второго (в первом
случае), тогда в проекциях на ось второй закон Ньютона примет вид

({
m1g − T = m1a
(
m2g − T = − m2a

Сложим 2 уравнения и выразим массу второго груза

m = m1-(g −-a)
2 g + a

3. Запишем второй закон Ньютона для второго случая

(
{ m1g − T′ − Fарх = 0

( m2g − T′ = 0

Вычтем из первого уравнения системы второе, выразив ускорение, с учетом того, что сила Архимеда
равна , а масса второго груза m (g − a)
m2 = --1-------
g + a

3 − 4 3
a = ---ρgV----= 1000-к-г/м--⋅-10-Н/к-г ⋅ 1,5-⋅ 10-м- ≈ 1,8 м/ с2
2m1 − ρV 2 ⋅ 0,5 кг − 1000 кг/м3 1, 5 ⋅ 10 −4 м3

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тела будем рассматривать моделью абсолютно твердого тела.

3. Обоснована применимость второго закона Ньютона для описания движения тел.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: сделаны рисунки
для обоих случаев с расстановкой всех сил действующих на тела системы, обосновано
равенство ускорений движения тел, второй закон Ньютона для каждого из тел системы для
первого и второго случаев в векторной форме и в проекции на координатную ось, закон
Архимеда).

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

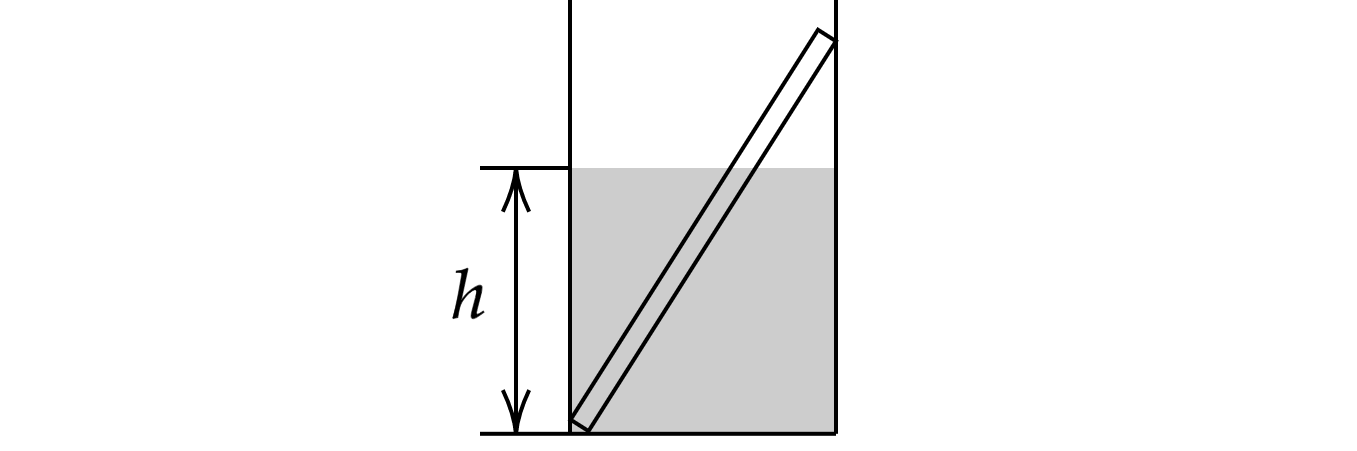
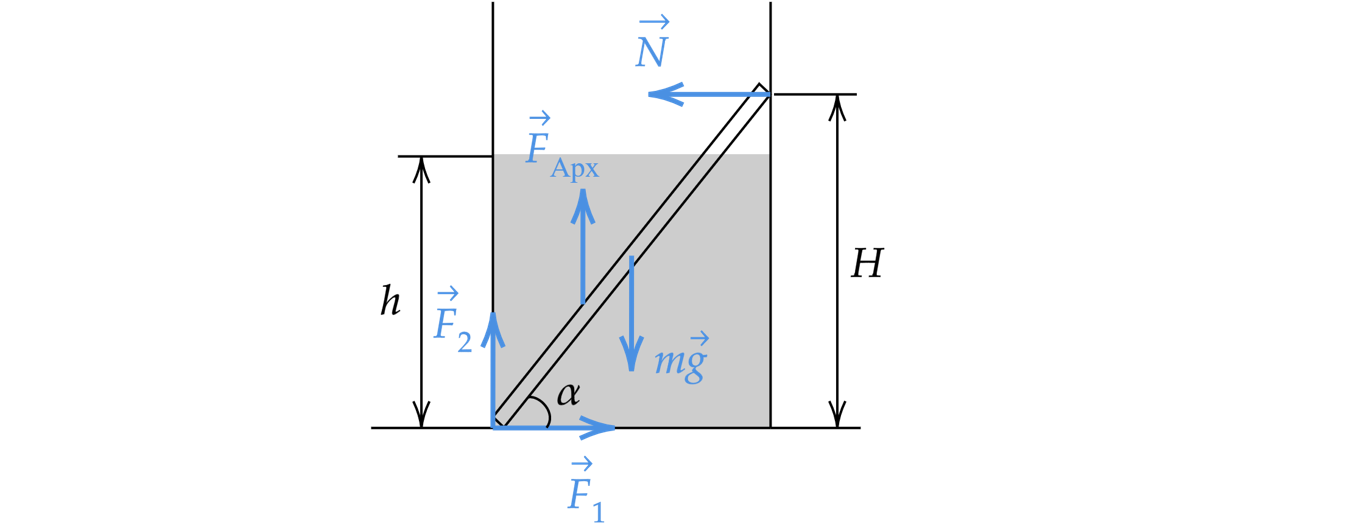
В гладкий высокий стакан радиусом 4 см поставили однородную алюминиевую палочку длиной 10 см и
массой 0,9 г, после чего в стакан налили до высоты h = 4 см воду. Найдите модуль силы , с которой
верхний конец палочки давит на стенку стакана. Сделайте рисунок с указанием сил, действующих на
палочку. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

5. Так как поверхность гладкая, то трение отсутствует и на доску действует сила реакции опоры со
стороны дна сосуда направленная перпендикулярно поверхности, также действует сила реакции опоры,
направленная со со стороны левой стенки вправо.

Решение

1. Найдем высоту палочки, относительно дна стакана

∘ -----------------------
√ 2------2- 2 2
H = l − 4R = 0,01 м − 4 ⋅ 0,0016 м = 0,06 м

где – длина палочки, – радиус стакана.
2. Сделаем рисунок с изображением всех сил, действующих на палочку.

3. Найдем силу Архимеда, действующую на палочку. Палочка погружена в жидкость на h
---
H от
своего объема, то есть

( )
h ρж mgh
F Арх = ρжg --V = --------
H ρ H

где – объем тела, – плотность палочки, – плотность жидкости.
4. Запишем правило моментов, относительно оси, проходящей перпендикулярно рисунку через точку
приложения сил и .

( )
h-
mgR − F арх 2ctgα − N H = 0

Выразим силу реакции опоры. С учетом третьего закона Ньютона она будет равна силе давления
палки на стенку сосуда.

( ) ( ( )2 )
R-- -h-- -R- ρж- h--
N = mg H − F арх 2H ctgα = mg H 1 − ρ H =

( ( ) )
0,-04 м 1000-кг/м3- 0,04-м- 2 − 3
F = N = 0,0009 кг ⋅ 10 Н/ кг0, 06 м 1 − 2700 кг/м3 0,06 м ≈ 5 ⋅ 10 Н

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тело будем рассматривать моделью твердого тела (форма и размеры
неизменны).

3. Описание того, что движение тела описывается совокупностью поступательного и вращательного
движения.

4. Сказаны условия равновесия тела относительно поступательного и вращательного
движения.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: правило моментов сил условия равновесия
твердого тела в ИСО, формула момента силы относительно оси вращения, закон Архимеда, формула
плотности вещества, третий закон Ньютона).

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Вертикальная труба с поршнем, плотно прилегающим к ее внутренним стенкам, опущена нижним
концом в воду. Вначале поршень находился в самом нижнем положении, на уровне воды, а затем его
медленно поднимают на высоту 20 м. Пренебрегая трением, найдите совершенную при этом работу (в
кДж). Площадь поршня 100 см Атмосферное давление 100 кПа. Какие законы Вы используете для
решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Описываем поршень моделью абсолютно твердого тела (форма и размеры неизменны).

3. Так как по условию сказано, трением пренебречь, то можно утверждать что вся работа идет на
поднятие поршня

Решение

Процесс поднятия поршня происходит в 2 этапа. Первый этап: давление под поршнем будет
положительным и равное

где – плотность воды, – высота подъезда поршня.
Вода будет заполнять весь объем под поршнем, а приложенная к поршню сила будет компенсировать
давление внутри, она будет равна

Она будет линейно возрастать. Это будет до момента, пока вода не поднимется на высоту,
равную

p 100 кП а
h0 = -0-= ----------3----- = 10 м
ρg 1000 кг/м ⋅ 10 ∕

При подъеме поршня на высоту давление станет равным нулю. После этого вода перестает
подниматься, а сила, приложенная к поршню, остается равной

Работа по поднятию равна сумме работ: работе по поднятию до высоты : 0-+-F1- poSh0-
A0 = 2 h0 = 2
(так как она линейно возрастает, то берем как среднее арифметическое от начального, до конечного) и
работе по поднятию от высоты и конечной высоты . Значит,
полная работа равна

( )
poSh0- h0- − 2 2
A = 2 + p0Sh1 − p0Sh0 = p0S h1 − 2 ) = 100 к Па ⋅ 10 м (20 м − 5 м = 15 кД ж

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тела будем рассматривать моделью абсолютно твердого тела.

3. Сказано, на что идет работа при поднятии поршня.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

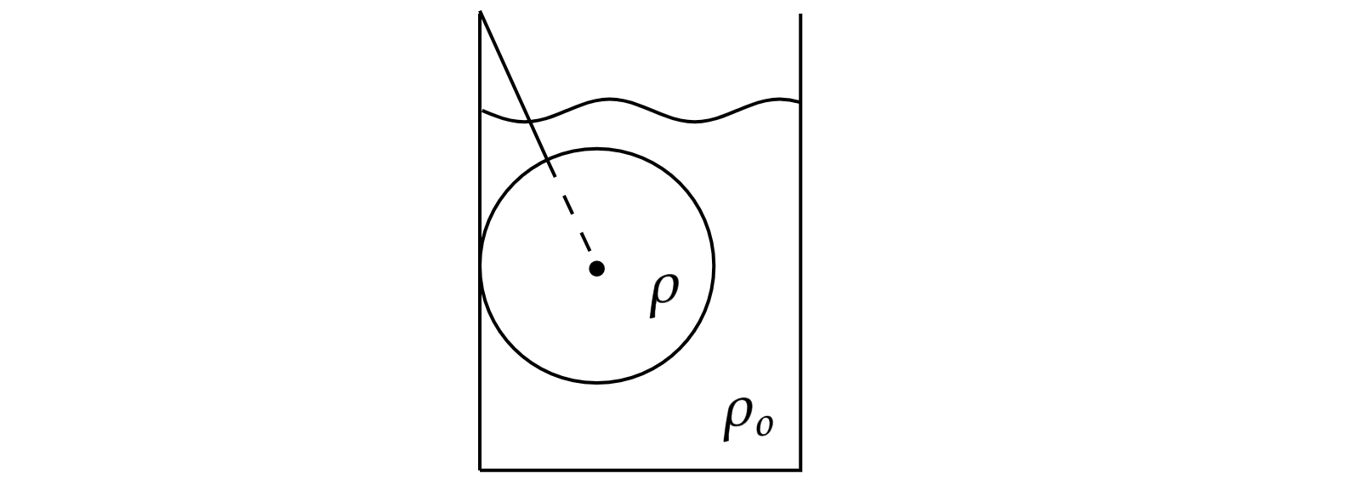
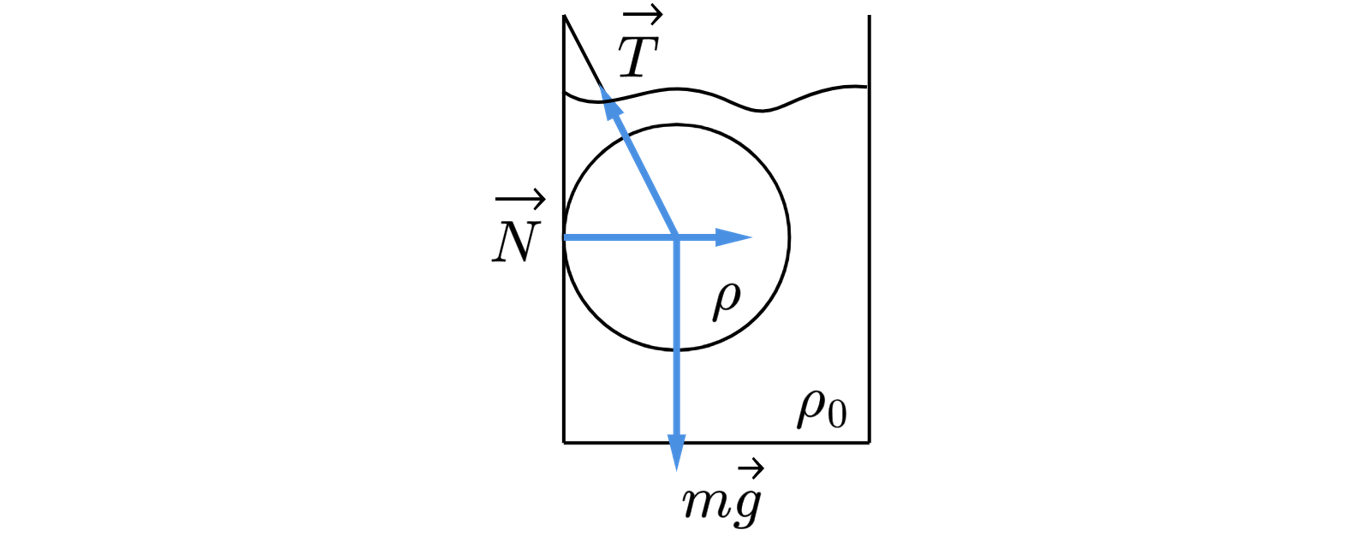
К стенке стакана с водой привязан алюминиевый шар массой m = 3 кг. Нить образует со стенкой
сосуда угол ∘
α = 30 . Найдите силу натяжения нити. Какие законы Вы используете для решения
задачи? Обоснуйте их применение.
Досрочная волна, 2018

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Описываем тело моделью твердого тела (форма и размеры тела неизменны, расстояние между
любыми двумя точками тела остаётся неизменным).

5. Шар целиком погружён в жидкость и отсутствует трение между шаром и станкой сосуда. Значит,
все вешние силы, действующие на шар, кроме силы натяжения нити, действуют по прямым,
проходящим через центр шара. Значит, сумма моментов этих сил относительно оси, проходящей через
центр шара, равна нулю. При равновесии шара в ИСО сумма моментов всех внешних сил равна нулю.
следовательно, и момент силы натяжения нити, относительно оси, проходящей через центр шара, тоже
равен нулю, поэтому сила натяжения нити действует по прямой, проходящей через центр
шара.

Решение

Второй закон Ньютона в этом случае

где – сила Архимеда, – сила натяжения нити, – ускорение тела.
Так как тело покоится, то его ускорение равно 0.
Запишем второй закон Ньютона на ось

С учетом того, что сила Архимеда равна

m
F А = ρ0gV = ρ0g-- (2)
ρ

– плотность жидкости, – объем погруженной части тела, – плотность алюминия.
Выразим из (1) силу натяжения нити , с учетом (2)

mg − ρ0gm--
--------ρ--- mg-(ρ-−-ρ0) 30 Н-(2700-к-г/м3-−-1000-кг/м3-)
T = cosα = ρ cosα = √3-- = 22 Н
2700 к г/м3 ⋅----
2

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тело будем рассматривать моделью твердого тела (форма и размеры
неизменны).

3. Описание того, что движение тела описывается совокупностью поступательного и вращательного
движения..

4. Сказаны условия равновесия тела относительно поступательного и вращательного
движения.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Будем использовать формулы механики для решения данной задачи.

3. Так как масло «легче»воды, то она будет сверху в трубе.

Решение

Воды будет общей жидкостью для двух сообщающихся сосудов.
Приравняем давление внутри трубки и вне ее.

где ρ м – плотность масла, ρ в – плотность воды, h м – высота столба масла, h в – высота столба
воды, – атмосферное давление.
Высоту столба жидкостей выразим через массу масла. Для этого воспользуемся формулами
массы:

где – плотность масла, – его объем.
Объем можно найти по формуле:

V = Sh,

где – высота столба масла.
Отсюда для масла

h = --m---- (2)
м ρ м ⋅ S

Из (1) выразим высоту воды

ρм
h в = --h м,
ρв

тогда с учётом (2):

h = --m---
в ρ в ⋅ S

Разность высот

m ( 1 1 ) 0,1 кг ( 1 1 )
Δh = h м − h в = -- ---− --- = --------2 ---------3 − ----------3 = 0,025 м = 2,5 см
S ρ м ρ в 0, 001 м 800 кг/м 1000 кг/м

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что решать задачу будем при помощи формул механики.

3. Сказано, что менее плотная жидкость находится сверху, нежели более плотная.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Описываем тело моделью материальной точки, так как в условиях данной задачи размерами тела
можно пренебречь.

Решение

Пусть – плотность жидкости, – первоначальный уровень воды, тогда после перерезания нити
уровень уменьшится на . Значит гидростатическое давление до перерезания нити

Сила давления на дно же равна

F = PS,

где – площадь дна сосуда. Так как есть еще сила натяжения нити, которая удерживает шар в
воде, но не действует на дно, то сила давления на дно равна

F = ρ ⋅ g ⋅ H ⋅ S − T
1

Во втором случае нить обрывается и шар всплывает и уровень уменьшается на , тогда сила
давления на дно будет равна

Поскольку масса шара и воды остается неизменным, то и сила давления на дно при равновесных
состояниях остается неизменной, а значит мы можем приравнять и

Выразим силу натяжения нити

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета.

2. Сказано, что тело будем рассматривать моделью материальной точки.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Источник

Гидростатика: задачи ненулевого уровня.

В этой статье собраны задачи по гидростатике из задачника Русакова и др. Задачи «крепкие» — тянут на подготовку к городскому этапу олимпиады. Вполне доступны для решения школьниками от 8 класса.

Задача 1. Сосуд без дна, имеющий форму и размеры, указанные на рисунке, стоит на гладком столе. Масса сосуда равна . В сосуд наливают жидкость. После того, как уровень достигает высоты , сосуд приподнимается под действием жидкости. Найти плотность жидкости.

Рисунок 1

Сосуд начнет приподниматься, когда сила давления воды снизу и сила тяжести сравняются.

Ответ:

Задача 2.

В жидкость опущена тонкостенная трубка диаметром , к которой прилегает цилиндрический диск диаметром и толщиной . Плотность диска больше плотности жидкости . На какой глубине диск оторвется, если трубку медленно вытаскивать из жидкости?

Рисунок 2

Рассмотрим диск. На него давит вода и снизу, и сверху. Поэтому, когда сила давления воды снизу станет меньше суммы силы давления воды сверху и силы тяжести, диск оторвется.

Сила давления воды снизу:

Сила давления воды сверху:

Тогда условие равенства нулю равнодействующей:

Ответ:

Задача 3. Шар массой , привязанный ко дну невесомой нитью, плавает на поверхности воды и погружен в нее наполовину. Сила натяжения нити равна . Найти плотность материала шара. Плотность воды считать известной.

Рисунок 3

Запишем условие равновесия шара:

Ответ:

Задача 4.

Однородное тело плавает на поверхности керосина так, что объем погруженной части составляет 0,5 всего объема тела. Определить долю погруженной части от полного объема тела, когда тело переместят в воду. Плотность керосина принять равной 800 кг/м.

Запишем условие плавания в керосине:

Мы нашли плотность тела, теперь перемещаем его в воду. Записываем условие плавания:

Где — объем погруженной в воду части.

Подставим ранее найденную плотность

Ответ: .

Задача 5.

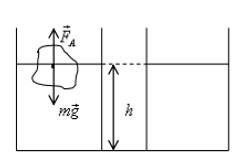
Шар массой наполовину погружен в воду и давит на дно с силой . Найти плотность материала шара. Плотность воды дана.

Рисунок 4

Сила давления шара на дно равна разности силы тяжести и силы Архимеда:

Ответ:

Задача 6.

Определите силу натяжения нити, связывающей два шарика объема 8 см, если верхний шарик плавает, наполовину погрузившись в воду. Нижний шарик в три раза тяжелее верхнего. Плотность воды известна, принять м/с.

Рисунок 5

Пусть — верхний шарик, тогда — нижний.

Записываем условия равновесия шариков:

Если уравнения сложить, получим

Теперь можно найти силу натяжения нити:

Ответ: 0,01 Н.

5

Роман
✉️
07.07.2020 16:17:05

Анна, не совсем понятно решение 3-ей задачи. Вы плотность шара выражаете через плотность этого же шара. В итоговой формуле должны быть известные величины: m, Т и плотность воды.

Анна Валерьевна
✨
09.07.2020 07:36:37

Конечно! Отвлеклась и не дорешала. Исправлено.

Aktrc
✉️
13.08.2020 16:34:01

Откуда берется радиус r во второй задаче?

Анна Валерьевна
✨
14.08.2020 05:43:48

Пояснила.

Татьяна
✉️
24.10.2020 12:31:16

большое спасибо за задачи

Источник

7. Механика (установление соответствия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Гидростатика

Тело, находящееся в воде или на поверхности, медленно, не останавливаясь, двигают по вертикали.

Установите соответствие между графиками и процессами, которые их описывают.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

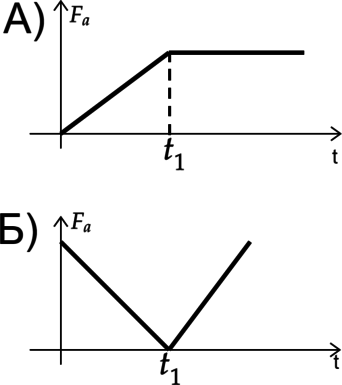
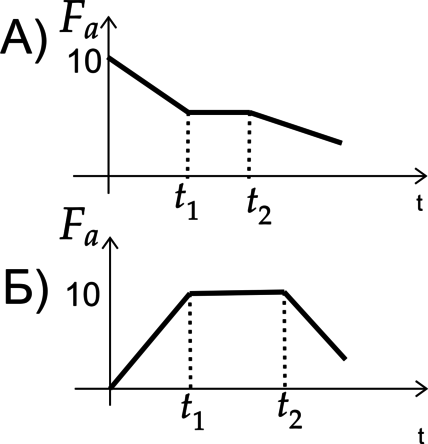
ГРАФИКИ

ПРОЦЕССЫ

1) Тело до (t_1) опускали вниз, а после (t_1) оно полностью погрузилось в воду.

2) Тело до (t_1) поднимали, а после оно находилось на поверхности.

3) Тело до (t_1) поднимали, а после опускали вниз.

4) Тело всё время находилось на одной глубине погружения.

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Сила Архимеда находится по формуле [F_a=rho g V] Где (rho) — плотность жидкости, а (V) — объем погруженной части тела. Так как сила Архимеда сначала увеличивалась, а затем была постояна, то объем погруженной части тоже увеличивался, а затем был постоянный, а значит тело погружали, пока оно не погрузилось полностью. Ответ — 1
Б) Сила Архимеда сначала уменьшалась, а затем увеличивалась, значит тоже самое происходило и с объемом тела. Ответ — 3

Ответ: 13

Тело массой (m) и объемом (V) плавает на поверхности жидкости плотностью (rho) и погружено на (dfrac{1}{4}V).

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

[begin{array}{ll}

text{Физические величины}&text{Формулы}\

text{А) Сила тяжести} & text{1)} dfrac{1}{4}rho g V \
text{Б) Плотность тела} &text{2)} rho g V \
&text{3)} dfrac{1}{4} rho \
&text{4)} rho \

end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как тело плавает, то силу тяжести уравновешивает сила Архимеда [F_text{т}=dfrac{1}{4}rho g V]

Ответ – 1

Б) Из пункта А) [mg= F_text{т}=dfrac{1}{4}rho V]

Заменим (m) на (rho_o cdot V), где (rho_0) – плотность тела. Получим [rho_0 cdot V= dfrac{1}{4}rho V]

Или [rho_o=dfrac{1}{4}rho]

Ответ – 3

Ответ: 13

Тело сделанное из железа плотностью (rho_0)=7800 кг/м(^3) и объемом (V)=0,001 м(^3) в первом случае погружают в воду, а во втором в ртуть.

Установите соответствие между физическими величинами и их значениями.

[begin{array}{ll}

text{Физические величины}&text{Значения}\

text{А) Сила Архимеда в воде} &1) 78text{ Н} \
text{Б) Сила Архимеда в ртути} &2) 10 text{ Н} \
&3) 136 text{ Н} \
&4) 100 text{ Н} \

end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как плотность железа больше плотности воды, то тело тонет. Значит сила Архимеда находится по формуле [F_a=rho_1 g V_text{т}]

Где (rho_1) — плотность воды, а (V_text{т}) — объем погруженной части (т.к. тело тонет, то он равен (V)).

Найдем силу Архимеда (F_a=1000text{ кг/м$^3$} cdot 10 text{ м/с$^2$} cdot 0,001 text{ м$^3$}= 10text{ Н} ). Ответ – 2

Б) Так как плотность железа меньше плотности ртути, то тело будет плавать на поверхности и сила Архимеда будет уравновешивать силу тяжести [F_a=F_text{т}=mg=rho_0cdot Vcdot g]

Найдем силу Архимеда (F_a= 7800text{ кг/м$^3$} cdot 0,001 text{ м$^3$} cdot 10 text{ м/с}^2= 78 text{ Н}). Ответ – 1

Ответ: 21

Тело объемом (V)=0,002 м(^3), находящееся в сосуде с водой плотностью (rho)=1000 кг/м(^3), двигают по вертикали.

Установите соответствие между графиками и процессами, которые их описывают.

ГРАФИКИ

ПРОЦЕССЫ

1) Тело до (t_1) погружали в жидкость, от (t_1) до (t_2) находилось полностью под водой, а от (t_2) поднимали вверх.

2) Тело до (t_1) поднимали, от (t_1) до (t_2) было на одной глубине погружений, от (t_2) поднимали вверх.

3) Тело до (t_1) погружали в жидкость, от (t_1) до (t_2) было на одной глубине погружений, от (t_2) поднимали вверх.

4) Тело всё время находилось на одной глубине погружения.

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

Найдем максимальную силу Архимеда по формуле (F_a=rho cdot g cdot V). [F_a=1000text{ кг/м$^3$} cdot 10 text{ Н/м} cdot 0,002 text{ м$^3$}= 20text{ Н}]

А) Заметим, что до (t_1) (F_a) уменьшалась, от (t_1) до (t_2) оставалась неизменной, после опять уменьшалась, значит и объем ведет себя также. Ответ – 2

Б) Проанализируем график до (t_1) (F_a) увеличивалась, от (t_1) до (t_2) оставалась неизменной, но не доходила до своего максимума, после уменьшалась, найдем подходящий. Ответ 1) не подходит, так как от (t_1) до (t_2) (F_a) не достигла максимума. Ответ – 3

Ответ: 23

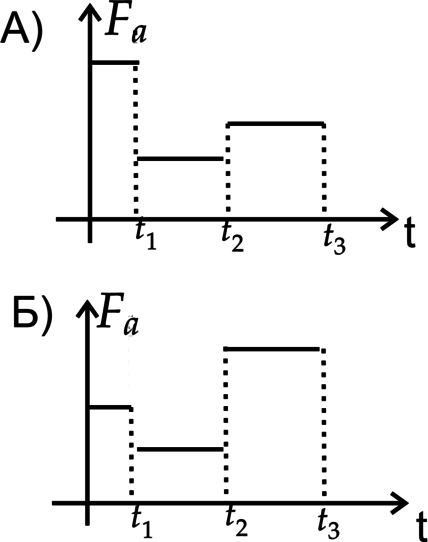
Тело поочередно погружали на полный объем в одну из трех жидкостей с плотностями (rho_1)=(rho), (rho_2)=(2rho) и (rho_3)=(4rho). Представлены два графика. Определите последовательность жидкостей в каждом опыте.

ГРАФИКИ

ПОЛЕДОВАТЕЛЬНОСТЬ

1) (rho_1), (rho_2), (rho_3)

2) (rho_2), (rho_3), (rho_1)

3) (rho_2), (rho_1), (rho_3)

4) (rho_3), (rho_1), (rho_2)

Сила Архимеда рассчитывается по формуле (F_a=rho g V), где (rho) — плотность жидкости. (V) — объем погруженной части тела. Так как (V) везде одинаковый, то (F_a) зависит только от (rho).

А) До (t_1) (F_a) максимальна, а значит первым идет жидкость с плотностью (rho_3). На втором этапе сила Архимеда минимальна, следовательно, плотность жидкости (rho_1). Последняя жидкость (rho_2). Ответ – 4

Б) Первый этап — (F_a) принимает среднее значение, значит жидкость с плотностью (rho_2), второй — минимальное, значит — (rho_1). Третья жидкость с максимальной плотностью — (rho_3). Ответ– 3

Ответ: 43

Тело массой (m) и объёмом (V) плавает на поверхности жидкости плотностью (rho). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

[begin{array}{ll}

text{Физические величины}&text{Формула}\

text{А) Сила Архимеда } &1) rho g V \
text{Б) Объём погружённой части тела } &2) V \
&3) mg \
&4) dfrac{m}{rho} \
end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как тело плавает на поверхности воды, то сила Архимеда уравновешивает силу тяжести, значит (F_a=mg). Ответ – 3

Б) Выразим объем погруженной части (V_text{п} ) из (F_a=rho g V_text{п}= mg), значит (V_text{п}=dfrac{m}{rho}). Ответ – 4

Ответ: 34

Тело массой (m) и объёмом (V) лежит на дне сосуда с жидкостью плотностью (rho). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

[begin{array}{ll}

text{Физические величины}&text{Формула}\

text{А) Сила Архимеда } &1) rho g V \
text{Б) Разность силы тяжести и силы Архимеда } &2) g(rho cdot V — m) \
&3) 0 \
&4) g(m — rho cdot V ) \
end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как тело лежит на дне сосда, то оно погружено на весь свой объем в жидкость и сила Архимеда находится по формуле: (F_a=rho g V). Ответ – 1

Б) Разность силы тяжести и силы Архимеда в этом случае (g(m — rho cdot V) ). Так как тело погружено на весь свой объем. Ответ – 4

Ответ: 14

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Скачать материал

Сейчас обучается 140 человек из 50 регионов

Сейчас обучается 31 человек из 20 регионов

Сейчас обучается 104 человека из 46 регионов

Краткое описание документа:

Сборник задач по теме «Гидростатика» для подготовки к ЕГЭ по физике.

(материал сайта ФИПИ)

1. Сосновый брус объёмом 0,06 м3 плавает в воде, погрузившись на 0,4 своего объёма. На брус действует выталкивающая (архимедова) сила, равная

1) 96 Н 2) 240 Н 3) 600 Н 4) 24 кН

2. Аэростат объемом 1000 м3 заполнен гелием Плотность гелия 0,18 кг/м3. Плотность воздуха 1,29 кг/м3. На аэростат действует выталкивающая сила

1) 1,29 кН 2) 12,9 кН 3) 180 кН 4) 1,8 кН

3. Пластиковый пакет с водой объемом 1 л полностью погрузили в воду. На него действует выталкивающая сила, равная

1) 0 2) 1 Н 3) 9 Н 4) 10 Н

4. Пластиковый пакет с водой объемом 1 л полностью погрузили в воду. На него действует выталкивающая сила, равная

1) 0 2) 1 Н 3) 9 Н 4) 10 Н

5. Два одинаковых бруска толщиной h каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Если в стопку добавить ещё один такой же брусок, то глубина её погружения увеличится на

1) h 2) 13 h 3) 12 h 4) 36. Шесть одинаковых брусков толщиной h каждый, связанные в стопку, плавают в воде так, что уровень воды приходится на границу между двумя средними брусками. Если из стопки убрать два бруска, то глубина ее погружения уменьшится на

1) h 2) 12h 3) 13h 4) 14h

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 460 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

05.04.2015
1047
0

04.04.2015
2579
0

Рейтинг:
4 из 5

04.04.2015
2269
2

04.04.2015
1061
1

04.04.2015
3038
2

Источник

В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».

За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.

Задачи по гидростатике с решениями

Задача №1 на гидростатику

Условие

B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?

Решение

По условию плавания тел:

V – объем погруженной в воду части льда. После таяния льда образуется объем воды:

Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.

Ответ: уровень не изменится.

Задача №2 на гидростатику

Условие

Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?

Решение

Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:

Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:

В одном кубическом метре – тысяча литров.

Ответ: 2 литра.

Задача №3 на гидростатику

Условие

Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.

Решение

Вспоминаем основное уравнение гидростатики и записываем:

Ответ: 150 кПа.

Задача №4 на гидростатику

Условие

Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.

Решение

Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.

Ответ: 2600 кг/м3.

Задача №5 на гидростатику

Условие

Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?

Решение

Формула для гидростатического давления:

Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.

Ответ: высота увеличилась в 5 раз.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Вопросы по гидростатике

Вопрос 1. Что такое гидростатический парадокс?

Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.

Вопрос 2. Какие есть внесистемные единицы изменения давления:

Ответ. Внесистемные единицы давления:

миллиметр ртутного столба;
бар;
атмосфера.

Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?

Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).

Вопрос 4. Что такое сообщающиеся сосуды?

Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.

Вопрос 5. Что такое гидравлический пресс?

Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.

Гидростатика: немного теории

Гидростатика – раздел физики, изучающий равновесие жидкостей.

Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?

Давление и плотность

Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.

Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:

Греческое «ро» — плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.

Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.

Закон Паскаля и основное уравнение гидростатики

Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.

Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.

В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.

В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.

Закон Архимеда и условия плавания тел

Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:

На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.

Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.

Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.

Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.

Источник

Практические задания ЕГЭ по физике на тему «Статика и Гидростатика» с ответами — теория и практика

30.09.2013

Практические задания подобраны с учётом специфики заданий ЕГЭ на реальном экзамене. Количество заданий поможет максимально качественно освоить этот раздел физики «Статика и Гидростатика».

Все практические задания содержат ответы в конце документа.

Дополнительный материал по теме «Статика и Гидростатика»:

Теория
Обучающие задания
Практические задания
Контрольная работа

Смотреть в PDF:

Или прямо сейчас: Скачайте в pdf файле.

Источник