Гипербола для егэ

Каталог заданий
Задания 10. Графики функций. Гиперболы

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

09
Янв 2022

Категория: 10 Графики функций

2022-01-09
2022-09-11

Автор: egeMax |

Нет комментариев

ЕГЭ Профиль №9. Гиперболаadmin2022-08-17T23:36:10+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Гипербола

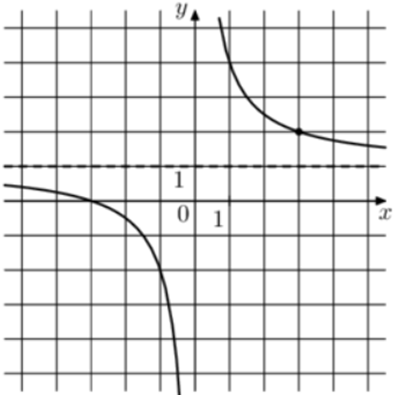
Задача 1. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)   Найдите  (fleft( { — 12} right).) Ответ ОТВЕТ: 0,75.
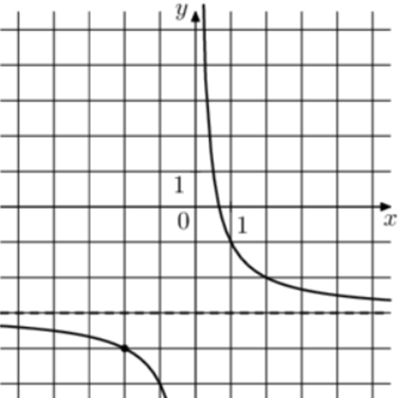
Задача 2. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {50} right).) Ответ ОТВЕТ: — 2,96.
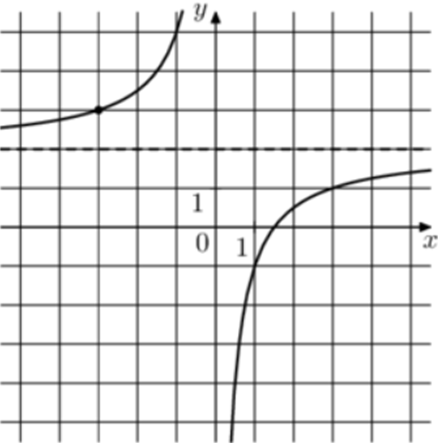
Задача 3. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {7,5} right).) Ответ ОТВЕТ: 1,6.
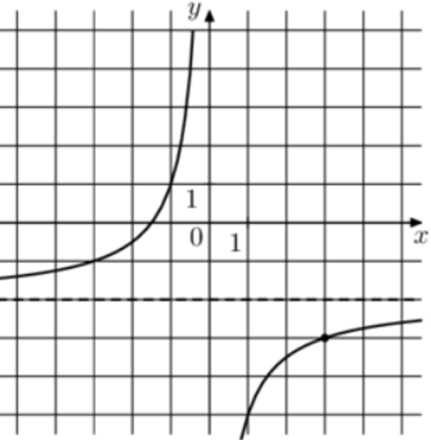
Задача 4. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите  (fleft( {0,25} right).) Ответ ОТВЕТ: — 14.
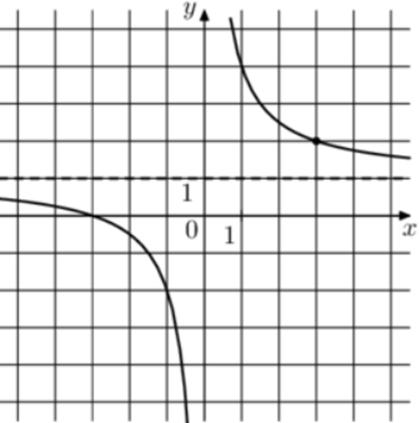
Задача 5. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 0,8. Ответ ОТВЕТ: — 15.
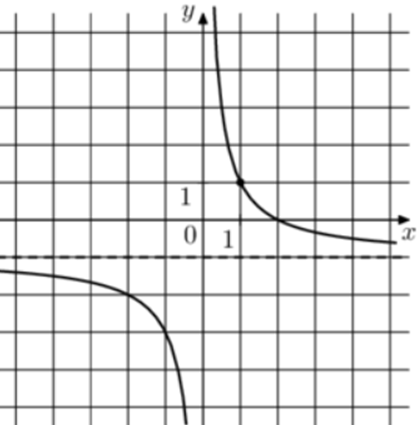
Задача 6. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 19. Ответ ОТВЕТ: 0,1.
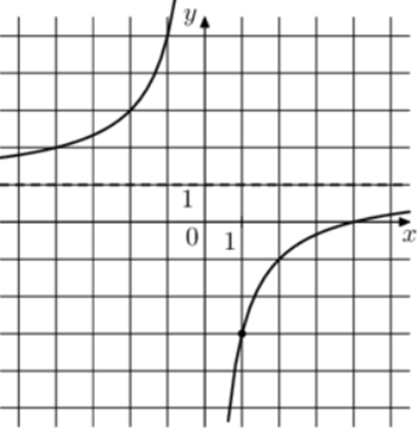
Задача 7. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно 0,75. Ответ ОТВЕТ: 16.
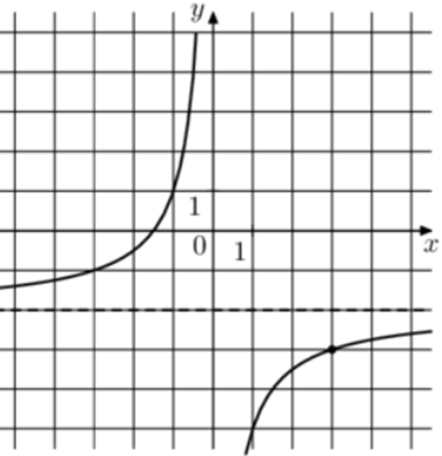
Задача 8. На рисунке изображён график функции  (fleft( x right) = frac{k}{x} + a.)  Найдите, при каком значении  x  значение функции равно ( — 9,5.) Ответ ОТВЕТ: 0,4.
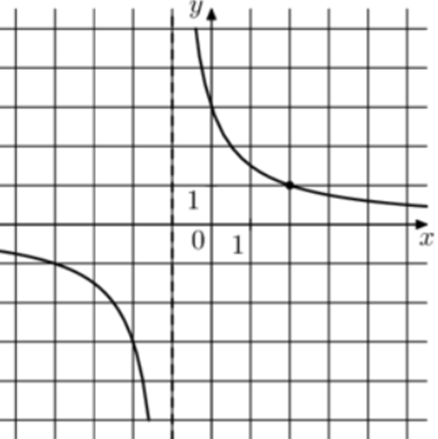
Задача 9. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {19} right).) Ответ ОТВЕТ: 0,15.
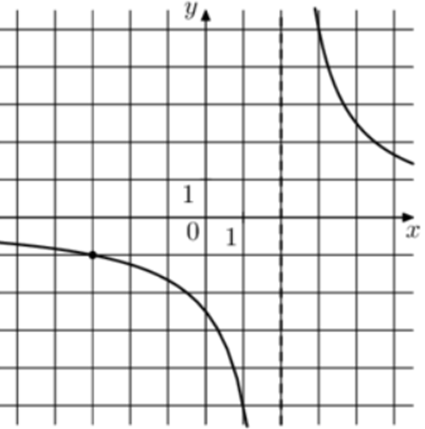
Задача 10. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( { — 4frac{2}{3}} right).) Ответ ОТВЕТ: — 0,75.
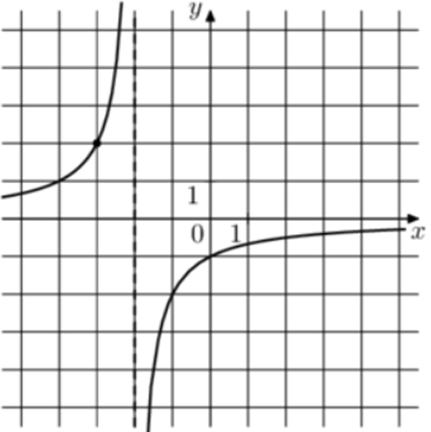
Задача 11. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {18} right).) Ответ ОТВЕТ: — 0,1.
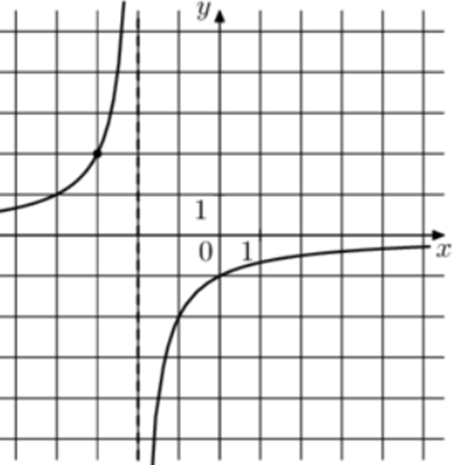
Задача 12. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите  (fleft( {6frac{1}{3}} right).) Ответ ОТВЕТ: — 0,24.
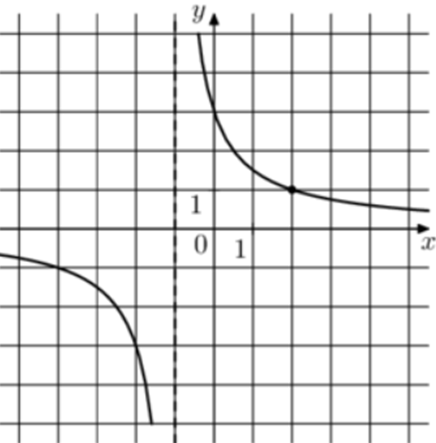
Задача 13. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) = 0,2.) Ответ ОТВЕТ: 14.
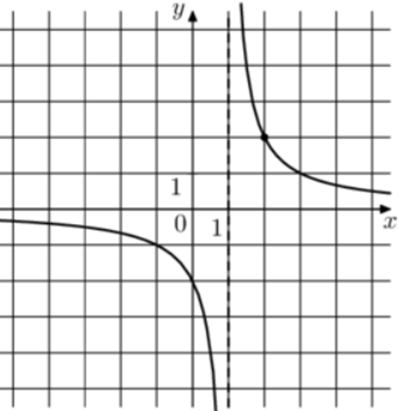
Задача 14. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) =  — 0,08.) Ответ ОТВЕТ: — 24.
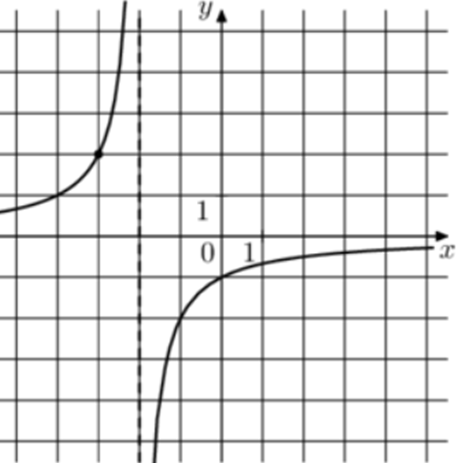
Задача 15. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) =  — 0,04.) Ответ ОТВЕТ: 48.
Задача 16. На рисунке изображён график функции  (fleft( x right) = frac{k}{{x + a}}.)  Найдите значение x, при котором  (fleft( x right) = 0,2.) Ответ ОТВЕТ: — 29.

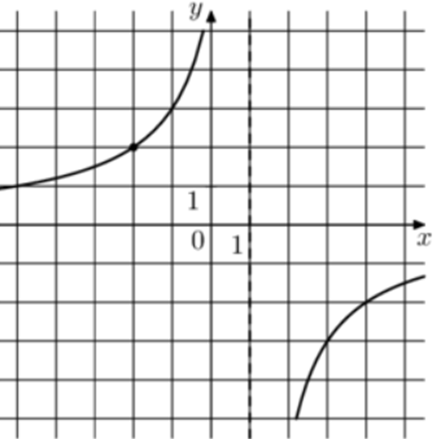Задача 17. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k. Ответ ОТВЕТ: 1.
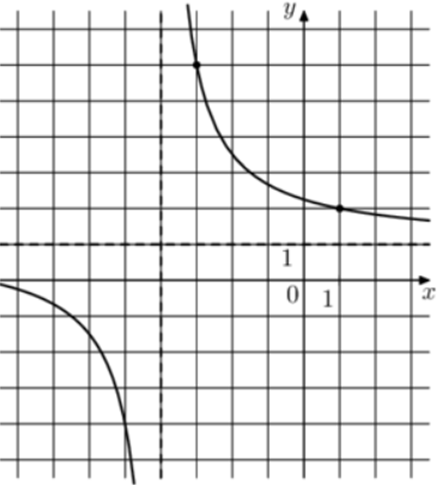Задача 18. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k. Ответ ОТВЕТ: 2.
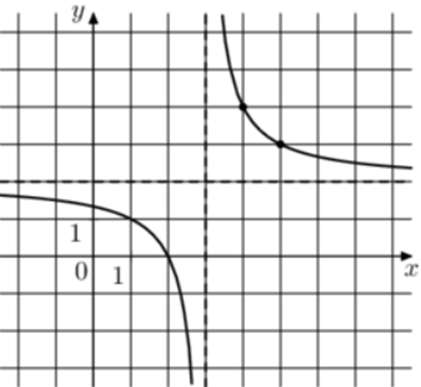Задача 19. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k. Ответ ОТВЕТ: 2.
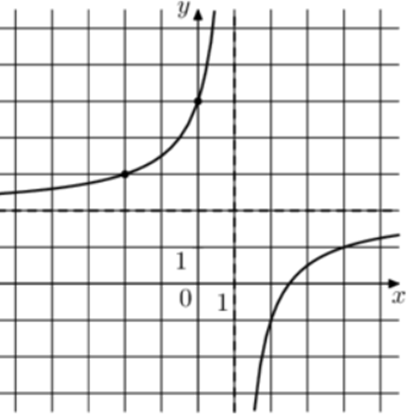Задача 20. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите k. Ответ ОТВЕТ: — 2.
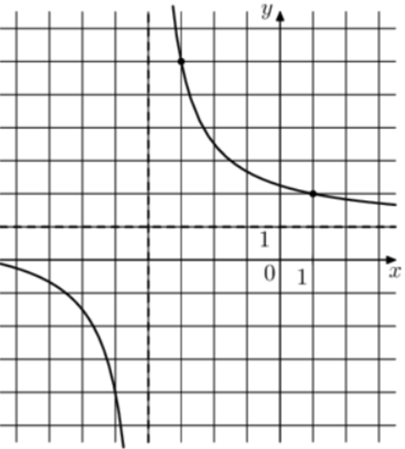
Задача 21. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a. Ответ ОТВЕТ: 9.
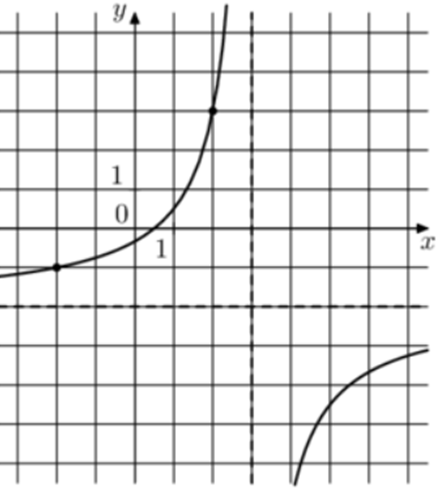
Задача 22. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a. Ответ ОТВЕТ: — 4.
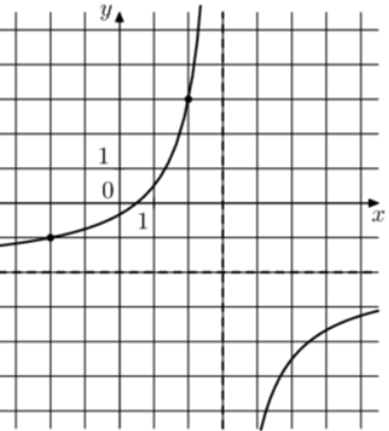
Задача 23. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a. Ответ ОТВЕТ: 1.
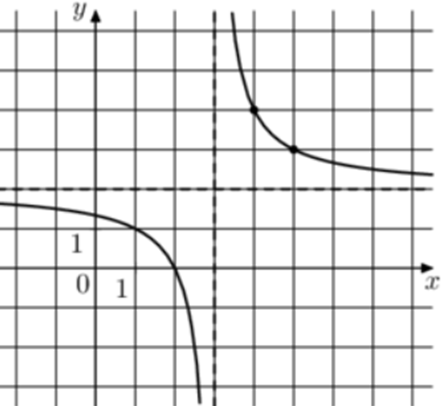
Задача 24. На рисунке изображён график функции  (fleft( x right) = frac{{k,x + a}}{{x + b}}.)  Найдите a. Ответ ОТВЕТ: — 5.
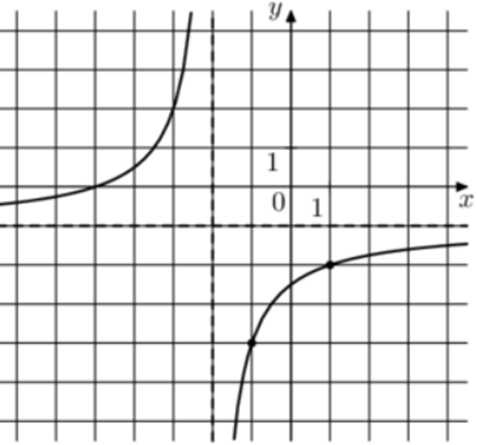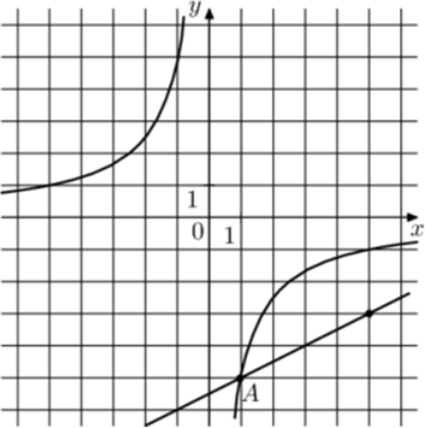
Задача 25. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 0,2.
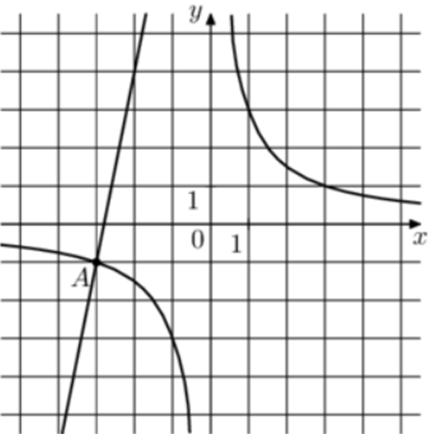Задача 26. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: — 6,25.
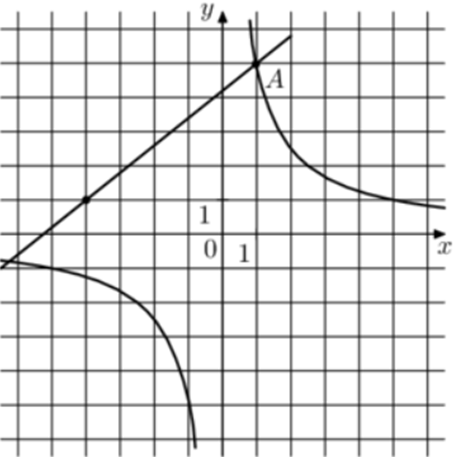Задача 27. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 10.
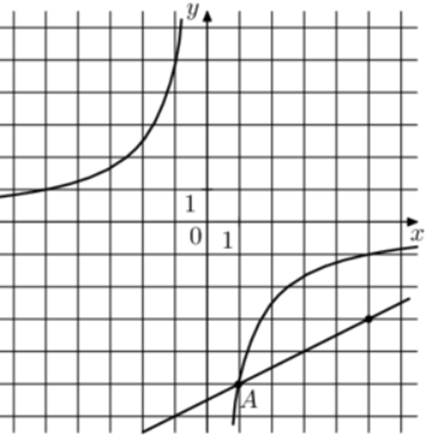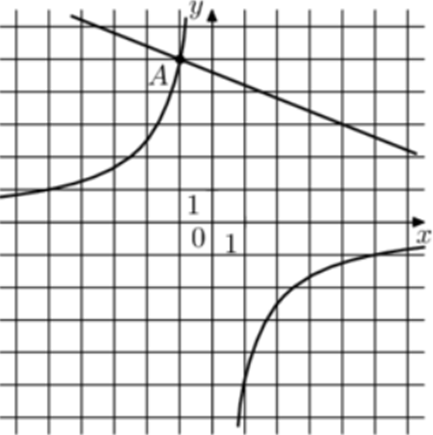
Задача 28. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 12,5.
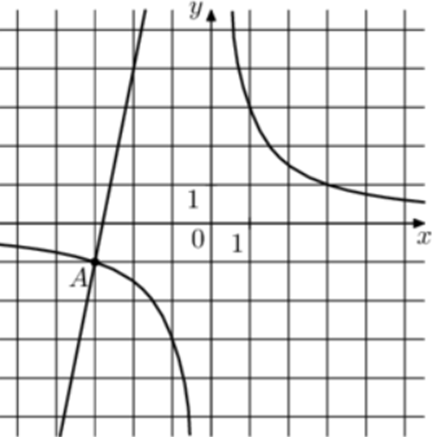
Задача 29. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B. Ответ ОТВЕТ: 15.
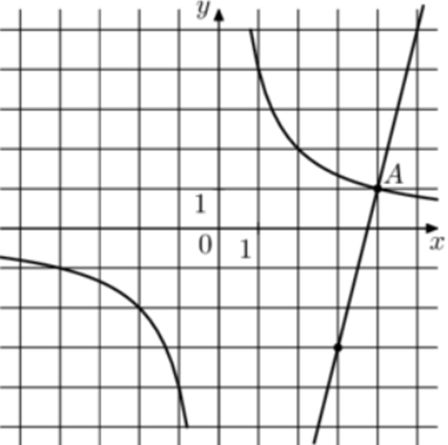
Задача 30. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 16.
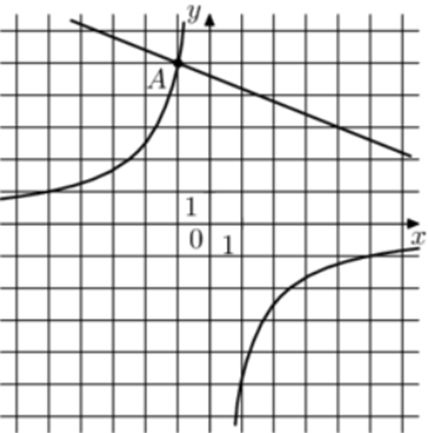
Задача 31. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 0,4.
Задача 32. На рисунке изображены графики функций  (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,)  которые пересекаются в точках  A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 0,5.

Выпускнику

Система подготовки к ЕГЭ – 2022

ЗАДАНИЕ 9

Графики функций

(Учитель математики: Салтыкова Р.А.)

2021

СОДЕРЖАНИЕ

Номер урока	Тема урока	Страница
1.	Гиперболы	3
Типовые примеры	4
Задания для самостоятельного решения	11
2.	Кусочно-линейная функция	15
Типовые примеры	15
3.	Параболы	22
Типовые примеры	23
4.	Синусоиды	27
Типовые примеры	28
5.	Литература	57

Тема 1. Гиперболы

ОСНОВНЫЕ
ПОНЯТИЯ И МЕТОДЫ РЕШЕНИЯ

Определение.

Функция вида

у = ,              (1)

где k –
число (причём k ≠ 0),
а x – переменная, называется обратной пропорциональностью.

Графиком прямой пропорциональности служит гипербола.

Заметим, что если известны координаты некоторой точки,
принадлежащей графику прямой пропорциональности, то из формулы (1) получаем
правило нахождения коэффициента k:

k = x ∙ y.

Если k>0, то
гипербола расположена в I и III координатных
четвертях.

Если k<0, то
гипербола расположена во II и IV координатных
четвертях.

У гиперболы есть асимптоты – координатные прямые Ох
(горизонтальная асимптота) и Оу (вертикальная асимптота).

Определение.

Функция вида

у = ,                     (2)

где a, b, c, d – числа, а x –
переменная, называется дробно-линейной функцией.

Графиком дробно-линейной функции также является
гипербола.

Для построения графика дробно-линейной функции с
помощью параллельного переноса графика прямой пропорциональности формулу (2)
удобнее записать в следующем виде:

у = ,                   (3)

где
a, b, c – числа, а
x –
переменная.

При этом коэффициент b
показывает, на сколько единиц необходимо перенести «основной» график по оси х,
а коэффициент с – по оси у.

Иными словами, в
точке (b; с) пересекаются асимптоты
графика функции

у = .                 

Например, для построения графика функции

у =

достаточно
построить график функции у = , а затем перенести его параллельно на
вектор (3; −2), то
есть на 3 единицы вправо и на 2 единицы вниз.

А для построения графика функции у =

надо
также построить график функции у =  и перенести его
параллельно на вектор (−3; −2), то есть на 3 единицы влево и на 2
единицы вниз.

Пример
1.1. 
На рисунке изображён график функции
вида f(х) =
, где числа a, b и c — целые.
Найдите f(13).

Решение.

1)    Заметим,
что асимптоты гиперболы пересекаются в точке (3; 2). Значит, b = −3, с = 2,
то есть гипербола задаётся формулой: f(х) =
.

2)    Для
нахождения коэффициента a перенесём систему
координат на вектор (3; 2), тем самым поместив её в точку пересечения
асимптот гиперболы. В новой системе координат данная функция «превращается» в
прямую пропорциональность у = , а значит, для нахождения
коэффициента a достаточно воспользоваться формулой а = x ∙ y,
подставив в неё координаты какой-нибудь точки графика вместо переменных х
и у. В новой системе координат выделенная на графике точка
имеет координаты (−1;−1). Значит, а = −1 ∙ (−1) = 1.

3)   
С
учётом полученных коэффициентов заданная формула перепишется в виде f(х)=. f(13)
=  =  = 0,1 + 2 = 2,1.

Ответ:
2,1.

Пример
1.2. 
На рисунке изображён график функции
вида f(х) =
, где числа a, b и c — целые.
Найдите f(10).

Решение.

1)    Асимптоты
гиперболы пересекаются в точке (2;−4). Значит, гипербола задаётся формулой:

f(х) =
.

2)    Перенесём
систему координат на вектор (2; −4), поместив её в точку пересечения асимптот
гиперболы. В новой системе координат выделим точку с координатами (3; 1).
Значит, а = 3 ∙ 1 = 3.

3)    С учётом
полученных коэффициентов заданная формула перепишется в виде у
=.

f(10)
=  =  = 0,375 – 4 = −3,625.

Ответ:
−3,625.

Пример
1.3. 
На рисунке изображён график функции
вида f(х) =
, где числа a, b и c — целые.
Найдите f(4).

Решение.

1)    Асимптоты
гиперболы пересекаются в точке (−1; −1). Значит, гипербола задаётся формулой:

f(х) =
.

2)    Перенесём
систему координат на вектор (−1;−1), поместив её в точку пересечения асимптот
гиперболы. В новой системе координат выделим точку с координатами (−3; 1).
Значит, а = −3 ∙ 1 = −3.

3)    С учётом
полученных коэффициентов заданная формула перепишется в виде у
=.

f(10)
=  =  = −0,6
– 1 = −1,6.

Ответ:
−1,6.

Пример
1.4. 
На рисунке изображён график функции
вида f(х) =
, где числа a, b и c — целые.
Найдите число a.

Решение.

1)   
Асимптоты
гиперболы пересекаются в точке (5;−1). Значит, гипербола задаётся формулой: f(х)=
.

2)    Перенесём
систему координат на вектор (5; −1), поместив её в точку пересечения асимптот
гиперболы. В новой системе координат выделим точку с координатами (−1; −1).

Значит, k = −1 ∙ (−1) = 1.

3)    С учётом
полученных коэффициентов заданная формула перепишется в виде:

f (х)
= =  = .

4)   Сопоставив полученную
формулу с исходной формулой f(х) = , получим, что a = −1.

Ответ:
−1.

Пример
1.5. 
На рисунке изображён график функции
вида f(х) =
, где числа a, b и c — целые.
Найдите значение х, при котором f(х) = −1,125.

Решение.

В примере 1.4 мы уже составили формулу, задающую
функцию, график которой изображён на рисунке:

f (х)
=,

f (х)
= ,

f (х)
=  .

По
условию, f (х)
= −1,125.

Составим уравнение:

 = −1,125.

Решение этого уравнения и является искомым значением х.

 =  .

−9 ∙ (х – 5) = 8 ∙ (−х + 6),

−9х + 45 = −8х + 48,

−х = 3,

х = −3.

Ответ:
−3.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Тема 2. Кусочно-линейная
функция

Пример 2.1. 
На рисунке изображён график функции вида f(x) = ax + |bx + c| + d,
где числа a, b, c и d — целые. Найдите корень уравнения ax + d = 0.

Решение.

Вспомним, что график линейной функции
задаётся формулой вида у = kх
+ m,
где k – это угловой
коэффициент прямой, а m
– ордината точки пересечения графика с осью Оу.

1)  
Если х≤2,
то f(x) = − х + 3,
так как на этом промежутке k
=  =
−1, а ось Оу пересекается с графиком в точке с ординатой
3.

В то же время на этом промежутке модуль
раскрывается со знаком минус:

f(x) = ax –
(bx + c) + d.

Упростим эту формулу:

f(x) = ax –
bx –
c + d = (а – b)х
+ (d
– c).

Имеем:

a – b = –1,
                                 d – c = 3.

2)  
Если х≥2,
то f(x) = 3 х −
5, так как на этом промежутке k
=  =
3, а ось Оу пересекается с продолжением этого графика в
точке с ординатой −5.

В то же время на этом промежутке модуль
раскрывается со знаком плюс:

f(x) = ax + (bx + c) + d.

Упростим эту формулу:

f(x) = ax + bx + c + d =
(а + b)х
+ (d + c).

Имеем:

a + b = 3,                                  d + c = −5.

3)   
Решим две системы уравнений:

       и             

Получаем,
что a
= 1, b
= 2, c
= −4, d
= −1.

4)   
Решим уравнение ax
+ d = 0:

1 ∙ х
– 1 = 0,

х = 1.

Ответ:
1.

Пример 2.2. 
На рисунке изображён график функции вида f(x) = ax + |bx + c| + d,
где числа a, b, c и d — целые. Найдите корень уравнения bx + c = 0.

Решение.

Графики функций, заданные формулой,
содержащей знак модуля, имеют точки излома в «нулях» модулей.

Заметим, что х = 2 – это точка, в
которой находится точка излома (вершина ломаной). Значит,

bx + c = 0 при
х = 2.

Ответ:
2.

Пример 2.3. 
На рисунке изображён график функции вида f(x) = ax + |bx + c| + d,
где числа a, b, c и d — целые. Найдите корень уравнения ax + d = 0.

Решение.

1)   
Для точек, находящихся левее точки излома,
имеем: f(x) = − х – 7,

так
как на этом промежутке k
=  =
−4, а ось Оу пересекается с графиком в точке с ординатой
–7.

В то же время на этом промежутке модуль
раскрывается со знаком минус:

f(x) = ax –
(bx + c) + d.

Упростим эту формулу:

f(x) = ax –
bx –
c + d = (а – b)х
+ (d
– c).

Имеем:

a – b = –4,
                                 d – c = –7.

2)   
Для точек, находящихся правее точки
излома, имеем:  

f(x) = − 5,

так
как на этом промежутке k
= 0,
а ось Оу пересекается с продолжением этого графика в точке с ординатой −5.

В то же время на этом промежутке модуль
раскрывается со знаком плюс:

f(x) = ax + (bx + c) + d.

Упростим эту формулу:

f(x) = ax + bx + c + d =
(а + b)х
+ (d + c).

Имеем:

a + b = 0,                                  d + c = −5.

3)   
Решим две системы уравнений:

       и             

Получаем,
что a
= –3, b
= 2, c
= 1, d
= −6.

4)   
Решим уравнение ax
+ d = 0:

–2 ∙ х
– 6 = 0,

х = –3.

Ответ:
–3.

Пример 2.4. 
На рисунке изображён график функции вида f(x) = ax – |bx + c| + d,
где числа a, b, c и d — целые. Найдите корень уравнения ax + d = 0.

Решение.

1)   
Для точек, находящихся левее точки излома,
имеем: f(x) = 4 х – 1,

так
как на этом промежутке k
=  =
4, а ось Оу пересекается с графиком в точке с ординатой
–1.

В то же время на этом промежутке модуль
раскрывается со знаком минус:

f(x) = ax + (bx + c) + d.

Упростим эту формулу:

f(x) = ax + bx + c + d =
(а + b)х
+ (d + c).

Имеем:

a + b = 4,                                  d + c = –1.

2)   
Для точек, находящихся правее точки
излома, имеем: 

f(x) = − 2х
+ 5,

так
как на этом промежутке k
=  = −2,
а ось Оу пересекается с продолжением этого графика в точке с ординатой 5.

В то же время на этом промежутке модуль
раскрывается со знаком плюс:

f(x) = ax −
(bx + c) + d.

Упростим эту формулу:

f(x) = ax −
bx −
c + d = (а − b)х
+ (d −
c).

Имеем:

a – b = –2,                                  d – c = 5.

3)   
Решим две системы уравнений:

       и             

Получаем,
что a
= 1, b
= 3, c
= –3, d
= 2.

4)    Решим
уравнение ax
+ d = 0:

1
∙
х
+ 2 = 0,

х
= –2.

Ответ:
–2.

Пример
2.5. 
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки
пересечения графиков.

Решение.

1)   Для первого
графика k = , а ось Оу пересекается с графиком в точке
с ординатой 7. Значит,
уравнение данной прямой имеет вид у₁ = х + 7.

2)   Для второго
графика k =  = 1,  а ось Оу пересекается с графиком в
точке с ординатой 1. Значит, уравнение данной прямой имеет
вид у₂ = х + 1.

3)    В точке
пересечения должно выполняться условие

у₁
= у₂.

Составим
уравнение и решим его:

х + 7 = х + 1,

3х
+ 14 = 2х + 2,

х
= –12.

Ответ:
–12.

Тема 3. Параболы

Парабола – это график квадратичной функции, которую
можно задать формулой у = k∙(х – m)²
+ n, где (m; n) –
координаты вершины параболы, а k – коэффициент
растяжения.

         Чтобы
найти коэффициент k, систему
координат переносят параллельно в точку с координатами (m; n), то есть
в вершину параболы. В новой системе координат уравнение параболы будет записано
в виде у = k∙х², откуда k = . Подставив в эту формулу координаты
какой-нибудь точки параболы в новой системе координат, можно вычислить значение
коэффициента k.

Пример
3.1. 
На рисунке изображён график функции
вида f(х) =
 + bx
+ c, где
числа a, b и c — целые. Найдите значение
f(3,5).

Решение.

1)   
Вершина данной параболы находится в точке
(6; 8), поэтому она будет задана уравнением

f(х)
= k∙(х
– 6)² + 8.

2)   
В новой системе координат выделим на
графике точку с координатами (2; –1)
и подставим их значения вместо х и у в формулу k
= :

k =  = .

3)    Тогда
данная функция будет задана формулой

f(х)
= ∙(х – 6)² + 8
=  ∙
х ² + 3х – 1.

4)   
Вычислим значение f(3,5):

f(3,5)
= ∙(3,5 – 6)² + 8
= 6,4375.

Ответ:
6,4375.

Пример
3.2. 
На рисунке изображён график функции
вида f(х) =
 + bx
+ c, где
числа a, b и c — целые. Найдите значение
дискриминанта уравнения f(х) = 0.

Решение.

В
задаче 3.1 мы уже составили уравнение этой параболы:

f(х)
=   ∙
х ² + 3х – 1.

Составим
и решим уравнение f(х)
= 0:

 ∙
х ² + 3х – 1 = 0,

D
= 3² – 4 ∙
 ∙
(-1) = 9 – 1 = 8.

Ответ:
8.

Пример
3.3. 
На рисунке изображён график функции
вида f(х) =
 + bx
+ c, где
числа a, b и c — целые. Найдите значение f(0).

Решение.

1)   
Вершина данной параболы находится в точке
(6; 6), поэтому она будет задана уравнением

f(х)
= k∙(х
– 6)² + 6.

2)   
В новой системе координат выделим на
графике точку с координатами (2; –2)
и подставим их значения вместо х и у в формулу k
= :

k =  = .

3)    Тогда
данная функция будет задана формулой

f(х)
= ∙(х – 6)² + 6
=  ∙
х ² + 6х – 12.

4)   
Вычислим значение f(0):

f(0)
= – 12.

Ответ:
–
12.

Пример
3.4. 
На рисунке изображён график функции
вида f(х) =
 + bx
+ c, где
числа a, b и c — целые. Найдите значение f(–18) – f(–3).

Решение.

1)   
Вершина данной параболы находится в точке
(2; 0), поэтому она будет задана уравнением

f(х)
= k∙(х
– 2)².

2)   
В новой системе координат выделим на
графике точку с координатами (2; 2) и подставим их значения вместо х
и у в формулу k
= :

k =  = .

3)    Тогда
данная функция будет задана формулой

f(х)
= ∙(х – 2)².

Вычислим значение f(–18) – f(–3):

f(–18)
=  ∙
(– 18 – 2)² =  ∙
(– 20)² = 200,

f(–3)
=  ∙
(– 3 – 2)² =  ∙
(– 5)² = 12,5,

f(–18) – f(–3) = 200 – 12,5 = 187,5.

Ответ:
187,5.

Тема 4. Синусоиды

Уравнение вида

f(х) = a ∙ cos (𝝎 x + 𝝋₀) + d

является уравнением гармонического
колебания.

Здесь
a – амплитуда колебаний (коэффициент
растяжения синусоиды вдоль оси Оу),

𝝎 – частота
колебаний (𝝎 = , где Т – период данной
функции),

𝝋₀
– начальная фаза колебаний (начальное отклонение по оси Ох от
состояния равновесия),

d – отклонение по оси Оу.

Пример
4.1.
На рисунке изображён график функции
вида f(х) =
a ∙
cos (b𝝅x + c) + d,
где числа a, b, c и d — целые. Найдите
значение f .

Решение.

1)    Определим
характеристики гармонического колебания:

а
=  = 2,

Т
= 4 – 2 = 2,

b𝝅 =  =
 =
𝝅, откуда b = 1,

с
= 0,

d
= –1.

Таким
образом, формула, задающая синусоиду, имеет вид:

f(х)
= 2 ∙ cos 𝝅x – 1.

2)   
В силу периодичности данной функции (Т =
2) имеем:

f  = f  = f  = f  = f   

f   = 2 ∙
cos   – 1 = 2 ∙ cos   – 1 =

= –2 ∙ cos   – 1 = –2 ∙   – 1 = – 2.

Ответ:
– 2.

Пример
4.2.
На рисунке изображён график функции вида f(х) =
a ∙
cos (b𝝅x + c) + d,
где числа a, b, c и d — целые. Найдите
значение f .

Решение.

1)    Определим
характеристики гармонического колебания:

а
=  = –1,

Т
= 1,5 – 0,5 = 1,

b𝝅 =  =
 =
2𝝅, откуда b = 2,

с
= 0,

d
= –2.

Таким
образом, формула, задающая синусоиду, имеет вид:

f(х)
= – cos 2𝝅x – 2.

2)   
В силу периодичности данной функции (Т =
2) и её чётности имеем:

f  = f  = f  = f  = f   

f   = – cos   – 2 = –  – 2 = – 2,5.

Ответ:
– 2,5.

Пример
4.3.
На рисунке изображён график функции
вида f(х) =
a ∙ cos  + d,
где числа a, b, c и d — целые. Найдите
значение f .

Решение.

1)    Определим
характеристики гармонического колебания:

а
=  = –2,

Т
= 6 – 2 = 4,

 =  =
 =
, откуда b = 2,

с
= 0,

d
= 1.

Таким
образом, формула, задающая синусоиду, имеет вид:

f(х) = –2 cos  + 1.

2)   
В силу периодичности данной функции (Т = 4)
и её чётности имеем:

f  = f  = f  = f  = f   

f   = –2 cos   +
1 = –2 ∙   + 1 = 0.

Ответ:
0.

Литература

СДАМ
ГИА: РЕШУ ЕГЭ. Образовательный портал для подготовки к экзаменам. Математика
профильного уровня — https://ege.sdamgia.ru/

ДЛЯ
ЗАМЕТОК