- »
- »
Уравнения с параметром. Задача 18 (С6)
Графический метод в задачах с параметром
Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.
Для начала рассмотрим уравнение с одной переменной (f(x)=0). Для того, чтобы решить его графическим методом, нужно построить график функции (y=f(x)). Точки пересечения графика с осью абсцисс (ось (х)) и будут решениями нашего уравнения.
Или рассмотрим уравнение (f(x)=g(x)). Точно так же строим на одной координатной плоскости графики функций (y=f(x)) и (y=g(x)), абсциссы точек их пересечения будут решениями уравнения.
Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.
Пример 1
Решить графическим методом уравнение (x^2+3x=5x+3).
Решение: Построим на одной координатной плоскости графики функций (y=x^2+3x) и (y=5x+3). См. рис.1.
(y=5x+3) – красный график; (y=x^2+3x) – синий график.
Из Рис.1 видно, что графики пересекаются в точках ((-1;2)) и ((3;18)). Таким образом, решением нашего уравнения будут: ({x}_{1}=-1; {x}_{2}=3).
Ответ: ({x}_{1}=-1; {x}_{2}=3).
Теперь рассмотрим уравнение с двумя переменными (f(x,y)=0). Решением этого уравнения будет множество пар точек ((x,y)), которые можно изобразить в виде графика на координатной плоскости ((xOy)). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую ((x,y=f(x))) или ((x=f(y),y)).
В качестве примера рассмотрим обыкновенное линейное уравнение (2x-5y=10). (1) Выражаем (x=frac{10+5y}{2}) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):
Все точки, принадлежащие этому графику, будут решениями нашего уравнения. Например, при (x=0) ⇔ (y=-2). Аналогично можно выразить (y=frac{2x-10}{5}). График будет выглядеть так (Рис. 3):
И, разумеется, будет задавать точно такие же пары решений (x) и (y).
Теперь перейдем к уравнениям с параметром. Заметим, что параметр – это обычная переменная, которая ничем не отличается от рассмотренных выше переменных (x) и (y). Поэтому, если мы вместо (y) в уравнении (1) запишем параметр (a), то суть уравнения от этого не поменяется. То есть уравнение (1) можно рассматривать относительно (x) с параметром (y) или наоборот. В дальнейшем параметр будем обозначать за (a).
Разберем уравнение с параметром (6x-5a=15). Будем работать в системе координат ((aOx)). Выразим (x=frac{15+5a}{6}) – это будет общий вид решения. Для того чтобы проиллюстрировать ответ, построим график (x(a)) (Рис. 4).
Пример 2
Найти все значения параметра (a), при которых корни уравнения (6x-5a=15) лежат на отрезке ([-5;5]).
График (x(a)) для этого же примера на рисунке 4.
Иногда для решения удобно построить график зависимости (a(x): a=frac{6x-15}{5}). Давайте так и поступим. Построим график (Рис. 5). И красной областью покажем интервал, который нас интересует по условию задачи. Из рисунка видно, что (a∈[-9;3]) (при (x=5) ⇔(a=3); и при (x=-5) ⇔(a=-9))
На мой взгляд, будет более наглядно, если показывать графический метод на примерах. Поэтому, давайте разберем примеры от простых к сложным, которые могут встретиться на ЕГЭ.
Пример 3
Определить, при каких значениях параметра (a) уравнение (x^2-3x-2a=0) имеет: а) 2 корня; б) 1 корень; в) не имеет корней;
Решение:
1 способ решения:
Приведем уравнение к виду (x^2-3x=2a). И построим графики (y=1/2*(x^2-3x)) (показан красной линией) и (y=a) (синяя линия). Обратите внимание, график (y=a) – это просто семейство прямых параллельных оси (x) в плоскости ((xOy)) (Рис. 6). Точки пересечения красной линии с семейством синих линий – это корни нашего уравнения. Если, например, (a=5), то графики (y=5) и (y=1/2*(x^2-3x)) имеют две общие точки, а значит, и два решения. При (a=-1.125) оба графика имеют только одну общую точку ((1.5;-1.125)) – это единственное решение.
Ответ:
При (a>-1.115) уравнение имеет два корня;
При (a=-1.125) уравнение имеет один корень;
При (a<-1.125) уравнение не имеет корней.
2 способ решения:
Таким же образом можно решить данное уравнение, построив графики в плоскости ((xOa)). Для этого выразим (a=1/2*(x^2-3x).)
Различным значениям параметра (a) можно поставить значения искомого (x), для это проведем горизонтальные линии.
Ответ:
При (a>-1.115) уравнение имеет два корня;
При (a=-1.125) уравнение имеет один корень;
При (a<-1.125) уравнение не имеет корней.
Пример 4
Решить уравнение: (cos^2x-2 cosx+a=0)
Сделаем замену (t=cosx,) тогда ( t^2-2t+a=0,) при (t∈[-1;1].)
Построим в плоскости ((tOa)) график нашей функции (a=2t-t^2:)
Точки пересечения горизонтальных (фиолетовых) прямых с графиком нашей функции соответствуют решениям. Но (t∈[-1;1]), покажем это при помощи зеленой области (Рис.8). Таким образом, нас устраивают решения, которые принадлежат кусочку параболы, попавшей в зеленую область. Как видно из рисунка, (a) может принимать значения (a∈[-3;1]), и каждому значению (a) из этой области соответствует единственное решение. Найдем его, решив уравнение (t^2-2t+a=0;)
$$ {t}_{1}=frac{4-sqrt{4-4a}}{2};$$
$$ {t}_{2}=frac{4+sqrt{4-4a}}{2}.$$
({t}_{2}) не подходит, так как он не удовлетворяет условию (t∈[-1;1]).
Сделаем обратную замену:
$$ cosx=frac{4-/sqrt{4-4a}}{2};$$
$$ x=±arccos(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$
Ответ: При (a∈[-3;1]); $$ x=±arccos(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$
Пример 5
Решить уравнение (sin^4x-(a-1) sin^2x-(2a+2)=0.)
Решение:
Сделаем замену: (t=sin^2x ) ⇔ (t^2-(a-1)t-2a-2=0;)
Обратите внимание: (t∈[0;1];)
Выразим (a=frac{t^2+t-2}{t+2}=frac{(t+2)(t-1)}{t+2}=t-1),при (t≠-2).
Таким образом, необходимо решить систему:
$$ begin{cases} a=t-1, \t∈[0;1]. end{cases} $$
Построим решения данной системы на координатной плоскости ((tOa)).
Красной линией показан график (a=t-1), а зеленая область показывает интервал, в котором могут лежать корни. Выделенная часть графика соответствует всем возможным корням при (a∈[-1;0].) Если (a) не принадлежит этому интервалу, то корней нет. Найдем эти решения:
$$ t=a+1,$$ $$sin^2x=a+1,$$ $$ 1-cos2x=a+1,$$ $$ cos2x=-a,$$
$$x=±1/2$$ $$ arccos(-a)+πn,n∈Z.$$
Ответ:При (a∈[-1;0];) $$ x=±1/2 arccos(-a)+πn,n∈Z.$$
Пример 6
Решить уравнение (9^{-|x+1|}-3^{1-|x+1|}-a=0.)
Сделаем замену (t=3^{-|x+1|}), получим (t^2-3t-a=0), где (t∈(0;1].)
Построим график функции (a(t)=t^2-3t), при (t∈(0;1]) в системе координат ((tOa)).
Зеленой областью покажем допустимый интервал, в котором могут находиться корни. Выделенная часть параболы соответствует корням нашего уравнения при (a∈[-2;0)). Таким образом, при (a<-2) и (a≥0) корней нет.
Решим уравнение (t^2-3t-a=0).
При (a∈[-2;0)) $$ {t}_{1}=frac{3-sqrt{9+4a}}{2};$$ $$ {t}_{2}=frac{3+sqrt{9+4a}}{2},$$ так как (t∈(0;1]), то ({t}_{2}) не подходит.
Сделаем обратную замену:
$$ 3^{-|x+1|}=frac{3-sqrt{9+4a}}{2};$$
$$-|x+1|=log_3 (frac{3-sqrt{9+4a}}{2});$$
$$|x+1|=-log_3 (frac{3-sqrt{9+4a}}{2});$$
$$x=-1±log_3 (frac{3-sqrt{9+4a}}{2}).$$
Ответ: (x=-1±log_3 (frac{3-sqrt{9+4a}}{2})) при (a∈[-2;0).)
Пример 7
Решить уравнение (sqrt{a(3^x+1)+9}=2-3^x.)
Сделаем замену (t=3^x, t>0) ⇔ (sqrt{a(t+1)+9}=2-t.)
Данному уравнению равносильна система:
$$ begin{cases} a(t+1)+9=(2-t)^2, \ 2-t ≥ 0, \ t > 0. end{cases} $$
$$ begin{cases} a=frac{(t-5)(t+1)}{t+1}, \ 0 < t ≤ 2. end{cases} $$
$$ begin{cases} a = t-5, \ 0 < t <= 2. end{cases}$$
Построим множество точек, которые удовлетворяют полученной системе:
При (a∈(-5;-3]) ⇔ (t=a+5,) сделаем обратную замену 3(^x=a+5), ⇔ (x=log_3 (a+5).)
При (a∈(-∞;-5]∪(-3;+∞)) корней нет.
Ответ: При (a∈(-5;-3]) ⇔ ( x=log_3 (a+5).)
Пример 8
Решить неравенство (9^x-(a-1) 3^x-a≥0)
Сделаем замену: (t=3^x,) ⇔ (t>0;)
Получаем
$$ begin{cases} t^2-(a-1)t-a≥0, \t>0. end{cases} $$
$$ t(t+1)≥a(t+1); $$
Заметим, что решение (t=-1) не подходит, так как (t>0). Поделим наше неравенство на
(t+1). Так как (t+1>0), то знак неравенства не меняется. Будьте внимательны! В случае, когда нам неизвестен знак выражения, на которое мы делим неравенство, необходимо рассмотреть два случая, когда выражение отрицательно (меняем знак неравенства) и когда положительно (не меняем).
$$ begin{cases} t≥a, \t>0. end{cases} $$
Построим график, получившейся системы неравенств на плоскости ((tOa)).
Оранжевой областью выделено решение первого неравенства системы, синей областью – второго неравенства. Их пересечение – это решение все системы.
Получаем, что при (a≤0) $$ t∈(0;+∞) ⇔ 3^x>0 ⇔ x∈(-∞;+∞)$$
При ( a>0) $$ t∈[a;+∞) ⇔ 3^x≥a ⇔ x≥log_3 a.$$
Ответ: при( a≤0) $$ x∈(-∞;+∞)$$
при (a>0) $$ x≥log_3 a.$$
Пример 9
Найти все значения параметра, при которых функция
$$ f(x)=ln{(p-1)*3^x-4*3^{x/2}+(p+2)} $$
определена при всех (x∈R.)
Решение:
Наша функция будет определена при условии, что выражение под логарифмом будет больше нуля:
$$ (p-1)*3^x-4*3^{x/2}+(p+2) > 0.$$
Сделаем замену: (t=3^{x/2},t > 0).
Получим
$$ begin{cases} (p-1)*t^2-4*t+p+2>0, \ t>0. end{cases} $$
Если (p=1),
$$ begin{cases} -4t+3>0, \ t>0; end{cases} $$
$$ begin{cases} t<0.75, \ t>0; end{cases} $$
Сделаем обратную замену: (0 < 3^{x/2} < 0.75.) Очевидно, что это неравенство не будет выполняться при всех (x), как того требует условие задачи.
Если (p≠-1,)
$$ begin{cases} pt^2-t^2-4t+p+2>0, \t>0; end{cases} $$
$$ begin{cases} p(t^2+1)>t^2+4t-2, \t>0; end{cases} $$
$$ begin{cases} p > frac{t^2+4t-2}{1+t^2}, \t>0. end{cases} $$
Теперь нужно построить график функции (p=frac{t^2+4t-2}{1+t^2}). Для этого исследуем функцию на монотонность и найдем экстремумы.
Найдем производную:
$$ p^{‘}=frac{-4(t-2)(t+1/2)}{1+t^2}^2 ;$$
Как видно из рисунка 13, точка ((-1/2;-3)) – точка минимума; а ((2;2)) – точка максимума.
Найдем асимптоты. Напомню, что вертикальные асимптоты бывают только в точках разрыва, поэтому наличие вертикальной асимптоты можно проверить, взяв предел от функции в точке разрыва. В нашем случае нет точек разрыва, поэтому вертикальных асимптот не будет.
График функции будет иметь горизонтальные асимптоты, если (lim_{t→+∞} p(t)=const) или (lim_{t→-∞} p(t)=const.) Проверим нашу функцию:
$$lim_{t→∞} frac{t^2+4t-2}{1+t^2}=1.$$
Значит, есть горизонтальная асимптота (p=1).
И асимптоты могут быть наклонными: Прямая (p=kt+b) будет наклонной асимптотой к нашему графику ( p=frac{t^2+4t-2}{1+t^2}), если существуют пределы (lim_{t→∞} {frac{p(t)}{t}}=k) и (lim_{t→∞} {(p(t)-kt)}=b.)
В нашей случае наклонной асимптоты не будет.
Подробнее можно посмотреть здесь.
Из полученных данных построим примерный график функции (p=frac{t^2+4t-2}{1+t^2}) :
На рисунке 14 при помощи штриховки показаны точки, которые будут корнями системы
$$ begin{cases} p < frac{t^2+4t-2}{1+t^2}, \ t > 0. end{cases}$$
Если (p>2),то (t>0) или (3^(x/2)>0), а значит и функция (f(x)) определена при любых (x∈R).
Ответ: (p∈(2;+∞).)
Пример 10
Найти при каких значениях параметра (a) система
$$ begin{cases} (2+log_{3} {(frac{1}{9} a+frac{1}{3}-frac{2}{9} y)}=log_{3}{(2a+x-y-6)}, \ sqrt{x}=2+y. end{cases}$$
имеет решение?
Решение:
Преобразуем исходную систему:
$$ begin{cases} a+3-2y=2a+x-y-6, \ frac{1}{9} a+frac{1}{3}-frac{2}{9} y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=3-2y-(2+y)^2+y+6, \ a+3-2y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=-y^2-5y+5, \ a>2y-3, \ x=(2+y)^2. end{cases}$$
Построим график полученной системы:
Из рисунка 15 видно, что (a∈(-19;11.25].)
Ответ: (a∈(-19;11.25].)
Пример 11
Найти значения параметра a, при которых система
$$ begin{cases} x+y-1=0, \ 2y=sqrt{ax-1} end{cases} $$
имеет единственное решение.
Решение:
Из второго уравнения следует, что (x=frac{y^2+1}{a}).
Тогда
$$ begin{cases} frac{y^2+1}{a}+y-1=0, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$
$$ begin{cases} a=frac{y^2+1}{1-y}, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$
Обратите внимание, что (y=1), (x=0) не может быть решением системы при любых значениях параметра (a).
Исследуем, полученную зависимость (a=frac{y^2+1}{1-y}) на монотонность и найдем экстремумы.
$$ {a}^{‘}=frac{2y(1-y)+(y^2+1)}{1-y}^2 ;$$
$$ {a}^{‘}=frac{-y^2+2y+1}{(1-y)^2} =-frac{(y-1-sqrt{2})(y-1+sqrt{2})}{(1-y)^2} ;$$
Из рисунка 16 видно, что ({y}_{1}=1-sqrt{2}) — точка минимума функции (a=frac{y^2+1}{1-y};) Ей соответствует значение (a=2sqrt{2}-2).
({y}_{2}=1+sqrt{2}) — точка максимума. (a=-2sqrt{2}-2).
Найдем асимптоты (см. пример 9):
$$lim_{y→1} {frac{y^2+1}{1-y}}=∞;$$
Значит (y=1) – вертикальная асимптота.
$$lim_{y→∞} {frac{y^2+1}{1-y}}=∞;$$
Значит горизонтальные асимптоты отсутствуют.
И проверим на наличие наклонных асимптот:
$$ lim_{y→∞} {frac{a(y)}{y}}=lim_{y→∞} {frac{(frac{y^2+1}{1-y})}{y}}=lim_{y→∞} {frac{y^2+1}{y-y^2 }}=$$
$$=lim_{y→∞} {frac{1+frac{1}{y^2}}{-1+frac{1}{y}}}=-1=k;$$
$$lim_{y→∞} {(a(y)-ky)}=lim_{y→∞} {frac{y^2+1}{1-y}+y}=lim_{y→∞} {frac{1+y}{1-y}}=-1;$$
Получим уравнение наклонной асимптоты (a=-y-1).
Красным показа график функции (a=frac{y^2+1}{1-y};) Зеленым – показаны найденные асимптоты; Синяя область удовлетворяет условию (y≥0);
Выделенная бардовым часть графика указывает на возможные корни исходной системы. По условию задачи необходимо найти такие значения параметра (a), чтобы система имела единственное решение. Таким образом, из рисунка следует, что при (a=-2sqrt{2}-2) и (a ≥ 1) система будет иметь единственное решение.
Ответ: (a=-2sqrt{2}-2) и (a≥1)
Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.
Использование свойств функции при решении заданий с параметром из ЕГЭ по математике профильного уровня. Симметрия функций и приемы решения.
Квадратные уравнения с параметром. Умение исследовать квадратный многочлен поможет решать задачи с параметром аналитическим методом. Квадратное уравнение решается при помощи дискриминанта или теоремы Виета.
Разбор линейных уравнений с параметром. Для того, чтобы решить такое уравнение, нужно найти все x при всех значениях параметра a
Решение показательных и логарифмических уравнений с параметром
Знакомимся с понятием параметра в уравнениях. Краткие рекомендации к выполнению.
Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.
Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.
Вот список тем, которые стоит повторить:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
2. Преобразование графиков функций.
3. Построение графиков функций.
4. Базовые элементы для решения задач с параметрами.
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.
Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).
1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.
Получим систему:
В первом уравнении выделим полный квадрат:
Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.
Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.
Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.
Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках
и
Координаты этих точек легко найти, подставим
в уравнение окружности.
Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.
Это значит, что
2. Найдите все значения a, при которых уравнение имеет единственное решение.
Уравнение равносильно системе:
Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).
Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.
Приводим подобные слагаемые в уравнении.
Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:
Решим систему графически:
Уравнение задает окружность с центром в точке
, где радиус
Неравенство задает полуплоскость, которая расположена выше прямой
, вместе с самой этой прямой.
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением
Пусть С — точка касания.
На координатной плоскости отметим точки и
, в которых прямая
пересекает оси Y и Х.
Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.
Тогда
Решая это уравнение, получаем, что
Ответ:
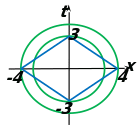
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.
График уравнения — окружность
с центром
и радиусом равным 2.
График уравнения — две симметричные окружности
и
радиуса 2 c центрами в точках
и
Второе уравнение при задает окружность
с центром в точке
и радиусом a.
Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.
Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности
или только правой
Если a — радиус окружности , то это значит, что
(только правая) или
(только левая).
Пусть А — точка касания окружности и окружности
Для точки А:
,
(как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),
В — точка касания окружности и окружности
Для точки В:
длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4;
Тогда для точки В получим:
Есть еще точки С и D, в которых окружность касается окружности
или окружности
соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:
, но
и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность
и система будет иметь не одно, а три решения.
Аналогично, для точки D:
и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность
и система будет иметь три решения.
Ответ: или
4. При каких значениях a система уравнений имеет 4 решения?
Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!
Просто выделили полный квадрат во втором уравнении.
Сделаем замену Система примет вид:
Вот теперь все видно! Рисовать будем в координатах
Графиком первого уравнения является ромб, проходящий через точки с координатами и
Графиком второго уравнения является окружность с радиусом и центром в начале координат.
Когда же система имеет ровно 4 решения?
1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.
Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.
Диагонали нашего ромба равны 8 и 6. Значит,
Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то
При этом
Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда
Мы получили ответ:
2) Есть второй случай, и мы его найдем.
Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.
Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.
Пусть радиус окружности равен 3. Тогда система имеет 6 решений.
А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!
Значит, Объединим случаи и запишем ответ:
Ответ:
Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Графический метод решения задач с параметрами» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Параметрические уравнения
Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр. На самом деле с каждым параметрическим уравнением может быть написано множество уравнений.
Способ решения параметрических уравнений
- Находим область определения уравнения.
- Выражаем a как функцию от $х$.
- В системе координат $хОа$ строим график функции, $а=f(х)$ для тех значений $х$, которые входят в область определения данного уравнения.
- Находим точки пересечения прямой, $а=с$, где $с∈(-∞;+∞)$ с графиком функции $а=f(х)$. Если прямая, а=с пересекает график, $а=f(х)$, то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение вида, $а=f(х)$ относительно $х$.
- Записываем ответ.
Общий вид уравнения с одним параметром таков:
$F(x, a) = 0$
При различных значениях, а уравнение $F(x, a) = 0$ может иметь различные множества корней, задача состоит в том, чтобы изучить все случаи, выяснить, что будет при любом значении параметра. При решении уравнений с параметром обычно приходится рассматривать много различных вариантов. Своевременное обнаружение хотя бы части невозможных вариантов имеет большое значение, так как освобождает от лишней работы.
Поэтому при решении уравнения $F(x, a) = 0$ целесообразно под ОДЗ понимать область допустимых значений неизвестного и параметра, то есть множество всех пар чисел ($х, а$), при которых определена (имеет смысл) функция двух переменных $F(x, а)$. Отсюда естественная геометрическая иллюстрация ОДЗ в виде некоторой области плоскости $хОа$.
ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):
1. Выражение, стоящее в знаменателе, не должно равняться нулю.
${f(x)}/{g(x)}; g(x)≠0$
2. Подкоренное выражение должно быть неотрицательным.
$√{g(x)}; g(x)≥0$.
3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.
${f(x)}/{√{g(x)}}; g(x) > 0$
4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.
$log_{f(x)}g(x) {tableg(x) > 0; f(x) > 0; f(x)≠1;$
Алгебраический способ решения квадратных уравнений с параметром $ax^2+bx+c=0$
Квадратное уравнение $ax^2+bx+c=0, а≠0$ не имеет решений, если $D < 0$;
Квадратное уравнение имеет два различных корня, когда $D > 0$;
Квадратное уравнение имеет один корень, если $D=0$
Тригонометрические тождества
1. $tgα={sinα}/{cosα}$
2. $ctgα={cosα}/{sinα}$
3. $sin^{2}α+cos^{2}α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^{2}α}$
$cosα=±√{1-sin^{2}α$
4. $tgα·ctgα=1$
5. $1+tg^{2}α={1}/{cos^{2}α}$
6. $1+ctg^{2}α={1}/{sin^{2}α}$
Формулы двойного угла
1. $sin2α=2sinα·cosα$
2. $cos2α=cos^{2}α-sin^{2}α=2cos^{2}α-1=1-2sin^{2}α$
3. $tg2α={2tgα}/{1-tg^{2}α}$
Формулы суммы и разности
$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$
$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$
$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$
$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$
Формулы произведения
$cosα·cosβ={cos{α-β}+cos{α+β}}/{2}$
$sinα·sinβ={cos{α-β}-cos{α+β}}/{2}$
$sinα·cosβ={sin{α+β}+sin{α-β}}/{2}$
Формулы сложения
$cos(α+β)=cosα·cosβ-sinα·sinβ$
$cos(α-β)=cosα·cosβ+sinα·sinβ$
$sin(α+β)=sinα·cosβ+cosα·sinβ$
$sin(α-β)=sinα·cosβ-cosα·sinβ$
Решение тригонометрического уравнения с параметром рассмотрим на примере.
Пример:
Найдите все значения параметра с, при каждом из которых уравнение $3cos2x-2sin2x=c$ имеет решение.
Решение:
Преобразуем данное уравнение к виду
$√{3^2+(-2)^2}(cos2xcosφ-sin2xsinφ)=c$
Воспользуемся тригонометрической формулой и свернем второй множитель как косинус суммы
$√{13}cos(2x+φ)=c$, где $φ=arccos{3}/{√{13}}$
Уравнение $√{13}cos(2x+φ)=c$ имеет решения тогда и только тогда, когда $-1≤ {c}/{√{13}} ≤ 1$, домножим полученное неравенство на $√{13}$ и получим
$-√{13} ≤ c ≤ √{13}$
Ответ: $-√{13} ≤ c ≤ √{13}$
Неравенства с параметром
Если имеется неравенство вида $F(a,x) ≤ G(a,x)$ то оно будет иметь одно решение, если $F'(a, x)=G'(a, x)$.
Системы уравнений:
Выделяют четыре основных метода решения систем уравнений:
- Метод подстановки: из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.
- Метод алгебраического сложения: путем сложения двух уравнений получить уравнение с одной переменной.
- Метод введения новых переменных: ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы.
- Графический метод решения: из каждого уравнения выражается $«у»$, получаются функции, графики которых необходимо построить и посмотреть координаты точек пересечения.
Логарифмические уравнения и системы уравнений
Основное логарифмическое тождество:
$a^{log_{a}b}=b$
Это равенство справедливо при $b> 0, a> 0, a≠1$
Свойства логарифмов:
Все свойства логарифмов мы будем рассматривать для $a> 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любых действительных чисел $m$ и $n$ справедливы равенства:
$log_{а}b^m=mlog_{a}b$;
$log_{a^m}b={1}/{m}log_{a}b$.
$log_{a^n}b^m={m}/{n}log_{a}b$
2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.
$log_a(bc)=log_{a}b+log_{a}c$
3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию
$log_a{b}/{c}=log_{a}b-log_{a}c$
4. При умножении двух логарифмов можно поменять местами их основания
$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a, b, c, d >0, a≠1, b≠1$.
5. $c^{log_{a}b}=b^{log_{a}b}$, где $а, b, c > 0, a≠1$
6. Формула перехода к новому основанию
$log_{a}b={log_{c}b}/{log_{c}a}$
7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение
$log_{a}b={1}/{log_{b}a}$
При решении систем, содержащих логарифмические уравнения, часто удается, избавившись от логарифма, заменить одно или оба уравнения системы рациональными уравнениями. После этого надо выразить одну переменную через другую и после постановки получить уравнение с одной переменной. Кроме того, часто встречаются задачи на замену переменной в пределах одного или обоих уравнений системы и системы, требующие отбора решений.
Логарифмические неравенства:
1. Определить ОДЗ неравенства.
2. По свойствам логарифма преобразовать неравенство к простому виду, желательно получить с двух сторон логарифмы по одинаковому основанию.
3. Перейти к подлогарифмическим выражениям, при этом надо помнить, что:
а) если основание больше единицы, то при переходе к подлогарифмическим выражениям знак неравенства остается прежним;
b) если основание меньше единицы, то при переходе к подлогарифмическим выражениям знак неравенства меняется на противоположный;
с) если в основании находится переменная, надо рассмотреть оба варианта.
4. Решить неравенство.
5. Выбрать решения с учетом ОДЗ из п.1
При решении логарифмических неравенств с переменной в основании легче всего воспользоваться тождественными преобразованиями:
$log_{a}f > b ↔ {table (f-a^b)(a-1) > 0; f > 0; a > 0;$
$log_{a}f+log_{a}g > 0 ↔ {table(fg-1)(a-1)> 0; f > 0,g > 0; a > 0;$
$log_{a}f+b > 0 ↔ {table(fa^b-1)(a-1) > 0; f > 0; a > 0;$
Системы, содержащие показательные уравнения
Свойства степеней
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n·a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
Основные методы решения систем, содержащих показательные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – положительность выражения $a^{f(x)}$, которую полезно учитывать, вводя соответствующее ограничение при замене переменной.
Показательные неравенства, сводящиеся к виду $a^{f(x)} ≥ a^{g(x)}$:
1. Преобразовать показательное уравнение к виду $a^{f(x)} ≥ a^{g(x)}$
2. Перейти показателям степеней, при этом если основание степени меньше единицы, то знак неравенства меняется на противоположный, если основание больше единицы – знак неравенства остается прежним.
3. Решить полученное неравенство.
4. Записать результат.
Показательные неравенства, которые можно разложить на множители или сделать замену переменной.
1. Для данного метода во всем неравенстве по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
2. Сделать замену переменной $a^{f(x)}=t, t>0$.
3. Получаем рациональное неравенство, которое можно решить методом интервалов путем разложения на множители выражения.
4. Делаем обратную замену с учетом того, что $t>0$. Получаем простейшее показательное неравенство $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Уравнения с многочленами
Многочлен может обозначаться записью $Р(х)$ — это означает, что многочлен зависит от «х», если записать $Р(х+1)$ — это означает, что в многочлене вместо «х» надо сделать замену на скобку $(х+1)$
Пример:
Найдите значение выражения: $4(p(2x)−2p(x+3))$, если $p(x)=x−6$
Решение:
В данном условии задан многочлен, зависящий от «х», как $p(x)=x−6$.
Чтобы было понятнее, назовем исходный многочлен основной формулой, тогда, чтобы записать $p(2x)$, в основной формуле заменим «х» на «2х».
$p(2x)=2х-6$
Аналогично $p(x+3)=(х+3)-6=х+3-6=х-3$
Соберем все выражение: $4(p(2x)−2p(x+3))=4((2х-6)-2(х-3))$
Далее осталось раскрыть скобки и привести подобные слагаемые
$4((2х-6)-2(х-3))=4(2х-6-2х+6)=4·0=0$
Ответ: $0$
Системы иррациональных уравнений
Основные методы решения систем, содержащих иррациональные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – надо расписать ОДЗ каждого уравнения, а в конце решения выбрать решение системы с учетом ОДЗ.
Чтобы решить иррациональное уравнение, необходимо:
1. Преобразовать заданное иррациональное уравнение к виду
$√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
2. Обе части уравнение возвести в квадрат
$√{f(x)}^2={g(x)}^2$ или $√{f(x)}^2=√{g(x)}^2$
3. Решить полученное рациональное уравнение.
4. Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
Графический метод в задачах с параметром
Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.
Для начала рассмотрим уравнение с одной переменной (f(x)=0). Для того, чтобы решить его графическим методом, нужно построить график функции (y=f(x)). Точки пересечения графика с осью абсцисс (ось (х)) и будут решениями нашего уравнения.
Или рассмотрим уравнение (f(x)=g(x)). Точно так же строим на одной координатной плоскости графики функций (y=f(x)) и (y=g(x)), абсциссы точек их пересечения будут решениями уравнения.
Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.
Решить графическим методом уравнение (x^2+3x=5x+3).
Решение: Построим на одной координатной плоскости графики функций (y=x^2+3x) и (y=5x+3). См. рис.1.
(y=5x+3) – красный график; (y=x^2+3x) – синий график.
Из Рис.1 видно, что графики пересекаются в точках ((-1;2)) и ((3;18)). Таким образом, решением нашего уравнения будут: (_<1>=-1; _<2>=3).
Теперь рассмотрим уравнение с двумя переменными (f(x,y)=0). Решением этого уравнения будет множество пар точек ((x,y)), которые можно изобразить в виде графика на координатной плоскости ((xOy)). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую ((x,y=f(x))) или ((x=f(y),y)).
В качестве примера рассмотрим обыкновенное линейное уравнение (2x-5y=10). (1) Выражаем (x=frac<10+5y><2>) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):
Графический метод решения задач с параметрами
Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.
Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.
Вот список тем, которые стоит повторить:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.
Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).
1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.
В первом уравнении выделим полный квадрат:
Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.
Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.
Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.
Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках и Координаты этих точек легко найти, подставим в уравнение окружности.
Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.
2. Найдите все значения a, при которых уравнение имеет единственное решение.
Уравнение равносильно системе:
Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).
Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.
Приводим подобные слагаемые в уравнении.
Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:
Решим систему графически:
Уравнение задает окружность с центром в точке , где радиус
Неравенство задает полуплоскость, которая расположена выше прямой , вместе с самой этой прямой.
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением
Пусть С — точка касания.
На координатной плоскости отметим точки и , в которых прямая пересекает оси Y и Х.
Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.
Решая это уравнение, получаем, что
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.
График уравнения — окружность с центром и радиусом равным 2.
График уравнения — две симметричные окружности и радиуса 2 c центрами в точках и
Второе уравнение при задает окружность с центром в точке и радиусом a.
Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.
Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности или только правой
Если a — радиус окружности , то это значит, что (только правая) или (только левая).
Пусть А — точка касания окружности и окружности
, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),
В — точка касания окружности и окружности
длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:
Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:
, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.
Аналогично, для точки D:
и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.
4. При каких значениях a система уравнений имеет 4 решения?
Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!
Просто выделили полный квадрат во втором уравнении.
Сделаем замену Система примет вид:
Вот теперь все видно! Рисовать будем в координатах
Графиком первого уравнения является ромб, проходящий через точки с координатами и
Графиком второго уравнения является окружность с радиусом и центром в начале координат.
Когда же система имеет ровно 4 решения?
1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.
Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.
Диагонали нашего ромба равны 8 и 6. Значит,
Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

Мы получили ответ:
2) Есть второй случай, и мы его найдем.
Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.
Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.
Пусть радиус окружности равен 3. Тогда система имеет 6 решений.
А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!
Значит, Объединим случаи и запишем ответ:
Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.
Задание 17. Уравнения и неравенства с параметром
Существует ровно три генеральных метода решения задач 17:
- Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;
- Графический метод — привлечение чертежа. Во многих задачах 17 достаточно начертить графики функций — и решение становится очевидным;
- Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.
Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.
Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)
Глава 1. Графический подход § 1. Вебинар по задачам 18: модуль и окружности 















источники:
http://ege-study.ru/graficheskij-metod-resheniya-zadach-s-parametrami/
http://www.berdov.com/ege/parametr/
Графический метод
в задачах с параметром
Введение.
Я выбрала эту тему, так как она является неотъемлемой частью изучения школьного курса алгебры. Готовя данную работу, я ставила цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. Мой реферат поможет понять применение графического метода решения уравнений с параметрами, узнать о происхождении, развитии этого метода.
В современной жизни изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами.
Для решения таких уравнений графический метод является весьма эффективным, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра а.
Задачи с параметрами представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков. Они обладают диагностической ценностью, так как с помощью них можно проверить знание основных разделов математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности и перспективные возможности успешного овладения курса математики в высших учебных заведениях.
В моём реферате рассмотрены часто встречающиеся типы заданий и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов, ведь уравнения с параметрами по праву считаются одними из самых сложных задач в курсе школьной математики. Именно такие задачи и попадают в список заданий на едином государственном экзамене ЕГЭ.
§1 Что такое параметр.
Толковый словарь определяет «параметр» как величину, характеризующую какое — нибудь основное свойство машины, устройства, системы или явления, процесса. (Ожегов С.И. , Шведова Н.Ю. Толковый словарь русского языка. Москва. 1999). Рассмотрение параметров — это всегда выбор. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и др. Перед выбором мы стоим и в различных жизненных ситуациях.
Что такое параметр в математике? Если вы вспомните некоторые основные уравнения (например, kx+l=0, ax²+bx+c=0), то обратите внимание, что при поиске их корней значения остальных переменных, входящих в уравнения, считаются фиксированными и заданными. Все разночтения в существующей литературе связаны с толкованием того, какими фиксированными и заданными могут быть эти значения остальных переменных.
Поскольку в школьных учебниках нет определения параметра, возьмем за основу следующий его простейший вариант.
Определение: параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Независимость параметра заключается в его «неподчинении» свойствам, вытекающим из условия задачи. Например, из неотрицательности левой части уравнения |x|=a–1 не следует неотрицательность значений выражения a–1, и если a–1
§2 Что означает «решить задачу с параметром»
и основные типы задач с параметрами.
Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.
Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.
На ЕГЭ встречаются два типа задач с параметрами. Первый «для каждого значения параметра найти все решения некоторого уравнения или неравенства». Второй «найти все значения параметра, при каждом из которых решения уравнения или неравенства удовлетворяют заданным условиям».
И ответы в задачах этих двух типов различаются по существу. В задачах первого типа ответ выглядит так: перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения. В ответах второго типа задач с параметром перечисляются все значения параметра, при которых выполнены условия задачи.
§3 Основные способы решения задач с параметром.
Аналитический — способ прямого решения, повторяющего стандартные процедуры нахождения ответа в уравнении без параметров.
Графический — в зависимости от условия задачи рассматривается положение графика функции в системе координат.
Графический способ. В зависимости от того, какая роль параметру отведена в задаче, можно соответственно выделить два основных графических приёма:
первый – построение графика на координатной плоскости (х;у),
второй – построение графика на координатной плоскости на (х;а).
На плоскости (х;у) или (х;а) функция y=f(x;a) задаёт семейство кривых, зависящих от параметра а. Понятно, что каждое семейство f обладает определёнными свойствами. Нас же в первую очередь будет интересовать с помощью какого преобразования плоскости (параллельный перенос, поворот и т.д.) можно перейти от одной прямой к какой-нибудь другой.
Если уравнение одной из фигур не зависит от изменяющегося параметра, то график этой фигуры неподвижен относительно системы координат. Если в уравнение другой фигуры входит параметр, то от его изменения зависит расположение и даже форма графика. Тогда суть решения уравнения состоит в определении числа точек пересечения графиков построенных уравнений, а значит в определении количества возможных решений в зависимости от конкретных числовых значений параметра.
Графический способ определения числа корней уравнения в зависимости от входящего в него параметра является более удобным, чем аналитический.
§4. «Базовые элементы» для решения задач с параметрами
Понятие функции — одно из ключевых в математике.
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись.
Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
1. Степенные
К этому типу относятся линейные, квадратичные, кубические,
,
,
Все они содержат выражения вида xα.
2. Показательные
Это функции вида y = ax
3. Логарифмические
y = logax.
4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
5. Обратные тригонометрические
Содержат arcsinx, arccosx, arctgx, arcctgx.
Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x2 · ex — произведение квадратичной и показательной функций; y = sin(ax) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
В задачах с параметрами Профильного ЕГЭ по математике встречаются не только графики функций (в школьном смысле этого слова), но и множества точек на плоскости.
Вот несколько уравнений и неравенств, задающих окружность, круг, ромбик, отрезок. Заметим, что окружность или ромбик, хотя и задаются уравнениями, не являются графиками функций в школьном смысле этого слова.
Задачи с параметрами на ЕГЭ по математике считаются одними из самых сложных. Однако на самом деле они похожи на конструктор, где вы собираете решение из готовых элементов. Чтобы уверенно решать задачи с параметрами, необходимо отлично знать типы элементарных функций и их графики. Преобразования графиков функций. И вот эти базовые элементы:
1. Уравнение задает окружность с центром в начале координат и радиусом
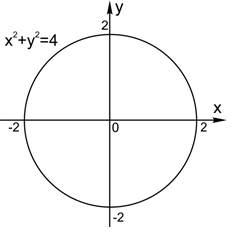
2. Уравнение задает окружность с центром в точке (a;b) и радиусом

3. Неравенство задает круг вместе с границей
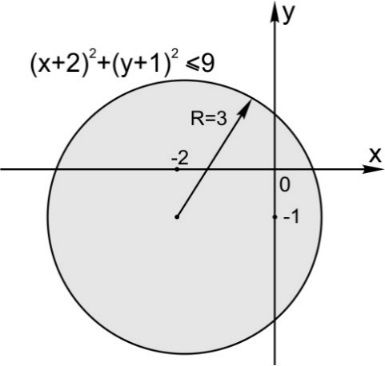
4. Уравнение задает верхнюю полуокружность с центром в начале координат и радиусом

5. Уравнение задает нижнюю полуокружность с центром в начале координат и радиусом
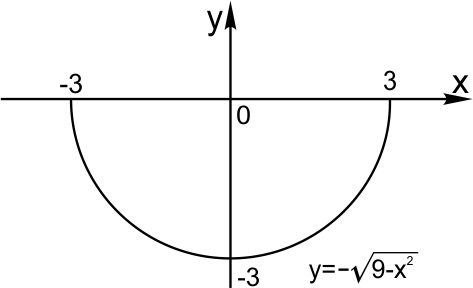
6. Уравнение задает верхнюю полуокружность центром в точке
и радиусом
7. Уравнение при положительных
и
задает ромбик, симметричный относительно начала координат.

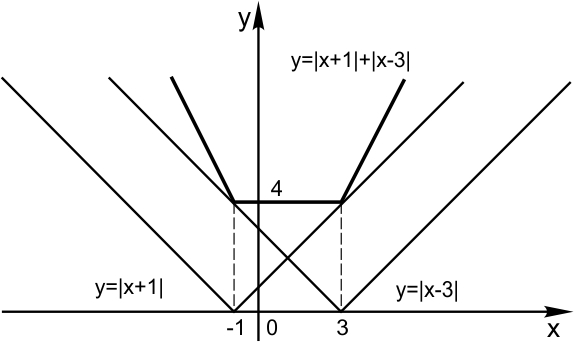
8. Уравнение (сумма модулей) задает график следующего вида:
§5 Преобразование графиков функций
В своей работе я рассмотрела основные преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Эта тема — полезная и очень интересная — выпадает из школьной программы. Для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Начнем со сдвигов графиков по Х и по Y.
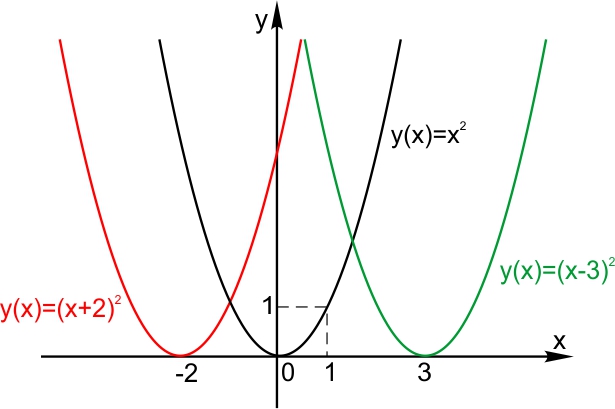
Сдвиг по горизонтали.
Пусть функция задана формулой и
Тогда график функции
сдвинут относительно исходной на а вправо. График функции
сдвинут относительно исходной на а влево.
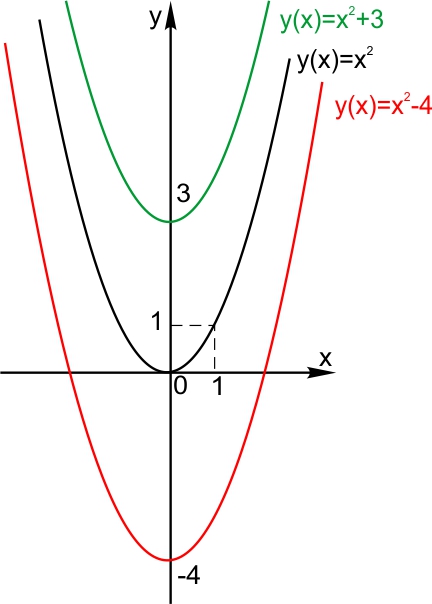
Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции
сдвинут относительно исходного на С вверх. График функции
сдвинут относительно исходного на С вниз.
Теперь растяжение графика или сжатие.
Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и
Тогда график функции
растянут относительно исходного в k раз по горизонтали, если
, и сжат относительно исходного в k раз по горизонтали, если

Растяжение (сжатие) по вертикали
Пусть функция задана формулой и
Тогда график функции
растянут относительно исходного в М раз по вертикали, если
, и сжат относительно исходного в М раз по вертикали, если
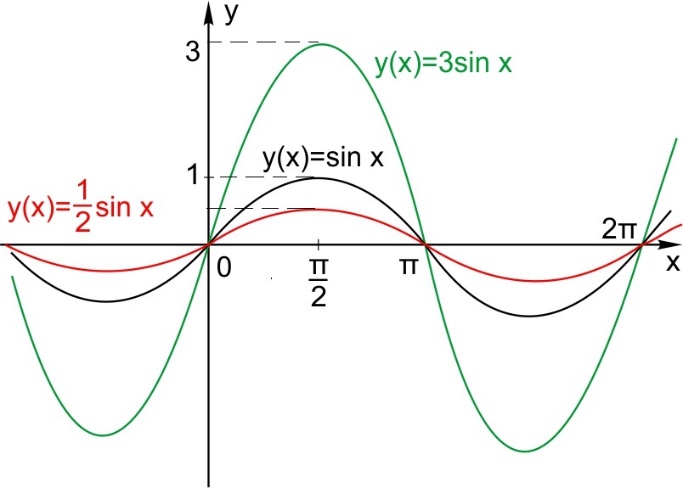
Отражение по горизонтали.
График функции симметричен графику функции
относительно оси Y.

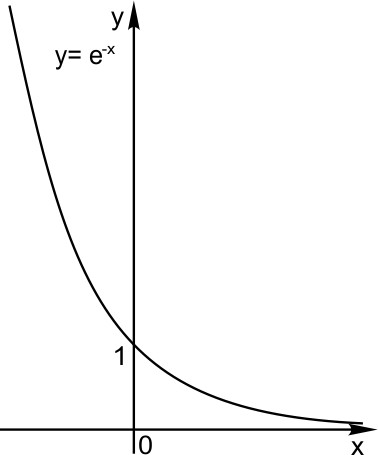
Отражение по вертикали.
График функции симметричен графику функции
относительно оси Х.
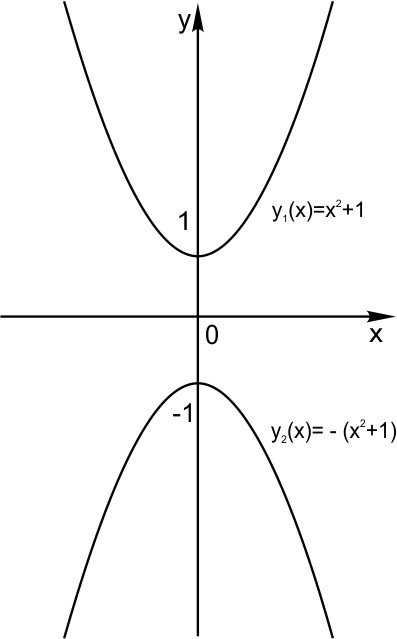
И еще два интересных преобразования.
Здесь в формулах присутствует знак модуля
Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
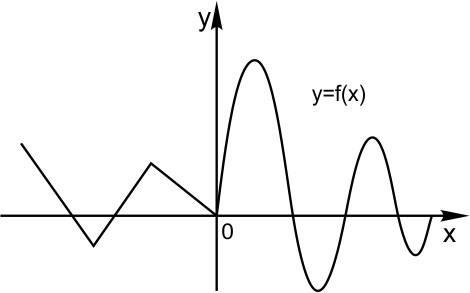
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
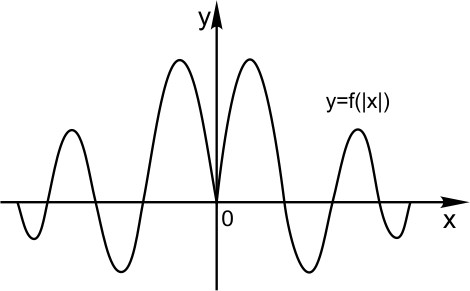
Теперь график функции Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
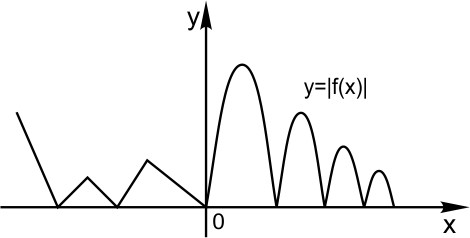
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
§6. Решение задач.
Задача 1. Сколько корней имеет уравнение | | x | – 2 | = a в зависимости от параметра a?
Решение. В системе координат (x; y) построим графики функций y = | | x | – 2 | и y = a. График функции y = | | x | – 2 | изображен на рисунке.
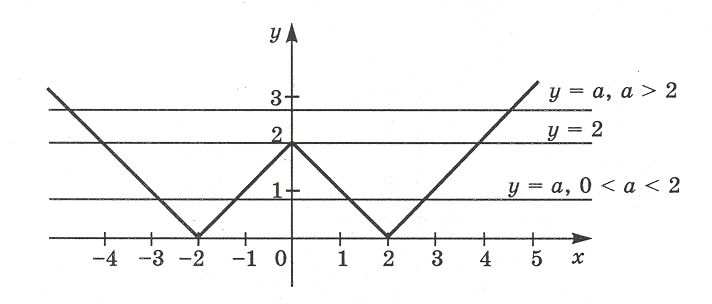
Графиком функции y = а является прямая, параллельная оси Ox или с ней совпадающая (при a = 0).
Из графика видно, что:
Если a = 0, то прямая y = a совпадает с осью Ox и имеет с графиком функции y = | | x | – 2 | две общие точки; значит, исходное уравнение имеет два корня (в данном случае корни можно найти: x1,2 = + 2).
Если 0 a Если a = 2, то прямая y = 2 имеет с графиком функции три общие точки. Тогда исходное уравнение имеет три корня.
Если a 2, то прямая y = a будет иметь с графиком исходной функции две точки, то есть данное уравнение будет иметь два корня.
Ответ: если a если a = 0, a 2, то два корня;
если a = 2, то три корня;
если 0 a
Задача 2. Сколько корней имеет уравнение | x2 – 2| x | – 3 | = a в зависимости от параметра a?
Решение. В системе координат (x; y) построим графики функций
y = | x2 – 2| x | – 3 | и y = a.
График функции y = | x2 – 2| x | – 3 | изображен на рисунке. Графиком функции y = a является прямая, параллельная Ox или с ней совпадающая (когда a = 0).
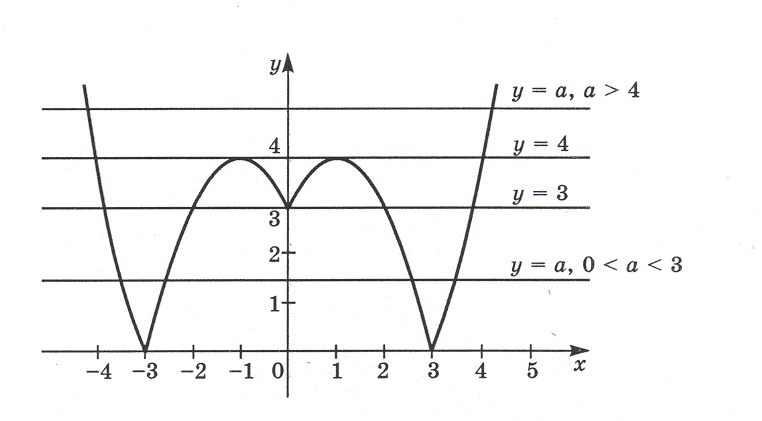
Из графика видно:
Если a = 0, то прямая y = a совпадает с осью Ox и имеет с графиком функции
y = | x2 – 2| x | – 3 | две общие точки, а также прямая y = a будет иметь с графиком функции y = | x2 – 2| x | – 3 | две общие точки при a 4. Значит, при a = 0 и a 4 исходное уравнение имеет два корня.
Если 0 a a имеет с графиком функции y = | x2 – 2| x | – 3 | четыре общие точки, а также прямая y=a будет иметь с графиком построенной функции четыре общие точки при a = 4. Значит, при 0 a a = 4 исходное уравнение имеет четыре корня.
Если a = 3, то прямая y = a пересекает график функции в пяти точках; следовательно, уравнение имеет пять корней.
Если 3 a Если a 2 – 2| x | – 3 |.
Ответ: если a если a = 0, a 4, то два корня;
если 0 a a = 4, то четыре корня;
если a = 3, то пять корней;
если 3 a
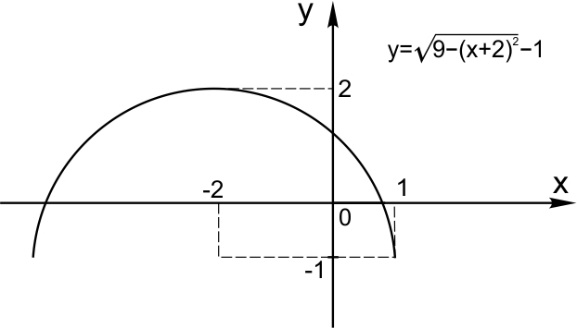
Задача 3. Найдите все значения а, при каждом из которых решения неравенства

Решение. Перенесем единицу:

Построим графики функций и

На рисунке видно, что неравенство имеет решения только при или

1)
Решения образуют отрезок длины 1, если

2) 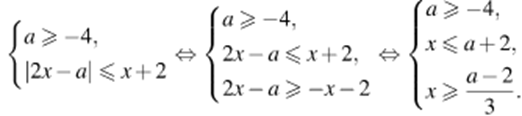
Решения образуют отрезок длины 1, если



Ответ: 

Задача 4. Сколько корней имеет уравнение
x + 2 = a | x – 1 |
в зависимости от параметра a?
Решение. Заметим, что x = 1 не является корнем данного уравнения, так как равенство 3 = a0 не может быть верным ни при каком значении параметра a. Разделим обе части уравнения на | x – 1 |(| x – 1 | 0), тогда уравнение примет вид В системе координат xOy построим график функции

График этой функции изображен на рисунке. Графиком функции y = a является прямая, параллельная оси Ox или с ней совпадающая (при a = 0).
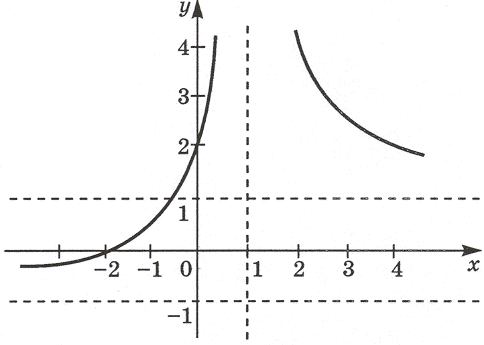
Далее рассуждая так же, как и в предыдущей задаче, получаем ответ.
Ответ: если a – 1, то корней нет;
если – 1 a 1, то один корень;
если a 1, то два корня.
Задача 5. При каких значениях параметра a уравнение
ax2 + | x – 1 | = 0 имеет три решения?
Решение. 1. Контрольным значением параметра для данного уравнения будет число a = 0, при котором уравнение примет вид 0 + | x – 1 | = 0, откуда x = 1. Следовательно, при a = 0 уравнение имеет один корень, что не удовлетворяет условию задачи.
2.Рассмотрим случай, когда a ax2 = – | x – 1 |. Заметим, что уравнение будет иметь решения только при a
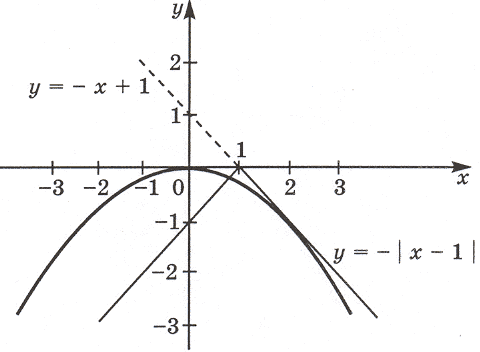
В системе координат xOy построим графики функций y = | x – 1 | и y = ax2. График функции y = | x – 1 | изображен на рисунке. Графиком функции y = ax2 является парабола, ветви которой направлены вниз, так как a
Уравнение будет иметь три решения только тогда, когда прямая y = – x + 1 будет касательной к графику функции y=ax2.
Пусть x0 — абсцисса точки касания прямой y = – x + 1 с параболой y = ax2. Уравнение касательной имеет вид
y = y(x0) + y ‘(x0)(x – x0).
Запишем условия касания:
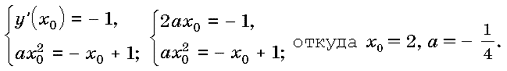
Данное уравнение можно решить без использования понятия производной.
Рассмотрим другой способ. Воспользуемся тем, что если прямая y = kx + b имеет единственную общую точку с параболой y = ax2 + px + q, то уравнение ax2 + px + q = kx + b должно иметь единственное решение, то есть его дискриминант равен нулю. В нашем случае имеем уравнение ax2 = – x + 1 (a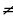
Ответ:
Задача 6. Найдите все значения 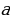
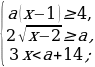
Преобразуем систему: 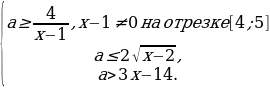
Построим прямоугольную систему координат xOa. Изобразим множество точек, координаты которых удовлетворяют системе неравенств.
Гипербола 

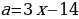
Поскольку система должна иметь хотя бы одно решение на отрезке [4; 5], определим наименьшую и наибольшую ординаты проекции выделенного на рисунке четырехугольника на ось ординат.
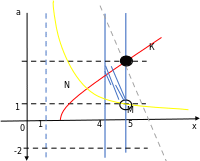
Найдём координаты точки P:
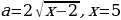
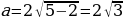
Проекции точек P и M дают искомое множество: заданная система неравенств имеет хотя бы одно решение на отрезке [4; 5] при 
Ответ: (1; 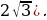
Задача 7. Найдите все значения а, при каждом из которых уравнение имеет единственный корень.
Запишем уравнение в виде 
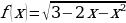
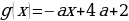
Рассмотрим функцию 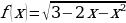

Таким образом, получаем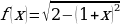
Г
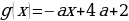
Уравнение имеет единственный корень, если графики функций имеют одну общую точку (т.е. прямая касается или пересекает полуокружность в единственной точке).
Рассмотрим рисунок: 1. Прямая МС является касательной к полуокружности, следовательно, МС и полуокружность пересекаются в единственной точке. Так как МС параллельна оси ОХ ( У точки М (4,2) и С(-1,2)), то угловой коэффициент 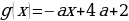
2. Проведем прямую через точки М(4;2) и А(-3;0) ( так как координаты известны). Прямая МА пересекает график полуокружности в двух точках, но такая ситуация не удовлетворяет условию задачи. Поэтому надо найти значения углового коэффициента, при которых вышеназванное условие не выполняется. Чтобы найти значения –а подставим координаты точек М и А в функцию 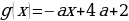
-4а+16а+2=2 3а+4а+2=0
12а=0 7а=-2
а=0. а=
Получаем, -а=0 и –а=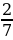
При условии 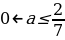
3. Проведем прямую МВ через точки М(4;2) и В(1;0). Чтобы найти значения –а подставим координаты точек М и А в функцию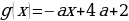
3а+4а+2=0 -а+4а+2=0
7а=-2 3а=-2
а=

Получаем –а=
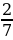
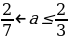
Ответ: а=0, 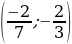
Задача 8. Найдите все значения 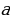
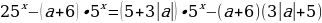
имеет единственное решение.
Аналитический способ:
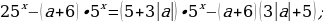
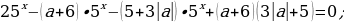
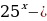
Пусть 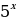
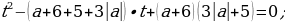
Исходное уравнение будет иметь единственное решение:
1 случай: еcли уравнение (*) имеет единственное решение (D=0);
2 случай: если уравнение (*) имеет два корня (D0), один из которых меньше нуля или равен нулю.
Пусть n=a+6, m=5+3|a|;
1 случай:
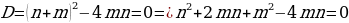

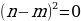
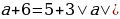

если a 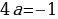
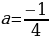

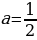
2 случай:


если nm, то:
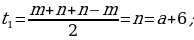
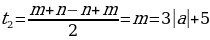
если n

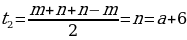
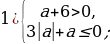
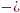

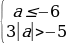
или 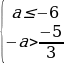
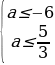

или 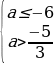
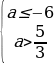
Ответ: 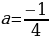
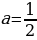

Графический способ:
Преобразуем исходное уравнение:
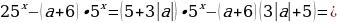

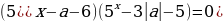
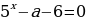
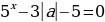
Построим графики функций 
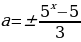
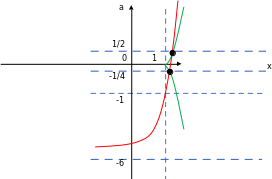
На чертеже заметим, что система имеет единственное решение при 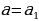
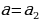


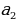
Если a0, то: 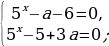
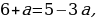

Если а 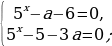
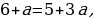

Ответ: 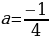
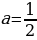

Задача 9. Найдите все значения 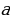
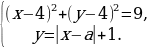
Первое уравнение системы является уравнением окружности с центром в точке 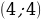

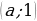
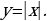

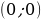
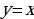
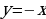

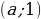

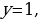

Ровно три общие точки фигуры имеют в следующих случаях:
1. Вершина прямого угла лежит в точке 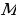

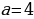
2. Одна из сторон прямого угла пересекает окружность в двух точках, а другая касается окружности в точке 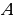
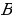



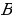
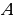
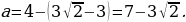
При 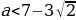
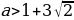
При 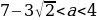
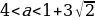
Ответ: 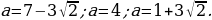

П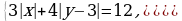
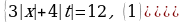
Пусть t = y – 3, тогда система примет вид:
Количество решений полученной системы совпадает с количеством решений исходной системы.
Построим графики уравнений (1) и (2) в системе координат Oxt. График первого уравнения – ромб, диагонали которого, равные 8 и 6, лежат на осях Ох и Оt, а графиком второго уравнения является окружность с центром в начале координат и радиусом r = |a|.
С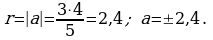
Во втором случае получаем 3 |a |
Ответ: а = ± 2,4; −4
Заключение
Работая над это темой, я провела большую работу: изучила литературу по выбранной теме; разобралась, что такое параметр и задачи с параметрами; познакомилась с методами их решения.
Выполняя практическую часть, было решено много уравнений, неравенств и их систем, я приобрела опыт и научилась решать определённый круг задач и пришла к некоторым выводам.
Решение каждого задания требует к себе индивидуального подхода, но при этом задачи с параметрами чем-то похожи на детский конструктор. Разобрав много таких примеров, можно заметить, как решение «собирается» из мелких деталей – хорошо знакомых нам фактов.
Для себя я выделила два основных способа решения №17 из ЕГЭ:
аналитический и графический.
Графический способ является наиболее наглядным, простым и доступным способом решения задач с параметрами. Если задачу с параметром можно нарисовать – рисуем. То есть применяем графический метод. Размытость в решение уравнения, неравенства или их системы с помощью графика, можно подкрепить аналитическим выводом, что поможет подтвердить правоту выбранного решения и ответа.
Сочетание аналитического способа решения с графической интерпретацией полученных результатов позволяет сделать процесс решения уравнений с параметрами более осознанным, способствуя при этом формированию элементов исследовательской деятельности.
Мне эта работа интересна.
Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность.
Список литературы
1.Корянов А.Г., Прокофьев А.А. Уравнения и неравенства с параметрами. Количество решений.
2.Шарыгин И.Ф., В.И.Голубев. Факультативный курс по математике. Решение задач. Учебное пособие для 11 класса. Москва «Просвещение». 1991 г.
3.Моденов В.П. Задачи с параметрами Москва «Экзамен» 2017
Интернет – ресурсы:
http://reshuege.ru «Решу ЕГЭ» — образовательный портал
https://egemaximum.ru/category/17/
34