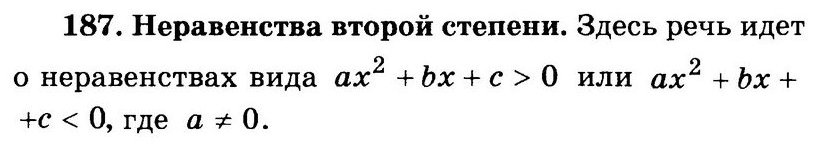СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Неравенства с параметром
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 17 № 507589
Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.
Аналоги к заданию № 507589: 507594 Все
Классификатор алгебры: Подвижная галочка
Методы алгебры: Использование косвенных методов
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 17 № 507594
Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1.
Аналоги к заданию № 507589: 507594 Все
Классификатор алгебры: Подвижная галочка
Методы алгебры: Использование косвенных методов
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 17 № 510547
Найдите все значения a, при каждом из которых множеством решений неравенства
является отрезок.
Аналоги к заданию № 510547: 484643 511315 Все
Классификатор алгебры: Подвижная галочка
Методы алгебры: Использование косвенных методов
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
4
Тип 17 № 505710
Найти все значения параметра a, при каждом из которых неравенство
выполняется для всех x из отрезка
Источник: А. Ларин: Тренировочный вариант № 59.
Классификатор алгебры: Неравенства с параметром
Методы алгебры: Замена переменной, Использование симметрий, оценок, монотонности, Формулы приведения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 17 № 537138
Найдите все значения параметра а из отрезка при которых неравенство
выполняется при любых
Источник: А. Ларин. Тренировочный вариант № 307. (Часть C)
Классификатор алгебры: Комбинация «кривых», Координаты (x, a), Неравенства с параметром
Методы алгебры: Перебор случаев
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
- »
- »
Уравнения с параметром. Задача 18 (С6)
Графический метод в задачах с параметром
Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.
Для начала рассмотрим уравнение с одной переменной (f(x)=0). Для того, чтобы решить его графическим методом, нужно построить график функции (y=f(x)). Точки пересечения графика с осью абсцисс (ось (х)) и будут решениями нашего уравнения.
Или рассмотрим уравнение (f(x)=g(x)). Точно так же строим на одной координатной плоскости графики функций (y=f(x)) и (y=g(x)), абсциссы точек их пересечения будут решениями уравнения.
Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.
Пример 1
Решить графическим методом уравнение (x^2+3x=5x+3).
Решение: Построим на одной координатной плоскости графики функций (y=x^2+3x) и (y=5x+3). См. рис.1.
(y=5x+3) – красный график; (y=x^2+3x) – синий график.
Из Рис.1 видно, что графики пересекаются в точках ((-1;2)) и ((3;18)). Таким образом, решением нашего уравнения будут: ({x}_{1}=-1; {x}_{2}=3).
Ответ: ({x}_{1}=-1; {x}_{2}=3).
Теперь рассмотрим уравнение с двумя переменными (f(x,y)=0). Решением этого уравнения будет множество пар точек ((x,y)), которые можно изобразить в виде графика на координатной плоскости ((xOy)). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую ((x,y=f(x))) или ((x=f(y),y)).
В качестве примера рассмотрим обыкновенное линейное уравнение (2x-5y=10). (1) Выражаем (x=frac{10+5y}{2}) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):
Все точки, принадлежащие этому графику, будут решениями нашего уравнения. Например, при (x=0) ⇔ (y=-2). Аналогично можно выразить (y=frac{2x-10}{5}). График будет выглядеть так (Рис. 3):
И, разумеется, будет задавать точно такие же пары решений (x) и (y).
Теперь перейдем к уравнениям с параметром. Заметим, что параметр – это обычная переменная, которая ничем не отличается от рассмотренных выше переменных (x) и (y). Поэтому, если мы вместо (y) в уравнении (1) запишем параметр (a), то суть уравнения от этого не поменяется. То есть уравнение (1) можно рассматривать относительно (x) с параметром (y) или наоборот. В дальнейшем параметр будем обозначать за (a).
Разберем уравнение с параметром (6x-5a=15). Будем работать в системе координат ((aOx)). Выразим (x=frac{15+5a}{6}) – это будет общий вид решения. Для того чтобы проиллюстрировать ответ, построим график (x(a)) (Рис. 4).
Пример 2
Найти все значения параметра (a), при которых корни уравнения (6x-5a=15) лежат на отрезке ([-5;5]).
График (x(a)) для этого же примера на рисунке 4.
Иногда для решения удобно построить график зависимости (a(x): a=frac{6x-15}{5}). Давайте так и поступим. Построим график (Рис. 5). И красной областью покажем интервал, который нас интересует по условию задачи. Из рисунка видно, что (a∈[-9;3]) (при (x=5) ⇔(a=3); и при (x=-5) ⇔(a=-9))
На мой взгляд, будет более наглядно, если показывать графический метод на примерах. Поэтому, давайте разберем примеры от простых к сложным, которые могут встретиться на ЕГЭ.
Пример 3
Определить, при каких значениях параметра (a) уравнение (x^2-3x-2a=0) имеет: а) 2 корня; б) 1 корень; в) не имеет корней;
Решение:
1 способ решения:
Приведем уравнение к виду (x^2-3x=2a). И построим графики (y=1/2*(x^2-3x)) (показан красной линией) и (y=a) (синяя линия). Обратите внимание, график (y=a) – это просто семейство прямых параллельных оси (x) в плоскости ((xOy)) (Рис. 6). Точки пересечения красной линии с семейством синих линий – это корни нашего уравнения. Если, например, (a=5), то графики (y=5) и (y=1/2*(x^2-3x)) имеют две общие точки, а значит, и два решения. При (a=-1.125) оба графика имеют только одну общую точку ((1.5;-1.125)) – это единственное решение.
Ответ:
При (a>-1.115) уравнение имеет два корня;
При (a=-1.125) уравнение имеет один корень;
При (a<-1.125) уравнение не имеет корней.
2 способ решения:
Таким же образом можно решить данное уравнение, построив графики в плоскости ((xOa)). Для этого выразим (a=1/2*(x^2-3x).)
Различным значениям параметра (a) можно поставить значения искомого (x), для это проведем горизонтальные линии.
Ответ:
При (a>-1.115) уравнение имеет два корня;
При (a=-1.125) уравнение имеет один корень;
При (a<-1.125) уравнение не имеет корней.
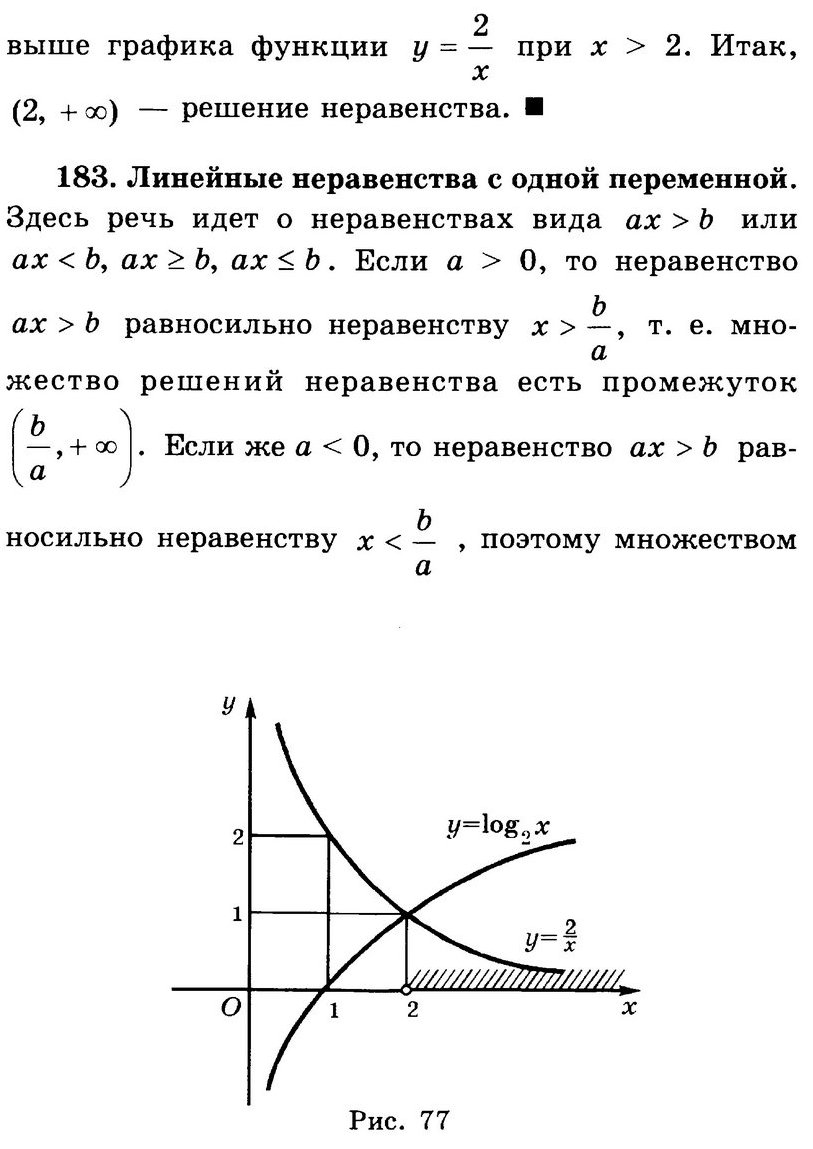
Пример 4
Решить уравнение: (cos^2x-2 cosx+a=0)
Сделаем замену (t=cosx,) тогда ( t^2-2t+a=0,) при (t∈[-1;1].)
Построим в плоскости ((tOa)) график нашей функции (a=2t-t^2:)
Точки пересечения горизонтальных (фиолетовых) прямых с графиком нашей функции соответствуют решениям. Но (t∈[-1;1]), покажем это при помощи зеленой области (Рис.8). Таким образом, нас устраивают решения, которые принадлежат кусочку параболы, попавшей в зеленую область. Как видно из рисунка, (a) может принимать значения (a∈[-3;1]), и каждому значению (a) из этой области соответствует единственное решение. Найдем его, решив уравнение (t^2-2t+a=0;)
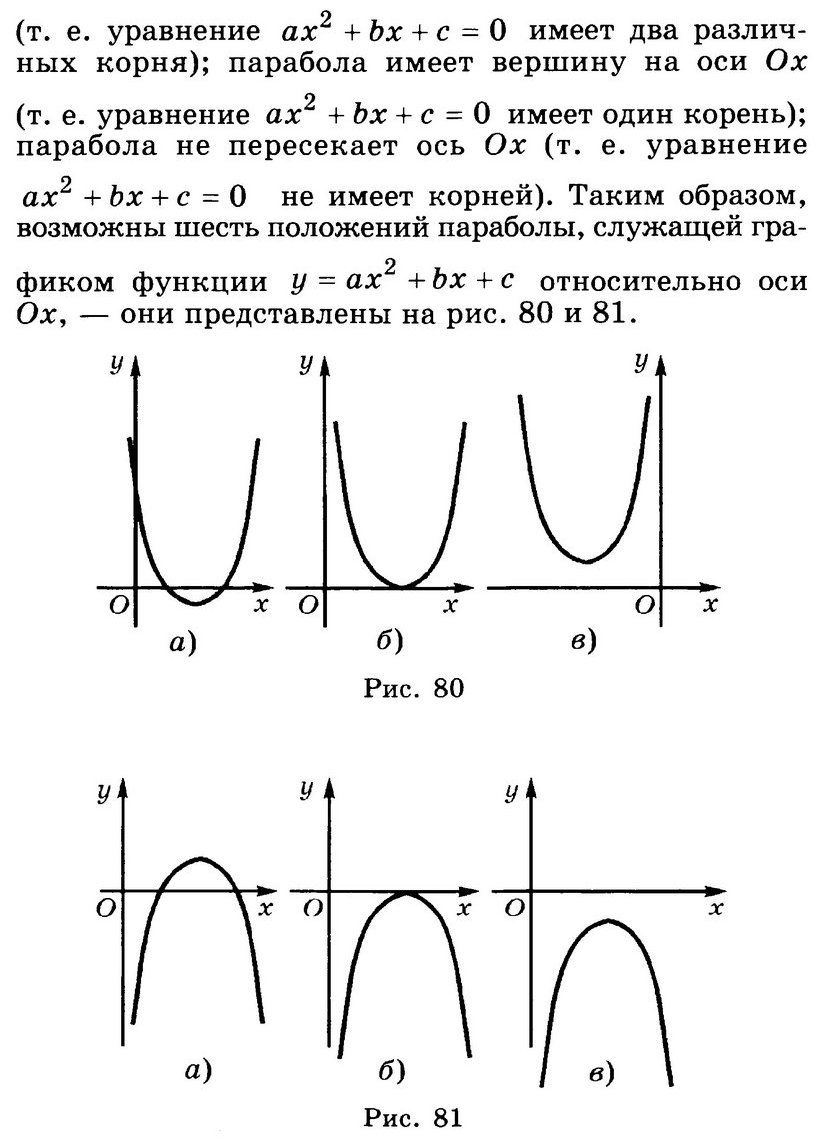
$$ {t}_{1}=frac{4-sqrt{4-4a}}{2};$$
$$ {t}_{2}=frac{4+sqrt{4-4a}}{2}.$$
({t}_{2}) не подходит, так как он не удовлетворяет условию (t∈[-1;1]).
Сделаем обратную замену:
$$ cosx=frac{4-/sqrt{4-4a}}{2};$$
$$ x=±arccos(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$
Ответ: При (a∈[-3;1]); $$ x=±arccos(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$
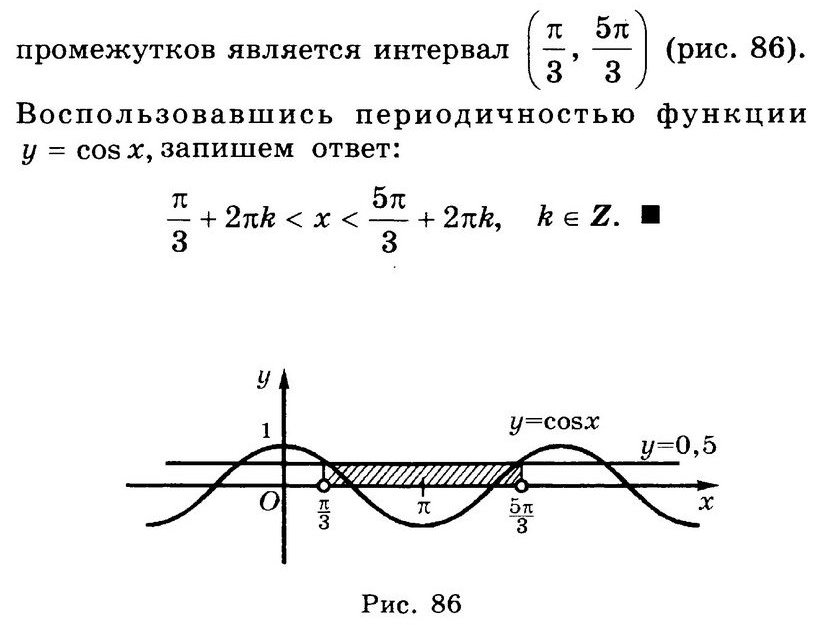
Пример 5
Решить уравнение (sin^4x-(a-1) sin^2x-(2a+2)=0.)
Решение:
Сделаем замену: (t=sin^2x ) ⇔ (t^2-(a-1)t-2a-2=0;)
Обратите внимание: (t∈[0;1];)
Выразим (a=frac{t^2+t-2}{t+2}=frac{(t+2)(t-1)}{t+2}=t-1),при (t≠-2).
Таким образом, необходимо решить систему:
$$ begin{cases} a=t-1, \t∈[0;1]. end{cases} $$
Построим решения данной системы на координатной плоскости ((tOa)).
Красной линией показан график (a=t-1), а зеленая область показывает интервал, в котором могут лежать корни. Выделенная часть графика соответствует всем возможным корням при (a∈[-1;0].) Если (a) не принадлежит этому интервалу, то корней нет. Найдем эти решения:
$$ t=a+1,$$ $$sin^2x=a+1,$$ $$ 1-cos2x=a+1,$$ $$ cos2x=-a,$$
$$x=±1/2$$ $$ arccos(-a)+πn,n∈Z.$$
Ответ:При (a∈[-1;0];) $$ x=±1/2 arccos(-a)+πn,n∈Z.$$
Пример 6
Решить уравнение (9^{-|x+1|}-3^{1-|x+1|}-a=0.)
Сделаем замену (t=3^{-|x+1|}), получим (t^2-3t-a=0), где (t∈(0;1].)
Построим график функции (a(t)=t^2-3t), при (t∈(0;1]) в системе координат ((tOa)).
Зеленой областью покажем допустимый интервал, в котором могут находиться корни. Выделенная часть параболы соответствует корням нашего уравнения при (a∈[-2;0)). Таким образом, при (a<-2) и (a≥0) корней нет.
Решим уравнение (t^2-3t-a=0).
При (a∈[-2;0)) $$ {t}_{1}=frac{3-sqrt{9+4a}}{2};$$ $$ {t}_{2}=frac{3+sqrt{9+4a}}{2},$$ так как (t∈(0;1]), то ({t}_{2}) не подходит.
Сделаем обратную замену:
$$ 3^{-|x+1|}=frac{3-sqrt{9+4a}}{2};$$
$$-|x+1|=log_3 (frac{3-sqrt{9+4a}}{2});$$
$$|x+1|=-log_3 (frac{3-sqrt{9+4a}}{2});$$
$$x=-1±log_3 (frac{3-sqrt{9+4a}}{2}).$$
Ответ: (x=-1±log_3 (frac{3-sqrt{9+4a}}{2})) при (a∈[-2;0).)
Пример 7
Решить уравнение (sqrt{a(3^x+1)+9}=2-3^x.)
Сделаем замену (t=3^x, t>0) ⇔ (sqrt{a(t+1)+9}=2-t.)
Данному уравнению равносильна система:
$$ begin{cases} a(t+1)+9=(2-t)^2, \ 2-t ≥ 0, \ t > 0. end{cases} $$
$$ begin{cases} a=frac{(t-5)(t+1)}{t+1}, \ 0 < t ≤ 2. end{cases} $$
$$ begin{cases} a = t-5, \ 0 < t <= 2. end{cases}$$
Построим множество точек, которые удовлетворяют полученной системе:
При (a∈(-5;-3]) ⇔ (t=a+5,) сделаем обратную замену 3(^x=a+5), ⇔ (x=log_3 (a+5).)
При (a∈(-∞;-5]∪(-3;+∞)) корней нет.
Ответ: При (a∈(-5;-3]) ⇔ ( x=log_3 (a+5).)
Пример 8
Решить неравенство (9^x-(a-1) 3^x-a≥0)
Сделаем замену: (t=3^x,) ⇔ (t>0;)
Получаем
$$ begin{cases} t^2-(a-1)t-a≥0, \t>0. end{cases} $$
$$ t(t+1)≥a(t+1); $$
Заметим, что решение (t=-1) не подходит, так как (t>0). Поделим наше неравенство на
(t+1). Так как (t+1>0), то знак неравенства не меняется. Будьте внимательны! В случае, когда нам неизвестен знак выражения, на которое мы делим неравенство, необходимо рассмотреть два случая, когда выражение отрицательно (меняем знак неравенства) и когда положительно (не меняем).
$$ begin{cases} t≥a, \t>0. end{cases} $$
Построим график, получившейся системы неравенств на плоскости ((tOa)).
Оранжевой областью выделено решение первого неравенства системы, синей областью – второго неравенства. Их пересечение – это решение все системы.
Получаем, что при (a≤0) $$ t∈(0;+∞) ⇔ 3^x>0 ⇔ x∈(-∞;+∞)$$
При ( a>0) $$ t∈[a;+∞) ⇔ 3^x≥a ⇔ x≥log_3 a.$$
Ответ: при( a≤0) $$ x∈(-∞;+∞)$$
при (a>0) $$ x≥log_3 a.$$
Пример 9
Найти все значения параметра, при которых функция
$$ f(x)=ln{(p-1)*3^x-4*3^{x/2}+(p+2)} $$
определена при всех (x∈R.)
Решение:
Наша функция будет определена при условии, что выражение под логарифмом будет больше нуля:
$$ (p-1)*3^x-4*3^{x/2}+(p+2) > 0.$$
Сделаем замену: (t=3^{x/2},t > 0).
Получим
$$ begin{cases} (p-1)*t^2-4*t+p+2>0, \ t>0. end{cases} $$
Если (p=1),
$$ begin{cases} -4t+3>0, \ t>0; end{cases} $$
$$ begin{cases} t<0.75, \ t>0; end{cases} $$
Сделаем обратную замену: (0 < 3^{x/2} < 0.75.) Очевидно, что это неравенство не будет выполняться при всех (x), как того требует условие задачи.
Если (p≠-1,)
$$ begin{cases} pt^2-t^2-4t+p+2>0, \t>0; end{cases} $$
$$ begin{cases} p(t^2+1)>t^2+4t-2, \t>0; end{cases} $$
$$ begin{cases} p > frac{t^2+4t-2}{1+t^2}, \t>0. end{cases} $$
Теперь нужно построить график функции (p=frac{t^2+4t-2}{1+t^2}). Для этого исследуем функцию на монотонность и найдем экстремумы.
Найдем производную:
$$ p^{‘}=frac{-4(t-2)(t+1/2)}{1+t^2}^2 ;$$
Как видно из рисунка 13, точка ((-1/2;-3)) – точка минимума; а ((2;2)) – точка максимума.
Найдем асимптоты. Напомню, что вертикальные асимптоты бывают только в точках разрыва, поэтому наличие вертикальной асимптоты можно проверить, взяв предел от функции в точке разрыва. В нашем случае нет точек разрыва, поэтому вертикальных асимптот не будет.
График функции будет иметь горизонтальные асимптоты, если (lim_{t→+∞} p(t)=const) или (lim_{t→-∞} p(t)=const.) Проверим нашу функцию:
$$lim_{t→∞} frac{t^2+4t-2}{1+t^2}=1.$$
Значит, есть горизонтальная асимптота (p=1).
И асимптоты могут быть наклонными: Прямая (p=kt+b) будет наклонной асимптотой к нашему графику ( p=frac{t^2+4t-2}{1+t^2}), если существуют пределы (lim_{t→∞} {frac{p(t)}{t}}=k) и (lim_{t→∞} {(p(t)-kt)}=b.)
В нашей случае наклонной асимптоты не будет.
Подробнее можно посмотреть здесь.
Из полученных данных построим примерный график функции (p=frac{t^2+4t-2}{1+t^2}) :
На рисунке 14 при помощи штриховки показаны точки, которые будут корнями системы
$$ begin{cases} p < frac{t^2+4t-2}{1+t^2}, \ t > 0. end{cases}$$
Если (p>2),то (t>0) или (3^(x/2)>0), а значит и функция (f(x)) определена при любых (x∈R).
Ответ: (p∈(2;+∞).)
Пример 10
Найти при каких значениях параметра (a) система
$$ begin{cases} (2+log_{3} {(frac{1}{9} a+frac{1}{3}-frac{2}{9} y)}=log_{3}{(2a+x-y-6)}, \ sqrt{x}=2+y. end{cases}$$
имеет решение?
Решение:
Преобразуем исходную систему:
$$ begin{cases} a+3-2y=2a+x-y-6, \ frac{1}{9} a+frac{1}{3}-frac{2}{9} y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=3-2y-(2+y)^2+y+6, \ a+3-2y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=-y^2-5y+5, \ a>2y-3, \ x=(2+y)^2. end{cases}$$
Построим график полученной системы:
Из рисунка 15 видно, что (a∈(-19;11.25].)
Ответ: (a∈(-19;11.25].)
Пример 11
Найти значения параметра a, при которых система
$$ begin{cases} x+y-1=0, \ 2y=sqrt{ax-1} end{cases} $$
имеет единственное решение.
Решение:
Из второго уравнения следует, что (x=frac{y^2+1}{a}).
Тогда
$$ begin{cases} frac{y^2+1}{a}+y-1=0, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$
$$ begin{cases} a=frac{y^2+1}{1-y}, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$
Обратите внимание, что (y=1), (x=0) не может быть решением системы при любых значениях параметра (a).
Исследуем, полученную зависимость (a=frac{y^2+1}{1-y}) на монотонность и найдем экстремумы.
$$ {a}^{‘}=frac{2y(1-y)+(y^2+1)}{1-y}^2 ;$$
$$ {a}^{‘}=frac{-y^2+2y+1}{(1-y)^2} =-frac{(y-1-sqrt{2})(y-1+sqrt{2})}{(1-y)^2} ;$$
Из рисунка 16 видно, что ({y}_{1}=1-sqrt{2}) — точка минимума функции (a=frac{y^2+1}{1-y};) Ей соответствует значение (a=2sqrt{2}-2).
({y}_{2}=1+sqrt{2}) — точка максимума. (a=-2sqrt{2}-2).
Найдем асимптоты (см. пример 9):
$$lim_{y→1} {frac{y^2+1}{1-y}}=∞;$$
Значит (y=1) – вертикальная асимптота.
$$lim_{y→∞} {frac{y^2+1}{1-y}}=∞;$$
Значит горизонтальные асимптоты отсутствуют.
И проверим на наличие наклонных асимптот:
$$ lim_{y→∞} {frac{a(y)}{y}}=lim_{y→∞} {frac{(frac{y^2+1}{1-y})}{y}}=lim_{y→∞} {frac{y^2+1}{y-y^2 }}=$$
$$=lim_{y→∞} {frac{1+frac{1}{y^2}}{-1+frac{1}{y}}}=-1=k;$$
$$lim_{y→∞} {(a(y)-ky)}=lim_{y→∞} {frac{y^2+1}{1-y}+y}=lim_{y→∞} {frac{1+y}{1-y}}=-1;$$
Получим уравнение наклонной асимптоты (a=-y-1).
Красным показа график функции (a=frac{y^2+1}{1-y};) Зеленым – показаны найденные асимптоты; Синяя область удовлетворяет условию (y≥0);
Выделенная бардовым часть графика указывает на возможные корни исходной системы. По условию задачи необходимо найти такие значения параметра (a), чтобы система имела единственное решение. Таким образом, из рисунка следует, что при (a=-2sqrt{2}-2) и (a ≥ 1) система будет иметь единственное решение.
Ответ: (a=-2sqrt{2}-2) и (a≥1)
Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.
Использование свойств функции при решении заданий с параметром из ЕГЭ по математике профильного уровня. Симметрия функций и приемы решения.
Квадратные уравнения с параметром. Умение исследовать квадратный многочлен поможет решать задачи с параметром аналитическим методом. Квадратное уравнение решается при помощи дискриминанта или теоремы Виета.
Разбор линейных уравнений с параметром. Для того, чтобы решить такое уравнение, нужно найти все x при всех значениях параметра a
Решение показательных и логарифмических уравнений с параметром
Знакомимся с понятием параметра в уравнениях. Краткие рекомендации к выполнению.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 — два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.
Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!
Темы для повторения:
New
Решаем задачи из сборника И. В. Ященко, 2021
Квадратичные неравенства
Метод интервалов
Уравнения и неравенства с модулем
Иррациональные неравенства
Показательные неравенства
Логарифмические неравенства
Метод замены множителя (рационализации)
Решение неравенств: основные ошибки и полезные лайфхаки
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15
Логарифмические неравенства повышенной сложности
Разберем неравенства разных типов из вариантов ЕГЭ по математике.
Дробно-рациональные неравенства
1. Решите неравенство:
Сделаем замену
Тогда , а
Получим:
Решим неравенство относительно t методом интервалов:
Получим:
Вернемся к переменной x:
Ответ:
Показательные неравенства
2. Решите неравенство
Сделаем замену Получим:
Умножим неравенство на
Дискриминант квадратного уравнения
Значит, корни этого уравнения:
Разложим квадратный трехчлен на множители.
. Вернемся к переменной x.
Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Ответ:
Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.
3. Решите неравенство
Сделаем замену Получим:
Вернемся к переменной
Первое неравенство решим легко: С неравенством
тоже все просто. Но что делать с неравенством
? Ведь
Представляете, как трудно будет выразить х?
Оценим Для этого рассмотрим функцию
Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом
Мы получили, что
Тогда , и это значит, что
Значение
не достигается ни при каких х.
Но если и
, то
Мы получили:
Ответ:
Логарифмические неравенства
4. Решите неравенство
Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.
Ответ:
Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!
5. Решите неравенство
ОДЗ:
Замена
Ответ:
А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.
6. Решите неравенство:
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Поскольку
Согласно методу замены множителя, выражение заменим на
Получим систему:
Решить ее легко.
Ответ: .
Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.
7. Решите неравенство:
ОДЗ:
Привести обе части к одному основанию не получается. Ищем другой способ.
Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.
Функции и
— монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.
Поскольку при x=9 значение монотонно возрастающей функции равно 4, при
значения этой функции меньше 4. Конечно, при этом
, то есть x принадлежит ОДЗ.
Ответ:
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Решение уравнений с помощью графиков
Решение линейных уравнений
Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.
Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.
Сейчас же я покажу тебе, как это сделать графическим способом.
Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)
Как его решить?
Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:
( displaystyle 2x=2+10)
( displaystyle 2x=12)
Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.
Иными словами, у нас будет:
( displaystyle {{y}_{1}}=2x)
( displaystyle {{y}_{2}}=12)
А теперь строим. Что у тебя получилось?
Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:
Наш ответ: ( displaystyle x=6)
Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!
Вариант 1. Напрямую
Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)
Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:
( displaystyle x=-frac{b}{2a})
( displaystyle y=-frac{{{b}^{2}}-4ac}{4a})
Ты скажешь «Стоп! Формула для ( displaystyle y) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.
Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!
Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:
( displaystyle x=frac{-2}{2}=-1)
( displaystyle y=-frac{{{2}^{2}}-4cdot left( -8 right)}{4}=-frac{4+32}{4}=-9)
Точно такой же ответ? Молодец!
И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).
Ты знаешь, что парабола симметрична относительно своей вершины, например:
Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:
Возвращаемся к нашей параболе.
Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?
Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).
При ( displaystyle x=0):
( displaystyle y={{0}^{2}}+0-8=-8)
При ( displaystyle x=2):
( displaystyle y={{2}^{2}}+2cdot 2-8=0)
Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:
Как ты думаешь, что является решением уравнения?
Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).
И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).
Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!
Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.
Что у тебя получилось? То же самое?
Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!
Решение смешанных неравенств
Теперь перейдем к более сложным неравенствам!
Как тебе такое:
( displaystyle 4x<{{x}^{3}})?
Жуть, правда? Честно говоря, я понятия не имею, как решить такое алгебраически… Но, оно и не надо. Графически ничего сложного в этом нет! Глаза боятся, а руки делают!
Первое, с чего мы начнем, – это с построения двух графиков:
( displaystyle {{y}_{1}}=4x)
( displaystyle {{y}_{2}}={{x}^{3}})
Я не буду расписывать для каждого таблицу – уверена, ты отлично справишься с этим самостоятельно (еще бы, столько прорешать примеров!).
Расписал? Теперь строй два графика.
Сравним наши рисунки?
У тебя так же? Отлично!
Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).
Смотри, что получилось в итоге:
А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!
На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).
Это и есть ответ!
Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!
Материалы для подготовки к ЕГЭ. Онлайн-Справочник по математике.
Раздел 5 «Неравенства» (§§ 17-18). Решение неравенств. Доказательство неравенств.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Раздел V. Неравенства
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
§ 17. Решение неравенств.
181. Основные понятия, связанные с решением неравенств.
182. Графическое решение неравенств с одной переменной.
183. Линейные неравенства с одной переменной.
184. Системы неравенств с одной переменной.
185. Совокупности неравенств с одной переменной.
186. Дробно-линейные неравенства.
187. Неравенства второй степени.
188. Графическое решение неравенств второй степени.
189. Неравенства с модулями.
190. Решение рациональных неравенств методом промежутков.
191. Показательные неравенства.
192. Логарифмические неравенства.
193. Иррациональные неравенства.
194. Тригонометрические неравенства.
195. Неравенства и системы неравенств с двумя переменными.
§ 18. Доказательство неравенств.
196. Метод оценки знака разности.
197. Синтетический метод доказательства неравенств.
198. Доказательство неравенств методом от противного.
199. Использование неравенств при решении уравнений.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Материалы для подготовки к ЕГЭ. Онлайн справочник по математике.
Раздел 5 «Неравенства» (§§ 17-18). Решение неравенств. Доказательство неравенств.
Просмотров:
2 709