График производной егэ профиль

Каталог заданий.
Применение производной к исследованию функций


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

На рисунке изображен график производной функции f левая круглая скобка x правая круглая скобка , определенной на интервале левая круглая скобка минус 6; 6 правая круглая скобка . Найдите промежутки возрастания функции f левая круглая скобка x правая круглая скобка . В ответе укажите сумму целых точек, входящих в эти промежутки.

2

На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.

3

На рисунке изображен график функции y  =  f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).

Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402

4

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье

5

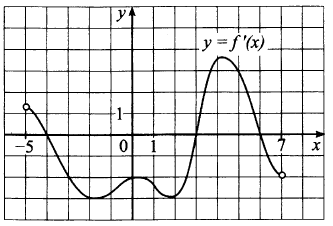
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург

Пройти тестирование по этим заданиям

Источник

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.

Геометрический смысл производной 

Вспомним, что производная — это скорость изменения функции.

Производная функции fleft ( x right ) в точке x_0 равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

boldsymbol{f

1. На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x_0 . Найдите значение производной функции f(x) в точке x_0 .

Производная функции f(x) в точке x_0 равна тангенсу угла наклона касательной, проведенной в точке x_0.

Достроив до прямоугольного треугольника АВС, получим:

f

Ответ: 0,25.

2. На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x_0.
Найдите значение производной функции y = f(x) в точке x_0.

Начнём с определения знака производной. Мы видим, что в точке x_0 функция убывает, следовательно, её производная отрицательна. Касательная в точке x_0 образует тупой угол alpha с положительным направлением оси X. Поэтому из прямоугольного треугольника мы найдём тангенс угла varphi , смежного с углом alpha.

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: tg varphi = 0, 25. Поскольку alpha + varphi = 180^{circ}, имеем:

tg alpha = tg(180^{circ} -varphi ) = - tg varphi = -0, 25.

Ответ: −0, 25.

Касательная к графику функции

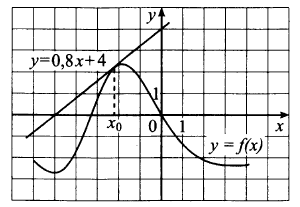
3. Прямая y = - 4x - 11 является касательной к графику функции y = x^3 + 7x^2 + 7x - 6.

Найдите абсциссу точки касания.

Запишем условие касания функции y=fleft(xright) и прямой y=kx+b в точке x_0 .

При x= x_0 значения выражений fleft(xright) и kx+b равны.

При этом производная функции fleft(xright) равна угловому коэффициенту касательной, то есть k.

left{ begin{array}{c}fleft(xright)=kx+b \f^{

left{ begin{array}{c}x^3+{7x}^2+7x-6=-4x-11 \{3x}^2+14x+7=-4 end{array}right..

Из второго уравнения находим x = -1 или x=-frac{11}{3}. Первому уравнению удовлетворяет только x = -1.

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону x(t) = t^2 - 3t - 29, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени t = 3 с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета: xleft(tright)=t^2-3t-29.

Найдем скорость материальной точки как производную от координаты по времени:

vleft(tright)=x В момент времени t=3 получим:

vleft(3right)=2cdot 3-3=3.

Ответ: 3.

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

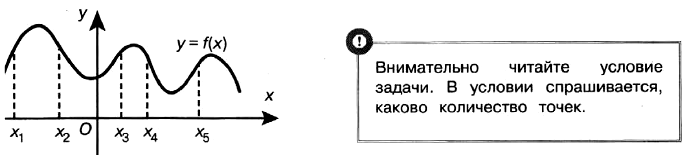
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если f, то функция f (x) возрастает.

Если f, то функция f (x) убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

f(x) возрастает точка максимума убывает точка минимума возрастает
f + 0 - 0 +

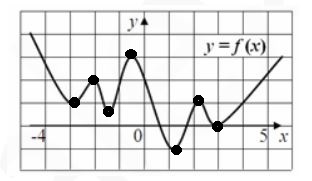
5. На рисунке изображен график функции y=f(x), определенной на интервале (-3; 9). Найдите количество точек, в которых производная функции f(x) равна 0.

Производная функции f { в точках максимума и минимума функции f(x). Таких точек на графике 5.

Ответ: 5.

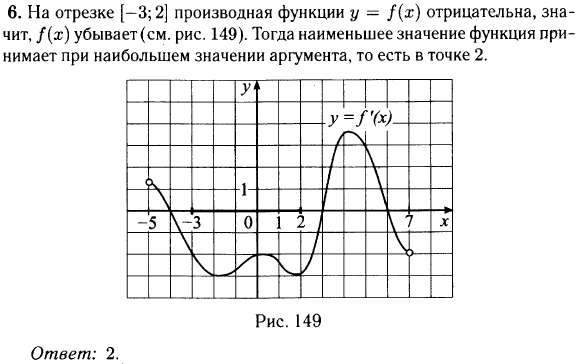
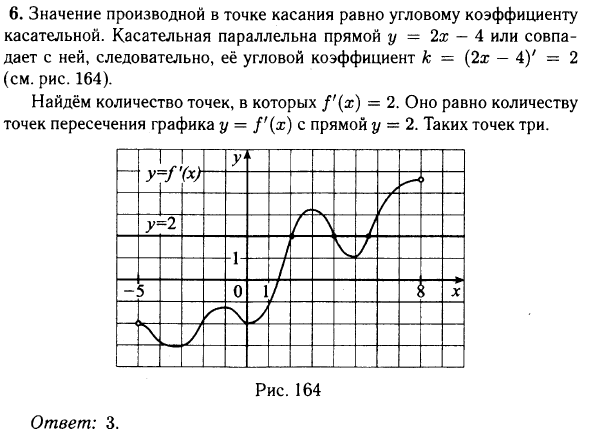
6. На рисунке изображён график y = f — производной функции f(x), определённой на интервале (-6; 5). В какой точке отрезка [-1; 3] функция f(x) принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке [-1;3] производная функции f(x) положительна.

Значит, функция f(x) возрастает на этом отрезке. Большим значениям х соответствует большее значение f(x). Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции y= f(x), определённой на интервале (-3; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 1.

Прямая y=1 параллельна оси абсцисс. Найдем на графике функции y = f(x) точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

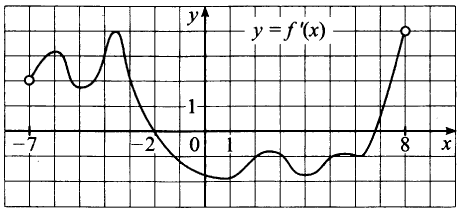
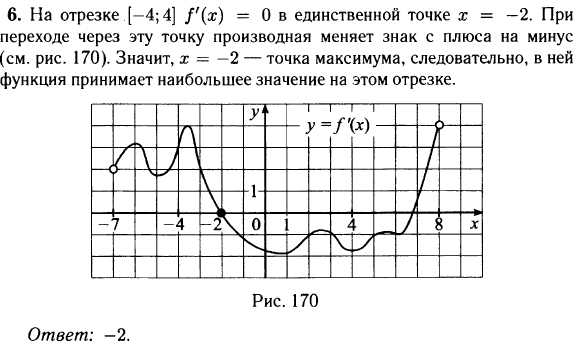
8. На рисунке изображен график производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x) на отрезке [-6; 9].

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке [-6; 9] такая точка всего одна! Это x=7.

Ответ: 1.

9. На рисунке изображен график производной функции f(x), определенной на интервале (-6; 5). Найдите точку экстремума функции f(x) на отрезке [-5; 4].

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке [- 5; 4] график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке x = -2. В этой точке производная меняет знак с минуса на плюс.

Значит, x= -2 является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x). Функции вида y = F(x) + C образуют множество первообразных функции y = f(x).

10. На рисунке изображён график y = F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-6; 6). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-4; 4] .

Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x).

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку [-4; 4] , в которых производная функции F(x) равна нулю. Это точки максимума и минимума функции F(x). На отрезке [-4; 4] таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:

$f'(x_0)={lim}↙{△x→0}{△f(x_0)}/{△x}$

Дифференцированием называют операцию нахождения производной.

Таблица производных некоторых элементарных функций

Функция Производная
$c$ $0$
$x$ $1$
$x^n$ $nx^{n-1}$
${1}/{x}$ $-{1}/{x^2}$
$√x$ ${1}/{2√x}$
$e^x$ $e^x$
$lnx$ ${1}/{x}$
$sinx$ $cosx$
$cosx$ $-sinx$
$tgx$ ${1}/{cos^2x}$
$ctgx$ $-{1}/{sin^2x}$

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$

Производная суммы (разности) равна сумме (разности) производных.

$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

Найти производную $f(x)=4x·cosx$

$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

$f(x)= cos(5x)$

$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

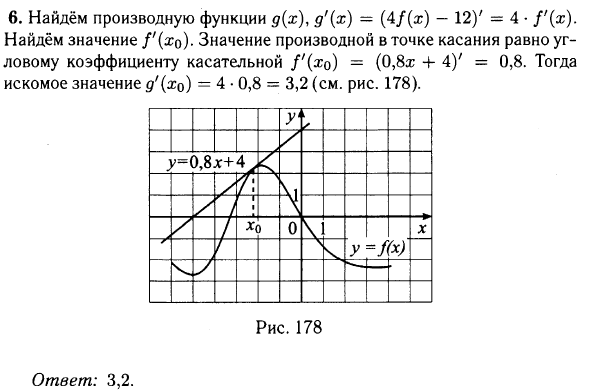
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Решение:

Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$

Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.

Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)

$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$

$f'(x_0) = tg ВАС = 0,25$

Ответ: $0,25$

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.

В ответ запишите количество данных точек.

Решение:

Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.

В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.

Ответ: $2$

Источник
Skip to content

ЕГЭ Профиль №6. Применение производной к исследованию функций

ЕГЭ Профиль №6. Применение производной к исследованию функцийadmin2022-08-17T20:42:09+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №6. Применение производной к исследованию функций

Задача 1. На рисунке изображен график функции  (y = fleft( x right)), определенной на интервале  (left( { — 8;6} right)). Определите количество целых точек, в которых производная функции (fleft( x right)) положительна.

Ответ

ОТВЕТ: 5.
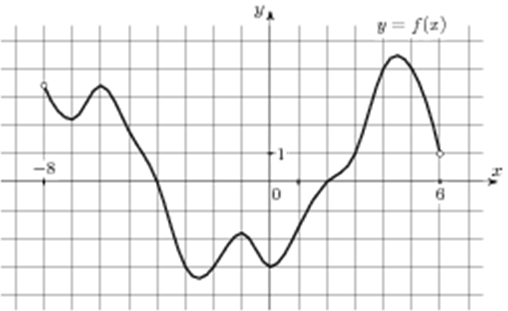Задача 2. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале(left( { — 1;10} right)). Определите количество целых точек, в которых производная функции отрицательна.

Ответ

ОТВЕТ: 6.
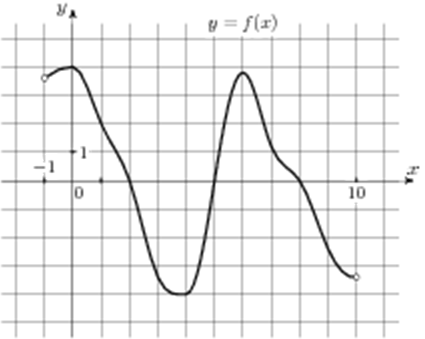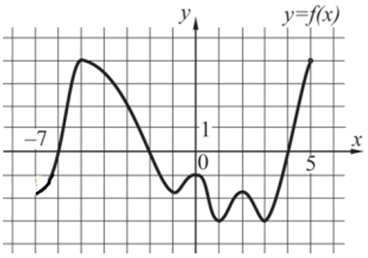
Задача 3. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале   (left( { — 7;5} right)). Найдите сумму точек экстремума функции (fleft( x right)).

Ответ

ОТВЕТ: 0.
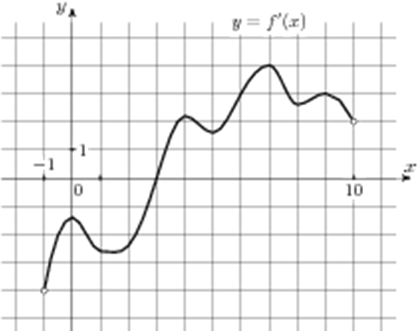
Задача 4. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 1;10} right)). В какой точке отрезка   (left[ {5;;9} right]) (fleft( x right)) принимает наибольшее значение?

Ответ

ОТВЕТ: 9.
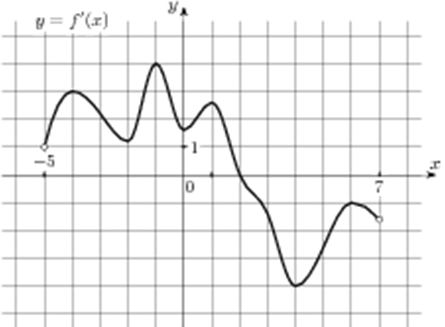
Задача 5. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале  (left( { — 5;7} right)). В какой точке отрезка (left[ {2;;6} right]) (fleft( x right)) принимает наименьшее значение?

Ответ

ОТВЕТ: 6.
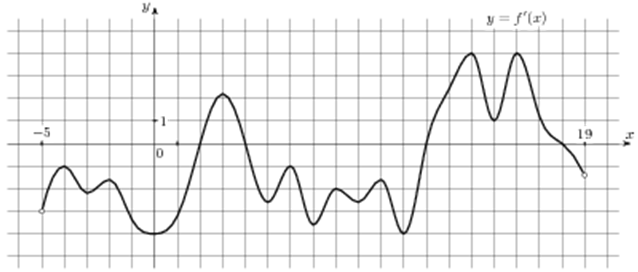
Задача 6. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 5;19} right)). Найдите количество точек максимума функции (fleft( x right)), принадлежащих отрезку    (left[ { — 3;;15} right]).

Ответ

ОТВЕТ: 1.
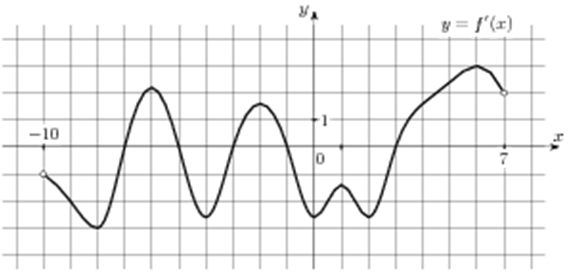
Задача 7. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 10;7} right)). Найдите количество точек минимума функции (fleft( x right)), принадлежащих отрезку (left[ { — 6;;2} right]).

Ответ

ОТВЕТ: 1.
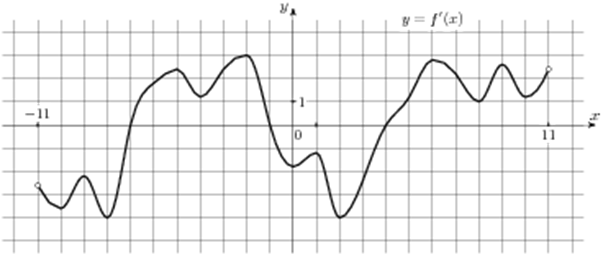
Задача 8. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале  (left( { — 11;11} right)). Найдите количество точек экстремума функции (fleft( x right)), принадлежащих отрезку   (left[ { — 8;;10} right]).

Ответ

ОТВЕТ: 3.
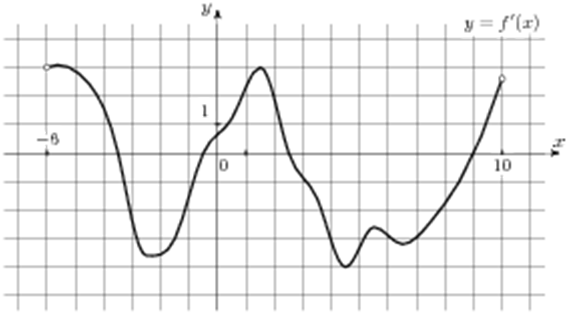
Задача 9. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 6;10} right)). Найдите промежутки возрастания функции (fleft( x right)). В ответе укажите сумму целых точек, входящих в эти промежутки.

Ответ

ОТВЕТ: 3.
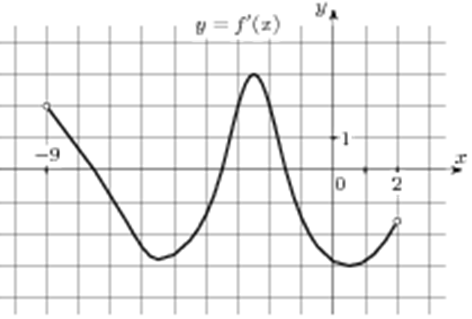
Задача 10. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 9;2} right)). Найдите промежутки убывания функции (fleft( x right)). В ответе укажите сумму целых точек, входящих в эти промежутки.

Ответ

ОТВЕТ: — 22.
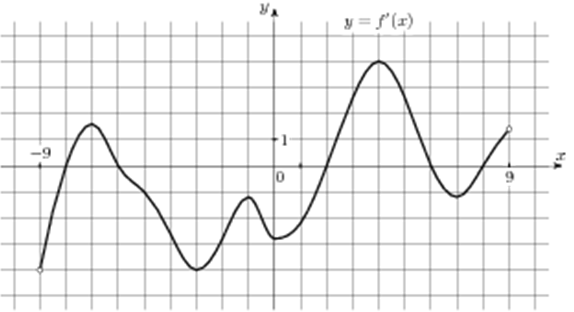
Задача 11. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 9;9} right)). Найдите промежутки возрастания функции (fleft( x right)). В ответе укажите длину наибольшего из них.

Ответ

ОТВЕТ: 4.
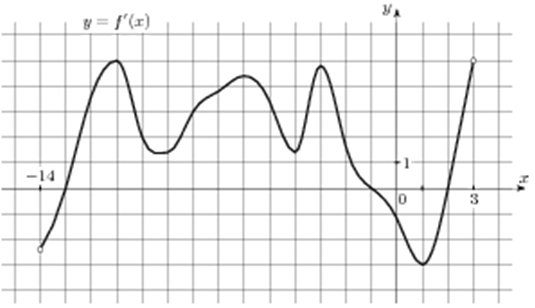
Задача 12. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 14;3} right)). Найдите промежутки убывания функции (fleft( x right)). В ответе укажите длину наибольшего из них.

Ответ

ОТВЕТ: 3.
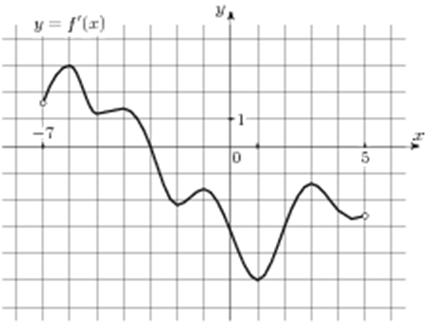
Задача 13. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале  (left( { — 7;5} right)). Найдите точку экстремума функции (fleft( x right)), принадлежащую отрезку (left[ { — 6;,4} right]).

Ответ

ОТВЕТ: — 3.
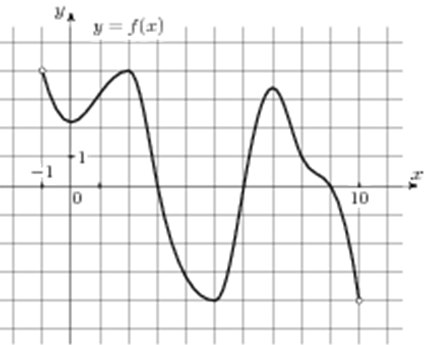
Задача 14. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале (left( { — 1;10} right)). Найдите количество точек, в которых производная функции (fleft( x right)) равна 0.

Ответ

ОТВЕТ: 4.
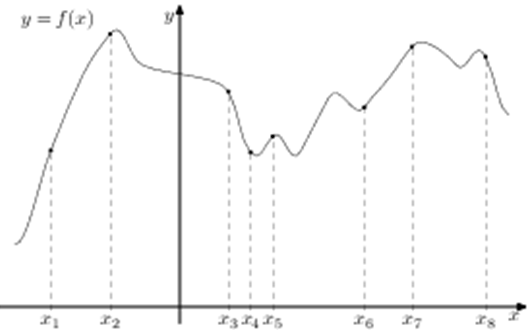
Задача 15. На рисунке изображён график функции (y = fleft( x right)) и восемь точек на оси абсцисс:  ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек производная функции (fleft( x right)) положительна?

Ответ

ОТВЕТ: 5.
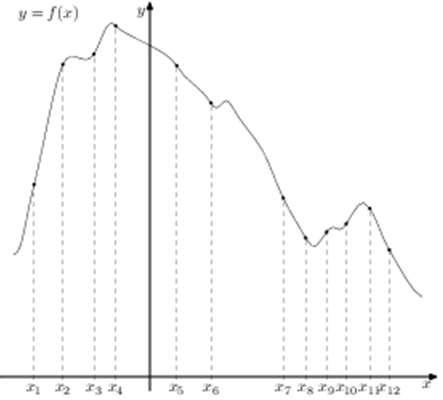
Задача 16. На рисунке изображён график функции (y = fleft( x right)) и двенадцать точек на оси абсцисс: ({x_1},,{x_2},;{x_3},,…,{x_{12}}.) В скольких из этих точек производная функции (fleft( x right)) отрицательна?

Ответ

ОТВЕТ: 7.
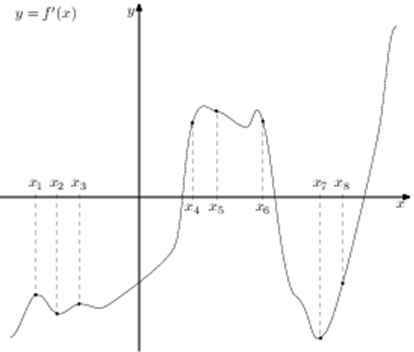
Задача 17. На рисунке изображён график (y = f’left( x right)) производной функции (fleft( x right)) и восемь точек на оси абсцисс:  ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек функция (fleft( x right)) возрастает?

Ответ

ОТВЕТ: 3.
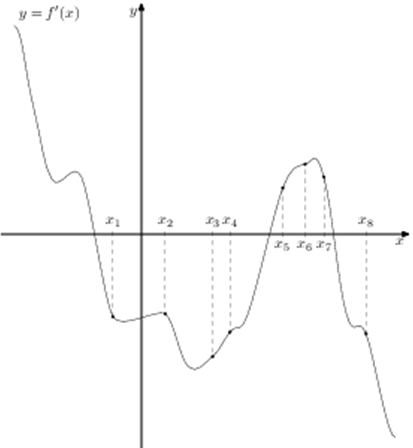
Задача 18. На рисунке изображён график (y = f’left( x right)) производной функции (fleft( x right)) и восемь точек на оси абсцисс:  ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек функция (fleft( x right)) убывает?

Ответ

ОТВЕТ: 5.
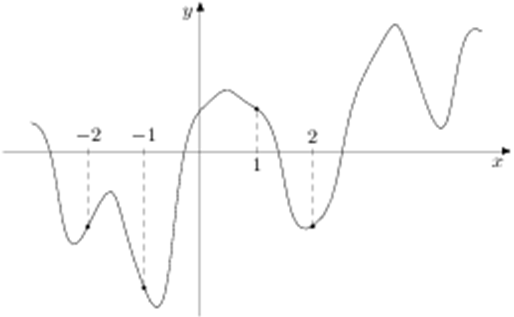
Задача 19. На рисунке изображен график функции (y = fleft( x right)) и отмечены точки   ( — 2,; — 1,;1,;2). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Ответ

ОТВЕТ: — 2.
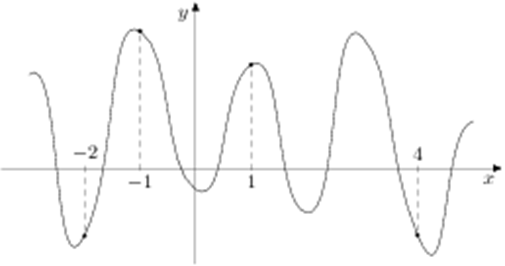
Задача 20. На рисунке изображен график функции (y = fleft( x right)) и отмечены точки ( — 2,; — 1,;1,;4). В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Ответ

ОТВЕТ: 4.
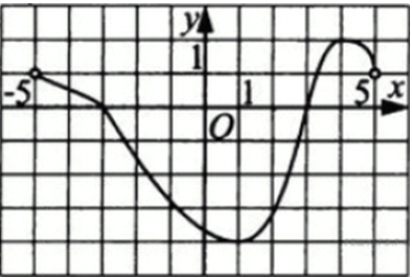
Задача 21. Функция (y = fleft( x right)) определена и непрерывна на отрезке (left[ { — 5;,5} right]). На рисунке изображён график её производной. Найдите точку x0, в которой функция принимает наименьшее значение, если   (fleft( { — 5} right) geqslant fleft( 5 right)).

Ответ

ОТВЕТ: 3.
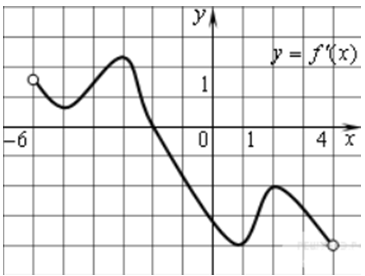
Задача 22. Функция (y = fleft( x right)) определена на промежутке (left( { — 6;,4} right)). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция (y = fleft( x right)) принимает наибольшее значение.

Ответ

ОТВЕТ: — 2.

Источник

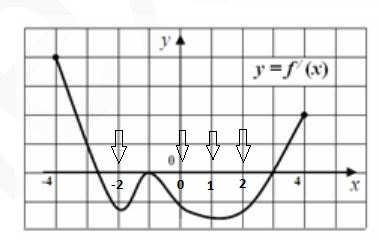
Задание 901

На графике производной функции у = f ‘ / (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых функция f (x) возрастает. В ответе укажите количество этих точек.

Ответ: 4

Скрыть

Так как дан график производной, то мы будем искать точки над осью OX (функция возрастает, производная положительна)

Задание 937

На графике производной функции у = f‘ / (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых угловой коэффициент касательной к графику функции f (x) положительный. В ответе укажите количество этих точек.

Ответ: 4

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Угловой коэффициент касательной к графику это и есть значение производной, следовательно, мы ищем, где производная положительная. Так как дан нам график производной, то мы просто найдем количество точек, которые располагаются над осью ОХ: x1,x3,x4,x6 всего 4

Задание 973

Прямая y=3х+4 является касательной к графику функции у=х2‐3x‐c. Найдите c.

Ответ: -13

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Так как прямая является касательной, то мы можем приравнять производные данных функций, чтобы найти абсциссу точки касания: 3 = 2x — 3. Отсюда x = 3. Так же мы можем приравнять сами функции и подставить найденную абсциссу:

3x+4=х2‐3x‐c

3*3+4=32-3*3-с

13=-c, отсюда с = -13

Задание 1013

Производная непрерывной функции f (x) равна нулю в каждой точке отрезка [‐5; 4]. Известно, что f (– 5) = – 5. Найдите f (4)

Ответ: -5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Раз производная равна нулю на всем промежутке и функция непрерывна, то функция не возрастает и не убывает, то есть сохраняет свое значение. Значит  f(– 5) =f(4)= – 5

Задание 1043

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  $$x(t)=6t^{2}-48t+17$$ (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 9 с.

Ответ: 60

Задание 1044

Мате­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну $$x(t)=frac{1}{2}t^{3}-3t^{2}+2t$$ (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость в (м/с) в мо­мент вре­ме­ни t = 6 с.

Ответ: 20

Задание 1045

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну $$x(t)=-t^{4}+6t^{3}+5t+23$$ (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость в (м/с) в мо­мент вре­ме­ни t = 3 с.

Ответ: 59

Задание 1046

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну $$x(t)=t^{2}-13t+23$$ (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). В какой мо­мент вре­ме­ни (в се­кун­дах) ее ско­рость была равна 3 м/с?

Ответ: 8

Задание 1047

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну $$x(t)=frac{1}{3}t^{3}-3t^{2}-5t+3$$ (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). В какой мо­мент вре­ме­ни (в се­кун­дах) ее ско­рость была равна 2 м/с?

Ответ: 7

Задание 1048

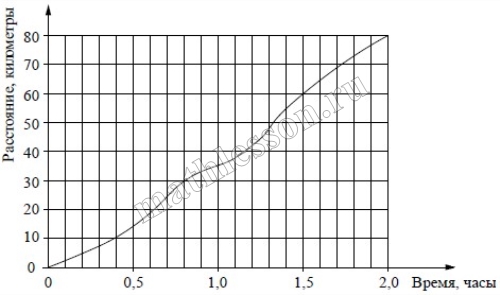
На ри­сун­ке по­ка­зан гра­фик дви­же­ния ав­то­мо­би­ля по марш­ру­ту. На оси абс­цисс от­кла­ды­ва­ет­ся время (в часах), на оси ор­ди­нат — прой­ден­ный путь (в ки­ло­мет­рах). Най­ди­те сред­нюю ско­рость дви­же­ния ав­то­мо­би­ля на дан­ном марш­ру­те. Ответ дайте в км/ч.

Ответ: 40

Задание 1097

К графику функции у = f (x) в точке с абсциссой х0 проведена касательная, которая перпендикулярна прямой, проходящей через точки (4; 3) и (3; ‐1) этого графика. Найдите f / (x0).

Ответ: -0,25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Пусть прямая, проходящая через точки (4; 3) и (3; ‐1) задается формулой y = k1x+b. Найдем k1, подставив имеющиеся координаты в уравнение прямой:

$$left{begin{matrix}3=4*k_{1}+b\ -1=3*k_{1}+bend{matrix}right.$$ Найдем $$k_{1}$$. Решив систему получим, что $$k_{1}=4$$ Далее воспользуемся свойством: если k1 и k2 угловые коэффициенты двух линейных функций, то их графики буду перпендикулярны в том случае, когда k1k2=-1. Получаем, что k2=-1/k1=-1/4=-0.25. А значение производной в точке и есть величина углового коэффициента.

Задание 1175

Функция у = f (x) определена на отрезке [‐4; 4]. На рисунке приведен график её производной. Найдите промежутки убывания функции. В ответе укажите сумму всех целых x, входящих в эти промежутки.

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Функция убывает, когда производная отрицательная. То есть мы смотрим, где график производной лежит под осью оХ, и выбираем оттуда целые значения Х (в задании надо сумму целых чисел). Важно выбрать значения, где производная равна 0, так как считается, что если функция определена в точках максимума или минимума, то эти точки входят в промежутки возрастания и убывания. Получаем точки -2; -1; 0 ; 1 ; 2 ;3

-2-1+0+1+2+3=3

Задание 1236

По графику функции у = f (x) определите количество точек на интервале (4;5), в которых касательная к графику параллельна оси абсцисс или совпадает с ней.

Ответ: 7

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Если касательная параллельна оси ОХ, то производная равна 0. Производная равна нулю на данном графике функции в точках максимума и минимума ( они отмечены жирной точкой ). Их всего 7

Задание 1277

На рисунке приведен график f ‘ (x) – производной функции у = f (x). Определите абсциссу точки графика функции у = f (x), в которой касательная параллельна прямой у = 2х – 1 или совпадает с ней.

Ответ: -3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Так как касательная к графику параллельна или совпадает с прямой y = 2x — 1, и при этом значение производной равно коэффициенту k линейной функции ( в нашем случае этот коэффициент равен 2 ), то и значение производной, которое мы ищем, равно 2. А так как нам дан график производной, то мы смело находим точку с ординатой (ось Оу) равную 2 и ищем абсциссу этой точки. Она равна -3

Задание 1290

На рисунке изображён график функции y=F(x) − одной из первообразных некоторой функции f(x), определённой на интервале (‐7;4). Пользуясь рисунком, определите значение функции f(x) в точке х=1.

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Нам дана первообразная F, нам необходимо найти значение функции f в точке. При подобном задании можно рассматривать следующую ситуацию, вместо F — рассматривается функция g, вместо функции f — производная g’. То есть нам дан график функции g(x), а надо найти значение производной g'(x) в точке x = 1. Как видим на графике, данная точка — точка минимум, значит значение производной и ответ — 0

Источник

ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 6

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 6 ЕГЭ профиль проверяет умение применять производную для решения прикладных задач. Такие задачи часто встречаются в физике и технических областях науки.

Задание состоит из текстовой задачи на определение физического, геометрического смысла производной, промежутков возрастания и убывания функции по её графику и графику её производной или первообразной. Ответом является целое число или конечная десятичная дробь.

При подготовке необходимо повторить правила нахождения производной, физический и геометрический смысл производной, понятие возрастания и убывания функции, понятие первообразной.

План выполнения задания № 6:

  1. Внимательно прочитайте задачу.
  2. Рассмотрите график. Определите, какой из графиков вам дан: функции, производной функции или первообразной функции. От ответа на данный вопрос зависит ход решения задачи.
  3. Определите по графику необходимые значения.
  4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

1) Задачи на Физический смысл производной

Задачи на применение физического смысла производной состоят из текста и выражения, описывающего уравнение движения материальной точки или тела.

Производная перемещения по времени выражает скорость движения: v(t) = x'(t) = at + v0.
Производная скорости по времени выражает ускорение движения: a(t) = v'(t).

Задача № 6 (1). Материальная точка движется прямолинейно по закону x(t) = 2t2 – 8t – 9, где х — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в м/с) в момент времени t = 5с.
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 4t – 8.
При t = 5 имеем: v(5) = 4 • 5 – 8 = 12.
Ответ: 12.
Комментарий. Иногда в ответе получаются отрицательные числа, которые учащиеся рассматривают как ошибочный ответ.

Задача № 6 (2). Тело движется прямолинейно по закону: x(t) = 2t3 + t – 1. В какой момент времени (в секундах) его ускорение будет равно 12 м/с2?
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 6t2 + 1.
Ускорение — это производная скорости по времени: a(t) = v'(t) = 12t.
Чтобы найти, в какой момент времени ускорение было 12 м/с2, решим уравнение: 12t = 12. Отсюда t = 1 c.
Ответ: 1.
Комментарий. Обратите внимание: в задании нужно найти, в какой момент времени ускорение (не скорость!) будет равно 12 м/с2.

2) Задачи на Геометрический смысл производной

Задание ориентировано на умение выпускников читать и анализировать графики, содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.

Геометрический смысл производной: угловой коэффициент касательной к графику функции в точке с абсциссой х0 равен производной этой функции в точке х0.
Геометрический смысл производной: k = tg a = f'(x)

Производная функции в точке с абсциссой х есть тангенс угла наклона касательной, проведённой к графику этой функции в точке (х0; f(x0)). При tg a > 0 производная функции положительна, при tg a < 0 производная отрицательна. При tg a = 0 производная равна нулю.

Точка х0 называется точкой максимума (минимума) функции, если существует такая окрестность точки х0, что для любого х из этой окрестности верно неравенство f(x) < f(x0)  (f(x) > f(x0)).

Задача № 6 (3). На рисунке изображён график функции y = f(x) и отмечены пять точек на оси абсцисс: х1, х2, х3, х4, х5. В скольких из этих точек производная функции f(x) отрицательна?
ЕГЭ по математике Профиль. Задание 6
Решение: Производная функции отрицательна в тех точках, которые принадлежат участкам убывания функции. Это точки х2, х4 — всего 2 точки.
Ответ: 2.

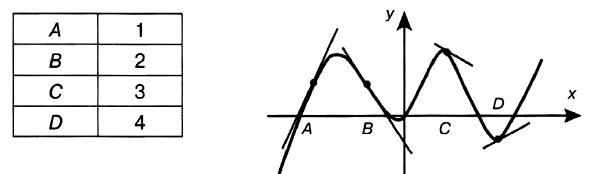
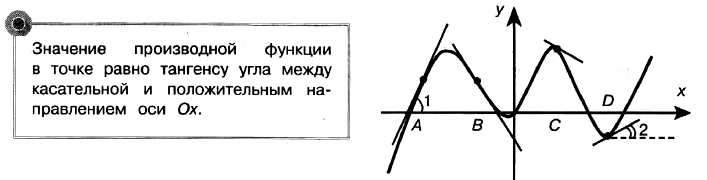
Задача № 6 (4). На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. Пользуясь графиком, определите, в какой из данных точек значение производной наибольшее. В ответе укажите число, которое ей соответствует по таблице.
ЕГЭ по математике Профиль. Задание 6
Решение: Производная функции положительна в точках А и D, так как в данных точках функция возрастает.
ЕГЭ по математике Профиль. Задание 6
Угол 1 больше угла 2, значит, тангенс первого угла больше тангенса второго угла, соответственно, значение производной в точке А больше значения производной в точке D.
Ответ: 1.

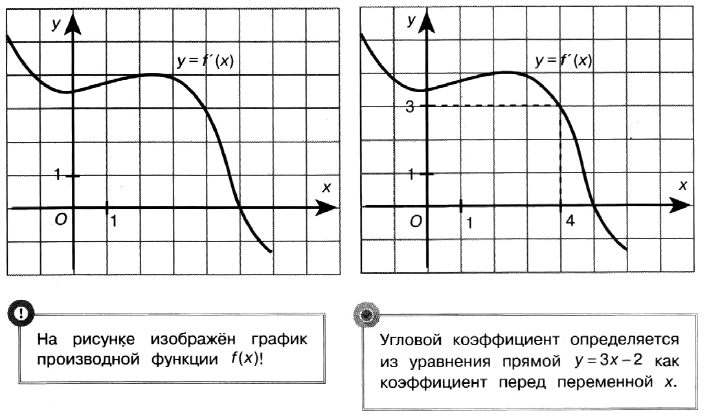
Задача № 6 (5). На рисунке изображён график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику параллельна прямой у = 3х–2 или совпадает с ней.
ЕГЭ по математике Профиль. Задание 6
Решение: Поскольку касательная параллельна прямой у = 3х – 2 или совпадает с ней, она имеет угловой коэффициент, равный 3 (у’ = 3). Найдём, при каких х производная принимает значение 3. Из графика видно, что значению у = 3 соответствует точка х = 4.
Ответ: 4.

3) Задачи на Применение
производной к исследованию функций

Задание содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.

  • Если функция y = f(x) имеет экстремум в точке х0, то в этой точке производная равна нулю или не существует.
  • Если f'(x) = 0 и при переходе через точку х0 значения производной меняют знак с «+» на «–», то х0 — точка максимума.
  • Если f'(x) = 0 и при переходе через точку х0 значения производной меняют знак с «–» на «+», то х0 — точка минимума.
  • Если f'(x) = 0 и при переходе через точку х0 значения производной не меняют знак, то х0 не является точкой экстремума.
  • Если в каждой точке х некоторого промежутка f'(х) > 0, то функция f(x) возрастает на этом промежутке.
  • Если в каждой точке х некоторого промежутка f'(х) < 0, то функция f{x) убывает на этом промежутке.

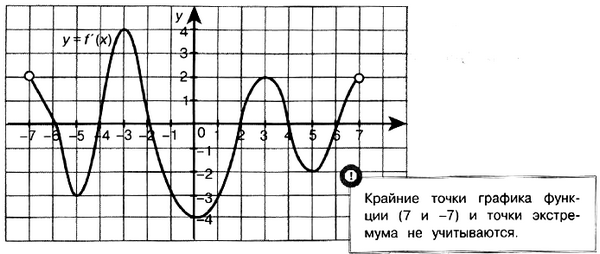
Задача № 6 (6). На рисунке изображён график производной функции f(x), определённой на интервале (–7; 7). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
ЕГЭ по математике Профиль. Задание 6
Решение: Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых её производная положительна, то есть промежуткам (–7; –6); (–4; –2); (2; 4); (6; 7). Данные промежутки содержат целые числа –3; 3. Их сумма равна 0.
Ответ: 0.
ПРИМЕЧАНИЕ: В ответе нужно указать сумму целых точек, входящих в промежутки возрастания.

4) Задачи на Первообразную

Функцию y = F(x) называют первообразной для функции y = f(x) на заданном промежутке х, если для всех х из этого промежутка верно равенство F'(x) = f(x).

Если функция y = F(x) является первообразной для функции y = f(x) на некотором промежутке, то и функция y = F(x) + C (С — постоянная) является первообразной для функции f на этом промежутке.

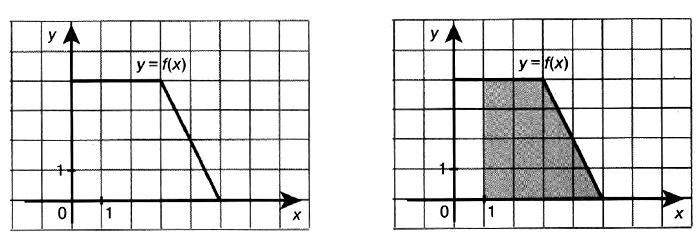
Пусть функция f(x) непрерывна на отрезке [а; b]. Тогда площадь трапеции, ограниченной линиями y = f(x); у = а; у = b и у = 0, равна F(b) – F(a), где F(x) — первообразная функции f(x).

Задача № 6 (7). На рисунке изображён график некоторой функции y = f(x). Пользуясь рисунком, вычислите F(5) – F(1), где F(x) — одна из первообразных функции f(x).
ЕГЭ по математике Профиль. Задание 6
Решение: Разность значений первообразной в точках 5 и 1 равна площади выделенной на рисунке трапеции.
Площадь трапеции ограничена точками 1 и 5.
Площадь трапеции вычисляется по формуле S = h • (a + b)/2.
Из рисунка видно, что а =2, b = 4, h = 4. Значит, F(5) – F(1) = 4 • (2 + 4)/2 = 12.
Ответ: 12.
ПРИМЕЧАНИЕ: Если результат отрицательный или равен нулю, значит, в вычислениях была допущена ошибка.

Тренировочные задания с самопроверкой

№ 6.1. На рисунке изображён график у = f’(x) – производной функции f(x), определённой на интервале (–5; 7). В какой точке отрезка [–3; 2] f(x) принимает наименьшее значение?
ЕГЭ по математике Профиль. Задание 6

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 6

№ 6.2. Прямая у = 5х + 4 параллельна касательной к графику функции у = х2 – 4х – 12. Найдите абсциссу точки касания.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 6

№ 6.3. На рисунке изображён график у = f‘(х) – производной функции f(х), определённой на интервале (–5; 8). Найдите количество точек, в которых касательная к графику функции f(х) параллельна прямой у = 2х – 4 или совпадает с ней.
ЕГЭ по математике Профиль. Задание 6

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 6

№ 6.4. На рисунке изображён график у = f‘(x) – производной функции f(x), определённой на интервале (–7; 8). Найдите, в какой точке отрезка [–4; 4] функция принимает наибольшее значение.
ЕГЭ по математике Профиль. Задание 6

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 6

№ 6.5. На рисунке изображены график функции у = f(x) и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции g(х) = 4f(x) – 12 в точке x0.
ЕГЭ по математике Профиль. Задание 6

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 6

Вы смотрели: ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
20 317

Источник

Справочник

Задание №7 профильная математика

Производной функции y=f(x)в точке x0 называется предел (если он существует
и конечен) отношения приращения функции к приращению аргумента при условии, что
последнее стремится к нулю. То есть,

  

Геометрический смысл производной

Физический смысл производной

Значение
производной функции в точке равно угловому коэффициенту касательной к графику
функции в этой точке (тангенсу угла между касательной и осью Ох)

f’(хo)
= k = tg α

Если точка движется вдоль оси х и ее
координата изменяется по закону  x(t), то мгновенная скорость точки:

V(t)=x’(t)

•     
Если f’(x) > 0 на
промежутке, то функция f(x)  возрастает на этом  промежутке.

Если f’(x) < 0 на промежутке, то функция f(x) убывает на
этом промежутке

•     
Если функция f(x)  возрастает
на промежутке, то  f’(x) > 0 на этом  промежутке.

Если функция f(x) убывает на
промежутке, то f’(x) < 0 на этом промежутке

Если прямые параллельны, то их угловые коэффициенты
равны

•     
Точка хo называется точкой максимума
функции f(х), если 
существует такая окрестность точки хo, что для всех х≠ хo
из этой окрестности выполняется неравенство f(х) <
f(хo).

•     
Точка хo называется точкой
минимума функции f(х), если
существует такая окрестность точки хo, что для всех х≠ хo
из этой  окрестности выполняется неравенство f(х)
> f(хo) = 0.

•     
Если хo – точка экстремума
функции f(х), то f’(хo) = 0.

Пусть функция f(х) дифференцируема на интервале (a;b), хo Є (a; b)   и  f’(хo) = 0, то:

• 
при переходе через стационарную точку хo
функции f(х) ее производная
меняет знак с «плюса» на «минус», то хo – точка максимума
функции f(х);

• 
при переходе через стационарную точку хo
функции f(х) ее производная меняет знак с «минуса» на
«плюс», то хo – точка минимума функции f(х).

Примеры заданий

№

Задание

Что делать?

1.     
 

На рисунке изображен график функции y=f(x) и касательная к нему в точке х0. Найдите значение производной
функции f(x) в точке x0.

 

Найти тангенс угла наклона касательной к оси
абсцисс (отношение противолежащего катета к прилежащему катету).

На рисунке выделены точки на касательной, на
которых как на гипотенузе надо достроить прямоугольный треугольник. Если α
<900, то tg α >0,

если α >900,
то tg α <0.

2.     
 

На рисунке изображен график функции y=f(x), определённый на интервале (-10;2). Найдите количество точек, в
которых производная функции f(x) равна 0.

Подсчитать количество точек
экстремума(минимумы и максимумы)

3.     
 

На рисунке изображен график функции y=f(x), определённый на интервале (-1;12). Найдите количество целых точек,
в которых производная функции отрицательна.

Подсчитать целые точки на промежутках убывания функции

4.     
 

На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 2, 3. В какой из этих точек значение
производной наибольшее? В ответе укажите эту точку.

x=-2, то f
↓ => f’ <0

x=-1, то f
имеет экстремум =>f’=0

x=2, то f ↑ => f’ >0

x=3, то f ↓ => f’ <0

5.     
 

На рисунке изображён график
дифференцируемой функции y=f(x), и отмечены
семь точек на оси абсцисс: х1, х2, х3, х4,
х5, х6, х7, х8,х9
. В скольких из этих точек производная функции  f(x) отрицательна?

В скольких точках функция убывает

6.     
 

На рисунке изображен график функции y=f’(x ) – производной функции f(x),
определённой на интервале (-6;5). Найдите промежутки убывания функции f(x). В ответе
укажите сумму целых точек, входящих в
эти промежутки.

Промежутки убывания функции =производная на
данном графике отрицательна, т.е.расположена ниже оси Ох. Найти сумму целых точек.

7.     
 

На рисунке изображен график функции y=f’(x ) – производной функции f(x),
определённой на интервале (-8;6). Найдите промежутки возрастания функции
f(x). В ответе укажите длину наибольшего
из них.

Промежутки возрастания функции =производная
на данном графике положительна, т.е.расположена выше оси Ох. Записать длину большего промежутка

8.     
 

На рисунке изображены график функции y=f’(x ) – производной функции f(x) и семь точек
на оси абсцисс: х1, х2, х3, х4,
х5, х6, х7. В скольких из этих точек функция 
f(x) возрастает?

Сосчитать количество точек, в которых
производная на данном графике положительна

9.     
 

Прямая y=6x+9 параллельна касательной к графику функции y=x2+7х-6. Найдите
абсциссу точки касания.

Если прямые параллельны, то их угловые
коэффициенты равны.

Найти производную функции (x2+7х-6)’=2x+7=kкас=6

=>  x=-0,5

10.   

Прямая y=-9x+5 параллельна касательной к графику функции y=аx2+15х+11. Найдите
a.

Найти производную функции (аx2+15х+11)’=2a+15=
-9

=> a= -12

11.   

На рисунке изображён график y=f’(x) – производной функции f(x), определённой на интервале (-9;3). Найдите
количество точек, в которых касательная к графику f(x) параллельна прямой y=2x-19 или совпадает с ней.

Провести горизонтальную прямую y=2 и
сосчитать количество точек пересечения с графиком.

12.   

На рисунке изображён график функции y=f(x), определённой на интервале (-3;9). Найдите количество точек, в которых
касательная к графику f(x) параллельна прямой y=12.

Т.к. угловой коэффициент прямой y=12 равен 0, то считаем количество
точек пересечения с осью Ох.

13.   

На рисунке изображен график производной
функции y=f’(x). Найдите абсциссу точки, в которых касательная
к графику функции y=f(x) параллельна оси абсцисс или  совпадает ней.

Находим точку на графике y=f’(x), в которой у=0, т.е.точку пересечения данного графика с осью Ох => -3

14.   

На рисунке изображен график производной
функции y=f’(x), определенной на интервале (-7;4). В какой
точке отрезка

[-6;-1] функция f(x) принимает наибольшее значение?

На отрезке [-6;-1] производная положительна
(лежит выше Ох)

=> функция возрастает, т.е. достигает
наибольшего значения при наибольшем значении аргумента => -1

Значит в х=-6 достигает наименьшего
значения.

15.   

На рисунке изображён график y=f’(x) – производной функции f(x), определённой
на интервале (-7;4). Найдите точку максимума функции f(x).

Находим точку на оси Ох, в которой
производная меняет свой знак с «+» на «-»

=> -1

16.   

На рисунке изображён график y=f’(x) – производной функции f(x), определённой
на интервале (-6;5). Найдите точку экстремума функции f(x),
принадлежащую отрезку [-5;4].

Находим точку на оси Ох, в которой
производная меняет свой знак =>  -2

17.   

На рисунке изображён график функции y=f(x), определённой на интервале (-5;7). Найдите сумму точек экстремума
функции f(x).

Считаем сумму «горбов и впадин» по оси Ох:
-3 + (-1) +0+2+3+5+6=12

18.   

На рисунке изображён график y=f’(x) – производной функции f(x), определённой
на интервале (-10;8). Найдите количество точек максимума функции f(x),
принадлежащих отрезку [-9;6].

Находим точки на оси Ох, в которой
производная меняет свой знак  с  «+» на «-»

=>  х= -4 и х=4 => 2

19.   

На рисунке изображён график y=f’(x) – производной функции f(x), определённой
на интервале (-16;4). Найдите количество точек экстремума функции f(x),
принадлежащих отрезку

[-14;2].

Считаем количество точек пересечения графика
производной на рисунке с осью Ох => 5

20.   

Материальная точка движется прямолинейно по
закону x(t)=t2-3t-29, где x – расстояние от точки отсчета в метрах, t – время в
секундах, измеренное с начала движения. Найдите её скорость (в метрах
в секунду) в момент времени t=3с.

V(t=3)=x’(t)=( t2-3t-29)’=

=2t-3=2*3-3=3

21.   

Материальная точка движется прямолинейно по
закону x(t)=1/6t3-2t2-4t+39, где x
– расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент
времени (в секундах) её скорость была равной 38м/с.

V(t)=x’(t)=( 1/6t3-2t2-4t+39)’=

=1/6 *3t2-2*2t-4=0.5t-4t-4

Если V=38, то 0.5t2-4t-4=38

                        0.5t2-4t-4-38=0

                       t2-8t-84=0

Решая уравнение через D,
находим t=14
Источник

Понравилась статья? Поделить с друзьями:
  • График проведения экзаменов по электробезопасности
  • График проведения экзаменов огэ 2022
  • График проведения экзаменов егэ
  • График проведения экзаменов в ростехнадзоре
  • График проведения экзаменов в 9 классе в 2022 году