Графики параболы егэ

Каталог заданий.
Параболы


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 10 № 509253

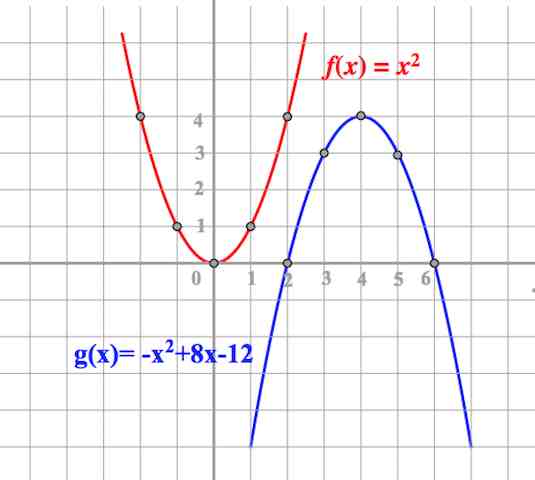
На рисунке изображены графики функций f левая круглая скобка x правая круглая скобка =4x в квадрате минус 25x плюс 41 и g левая круглая скобка x правая круглая скобка =ax в квадрате плюс bx плюс c, которые пересекаются в точках A и B. Найдите абсциссу точки B.

Аналоги к заданию № 509253: 509254 509255 509259 509262 509263 509264 509268 509256 509257 509258 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

2

Тип 10 № 562060

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение f левая круглая скобка 3,5 правая круглая скобка .

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

3

Тип 10 № 562061

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение дискриминанта уравнения f левая круглая скобка x правая круглая скобка =0.

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

1 комментарий · Сообщить об ошибке · Помощь

4

Тип 10 № 562153

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение f левая круглая скобка 13 правая круглая скобка .

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

5

Тип 10 № 562154

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение f левая круглая скобка 10 правая круглая скобка .

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Квадратичная функция (парабола)

Все знают, как выглядит парабола y = x2. В седьмом классе мы рисовали таблицу:

x -3 -2 -1 0 1 2 3
y 9 4 1 0 1 4 9

После этого по точкам строили график:

Параболу y = ax2 + bx + c мы не станем строить каждый раз «по точкам» — для выпускника школы это просто несолидно. Ведь нам надо знать закономерности поведения данной функции. А эти закономерности таковы.

1. Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a < 0 — вниз.

На рисунке приведены две параболы y = ax2 с равными по модулю, но противоположными по знаку значениями a.


2. Абсолютная величина коэффициента a отвечает за «раскрыв» параболы. Чем больше |a|, тем у́же парабола (больше прижата к оси Y ). Наоборот, чем меньше |a|, тем шире парабола (больше прижата к оси X).

На рисунке приведены две параболы y = a1x2 и y = a2x2, у которых a2 > a1 > 0.


3. Абсцисса вершины параболы y = ax2 + bx + c находится по формуле:


Для нахождения ординаты вершины y0 удобнее всего подставить x0 в уравнение параболы. Но вообще, полезно помнить, что


где D = b2 − 4ac — дискриминант.

4. Точки пересечения параболы y = ax2 + bx + c с осью X находятся с помощью решения квадратного уравнения
ax2 + bx + c = 0. Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X.

5. Точка пересечения с осью Y находится легко: мы просто подставляем x = 0 в уравнение параболы. Получается точка (0, c).

А теперь покажем, как с помощью графика функции y = ax2 + bx + c решать квадратные неравенства.

1. Часто на тестировании мы предлагаем решить неравенство

x2 < 400.

Справляются далеко не все. Очень часто, не задумываясь, выдают «ответ»: x < ± 20.

Однако сама эта запись — абсурдна! Представьте, что вы слышите прогноз погоды: «Температура будет меньше плюс-минус двадцати градусов». Что, спрашивается, надеть — рубашку или шубу? :-)

Давайте решим это неравенство с помощью графика. Изобразим схематично график функции y = x2 и отметим все значения x, для которых y < 400.


Теперь мы видим правильный ответ: x ∈ (−20; 20).

2. Решим неравенство: x2 − 3x − 10 ≥ 0.

Графиком функции y = x2 − 3x − 10 служит парабола, ветви которой направлены вверх. Решая квадратное уравнение x2 − 3x − 10 = 0, находим x1 = −2 и x2 = 5 — в этих точках парабола пересекает ось X. Нарисуем схематично нашу параболу:


Мы видим, что при x ∈ (−2; 5) значения функции отрицательны (график проходит ниже оси X). В точках −2 и 5 функция обращается в нуль, а при x < −2 и x > 5 значения функции положительны. Следовательно, наше неравенство выполняется при .

Обратите внимание, что для решения неравенства нам достаточно было схематично изобразить параболу. Ось Y вообще не понадобилась!

3. Ещё одно неравенство: x2 + 2x + 4 > 0.

Ветви параболы y = x2 + 2x + 4 направлены вверх. Дискриминант отрицателен, т. е. уравнение x2 + 2x + 4 = 0 не имеет корней. Стало быть, нет и точек пересечения параболы с осью X.

Раз ветви параболы направлены вверх и она не пересекает ось X — значит, парабола расположена над осью X.


Получается, что значения функции положительны при всех возможных x. Иными словами, решения нашего неравенства — это все действительные числа.

Ответ: .

Квадратные неравенства являются неотъемлемой частью ЕГЭ. Разберём типичные примеры из банка заданий ЕГЭ.

4. Завиcимоcть объeма cпроcа q (тыc. руб.) на продукцию предприятия-монополиcта от цены p (тыc. руб.) задаeтcя формулой q = 100 − 10p. Выручка предприятия за меcяц r (в тыc. руб.) вычиcляетcя по формуле r(p) = q · p. Определите наибольшую цену p, при которой меcячная выручка r(p) cоcтавит не менее 240 тыc. руб. Ответ приведите в тыc. руб.

Подставим выражение для q в формулу выручки:

r(p) = qp = (100 − 10p)p = 100p − 10p2.

Выручка должна быть не менее (то есть больше или равна) 240 тысяч рублей. Поскольку цена p уже выражена в тысячах рублей, мы можем записать это условие в виде неравенства:

100p − 10p2 ≥ 240.

Переносим всё вправо и делим на 10:

p2 − 10p + 24 ≤ 0.

Для схематичного построения параболы находим корни уравнения p2 − 10p + 24 = 0. Они равны 4 и 6. Остаётся сделать рисунок.

Решением нашего неравенства служит отрезок [4; 6]. Нас просили найти наибольшее p. Оно равно 6.

Ответ: 6.

5. Выcота над землёй подброшенного вверх мяча меняетcя по закону h(t) = 1,6 + 8t − 5t2, где h — выcота в метрах, t — время в cекундах, прошедшее c момента броcка. Cколько cекунд мяч будет находитьcя на выcоте не менее трёх метров?

Итак, требуется, чтобы выполнялось неравенство h(t) ≥ 3. Подставляем сюда выражение для h:

1,6 + 8t − 5t2 ≥ 3.

Собираем всё справа:

5t2 − 8t + 1,4 ≤ 0.

Корни соответствующего уравнения 5t2 −8t+1,4 = 0 равны t1 = 0,2 и t2 = 1,4. Как дальше действовать — мы знаем.


Таким образом, через t1 = 0,2 секунды после начала полёта мяч оказался на высоте 3 метра. Мяч продолжал лететь вверх, высота увеличивалась; затем началось снижение, высота уменьшалась, и в момент времени t = 1,4 секунды снова стала равна трём метрам над землей.

Получается, что мяч находился на высоте не менее трёх метров в течение t2 − t1 = 1,2 секунд. В бланк ответов вписываем десятичную дробь 1,2.

6. Завиcимоcть температуры (в градуcах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экcпериментально и на иccледуемом интервале температур определяетcя выражением T(t) = T0 + bt + at2, где t — время в минутах, T0 = 1400 К, a = −10 К/мин, b = 200 К/мин. Извеcтно, что при температуре нагревателя cвыше 1760 К прибор может иcпортитьcя, поэтому его нужно отключать. Определите, через какое наибольшее время поcле начала работы нужно отключать прибор. Ответ выразите в минутах.

Согласно условию, зависимость температуры нагревательного элемента от времени определяется формулой:

T(t) = 1400 + 200t − 10t2.

В нормальном режиме работы прибора должно выполняться неравенство T ≤ 1760, или

1400 + 200t − 10t2 ≤ 1760.

Переносим всё вправо и делим на 10:

t2 − 20t + 36 ≥ 0.

Находим t1 = 2, t2 = 18 и делаем рисунок:

Получаем решения нашего неравенства:

left [ begin{array}{c}tleq 2,\tgeq 18.\end{array} right.

Остаётся понять: в какой же момент отключать прибор? Для этого надо представить физическую картину процесса.

Мы включаем прибор в момент времени t = 0. Температура нагревателя повышается и при t = 2 мин достигает 1760 К. Затем повышение температуры продолжается, в результате чего прибор может испортиться. Поэтому ясно, что отключать его надо при t = 2.

А что же решения t ≥ 18? Они не имеют физического смысла. Войдя в зону температур T > 1760, прибор испортится, и формула T(t) = 1400+200t−10t2, справедливая для исправного прибора, перестанет адекватно отражать реальность.

Поэтому в бланк ответов вписываем число 2.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратичная функция (парабола)» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник
Skip to content

ЕГЭ Профиль №10. Парабола

ЕГЭ Профиль №10. Параболаadmin2023-01-10T14:17:50+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №10. Парабола

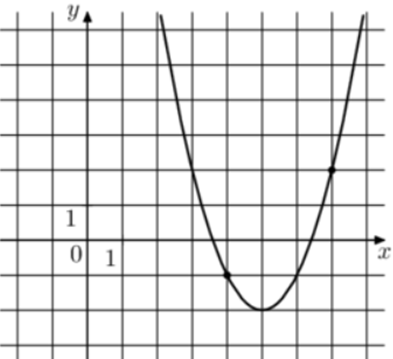
Задача 1. На рисунке изображён график функции  (fleft( x right) = 2{x^2} + b,x + c.)  Найдите  (fleft( { — 5} right).)

Ответ

ОТВЕТ: 31.
Решение

Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 2 + b + c,,,,}\{ — 2 = 8 — 2b + c}end{array}} right.)

Вычтем из первого уравнения второе:  (3 =  — 6 + 3b,,,,,,, Leftrightarrow ,,,,,,,b = 3.)

Тогда: (1 = 2 + 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c =  — 4.) 

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} + 3x — 4)  и  (fleft( { — 5} right) = 2 cdot {left( { — 5} right)^2} + 3 cdot left( { — 5} right) — 4 = 31.) 

Ответ: 31.
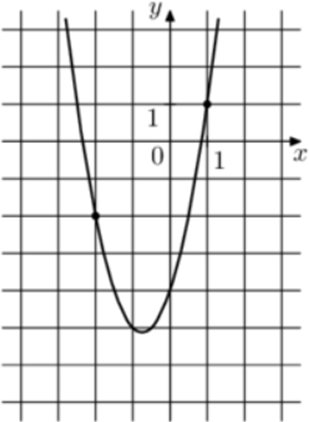
Задача 2. На рисунке изображён график функции  (fleft( x right) = {x^2} + b,x + c.)  Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: 34.
Решение

1 Способ

Парабола проходит через точки (left( {4; — 1} right)) и (left( {6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 16 + 4b + c,,,,}\{ — 1 = 36 + 6b + c,,,}end{array}} right.)

Вычтем из первого уравнения второе:  (0 =  — 20 — 2b,,,,,,, Leftrightarrow ,,,,,,,b =  — 10.)

Тогда: ( — 1 = 16 — 40 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 23.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = {x^2} — 10x + 23)   и   (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.)   

Ответ: 34.

2 Способ

Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2)   и   (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.)

Ответ: 34.
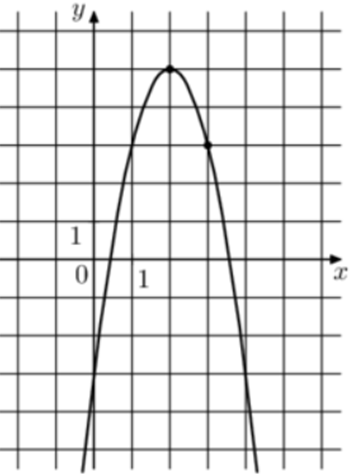
Задача 3. На рисунке изображён график функции  (fleft( x right) =  — 2{x^2} + b,x + c.)  Найдите  (fleft( 6 right).)

Ответ

ОТВЕТ: — 27.
Решение

1 Способ

Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно:  (left{ {begin{array}{*{20}{c}}{3 =  — 2 + b + c,,,,,,,,}\{3 =  — 18 + 3b + c,,,}end{array}} right.)Вычтем из первого уравнения второе: (0 = 16 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = 8.)Тогда: (3 =  — 2 + 8 + c,,,,,,,, Leftrightarrow ,,,,,,,,c =  — 3.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — 2{x^2} + 8x — 3)  и  (fleft( 6 right) =  — 2 cdot {6^2} + 8 cdot 6 — 3 =  — 27.)   

Ответ: – 27.

2 Способ

Заметим, что графиком является парабола (fleft( x right) =  — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) =  — 2{left( {x — 2} right)^2} + 5)   и   (fleft( 6 right) =  — 2 cdot {left( {6 — 2} right)^2} + 5 =  — 27.)

Ответ: – 27.
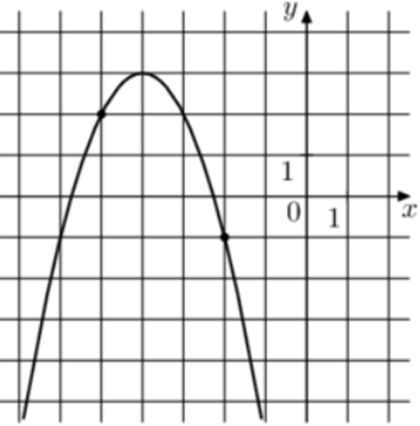
Задача 4. На рисунке изображён график функции  (fleft( x right) =  — {x^2} + b,x + c.)  Найдите  (fleft( { — 8} right).)

Ответ

ОТВЕТ: — 13.
Решение

1 Способ

Парабола проходит через точки (left( { — 3;2} right))  и  (left( { — 5;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 =  — 9 — 3b + c,,,,,,,,}\{2 =  — 25 — 5b + c,,,}end{array}} right.)

Вычтем из первого уравнения второе:  (0 = 16 + 2b,,,,,,, Leftrightarrow ,,,,,,,b =  — 8.)

Тогда: (2 =  — 9 + 24 + c,,,,,,,, Leftrightarrow ,,,,,,,,c =  — 13.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — {x^2} — 8x — 13)   и   (fleft( { — 8} right) =  — {left( { — 8} right)^2} + 8 cdot left( { — 8} right) — 13 =  — 13.)   

Ответ: – 13.

2 Способ

Заметим, что графиком является парабола (fleft( x right) =  — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид:

(fleft( x right) =  — {left( {x + 4} right)^2} + 3)   и   (fleft( { — 8} right) =  — {left( { — 8 + 4} right)^2} + 3 =  — 13.)

Ответ: – 13.
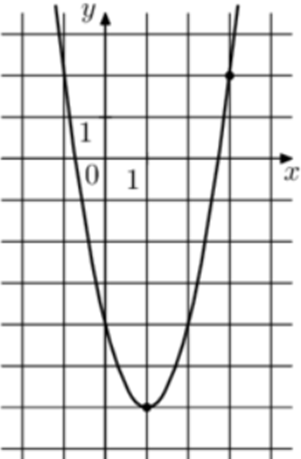
Задача 5. На рисунке изображён график функции  (fleft( x right) = a,{x^2} — 4,x + c.)  Найдите  (fleft( { — 3} right).)

Ответ

ОТВЕТ: 26.
Решение

1 Способ

Парабола проходит через точки (left( {1; — 6} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 6 = a — 4 + c,,,,,,,,}\{2 = 9a — 12 + c,,,}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 8 =  — 8a + 8,,,,,,, Leftrightarrow ,,,,,,,a = 2.)

Тогда:  ( — 6 = 2 — 4 + c,,,,,,,, Leftrightarrow ,,,,,,,,c =  — 4.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} — 4x — 4)   и   (fleft( { — 3} right) = 2 cdot {left( { — 3} right)^2} — 4 cdot left( { — 3} right) — 4 = 26.)   

Ответ: 26.

2 Способ

Заметим, что графиком является парабола (fleft( x right) = 2{x^2}), вершина которой находится в точке (left( {1; — 6} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = 2{left( {x — 1} right)^2} — 6)  и  (fleft( { — 3} right) = 2 cdot {left( { — 3 — 1} right)^2} — 6 = 26.)

Ответ: 26.
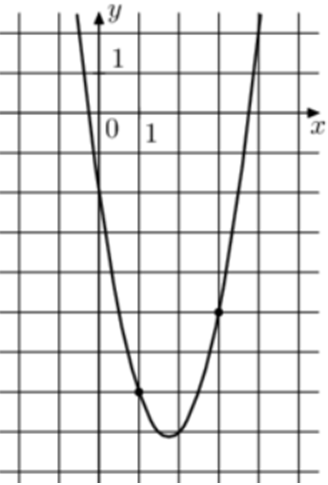
Задача 6. На рисунке изображён график функции  (fleft( x right) = a,{x^2} — 7,x + c.)  Найдите  (fleft( 7 right).)

Ответ

ОТВЕТ: 47.
Решение

Парабола проходит через точки (left( {1; — 7} right)) и (left( {3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 7 = a — 7 + c,,,,,,,,}\{ — 5 = 9a — 21 + c,,,}end{array}} right.)

Вычтем из первого уравнения второе: ( — 2 =  — 8a + 14,,,,,,, Leftrightarrow ,,,,,,,a = 2.)

Тогда:  ( — 7 = 2 — 7 + c,,,,,,,, Leftrightarrow ,,,,,,,,c =  — 2.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} — 7x — 2)   и   (fleft( 7 right) = 2 cdot {7^2} — 7 cdot 7 — 2 = 47.)   

Ответ: 47.
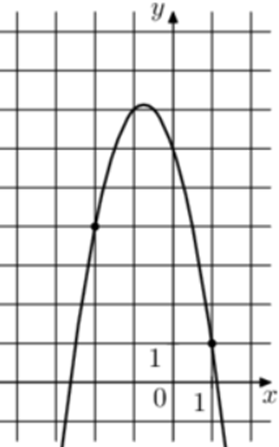
Задача 7. На рисунке изображён график функции  (fleft( x right) = a,{x^2} — 3,x + c.)  Найдите  (fleft( { — 4} right).)

Ответ

ОТВЕТ: — 14.
Решение

Парабола проходит через точки (left( {1;1} right)) и (left( { — 2;4} right)). Следовательно:  (left{ {begin{array}{*{20}{c}}{1 = a — 3 + c,,,,,,,,}\{4 = 4a + 6 + c,,,}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 3 =  — 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a =  — 2.)

Тогда: (1 =  — 2 — 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 6.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — 2{x^2} — 3x + 6)   и   (fleft( { — 4} right) =  — 2 cdot {left( { — 4} right)^2} — 3 cdot left( { — 4} right) + 6 =  — 14.)   

Ответ: – 14.
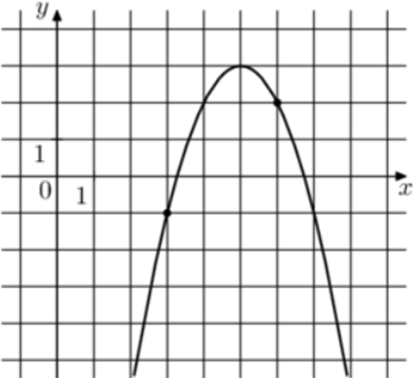
Задача 8. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + 10,x + c.)  Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: — 33.
Решение

1 Способ

Парабола проходит через точки (left( {3; — 1} right)) и (left( {4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 9a + 30 + c}\{2 = 16a + 40 + c}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 3 =  — 7a — 10,,,,,,, Leftrightarrow ,,,,,,,a =  — 1.)

Тогда: ( — 1 =  — 9 + 30 + c,,,,,,,, Leftrightarrow ,,,,,,,,c =  — 22.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — {x^2} + 10x — 22)   и   (fleft( { — 1} right) =  — {left( { — 1} right)^2} + 10 cdot left( { — 1} right) — 22 =  — 33.)   

Ответ: – 33.

2 способ

Заметим, что графиком является парабола (fleft( x right) =  — {x^2}), вершина которой находится в точке (left( {5;3} right)). Следовательно, ее уравнение будет иметь вид:

(fleft( x right) =  — {left( {x — 5} right)^2} + 3)  и  (fleft( { — 1} right) =  — {left( { — 1 — 5} right)^2} + 3 =  — 33.)

Ответ: – 33.
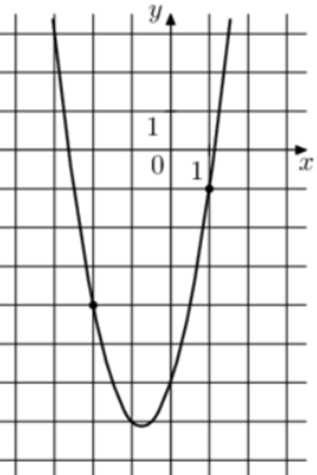
Задача 9. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x — 6.)  Найдите  (fleft( { — 6} right).)

Ответ

ОТВЕТ: 48.
Решение

Парабола проходит через точки (left( {1; — 1} right)) и (left( { — 2; — 4} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6,,,,,,,,,,,,,,,,,,,,,}\{ — 4 = 4a — 2b — 6left| {:left( { — 2} right)} right.,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6}\{2 =  — 2a + b + 3}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 3 = 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = 2.)

Тогда: ( — 1 = 2 + b — 6,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} + 3x — 6)   и   (fleft( { — 6} right) = 2 cdot {left( { — 6} right)^2} + 3 cdot left( { — 6} right) — 6 = 48.)   

Ответ: 48.
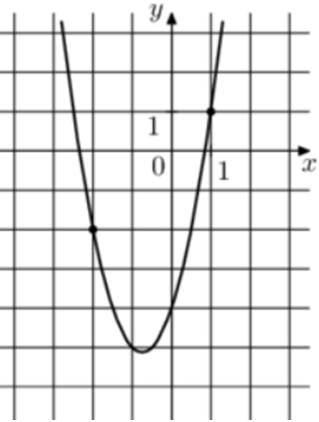
Задача 10. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x — 4.)  Найдите  (fleft( { — 4} right).)

Ответ

ОТВЕТ: 16.
Решение

Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,,,,,,,,,,,,,,,,,,,}\{-2 = 4a — 2b — 4left| {:left( { — 2} right)} right.,,,}end{array},,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,}\{1 =  — 2a + b + 2}end{array}} right.} right.)

Вычтем из первого уравнения второе:  (0 = 3a — 6,,,,,,, Leftrightarrow ,,,,,,,a = 2.)

Тогда: (1 = 2 + b — 4,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} + 3x — 4)    и    (fleft( { — 4} right) = 2 cdot {left( { — 4} right)^2} + 3 cdot left( { — 4} right) — 4 = 16.)   

Ответ: 16.
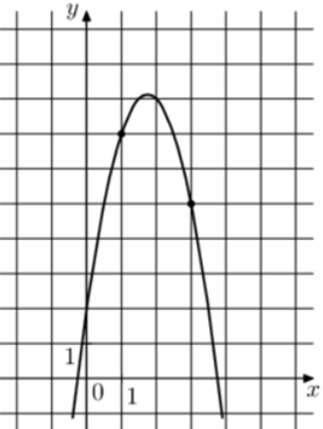
Задача 11. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + 2.)  Найдите  (fleft( { — 3} right).)

Ответ

ОТВЕТ: — 37.
Решение

Парабола проходит через точки (left( {1;7} right)) и (left( {3;5} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{7 = a + b + 2,,,,,,,,}\{5 = 9a + 3b + 2,,,,}end{array},,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b,,,,,,,,,,,,}\{3 = 9a + 3bleft| {:3} right.}end{array}} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b}\{1 = 3a + b}end{array}} right.,,,,,,,,,)

Вычтем из первого уравнения второе:  (4 =  — 2a,,,,,,, Leftrightarrow ,,,,,,,a =  — 2.)

Тогда: (5 =  — 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — 2{x^2} + 7x + 2)   и   (fleft( { — 3} right) =  — 2 cdot {left( { — 3} right)^2} + 7 cdot left( { — 3} right) + 2 =  — 37.)   

Ответ: – 37.
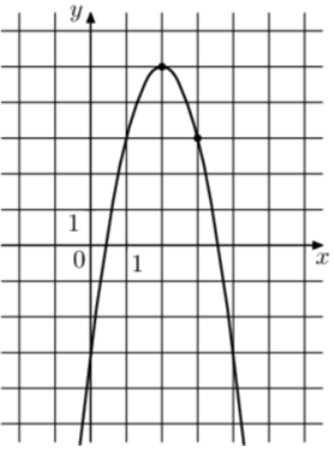
Задача 12. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x — 3.)  Найдите  (fleft( 8 right).)

Ответ

ОТВЕТ: — 67.
Решение

1 Способ

Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{3 = a + b — 3,,,,,,,,,,,,,,,,,,}\{3 = 9a + 3b — 3left| {:3} right.,,,,,}end{array},,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{3 = a + b — 3}\{1 = 3a + b — 1}end{array}} right.} right.)

Вычтем из первого уравнения второе:  (2 =  — 2a — 2,,,,,,, Leftrightarrow ,,,,,,,a =  — 2.)

Тогда: (3 =  — 2 + b — 3,,,,,,,, Leftrightarrow ,,,,,,,,b = 8.)  

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — 2{x^2} + 8x — 3)   и   (fleft( 8 right) =  — 2 cdot {8^2} + 8 cdot 8 — 3 =  — 67.)   

Ответ: – 67.

2 Способ

Заметим, что графиком является парабола (fleft( x right) =  — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) =  — 2{left( {x — 2} right)^2} + 5)  и  (fleft( 8 right) =  — 2 cdot {left( {8 — 2} right)^2} + 5 =  — 67.)

Ответ: – 67.
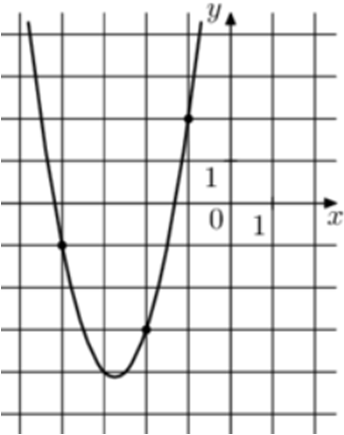
Задача 13. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( { — 7} right).)

Ответ

ОТВЕТ: 32.
Решение

Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2; — 3} right)) и (left( { — 4; — 1} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,}\{ — 3 = 4a — 2b + c}\{ — 1 = 16a — 4b + c}end{array}} right.)

Вычтем из первого уравнения второе:  (5 =  — 3a + b.)

Вычтем из первого уравнения третье:   (3 =  — 15a + 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,1 =  — 5a + b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{5 =  — 3a + b}\{1 =  — 5a + b}end{array}} right.)

Вычтем из первого уравнения второе:  (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.)

Тогда: (5 =  — 3 cdot 2 + b,,,,,, Leftrightarrow ,,,,,,b = 11)    и    (2 = 2 — 11 + c,,,,, Leftrightarrow ,,,,,c = 11.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} + 11x + 11)   и   (fleft( { — 7} right) = 2 cdot {left( { — 7} right)^2} + 11 cdot left( { — 7} right) + 11 = 32.)

Ответ: 32.
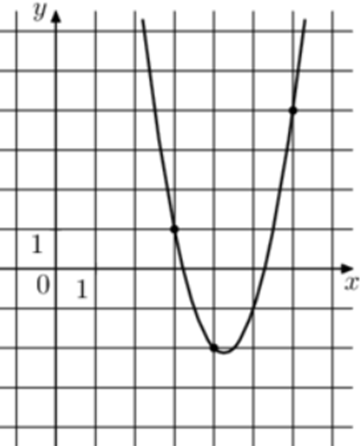
Задача 14. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( {10} right).)

Ответ

ОТВЕТ: 64.
Решение

Парабола проходит через точки (left( {3;1} right)), (left( {4; — 2} right)) и (left( {6;4} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{1 = 9a + 3b + c,,,,,,,,,}\{ — 2 = 16a + 4b + c}\{4 = 36a + 6b + c}end{array}} right.)

Вычтем из первого уравнения второе:  (3 =  — 7a — b)

Вычтем из первого уравнения третье:  ( — 3 =  — 27a — 3bleft| {:left( { — 3} right),,,,,,,,, Leftrightarrow ,,,,,,,,,1 = 9a + b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{3 =  — 7a — b}\{1 = 9a + b}end{array}} right.)

Прибавим к первому уравнению второе:  (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.)

Тогда: (3 =  — 7 cdot 2 — b,,,,,,, Leftrightarrow ,,,,,,,b =  — 17)  и   (1 = 9 cdot 2 + 3 cdot left( { — 17} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = 34.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} — 17x + 34)  и  (fleft( {10} right) = 2 cdot {10^2} — 17 cdot 10 + 34 = 64.)

Ответ: 64.
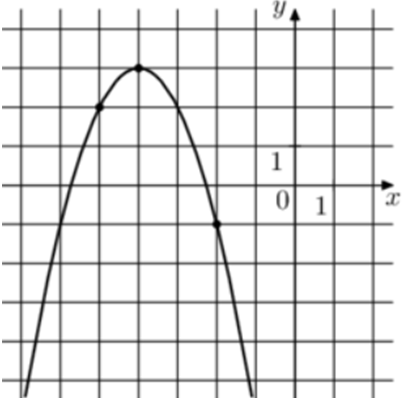
Задача 15. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( 2 right).)

Ответ

ОТВЕТ: — 33.
Решение

1 Способ

Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 5;2} right)) и (left( { — 6; — 1} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 25a — 5b + c,,,,,,,}\{ — 1 = 36a — 6b + c,,,}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 3 =  — 21a + 3bleft| {:3,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 =  — 7a + b} right..)

Вычтем из первого уравнения третье:  (0 =  — 32a + 4bleft| {:4,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 =  — 8a + b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{ — 1 =  — 7a + b}\{0 =  — 8a + b}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a =  — 1.)

Тогда: ( — 1 =  — 7 cdot left( { — 1} right) + b,,,,,, Leftrightarrow ,,,,,,b =  — 8)    и   ( — 1 = 4 cdot left( { — 1} right) — 2 cdot left( { — 8} right) + c,,,,,, Leftrightarrow ,,,,,,c =  — 13.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — {x^2} — 8x — 13)   и   (fleft( 2 right) = -{2^2} — 8 cdot 2 — 13 =  — 33.)

Ответ: – 33.

2 Способ

Заметим, что графиком является парабола (fleft( x right) =  — {x^2}) вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) =  — {left( {x + 4} right)^2} + 3)    и    (fleft( 2 right) =  — {left( {2 + 4} right)^2} + 3 =  — 33.)

Ответ: – 33.
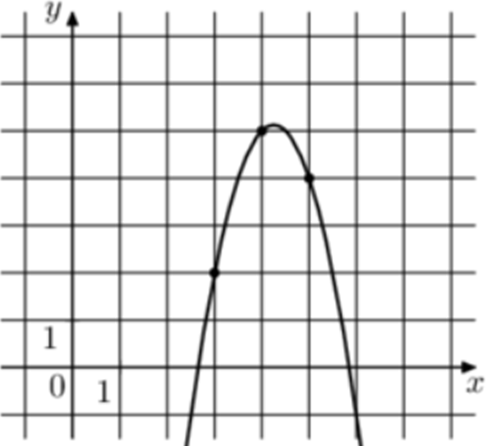
Задача 16. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: — 50.
Решение

Парабола проходит через точки (left( {3;2} right)), (left( {4;5} right)) и (left( {5;4} right)).  Следовательно:

(left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{5 = 16a + 4b + c,,,,,,}\{4 = 25a + 5b + c,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: ( — 3 =  — 7a — b.)

Вычтем из первого уравнения третье:  ( — 2 =  — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 =  — 8a — b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{ — 3 =  — 7a — b}\{ — 1 =  — 8a — b}end{array}} right.)

Прибавим к первому уравнению второе:  ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a =  — 2.)

Тогда:  ( — 3 =  — 7 cdot left( { — 2} right) — b,,,,,,, Leftrightarrow ,,,,,,,b = 17)   и   (2 = 9 cdot left( { — 2} right) + 3 cdot 17 + c,,,,,, Leftrightarrow ,,,,,,c =  — 31.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — 2{x^2} + 17x — 31)   и   (fleft( { — 1} right) =  — 2 cdot {left( { — 1} right)^2} + 17 cdot left( { — 1} right) — 31 =  — 50.)

Ответ: – 50.
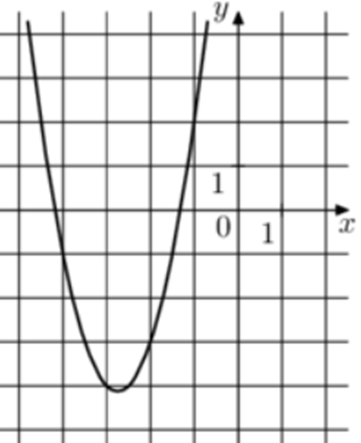
Задача 17. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( 2 right).)

Ответ

ОТВЕТ: 41.
Решение

Парабола проходит через точки (left( { — 2; — 3} right)), (left( { — 3; — 4} right)) и (left( { — 4; — 1} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 3 = 4a — 2b + c,,,,,,,,,}\{ — 4 = 9a — 3b + c,,,,,,,,}\{ — 1 = 16a — 4b + c,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: (1 =  — 5a + b.)

Вычтем из первого уравнения третье:  ( — 2 =  — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 =  — 6a + b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{1 =  — 5a + b}\{ — 1 =  — 6a + b}end{array}} right.)

Прибавим к первому уравнению второе:  (2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.)

Тогда: (1 =  — 5 cdot 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 11)   и   ( — 3 = 4 cdot 2 — 2 cdot 11 + c,,,,,,, Leftrightarrow ,,,,,,,c = 11.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = 2{x^2} + 11x + 11)  и  (fleft( 2 right) = 2 cdot {2^2} + 11 cdot 2 + 11 = 41.)

Ответ: 41.
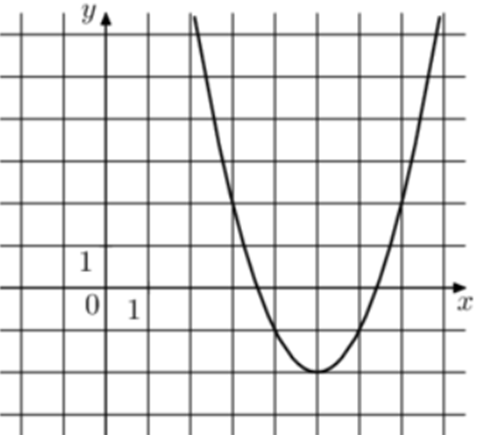
Задача 18. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: 34.
Решение

1 Способ

Парабола проходит через точки (left( {3;2} right)), (left( {4; — 1} right)) и (left( {5; — 2} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{ — 1 = 16a + 4b + c,,,,,,,}\{ — 2 = 25a + 5b + c,,,}end{array}} right.)

Вычтем из первого уравнения второе: (3 = -7a — b.)

Вычтем из первого уравнения третье:  (4 =  — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,,,2 =  — 8a — b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{3 =  — 7a — b}\{2 =  — 8a — b}end{array}} right.)

Вычтем из первого уравнения второе:  (1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 1.)

Тогда: (3 =  — 7 — b,,,,,,, Leftrightarrow ,,,,,,,b =  — 10)   и   (2 = 9 cdot 1 + 3 cdot left( { — 10} right) + c,,,,,, Leftrightarrow ,,,,,,c = 23.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) = {x^2} — 10x + 23)  и  (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.)

Ответ: 34.

2 Способ

Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2)   и   (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.)

Ответ: 34.
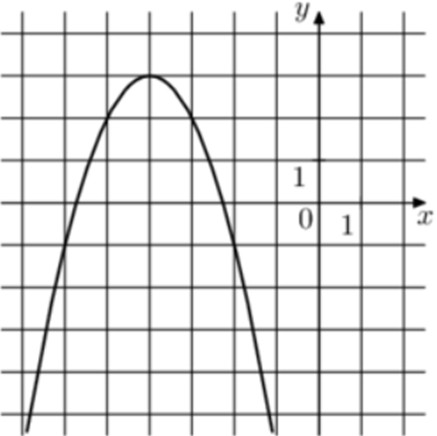
Задача 19. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( { — 8} right).)

Ответ

ОТВЕТ: — 13.
Решение

1 Способ

Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 3;2} right)) и (left( { — 4;3} right)).  Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 9a — 3b + c,,,,,,,}\{3 = 16a — 4b + c,,,}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 3 =  — 5a + b.)

Вычтем из первого уравнения третье:  ( — 4 =  — 12a + 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 2 =  — 6a + b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{ — 3 =  — 5a + b}\{ — 2 =  — 6a + b}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a =  — 1.)

Тогда: ( — 3 =  — 5 cdot left( { — 1} right) + b,,,,,,, Leftrightarrow ,,,,,,,b =  — 8)    и   ( — 1 = 4 cdot left( { — 1} right) — 2 cdot left( { — 8} right) + c,,,,,, Leftrightarrow ,,,,,,c =  — 13.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — {x^2} — 8x — 13)   и   (fleft( { — 8} right) =  — {left( { — 8} right)^2} — 8 cdot left( { — 8} right) — 13 =  — 13.)

Ответ: – 13.

2 Способ

Заметим, что графиком является парабола (fleft( x right) =  — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид:

(fleft( x right) =  — {left( {x + 4} right)^2} + 3)   и   (fleft( { — 8} right) =  — {left( { — 8 + 4} right)^2} + 3 =  — 13.)

Ответ: – 13.
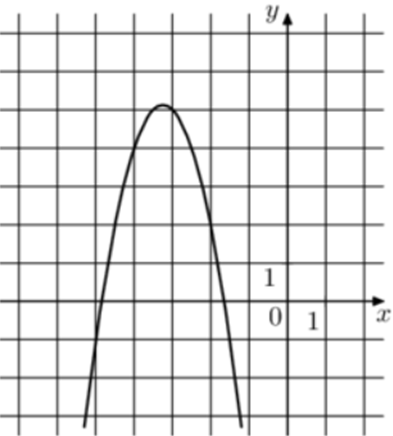
Задача 20. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( { — 6} right).)

Ответ

ОТВЕТ: — 10.
Решение

Парабола проходит через точки (left( { — 2;2} right)), (left( { — 3;5} right)) и (left( { — 4;4} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{2 = 4a — 2b + c,,,,,,,,,}\{5 = 9a — 3b + c,,,,,,,,}\{4 = 16a — 4b + c,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: ( — 3 =  — 5a + b.)

Вычтем из первого уравнения третье:  ( — 2 =  — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 =  — 6a + b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{ — 3 =  — 5a + b}\{ — 1 =  — 6a + b}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a =  — 2.)

Тогда: ( — 3 =  — 5 cdot left( { — 2} right) + b,,,,,,, Leftrightarrow ,,,,,,b =  — 13)   и   (2 = 4 cdot left( { — 2} right) — 2 cdot left( { — 13} right) + c,,,,,,, Leftrightarrow ,,,,,,,c =  — 16.)

Следовательно, уравнение параболы имеет вид:

(fleft( x right) =  — 2{x^2} — 13x — 16)  и  (fleft( { — 6} right) =  — 2 cdot {left( { — 6} right)^2} — 13 cdot left( { — 6} right) — 16 =  — 10.)

Ответ: – 10.
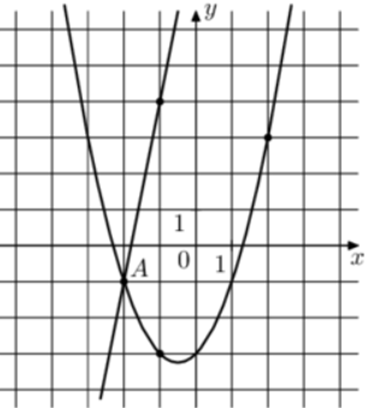
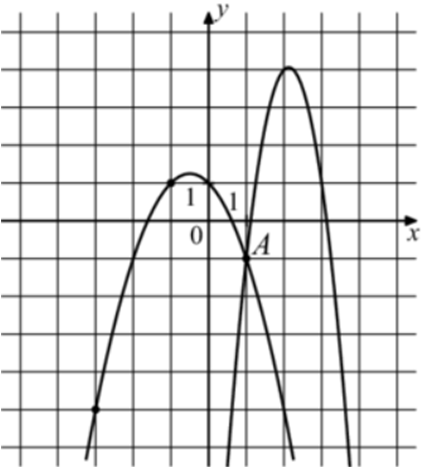
Задача 21. На рисунке изображены графики функций (fleft( x right) = 5x + 9) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 6.
Решение

Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 1; — 3} right)) и (left( {1; — 1} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{ — 3 = a — b + c,,,,,,,,,,,,,,,}\{ — 1 = a + b + c,,,,,,,,,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе:  (2 = 3a — b.)

Вычтем из первого уравнения третье:  (0 = 3a — 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = a — b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{2 = 3a — b}\{0 = a — b,,,}end{array}} right.)

Вычтем из первого уравнения второе:  (2 = 2a,,,,, Leftrightarrow ,,,,a = 1.)

Тогда: (0 = 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 1)   и   ( — 1 = 4 cdot 1 — 2 cdot 1 + c,,,,,,, Leftrightarrow ,,,,,,,c =  — 3.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) = {x^2} + x — 3.)

Чтобы найти координаты точек пересечения прямой  (fleft( x right) = 5x + 9)  и параболы (gleft( x right) = {x^2} + x — 3) необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y = {x^2} + x — 3}\{y = 5x + 9,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,{x^2} + x — 3 = 5x + 9,,,,,, Leftrightarrow ,,,,,,{x^2} — 4x — 12 = 0,,,,, Leftrightarrow ,,,,,{x_1} =  — 2,,,,{x_2} = 4.)

Значение (x =  — 2) является абсциссой точки  А. Следовательно, абсцисса точки  В  равна 4.

Ответ: 4.
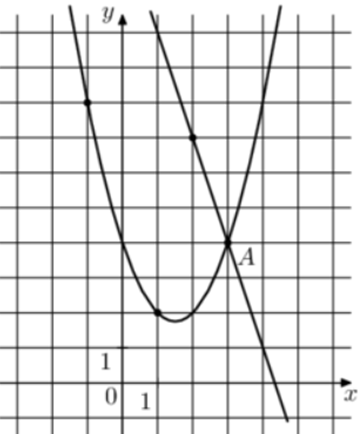
Задача 22. На рисунке изображены графики функций (fleft( x right) =  — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 3.
Решение

Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: (0 =  — 3a — b.)

Вычтем из первого уравнения третье:  ( — 2 =  — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 1 =  — 4a — b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{0 =  — 3a — b}\{ — 1 =  — 4a — b,,,}end{array}} right.)

Вычтем из первого уравнения второе:  (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.)

Тогда: (0 =  — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b =  — 3)   и   (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) = {x^2} — 3x + 4.)

Чтобы найти координаты точек пересечения прямой  (fleft( x right) =  — 3x + 13)  и параболы  (gleft( x right) = {x^2} — 3x + 4)  необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y =  — 3x + 13,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,{x^2} — 3x + 4 =  — 3x + 13,,,,,,, Leftrightarrow ,,,,,,,{x^2} = 9,,,,,,, Leftrightarrow ,,,,,{x_1} = 3,,,,{x_2} =  — 3.)

Значение (x = 3) является абсциссой точки  А.  Следовательно, абсцисса точки  В  равна – 3.

Ответ: – 3.
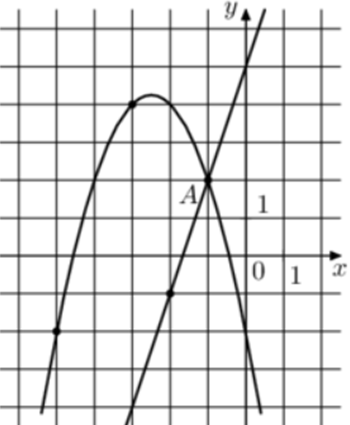
Задача 23. На рисунке изображены графики функций (fleft( x right) = 3x + 5) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 7.
Решение

Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2;4} right)) и (left( { — 4;2} right)).  Следовательно:

(left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = 4a — 2b + c,,,,,,,,,,,,,,,}\{2 = 16a — 4b + c,,,,,,,,,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: ( — 2 =  — 3a + b.)

Вычтем из первого уравнения третье:  (0 =  — 15a + 3bleft| {:3,,,,,,,, Leftrightarrow ,,,,,,,0 =  — 5a + b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{ — 2 =  — 3a + b}\{0 =  — 5a + b,,,}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 2 = 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a =  — 1.)

Тогда: ( — 2 =  — 3 cdot left( { — 1} right) + b,,,,,,,, Leftrightarrow ,,,,,,,,b =  — 5)  и   (2 =  — 1 + 5 + c,,,,,,, Leftrightarrow ,,,,,,,c =  — 2.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) =  — {x^2} — 5x — 2.)

Чтобы найти координаты точек пересечения прямой  (fleft( x right) = 3x + 5)  и параболы  (gleft( x right) =  — {x^2} — 5x — 2)  необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y =  — {x^2} — 5x — 2}\{y = 3x + 5,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,, — {x^2} — 5x — 2 = 3x + 5,,,,,, Leftrightarrow ,,,,,{x^2} + 8x + 7 = 0,,,,,, Leftrightarrow ,,,,,{x_1} =  — 1,,,,{x_2} =  — 7.)

Значение (x =  — 1)  является абсциссой точки  А. Следовательно, абсцисса точки  В  равна – 7.

Ответ: – 7.
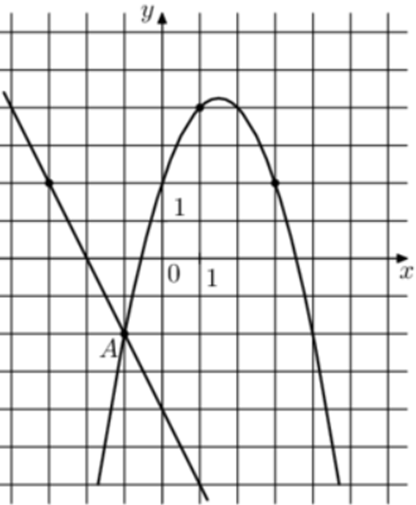
Задача 24. На рисунке изображены графики функций (fleft( x right) =  — 2x — 4) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 6.
Решение

Парабола проходит через точки (left( { — 1; — 2} right)), (left( {1;4} right)) и (left( {3;2} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: ( — 6 =  — 2b,,,,,,, Leftrightarrow ,,,,,,b = 3.)

Вычтем из первого уравнения третье:  ( — 4 =  — 8a — 4bleft| {:left( { — 2} right),,,,,,,,, Leftrightarrow ,,,,,,,,2 = 4a + 2b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{b = 3,,,,,,,,,,,,,,,,}\{2 = 4a + 2b,,,}end{array},,,,, Leftrightarrow ,,,,,,2 = 4a + 2 cdot 3,,,,,,,, Leftrightarrow ,,,,,,,,,a =  — 1} right..)

Тогда: ( — 2 =  — 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,,c = 2.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) =  — {x^2} + 3x + 2.)

Чтобы найти координаты точек пересечения прямой (fleft( x right) =  — 2x — 4) и параболы (gleft( x right) =  — {x^2} + 3x + 2) необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y =  — {x^2} + 3x + 2}\{y =  — 2x — 4,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — ,{x^2} + 3x + 2 =  — 2x — 4,,,,,, Leftrightarrow ,,,,,{x^2} — 5x — 6 = 0,,,,, Leftrightarrow ,,,,,{x_1} =  — 1,,,,{x_2} = 6.)

Значение (x =  — 1)  является абсциссой точки  А. Следовательно, абсцисса точки  В  равна 6.

Ответ: 6.
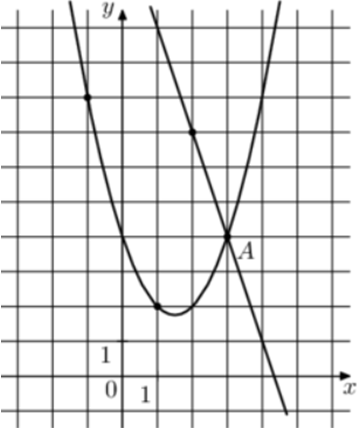
Задача 25. На рисунке изображены графики функций (fleft( x right) =  — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 22.
Решение

Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: (0 =  — 3a — b.)

Вычтем из первого уравнения третье:  ( — 2 =  — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,, — 1 =  — 4a — b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{0 =  — 3a — b}\{ — 1 =  — 4a — b}end{array}} right.)

Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.)

Тогда: (0 =  — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b =  — 3)   и   (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) = {x^2} — 3x + 4.)

Чтобы найти координаты точек пересечения прямой  (fleft( x right) =  — 3x + 13)  и параболы  (gleft( x right) = {x^2} — 3x + 4)  необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y =  — 3x + 13,,,,}end{array}} right.,,, Leftrightarrow ,,,{x^2} — 3x + 4 = 13 — 3x,,, Leftrightarrow ,,,{x^2} = 9,,,, Leftrightarrow ,,,{x_1} = 3,,,,{x_2} =  — 3,,, Leftrightarrow ,,,{y_1} = 4,,,{y_2} = 22.)

Следовательно,  (Aleft( {3;4} right))  и  (Bleft( { — 3;22} right)).  Таким образом, ордината точки В равна 22.

Ответ: 22.
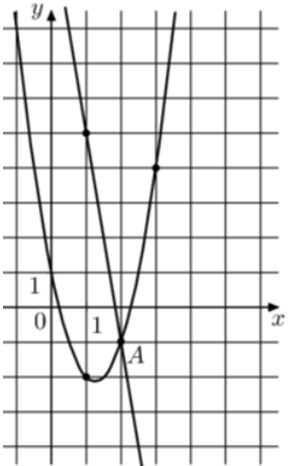
Задача 26. На рисунке изображены графики функций (fleft( x right) =  — 6x + 11) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 26.
Решение

Парабола проходит через точки (left( {1; — 2} right)), (left( {2; — 1} right)) и (left( {3;4} right)).  Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 2 = a + b + c}\{ — 1 = 4a + 2b + c}\{4 = 9a + 3b + c}end{array}} right.)

Вычтем из первого уравнения второе: ( — 1 =  — 3a — b.)

Вычтем из первого уравнения третье:  ( — 6 =  — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 3 =  — 4a — b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{ — 1 =  — 3a — b}\{ — 3 =  — 4a — b}end{array}} right.)

Вычтем из первого уравнения второе:  (2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.)

Тогда: ( — 1 =  — 3 cdot 2 — b,,,,,,,, Leftrightarrow ,,,,,,,,b =  — 5)   и   ( — 2 = 2 — 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = 1.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) = 2{x^2} — 5x + 1.)

Чтобы найти координаты точек пересечения прямой  (fleft( x right) =  — 6x + 11)  и параболы  (gleft( x right) = 2{x^2} — 5x + 1)  необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y = 2{x^2} — 5x + 1}\{y =  — 6x + 11,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,2{x^2} — 5x + 1 =  — 6x + 11,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + x — 10 = 0,,,,,,,,, Leftrightarrow ,,,,,)

( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} =  — frac{5}{2},,,,,,,,, Leftrightarrow ,,,,,,,{y_1} =  — 1,,,,,{y_2} = 26.)

Следовательно,  (Aleft( {2; — 1} right))  и  (Bleft( { — frac{5}{2};26} right)).  Таким образом, ордината точки В равна 26.

Ответ: 26.
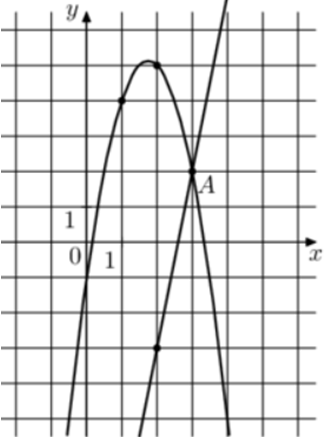
Задача 27. На рисунке изображены графики функций (fleft( x right) = 5x — 13) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 23.
Решение

Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)).  Следовательно:

(left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе:   ( — 1 =  — 3a — b.)

Вычтем из первого уравнения третье:   (2 =  — 8a — 2bleft| {:2,,,,,,, Leftrightarrow ,,,,,,1 =  — 4a — b} right..)

Таким образом, получим систему уравнений:   (left{ {begin{array}{*{20}{c}}{ — 1 =  — 3a — b}\{1 =  — 4a — b}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a =  — 2.)

Тогда: ( — 1 =  — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7)   и   (4 =  — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c =  — 1.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) =  — 2{x^2} + 7x — 1.)

Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x — 13) и параболы (gleft( x right) =  — 2{x^2} + 7x — 1) необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y =  — 2{x^2} + 7x — 1}\{y = 5x — 13,,,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = 5x — 13,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 2x — 12 = 0,,,,,,,,, Leftrightarrow ,,,,,)

( Leftrightarrow ,,,,,,,,{x_1} = 3,,,,,,{x_2} =  — 2,,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 2,,,,,{y_2} =  — 23.)

Следовательно,  (Aleft( {3;2} right))  и  (Bleft( { — 2; — 23} right)).  Таким образом, ордината точки В равна – 23.

Ответ: – 23.
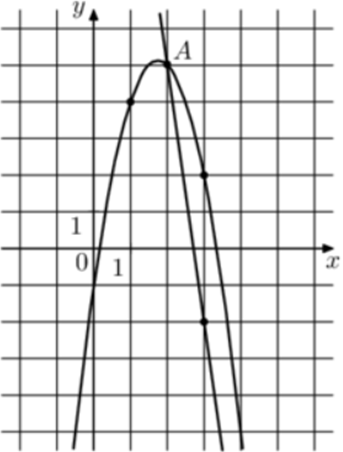
Задача 28. На рисунке изображены графики функций (fleft( x right) =  — 7x + 19) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 16.
Решение

Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)).  Следовательно:

(left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)

Вычтем из первого уравнения второе: ( — 1 =  — 3a — b.)

Вычтем из первого уравнения третье:  (2 =  — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,,1 =  — 4a — b} right..)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{ — 1 =  — 3a — b}\{1 =  — 4a — b}end{array}} right.)

Вычтем из первого уравнения второе:  ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a =  — 2.)

Тогда: ( — 1 =  — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7)   и   (4 =  — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c =  — 1.)

Следовательно, уравнение параболы имеет вид:   (gleft( x right) =  — 2{x^2} + 7x — 1.)

Чтобы найти координаты точек пересечения прямой  (fleft( x right) =  — 7x + 19)  и параболы  (gleft( x right) =  — 2{x^2} + 7x — 1)  необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y =  — 2{x^2} + 7x — 1}\{y =  — 7x + 19,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 =  — 7x + 19,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 14x + 20 = 0,,,,,,,,, Leftrightarrow ,,,,,)

( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = 5,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 5,,,,,{y_2} =  — 16.)

Следовательно, (Aleft( {2;5} right)) и (Bleft( {5; — 16} right)). Таким образом, ордината точки В равна – 16.

Ответ: – 16.
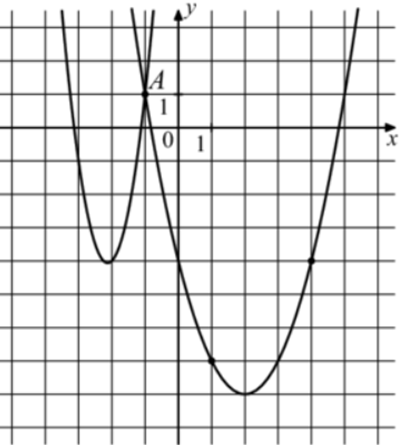
Задача 29. На рисунке изображены графики функций (fleft( x right) = 4{x^2} + 17x + 14) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 6.
Решение

График функции (fleft( x right) = 4{x^2} + 17x + 14) пересекает ось ординат в точке (left( {0;14} right)). Значит, график (y = fleft( x right)) изображён слева, а график (gleft( x right) = a{x^2} + bx + c) справа. Заметим, что графиком функции (y = gleft( x right)) является парабола (gleft( x right) = {x^2}), вершина которой находится в точке (left( {2; — 8} right)). Следовательно, ее уравнение будет иметь вид: (gleft( x right) = {left( {x — 2} right)^2} — 8 = {x^2} — 4x — 4.)

Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y = 4{x^2} + 17x + 14}\{y = {x^2} — 4x — 4,,,,,,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,4{x^2} + 17x + 14 = {x^2} — 4x — 4,,,,,,, Leftrightarrow ,,,,,,,3{x^2} + 21x + 18 = 0left| {:3,,,,, Leftrightarrow } right.)

( Leftrightarrow ,,,,,,,{x^2} + 7x + 6 = 0,,,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} =  — 1,,,,{x_2} =  — 6.)

Значение  (x =  — 1)  является абсциссой точки А.  Следовательно, абсцисса точки В равна  – 6.

Ответ: – 6.
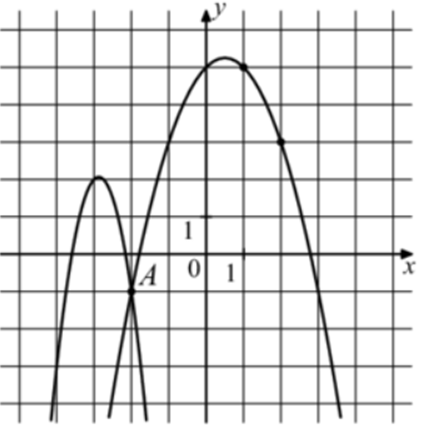
Задача 30. На рисунке изображены графики функций (fleft( x right) =  — 4{x^2} — 23x — 31) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 6.
Решение

График функции (fleft( x right) =  — 4{x^2} — 23x — 31) пересекает ось ординат в точке (left( {0; — 31} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( { — 2; — 1} right)), (left( {1;5} right)) и (left( {2;3} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c}\{5 = a + b + c,,,,,,}\{3 = 4a + 2b + c}end{array}} right.)

Вычтем из первого уравнения второе:   ( — 6 = 3a — 3b.)

Вычтем из первого уравнения третье:   ( — 4 =  — 4b,,,,,, Leftrightarrow ,,,,,b = 1.)

Тогда:   ( — 6 = 3a — 3,,,,,, Leftrightarrow ,,,,,,a =  — 1)    и    ( — 1 =  — 4 — 2 + c,,,,,, Leftrightarrow ,,,,,,,c = 5.)

Следовательно:   (gleft( x right) =  — {x^2} + x + 5.)

Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y =  — 4{x^2} — 23x — 31}\{y =  — {x^2} + x + 5,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — 4{x^2} — 23x — 31 =  — {x^2} + x + 5,,,,, Leftrightarrow ,,,,,3{x^2} + 24x + 36 = 0left| {:3,,,, Leftrightarrow ,} right.)

( Leftrightarrow ,,,,,,{x^2} + 8x + 12 = 0,,,,,,,, Leftrightarrow ,,,,,,{x_1} =  — 2,,,,,,{x_2} =  — 6.)

Значение  (x =  — 2)  является абсциссой точки  А. Следовательно, абсцисса точки В равна  – 6.

Ответ: – 6.
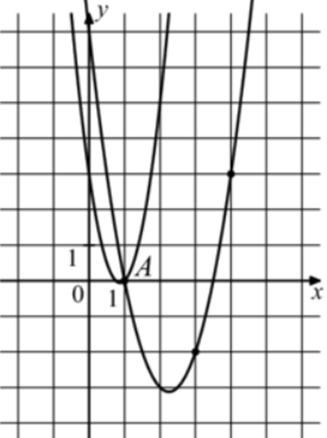
Задача 31. На рисунке изображены графики функций (fleft( x right) = 4{x^2} — 7x + 3) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 33.
Решение

График функции (fleft( x right) = 4{x^2} — 7x + 3) пересекает ось ординат в точке (left( {0;3} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( {1;0} right)), (left( {3; — 2} right)) и (left( {4;3} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{0 = a + b + c,,,,,,,,}\{ — 2 = 9a + 3b + c}\{3 = 16a + 4b + c}end{array}} right.)

Вычтем из первого уравнения второе:   (2 =  — 8a — 2bleft| {: 2,,,,,,, Leftrightarrow ,,,,,,,,1 =  — 4a — b.} right.)

Вычтем из первого уравнения третье:   ( — 3 =  — 15a — 3bleft| {:3} right.,,,,,, Leftrightarrow ,,,,, — 1 =  — 5a — b.)

Таким образом, получим систему уравнений:  (left{ {begin{array}{*{20}{c}}{1 =  — 4a — b}\{ — 1 =  — 5a — b}end{array}} right.)

Вычтем из первого уравнения второе:   (2 = a,,,,,,, Leftrightarrow ,,,,,,,a = 2.)

Тогда:   (1 =  — 4 cdot 2 — b,,,,,, Leftrightarrow ,,,,,,b =  — 9)   и   (0 = 2 — 9 + c,,,,,,, Leftrightarrow ,,,,,,,c = 7.)

Следовательно:   (gleft( x right) = 2{x^2} — 9x + 7.)

Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y = 4{x^2} — 7x + 3}\{y = 2{x^2} — 9x + 7}end{array},,,,,,, Leftrightarrow ,,,,,,4{x^2} — 7x + 3 = 2{x^2} — 9x + 7,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + 2x — 4 = 0left| {:2,,,,, Leftrightarrow } right.} right.)

( Leftrightarrow ,,,,,,,{x^2} + x — 2 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} =  — 2,,,,,,,,,,,,,,{y_1} = 0,,,,{y_2} = 33.)

Следовательно,  (Aleft( {1;0} right))  и  (Bleft( { — 2;33} right)).  Таким образом, ордината точки В равна 33.

Ответ: 33.
Задача 32. На рисунке изображены графики функций (fleft( x right) =  — 4{x^2} + 17x — 14) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 29.
Решение

График функции (fleft( x right) =  — 4{x^2} + 17x — 14) пересекает ось ординат в точке (left( {0; — 14} right)). Значит график функции (y = fleft( x right)) изображен справа, а график (gleft( x right) = a{x^2} + bx + c) слева, который проходит через точки (left( {1; — 1} right)), (left( { — 1;1} right)) и (left( { — 3; — 5} right)). Следовательно:

(left{ {begin{array}{*{20}{c}}{ — 1 = a + b + c,,,,,,}\{1 = a — b + c,,,,,,,,}\{ — 5 = 9a — 3b + c}end{array}} right.)

Вычтем из первого уравнения второе:   ( — 2 = 2b,,,,,,, Leftrightarrow ,,,,,,,b =  — 1.)

Вычтем из первого уравнения третье:   (4 =  — 8a + 4b,,,,, Leftrightarrow ,,,,,4 =  — 8a — 4,,,,,, Leftrightarrow ,,,,,,a =  — 1.)

Тогда:  ( — 1 =  — 1 — 1 + c,,,,,, Leftrightarrow ,,,,,,,c = 1.)   Следовательно:   (gleft( x right) =  — {x^2} — x + 1.)

Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений:

(left{ {begin{array}{*{20}{c}}{y =  — 4{x^2} + 17x — 14}\{y =  — {x^2} — x + 1,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,, — 4{x^2} + 17x — 14 =  — {x^2} — x + 1,,,,,, Leftrightarrow ,,,,,3{x^2} — 18x + 15 = 0left| {:3,,,,, Leftrightarrow } right.)

( Leftrightarrow ,,,,,,,{x^2} — 6x + 5 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 5,,,,,,,,,{y_1} =  — 1,,,,{y_2} =  — 29.)

Следовательно,  (Aleft( {1; — 1} right))  и  (Bleft( {5; — 29} right)).  Таким образом, ордината точки В равна – 29.

Ответ: – 29.

Источник

Функция вида y=ax^2+bx+c , где aneq 0 называется квадратичной функцией. 

График квадратичной функции – парабола. 

парабола, построение параболы, график парабола

Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА 

y=x^2, то есть a=1, b=0, c=0

Для построения заполняем таблицу, подставляя значения x в формулу:

parabola2

Отмечаем  точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

классическая парабола, парабола, построение параболы

Нетрудно заметить, что если мы возьмем случай a=-1, b=0, c=0, то есть y=-x^2, то мы получим параболу, симметричную y=x^2 относительно оси (ох). Убедиться  в этом несложно, заполнив аналогичную таблицу:

парабола, построение параболы

II СЛУЧАЙ,  «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать a=2, a=-3, a=0.5? Как изменится поведение параболы? При |a|>1 парабола  y=ax^2 изменит форму, она “похудеет” по сравнению с параболой y=x^2 (не верите – заполните соответствующую таблицу – и убедитесь сами):

парабола, построение параболы, ветви параболы, коэффициенты параболы, дискриминант

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы y=x^2 (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях x  ордината  y  каждой точки умножилась на 4.  Это произойдет со всеми ключевыми точками исходной  таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при |a|<1 парабола y=ax^2  «станет шире»  параболы y=x^2:

парабола, построение параболы, ветви параболы, коэффициенты параболы, дискриминант, ветви вниз

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ  «С»

 Теперь давайте введем в игру c (то есть рассматриваем случай, когда cneq 0), будем рассматривать параболы вида y=ax^2+c. Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы y=ax^2 вдоль оси (oy) вверх или вниз в зависимости от знака c:

парабола, построение параболы, сдвиг параболы, ветви параболы, коэффициенты параболы, дискриминант

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси (oy) и будет, наконец, “гулять” по всей координатной плоскости? Когда b перестанет быть равным 0.

Здесь для построения параболы y=ax^2+bx+c нам понадобится формула для вычисления вершины: x_o=frac{-b}{2a},   y_o=y(x_o).

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу y=ax^2, что уже нам по силам. Если  имеем дело со случаем a=1, то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с a=2, например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы y=x^2-4x-2:

x_o=frac{4}{2}=2,  y_o=(2)^2-4cdot 2 -2=-6. Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы y=x^2,  ведь a=1 в нашем случае.

парабола, построение параболы, ветви параболы, дискриминант

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку (0;c).  Действительно, подставив в формулу y=ax^2+bx+c x=0, получим, что y=c. То есть ордината точки пересечения параболы  с осью (оу), это c.   В нашем примере (выше), парабола пересекает ось ординат в точке -2, так как c=-2.

2) осью симметрии параболы является прямая x=frac{-b}{2a}, поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая y к 0, мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение ax^2+bx+c=0. В зависимости от дискриминанта, будем получать одну (D=0,  x=-frac{b}{2a}), две (D>0, x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}) или нИсколько (D<0) точек пересечения с осью (ох). В предыдущем примере у нас  корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения  с осью (ох) у нас будут (так как D>0), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана  в виде y=ax^2+bx+c

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины (x_o;y_o) параболы по формуле x_o=frac{-b}{2a},   y_o=y(x_o).

3) находим точку пересечения параболы с осью (оу) по свободному члену c, строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение c велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу y=ax^2. Если |a|>1, то парабола y=ax^2 становится у’же по сравнению с y=x^2, если |a|<1, то парабола расширяется по сравнению с y=x^2

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение ax^2+bx+c=0

Пример 1

алгоритм построения параболы, парабола

Пример  2

парабола, построение параболы, ветви параболы, коэффициенты параболы, дискриминант

Замечание 1. Если же парабола изначально нам задана в виде y=a(x-m)^2+n, где m, n – некоторые числа (например, y=(x-5)^2-1), то построить ее будет еще легче, потому что нам уже заданы координаты вершины (m, n). Почему?

Возьмем квадратный трехчлен ax^2+bx+c и выделим в нем полный квадрат: ax^2+bx+c=a(x^2+frac{b}{a}x+frac{c}{a})=a((x^2+2frac{b}{2a}x+frac{b^2}{4a^2})-frac{b^2}{4a^2}+frac{c}{a})=a(x+frac{b}{2a})^2-frac{b^2}{4a}+c. Посмотрите, вот мы и получили, что m=frac{-b}{2a}, n=-frac{b^2}{4a}+c=y(frac{-b}{2a}). Мы с вами ранее называли   вершину параболы (x_o; y_o), то есть теперь x_o=m, y_o=n.

Например,  y=-frac{1}{3}{(x+2)}^2+6. Отмечаем на плоскости вершину параболы (-2; 6), понимаем, что ветви направлены вниз, парабола расширена (относительно y=x^2). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

парабола с ветвями вниз

Замечание 2. Если парабола задана в виде, подобном этому y=x(x-4) (то есть y представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае  – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Источник

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

задача с гиперболой

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

находим две точки с целыми координатами

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

составляем уравнения

3. Решаем эту систему и получаем готовую формулу.

решаем систему

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

отвечаем на вопрос задачи

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

Пример с логарифмической функцией

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

преобразование графиков функций

Для использования этого способа надо знать, как выглядят изначальные функции:

Виды функций

И понимать, как меняются функции от преобразований:

Преобразование графиков функций

примеры преобразований функций

Преобразование показательной функции Преобразование гипербол

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

как по формуле определить какие были преобразования с функцией

Пример:

пример с функцией обратной пропорциональности

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

показательная и логарифмическая функция

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

пример с логарифмической функцией

пример с логарифмической функцией

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

что значит найти f от числа

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

найдите, при каком значении x значение функции равно 8

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

найдите точку пересечения функций

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

найдите ординату точки пересечения

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

найдите k

Источник

В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы. Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике. 

Способы решения номера

9 задание по математике профильного уровня 2022 получится решить четырьмя методами. 

Первый вариант

Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом: 

Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки: 

Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты: 

16a — 4b + c = -3

Аналогичным образом записываем выражение, используя две остальные точки: 

9a — 3b + c = -2

4a — 2b + c = 1

Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем: 

b = 8;

c = 13. 

Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы: 

f(x) = x2 + 8x + 13

f(-12) = 144 — 96 + 13 = 61

Второй вариант

Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы: 

Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x2, сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x0 = -b / 2a. По рисунку видно: x0 = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще. 

Третий вариант

9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример: 

y = x2

Сдвиг влево записывается: 

y = (x + 4)2

Сдвиг вниз: 

y = (x + 4)2 — 3

Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61. 

Четвертый вариант

Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат: 

Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!

В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum. 

Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации! 

Источник

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида y=ax^2+bx+c, где a<>0  называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции y=x^2 имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции y=x^2, составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции y=x^2 при любых значениях остальных коэффициентов.

График  функции y=-x^2 имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции y=-x^2 симметричен графику функции y=x^2 относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика  функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты  точек  пересечения графика функции y=f(x) с осью ОХ, нужно решить уравнение f(x)=0.

В случае квадратичной функции y=ax^2+bx+c нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: D=b^2-4ac, который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если D<0 ,то уравнение ax^2+bx+c=0 не имеет решений, и, следовательно, квадратичная парабола y=ax^2+bx+c не имеет точек пересечения с осью ОХ. Если a>0 ,то график функции выглядит как-то так:

2. Если D=0 ,то уравнение ax^2+bx+c=0  имеет одно решение, и, следовательно, квадратичная парабола y=ax^2+bx+c  имеет одну точку пересечения с осью ОХ. Если a>0 ,то график функции выглядит примерно так:

3.  Если D>0 ,то уравнение ax^2+bx+c=0  имеет два решения, и, следовательно, квадратичная парабола y=ax^2+bx+c  имеет две точки пересечения с осью ОХ:

x_1={-b+sqrt{D}}/{2a},  x_2={-b-sqrt{D}}/{2a}

Если a>0 ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

x_0=-{b/{2a}}

y_0=-{D/{4a}}=y(x_0)

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы y=ax^2+bx+c с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы y=ax^2+bx+c с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c.

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны  на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой y=ax^2+bx+c.

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции y=2x^2+3x-5

1. Направление ветвей параболы.

Так как a=2>0 ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена 2x^2+3x-5

D=b^2-4ac=9-4*2*(-5)=49>0  sqrt{D}=7

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение: 2x^2+3x-5=0

x_1={-3+7}/4=1,  x_1={-3-7}/4=-2,5

3.   Координаты  вершины параболы:

x_0=-{b/{2a}}=-3/4 =-0,75

y_0=-{D/{4a}}=-49/8=-6,125

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

y=2x^2+3x-5

Кррдинаты вершины параболы

x_0=-{b/{2a}}=-3/4 =-0,75

y_0=-{D/{4a}}=-49/8=-6,125

Ближайшие к вершине точки, расположенные  слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы  соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их  в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2.  Уравнение квадратичной функции имеет вид y=a(x-x_0)^2+y_0 — в этом уравнении x_0;y_0 — координаты вершины параболы

или в уравнении квадратичной функции y=ax^2+bx+c a=1, и второй коэффициент — четное число.

Построим для примера график функции y=2(x-1)^2+4.

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

  • сначала построить график функции y=x^2,
  • затем одинаты всех точек графика умножить на 2,
  • затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
  • а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение  графика функции y=x^2+4x+5. В уравнении этой функции a=1, и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат: x^2+4x+5=x^2+4x+4-4+5=(x^2+4x+4)+1=(x+2)^2+1

Следовательно,  координаты вершины параболы: x_0=-2, y_0=1. Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3.  Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда x_1=2; x_2=-1

2. Координаты вершины параболы: x_0={x_1+x_2}/2={2-1}/2=1/2

y_0=y(-1)=({1/2}-2)({1/2}+1)=-9/4=-2,25

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на  координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида Подготовка к ГИА и ЕГЭ.

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции Подготовка к ГИА и ЕГЭ от значения коэффициента Подготовка к ГИА и ЕГЭ,
— сдвига графика функции Подготовка к ГИА и ЕГЭ вдоль оси Подготовка к ГИА и ЕГЭ от значения  Подготовка к ГИА и ЕГЭ,

— сдвига графика функции Подготовка к ГИА и ЕГЭ вдоль оси Подготовка к ГИА и ЕГЭ от значения  Подготовка к ГИА и ЕГЭ
— направления ветвей параболы от знака коэффициента Подготовка к ГИА и ЕГЭ
— координат вершины параболы Подготовка к ГИА и ЕГЭ от значений Подготовка к ГИА и ЕГЭ и Подготовка к ГИА и ЕГЭ:

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

Источник

Понравилась статья? Поделить с друзьями:
  • Грибоедов горе от ума анализ произведения для егэ
  • Грибная клетка рисунок егэ
  • Гржимайло биология егэ скачать
  • Греческих богинь егэ
  • Греческие философы хорошо понимали то что математическая егэ