Графики тригонометрических функций егэ профиль теория

Параметрические уравнения

Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр. На самом деле с каждым параметрическим уравнением может быть написано множество уравнений.

Способ решения параметрических уравнений

1. Находим область определения уравнения.
2. Выражаем a как функцию от $х$.
3. В системе координат $хОа$ строим график функции, $а=f(х)$ для тех значений $х$, которые входят в область определения данного уравнения.
4. Находим точки пересечения прямой, $а=с$, где $с∈(-∞;+∞)$ с графиком функции $а=f(х)$. Если прямая, а=с пересекает график, $а=f(х)$, то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение вида, $а=f(х)$ относительно $х$.
5. Записываем ответ.

Общий вид уравнения с одним параметром таков:

$F(x, a) = 0$

При различных значениях, а уравнение $F(x, a) = 0$ может иметь различные множества корней, задача состоит в том, чтобы изучить все случаи, выяснить, что будет при любом значении параметра. При решении уравнений с параметром обычно приходится рассматривать много различных вариантов. Своевременное обнаружение хотя бы части невозможных вариантов имеет большое значение, так как освобождает от лишней работы.

Поэтому при решении уравнения $F(x, a) = 0$ целесообразно под ОДЗ понимать область допустимых значений неизвестного и параметра, то есть множество всех пар чисел ($х, а$), при которых определена (имеет смысл) функция двух переменных $F(x, а)$. Отсюда естественная геометрическая иллюстрация ОДЗ в виде некоторой области плоскости $хОа$.

ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):

1. Выражение, стоящее в знаменателе, не должно равняться нулю.

${f(x)}/{g(x)}; g(x)≠0$

2. Подкоренное выражение должно быть неотрицательным.

$√{g(x)}; g(x)≥0$.

3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.

${f(x)}/{√{g(x)}}; g(x) > 0$

4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.

$log_{f(x)}g(x) {tableg(x) > 0; f(x) > 0; f(x)≠1;$

Алгебраический способ решения квадратных уравнений с параметром $ax^2+bx+c=0$

Квадратное уравнение $ax^2+bx+c=0, а≠0$ не имеет решений, если $D < 0$;

Квадратное уравнение имеет два различных корня, когда $D > 0$;

Квадратное уравнение имеет один корень, если $D=0$

Тригонометрические тождества

1. $tgα={sinα}/{cosα}$

2. $ctgα={cosα}/{sinα}$

3. $sin^{2}α+cos^{2}α=1$ (Основное тригонометрическое тождество)

Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса

$sinα=±√{1-cos^{2}α}$

$cosα=±√{1-sin^{2}α$

4. $tgα·ctgα=1$

5. $1+tg^{2}α={1}/{cos^{2}α}$

6. $1+ctg^{2}α={1}/{sin^{2}α}$

Формулы двойного угла

1. $sin2α=2sinα·cosα$

2. $cos2α=cos^{2}α-sin^{2}α=2cos^{2}α-1=1-2sin^{2}α$

3. $tg2α={2tgα}/{1-tg^{2}α}$

Формулы суммы и разности

$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$

$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$

$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$

$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$

Формулы произведения

$cosα·cosβ={cos{α-β}+cos{α+β}}/{2}$

$sinα·sinβ={cos{α-β}-cos{α+β}}/{2}$

$sinα·cosβ={sin{α+β}+sin{α-β}}/{2}$

Формулы сложения

$cos(α+β)=cosα·cosβ-sinα·sinβ$

$cos(α-β)=cosα·cosβ+sinα·sinβ$

$sin(α+β)=sinα·cosβ+cosα·sinβ$

$sin(α-β)=sinα·cosβ-cosα·sinβ$

Решение тригонометрического уравнения с параметром рассмотрим на примере.

Неравенства с параметром

Если имеется неравенство вида $F(a,x) ≤ G(a,x)$ то оно будет иметь одно решение, если $F'(a, x)=G'(a, x)$.

Системы уравнений:

Выделяют четыре основных метода решения систем уравнений:

1. Метод подстановки: из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.
2. Метод алгебраического сложения: путем сложения двух уравнений получить уравнение с одной переменной.
3. Метод введения новых переменных: ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы.
4. Графический метод решения: из каждого уравнения выражается $«у»$, получаются функции, графики которых необходимо построить и посмотреть координаты точек пересечения.

Логарифмические уравнения и системы уравнений

Основное логарифмическое тождество:

$a^{log_{a}b}=b$

Это равенство справедливо при $b> 0, a> 0, a≠1$

Свойства логарифмов:

Все свойства логарифмов мы будем рассматривать для $a> 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log_{а}b^m=mlog_{a}b$;

$log_{a^m}b={1}/{m}log_{a}b$.

$log_{a^n}b^m={m}/{n}log_{a}b$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_a(bc)=log_{a}b+log_{a}c$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_a{b}/{c}=log_{a}b-log_{a}c$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a, b, c, d >0, a≠1, b≠1$.

5. $c^{log_{a}b}=b^{log_{a}b}$, где $а, b, c > 0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

При решении систем, содержащих логарифмические уравнения, часто удается, избавившись от логарифма, заменить одно или оба уравнения системы рациональными уравнениями. После этого надо выразить одну переменную через другую и после постановки получить уравнение с одной переменной. Кроме того, часто встречаются задачи на замену переменной в пределах одного или обоих уравнений системы и системы, требующие отбора решений.

Логарифмические неравенства:

1. Определить ОДЗ неравенства.

2. По свойствам логарифма преобразовать неравенство к простому виду, желательно получить с двух сторон логарифмы по одинаковому основанию.

3. Перейти к подлогарифмическим выражениям, при этом надо помнить, что:

а) если основание больше единицы, то при переходе к подлогарифмическим выражениям знак неравенства остается прежним;

b) если основание меньше единицы, то при переходе к подлогарифмическим выражениям знак неравенства меняется на противоположный;

с) если в основании находится переменная, надо рассмотреть оба варианта.

4. Решить неравенство.

5. Выбрать решения с учетом ОДЗ из п.1

При решении логарифмических неравенств с переменной в основании легче всего воспользоваться тождественными преобразованиями:

$log_{a}f > b ↔ {table (f-a^b)(a-1) > 0; f > 0; a > 0;$

$log_{a}f+log_{a}g > 0 ↔ {table(fg-1)(a-1)> 0; f > 0,g > 0; a > 0;$

$log_{a}f+b > 0 ↔ {table(fa^b-1)(a-1) > 0; f > 0; a > 0;$

Системы, содержащие показательные уравнения

Свойства степеней

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n·a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n·m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

Основные методы решения систем, содержащих показательные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – положительность выражения $a^{f(x)}$, которую полезно учитывать, вводя соответствующее ограничение при замене переменной.

Показательные неравенства, сводящиеся к виду $a^{f(x)} ≥ a^{g(x)}$:

1. Преобразовать показательное уравнение к виду $a^{f(x)} ≥ a^{g(x)}$

2. Перейти показателям степеней, при этом если основание степени меньше единицы, то знак неравенства меняется на противоположный, если основание больше единицы – знак неравенства остается прежним.

3. Решить полученное неравенство.

4. Записать результат.

Показательные неравенства, которые можно разложить на множители или сделать замену переменной.

1. Для данного метода во всем неравенстве по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.

2. Сделать замену переменной $a^{f(x)}=t, t>0$.

3. Получаем рациональное неравенство, которое можно решить методом интервалов путем разложения на множители выражения.

4. Делаем обратную замену с учетом того, что $t>0$. Получаем простейшее показательное неравенство $a^{f(x)}=t$, решаем его и результат записываем в ответ.

Уравнения с многочленами

Многочлен может обозначаться записью $Р(х)$ — это означает, что многочлен зависит от «х», если записать $Р(х+1)$ — это означает, что в многочлене вместо «х» надо сделать замену на скобку $(х+1)$

Системы иррациональных уравнений

Основные методы решения систем, содержащих иррациональные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – надо расписать ОДЗ каждого уравнения, а в конце решения выбрать решение системы с учетом ОДЗ.

Чтобы решить иррациональное уравнение, необходимо:

1. Преобразовать заданное иррациональное уравнение к виду

$√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$

2. Обе части уравнение возвести в квадрат

$√{f(x)}^2={g(x)}^2$ или $√{f(x)}^2=√{g(x)}^2$

3. Решить полученное рациональное уравнение.

4. Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)

16
Сен 2022

Категория: 10 Графики функций

2022-09-16
2022-09-16

Задача 1. На рисунке изображён график функции   Найдите

Решение: + показать

---

Задача 2. На рисунке изображён график функции   Найдите

Решение: + показать

---

Задача 3. На рисунке изображён график функции   Найдите

Решение: + показать

---

Задача 4. На рисунке изображён график функции   Найдите

Решение: + показать

---

Задача 5. На рисунке изображён график функции   Найдите

Решение: + показать

---

Задача 6. На рисунке изображён график функции где и – целые.  Найдите

Решение: + показать

---

Задача 7. На рисунке изображён график функции где и – целые.  Найдите

Решение: + показать

---

Пройти тест

Автор: egeMax |

Нет комментариев

Чтобы найти (displaystyle fbigg(frac{pi}{6}bigg){small,}) найдём сначала неизвестные коэффициенты (displaystyle a) и (displaystyle b{small.})

Для этого составим систему уравнений относительно (displaystyle a) и (displaystyle b) и решим её.

Заметим, что точки, отмеченные на графике функции (displaystyle f(x)=asin x +b{ small ,})
имеют координаты (displaystyle Big(color{blue}{0};color{blue}{-frac{1}{2}}Big)) и (displaystyle Big(color{green}{frac{pi}{2}};color{green}{1}Big){small .})

Значит,

• при подстановке координат (displaystyle x=color{blue}{0}) и (displaystyle y=color{blue}{-frac{1}{2}}) в уравнение (displaystyle y=asin x +b) получим верное равенство;
• при подстановке координат (displaystyle x=color{green}{frac{pi}{2}}) и (displaystyle y=color{green}{1}) в уравнение (displaystyle y=asin x +b) получим верное равенство.

Таким образом, получаем систему уравнений:

(displaystyle left{begin{aligned}color{blue}{-frac{1}{2}}&=acdot sin color{blue}{0}+b{ small ,}\color{green}{1}&=acdot sincolor{green}{frac{pi}{2}}+b{ small .}end{aligned}right. )

Подставим вместо  (displaystyle sin color{blue}{0}) и (displaystyle sincolor{green}{frac{pi}{2}}) их значения.

(displaystyle sin{0}=0) 

(displaystyle sin frac{pi}{2}=1) 

Подставляя, получаем:

(displaystyle left{begin{aligned}{-frac{1}{2}}&=acdot 0+b{ small ,}\{1}&=acdot1+bend{aligned}right. )

или

(displaystyle left{begin{aligned}{-frac{1}{2}}&=b{ small ,}\{1}&=a+b{ small .}end{aligned}right. )

Решим полученную систему уравнений.

Решение данной системы уравнений (displaystyle a=frac{3}{2}) и (displaystyle b=-frac{1}{2})

Тогда исходная функция имеет вид:

(displaystyle f(x)=frac{3}{2}sin x -frac{1}{2}{ small .}) 

Найдём (displaystyle fbigg(frac{pi}{6}bigg){ small:})

(displaystyle fbigg(frac{pi}{6}bigg)=frac{3}{2}cdot sin frac{pi}{6} -frac{1}{2}{ small .}) 

Значение (displaystyle sin frac{pi}{6} )– табличное. Подставим его:

Подсказка – табличные значения

(displaystyle fbigg(frac{pi}{6}bigg)=frac{3}{2}cdot sin frac{pi}{6} -frac{1}{2}= frac{3}{2}cdot frac{1}{2} -frac{1}{2}=frac{3}{4}-frac{2}{4}=frac{1}{4}=0{,}25{small.})

Ответ: (displaystyle fbigg(frac{pi}{6}bigg)=0{,}25{small.})

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 60    1–20 | 21–40 | 41–60

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 60    1–20 | 21–40 | 41–60

Методические материалы по математике, нацеленные главным образом на подготовку к ЕГЭ.

Алгебра и анализ

Метод интервалов: interval.pdf
Уравнения и неравенства с модулем: modul.pdf
Что такое функция: function.pdf
Чтение графика функции: grafik.pdf
Степени и корни: power.pdf
Производная: der.pdf
Геометрический смысл производной: dergeom.pdf

Тригонометрия

Тригонометрический круг: trigcircle.pdf
Тригонометрические формулы: trigform.pdf
Простейшие тригонометрические уравнения. 1: treq1.pdf
Простейшие тригонометрические уравнения. 2: treq2.pdf
Тригонометрические уравнения: trigequations.pdf
Углы в тригонометрии: trigangles.pdf Задачи: protrigangles.pdf
Тригонометрическая окружность: trigok.pdf Задачи: protrigok.pdf
Тригонометрические функции. Синус и косинус: sincos.pdf
Тригонометрические функции. Тангенс и котангенс: tangens.pdf Задачи: protrigfun.pdf
Основное тригонометрическое тождество: ott.pdf Задачи: proott.pdf
Формулы сложения: fadd.pdf Задачи: profadd.pdf
Формулы приведения: fpriv.pdf Задачи: profpriv.pdf
Формулы двойного и половинного угла: fda.pdf Задачи: profda.pdf
Суммы и произведения тригонометрических функций: trigsum.pdf Задачи: protrigsum.pdf
Тригонометрические формулы (резюме): trigform.pdf
Обратные тригонометрические функции: trigeqprost.pdf
Тригонометрические уравнения: trigequations.pdf

Планиметрия

О первичных понятиях, или Зачем аксиомы в геометрии: primaries.pdf

Стереометрия

Многогранники в задаче С2: sm.pdf
Пирамида: piramida.pdf
Призма: prizma.pdf
Взаимное расположение прямых в пространстве: ll.pdf
Угол между скрещивающимися прямыми: lla.pdf Задачи: prolla.pdf
Взаимное расположение прямой и плоскости: lp.pdf
Теорема о трёх перпендикулярах: ttp.pdf
Угол между прямой и плоскостью: lpa.pdf Задачи: lpa.pdf
Взаимное расположение плоскостей: pp.pdf
Угол между плоскостями: ppa.pdf Задачи: proppa.pdf
Расстояние от точки до прямой: dpl.pdf Задачи: prodpl.pdf
Расстояние от точки до плоскости: dpp.pdf Задачи: prodpp.pdf
Расстояние между скрещивающимися прямыми: dll.pdf Задачи: prodll.pdf
Метод объёмов: vol.pdf
Задачи на сечения многогранников: prosec.pdf

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Самый наглядный способ представления информации – графический. Этот тезис применим и в математике. А при правильном подходе график может дать гораздо больше информации о поведении функции, чем просто положении точек на координатной плоскости.

Что может рассказать график $ y=f(x) $?

1. Область определения функции – значения аргумента $ x $, которые можно «подать на вход». Аргумент откладывается на горизонтальной оси.

2. Область значения функции – значения функции $ y $, получаемые «на выходе». Значения отмечаются на вертикальной оси.

3. Непрерывность функции. Для всех ли аргументов существуют значения?

4. Промежутки монотонности функции (возрастания или убывания).

Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции то есть  $ x_{1} < x_{2}Rightarrow y_{1} < y_{2} $.

Если же большему значению аргумента соответствует меньшее значение функции (то есть  $ x_{1} < x_{2}Rightarrow y_{1} > y_{2} $), то функция называется убывающей.

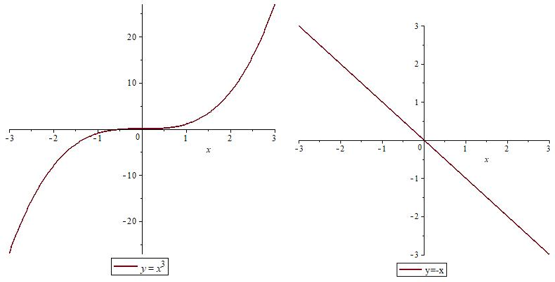
Существуют функции, которые всегда возрастают (например,  $ y=x^{3} $) или всегда убывают (например,  $ y=-x $).

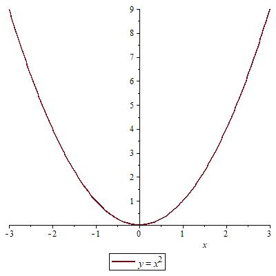
Но чаще функции имеют несколько промежутков возрастания и убывания. Например, функция  $ y=x^{2} $ убывает при  $ x in (0; +infty) $ и возрастает при  $ x in (- infty; 0) $.

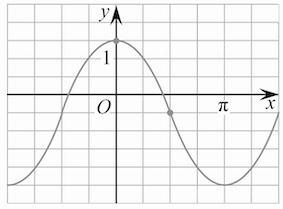
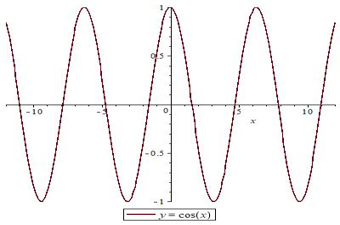
А график функции косинус имеет множество таких промежутков, сменяющих друг друга.

5. Точки минимума и максимума.

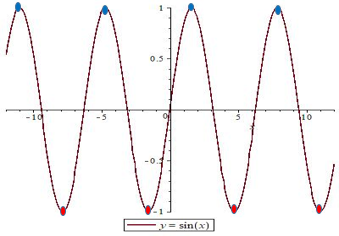
Значения аргумента, в которых функция перестает возрастать и начинает убывать, называются точками максимума. Если же в них, наоборот, функция перестает убывать и начинает возрастать – точками минимума. На графике  $ y = sin(x) $ красным отмечены точки минимума, синим – максимума.

Всегда возрастающие и убывающие функции таких точек не имеют.

6. Ограниченность функции. Есть ли значения, за которые функция «не заходит»?

Функции могут быть неограниченными; ограниченными сверху, снизу, слева, справа, а также сразу с нескольких сторон.

Уже знакомая нам функция косинуса, например, ограничена и сверху, и снизу. Парабола  $ y=x^{2} $ ограничена снизу. А график функции  $ y=x^{3} $неограничен нигде.

7. Четность функции.

Функция называется четной, если выполняется равенство  $ f(-x)=f(x) $. Такой функцией является парабола  $ y=x^{2} $ так как верно, что  $ -x^{2} = x^{2} $. Наглядным признаком четности является симметрия графика относительно оси ОY.

Если выполняется равенство $ f(-x)=-f(x) $, то функция считается нечетной. Примером такого типа функций может служить кубическая парабола  $ y=x^{3} $ для которой  $ (-x)^{3} = -x^{3} $. График нечетной функции будет симметричен относительно начала координат.

Не всякую функцию можно отнести одной из этих групп. Если не выполняется ни одно из названных условий, говорят, что функция не обладает четностью.

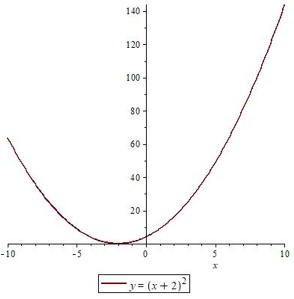
Рассмотрим функцию $ y = (x+2)^{2} $ и исследуем ее $ на четность.

$ y(-x) = (-x+2)^{2} = (-1(x-2))^{2} = (-1)^{2} cdot (x-2)^{2} = (x-2)^{2} $

Видно, что   $ (x-2)^{2} neq (x+2)^{2} = y(x);$ и $ (x-2)^{2} neq -(x+2)^{2} = -y(x) $

То есть данная функция не является ни четной, ни нечетной.

8. Периодичность функции.

Если с какого-то момента график функции начинает повторяться, то такая функция называется периодичной. Таким свойством обладают все тригонометрические функции.

Помимо вышеназванных свойств у функций и их графиков есть особенные признаки, которые позволяют быстро и схематично их изобразить. Рассмотрим самые часто встречающиеся в математике зависимости.

Линейная функция

Формула	$ y=kx+b, k neq 0 $
График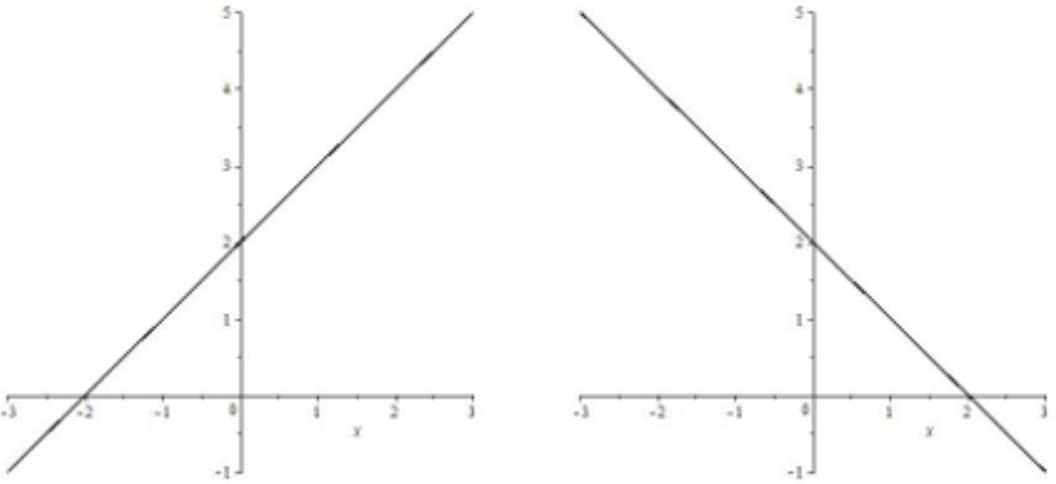
Особые свойства	$ k=tga $ тангенс угла наклона, $ b $ точка пересечения с $ OY $
Область определения	$ R $
Область значения	$ R $
Непрерывность	да
Монотонность	$ k > 0 $ — возростает, $ k < 0 $ — убывает
Точки минимума и максимума	нет
Ограниченность	неограничено
Четность	нечетная
Периодичность	нет

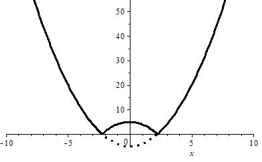
Квадратичная функция (парабола)

Формула	$ y=ax^{2}+bx+c, a neq 0 $
График
Особые свойства	$ a > 0 $ ветви направлены вверх, $ a < 0 $ $ b $ — точка пересечения с $ OY $ $ x_{вершины}=frac{-b}{2a} $
Область определения	$ R $
Область значения	$ R $
Непрерывность	да
Монотонность	При $ a > 0 (-infty;x_{вершины}) $ — убывает $ x_{вершины};+infty $ — возростает. При $ a < 0 $ — наоборот.
Точки минимума и максимума	$ a > 0 x_{вершины} $ — точка минимума, при $ a < 0 $ — максимума
Ограниченность	При $ a > 0 $ ограничена снизу, при $ a < 0 $ — сверху
Четность	$ b=0 $ — четная, $ b neq 0 $ — не обладает четностью
Периодичность	нет

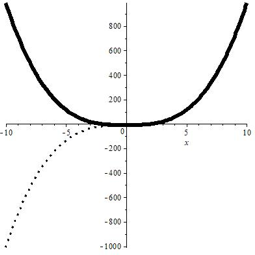
Кубическая парабола

Формула	$ y=ax^{3}+b, a neq 0 $
График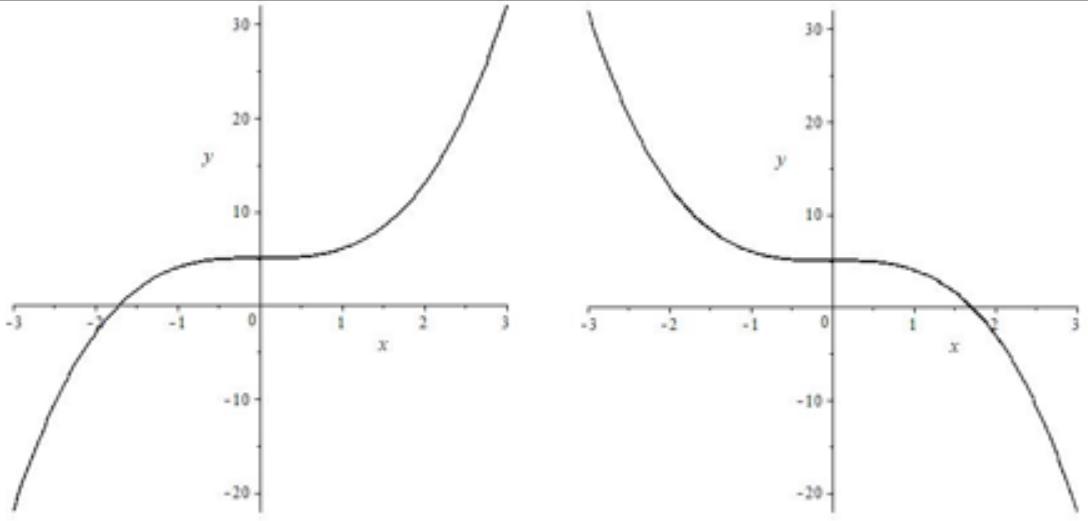
Особые свойства	$ b $ — точка пересечения с $ OY $
Область определения	$ R $
Область значения	$ R $
Непрерывность	да
Монотонность	При $ a > 0 $ — возростает, $ a < 0 $ — убывает.
Точки минимума и максимума	нет
Ограниченность	Неограничена
Четность	$ b=0 $ — нечетная, иначе — не обладает четностью
Периодичность	нет

Квадратный корень

Формула	$ y=a sqrt {x}, a neq 0 $
График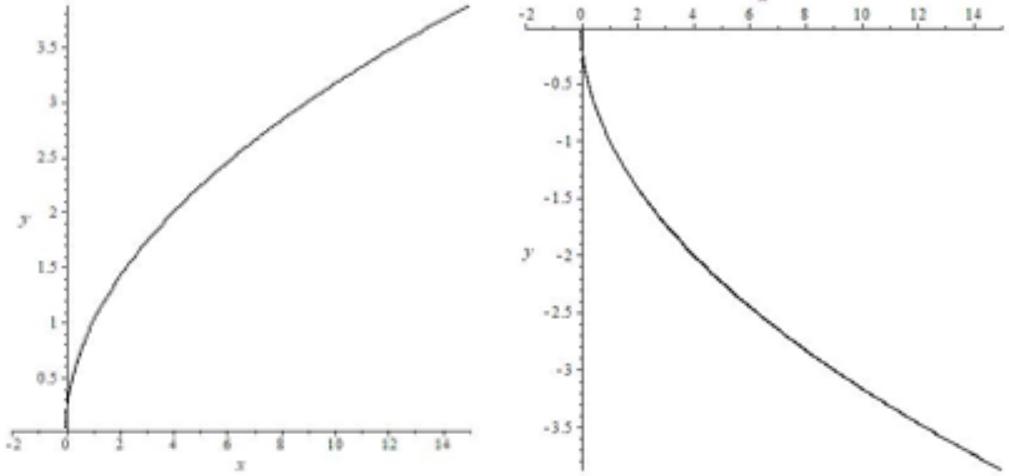
Особые свойства	График располагается справа от нуля
Область определения	$ x geq 0 $
Область значения	$ a geq 0 Rightarrow y geq 0 $ $ a leq 0 Rightarrow y leq 0 $
Непрерывность	да
Монотонность	При $ a > 0 $ — возростает, $ a < 0 $ — убывает.
Точки минимума и максимума	$ a > 0 — x = 0 $ точка минимума, $ a < 0 — x = 0 $ точка максимума
Ограниченность	При $ a > 0 $ ограничена снизу и слева, при $ a < 0 $ — сверху и слева
Четность	Не обладает четностью
Периодичность	нет

Гипербола

Формула	$ y= frac{k}{x}, k neq 0 $
График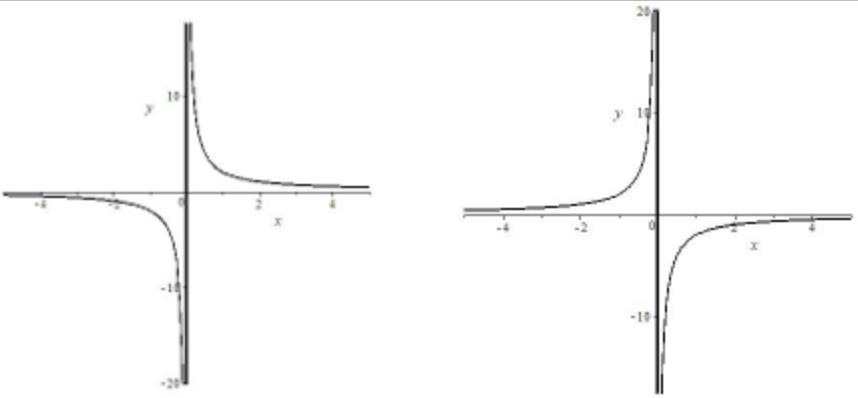
Особые свойства	График имеет 2 асимптоты (прямые, к которым бесконечно приближается, но никогда не пересекает) $ x=0, y=0 $
Область определения	$ x neq 0 $
Область значения	$ y neq 0 $
Непрерывность	Разрыв в точке $ x neq 0 $
Монотонность	$ k > 0 $ убывает $ (-infty ; 0) $, возрастает $ (0;+infty) $ \ $ k < 0 $ возрастает $ (-infty ; 0) $, убывает $ (0;+infty) $
Точки минимума и максимума	нет
Ограниченность	Неограничена
Четность	Нечетная
Периодичность	Нет

Окружность

Формула	$ (x-a)^{2} + (y-b)^{2}= R^{2} $
График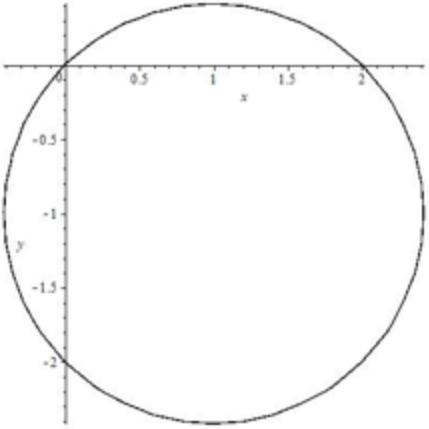
Особые свойства	Центр окружности в точке $ a, b $, радиус $ R $
Область определения	$ R $
Область значения	$ R $
Непрерывность	Да
Монотонность
Точки минимума и максимума	нет
Ограниченность	С 4 сторон
Четность	При $ a=b=0 $ — четная, иначе не обладает четностью
Периодичность	Нет

Показательная функция

Формула	$ y=a^{x}, a > 0, a neq 1 $
График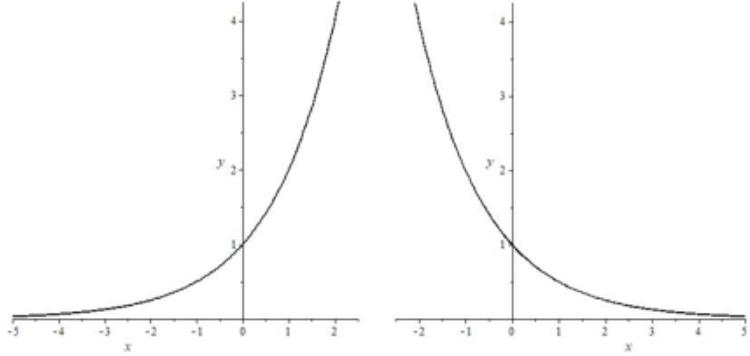
Особые свойства	Все показательные функции проходят через точку (0,1)
Область определения	$ R $
Область значения	$ (0;+infty) $
Непрерывность	Да
Монотонность	$ a > 1 $ — возрастает, $ 0 < a < 1 $ — убывает
Точки минимума и максимума	нет
Ограниченность	Ограничена с низу
Четность	Не обладает четностью
Периодичность	Нет

Логарифмическая функция

Формула	$ y=log_{a}x, a > 0, a neq 1 $
График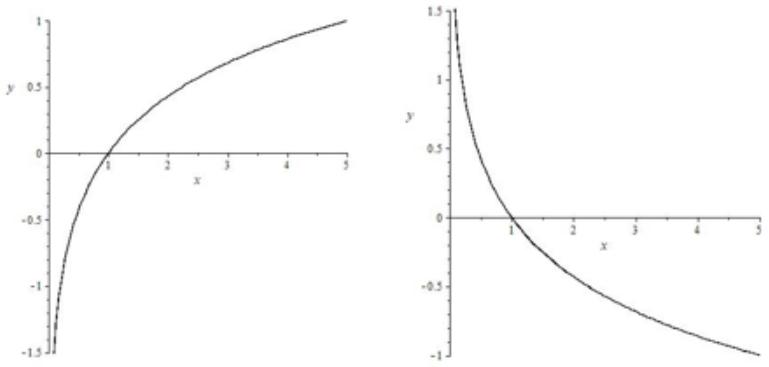
Особые свойства	Все показательные функции проходят через точку (1,0)
Область определения	$ (0;+infty) $
Область значения	$ R $
Непрерывность	Да
Монотонность	$ a > 1 $ — возрастает, $ 0 < a < 1 $ — убывает
Точки минимума и максимума	нет
Ограниченность	Нет
Четность	Нет
Периодичность	Нет

Синус

Формула	$ y=sin(x) $
График
Особые свойства
Область определения	$ R $
Область значения	[-1;1]
Непрерывность	Да
Монотонность	Да
Точки минимума и максимума	Точки минимума $ frac{pi}{2}+2pi k, kin Z $, точки минимума $ -frac{pi}{2}+2pi k, kin Z $
Ограниченность	Сверху и снизу
Четность	Нечетная
Периодичность	Период $ 2pi $

Косинус

Формула	$ y=cos(x) $
График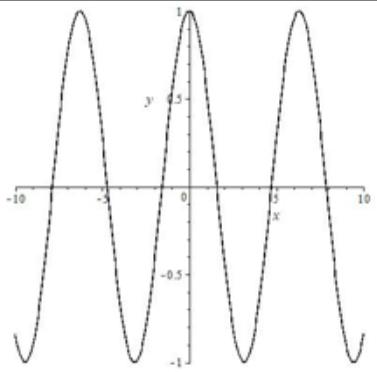
Особые свойства
Область определения	$ R $
Область значения	[-1;1]
Непрерывность	Да
Монотонность	Да
Точки минимума и максимума	Точки минимума $ 2pi k, kin Z $, точки минимума $ pi+2pi k, kin Z $
Ограниченность	Сверху и снизу
Четность	Четная
Периодичность	Период $ 2pi $

Тангенс

Формула	$ y=tgx $
График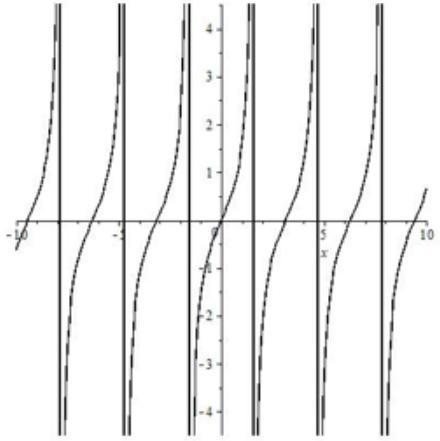
Особые свойства	Имеет бесконечное число асимптот
Область определения	$ x neq frac{pi}{2}+pi k, kin Z $
Область значения	$ R $
Непрерывность	Разрыв в точках $ (-frac{pi}{2}+pi k; frac{pi}{2}+pi k), k in Z $
Монотонность	Возрастает на каждом промежутке $ x neq frac{pi}{2}+pi k, kin Z $
Точки минимума и максимума	Нет
Ограниченность	Нет
Четность	Четная
Периодичность	Период $ pi $

Котангенс

Формула	$ y=ctgx $
График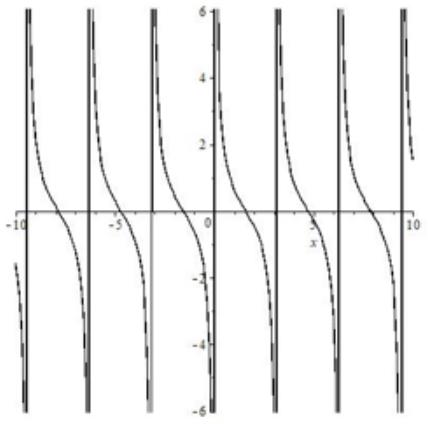
Особые свойства	Имеет бесконечное число асимптот
Область определения	$ x neq pi k, kin Z $
Область значения	$ R $
Непрерывность	Разрыв в точках $ x = pi k, kin Z $
Монотонность	Убывает на каждом промежутке $ (pi k, pi + pi k), k in Z $
Точки минимума и максимума	Нет
Ограниченность	Нет
Четность	Нечетная
Периодичность	Период $ pi $

Преобразование графиков функции

График любой зависимости можно построить по точкам. Но в некоторых случаях гораздо проще преобразовать график какой-либо известной функции с помощью сдвигов, отражений и растяжений.

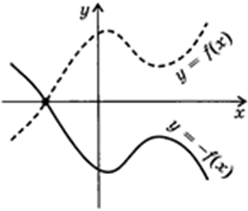
1. Симметрия относительно оси  $ OX: f(x) rightarrow — f(x) $

Все абсциссы остаются неизменными, а все ординаты меняют знак на противоположный.

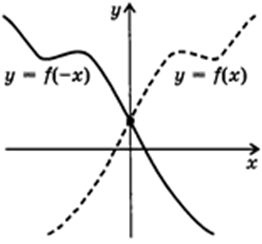
2. Симметрия относительно оси  $ OY: f(x) rightarrow f(-x) $

Все ординаты графика остаются неизменными, а абсциссы меняют знак на противоположный.

При таком преобразовании четной функции, график остается неизменным.

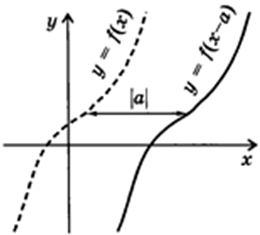
3. Сдвиг вдоль оси $ OX: f(x) rightarrow f(x-a) $

Ординаты остаются неизменными, а абсциссам прибавляется  $ a $. Если  $ a > 0 $, то график сдвигается вправо, иначе – влево.

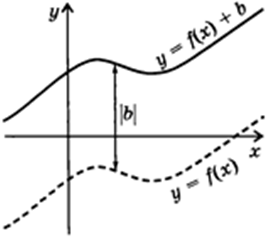
4. Сдвиг вдоль оси  $ OY: f(x) rightarrow f(x)+b $

Абсциссы не меняются, а к ординатам прибавляется  $ : b $. При  $ b > 0 $ график сдвигается вверх, иначе – вниз.

Обратите внимание, что в пункте 3. перед $ a $ стоит знак «–», в то время как в 4. перед  $ b $ стоит «+». При этом знаки параметров  $ a,b $ могут быть любыми.

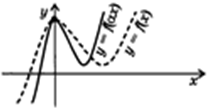
5. Сжатие и растяжение вдоль оси  $ OX: f(x) rightarrow f(ax), a > 0 $

Ординаты остаются неизменными, а абсциссы делятся на $ a $. Точки пересечения графика функции с осью  $ OY $ остаются на месте.

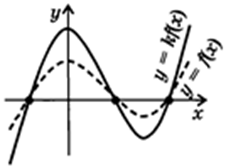
6. Сжатие и растяжение вдоль оси  $ OY: f(x) rightarrow kf(x), k > 0 $

Абсциссы остаются неизменными, а ординаты умножаются на $ k $. Точки пересечения графика функции с осью  $ OX $ остаются на месте.

7. Модуль функции: $ f(x) rightarrow|;f(x);| $

Точки с положительными ординатами остаются на месте, точки с отрицательными ординатами отбражаются симметрично относительно оси  $ OX $.

8. Модуль аргумента: $ f(x) rightarrow f(|x|) $

Точки, соответствующие отрицательным абсциссами, стираются. Точки с положительными абсциссами остаются на месте, а так же отображаются симметрично относительно оси  $ OY $. Функция становится четной.

Приведенные выше преобразования можно комбинировать и выполнять друг за другом.

Пример 1.

Построите график функции $ y=-2(x-3)^{2}+4 $.

Данный график можно получить из $ y=x^{2} $ последовательными сжатием вдоль оси  $ OY $ в 2 раза, сдвигом вдоль оси  $ OX $ на 3 вправо, сдвигом вдоль оси  $ OY $ на 4 вверх и отражением относительно оси  $ OX $.