Демонстрационная версия ЕГЭ−2023 по информатике
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 39 | 3 | |||||
| П2 | 39 | 8 | 5 | ||||
| П3 | 3 | 2 | |||||
| П4 | 8 | 53 | |||||
| П5 | 5 | 21 | 30 | ||||
| П6 | 2 | 21 | 13 | ||||
| П7 | 53 | 30 | 13 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт B и из пункта F в пункт A.
В ответе запишите целое число.
Ответ:
2
Миша заполнял таблицу истинности логической функции F
¬ (y → x) ∨ (z → w) ∨ ¬z,
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| 0 | 0 | |||
| 0 | 1 | 0 | ||
| 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
Пример. Функция F задана выражением ¬ x ∨ y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
В этом случае первому столбцу соответствует переменная y, а второму столбцу — переменная x. В ответе следует написать: yx.
Ответ:
3
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
Задание 3
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок, шт. |
Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количество в упаковке |
Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите общий вес (в кг) крахмала картофельного, поступившего в магазины Заречного района за период с 1 по 8 июня включительно.
В ответе запишите только число.
Ответ:
4
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н — 1111, З — 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны.
Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Ответ:
5
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.
Полученная таким образом запись является двоичной записью искомого числа R.
Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе запишите это число в десятичной системе счисления.
Ответ:
6
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм: Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Ответ:
7
Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла — 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
Ответ:
8
Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6.
Ответ:
9
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел.
Задание 9
Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
— в строке только одно число повторяется ровно два раза, остальные числа различны;
— среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.
В ответе запишите только число.
Ответ:
10
Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует. В ответе запишите только число.
Задание 10
Ответ:
11
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число — количество Кбайт.
Ответ:
12
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке.
Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.
Ответ:
13
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
Ответ:
14
Операнды арифметического выражения записаны в системе счисления с основанием 15:
123x515 + 1x23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Ответ:
15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A ≥ 100)
тождественно истинна (т. е. принимает значение 1) при любом натуральном значении переменной х?
Ответ:
16
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n · F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?
Ответ:
17
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от −10 000 до 10 000 включительно. Определите количество пар последовательности, в которых только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Задание 17
Ответ:
18
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
18.xlsx
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 38 и 22.
Ответ:
19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 129 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Ответ:
20
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 129 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Ответ:
21
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 129 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
Ответ:
22
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы — время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) |
ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1; 2 |
| 4 | 7 | 3 |
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Выполните задания, используя данные из файла ниже:
Задание 22
Ответ:
23
Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Программа для исполнителя — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Ответ:
24
Текстовый файл состоит из символов A, C, D, F и O.
Определите максимальное количество идущих подряд пар символов вида
согласная + гласная.
Для выполнения этого задания следует написать программу.
24.txt
Ответ:
25
Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:
— символ «?» означает ровно одну произвольную цифру;
— символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность.
Например, маске 123*4?5 соответствуют числа 123405 и 12300405.
Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце — соответствующие им результаты деления этих чисел на 2023.
Количество строк в таблице для ответа избыточно.
26
В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки — подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т. д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки.
Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные.
Задание 26
В первой строке входного файла находится число N — количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое — в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Пример входного файла:
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы.
При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т. е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Ответ:
27
У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные
Файл A
Файл B
Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) — количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем — для файла B.
Пример организации исходных данных во входном файле:
6
1 100
2 200
5 4
7 3
8 2
10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит:
1 · 2 + 3 · 1 + 5 · 1 + 6 · 1 + 8 · 2.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
Старый каталог
Каталог заданий по типам по темам
?
1. Анализ информационных моделей
49
2. Построение таблиц истинности логических выражений
60
3. Поиск информации в реляционных базах данных
23
4. Кодирование и декодирование информации
70
5. Анализ и построение алгоритмов для исполнителей
81
6. Определение результатов работы простейших алгоритмов
31
7. Кодирование и декодирование информации. Передача информации
64
8. Перебор слов и системы счисления
144
10. Поиск символов в текстовом редакторе
36
11. Вычисление количества информации
121
12. Выполнение алгоритмов для исполнителей
76
13. Поиск путей в графе
177
14. Кодирование чисел. Системы счисления
96
15. Преобразование логических выражений
100
16. Рекурсивные алгоритмы
87
17. Обработки числовой последовательности
36
19. Выигрышная стратегия. Задание 1
110
20. Выигрышная стратегия. Задание 2
110
21. Выигрышная стратегия. Задание 3
110
22. Многопроцессорные системы
36
23. Оператор присваивания и ветвления. Перебор вариантов, построение дерева
84
24. Обработка символьных строк
37
25. Обработка целочисленной информации
36
26. Обработка целочисленной информации
35
Дополнительные задания для подготовки
Задания Д1. Анализ информационных моделей
106
Задания Д1. Кодирование и операции над числами в разных системах счисления
90
Задания Д2. Кодирование цвета
4
Задания Д2. Построение таблиц истинности логических выражений
26
Задания Д3. Анализ информационных моделей
30
Задания Д3. Базы данных. Файловая система
159
Задания Д4. Базы данных. Файловая система
2
Задания Д4. Кодирование и декодирование информации
54
Задания Д5. Анализ и построение алгоритмов для исполнителей
106
Задания Д5. Разные задачи
1
Задания Д6. Анализ программ
184
Задания Д6. Символьные строки
9
Задания Д7. Анализ диаграмм и электронных таблиц
171
Задания Д7. Базы данных. Файловая система
91
Задания Д7. Кодирование и декодирование информации. Передача информации
127
Задания Д8. Кодирование и декодирование информации
54
Задания Д8. Перебор слов и системы счисления
54
Задания Д9. Анализ и построение алгоритмов для исполнителей
85
Задания Д10. Анализ диаграмм и электронных таблиц
76
Задания Д11. Вычисление количества информации
69
Задания Д11. Кодирование и декодирование информации. Передача информации
77
Задания Д12. Выполнение алгоритмов для исполнителей
103
Задания Д12. Организация компьютерных сетей. Адресация
155
Задания Д12. Построение таблиц истинности логических выражений
91
Задания Д13. Выполнение алгоритмов для исполнителей
30
Задания Д14. Запросы для поисковых систем с использованием логических выражений
49
Задания Д14. Кодирование чисел. Системы счисления
51
Задания Д15. Преобразование логических выражений
44
Задания Д16. Обработка массивов и матриц
44
Задания Д16. Рекурсивные алгоритмы
81
Задания Д17. Анализ программы с циклами и условными операторами
1
Задания Д17. Запросы для поисковых систем с использованием логических выражений
118
Задания Д18. Оператор присваивания и ветвления
32
Задания Д19 C4. Обработка символьных строк
60
Задания Д19. Обработка массивов и матриц
93
Задания Д21. Анализ программ с циклами и подпрограммами
72
Задания Д22. Анализ программы с циклами и условными операторами
109
Задания Д23. Логические уравнения
116
Задания Д23. Оператор присваивания и ветвления. Перебор вариантов, построение дерева
9
Задания Д24 C1. Исправление ошибок в программе
153
Задания Д25 C2. Алгоритмы обработки массивов
185
Задания Д26 C3. Выигрышная стратегия
152
Задания Д27 C4. Программирование
122
Подборка тренировочных вариантов ЕГЭ 2023 по информатике для 11 класса из различных источником с ответами.
Соответствуют демоверсии 2023 года.
→ тренировочные варианты ЕГЭ по информатике прошлого года
Тренировочные варианты ЕГЭ 2023 по информатике
Ссылки на доп. файлы находятся в вариантах.
| vk.com/ege100ballov | ||
| Вариант 2 | скачать | |
| Вариант 3 | скачать | |
| Вариант 4 | скачать | |
| Вариант 5 | скачать | |
| Вариант 6 | скачать | |
| Вариант 7 | скачать | |
| vk.com/inform_web | ||
| Вариант 1 (уровень сложности — простой) | скачать | |
| Вариант 2 (уровень сложности — простой) | скачать | разбор |
| Вариант 3 (уровень сложности — простой) | скачать | разбор |
| Вариант 4 (уровень сложности — обычный) | скачать | |
| Вариант 5 (уровень сложности — обычный) | скачать |
Примеры заданий:
1. Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.
2. На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N. К этой записи дописываются справа ещё два разряда по следующему правилу:
2) Если число чётное, в конец числа (справа) дописывается 1, в противном случае справа дописывается 0.
3) Предыдущий пункт повторяется для записи с добавленной цифрой. Например, двоичная запись 1001 числа 9 будет преобразована в 100101.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.
Укажите максимальное число N, для которого результат работы алгоритма будет меньше 171. В ответе это число запишите в десятичной системе счисления.
3. Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
4. На вход регистратору поступает одно из 1500 значений. Каждое значение записывается в память компьютера с помощью одинакового и минимально возможного количества бит. Сколько бит понадобится для хранения 153 измерений?
5. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может увеличить количество камней в два раза или в три раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 100. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в куче будет 100 или больше камней. В начальный момент в куче S камней; 1 ≤ S ≤ 99.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети.
Укажите минимальное значение S, когда такая ситуация возможна
Связанные страницы:
1.
1 задание. Демо ЕГЭ 2023 информатика, ФИПИ:
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| 1 | — | 39 | 3 | ||||
| 2 | 39 | — | 8 | 5 | |||
| 3 | 3 | — | 2 | ||||
| 4 | 8 | — | 53 | ||||
| 5 | 5 | — | 21 | 30 | |||
| 6 | 2 | 21 | — | 13 | |||
| 7 | 53 | 30 | 13 | — |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова сумма протяжённостей дорог из пункта D в пункт B и из пункта F в пункт A.
В ответе запишите целое число.
Ответ: 58
🎦 Видео на RuTube
✍ Решение:
- Рядом с каждой вершиной проставим количество ребер вершины и в скобках — количество ребер у «соседей»:
- Выберем уникальные вершины, значения которых вместе с соседними вершинами отличаются от всех:
B = 2(3,3) A = 3(3,3,3)
B 2(3,3):Найдем строки в таблице с двумя вершинами:
№1: 39 и 3 = 2(3,2) , т.к. 1 сосед =(39,8,5) и 2 сосед=2(3,2). Данная строка не подходит, так как мы ищем 2(3,3)
№3: 3 и 2 = 3(2,2) не подходит
№4: 8 и 53 = 2(3,3) => B = №4
А 3(3,3,3):Найдем строки в таблице с двумя вершинами:
№2: 39 и 8 и 5 = 3(3,2,3) не подходит
№5: 5 и 21 и 30 = 3(3,3,3) => A = №5
B, и видим соседей — D(2,3,3) и F(2,2,3).№4=B пересекается с №2(2,2,3) и №7(2,3,3). Делаем вывод, что №2=F, №7=D.DB=53, FA=5 53+5 = 58
Ответ: 58
2.
2 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Миша заполнял таблицу истинности логической функции F
¬(y → x) ∨ (z → w) ∨ ¬z
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | |||
| 0 | 1 | 0 | ||
| 1 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.).
Ответ: yxzw
Решение подобного задания (теоретическое):
🎦 RuTube
3.
3 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок внесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок | Цена |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Единица измерения | Количество в упаковке | Производитель |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите общий вес (в кг) крахмала картофельного, поступившего в магазины Заречного района за период с 1 по 8 июня включительно.
В ответе запишите только число.
Ответ: 355
🎦 Видео на RuTube здесь
4.
4 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны:
Н – 1111 З – 110
Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны.
Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Ответ: 14
🎦 Видео на RuTube здесь
5.
5 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.
Полученная таким образом запись является двоичной записью искомого числа R.
Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе это число запишите в десятичной системе счисления.
Ответ: 16
🎦 Видео на RuTube здесь (программирование Pascal)
🎦 Видео на RuTube здесь (аналитическое решение)
6.
6 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды:
Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова,
и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.
1. Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным
алгоритмом. Точки на линии учитывать не следует.
ИЛИ:
2. Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90] Поднять хвост Вперёд 3 Направо 90 Вперёд 5 Налево 90 Опустить хвост Повтори 2 [Вперёд 70 Направо 90 Вперёд 80 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными
алгоритмом линиями, включая точки на границах этого пересечения.
Ответ:1. 38 ИЛИ 2. 128
7.
7 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось.
Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
Ответ: 98
✍ Решение:
- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:
I = β * ƒ * t * S
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов
1 состояние: S = 1 канал I = 28 Мбайт 2 состояние: S = 2 канала β = в 3,5 раза выше ƒ = в 2 раза ниже I = ?
S), а стало два канала связи, то файл увеличился в 2 раза:I = I * 2
β) увеличилась в 3,5 раза, то и объем (I) увеличится в 3,5 раза (пропорциональная зависимость):I = I * 3,5
ƒ) уменьшилась в 2 раза, значит, объем (I) тоже уменьшится в 2 раза:I = I / 2
I = 28 Мбайт * 2 * 3,5 / 2 = 98 Мбайт
Ответ: 98
8.
8 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Ответ: 2961
Видео на RuTube здесь
9.
9 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
В ответе запишите только число.
Ответ: 2241
🎦 Видео на RuTube здесь (Excel)
10.
10 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует.
В ответе запишите только число.
Ответ: 45
11.
11 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.
Ответ: 22016
✍ Решение:
- Основной формулой для решения данной задачи является:
- Чтобы найти количество бит, необходимое для хранения одного идентификатора, для начала нужно найти количество бит, необходимых для хранения 1 символа в идентификаторе. По формуле получаем:
Q = 2N
где Q — количество вариантов символов, которые можно закодировать с помощью N бит.
1650+10 = 2N -> N ~ 11 бит (т.к. 10 мало)
250 * 11 = 2750 бит всего на идентификатор
2750 бит / 8 =343,75 ~ 344 байт
344 * 65536 : 210 => выразим в степени двойки => 65536 =216 344 * 216 : 210 = 344*26 = 22016
Ответ: 22016
12.
12 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Дана программа для Редактора:
НАЧАЛО ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0) ЕСЛИ нашлось (>1) ТО заменить (>1, 22>) КОНЕЦ ЕСЛИ ЕСЛИ нашлось (>2) ТО заменить (>2, 2>) КОНЕЦ ЕСЛИ ЕСЛИ нашлось (>0) ТО заменить (>0, 1>) КОНЕЦ ЕСЛИ КОНЕЦ ПОКА КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке.
Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.
Ответ: 5
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
begin for var n := 1 to 1000 do begin var s := '>' + 39 * '0' + n * '1' + 39 * '2'; while ('>1' in s) or ('>2' in s) or ('>0' in s) do begin if '>1' in s then s := s.Replace('>1', '22>', 1); if '>2' in s then s := s.Replace('>2', '2>', 1); if '>0' in s then s := s.Replace('>0', '1>', 1); end; var sum := s.CountOf('1') + s.CountOf('2') * 2; var isPrime := true; for var i := 2 to sum - 1 do begin if sum.Divs(i) then begin isPrime := false; break end; end; if isPrime then begin print(n); exit; end; end; end. |
🎦 Видео на RuTube здесь
13.
13 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
Ответ: 21
14.
14 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Операнды арифметического выражения записаны в системе счисления с основанием 15.
123x515 + 1x23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления.
Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Ответ: 8767
🎦 Видео решения на Паскале (RuTube) здесь
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
uses school; begin foreach var x in '0123456789abcde' do begin var a := dec('123' + x + '5', 15); var b := dec('1' + x + '233', 15); var sum := a + b; if sum mod 14 = 0 then begin print(sum / 14); break; end end; end. |
| Python: |
| С++: |
15.
15 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A ≥ 100)
тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х?
Ответ: 94
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 2 = 0) <= (x mod 3 <> 0)) or (x + A >= 100)) =false then begin ok := 0; break; end; end; if (ok = 1) then print(A) end; end. |
Питон:
1 2 3 4 5 6 |
for A in range(1,1000): OK = 1 for x in range(1,1000): OK *= ((x % 2 == 0) <= (x % 3 != 0)) or (x + A >= 100) if OK: print( A ) |
C++:
16.
16 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1; F(n) = n × F(n − 1), если n > 1
Чему равно значение выражения F(2023) / F(2020)?
Ответ: 8266912626
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
Решается только с типом данных BigInteger!
1 2 3 4 5 6 7 8 9 10 11 |
function F(n: biginteger): biginteger; begin if n = 1 then F := 1 else if n > 1 then F := n * F(n - 1) end; begin print(F(2023)/F(2020)) end. |
Питон:
C++:
Ответ: 8266912626
17.
17 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Ответ: 180 190360573
18.
18 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщенными линиями.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
Ответ: 1099 1026
19.
19 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Ответ: 64
20.
20 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
Найденные значения запишите в ответе в порядке возрастания.
Ответ: 32 63
21.
21 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них.
Ответ: 62
22.
22 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.
Ответ: 17
✍ Решение:
-
Откроем файл и проанализируем таблицу:
- В столбце
Суказаны номера процессов, после которых запускается процесс, указанный в столбцеА. - Если в столбце
Сдля некоторой строки указан0, значит процесс этой строки запускается сразу, не ожидая выполнения других процессов. То есть, процессы 1, 2, 9 и 10 запускаются одновременно и сразу после запуска системы процессов. При этом, процесс 1 будет выполняться 4 мс (столбецВ), а, к примеру, процесс 10 будет выполняться 8 мc. - Уменьшим ширину столбцов
D:V(примерный диапазон), и пронумеруем данные столбцы, начиная с 1, используя автозаполнение: - Далее, начиная с процессов, которые запускаются параллельно (цифра
0в столбцеС), выделяем вправо количество столбцов, равное количеству миллисекунд в столбцеВ. Заливаем их цветом: - Затем в столбце
Сищем те строки, в которых используются уже заполненные процессы. Так, процесс №3 запускается последовательно за процессом 1 и 2. Так как процесс №1 длится дольше — 4 мс, то заливаем цветом столбцы для процесса №3 вправо, после уровня залитых ячеек для процесса №1: - Теперь можно залить цветом данные о процессах 4 и 5, так как эти процессы следуют за процессом №3.
- Следуя той же логике, закрашиваем данные по всем процессам:
- Видим, что самая крайняя справа заполненная ячейка соответствует числу 17.
23.
23 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Программа для исполнителя – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы.
Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Ответ: 98
24.
24 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Текстовый файл состоит из символов A, C, D, F и O.
Определите максимальное количество идущих подряд пар символов вида
согласная + гласная
в прилагаемом файле.
Для выполнения этого задания следует написать программу.
Ответ: 95
25.
25 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:
?» означает ровно одну произвольную цифру;*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность.Например, маске 123*4?5 соответствуют числа 123405 и 12300405.
Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им
результаты деления этих чисел на 2023.
Количество строк в таблице для ответа избыточно.
... ... ... ... ... ...
Ответ:
162139404 80148 1321399324 653188 1421396214 702618 1521393104 752048
26.
26 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д.
Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите
наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные
В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле
5 43 40 32 40 30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Ответ: 2767 51
27.
27 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
A
B
Задание выполняется с использованием прилагаемых файлов
У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера,
соответствующие расстоянию от нулевой отметки до конкретного пункта.
Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные
Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000).
Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
6 1 100 2 200 5 4 7 3 8 2 10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 · 2 + 3 · 1 + 5 · 1 + 6 · 1 + 8 · 2.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Ответ: 51063 5634689219329
ЕГЭ по информатике -> демоверсия ЕГЭ 2023
Продолжаем решать демоверсию ЕГЭ по информатике 2023.
Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
В этой статье разберём задания 16-21 из демоверсии ЕГЭ по информатике 2023.
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
Задание 16
Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?
Решение:
Если мы просто перепечатаем функцию, как мы делали на экзамене в 2022 году, то программа откажится это вычислять. Здесь слишком большая глубина рекурсии.
Тогда посмотрим внимательно на функцию. Оказывается это функция факториала. Это действие означает n! = 1*2*3*…*n.
F(2023) / F(2020) = (2023 * 2022 * 2021 * 2020!) / 2020! = 2023 * 2022 * 2021
Выражение 2020! просто сокращается. В ответе напишем 2023 * 2022 * 2021 = 8266912626.
Ответ: 8266912626
Задание 17
В файле содержится последовательность целых чисел. Элементы
последовательности могут принимать целые значения от –10 000 до 10 000
включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары
не меньше квадрата максимального элемента последовательности,
оканчивающегося на 3. В ответе запишите два числа: сначала количество
найденных пар, затем максимальную из сумм квадратов элементов таких
пар. В данной задаче под парой подразумевается два идущих подряд
элемента последовательности.
Решение:
В начале нужно найти максимальное число последовательности, оканчивающегося на 3.
f=open('17.txt') mx=-10000 for s in f.readlines(): x=int(s) if abs(x)%10==3: mx = max(mx, x) print(mx)
Получается число 9973.
Напишем основную программу:
f=open('17.txt') k=0 mx=0 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if ((abs(n1)%10==3) != (abs(n2)%10==3)) and (n1**2 + n2**2 >= 9973**2): k=k+1 mx = max(mx, n1**2 + n2**2) n1=n2 print(k, mx)
Как решать подобные задачи было рассказано в видеокурсе.
Здесь нужно помнить, что числа отрицательные. Поэтому при нахождении последней цифры, нужно использовать функцию модуля abs.
Так же здесь интересное логическое выражение «в которых только одно число оканчивается на 3». Это операция xor — отрицание равносильности.
Ответ:
Задание 18
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Решение:
Открываем файл в программе Excel.
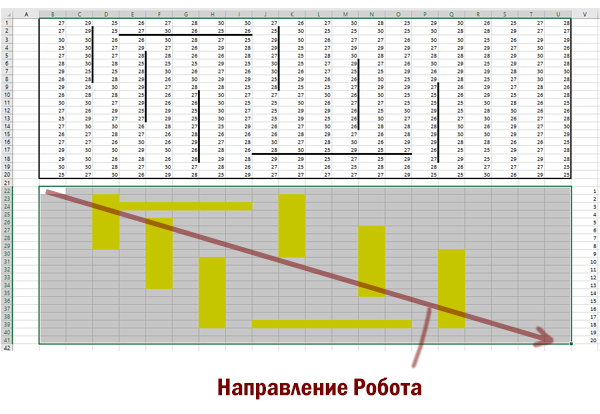
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
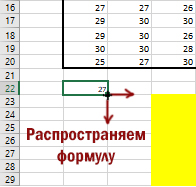
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
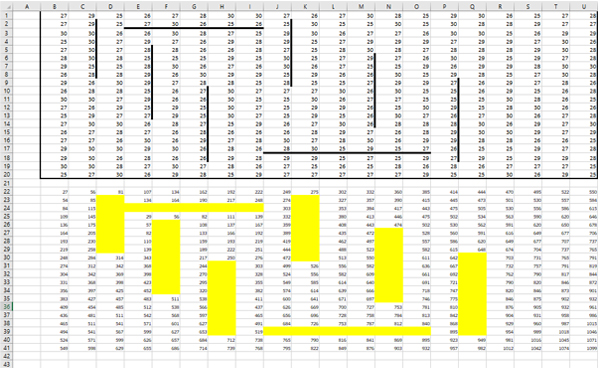
Распространим формулу на всё пространство, не трогая закрашенные клетки.
Получается такая картина:
Для вертикальных подкрашенных полосок, Робот может попасть только сверху! Поэтому пишем формулу для ячейки, к примеру, для D23:
=D22+D2
Распространяем формулу по всему закрашенному столбцу. Аналогично делаем для всех вертикальны подкрашенных полосок.
В ячейки для горизонтально подкрашенных полосок, Робот может попасть только слева! Поэтому пишем формулу, к примеру, для ячейки E24:
=D24+E3
Распространяем формулу по всей закрашенной строчке. Алагоично делаем со всеми горизонтальными полосками.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 1099.
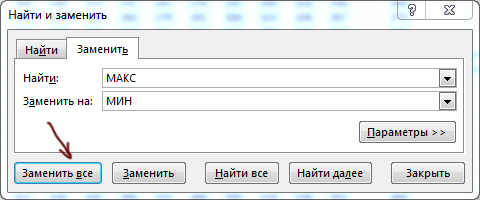
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 1026.
Ответ:
Задание 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит
куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход
игрок может добавить в кучу один камень или увеличить количество камней
в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть
неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится
не менее 129. Победителем считается игрок, сделавший последний ход,
т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может
выиграть при любых ходах противника. Описать стратегию игрока – значит
описать, какой ход он должен сделать в любой ситуации, которая ему может
встретиться при различной игре противника. В описание выигрышной
стратегии не следует включать ходы играющего по этой стратегии игрока,
не являющиеся для него безусловно выигрышными, т.е. не являющиеся
выигрышными независимо от игры противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход,
но при любом ходе Пети Ваня может выиграть своим первым ходом.
Решение:
Решим задачу с помощью шаблона на языке программирования Python. Если хотите ознакомится с аналитическим решением задач на теорию игр, можете посмотреть мои статьи по 19 Заданию, 20 Заданию, 21 Заданию. Но с помощью шаблонов на экзамене решать быстрее и легче. Об этом подходе можете найти в видеокурсе.
Введём параметр p, который будет олицетворять позицию игры (ход).
| Начальная позиция | Ход Пети | Ход Вани | Ход Пети | Ход Вани | Ход Пети | |
| p | 1 | 2 | 3 | 4 | 5 | 6 |
def F(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Заводим функцию F. Т.к. у нас одна куча, то она принимает параметры: x — количество камней в куче, p-позиция игры.
Дальше описываем победу. Если x>=29 и позиция равна 3 (1 Ход Вани), то возвращаем True, что означает победу.
Если, позиция уже равна 3, но камней меньше, чем должно быть для победы, то возвращаем False (проигрыш).
Третье условие. Если кто-то выиграл, но на первых двух условиях мы не вышли из функции, то, значит, выиграл не тот, кто нам нужен, следовательно, возвращаем Fasle.
Если мы не вышли на первых трёх условиях, то, значит, продолжаем прокручивать ходы, рекурсивно запускаем функцию F.
Для нечётных p (это ходы Вани), возвращаем разные ходы через and, т.к. он должен побеждать в любом случае. При этом увеличиваем на 1 значение p.
Для чётных p (это ходы Пети), возвращаем ходы через or.
В конце перебираем все возможные значения для s через цикл for, ищём те значения, которые подходят по условию задачи.
Ответ: 64
Задание 20
Для игры, описанной в задании 19, найдите два наименьших таких значения S, при
которых у Пети есть выигрышная стратегия, причём одновременно
выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как
будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение:
Задача точно такая же, как и в 19 задании, только теперь обязательно должен побежать Петя на своём втором ходу (p=4), при любой игре Вани.
Пишем тот же шаблон, немного отредактировав его.
def F(x, p): if x>=129 and p==4: return True if x<129 and p==4: return False if x>=129: return False if p%2==0: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Получается 32 и 63.
Ответ:
Задание 21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором
одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
Решение:
Опять используем прошлый шаблон, но немного модернизируем.
def F(x, p): if x>=129 and (p==3 or p==5): return True if x<129 and p==5: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) def F1(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F1(x+1, p+1) and F1(x*2, p+1) else: return F1(x+1, p+1) or F1(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s) print() for s in range(1, 129): if F1(s, 1): print(s)
Здесь Ваня должен выигрывать либо на первом своём ходе (p=3), либо на втором своём ходе (p=5).
Т.к. Ваня не должен гарантированно выиграть своим первым ходом, то мы создаём ещё одну функцию F1, похожую на основную функцию F, которая вычисляет, когда Ваня именно гарантированно выигрывает на своём первом ходе (p=3). И, затем, мы из тех чисел, которые получились в первой функции F, исключаем числа, которые получились во второй функции F1.
В первой функции получилось 62,64, а во второй 64. Получается ответ 62.
Ответ: 62
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
Канал видеоролика: ЕГЭ по информатике
Смотреть видео:
#информатика #егэинформатика #икт #экзамены #егэ_2020 #мгту #школьникам #помощь_студентам #подготовкакэкзаменам
Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):
С этим видео ученики смотрят следующие ролики:

Решение задания №1. Демоверсия ЕГЭ по информатике — 2023
ЕГЭ по информатике

Решение задания №2. Демоверсия ЕГЭ по информатике — 2023
ЕГЭ по информатике

Решение задания №3. Демоверсия ЕГЭ по информатике — 2023
ЕГЭ по информатике

Решение задания №4. Демоверсия ЕГЭ по информатике — 2023
ЕГЭ по информатике
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
25.08.2022