Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было семь камней, во второй куче — S камней; 1 ≤ S ≤ 69.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Задания
Версия для печати и копирования в MS Word
Тип 1 № 27416 
В следующем высказывании выделите простые, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное выражение.
Новый год мы встретим на даче или на Красной площади.
А =
В =
Источник/автор: Венера Шагитовна
Спрятать ответ
·
Хотите готовиться со мной к ЕГЭ?
Пишите: ydkras@mail.ru
Немного обо мне.
В задачах 19-21 ЕГЭ по информатике требуется проанализировать некую простую игру. Однако хотя игра и проста, её анализ может оказаться достаточно хитрым делом. Поэтому приходит мысль: а нельзя ли, чтобы этот анализ выполнил компьютер? (Спойлер: Можно!)
Немного теории.
Основную идею, лежащую в основе теории игр, подобных описанным в задачах ЕГЭ, можно выразить в двух словах: игроки умные. Это означает, что если у кого-то из игроков в текущей позиции есть возможность сделать выигрышный ход, то он этот ход сделает.
Таким образом, если в текущей позиции у игрока есть хотя бы один ход, ведущий к выигрышу, то это — выигрышная позиция для данного игрока.
Если же в ответ на любой ход текущего игрока его противник выигрывает, то для текущего игрока такая ситуация — проигрышная.
Теперь более-менее понятно, как должна выглядеть программа, анализирующая ход игры. Прежде всего она должна проверить, не выиграл ли уже кто-то из игроков. Если это так — то дальнейший анализ позиции не требуется.
Затем нужно просмотреть все возможные ходы текущего игрока. Если них есть хоть один выигрышный для него — в данной позиции он выиграл. Если же при любом его ходе выигрывает его противник — то можно считать, что данный игрок уже проиграл.
Если же неверно ни первое, ни второе — то ситуация неопределенная.(Вообще-то для игр из задач ЕГЭ всегда можно сказать, кто из игроков выиграет, такая неопределенность возникает только из-за ограничения на число ходов.)
Данную процедуру следует рекурсивно применять к позициям, возникающим по ходу игры.
А теперь — практика.
Решим программно задачи 19-21 из 8 варианта с сайта Полякова. Условие выглядит следующим образом:
(№ 3084) (А. Кабанов) Два игрока, Петя и Ваня, играют в следующую игру.
Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход
делает Петя. За один ход игрок может
а) добавить в кучу один камень;
б) увеличить количество камней в куче в два раза;
в) увеличить количество камней в куче в три раза.
Игра
завершается в тот момент, когда количество камней в куче становится не
менее 43. Если при этом в куче оказалось не более 72 камней, то
победителем считается игрок, сделавший последний ход. В противном случае
победителем становится его противник. В начальный момент в куче было S
камней, 1≤S≤42.
Ответьте на следующие вопросы:
Вопрос 1. Найдите минимальное значение S, при котором Ваня выигрывает своим первым ходом при любой игре Пети.
Вопрос 2. Сколько существует значений S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Вопрос 3. Найдите минимальное и максимальное значения S, при которых одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Найденные значения запишите в ответе в порядке возрастания.
Приведем текст рекурсивной функции hod на языке Питон, которая по сути и решает данную задачу.
def hod(number,limit,s):
player = (number+1)%2 + 1 # номер текущего игрока (1 или 2)
rival = 3 — player # Номер его противника (2 или 1)
#Анализ позиции
if s >= 43 and s <= 72: return rival # текущий игрок проиграл
if s > 72 : return player # проиграл противник
if number > limit: return 0 # ситуация неопределенная из-за ограничений на количество ходов
# Делаем ходы и проверяем результаты
rc1 = hod(number+1,limit,3*s)
if rc1 == player: return player
rc2 = hod(number+1,limit,2*s)
if rc2 == player: return player
rc3 = hod(number+1,limit,s+1)
if rc3 == player: return player
if rc1 == rival and rc2 == rival and rc3 == rival: return rival
return 0
Функция имеет три параметра: number (номер хода), limit (ограничение на количество ходов) и s (количество камней в куче). При первом обращении следует задавать значение number, равное 1 (т.е. ходы мы нумеруем с единицы).
Переменная player принимает значение 1 для нечетных номеров ходов (т.е. ходы 1, 3 и т.д. совершает первый игрок) и значение 2 — для четных номеров. Переменная rival, наоборот, равна 2 для нечетных номеров ходов и 1 — для четных. Таким образом, player — это номер игрока, который делает текущий ход, а rival — номер его противника.
Прежде всего функция проверяет, не завершилась ли игра. Если число камней S не менее 43 и не более 72, то это означает, что текущий игрок проиграл: перед этим его противник сделал победный ход. Функция завершается, вернув значение rival. Если же число камней более 72, то соперник текущего игрока только что сделал проигрышный для себя ход, и выиграл текущий игрок. Программа возвращает значение player.
Далее проверяется ограничение на число ходов. Если это ограничение превышено (number>limit), то дальнейшие ходы не выполняются и программа возвращает значение 0 (т.е. победитель не определён).
Далее осуществляются рекурсивные вызовы функции hod с параметром number+1 (т.е. номер хода увеличен на единицу), с тем же самым значением limit и числом камней в куче 3S, 2S и S+1 (согласно условиям задачи).
Рекомендую сначала проверять значения, как можно сильнее отличающиеся от исходного (т.е. 3S и 2S) и потом S+1. Это позволяет уменьшить число вершин «дерева игры», которые анализирует программа. С этой же целью программа, обнаружив выигрышный для текущего игрока ход (т.е. результат вызова функции равен player), немедленно возвращает значение player и не выполняет дальнейших проверок ходов.
Если все три результата ходов равны rival, то в данной позиции все ходы текущего игрока приводят к его проигрышу, и программа возвращает значение rival.
Если же для текущего игрока нет ни одного выигрышного хода, но у него есть ходы, не приводящие к его проигрышу, то ситуация неопределённая, и программа возвращает 0.
Теперь проведем анализ данной игры и получим ответы на заданные в задаче вопросы.
Первый вопрос: каково минимальное значение S, при котором второй игрок выигрывает своим первым ходом? Для ответа на него достаточно вызвать функцию для всех значений S таких, что 1<=S<=42, с ограничением на количество ходов, равным 2 (т.е. игроки делают по одному ходу). Если функция hod вернет значение, равное 2, то при данном начальном значении S второй игрок выигрывает в любом случае.
Второй вопрос: сколько имеется значений S, при которых первый игрок не может выиграть своим первым ходом, но гарантированно выигрывает вторым?
Для этого надо запустить программу два раза, первый раз с ограничением на число ходов 1, а второй раз — с ограничением 3. Если в первом случае программа вернет значение 0 (нет победителя), а второй — 1, то при данном S первый игрок не может гарантированно выиграть своим первым ходом, но непременно выигрывает вторым. Вместо ограничений 1 и 3 можно взять 2 и 4: дополнительный ход второго игрока (если он возможен) ничего не меняет.
Наконец, последний вопрос: при каких значениях S второй игрок не может гарантированно выиграть первым ходом, но обязательно выиграет вторым? Для этого надо опять запустить функцию дважды, с ограничением на число ходов 2 и 4. Если в первом случае функция вернет 0, а во втором — 2, то это искомое значение.
Вот программа, которая выполняет данные проверки:
for s in range(1,43):
h2 = hod(1,2,s)
h4 = hod(1,4,s)
rez = »
if h2 == 2: rez = ‘*** 19 ***’
if h2 == 0:
if h4 == 1: rez = ‘*** 20 ***’
if h4 == 2: rez = ‘*** 21 ***’
print(s,h2, h4, rez)
Результат выполнения программы следующий (из него исключены строки, которые не дают ответов не поставленные вопросы):
7 0 1 *** 20 ***
12 0 2 *** 21 ***
13 0 1 *** 20 ***
14 2 2 *** 19 ***
39 0 2 *** 21 ***
40 0 1 *** 20 ***
41 2 2 *** 19 ***
Следовательно, ответы на вопросы задачи таковы:
Вопрос 1: такие значения — 14 и 41, минимальное — 14.
Вопрос 2: такие значения — 7, 13 и 40, всего их 3.
Вопрос 3: такие значения — 12 и 39. Минимальное — 12, а максимальное — 39.
А теперь решим задачи 19-21 из демонстрационного варианта ФИПИ 2022 г.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.19. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
20. Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.21. Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
Вопросы по сути те же, что и в задаче с сайта Полякова, однако правила игры другие.
Перепишем функцию hod для данных правил:
def hod(number,limit,s):
player = (number+1)%2 + 1 # номер текущего игрока (1 или 2)
rival = 3 — player # Номер его противника (2 или 1)
#Анализ позиции
if s >= 29: return rival # текущий игрок проиграл
if number > limit: return 0 # ситуация неопределенная из-за ограничений на количество ходов
# Делаем ходы и проверяем результаты
rc1 = hod(number+1,limit,2*s)
if rc1 == player: return player
rc2 = hod(number+1,limit,s+1)
if rc2 == player: return player
if rc1 == rival and rc2 == rival: return rival
return 0
Основная программа выглядит так же, как и в предыдущем случае. Единственное изменение — вместо range(1,43) в ней записано range(1,29).
Результат выполнения программы следующий (в нём опять-таки опущены несущественные строки):
7 0 1 *** 20 ***
12 0 2 *** 21 ***
13 0 1 *** 20 ***
14 2 2 *** 19 ***
Отсюда видно, что ответ на задачу 19 — 14, на задачу 20 — 7 и 13, а на задачу 21 — 12. Это совпадает с приведенными в варианте ответами.
Если Петя глуповат…
При составлении программы мы предполагали, что игроки — умные и ошибочных ходов не делают. Но на сайте «Решу ЕГЭ» очень часто встречаются задачи, где один из игроков дает маху. Вот пример задачи 19 (задача 27416):
Два
игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две
кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один
ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза.
Например, пусть в одной куче 10 камней, а в другой 5 камней; такую
позицию в игре будем обозначать (10, 5). Тогда за один ход можно
получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10).
Для того чтобы делать ходы, у каждого игрока есть неограниченное
количество камней.Игра завершается в тот
момент, когда суммарное количество камней в кучах становится не менее
77. Победителем считается игрок, сделавший последний ход, т. е. первым
получивший такую позицию, при которой в кучах будет 77 или больше
камней.В начальный момент в первой куче было семь камней, во второй куче — S камней; 1 ≤ S ≤ 69.
Будем
говорить, что игрок имеет выигрышную стратегию, если он может выиграть
при любых ходах противника. Описать стратегию игрока — значит, описать,
какой ход он должен сделать в любой ситуации, которая ему может
встретиться при различной игре противника. В описание выигрышной
стратегии не следует включать ходы играющего по этой стратегии игрока,
не являющиеся для него безусловно выигрышными, т. е. не являющиеся
выигрышными независимо от игры противника.Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Сначала напишем нашу функцию hod для данной задачи: она всё равно потребуется для задач 20 и 21. Впрочем, отличий от первого варианта не так много. Во-первых, так как у нас теперь две кучи, у функции есть два параметра s1 и s2: число камней в первой и второй кучах. Условие завершения игры теперь выглядит так: s1+s2>=77. Так как теперь у каждого игрока есть четыре возможных хода, то проверяется не три, а четыре альтернативы.
def hod(number,limit,s1,s2):
player = (number+1)%2 + 1 # номер текущего игрока (1 или 2)
rival = 3 — player # Номер его противника (2 или 1)
#Анализ позиции
if s1+s2 >= 77: return rival # текущий игрок проиграл
if number > limit: return 0 # ситуация неопределенная из-за ограничений на количество ходов
# Делаем ходы и проверяем результаты
rc1 = hod(number+1,limit,2*s1,s2)
if rc1 == player: return player
rc2 = hod(number+1,limit,s1,2*s2)
if rc2 == player: return player
rc3 = hod(number+1,limit,s1+1,s2)
if rc3 == player: return player
rc4 = hod(number+1,limit,s1,s2+1)
if rc4 == player: return player
if rc1 == rival and rc2 == rival and rc3 == rival and rc4 == rival: return rival
return 0
Но как быть с тем, что наша функция предполагает безошибочную игру, а условие задачи подразумевает, что первый игрок сделал ошибочный ход? А очень просто: надо вызвать функцию четыре раза с позициями, которые могут получиться после первого хода Пети. В параметрах функции надо указать, что это — второй ход, и задать ограничение на количество ходов, равное двум. Если хотя бы в одном случае функция даст ответ, что выиграл второй игрок, то это и будет ответом на вопрос задачи.
Таким образом, основная программа выглядит так:
s1=7
for s2 in range(1,70):
if hod(2,2,s1*2,s2)==2 or hod(2,2,s1,s2*2)==2 or hod(2,2,s1+1,s2)==2 or hod(2,2,s1,s2+1)==2:
print(s2)
break
Она дает правильный ответ: 18 камней.
Когда основная функция написана, не представляет сложности решить задачи 20 и 21. Вот их вопросы (правила игры, естественно, те же самые):
20: Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
21: Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Основная программа опять-таки похожа на первый вариант, отличия незначительные:
s1=7
for s2 in range(1,70):
h2 = hod(1,2,s1,s2)
h4 = hod(1,4,s1,s2)
rez = »
if h2 == 0:
if h4 == 1: rez = ‘*** 20 ***’
if h4 == 2: rez = ‘*** 21 ***’
print(s2,h2, h4, rez)
Результат работы программы (опять-таки опущены несущественные строки):
30 0 2 *** 21 ***
31 0 1 *** 20 ***
33 0 2 *** 21 ***
34 0 1 *** 20 ***
Таким образом, ответ на вопрос задачи 20 — это 31 и 34, а на вопрос задачи 21 — 30 (напомню, что там требуется минимальное значение из двух ответов: 30 и 33).
Итак, мы убедились, что задачи 19-21 ЕГЭ по информатике можно решить программно, и решение — не слишком сложное.
(c) Ю.Д.Красильников, 2021 г.
В решение заданий демо-версии используется язык программирования Python.
|
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число. |
На графе расставим веса вершин. Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6. Сумма дорог BD + AF = 53 + 5 = 58 Ответ: 58 |
||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции F F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.
Решение на Python Ответ: YXZW |
||||||||||||||||||
Задание 3. Базы данных. Файловая система В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в На рисунке приведена схема указанной базы данных. Используя информацию из приведённой базы данных, определите общий вес |
На третьем листе книги применим фильтр по району и получим ID четырех магазинов. На втором листе применим фильтр по товару и получим ID товара. На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим: Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг. Ответ: 355 |
||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков? |
Ответ: 14 |
||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему 1. Строится двоичная запись числа N. Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число |
Минимальное R, большее 40, это 41. ИЛИ программное решение Ответ: 16
|
||||||||||||||||||
|
Задание 6. Определение результатов работы простейших алгоритмов Исполнитель Черепаха действует на плоскости с декартовой системой координат. Черепахе был дан для исполнения следующий алгоритм: Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения. |
Сначала нужно построить фигуру. Далее мы находим уравнения прямых, которыми ограничена фигура и решаем ИЛИ Ответ: 1 задание — 38, 2 задание — 128 |
||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно. |
I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц), i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро) I1 = ν ⋅ i ⋅ t I2 = 3,5 · 28 = 98 Ответ: 98 |
||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. |
* * * * * — пятизначное число. 6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029 Ответ: 2961 |
||||||||||||||||||
Задание 9. Работа с таблицами Файл с данными Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: |
Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке. Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6. Далее мы найдем среднее арифметическое неповторяющихся значений. Затем найдем сумму повторяющихся значений. Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия. Ответ: 2241 |
||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе Файл с данными Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует. |
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз. Ответ: 45 |
||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт. |
I = K · i, N = 2 i ID : ****….**** – всего 250 различных символов в наборе N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 211, значит для кодирования одного символа нужно 11 бит. IID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт I65536 = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего Ответ: 22016 |
||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Дана программа для Редактора: |
def pr(n): #функция определяет простое ли число for n in range(100): #перебираем n if ‘>2’ in s: if ‘>0’ in s: sum_s = 0 Ответ: 5 |
||||||||||||||||||
|
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. |
Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л. Ответ: 21 |
||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Операнды арифметического выражения записаны в системе счисления с основанием 15. |
for x in range(15): if n%14 == 0: Ответ: 8767 |
||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение |
def deli(n,m): for A in range(1,1000): if Ok: Ответ: 94 |
||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n – натуральное число, |
F(2023) = 2023! = 2023 ⋅ 2022! F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 = = 8266912626 Ответ: 8266912626 |
||||||||||||||||||
Задание 17. Проверка на делимость Файл с данными В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых |
f= open(’17.txt’) k = 0 for i in p: for i in range(1,len(p)): #Осторожно, скобки! print(k,PP) Ответ: 180 190360573 |
||||||||||||||||||
Задание 18. Робот-сборщик монет Файл с данными Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен. Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1. Далее делаем замену всех формул МАКС на МИН. Ответ: 1099 1026 |
||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом. Ответ: 64 |
||||||||||||||||||
|
Задание 20. Выигрышная стратегия. Задание 2 Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
Найденные значения запишите в порядке возрастания. |
Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом. Ответ: 32 63 |
||||||||||||||||||
|
Задание 21. Выигрышная стратегия. Задание 3 Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них. |
Ответ: 62 |
||||||||||||||||||
|
Задание 22. Многопроцессорные системы В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно. |
В независимых процессах время считается от 0, Ответ: 17 |
||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. |
def f(x, y): print (f(1,10) * f(10, 35)) Ответ: 98 |
||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Файл с данными Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная |
f=open(’24.txt’) PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’] for i in range(1, len(p), 2): Ответ: 95 |
||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Назовём маской числа последовательность цифр, в которой также могут Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка. |
Самый простой способ использовать библиотеку fnmatch. или так полным перебором: y = {»,’0′,’00’,’000′} for x in range (1000): Ответ: 162139404 80148 |
||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. |
|||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Файл А Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Ответ: 51063 5634689219329 |
1. Тип 1 № 28678
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги АГ больше, чем длина дороги ВГ. Определите длину дороги БЖ. В ответе запишите целое число — длину дороги в километрах.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 10 | 7 | 8 | ||||
| 2 | 12 | 20 | 19 | ||||
| 3 | 10 | 12 | 14 | 15 | |||
| 4 | 7 | 9 | 11 | ||||
| 5 | 8 | 9 | 23 | ||||
| 6 | 20 | 14 | 11 | ||||
| 7 | 19 | 15 | 23 |
2. Тип 2 № 15787
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | |||
| 1 | 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 37485
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
3.xlsx
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок, шт. |
Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количество в упаковке |
Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите, сколько килограмм творожка детского сладкого было продано в магазинах Заречного района за период с 1 по 10 июня включительно.
В ответе запишите только число.
4. Тип 4 № 27401
Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв П и Р — кодовые слова неизвестны.
Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.
5. Тип 5 № 9756
Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Перемножаются первая и вторая, а также вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 631. Произведение: 6 * 3 = 18; 3 * 1 = 3. Результат: 318.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 621.
6. Тип 6 № 47316
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 9 Направо 90 Вперёд 3 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
7. Тип 7 № 27404
Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
8. Тип 8 № 13406
Ольга составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Ольга использует 4-буквенные слова, в которых есть только буквы A, B, C, D, X, Y, Z. При этом первая буква кодового слова — это буква X, Y или Z, а далее в кодовом слове буквы X, Y и Z не встречаются. Сколько различных кодовых слов может использовать Ольга?
9. Тип 9 № 27520
Откройте файл электронной таблицы, содержащей вещественные числа — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Задание 9
Сколько раз встречалась температура, которая равна максимальному значению?
10. Тип 10 № 27582
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «дом» или «Дом» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «дом», такие как «дома», «домой» и т. д., учитывать не следует. В ответе укажите только число.
Задание 10
11. Тип 11 № 13597
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 62-символьного набора, содержащего все латинские буквы (заглавные и строчные) и десятичные цифры. В базе данных для хранения сведений о каждом пользователе отведено одинаковое минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым минимально возможным количеством бит. Кроме, собственно, пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; одно и то же для всех пользователей.
Для хранения сведений о 20 пользователях потребовалось 700 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число – количество байт.
12. Тип 12 № 16817
Исполнитель Редактор получает на вход строку цифр и преобразует её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 80 единиц?
НАЧАЛО
ПОКА нашлось (11111)
заменить (111, 2)
заменить (222, 1)
КОНЕЦ ПОКА
КОНЕЦ
13. Тип 13 № 9199
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р, Т, Ф. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Ф?
14. Тип 14 № 38948
Значение выражения 436 + 3 · 420 + 415 + 2 · 47 + 49 записали в системе счисления с основанием 16. Сколько разных цифр встречается в этой записи?
15. Тип 15 № 26990
Для какого наибольшего целого неотрицательного числа A выражение
(x > A) ∨ (y > A) ∨ (2y + x < 110)
тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?
16. Тип 16 № 4647
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(2) = 2
F(n) = 2 * F(n–1) + (n – 2) * F(n–2), при n >2
Чему равно значение функции F(6)?
В ответе запишите только натуральное число.
17. Тип 17 № 37361
В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых сумма элементов кратна 126, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.
17.txt
Ответ:
18. Тип 18 № 39247
Робот стоит в левом верхнем углу прямоугольного поля, в каждой клетке которого записано натуральное число. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз. Выходить за пределы поля робот не может. В начальный момент запас энергии робота равен числу, записанному в стартовой клетке. После каждого шага робота запас энергии изменяется по следующим правилам: если число в очередной клетке меньше, чем в предыдущей, запас увеличивается на величину этого числа, если больше — уменьшается на эту же величину.
Определите максимальный и минимальный запас энергии, который может быть у робота после перехода в правую нижнюю клетку поля. В ответе запишите два числа: сначала максимально возможное значение, затем минимальное.
Исходные данные записаны в электронной таблице.
Задание 18
Пример входных данных (для таблицы размером 4 × 4):
| 200 | 8 | 69 | 50 |
| 87 | 35 | 7 | 17 |
| 32 | 1 | 9 | 32 |
| 44 | 12 | 80 | 43 |
При указанных входных данных максимальное значение получается при движении по маршруту 200 + 87 + 35 + 7 − 9 − 80 + 43 = 283, а минимальное при движении по маршруту 200 + 8 − 69 + 7 − 17 − 32 − 43 = 54.
Ответ:
19. Тип 19 № 27915
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу один камень, или
добавить в кучу два камня, или
увеличить количество камней в куче в два раза.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 11, 12 или 20 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче превышает 33. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 34 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 33.
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20. Тип 20 № 27916
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу один камень, или
добавить в кучу два камня, или
увеличить количество камней в куче в два раза.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 11, 12 или 20 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче превышает 33. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 34 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 33.
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите три таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
21. Тип 21 № 27917
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу один камень, или
добавить в кучу два камня, или
увеличить количество камней в куче в два раза.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 11, 12 или 20 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче превышает 33. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 34 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 33.
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22. Тип 22 № 47593
В файле 22_12.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 13633
Исполнитель А17 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
3. Умножить на 3
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья – умножает на 3.
Программа для исполнителя А17 – это последовательность команд.
Сколько существует программ, для которых при исходном числе 2 результатом является число 30 и при этом траектория вычислений содержит число 15?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
24. Тип 24 № 39253
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите максимальное количество идущих подряд символов, среди которых не более одной буквы D.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Задание 24
25. Тип 25 № 28123
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [125 256; 125 330], числа, имеющие ровно шесть различных чётных натуральных делителей. Для каждого найденного числа запишите эти шесть делителей в шесть соседних столбцов на экране с новой строки. Делители в строке должны следовать в порядке возрастания.
Например, в диапазоне [2; 48] ровно шесть чётных различных натуральных делителей имеют числа 24, 36 и 40, поэтому для этого диапазона вывод на экране должна содержать следующие значения:
2 4 6 8 12 24
2 4 6 12 18 36
2 4 8 10 20 40
Ответ:
26. Тип 26 № 27886
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
Задание 26
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 2000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
Ответ:
27. Тип 27 № 39256
Дана последовательность натуральных чисел. Необходимо найти максимально возможную сумму её непрерывной подпоследовательности, в которой количество нечётных элементов кратно k = 10.
Входные данные.
Файл A
Файл B
Первая строка входного файла содержит целое число N — общее количество чисел в наборе. Каждая из следующих N строк содержит одно число. Гарантируется, что общая сумма всех чисел не превышает 2 · 109.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла A, затем для файла B.
Ответ:
Просмотр содержимого документа
«ЕГЭ 2023 Январь Информатика Вариант 15»
Сегодня научимся решать 12 задание из ЕГЭ по информатике 2022.
В основном 12 задание решается шаблонно с помощью Питона, но есть и задачи, в которых нужен особый подход.
Перейдём к классической задачке из ЕГЭ по информатике 2022.
Задача (Классическая)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (2222) ИЛИ нашлось (666)
ЕСЛИ нашлось (2222)
ТО заменить (2222, 6)
ИНАЧЕ заменить (666, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 239 идущих подряд цифр 6? В ответе запишите полученную строку.
Решение:
Решим задачу с помощью программы на Python’е.
s = '6'*239 while ('2222' in s) or ('666' in s): if '2222' in s: s = s.replace('2222', '6', 1) else: s = s.replace('666', '2', 1) print(s)
Здесь в начале формируется строка, состоящая из 239 шестёрок. Потом эта строка подаётся в программу. Программу переводим с русского языка на язык Питон.
Третий параметр в функции replace обозначает, что замену нужно производить один раз. Это в точности соответствует предложенной функции заменить.
Ответ получается 2266.
Ответ: 2266
В следующей типовой задаче из ЕГЭ по информатике 2022 нужно сообразить один момент.
Задача (Нужно сообразить)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (21) ИЛИ нашлось (31) ИЛИ нашлось (23)
ЕСЛИ нашлось (21)
ТО заменить (21, 12)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (31)
ТО заменить (31, 13)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (23)
ТО заменить (23, 32)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, содержащая 50 цифр 1, 50 цифр 2 и 50 цифр 3, расположенных в произвольном порядке. Запишите без разделителей символы, которые имеют порядковые номера 10, 90 и 130 в получившейся строке.
Решение:
Здесь сказали, что начальный порядок цифр в строке неизвестен. А просят написать конкретные данные на выходе. Отсюда делаем вывод, что любой порядок в начале приводит к одному и тому же результату.
В строке заведём цифры по порядку: в начале единицы, потом двойки, потом тройки.
s = '1'*50 + '2'*50 + '3'*50 while ('21' in s) or ('31' in s) or ('23' in s): if '21' in s: s = s.replace('21', '12', 1) if '31' in s: s = s.replace('31', '13', 1) if '23' in s: s = s.replace('23', '32', 1) print(s[9] + s[89] + s[129])
Чтобы обратится к конкретному символу в строке, используем конструкцию s[позиция символа]. Но нумерация начинается с нуля.
В ответе запишем 132.
Ответ: 132
В следующей примерной задаче из ЕГЭ по информатике 2022 опять используем Питон.
Задача (Снова программируем)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
НАЧАЛО ПОКА нашлось (111) заменить (111, 22) заменить (222, 11) КОНЕЦ ПОКА КОНЕЦ
Известно, что исходная строка содержала более 70 единиц и не содержала других цифр. Укажите минимально возможную длину исходной строки, при которой в результате работы этой программы получится строка, содержащая максимально возможное количество единиц.
Решение:
Здесь мы попробуем с помощью программы формировать строчки с разной длиной и смотреть, какое количество единиц получится на выходе.
for i in range(71, 1000): s = '1'*i while '111' in s: s = s.replace('111', '22', 1) s = s.replace('222', '11', 1) print(i, s.count('1'))
Посмотрев результаты, понимаем, что максимальное количество единиц в окончательной строке равно 4. А минимальное количество единиц в изначальной строке, чтобы получилось в итоге 4 единицы, равно 73.
Ответ: 73
Ещё один частый гость в тренировочных вариантах из ЕГЭ по информатике 2022.
Задача (Сумма цифр + непонятный символ)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>1)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>3)
ТО заменить (>3, 1>2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 28 цифр 1, 18 цифр 2 и 35 цифр 3, расположенных в произвольном порядке. Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
Решение:
Здесь снова результат будет одним и тем же независимо от того, как будут расположены числа в начале.
s = '>' + '1'*28 + '2'*18 + '3'*35 while ('>1' in s) or ('>2' in s) or ('>3' in s): if '>1' in s: s = s.replace('>1', '22>', 1) if '>2' in s: s = s.replace('>2', '2>1', 1) if '>3' in s: s = s.replace('>3', '1>2', 1) # Находим сумму цифр в строке sm=0 for i in range(0, len(s)): if s[i]!='>': sm = sm + int(s[i]) print(sm)
Чтобы найти сумму цифр, мы пробегаем по всей строке с помощью цикла range. Если символ не равен «>», то превращаем его в число с помощью функции int() и суммируем в переменную sm.
Получается 465.
Ответ: 465
Задача (Трудно запрограммировать)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (11)
ЕСЛИ нашлось(112)
ТО заменить (112, 5)
ИНАЧЕ заменить (11, 3)
КОНЕЦ ПОКА
КОНЕЦ
Исходная строка содержит 23 единицы и 5 двоек, других цифр нет, точный порядок расположения цифр неизвестен. Какую наибольшую сумму цифр может иметь строка, которая получится после выполнения программы?
Решение:
Здесь не важно, по какой ветке будет идти программа, прирост в сумме цифр будет всегда равен 1. Поэтому можно расположить в начале только 1, а затем все двойки в исходной строке.
Одиннадцать раз символы ’11’ превратятся в ‘3’. Тогда 11 * 3 = 33. Останутся цифры ‘122222’. Их сумма равна 11.
В ответе получается 33 + 11 = 44.
Ответ: 44
Задача (Крепкий орешек)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (01) или нашлось (02)
заменить (01, 2202)
заменить (02, 10)
КОНЕЦ ПОКА
КОНЕЦ
Известно, что начальная строка начиналась с нуля, а далее содержала только единицы и двойки. После выполнения данной программы получилась строка, содержащая 40 единиц и 64 двойки. Сколько двоек было в исходной строке ?
Решение:
Посмотрим, во что превращается 1:
01 -> 2202 -> 2210
Посмотрим, во что превращается 2:
02 -> 10
Т.е. в окончательном результате двойки могли возникнуть только из 1. Двоек получается в два раза больше, чем было изначально единиц.
Получается, что изначальное количество единиц равно 64 / 2 = 32. Эти 32 единицы так же принесли 32 единицы. Всего 40 единиц стало. Значит, ещё 8 единиц получилось в результате преобразования 02 -> 10. Т.е. двоек будет 8.
Теперь попробуем решить задачу с помощью программы. Здесь неизвестно количество единиц и двоек. Поэтому придётся создавать вложенные циклы. Предположим, что количество единиц и двоек меньше 100, чтобы программа отработала за адекватное время.
for i in range(1, 100): for j in range(1, 100): s = '0' + '1'*i + '2'*j while ('01' in s) or ('02' in s): s = s.replace('01', '2202', 1) s = s.replace('02', '10', 1) if s.count('1')==40 and s.count('2')==64: print(j)
Получается количество двоек равно восьми.
Ответ: 8
Решим задачу про Робота, которая в последнее время редко встречается на экзамене по информатике.
Задача (Робот)
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх , вниз , влево , вправо .
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно | снизу свободно | слева свободно | справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
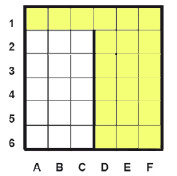
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободнo
ТО вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
|
|
Решение:
Проанализируем внимательно программу для Робота.
В программе есть главный цикл, внутри цикла проверяется сначала возможность двигаться вправо. Если есть такая возможность, робот будет двигаться до упора с помощью ещё одного цикла. Потом после того как больше нет возможности двигаться вправо, с помощью основного цикла и записанного условия будет перемещаться вниз, пока есть такая возможность.
Если нет возможности двигаться ни вправо, ни вниз, то Робот завершает программу.
Поняв этот алгоритм не сложно отметить те клетки, стартовав с которых, Робот остановится на клетке F6.
Ещё раз, Робот до упору будет двигаться вправо, потом до упору вниз, насколько это возможно. Вот алгоритм в двух словах.
Важно в этих задачах простыми словами сформулировать алгоритм, чтобы можно было проверять целые блоки лабиринта.
Количество клеток, удовлетворяющие условию будет 21.
Ответ: 21
12 Задание из ЕГЭ по информатике 2021 выглядит обычно объёмным, но на деле описываются обычные конструкции (Циклы и условия), которые есть в большинстве языках программирования.
Задача (Чертёжник)
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнить команду сместиться на(a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на(2, -3) переместит Чертёжника в точку (6, -1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (число повторений и величины смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на(8, -60)
ПОВТОРИ ... РАЗ
сместиться на(..., ...)
сместиться на(4, -6)
КОНЕЦ ПОВТОРИ
сместиться на(-35, -3)
КОНЕЦ
В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшие число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ» ?
Решение:
Эта задача похоже на задачу Кузнечик, которую рассматривали в 5 задании.
Напишем для переменной x уравнение.
8 + n * x + n * 4 — 35 = 0
Всё выражение приравниваем к нулю, т.к. Чертёжник возвращается в исходную точку, т.е. как ни ходил Чертёжник, он никуда в итоге не сдвинулся.
n — положительное целое число, количество повторений.
x — целое число, смещение по координате x.
n * x + n * 4 = 27
n * ( x + 4 ) = 27
Нужно подобрать x и n, чтобы равенство было верным.
Число n может быть 27, 9, 3, 1. Нам нужно выбрать число n, как можно больше.
Проверим число 27! Тогда выражение x + 4 = 1 => x = -3. Теперь нужно проверить это число для координаты y.
-60 + n * y — n * 6 — 3 = 0
27 * y — 27 * 6 = 63
27 * ( y — 6 ) = 63
Видим, что нельзя подобрать такое целое число для 27, чтобы при умножении получалось 63.
Проверим число 9! Тогда выражение x + 4 = 3 => x = -1. Теперь нужно проверить это число для координаты y.
-60 + n * y — n * 6 — 3 = 0
9 * y — 9 * 6 = 63
9 * ( y — 6 ) = 63
Видим, что можно подобрать такое целое число для 9, чтобы при умножении получалось 63. Это число 7. Значит, y — 6 = 7 => y = 13
Мы подобрали все нужные числа и нашли наибольшее число n=9.
Ответ: 9
Некоторые формулировки задач были взяты с сайтов:
https://kpolyakov.spb.ru/
https://inf-ege.sdamgia.ru/
Счастливых экзаменов по информатике!
почему 5-ую задачу сложно запрограммировать? тут ведь тоже произвольный порядок
я пробовал в программе ставить сначала единицы, а потом двойки и наоборот — сначала двойки а потом единицы
печатаю s и суммирую цифры
получается везде 44
Если бы сама программа была немного другая, то могло и не получится. Т.е. тут нужно самостоятельно провести анализ, при каком расположении цифр сумма будет максимальной.
Обожаю ваш сайт! Спасибо за пояснение усложненных задач.