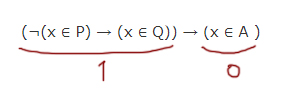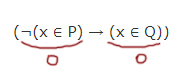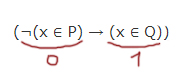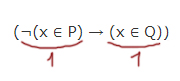На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Дано логическое выражение, зависящее от 5 логических переменных:
z1 ∧ ¬z2 ∧ ¬z3 ∧ ¬z4 ∧ z5
Сколько существует различных наборов значений переменных, при которых выражение ложно?
1) 1
2) 2
3) 31
4) 32
2
Дан фрагмент таблицы истинности выражения F:
| x1 | x2 | x3 | x4 | x5 | F |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 |
Какое выражение соответствует F?
1) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5
2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5
4) ¬x1 ∧ x2 ∧ x3 ∧ x4 ∧ ¬x5
Источник: Яндекс: Тренировочная работа ЕГЭ по информатике. Вариант 1.
3
Дан фрагмент таблицы истинности выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
Каким выражением может быть F?
1) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6
2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 ∨ ¬x6
3) x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ x6
4) ¬x1 ∧ ¬x2 ∧ x3 ∧ x4 ∧ x5 ∧ x6
Источник: Яндекс: Тренировочная работа ЕГЭ по информатике. Вариант 2.
4
Дан фрагмент таблицы истинности выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
5
Дан фрагмент таблицы истинности выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Пройти тестирование по этим заданиям
Алгебра логики: Конъюнкция, Дизъюнкция, Импликация, Эквивалентность
Лада Есакова, преподаватель информатики и математики, автор книги «Информатика. Полный курс подготовки к ЕГЭ».
Ну а теперь, ребята, самая «вкусная» тема теоретической части ЕГЭ – это булева алгебра, она же алгебра логики.
Сначала я хочу задать вам вопрос: для чего вообще придумали такой аппарат как булева алгебра, кроме того, чтобы мучить маленьких детей?
Раз у нас есть такая возможность пообщаться с компьютером, поручить ему какие-то задачи на выполнение, неплохо бы нам научиться говорить с ним на одном языке. То есть перевести наши желания и намерения на его компьютерный язык.
А кто такой компьютер? Если очень упрощенно, то это некоторое устройство, у которого на проводники подается либо не подается ток. Так вот в зависимости от того, есть ток или его нет на входящих проводниках, происходят определенные действия. Обозначим это 0 и 1: 0 – нет тока, 1 – есть ток. Вот именно в таких терминах нам и надо разговаривать с компьютером.
Рассматривая задачи, в том числе и 27, сложную задачу, считаем, что мы крутые программисты, если мы написали программный код на каком-то языке программирования. А компьютер нас поймет? Нет. Он знает только 0 и 1. Как же нам тогда до него достучаться?
После программистов высокого уровня в дело вступают Боги от программирования – это люди, которые пишут компиляторы, драйверы, операционные системы и которые уже непосредственно пытаются достучаться до компьютерного железа.
Что такое уже перевод программы в машинные коды? У меня нет цели рассказать, как это работает детально, я расскажу очень упрощенно, чтобы просто было понятно, для чего это нужно.
Если на один компьютерный разъем ток не поступил, а на другой поступил, мне нужно, чтобы получился 0. Я уже говорю терминами 0 и 1, нет тока или есть ток.
Если на оба разъема ток не поступил, тоже будет 0.
Если наоборот на первый поступил, а на второй не поступил, – то я тоже хочу 0. И в случае, если на оба разъема ток поступил, тогда пусть будет у меня 1
Например, у меня другая схема, в которую входит три проводника, и, в зависимости от того, что пришло на входы, я тоже хочу какое-то значение. Например, вот так. Не буду расписывать все варианты
По сути, у меня единственный возможный способ общаться с компьютером – это завести много функций от разного числа переменных, которые могут быть только 0 и 1 и которые на выходе дают тоже 0 или 1.
Можно посмотреть функцию от двух переменных и назвать ее f(1), функцию от трех переменных назовем f(2). Будут и другие функции, которые запишем в таблицы, переплету в многотомники и поставлю на полку. В случае, если мне нужно найти какую-то схему, достаю том, листаю страницы и нахожу то, что мне нужно.
Для компьютера это будет нормально, его устроит, если я выстрою с ним такой диалог. А вот человека такая схема работы не устроит, потому что людям очень сложно оперировать большими объемами информации без логического обоснования. Нам проще понять, как это работает, чем зубрить большое количество таблиц. Поэтому человек для облегчения своей жизни ввел аналогию – истину и ложь.
Наверняка вы помните детсадовские игры, когда можно задавать только вопросы, на которые можно ответить «да» или «нет», и нужно что-то угадать. Наверное, у детей изначально подсознательно заложена склонность к двоичному коду.
Поэтому человек поставил в соответствие аппарат логических высказываний, и теперь за 0 мы принимаем ложь, за 1 – истину. И выяснилось, что если я такими операциями буду оперировать, то все операции от трех, четырех, пяти и т. д. переменных я могу свести к функциям от двух переменных. А к каким же функциям?
Первая функция – это функция отрицания. Ее можно обозначить несколькими способами — .
Посмотрим, как это работает.
Если у меня высказывание ложное (например, я показываю маркер, а говорю, что это апельсин)
А если я показываю маркер и говорю, что это не апельсин, то это истина
Если я наоборот говорю, что это маркер и показываю его, то это истина, а если я говорю, что это не маркер, это будет ложь
Следующая операция – это логическое ИЛИ, она же записывается как .
Покажу как это работает.
Функция от двух переменных работает следующим образом: например, я говорю, что это апельсин или это яблоко (то есть два ложных высказывания), в сумме получается 0; если я говорю, что это апельсин или это маркер, в целом я сказала правду, потому что одно из утверждений является истинным, то получается 1; если я говорю, что это маркер или это банан, опять же это правда; и наконец, если я говорю, что это маркер или это маркер, то есть два верных утверждения, это тоже правда
Вот таким образом работает функция. Акцентирую ваше внимание, что мне ненужно запоминать эти наборы. Конечно, они запомнятся после несколько десятков прорешанных задач, но эту таблицу истинности не надо запоминать, это вытекает из логики.
Далее логическое И — , &, знак умножения.
Посмотрим, как оно работает. Если я говорю два ложных утверждения – это яблоко и это банан – это ложь. Если я говорю, что это яблоко и это маркер – одно высказывание истина, но я же настаиваю на том, что и то, и другое должно выполняться, поэтому это ложь. Если я говорю, что это маркер и это банан, то это тоже ложь. И если я говорю два истинных утверждения – это маркер и это маркер – да, это правда
А умножение, потому что если 1 умножить на 0 или 0 на 1, то тоже будет 0, и только в случае умножения 1 на 1 получится 1.
Вот именно к этим операциям можно свести и все остальные, но не всегда удобно, поэтому еще две функции используется в курсе школьной программы – это импликация и эквивалентность.
Импликацию можно свести к вышеперечисленным, но удобнее ее использовать по-другому.
Импликация – это логическое следование
Не будем зубрить таблицу истинности, а попробуем понять.
Если у меня есть ложное высказывание (например, 2 больше 5), могу ли я получить из него ложь разрешенными функциями? Легко! Добавлю к двум частям неравенства единицу и получу ложь: 2>5, 3>6.
То есть мы можем получить изо лжи ложь.
А могу ли я изо лживого высказывания получить истину? Тоже могу. -5 больше -3. Это ложь? Ложь. А применим-ка разрешенную операцию – возведение в квадрат. И запросто получим истину: -5>-3, 25>9. То есть изо лжи истину мы тоже можем получить.
А вот из истины получить ложь никак не получится. Из истины можно получить только истину.
Ну и из истины истину получить, конечно же, возможно.
То есть не всегда удобно приводить импликацию к другим функциям. Потому что это замечательная функция, которая 0 дает в единственном случае, когда из истины следует ложь.
И последняя функция, часто употребляемая, – это функция эквивалентности, обозначается логическим равенством или взаимными стрелками
Здесь все очень просто. 0 равен 0? Да. 0 = 1? Нет. 1 равна 0? Нет. 1 равна 1? Да.
Мы логически обосновали все пять функций, и это избавляет нас от необходимости зубрить таблицы истинности. Да, мы их запомним в процессе решения задач, но гораздо проще логически понять, в чем суть вопроса.
Теперь приоритеты этих функций.
Если у нас не стоят никакие скобки, то все действия, как и в математике, имеют некоторый приоритет.
Вот такая cтрока без скобок
Первый приоритет имеет отрицание , оно прямо приклеивается к тому высказыванию, рядом с которым стоит
, поэтому я всегда настаиваю использовать вот такой символ, черточку сверху
, потому что это гораздо понятнее, что оно относится к высказыванию.
Следующий приоритет – умножение . То есть в нашем выражении у нас будет вот так
Третий приоритет у сложения , То есть вот так
.
А дальше одинаковый приоритет имеют эквивалентность и импликация , слева на право. В нашем случае сначала выполнится сравнение на эквивалентность, а потом из этого импликация
.
Все видео по информатике
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Алгебра логики: Конъюнкция, Дизъюнкция, Импликация, Эквивалентность» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
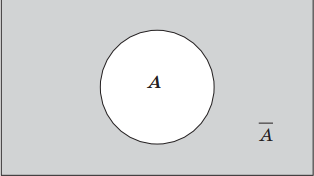
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖{-}$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖{-}$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
или
Высказывание $A↖{-}$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖{-}$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
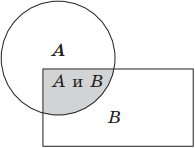
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
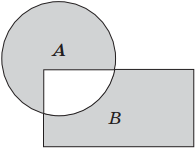
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
или
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если…, то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖{-} ∧B) ∧ (A ∧ B↖{-})$ |
| Импликация | А → В | $A↖{-} ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖{-} ∧ B↖{-}) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Последовательность выполнения операций следующая: сначала выполняются операции сравнения в скобках, затем дизъюнкция, и последней выполняется операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации имеет вид
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда получаем:
1) для X = 1:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) для X = 12:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) для X = 3:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
Пример 2. Указать множество целых значений X, для которых истинно выражение ¬((X > 2) → (X > 5)) .
Решение. Операция отрицания применена ко всему выражению ((X > 2) → (X > 5)) , следовательно, когда выражение ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) →(X > 5)) ложно. Поэтому необходимо определить, для каких значений X выражение ((X > 2) → (X > 5)) ложно. Операция импликации принимает значение «ложь» только в одном случае: когда из истины следует ложь. А это выполняется только для X = 3; X = 4; X = 5.
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
- выражения, которые используют операции сравнения («больше», «меньше», «равно», «не равно» и т. п.) и принимают логические значения (например, выражение а > b , где а = 5 и b = 7, равно значению «ложь»);
- непосредственные логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина).
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a — π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) ba + ab > a + b, после подстановки получим: 32 + 23 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (ba + ab > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
4) sin(π/a — π/b) < 1 = sin(π/2 — π/3) < 1 = истина.
После этих вычислений окончательно получим: истина ∨ А ∧ истина ∧ ¬В ∧ ¬истина.
Теперь должны быть выполнены операции отрицания, затем логического умножения и сложения:
5) ¬В = ¬ложь = истина; ¬истина = ложь;
6) A ∧ истина ∧ истина ∧ ложь = истина ∧ истина ∧ истина ∧ ложь = ложь;
7) истина ∨ ложь = истина.
Таким образом, результат логического выражения при заданных значениях— «истина».
Примечание. Учитывая, что исходное выражение есть, в конечном итоге, сумма двух слагаемых, и значение одного из них 1 ≤ a = 1 ≤ 2 = истина, без дальнейших вычислений можно сказать, что результат для всего выражения тоже «истина».
Тождественные преобразования логических выражений
В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| Переместительный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Сочетательный | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | ${A ∨ B}↖{-}$ = $A↖{-} ∧ B↖{-}$ | ${A ∧ B}↖{-}$ = $A↖{-} ∨ B↖{-}$ |
| Идемпотенции | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Склеивания | (A ∧ B) ∨ (A↖{-} ∧ B) = B | (A ∨ B) ∧ (A↖{-} ∨ B) = B |
| Операция переменной с ее инверсией | $A ∨ A↖{-}$ = 1 | $A ∧ A↖{-}$ = 0 |
| Операция с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойного отрицания | $A↖{=}$ = A |
Доказательства этих утверждений производят на основании построения таблиц истинности для соответствующих записей.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее по сравнению с исходной число операций, либо меньшее число переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т. п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Для преобразования здесь можно применить закон идемпотенции, распределительный закон; операцию переменной с инверсией и операцию с константой.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для упрощения применяется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
При преобразовании применяются правило де Моргана, операция переменной с ее инверсией, операция с константой
Примеры решения задач
Пример 1. Найти логическое выражение, равносильное выражению A ∧ ¬(¬B ∨ C) .
Решение. Применяем правило де Моргана для В и С: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равносильное исходному: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Ответ: A ∧ B ∧ ¬C.
Пример 2. Указать значение логических переменных А, В, С, для которых значение логического выражения (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации ложна только в случае, когд а из истинной посылки следует ложь. Следовательно, для заданного выражения посылка A ∨ B должна принимать значение «истина», а следствие, т. е. выражение B ∨ ¬C ∨ B , — «ложь».
1) A ∨ B — результат дизъюнкции — «истина», если хотя бы один из операндов — «истина»;
2) B ∨ ¬C ∨ B — выражение ложно, если все слагаемые имеют значение «ложь», т. е. В — «ложь»; ¬C — «ложь», а следовательно, переменная С имеет значение «истина»;
3) если рассмотреть посылку и учесть, что В — «ложь», то получим, что значение А — «истина».
Ответ: А — истина, В — ложь, С — истина.
Пример 3. Каково наибольшее целое число X, при котором истинно высказывание (35 < X · X) → (X < (X — 3)) ?
Решение. Запишем таблицу истинности для операции импликации:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Выражение X < (X — 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Ответ: X = 5.
Использование логических выражений для описания геометрических областей
Логические выражения могут быть использованы для описания геометрических областей. В этом случае задача формулируется так: записать для заданной геометрической области такое логическое выражение, которое принимает значение «истина» для значений x, y тогда и только тогда, когда любая точка с координатами (x; y) принадлежит геометрической области.
Рассмотрим описание геометрической области с помощью логического выражения на примерах.
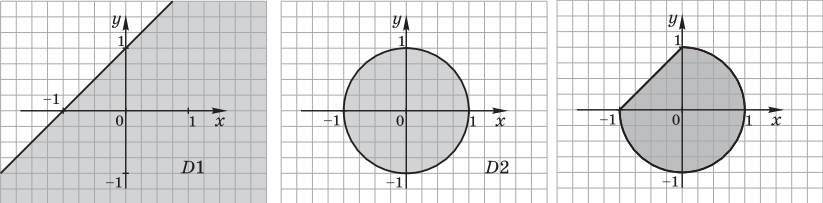
Пример 1. Задано изображение геометрической области. Записать логическое выражение, описывающее множество точек, принадлежащих ей.
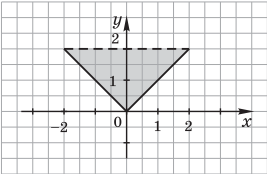
1) 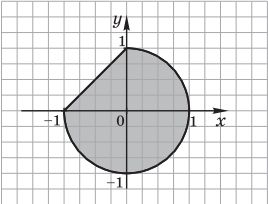
Решение. Заданную геометрическую область можно представить в виде набора следующих областей: первая область — D1 — полуплоскость ${x}/{-1} +{y}/{1} ≤ 1$, вторая — D2 — круг с центром в начале координат $x^2 + y^2 ≤ 1$. Их пересечение D1 $∩$ D2 представляет собой искомую область.
Результат: логическое выражение ${x}/{-1}+{y}/{1} ≤ 1 ∧ x^2 + y^2 ≤ 1$.
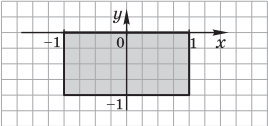
2)
Эту область можно записать так: |x| ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1 .
Примечание. При построении логического выражения используются нестрогие неравенства, а это значит, что границы фигур также принадлежат заштрихованной области. Если использовать строгие неравенства, то границы учитываться не будут. Границы, не принадлежащие области, обычно изображаются пунктиром.
Можно решить обратную задачу, а именно: нарисовать область для заданного логического выражнения.
Пример 2. Нарисовать и заштриховать область, для точек которой выполняется логическое условие y ≥ x ∧ y + x ≥ 0 ∧ y < 2 .
Решение. Искомая область представляет собой пересечение трех полуплоскостей. Строим на плоскости (x, y) прямые y = x; y = –x; y = 2. Это границы области, причем последняя граница y = 2 не принадлежит области, поэтому ее наносим пунктирной линией. Для выполнения неравенства y ≥ x нужно, чтобы точки находились слева от прямой y = x, а неравенство y = –x выполняется для точек, которые находятся справа от прямой y = –x. Условие y < 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:
Использование логических функций для описания электрических схем
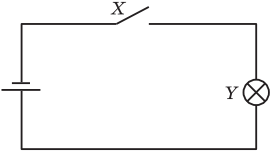
Логические функции очень удобны для описания работы электрических схем. Так, для схемы, представленной на рис., где значение переменной X — это состояние выключателя (если он включен, значение X — «истина», а если выключен — «ложь»), это значение Y — это состояние лампочки (если она горит — значение «истина», а если нет — «ложь»), логическая функция запишется так: Y = X . Функцию Y называют функцией проводимости.
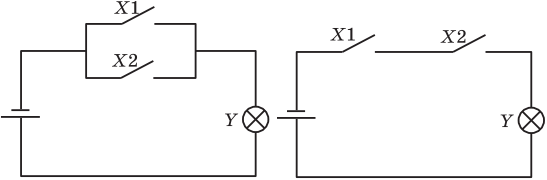
Для схемы, представленной на рис., логическая функция Y имеет вид: Y = X1 ∪ X2, т. к. достаточно одного включенного выключателя, чтобы горела лампочка. В схеме на рис., для того чтобы горела лампочка, должны быть включены оба выключателя, следовательно, функция проводимости имеет вид: Y = X1 ∧ X2 .
Для более сложной схемы функция проводимости будет иметь вид: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).
Схема также может содержать контакты на замыкание. В этом случае размыкаемый контакт как выключатель обеспечивает загорание лампочки, когда кнопка отпущена, а не нажата. Для таких схем размыкающий выключатель описывается отрицанием.
Две схемы называются равносильными, если через одну из них ток проходит тогда, когда он проходит и через другую. Из двух равносильных схем более простой считается схема, функция проводимости которой содержит меньшее число элементов. Задача нахождения наиболее простых схем среди равносильных очень важна.
Использование аппарата алгебры логики при проектировании логических схем
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера. Любая информация при обработке на компьютере представляется в двоичной форме, т. е. кодируется некоторой последовательностью 0 и 1. Обработку двоичных сигналов, соответствующих 0 и 1, выполняют в компьютере логические элементы. Логические элементы, которые выполняют основные логические операции И, ИЛИ, НЕ, представлены на рис.
Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу компьютера.
Технически компьютерный логический элемент реализуется в виде электрической схемы, которая представляет собой соединение различных деталей: диодов, транзисторов, резисторов, конденсаторов. На вход логического элемента, который называют также вентилем, поступают электрические сигналы высокого и низкого уровней напряжения, на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы: 1 — 0; ИСТИНА — ЛОЖЬ. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических схем описывают с помощью таблиц истинности. Условное обозначение на схеме ИЛИ знак «1» — от устаревшего обозначения дизъюнкции как «>=1» (значение дизъюнкции равно 1, если сумма двух операндов больше или равна 1). Знак «&» на схеме И является сокращенной записью английского слова and.
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы ${X1}↖{-} ∧ X2 ∨ {X1 ∨ X2}↖{-} ∨ X1$.
| X1 | X2 | ${X1}↖{-}$ | ${X1}↖{-}$ X2 | X1 ∧ X2 | ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
- в таблице истинности функции выбирают наборы аргументов, для которых логические формы равны 1 («истина»);
- все выбранные логические наборы как логические произведения аргументов записывают, последовательно соединив их между собой операцией логической суммы (дизъюнкции);
- для аргументов, которые являются ложными, в построенной записи проставляют операцию отрицания.
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Ответ: F(X1, X2) = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
- в таблице истинности выбирают наборы аргументов, для которых логические формы равны 0 («ложь»);
- все выбранные логические наборы как логические суммы аргументов записывают последовательно, соединив их между собой операцией логического произведения (конъюнкции);
- для аргументов, которые являются истинными, в построенной записи проставляют операцию отрицания.
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Ответ: X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2 = X1 ∧ ${X1}↖{-}$ ∨ X1 ∧ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ ${X2}↖{-}$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ 0 = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 = X2 ∧ (X1 ∨ ${X1}↖{-}$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ ${X3}↖{-}$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∪ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∨ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ = X2 ∧ X3 ∧ (X1 ∨ ${X1}↖{-}$) ∨ X1 ∧ ${X3}↖{-}$ ∧ (X2 ∨ ${X2}↖{-}$) = X2 ∧ X3 ∨ X1 ∧ ${X3}↖{-}$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 65.9%
Ответом к заданию 2 по информатике может быть цифра (число) или слово.
Задача 1
Дано логическое выражение, зависящее от 6 логических переменных:
¬(A → F) ∧ B ∧ ¬C ∧ (D → E).
Сколько существует различных наборов значений переменных, при которых выражение ложно?
Решение
Заметим, что все скобки и выражения связаны конъюнкцией, для которой сложно получить единицу. Поэтому будет решать от обратного. Посчитаем количество наборов, когда выражение истинно, тогда:
¬(A → F) = 1, тогда $A → F = 0$, следовательно, A = 1, F = 0.
B = 1.
¬C = 1, значит C = 0.
(D → E) = 1, тогда возможно 3 варианта: D = 0, E = 0; D = 0, E = 1; D = 1, E = 1.
Перемножим количество подходящих значений для каждой переменной: A, B, C, F — по одному набору, D и E — 3 набора. Итого:
1 х 3 = 3 набора, для которых вся функция истинна. Но нам нужно, чтобы функция была ложна. Найдём общее количество наборов по формуле $k = 2^N$, где N — количество переменных. У нас 6 переменных, значит всего наборов 64. Из них 3 нам не подходят. Тогда количество подходящих (ложных) наборов:
64 — 3 = 61.
Или при помощи программы на С++:
#include <iostream>
#include <algorithm>
#include <fstream>using namespace std;
bool f(int A, int B, int C, int D, int E, int F){
return (!(!A || F) && B && !C && (!D || E));
}int main() {
int count = 0;
for (int A = 0; A <= 1; ++A)
for (int B = 0; B <= 1; ++B)
for (int C = 0; C <= 1; ++C)
for (int D = 0; D <= 1; ++D)
for (int E = 0; E <= 1; ++E)
for (int F = 0; F <= 1; ++F)
if (f(A, B, C, D, E, F) == false)
count++;
cout << count;
return 0;
}
Ответ: 61.
Ответ: 61
Задача 2
Дано логическое выражение, зависящее от 5 логических переменных:
$(A ∨ ¬B) ∧ (¬C ∨ D ∨ ¬E)$.
Сколько существует различных наборов значений переменных, при которых выражение ложно?
Решение
В первой скобке 2 переменных, значит для неё будет 4 набора. Поскольку переменные соединяются дизъюнкцией, выражение ложно ровно в одном случае, а в трёх оставшихся — истинно.
Во второй скобке 3 переменных, значит для неё будет 8 наборов. Поскольку переменные соединяются дизъюнкцией, выражение ложно ровно в одном случае, а в семи оставшихся — истинно.
Конъюнкция ложна, когда хотя бы одна скобка ложна. Рассмотрим 3 случая:
Первая скобка ложна, вторая истинна. Первая скобка ложна в 1 случае из 4, вторая истинна в 7 случаях из 8. Итого 7 · 1 = 7.
Первая скобка истинна, вторая ложна. Первая скобка истинна в 3 случаях из 4, вторая ложна в 1 случае из 4. Итого 1 · 3 = 3.
Первая скобка ложна, вторая ложна. Первая скобка ложна в 1 случае из 4, вторая ложна в 1 случае из 8. Итого 1 · 1 = 1.
Суммарно: 7 + 3 + 1 = 11.
Ответ: 11.
Ответ: 11
Задача 3
Дано логическое выражение, зависящее от 5 логических переменных:
(¬A ∧ B ∧ C) ∨ (¬D ∧ ¬E).
Сколько существует различных наборов значений переменных, при которых выражение истинно?
Решение
В первой скобке 3 переменных, значит для неё будет 8 наборов. Поскольку переменные соединяются конъюнкцией, выражение истинно ровно в одном случае, а в семи оставшихся — ложно.
Во второй скобке 2 переменных, значит для неё будет 4 набора. Поскольку переменные соединяются конъюнкцией, выражение истинно ровно в одном случае, а в трёх оставшихся — ложно.
Дизъюнкция истинна, когда хотя бы одна скобка истинна. Рассмотрим 3 случая:
Первая скобка ложна, вторая истинна. Первая скобка ложна в 7 случаях из 8, вторая истинна в 1 случае из 4. Итого 7 · 1 = 7.
Первая скобка истинна, вторая ложна. Первая скобка истинна в 1 случае из 8, вторая ложна в 3 случаях из 4. Итого 1 · 3 = 3.
Первая скобка истинна, вторая истинна. Первая скобка истинна в 1 случае из 8, вторая истинна в 1 случае из 4. Итого 1 · 1 = 1.
Суммарно: 7 + 3 + 1 = 11.
Ответ: 11.
Ответ: 11
Задача 4
Логическая функция F задаётся выражением ((x∧z)∨¬x)∧¬w∧y. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F является истиной. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Строим таблицу истинности для логической функции любым способом и находим наборы, при которых функция ложна. Например, при помощи программы:
bool f(int x, int y, int z, int w){
return (((x && z) || !x) && !w && y);
}int main() {
cout << "x y z w F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
for (int w = 0; w <= 1; ++w)
if (f(x, y, z, w) == true)
cout << x << " " << y << " "
<< z << " " << w << " " << f(x, y, z, w) << endl;
return 0;
}
Получили наборы:
x y z w F
0 1 0 0 1
0 1 1 0 1
1 1 1 0 1
Начинаем сопоставление с исходной тбалицей:
1) столбец без единиц четвёртый в таблице из условия — это W
2) столбец с одной единицей третий в исходной таблице — это X
3) столбей с тремя единицами — это Y
4) столбец с двумя единицами — это Z
Результат: YZXW
Ответ: yzxw
Задача 5
Логическая функция F задаётся выражением (y → w) ∨ (¬x ∧ z). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Строим таблицу истинности для логической функции любым способом и находим наборы, при которых функция ложна. Например, при помощи программы:
bool f(int x, int y, int z, int w){
return ((!y || w) || (!x && z));
}int main() {
cout << "x y z w F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
for (int w = 0; w <= 1; ++w)
if (f(x, y, z, w) == false)
cout << x << " " << y << " "
<< z << " " << w << " " << f(x, y, z, w) << endl;
return 0;
}
Получили наборы:
x y z w F
0 1 0 0 0
1 1 0 0 0
1 1 1 0 0
Начинаем сопоставление с исходной тбалицей:
1) столбец без единиц второй в таблице из условия — это W
2) столбец с одной единицей третий в исходной таблице — это Z
3) столбей с тремя единицами — это Y
4) столбец с двумя единицами — это X
Результат: xwzy
Ответ: xwzy
Задача 6
Дан фрагмент таблицы истинности выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Сколько строк таблицы удовлетворяют выражению: F = (x1 ∨ x2 ∨ x3) ∧ x4 ∧ (x5 ∨ x6 ∨ x7) ∧ x8?
Решение
Данное выражение является конъюнкцией четырёх выражений. Конъюнкция нескольких высказываний истинна тогда и только тогда, когда истинными являются все входящие в неё высказывания. Следовательно, x4 = 1, x8 = 1 и в наборах значений переменных (x1, x2, x3), (x5, x6, x7) должна быть хотя бы одна 1.
Этим условиям удовлетворяют три последние строки таблицы. В каждой из этих строк значение функции F = 1. Следовательно, эти строки удовлетворяют заданному логическому выражению.
Чтобы остальные строки удовлетворяли заданному выражению, значение F должно быть равно 0. В таблице количество таких строк равно 5.
Всего значения 8 строк таблицы удовлетворяют заданному выражению.
Ответ: 8
Задача 7
Логическая функция F задаётся выражением (¬x → y) ∧ (z → y). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Переменная 1 ??? |
Переменная 2 ??? |
Переменная 3 ??? |
Функция F |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая 1-му столбцу; затем — буква, соответствующая 2-му столбцу; затем — буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x ∨ ¬y, зависящее от двух переменных x и y, и таблица истинности:
| Переменная 1 ??? |
Переменная 2 ??? |
Функция F |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение
Преобразуем исходное выражение.
(¬x → y) ∧ (z → y) = (x ∨ y) ∧ (¬z ∨ y) = y ∨ (x ∧ ¬z).
Так как дизъюнкция ложна только в том случае, когда ложны оба высказывания, входящие в неё, то переменной y должен соответствовать тот столбец, в котором значение 0 стоит в тех же строках, что и в столбце F. Следовательно, переменной y соответствует третий столбец.
Рассмотрим строку, в которой значение функции отличается от значения переменной y. Такой строкой является четвёртая снизу. Здесь переменная y = 0, а значение функции F = 1. Это означает, что x ∧ ¬z = 1. В рассматриваемой строке значение первого столбца 0, а второго 1. Пусть x = 0, z = 1. При этих значениях логическое выражение x ∧ ¬z ложно, что не соответствует табличному значению функции F = 1. Следовательно, x = 1, z = 0. Значит, первый столбец соответствует переменной z, а второй—x.
Или при помощи программы на С++:
Выводим только ложные наборы, потому что их меньше
#include <iostream>
#include <algorithm>
#include <fstream>using namespace std;
bool f(int x, int y, int z){
return ((x || y) && (!z || y));
}int main() {
cout << "x y z F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
if (f(x, y, z) == false)
cout << x << " " << y << " "
<< z << " " << f(x, y, z) << endl;
return 0;
}
Ответ: zxy
Задача 8
Логическая функция F задаётся выражением ((¬z∨¬x)∧z)∨w∨¬y. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Задача 9
Логическая функция F задаётся выражением (y ∧ (w → x)) → g. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, w, g.
| F | ||||
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
В ответе напишите буквы x, y, w, g в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Задача 10
Логическая функция F задаётся выражением (x → y) → (w → g). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, w, g.
| F | ||||
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
В ответе напишите буквы x, y, w, g в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Задача 11
Логическая функция F задаётся выражением (x = y) ∨ ¬(y → w) ∨ z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| F | ||||
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | ||
| 0 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Если бы функция F была задана выражением x ∨ ¬y, зависящим от двух переменных x и y, а фрагмент таблицы истинности имел бы вид:
тогда 1-му столбцу соответствовала бы переменная y, а 2-му столбцу — переменная x. В ответе следовало бы написать: yx.
Задача 12
Логическая функция F задаётся выражением (x = y)∨(x∧w)∨¬z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| F | ||||
| 1 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Если бы функция F была задана выражением x ∨ ¬y, зависящим от двух переменных x и y, а фрагмент таблицы истинности имел бы вид:
тогда 1-му столбцу соответствовала бы переменная y, а 2-му столбцу — переменная x. В ответе следовало бы написать: yx.
- Уроки Информатики
- 11 класс
- Подготовка к ЕГЭ

Основано на: демонстрационных вариантах ЕГЭ по информатике за 2015 год, на учебнике Босовой Людмилы Леонидовны
В предыдущей части 1 мы разобрали с вами логические операции Дизъюнкция и Конъюнкция, нам с вами осталось разобрать инверсию и перейти к решению задания ЕГЭ.
Инверсия
Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Для записи инверсии используются следующие знаки: НЕ, `¯` , `¬`
Инверсия определяется следующей таблицей истинности:
Инверсию иначе называют логическим отрицанием.
Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.
Логические операции имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.
И так, перед нами задание №2 из ЕГЭ по информатике 2015 года
Задание:
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
x1 x2 x3 x4 x5 x6 x7 x8 F 0 1 0 1 0 1 1 1 1 Каким выражением может быть F?
1) x1 / ¬x2 / x3 / ¬x4 / x5 / x6 / ¬x7 / ¬x8
2) x1 / x2 / x3 / ¬x4 / ¬x5 / ¬x6 / ¬x7 / ¬x8
3) ¬x1 / x2 / ¬x3 / x4 / x5 / ¬x6 / x7 / x8
4) x1 / ¬x2 / x3 / ¬x4 / ¬x5 / ¬x6 / ¬x7 / ¬x8
Значительно облегчает решение задания то, что в каждом варианте сложного выражения F только одна логическая операция: умножение или сложение. В случае умножения / если хотя бы одна переменная будет равна нулю, то значение всего выражения F так же должно быть равно нулю. А в случае со сложением V если хотя бы одна переменная будет равна единице, то значение всего выражения F должно быть равно 1.
Тех данных, которые есть в таблице по каждой из 8 переменных выражения F, нам вполне достаточно для решения.
Проверим выражение номер 1:
- по первой строчке таблицы x2=0, х8=1 мы с вами видим что F=0 (? / 1 / ? / ? / ? / ? / ? / 0)
- по второй строчке таблицы x1=1, х4=0 мы с вами видим что F возможно и может быть равным = 1, если все остальные переменные равны 1 (1 / ? / ? / 1 / ? / ? / ? / ?)
- по третьей строчке таблицы x4=1, х8=1 мы с вами видим что F=0 (? / ? / ? / 0 / ? / ? / ? / 0), а в таблице у нас F=1, и это значит, что выражение под номером один нам ТОЧНО НЕ ПОДХОДИТ.
Проверим выражение номер 2:
- по первой строчке таблицы x2=0, х8=1 мы с вами видим что F возможно и может быть равным = 0, если все остальные переменные равны 0 (? V 0 V ? V ? V ? V ? V ? V 0)
- по второй строчке таблицы x1=1, х4=0 мы с вами видим что F = 1 (1 V ? V ? V 1 V ? V ? V ? V ?)
- по третьей строчке таблицы x4=1, х8=1 мы с вами видим что F возможно и может быть равным = 1, если хотя бы одна из оставшихся переменных будет равна 1 (? V ? V ? V 0 V ? V ? V ? V 0)
Проверим выражение номер 3:
- по первой строчке таблицы x2=0, х8=1 мы с вами видим что F=0 (? / 0 / ? / ? / ? / ? / ? / 1)
- по второй строчке таблицы x1=1, х4=0 мы с вами видим что F =0 (0 / ? / ? / 0 / ? / ? / ? / ?), а в таблице у нас F=1, и это значит, что выражение под номером три нам ТОЧНО НЕ ПОДХОДИТ.
Проверим выражение номер 4:
- по первой строчке таблицы x2=0, х8=1 мы с вами видим что F=1 (? V 1 V ? V ? V ? V ? V ? V 0), а в таблице у нас F=0, и это значит, что выражение под номером четыре нам ТОЧНО НЕ ПОДХОДИТ.
В решении задания на едином государственном экзамене вам нужно поступать точно таким же образом: отбрасывать те варианты, которые точно не подходят по тем данным, которые есть в таблице. Оставшийся возможный вариант (как в нашем случае вариант номер 2) и будет правильным ответом.
Все статьи раздела
- Коменты VK
- Анонимные коменты, G+ или Facebook
Сегодняшний урок посвящён 15 заданию из ЕГЭ по информатике 2022.
Темой этого урока связана с преобразованием логических выражений.
Теорию для преобразования логических выражений Вы можете посмотреть в этой статье. Как можно работать с логическими выражениями на питоне, можно прочитать в этой статье.
Перейдём к практике решения задач 15 задания из ЕГЭ по информатике 2022.
Задача (Неравенство, одна переменная)
Какое количество натуральных чисел удовлетворяет логическому условию:
¬(X2 ≥ 9) ∨ ¬((X < 7) ∨ (X ≥ 10)) ?
Решение:
Первый способ (с помощью питона).
k=0 for x in range(1, 1000): if not(x**2 >= 9) or not((x < 7) or (x>=10)): k = k + 1 print(k)
Здесь перебираем с помощью цикла for натуральные числа от 1 до 1000.
Если логическое выражение выдаёт истину, то мы подсчитываем такой вариант.
Программа напечатает число 5.
Второй способ (с помощью рассуждений).
Натуральные числа — это целые, положительные числа. Например: 1, 2, 3, 4, и т. д.
Преобразуем первое выражение ¬(X2 ≥ 9) = (X2 < 9). Отрицание внесли в скобки. В этом случае знак, который находится в скобках, нужно поменять на противоположный.
Важно: Если было строгое неравенство, то оно станет нестрогим, и наоборот, если было неравенство нестрогим, то оно станет строгим.
Получается, что выражение (X2 < 9) будет истинно только при двух значениях: X = 1, X = 2.
Во втором выражении ¬((X < 7) ∨ (X ≥ 10)) удобно применить формулу Де Моргана.
Формула де Моргана:
¬(A ∨ B) = ¬A ∧ ¬B
¬(A ∧ B) = ¬A ∨ ¬B
Преобразуем выражение по формуле де Моргана и внесём отрицание в скобки:
¬((X < 7) ∨ (X ≥ 10)) = ¬(X < 7) ∧ ¬(X ≥ 10) = (X ≥ 7) ∧ (X < 10)
Получилось выражение (X ≥ 7) ∧ (X < 10). Между двумя выражениями стоит логическое умножение. Значит, одновременно должны выполняться и первое неравенство, и второе. Таким образом, получается, что подходят три значение для выражения (X ≥ 7) ∧ (X < 10). Это X = 7, X = 8, X = 9.
Обратимся к самому начальному логическому условию. Там два выражения соединятся логическим сложением. Значит, мы должны объединить те случаи, когда у нас первое выражение становится истинным (X=1, X=2), и те случаи, когда второе выражение становится истинным (X = 7, X = 8, X = 9).
Получается всего 5 натуральных чисел удовлетворяют изначальному логическому условию.
Ответ: 5
Разберём ещё одну разминочную задачу для подготовки к ЕГЭ по информатике 2022.
Задача (Неравенство, две переменные)
Для какого наибольшего целого неотрицательного числа A выражение
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 205)
тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x >= A) or (y >= A) or (x * y <= 205): k=k+1 if k==90000: print(A)
В первом цикле перебираем значения для A. Здесь мы пытаемся подобрать ответ в диапазоне от 0 до 300. Этот диапазон меньше, чем в прошлой задаче. Потому что здесь три вложенных цикла, и если перебирать числа от 0 до 1000, то программа может работать очень долго. При необходимости можно указать другой диапазон.
Для каждого A устанавливаем счётчик k в ноль.
Затем перебираем все числа в диапазоне от 1 до 300 (включительно) для переменных x и y, тем самым имитируем фразу «для любых x и y».
Если логическое выражение сработает при каждом значении x и y, то считается, что значение A нам подходит, и в счётчике по окончанию вложенных циклов будет значение 90000 (300 * 300 = 90000).
Наибольшее число, которое напечатает программа равно 15.
Второй способ (с помощью рассуждений).
Здесь есть три выражения в скобках, которые соединены логическим сложением. При логическом сложении достаточно хотя бы одного выражения, где будет истина, чтобы всё общее выражение было истинно.
Если мы сделаем A слишком большим, к примеру A = 250, то найдутся такие x = 16, y = 16, при которых все три условия в скобках не будут выполняться, и, значит, всё общее выражение будет ложным.
Следовательно, нам нужно выбрать таким A, чтобы не было возможности подобрать x, y, при которых все три выражения ложны.
Сделаем так: пока x и y меньше A, должно «работать» третье выражение в скобках. Как только x или y сравняются с A — начинают «работать» первое или второе выражение.
До какого же максимального значения могут дойти x и y, чтобы перемножение этих двух чисел было меньше или равно 205 (x * y <= 205) ?
15 * 15 = 225
14 * 14 = 196
Получается, пока числа x и y меньше 15, «выручает» третье выражение (x * y ≤ 205), как только станут x ≥ 15 и y ≥ 15, будут «работать» первое и второе выражение.
Отсюда получаем, что максимальное число A = 15
Ответ: 15
Задача (Функция ДЕЛ)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула
¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(x, A) or (not(D(x, 6)) or not(D(x, 9))): k=k+1 if k==1000: print(A)
Здесь мы формируем функцию ДЕЛ (функцию D). Если n делится на m, то функция возвращает Истину, в противном случае функция возвращает Ложь.
Далее решаем примерно так же, как и в прошлых задачах: для каждого числа A перебираем все значения x. Следование расписываем по формуле A ⟶ B = ¬A ∨ B.
Наибольшее число здесь получается равно 18.
Второй способ (с помощью рассуждений).
Рассмотрим случай, когда в левой части логического выражения будет 1, а в правой 0. В остальных случаях беспокоится не за что, потому что вся формула будет выдавать истину.
Посмотрим, когда в правой части получается ноль. Функция ДЕЛ(x, 6) должна выдавать истину. Т.е. x должен делится на 6. А функция ¬ДЕЛ(x, 9) должна выдавать ноль. Т.е. без отрицания ДЕЛ(x, 9) должна выдавать истину. Значит, x так же делится на 9.
x делится на 6 => x = 2*3*n, n ∈ N
x делится на 9 => x = 3*3*n, n ∈ N
Чтобы выполнялся случай, когда в правой части получается ноль, икс должен быть равен x = 3*3*2*n (n ∈ N). Т.е. получается, что икс должен быть кратен 18.
Т.е. получается, что когда x делится на 18, в правой части логического выражения будет получатся ноль. Чтобы спасти ситуацию, мы должны в левой части логического выражения не получать 1. Следовательно, ¬ДЕЛ(x, А) должно выдавать ноль. Значит, ДЕЛ(x, А) должно выдавать 1. Таким образом, приходим к выводу, что A должно равняться 18.
Если получится опасная ситуация, когда x кратен 18, то она будет нейтрализована, ведь в левой части будет получатся ноль.
Ответ: 18
Ещё один важный тип задач 15 задания ЕГЭ по информатике 2022
Задача (Поразрядная конъюнкция)
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102 & 01012 = 4
Для какого наименьшего неотрицательного целого числа A формула
x&51 ≠ 0 → (x&A = 0 → x&25 ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?
Решение:
Первый способ (с помощью питона).
for A in range(0, 1000): k=0 for x in range(0, 1000): if x&51==0 or (x&A!=0 or x&25!=0): k=k+1 if k==1000: print(A)
Здесь следование преобразовываем по формуле: A ⟶ B = ¬A ∨ B. Так же и A, и x неотрицательные числа. Поэтому мы перебираем их диапазон, начиная с нуля. Из-за этого в цикле, который перебирает переменную x, мы устанавливаем верхнюю границы равной 1000, а не 1001. Тогда тоже будет 1000 повторений в этом цикле.
Наименьшее число равно 34.
Второй способ (с помощью рассуждений).
Переведём числа 51 и 25 в двоичную систему.
51 = 1100112
25 = 110012
Формула будет тождественно ложна, когда
Этого допустить нельзя!
При каком x получается в левой выражении формулы истина ? Если у икса в двоичном представлении в тех разрядах, где у числа 51 стоят 1, будет хотя бы в одном месте 1.
Рассмотрим правое выражение формулы. Ноль получается в единственном случае:
Рассмотрим выражение x&25 ≠ 0. Чтобы в этом логическом выражении получился ноль, нужно x&25 = 0. Посмотрим на двоичное представление числа 25. В тех разрядах, где стоят единицы, у икс должны быть нули (для x&25 = 0).
Сформулируем окончательное условие для x, при котором возникает опасность превращение общей формулы в ложь.
Нам нужно «поломать эту песенку» с помощью x&A = 0. Т.е. нельзя допускать, чтобы это выражение было истинно.
Получается, что A = 1000102. Это наименьшее из возможных число, при котором мы точно себя обезопасим от того, что вся формула будет ложна.
A = 1000102 в десятичной системе будет 34.
Ответ: 34
Ещё один тип задач 15 задания ЕГЭ по информатике
Задача (числовая прямая)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула (¬(x ∈ P) → (x ∈ Q)) → (x ∈ A ) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) or F(8, 19, x))) or F(a, b, x): k=k+1 if k==400: mn= min(mn, b-a) print(mn)
Получается ответ 14. Более подробно, как решать задачи на ОТРЕЗКИ из 15 задания ЕГЭ по информатике на Python, можете посмотреть в этой статье.
Второй способ (с помощью рассуждений).
Если будут такие варианты:
То нам беспокоится не о чём. Потому что формула всегда будет истинна! (см. таблицу истинности для следования →)
Нас же будет интересовать этот случай.
При таком раскладе вся формула будет ложна! Нам нужно этого не допустить при любом значении x!
Единица получается в первом подвыражении в трёх случаях:
1) Случай
Выражение ¬(x ∈ P) получается ложно, когда (x ∈ P) будет истинно! Получается при x ∈ [5, 13] выражение ¬(x ∈ P) — ложно!
Выражение (x ∈ Q) ложно, когда x ∉ [8, 19]
Какой же минимальной длины должен быть отрезок A, чтобы этот случай не проходил при любом x ? При этом случае отрезок A должен быть равен [5, 8). Тогда левое выражение пусть и может стать единицей при x ∈ [5, 8), но выражение (x ∈ A) будет также равно 1 при x ∈ [5, 8)! И схема 1 → 0 не пройдёт. Будет 1 → 1.
Для 1 случая A=[5, 
2) Случай
При каких x выражение ¬(x ∈ P) обращается в ноль, мы уже рассматривали: x ∈ [5, 13].
Второе выражение «выдаёт» 1 при x ∈ [8, 19].
Получается, что при при x ∈ [8; 13] первое выражение в скобках в главной формуле будет тождественно истинно!
С помощью отрезка A нужно это нейтрализовать путём превращения второго выражения в скобках в главной формуле в 1, пока x ∈ [8; 13]. Значит, для этого случая A = [8; 13]
3) Случай
В выражении ¬(x ∈ P) единица получается, когда в выражении (x ∈ P) получается ноль. Тогда x ∉ [5, 13]!
Чтобы во втором выражении (x ∈ Q) была единица, нужно, чтобы x ∈ [8, 19].
Получается, что 3 случай выполняется, если x ∈ (13, 19].
С помощью отрезка A нужно этому противодействовать! Нужно чтобы выражение (x ∈ A) было всегда 1 при x ∈ (13, 19]. Тогда A должно быть (13, 19].
Следовательно, для третьего случая A=(13, 19].
Нам нельзя допустить ни одного случая! Поэтому, объединив все случаи, получаем, что A=[5, 19].
Длина отрезка равна 14.
Ответ: 14
Ещё одна задача про числовую прямую из банка тренировочных заданий ЕГЭ по информатике 2021.
Задача (Числовая прямая, закрепление)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ ¬(x ∈ A)) → ((x ∈ Q) ∧ ¬(x ∈ A)) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) and not(F(a, b, x)))) or (F(8, 19, x) and not(F(a, b, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Второй способ (с помощью рассуждений).
Формула может быть ложна, когда
Во всех остальных случаях, формула всегда верна.
Чтобы выражение ((x ∈ P) ∧ ¬(x ∈ A)) было тождественно 1, выражение (x ∈ P) обязательно должно быть тождественно 1. А, значит, x ∈ [5, 13] — это опасная зона, при которой появляется возможность обратить всю формулу в ноль!
Мы можем сразу пресечь эту опасность с помощью отрезка A. Выбрать такой отрезок, чтобы он всегда «выдавал» ложь при x ∈ [5, 13]. Для этого достаточно выбрать A=[5, 13]! Но вдруг его можно сделать ещё более маленьким за счёт правой части формулы ?
Предположим, что отрезок A сделали ещё меньшим. Тогда при каком-то x (x ∈ [5, 13]) выражение ¬(x ∈ A) будет «выдавать» 1! Причём такое же выражение стоит и в правой части формулы! Там тоже будет 1 для выражения ¬(x ∈ A).
Нас же в этом случае должно выручить выражение (x ∈ Q). Если оно «выдаст» 1 в этот «сложный» момент, то мы спасены! Ведь тогда получается, что правая часть всей формулы будет «выдавать» не 0, а 1. Посмотрим при каких x из отрезка [5, 13] приходит это спасение.
Видим, что в интервале x ∈ [8, 13] нас спасает выражение (x ∈ Q).
Значит, отрезок A можно сократить до A=[5, 8).
Длина отрезка будет равна 3!
Ответ: 3
Задачи для закрепления
Задача (Неравенство, две переменные, закрепление)
Для какого наибольшего целого неотрицательного числа A выражение
(x < A) ∧ (y < A) ∧ (x * y > 603)
тождественно ложно, т.е. принимает значение 0 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if not( (x < A) and (y < A) and (x * y > 603) ): k=k+1 if k==90000: print(A)
Т.к. выражение должно быть ЛОЖНО, то обернём логическое выражение в функцию not(). Видим, что программа не сильно отличается от прошлой задачи. Данный шаблон подходит для большинства задач подобного типа.
Наибольшее число получается равно 25.
Второй способ (с помощью рассуждений).
В этой задаче нужно, чтобы общее выражение было ложно!
Если мы поставим отрицание над всем выражением, то можно искать такое максимальное A, при котором всё выражение тождественно истинно, а не ложно!
¬((x < A) ∧ (y < A) ∧ (x * y > 603)) = ¬(x < A) ∨ ¬(y < A) ∨ ¬(x * y > 603)
Здесь применили формулу де Моргана! Т.е. каждое подвыражение получило отрицание + соединительная логическая операция (логическое умножение) сменилась на противоположную операцию (логическое сложение).
Внесём отрицание в скобки. Получается:
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 603)
Получили ситуацию, как в прошлой задаче! Напомню, что теперь нужно, чтобы общее выражение было истинно.
Найдём максимальное число, до которого могут «подняться» x и y, чтобы ещё работало третье выражение!
Обратите внимание, что x и y — симметричны. Значит, что верхняя планка для x и y будет одно и тоже число.
Поэтому вспоминаем таблицу квадратов.
25 * 25 = 625
24 * 24 = 576
Получается, что максимальное число до которого могут «дойти» x и y, чтобы «работало» третье выражение, равно 24.
Тогда, начиная с 25 для x и y, должны работать первое и второе выражение.
Получается, что максимальное число для A равно 25.
Ответ: 25
Ещё одна задачка подобного типа из тренировочных упражнений 15 задания ЕГЭ по информатике.
Задача (Неравенство, две переменные, закрепление)
Для какого наименьшего целого числа A формула
(3 * x + y < A) ∨ (x < y) ∨ (16 ≤ x)
тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(-300, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (3*x + y < A) or (x < y) or (16 <= x): k=k+1 if k==90000: print(A)
Наименьшее число равно 61. Здесь не сказали, что A принимает неотрицательные значения, поэтому мы включили в диапазон для A числа, которые меньше нуля. Из-за этого увеличилось время выполнения программы, но ответ получим за приемлемое время.
Второй способ (с помощью рассуждений).
Чтобы вся формула была тождественно истинна, нужно, чтобы хотя бы одно выражение «выдавало» истину, т.к. выражения в формуле соединяются с помощью логического сложения!
Взглянем на третье выражение. Пока x ≥ 16, всё идёт как надо. Третье выражение будет истинно, и, значит, вся формула будет истинна.
Но если x ≤ 15, то нужно, чтобы нас «спасало» первое или второе выражение.
Рассмотрим второе выражение. Пока y > x (x ≤ 15) => y > 15, у нас всё нормально, второе выражение будет истинно, и вся формула будет истинна.
Теперь обратим внимание на первое выражение. Оно должно нас «спасать», когда третье и второе выражение «не спасло»! Это возможно, если x ≤ 15 (иначе «спасло» бы третье выражение), а так же y ≤ 15 (иначе «спасало» бы второе выражение).
Но, чтобы первое выражение было всегда истинно при x ≤ 15 и y ≤ 15, мы должны подобрать число A при максимальных x и y (x=15, y=15)! Ведь для более маленьких значений выражение (3 * x + y < A) точно будет истинно.
Получается:
3 * 15 + 15 < A
60 < A
Нужно найти наименьшее число для A, при котором A > 60. Тогда там, где не «спасли» третье и второе выражение, точно «спасёт» первое выражение. Получается A = 61.
Ответ: 61
Задача (ЕГЭ по информатике, Москва, 2020)
Для какого наибольшего целого неотрицательного числа A выражение
(x > A) ∨ (y > x) ∨ (2 * y + x < 110)
тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x > A) or (y > x) or (2 * y + x < 110): k=k+1 if k==90000: print(A)
Максимальное число получается равно 36.
Второй способ (с помощью рассуждений).
Пока y > x, второе подвыражение всегда истинно, значит, и всё выражение истинно.
Теперь будем рассматривать случай y ≤ x.
Рассмотрим третье подвыражение. Найдём максимальные значения для x и для y, которые они одновременно могут принимать, и при которых ещё выполняется третье условие.
Т.к. мы рассматриваем случай y ≤ x, то максимальное число для y будет xmax т.е. ymax = xmax.
Тогда
2 * xmax + xmax < 110
3 * xmax < 110
36 * 3 = 108
37 * 3 = 111
xmax = ymax = 36
Если x «перевалит» за 36, и при этом y ≤ x (иначе «спасает» второе подвыражение), то должно «спасать» первое выражение.
Получается, что наибольшее значение A будет равно 36.
Ответ: 36
Следующий тип задач часто можно встретить в тренировочных вариантах ЕГЭ по информатике 2022.
Задача (С функцией ДЕЛ, закрепление)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула
ДЕЛ(120, A) ∧ ((ДЕЛ(x, 70) ∧ ДЕЛ(x, 30)) → ДЕЛ(x, A))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(120, A) and (not(D(x, 70) and D(x, 30)) or D(x, A)): k=k+1 if k==1000: print(A)
Наибольшее число получается равно 30.
Второй способ (с помощью рассуждений).
Рассмотрим левую часть логического выражения. Мы видим, что число 120 должно делится на A. Значит, для A уже есть некоторое ограничение (A <= 120).
Рассмотрим правую часть выражения. Изучим, когда она превращается в ноль. Тогда
Т.е. x должен делится на 70 и одновременно x должен делится на 30.
x = 70*n = 2*5*7*n (n ∈ N)
x = 30*n = 2*5*3*n (n ∈ N)
Чтобы одновременно выполнялись два условия, икс должен быть равен x = 2*5*7*3*n (n ∈ N).
Для того, чтобы правое выражение не превращалось в ноль, x как раз должен делится на число 2*5*7*3. Тогда будет 1->1. Т.е. число A должно равняться 2*5*7*3. Но мы сказали, что A <= 120, плюс, должно являться делителем числа 120. Значит, должны снизить значение для A.
Рассмотрим значение 2*5*7 для числа A (Предыдущее число, но без тройки). Для правой части оно подходит, т.к. «при малейшей» возможности превращения правого выражения в ноль (т.е. ДЕЛ(x, 70) = True), у нас будет спасаться ситуация, т.к. ДЕЛ(x, A) так же
будет равно 1. И снова получаем 1->1. Но это значение не подходит для левой части, ведь тогда A не является делителем числа 120.
Приходится брать число 2*5*3 (без семёрки). Здесь ситуация аналогично предыдущему случаю, только теперь это число является делителем числа 120.
В ответе напишем 30.
Ответ: 30
Задача (Поразрядная конъюнкция, закрепление)
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение:
Первый способ (с помощью питона).
for A in range(1, 1000): k=0 for x in range(1, 1001): if (x&49==0) or ((x&33!=0) or (x&A!=0)): k=k+1 if k==1000: print(A)
Наименьшее число равно 16.
Второй способ (с помощью рассуждений).
Переведём числа 49 и 33 в двоичную систему.
4910 = 1100012
3310 = 1000012
Рассмотрим случай, когда функция стремится превратится в ноль.
Чтобы левое выражение выдавало истину, икс должен иметь 1 (единицу) в первом разряде или во второй разряде, или в последнем разряде (в 6-ти битном числе).
Рассмотрим правое выражение. Посмотрим, когда выражение (X & 33 = 0) выдаёт истину. Первый бит и последний бит должен быть равен нулю. Т.е получается, что в 6-ти битном числе нас интересует второй бит. Если он будет равен 1 и при этом первый бит и последний будут равны 0, то возникает опасная ситуация, которую нужно спасть.
При выше описанных условиях выражение (X & A ≠ 0) должно выдавать истину. Тогда наименьшее A равно 100002 = 162.
Ответ: 16
Задача (числовая прямая, закрепление 2)
На числовой прямой даны два отрезка: P = [20, 30] и Q = [35, 60]. Найдите наименьшую возможную длину отрезка A, при котором формула
¬(x ∈ A) ∧ ((x ∈ P) ∨ (x ∈ Q))
тождественно ложна, то есть принимает значение 0 при любых x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not(not(F(a, b, x)) and (F(20, 30, x) or F(35, 60, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Ответ будет 40.
Второй способ (с помощью рассуждений).
Рассмотрим наоборот, когда логическое выражение выдаёт истину.
В правой части получается 1, когда x ∈ P или x ∈ Q. Именно в эти моменты выражение ¬(x ∈ A) должно спасать ситуацию и выдавать 0. Тогда без отрицания (x ∈ A) должно выдавать 1. Чтобы покрыть два отрезка, берём A=[20; 60].
Минимальная длина получается 60-20=40.
Ответ: 40
На этом всё! Увидимся в новых уроках по подготовке к ЕГЭ по информатике!
Добрый день! А как в 5 задаче (про числовую прямую) получился ответ 14?
В конце же получается, что A принадлежит [5, 19], то есть длина отрезка 15.
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 — 15 штук
Или я что-то неправильно понял?
Считается количество единиц, а не сколько целых чисел в этом отрезке.
И в самой последней задаче на закрепление, у вас, видимо, та же ошибка. Не 40, а 41 должно быть?
Как решать 15 задание с «~» тильдой на питоне?
Как например это задание:
На числовой прямой даны два отрезка: P = [7, 14] и Q = [9, 11]. Укажите наибольшую возможную длину промежутка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)
Грамотное объяснение. Безумно здорово, что есть объяснения как на питон (перебором) так и чисто в математической форме, потому что в информатике оба подхода, мне кажется, равносильны. Спасибо