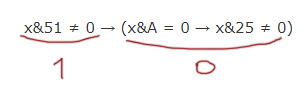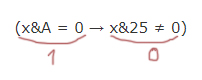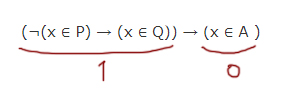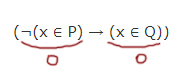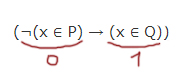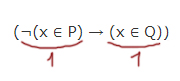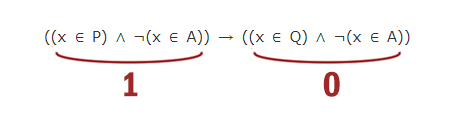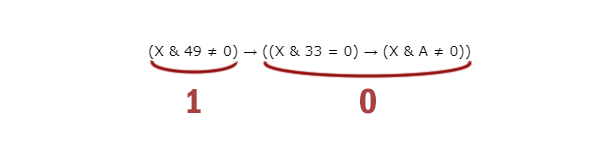На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Всего: 191 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.
Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наибольшего целого числа А формула
x&51 = 0 ∨ (x&41 = 0 → x&А = 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.
Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x&51 = 0 ∨ (x&41 = 0 → x&А = 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
На числовой прямой даны два отрезка: P = [17, 46] и Q = [22, 57]. Отрезок A таков, что приведённая ниже формула истинна при любом значении переменной х:
¬(x ∈ A) →(((x ∈ P) ⋀ (x ∈ Q)) → (x ∈ A))
Какова наименьшая возможная длина отрезка A?
На числовой прямой даны два отрезка: Р = [30, 45] и Q = [40, 55]. Какова наименьшая возможная длина интервала A, что обе приведённые ниже формулы истинны при любом значении переменной х:
( ¬(x ∈ A) → (¬(x ∈ P)) )
((x ∈ Q)→ (x ∈ A))
На числовой прямой даны два отрезка: Р = [3, 38] и Q = [21, 57]. Какова наибольшая возможная длина интервала A, что логическое выражение
((х ∈ Q) → (х ∈ Р)) → ¬(х ∈ A)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: P = [1, 39] и Q = [23, 58]. Какова наибольшая возможная длина интервала A, что логическое выражение
((x ∈ P) → ¬(x ∈ Q)) → ¬(x ∈ А)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
(x ∈ D) → ((¬(x ∈ C)∧ ¬(x ∈ A)) → ¬(x ∈ D))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Источник: Демонстрационная версия ЕГЭ−2022 по информатике
На числовой прямой даны два отрезка: P = [4, 15] и Q = [12, 20].
Укажите наименьшую возможную длину отрезка A, для которого выражение
((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: P = [20, 50] и Q = [30,65]. Отрезок A таков, что формул
¬(x ∈ A) → ((x ∈ P) →¬ (x ∈ Q))
истинна при любом значении переменной x. Какова наименьшая возможная длина отрезка A?
Источник: ЕГЭ по информатике 23.03.2016. Досрочная волна
На числовой прямой задан отрезок A. Известно, что формула
((x ∈ A) → (x2 ≤ 100)) ∧ ((x2 ≤ 64) → (x ∈ A))
тождественно истинна при любом вещественном x. Какую наименьшую длину может иметь отрезок A?
На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Какова наибольшая возможная длина интервала A, что формула
( (x ∈ А) → (x ∈ P) ) ∨ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны три отрезка: P = [10, 40], Q = [5, 15] и R = [35, 50]. Какова наименьшая возможная длина промежутка A, что формула
( (x ∈ А) ∨ (x ∈ P) ) ∨ ((x ∈ Q)→ (x ∈ R))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: P = [12, 62] и Q = [32, 92].
Какова наименьшая возможная длина интервала A, что формула
(¬(x ∈ А) ∧ (x ∈ Q)) → (x ∈ P)
тождественно истинна, т. е. принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: P = [8, 39] и Q = [23, 58].
Какова наименьшая возможная длина интервала A, при которой выражение
((x ∈ P) ∨ (x ∈ А)) → ((x ∈ Q) ∨ (x ∈ А))
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: P = [17, 54] и Q = [37, 83]. Какова наименьшая возможная длина интервала A, что формула
(x ∈ P) → (((x ∈ Q) ∧ ¬(x ∈ A)) → ¬(x ∈ P))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Источник: ЕГЭ по информатике 2021. Досрочная волна
Элементами множества А являются натуральные числа. Известно, что выражение
(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Элементами множества А являются натуральные числа. Известно, что выражение
(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {4, 8, 12, 16}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
На числовой прямой даны два отрезка: Р = [22, 72] и Q = [42, 102]. Какова наименьшая возможная длина интервала A, что логическое выражение
¬(¬(х ∈ А) ∧ (х ∈ Р)) ∨ (х ∈ Q)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: Р = [12, 62] и Q = [52, 92]. Какова наименьшая возможная длина интервала A, что логическое выражение
¬(¬(х ∈ А) ∧ (х ∈ Р)) ∨ (х ∈ Q)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
На числовой прямой даны два отрезка: P = [3, 13] и Q = [12, 22]. Какова наибольшая возможная длина интервала A, что формула
((х ∈ A) → (х ∈ Р)) ∨ (х ∈ Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Всего: 191 1–20 | 21–40 | 41–60 | 61–80 …
Сегодняшний урок посвящён 15 заданию из ЕГЭ по информатике 2022.
Темой этого урока связана с преобразованием логических выражений.
Теорию для преобразования логических выражений Вы можете посмотреть в этой статье. Как можно работать с логическими выражениями на питоне, можно прочитать в этой статье.
Перейдём к практике решения задач 15 задания из ЕГЭ по информатике 2022.
Задача (Неравенство, одна переменная)
Какое количество натуральных чисел удовлетворяет логическому условию:
¬(X2 ≥ 9) ∨ ¬((X < 7) ∨ (X ≥ 10)) ?
Решение:
Первый способ (с помощью питона).
k=0 for x in range(1, 1000): if not(x**2 >= 9) or not((x < 7) or (x>=10)): k = k + 1 print(k)
Здесь перебираем с помощью цикла for натуральные числа от 1 до 1000.
Если логическое выражение выдаёт истину, то мы подсчитываем такой вариант.
Программа напечатает число 5.
Второй способ (с помощью рассуждений).
Натуральные числа — это целые, положительные числа. Например: 1, 2, 3, 4, и т. д.
Преобразуем первое выражение ¬(X2 ≥ 9) = (X2 < 9). Отрицание внесли в скобки. В этом случае знак, который находится в скобках, нужно поменять на противоположный.
Важно: Если было строгое неравенство, то оно станет нестрогим, и наоборот, если было неравенство нестрогим, то оно станет строгим.
Получается, что выражение (X2 < 9) будет истинно только при двух значениях: X = 1, X = 2.
Во втором выражении ¬((X < 7) ∨ (X ≥ 10)) удобно применить формулу Де Моргана.
Формула де Моргана:
¬(A ∨ B) = ¬A ∧ ¬B
¬(A ∧ B) = ¬A ∨ ¬B
Преобразуем выражение по формуле де Моргана и внесём отрицание в скобки:
¬((X < 7) ∨ (X ≥ 10)) = ¬(X < 7) ∧ ¬(X ≥ 10) = (X ≥ 7) ∧ (X < 10)
Получилось выражение (X ≥ 7) ∧ (X < 10). Между двумя выражениями стоит логическое умножение. Значит, одновременно должны выполняться и первое неравенство, и второе. Таким образом, получается, что подходят три значение для выражения (X ≥ 7) ∧ (X < 10). Это X = 7, X = 8, X = 9.
Обратимся к самому начальному логическому условию. Там два выражения соединятся логическим сложением. Значит, мы должны объединить те случаи, когда у нас первое выражение становится истинным (X=1, X=2), и те случаи, когда второе выражение становится истинным (X = 7, X = 8, X = 9).
Получается всего 5 натуральных чисел удовлетворяют изначальному логическому условию.
Ответ: 5
Разберём ещё одну разминочную задачу для подготовки к ЕГЭ по информатике 2022.
Задача (Неравенство, две переменные)
Для какого наибольшего целого неотрицательного числа A выражение
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 205)
тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x >= A) or (y >= A) or (x * y <= 205): k=k+1 if k==90000: print(A)
В первом цикле перебираем значения для A. Здесь мы пытаемся подобрать ответ в диапазоне от 0 до 300. Этот диапазон меньше, чем в прошлой задаче. Потому что здесь три вложенных цикла, и если перебирать числа от 0 до 1000, то программа может работать очень долго. При необходимости можно указать другой диапазон.
Для каждого A устанавливаем счётчик k в ноль.
Затем перебираем все числа в диапазоне от 1 до 300 (включительно) для переменных x и y, тем самым имитируем фразу «для любых x и y».
Если логическое выражение сработает при каждом значении x и y, то считается, что значение A нам подходит, и в счётчике по окончанию вложенных циклов будет значение 90000 (300 * 300 = 90000).
Наибольшее число, которое напечатает программа равно 15.
Второй способ (с помощью рассуждений).
Здесь есть три выражения в скобках, которые соединены логическим сложением. При логическом сложении достаточно хотя бы одного выражения, где будет истина, чтобы всё общее выражение было истинно.
Если мы сделаем A слишком большим, к примеру A = 250, то найдутся такие x = 16, y = 16, при которых все три условия в скобках не будут выполняться, и, значит, всё общее выражение будет ложным.
Следовательно, нам нужно выбрать таким A, чтобы не было возможности подобрать x, y, при которых все три выражения ложны.
Сделаем так: пока x и y меньше A, должно «работать» третье выражение в скобках. Как только x или y сравняются с A — начинают «работать» первое или второе выражение.
До какого же максимального значения могут дойти x и y, чтобы перемножение этих двух чисел было меньше или равно 205 (x * y <= 205) ?
15 * 15 = 225
14 * 14 = 196
Получается, пока числа x и y меньше 15, «выручает» третье выражение (x * y ≤ 205), как только станут x ≥ 15 и y ≥ 15, будут «работать» первое и второе выражение.
Отсюда получаем, что максимальное число A = 15
Ответ: 15
Задача (Функция ДЕЛ)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула
¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(x, A) or (not(D(x, 6)) or not(D(x, 9))): k=k+1 if k==1000: print(A)
Здесь мы формируем функцию ДЕЛ (функцию D). Если n делится на m, то функция возвращает Истину, в противном случае функция возвращает Ложь.
Далее решаем примерно так же, как и в прошлых задачах: для каждого числа A перебираем все значения x. Следование расписываем по формуле A ⟶ B = ¬A ∨ B.
Наибольшее число здесь получается равно 18.
Второй способ (с помощью рассуждений).
Рассмотрим случай, когда в левой части логического выражения будет 1, а в правой 0. В остальных случаях беспокоится не за что, потому что вся формула будет выдавать истину.
Посмотрим, когда в правой части получается ноль. Функция ДЕЛ(x, 6) должна выдавать истину. Т.е. x должен делится на 6. А функция ¬ДЕЛ(x, 9) должна выдавать ноль. Т.е. без отрицания ДЕЛ(x, 9) должна выдавать истину. Значит, x так же делится на 9.
x делится на 6 => x = 2*3*n, n ∈ N
x делится на 9 => x = 3*3*n, n ∈ N
Чтобы выполнялся случай, когда в правой части получается ноль, икс должен быть равен x = 3*3*2*n (n ∈ N). Т.е. получается, что икс должен быть кратен 18.
Т.е. получается, что когда x делится на 18, в правой части логического выражения будет получатся ноль. Чтобы спасти ситуацию, мы должны в левой части логического выражения не получать 1. Следовательно, ¬ДЕЛ(x, А) должно выдавать ноль. Значит, ДЕЛ(x, А) должно выдавать 1. Таким образом, приходим к выводу, что A должно равняться 18.
Если получится опасная ситуация, когда x кратен 18, то она будет нейтрализована, ведь в левой части будет получатся ноль.
Ответ: 18
Ещё один важный тип задач 15 задания ЕГЭ по информатике 2022
Задача (Поразрядная конъюнкция)
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102 & 01012 = 4
Для какого наименьшего неотрицательного целого числа A формула
x&51 ≠ 0 → (x&A = 0 → x&25 ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?
Решение:
Первый способ (с помощью питона).
for A in range(0, 1000): k=0 for x in range(0, 1000): if x&51==0 or (x&A!=0 or x&25!=0): k=k+1 if k==1000: print(A)
Здесь следование преобразовываем по формуле: A ⟶ B = ¬A ∨ B. Так же и A, и x неотрицательные числа. Поэтому мы перебираем их диапазон, начиная с нуля. Из-за этого в цикле, который перебирает переменную x, мы устанавливаем верхнюю границы равной 1000, а не 1001. Тогда тоже будет 1000 повторений в этом цикле.
Наименьшее число равно 34.
Второй способ (с помощью рассуждений).
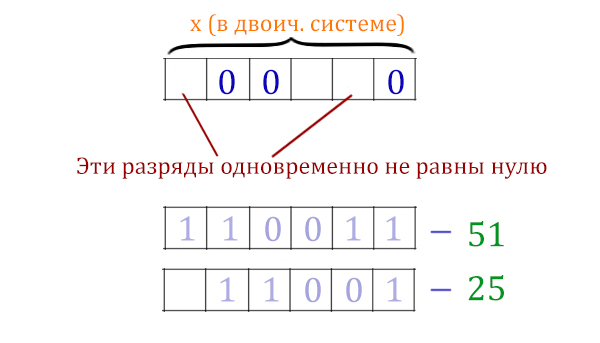
Переведём числа 51 и 25 в двоичную систему.
51 = 1100112
25 = 110012
Формула будет тождественно ложна, когда
Этого допустить нельзя!
При каком x получается в левой выражении формулы истина ? Если у икса в двоичном представлении в тех разрядах, где у числа 51 стоят 1, будет хотя бы в одном месте 1.
Рассмотрим правое выражение формулы. Ноль получается в единственном случае:
Рассмотрим выражение x&25 ≠ 0. Чтобы в этом логическом выражении получился ноль, нужно x&25 = 0. Посмотрим на двоичное представление числа 25. В тех разрядах, где стоят единицы, у икс должны быть нули (для x&25 = 0).
Сформулируем окончательное условие для x, при котором возникает опасность превращение общей формулы в ложь.
Нам нужно «поломать эту песенку» с помощью x&A = 0. Т.е. нельзя допускать, чтобы это выражение было истинно.
Получается, что A = 1000102. Это наименьшее из возможных число, при котором мы точно себя обезопасим от того, что вся формула будет ложна.
A = 1000102 в десятичной системе будет 34.
Ответ: 34
Ещё один тип задач 15 задания ЕГЭ по информатике
Задача (числовая прямая)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула (¬(x ∈ P) → (x ∈ Q)) → (x ∈ A ) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) or F(8, 19, x))) or F(a, b, x): k=k+1 if k==400: mn= min(mn, b-a) print(mn)
Получается ответ 14. Более подробно, как решать задачи на ОТРЕЗКИ из 15 задания ЕГЭ по информатике на Python, можете посмотреть в этой статье.
Второй способ (с помощью рассуждений).
Если будут такие варианты:
То нам беспокоится не о чём. Потому что формула всегда будет истинна! (см. таблицу истинности для следования →)
Нас же будет интересовать этот случай.
При таком раскладе вся формула будет ложна! Нам нужно этого не допустить при любом значении x!
Единица получается в первом подвыражении в трёх случаях:
1) Случай
Выражение ¬(x ∈ P) получается ложно, когда (x ∈ P) будет истинно! Получается при x ∈ [5, 13] выражение ¬(x ∈ P) — ложно!
Выражение (x ∈ Q) ложно, когда x ∉ [8, 19]
Какой же минимальной длины должен быть отрезок A, чтобы этот случай не проходил при любом x ? При этом случае отрезок A должен быть равен [5, 8). Тогда левое выражение пусть и может стать единицей при x ∈ [5, 8), но выражение (x ∈ A) будет также равно 1 при x ∈ [5, 8)! И схема 1 → 0 не пройдёт. Будет 1 → 1.
Для 1 случая A=[5, 
2) Случай
При каких x выражение ¬(x ∈ P) обращается в ноль, мы уже рассматривали: x ∈ [5, 13].
Второе выражение «выдаёт» 1 при x ∈ [8, 19].
Получается, что при при x ∈ [8; 13] первое выражение в скобках в главной формуле будет тождественно истинно!
С помощью отрезка A нужно это нейтрализовать путём превращения второго выражения в скобках в главной формуле в 1, пока x ∈ [8; 13]. Значит, для этого случая A = [8; 13]
3) Случай
В выражении ¬(x ∈ P) единица получается, когда в выражении (x ∈ P) получается ноль. Тогда x ∉ [5, 13]!
Чтобы во втором выражении (x ∈ Q) была единица, нужно, чтобы x ∈ [8, 19].
Получается, что 3 случай выполняется, если x ∈ (13, 19].
С помощью отрезка A нужно этому противодействовать! Нужно чтобы выражение (x ∈ A) было всегда 1 при x ∈ (13, 19]. Тогда A должно быть (13, 19].
Следовательно, для третьего случая A=(13, 19].
Нам нельзя допустить ни одного случая! Поэтому, объединив все случаи, получаем, что A=[5, 19].
Длина отрезка равна 14.
Ответ: 14
Ещё одна задача про числовую прямую из банка тренировочных заданий ЕГЭ по информатике 2021.
Задача (Числовая прямая, закрепление)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ ¬(x ∈ A)) → ((x ∈ Q) ∧ ¬(x ∈ A)) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) and not(F(a, b, x)))) or (F(8, 19, x) and not(F(a, b, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Второй способ (с помощью рассуждений).
Формула может быть ложна, когда
Во всех остальных случаях, формула всегда верна.
Чтобы выражение ((x ∈ P) ∧ ¬(x ∈ A)) было тождественно 1, выражение (x ∈ P) обязательно должно быть тождественно 1. А, значит, x ∈ [5, 13] — это опасная зона, при которой появляется возможность обратить всю формулу в ноль!
Мы можем сразу пресечь эту опасность с помощью отрезка A. Выбрать такой отрезок, чтобы он всегда «выдавал» ложь при x ∈ [5, 13]. Для этого достаточно выбрать A=[5, 13]! Но вдруг его можно сделать ещё более маленьким за счёт правой части формулы ?
Предположим, что отрезок A сделали ещё меньшим. Тогда при каком-то x (x ∈ [5, 13]) выражение ¬(x ∈ A) будет «выдавать» 1! Причём такое же выражение стоит и в правой части формулы! Там тоже будет 1 для выражения ¬(x ∈ A).
Нас же в этом случае должно выручить выражение (x ∈ Q). Если оно «выдаст» 1 в этот «сложный» момент, то мы спасены! Ведь тогда получается, что правая часть всей формулы будет «выдавать» не 0, а 1. Посмотрим при каких x из отрезка [5, 13] приходит это спасение.
Видим, что в интервале x ∈ [8, 13] нас спасает выражение (x ∈ Q).
Значит, отрезок A можно сократить до A=[5, 8).
Длина отрезка будет равна 3!
Ответ: 3
Задачи для закрепления
Задача (Неравенство, две переменные, закрепление)
Для какого наибольшего целого неотрицательного числа A выражение
(x < A) ∧ (y < A) ∧ (x * y > 603)
тождественно ложно, т.е. принимает значение 0 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if not( (x < A) and (y < A) and (x * y > 603) ): k=k+1 if k==90000: print(A)
Т.к. выражение должно быть ЛОЖНО, то обернём логическое выражение в функцию not(). Видим, что программа не сильно отличается от прошлой задачи. Данный шаблон подходит для большинства задач подобного типа.
Наибольшее число получается равно 25.
Второй способ (с помощью рассуждений).
В этой задаче нужно, чтобы общее выражение было ложно!
Если мы поставим отрицание над всем выражением, то можно искать такое максимальное A, при котором всё выражение тождественно истинно, а не ложно!
¬((x < A) ∧ (y < A) ∧ (x * y > 603)) = ¬(x < A) ∨ ¬(y < A) ∨ ¬(x * y > 603)
Здесь применили формулу де Моргана! Т.е. каждое подвыражение получило отрицание + соединительная логическая операция (логическое умножение) сменилась на противоположную операцию (логическое сложение).
Внесём отрицание в скобки. Получается:
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 603)
Получили ситуацию, как в прошлой задаче! Напомню, что теперь нужно, чтобы общее выражение было истинно.
Найдём максимальное число, до которого могут «подняться» x и y, чтобы ещё работало третье выражение!
Обратите внимание, что x и y — симметричны. Значит, что верхняя планка для x и y будет одно и тоже число.
Поэтому вспоминаем таблицу квадратов.
25 * 25 = 625
24 * 24 = 576
Получается, что максимальное число до которого могут «дойти» x и y, чтобы «работало» третье выражение, равно 24.
Тогда, начиная с 25 для x и y, должны работать первое и второе выражение.
Получается, что максимальное число для A равно 25.
Ответ: 25
Ещё одна задачка подобного типа из тренировочных упражнений 15 задания ЕГЭ по информатике.
Задача (Неравенство, две переменные, закрепление)
Для какого наименьшего целого числа A формула
(3 * x + y < A) ∨ (x < y) ∨ (16 ≤ x)
тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(-300, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (3*x + y < A) or (x < y) or (16 <= x): k=k+1 if k==90000: print(A)
Наименьшее число равно 61. Здесь не сказали, что A принимает неотрицательные значения, поэтому мы включили в диапазон для A числа, которые меньше нуля. Из-за этого увеличилось время выполнения программы, но ответ получим за приемлемое время.
Второй способ (с помощью рассуждений).
Чтобы вся формула была тождественно истинна, нужно, чтобы хотя бы одно выражение «выдавало» истину, т.к. выражения в формуле соединяются с помощью логического сложения!
Взглянем на третье выражение. Пока x ≥ 16, всё идёт как надо. Третье выражение будет истинно, и, значит, вся формула будет истинна.
Но если x ≤ 15, то нужно, чтобы нас «спасало» первое или второе выражение.
Рассмотрим второе выражение. Пока y > x (x ≤ 15) => y > 15, у нас всё нормально, второе выражение будет истинно, и вся формула будет истинна.
Теперь обратим внимание на первое выражение. Оно должно нас «спасать», когда третье и второе выражение «не спасло»! Это возможно, если x ≤ 15 (иначе «спасло» бы третье выражение), а так же y ≤ 15 (иначе «спасало» бы второе выражение).
Но, чтобы первое выражение было всегда истинно при x ≤ 15 и y ≤ 15, мы должны подобрать число A при максимальных x и y (x=15, y=15)! Ведь для более маленьких значений выражение (3 * x + y < A) точно будет истинно.
Получается:
3 * 15 + 15 < A
60 < A
Нужно найти наименьшее число для A, при котором A > 60. Тогда там, где не «спасли» третье и второе выражение, точно «спасёт» первое выражение. Получается A = 61.
Ответ: 61
Задача (ЕГЭ по информатике, Москва, 2020)
Для какого наибольшего целого неотрицательного числа A выражение
(x > A) ∨ (y > x) ∨ (2 * y + x < 110)
тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x > A) or (y > x) or (2 * y + x < 110): k=k+1 if k==90000: print(A)
Максимальное число получается равно 36.
Второй способ (с помощью рассуждений).
Пока y > x, второе подвыражение всегда истинно, значит, и всё выражение истинно.
Теперь будем рассматривать случай y ≤ x.
Рассмотрим третье подвыражение. Найдём максимальные значения для x и для y, которые они одновременно могут принимать, и при которых ещё выполняется третье условие.
Т.к. мы рассматриваем случай y ≤ x, то максимальное число для y будет xmax т.е. ymax = xmax.
Тогда
2 * xmax + xmax < 110
3 * xmax < 110
36 * 3 = 108
37 * 3 = 111
xmax = ymax = 36
Если x «перевалит» за 36, и при этом y ≤ x (иначе «спасает» второе подвыражение), то должно «спасать» первое выражение.
Получается, что наибольшее значение A будет равно 36.
Ответ: 36
Следующий тип задач часто можно встретить в тренировочных вариантах ЕГЭ по информатике 2022.
Задача (С функцией ДЕЛ, закрепление)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула
ДЕЛ(120, A) ∧ ((ДЕЛ(x, 70) ∧ ДЕЛ(x, 30)) → ДЕЛ(x, A))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(120, A) and (not(D(x, 70) and D(x, 30)) or D(x, A)): k=k+1 if k==1000: print(A)
Наибольшее число получается равно 30.
Второй способ (с помощью рассуждений).
Рассмотрим левую часть логического выражения. Мы видим, что число 120 должно делится на A. Значит, для A уже есть некоторое ограничение (A <= 120).
Рассмотрим правую часть выражения. Изучим, когда она превращается в ноль. Тогда
Т.е. x должен делится на 70 и одновременно x должен делится на 30.
x = 70*n = 2*5*7*n (n ∈ N)
x = 30*n = 2*5*3*n (n ∈ N)
Чтобы одновременно выполнялись два условия, икс должен быть равен x = 2*5*7*3*n (n ∈ N).
Для того, чтобы правое выражение не превращалось в ноль, x как раз должен делится на число 2*5*7*3. Тогда будет 1->1. Т.е. число A должно равняться 2*5*7*3. Но мы сказали, что A <= 120, плюс, должно являться делителем числа 120. Значит, должны снизить значение для A.
Рассмотрим значение 2*5*7 для числа A (Предыдущее число, но без тройки). Для правой части оно подходит, т.к. «при малейшей» возможности превращения правого выражения в ноль (т.е. ДЕЛ(x, 70) = True), у нас будет спасаться ситуация, т.к. ДЕЛ(x, A) так же
будет равно 1. И снова получаем 1->1. Но это значение не подходит для левой части, ведь тогда A не является делителем числа 120.
Приходится брать число 2*5*3 (без семёрки). Здесь ситуация аналогично предыдущему случаю, только теперь это число является делителем числа 120.
В ответе напишем 30.
Ответ: 30
Задача (Поразрядная конъюнкция, закрепление)
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение:
Первый способ (с помощью питона).
for A in range(1, 1000): k=0 for x in range(1, 1001): if (x&49==0) or ((x&33!=0) or (x&A!=0)): k=k+1 if k==1000: print(A)
Наименьшее число равно 16.
Второй способ (с помощью рассуждений).
Переведём числа 49 и 33 в двоичную систему.
4910 = 1100012
3310 = 1000012
Рассмотрим случай, когда функция стремится превратится в ноль.
Чтобы левое выражение выдавало истину, икс должен иметь 1 (единицу) в первом разряде или во второй разряде, или в последнем разряде (в 6-ти битном числе).
Рассмотрим правое выражение. Посмотрим, когда выражение (X & 33 = 0) выдаёт истину. Первый бит и последний бит должен быть равен нулю. Т.е получается, что в 6-ти битном числе нас интересует второй бит. Если он будет равен 1 и при этом первый бит и последний будут равны 0, то возникает опасная ситуация, которую нужно спасть.
При выше описанных условиях выражение (X & A ≠ 0) должно выдавать истину. Тогда наименьшее A равно 100002 = 162.
Ответ: 16
Задача (числовая прямая, закрепление 2)
На числовой прямой даны два отрезка: P = [20, 30] и Q = [35, 60]. Найдите наименьшую возможную длину отрезка A, при котором формула
¬(x ∈ A) ∧ ((x ∈ P) ∨ (x ∈ Q))
тождественно ложна, то есть принимает значение 0 при любых x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not(not(F(a, b, x)) and (F(20, 30, x) or F(35, 60, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Ответ будет 40.
Второй способ (с помощью рассуждений).
Рассмотрим наоборот, когда логическое выражение выдаёт истину.
В правой части получается 1, когда x ∈ P или x ∈ Q. Именно в эти моменты выражение ¬(x ∈ A) должно спасать ситуацию и выдавать 0. Тогда без отрицания (x ∈ A) должно выдавать 1. Чтобы покрыть два отрезка, берём A=[20; 60].
Минимальная длина получается 60-20=40.
Ответ: 40
На этом всё! Увидимся в новых уроках по подготовке к ЕГЭ по информатике!
Добрый день! А как в 5 задаче (про числовую прямую) получился ответ 14?
В конце же получается, что A принадлежит [5, 19], то есть длина отрезка 15.
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 — 15 штук
Или я что-то неправильно понял?
Считается количество единиц, а не сколько целых чисел в этом отрезке.
И в самой последней задаче на закрепление, у вас, видимо, та же ошибка. Не 40, а 41 должно быть?
Как решать 15 задание с «~» тильдой на питоне?
Как например это задание:
На числовой прямой даны два отрезка: P = [7, 14] и Q = [9, 11]. Укажите наибольшую возможную длину промежутка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)
Грамотное объяснение. Безумно здорово, что есть объяснения как на питон (перебором) так и чисто в математической форме, потому что в информатике оба подхода, мне кажется, равносильны. Спасибо
2 июля 2022
В закладки
Обсудить
Жалоба
Упрощение логических выражений
Конспект урока.
upra-l.docx
upra-l.pdf
Задания по практической работе
1. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˄ L ˅ ¬ ( L ˅ M ) ) ~ M ˄ N ˅ M
2. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˅ K ˄ M ~ ( L ˅ N ) ˄ ¬ ( N ˄ K ) )
3. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˄ ( K → L ) ˅ ( K ˅ N ) ˄ ( M ˅ N ) )
4. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: N ˄ ¬ ( L ˄ N ) → ( ¬ ( N ˅ K ) ˅ K ˄ M )
5. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˅ K ˄ M ~ ( L ˅ N ) ˄ ¬ ( N ˄ L ) )
Контрольные вопросы
1. Что такое логика и алгебра логики?
2. Что такое логическое высказывание? Какие они бывают?
3. Что такое логические операции и выражения? Какие они бывают?
4. По каким правилам выполняется упрощение логических операций?
Автор: Волков Р.Ю.
Информатика, 10 класс. Урок № 12.
Тема — Преобразование логических выражений
Перечень вопросов, рассматриваемых в теме: основные законы алгебры логики, преобразование логических выражений, логические функции, построение логического выражения с данной таблицей истинности и его упрощение, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ).
Глоссарий по теме: основные законы алгебры логики, логические функции, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ)
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса
— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)
Открытые электронные ресурсы по теме:
http://lbz.ru/metodist/authors/informatika/3/eor10.php
http://kpolyakov.spb.ru/school/ege.htm
Теоретический материал для самостоятельного изучения.
Способ определения истинности логического выражения путем построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т.к. за счет существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.
Основные законы алгебры логики
Справедливость законов можно доказать построением таблиц истинности.
Пример 1. Упростим логическое выражение
Последовательно применим дистрибутивный закон и закон исключенного третьего:
В общем случае можно предложить следующую последовательность действий:
- Заменить операции строгая дизъюнкция, импликация, эквиваленция на их выражения через операции конъюнкция, дизъюнкция, инверсия;
- Раскрыть отрицания сложных выражений по законам де Моргана.
- Используя законы алгебры логики, упростить выражение.
Пример 2. Упростим логическое выражение 
Здесь последовательно использованы замена операции импликация, закон де Моргана, распределительный закон, закон противоречия и операция с константой, закон идемпотентности и поглощения.
Аналогичные законы выполняются для операции объединения, пересечения и дополнения множеств. Например:
Пример 3. На числовой прямой даны отрезки B = [2;12] и C = [7;18]. Каким должен быть отрезок A, чтобы предикат 
Преобразуем исходное выражение, избавившись от импликации:
A, B, C — множества. Для них можно записать 
Будем считать, что
Тогда 
Так как множество B — это отрезок [2;12], а множество 



Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

Введем обозначения:
Перепишем исходное выражение в наших обозначениях и преобразуем его:

Рассмотрим предикат 

Рассмотрим предикат 

Рассмотрим предикат 
По условию задачи надо, чтобы 
Запишем это выражение для рассмотренных множеств истинности:
Так как 

Объединением множеств M и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством K будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т.е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.
Искомое число a должно быть таким, чтобы при любом неотрицательном целом значении переменной х: 
Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.
Совокупность значений n аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно
.
Для n=2 существует 16 различных логических функций. Рассмотрим их подробнее.
|
A |
B |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
F16 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
F1(A,B) = 0 — константа «ложь»;
F2(A,B) = A&B — конъюнкция;
F3(A,B) = 
F4(A,B) = A — функция, равная первому аргументу;
F5(A,B) = 
F6(A,B) = B — функция, равная второму аргументу;
F7(A,B) = 
F8(A,B) = A˅B — дизъюнкция;
F9(A,B) = 
F10(A,B) = 
F11(A,B) = 
F12(A,B) = 
F13(A,B) = 
F14(A,B) = 
F15(A,B) = 
F16(A,B) = 1 — константа «истина».
С увеличением числа аргументов количество логических функций резко возрастает. Отметим, что путем преобразований функция любого количества переменных может быть выражена через функции только двух переменных. Более того, можно использовать не все, а лишь некоторые логические функции двух переменных. Например:
- F2 и F11 (конъюнкция и отрицание второго аргумента);
- F8 и F13 (дизъюнкция и отрицание первого аргумента);
- F9 (стрелка Пирса, отрицание дизъюнкции);
- F15 (штрих Шеффера, отрицание конъюнкции).
Последние два примера говорят о том, что при желании всю алгебру логики можно свести к одной функции.
Любую логическую формулу путем тождественных преобразований можно привести к формуле, содержащей только операции отрицания, конъюнкции и дизъюнкции:
Такой способ представления логической формулы называется нормальной формой.
При решении задач часто требуется по таблице истинности логической формулы записать ее аналитическое выражение. Для этого используются понятия совершенной дизъюнктивной нормальной формы (СДНФ) и совершенной конъюнктивной нормальной формы (СКНФ).
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, в которой каждая переменная встречается не более одного раза (либо сама, либо ее отрицание). Например, запись 
Аналогично, выражение 
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций. Например, выражение 
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций. Например, выражение 
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные (либо сами, либо их отрицания). Например, выражение 

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные (либо сами, либо их отрицания). Например, выражение 
Для всякой таблицы истинности можно составить соответствующее ей логическое выражение. Для этого необходимо:
- Отметить в таблице истинности наборы переменных, при которых значение логического выражения равно единице;
- Для каждого отмеченного набора записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — её отрицание;
- Все полученные конъюнкции связать операциями дизъюнкции.
Пример 5. Имеется следующая таблица истинности:
После выполнения первых двух шагов алгоритма получим:
После выполнения третьего шага получаем логическое выражение:
Попробуем упростить полученное выражение. Прежде всего, вынесем за скобки 
Автор материалов — Лада Борисовна Есакова.
В компьютере вся информация представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Собственно, и цифр как таковых у компьютера нет, а есть электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, который может принимать значения “высокий уровень электрического напряжения” (принимаемый нами за 1) и “низкий уровень электрического напряжения” (принимаемый за 0). Для различных действий над этими нулями и единичками нам необходимы специальные операции, которые работают с двоичными переменными. Такие операции называются логическими операциями.
Логические операции и их аргументы принимают только два значения: 1 (“истина”) и 0 (“ложь”).
Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных.
Количество строк в таблице истинности выражения от N переменных равно 2N.
Основные логические операции:
1). Логическое умножение (конъюнкция, логическое И). Обозначается: AND, &, /.
Таблица истинности:
|
A |
B |
А&В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
2). Логическое сложение (дизъюнкция, логическое ИЛИ). Обозначается: OR, |, /.
Таблица истинности:
|
A |
B |
A / B |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
3). Логическое отрицание (инверсия, логическое НЕ). Обозначается: NOT, ¬, .
Таблица истинности:
4). Логическое следование (импликация). Обозначается: →.
Таблица истинности:
|
A |
B |
A → B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
5). Логическое равенство (эквивалентность). Обозначается: ↔, ~.
Таблица истинности:
|
A |
B |
A ~ B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Порядок (приоритет) выполнения логических операций:
Если в выражении нет скобок, то операции выполняются в следующем порядке:
— Логическое отрицание (инверсия, логическое НЕ);
— Логическое умножение (конъюнкция, логическое И);
— Логическое сложение (дизъюнкция, логическое ИЛИ);
— Логическое следование (импликация);
— Логическое равенство (эквивалентность).
Выбор выражения по таблице истинности
Пример 1.
Дан фрагмент таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Решение:
Все представленные варианты ответа — дизъюнкции трёх конъюнкций. Все значения F в таблице равны нулю. Дизъюнкция равна нулю, когда все слагаемые равны нулю.
Рассмотри поочерёдно все четыре выражения.
1) В первой строке таблицы x1=1 и x2=1, значит x1∧x2=1. Выражение не подходит.
2) Во второй строке таблицы x1=1 и x3=1, значит x1∧x3=1. Выражение не подходит.
3) Подставим в третье выражение поочередно значения всех строк таблицы:
Первая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (1 ∧ 0) ∨ (0 ∧ 0) ∨ (0 ∧ 1) = 0 ∨ 0 ∨ 0 = 0
Вторая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 0) ∨ (0 ∧ 1) ∨ (1 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Третья строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 1) ∨ (1 ∧ 0) ∨ (0 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Выражение подходит.
4) В третьей строке таблицы x1=1 и x4=1, значит x1∧x4=1. Выражение не подходит.
Ответ:3
Пример 2.
Для таблицы истинности функции F известны значения только некоторых ячеек:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
0 |
1 |
|||||
|
0 |
0 |
1 |
|||||
|
0 |
1 |
0 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
Решение:
Рассмотри поочерёдно все четыре выражения.
1) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. В первой строке x6 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
2) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. Подставим во второе выражение поочередно значения всех строк таблицы:
Первая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ 0 ∨ ¬x7 может принимать значение 1, если хотя бы один из операндов равен 1.
Вторая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 1 ∨ ¬x5 ∨ x6 ∨ 1 = 1
Третья строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = 0 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ x6 ∨ ¬x7 может принимать значение 0, если все остальные операнды равны 0.
3) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. Во второй строке x4 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
4) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. В третьей строке x4 = 1, значит и все выражение F равно 1, что не соответствует таблице истинности.
Ответ:2
Пример 3.
Логическая функция F задаётся выражением (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
|
Перем. 1 |
Перем. 2 |
Перем. 3 |
Функция |
|
??? |
??? |
??? |
F |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
Выражение (¬z) ∧ x ∨ x ∧ y является дизъюнкцией двух конъюнкций:
((¬z) ∧ x) ∨ (x ∧ y) . В обеих конъюнкциях присутствует x. Т. е. при x = 0 все выражение равно 0. Это выполняется только при Перем.3 = x.
Выражение равно 1, если x =1 и выполняется хотя бы одно из условий: y = 1 или z = 0. Из четвертой строки следует, что Перем.1 = z, а Перем.2 = y.
Ответ: zyx
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №2. Построение таблиц истинности логических выражений. Выбор выражения, соответствующего условию.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023