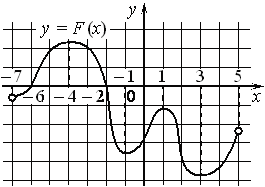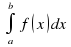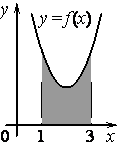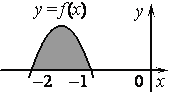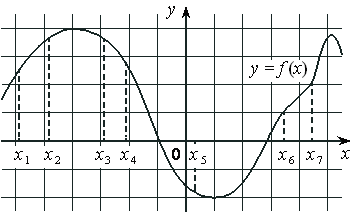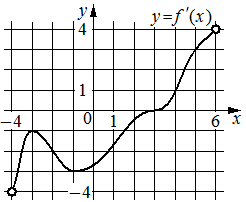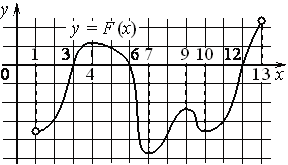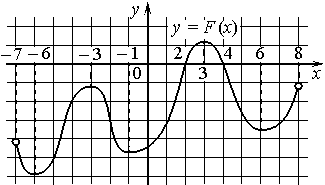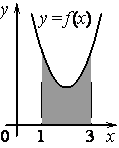Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
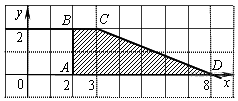
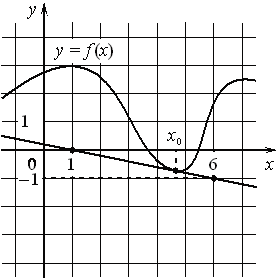
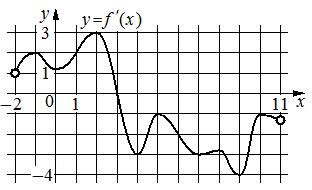
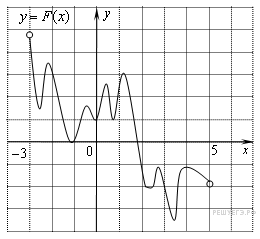
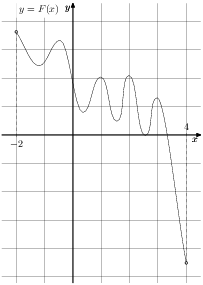
На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
2
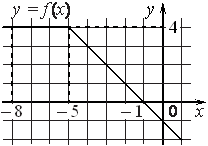
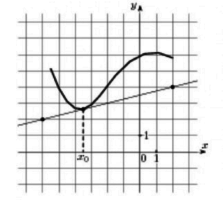
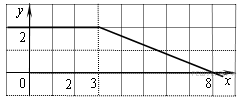
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1.
4
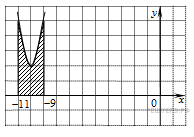
На рисунке изображён график некоторой функции y = f(x). Функция — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
5
На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл
Пройти тестирование по этим заданиям
Формулы для профильного ЕГЭ-2022 по математике
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Все формулы для профильного ЕГЭ-2022 по математике
Все формулы для базового ЕГЭ-2022 по математике
Файл к занятию 23
Нахождение наибольшего и наименьшего значения функции на отрезке
Задание 1. Найдите наибольшее значение функции y=x5+20x3−65x на отрезке [− 4; 0]. Ответ: 44
Задание 2. Найдите наибольшее значение функции y =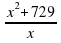
Задание 3. Найдите наименьшее значение функции y= 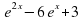
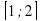
Ответ: -6
Дополнительно. Найдите наименьшее значение функции y=e2x−2ex+8 на отрезке [− 2; 1]. Ответ: 7
Задание 4. Найдите наибольшее значение функции y=15x−3sinx+5 на отрезке [− π/2; 0]. Ответ: 5
Дополнительно. Найдите наибольшее значение функции y=59x−56sinx+42 на отрезке [− π/2; 0]. Ответ: 42
Задание 5. Найдите наименьшее значение функции y=13cosx+17x+21 на отрезке [0; 3π/2]. Ответ: 34
Задание 6. Найдите наибольшее значение функции y=25x−25tgx+41 на отрезке [0; π/4]. Ответ: 41
Задание 7. Найдите наименьшее значение функции y= 3x—ln(x+3)3 на отрезке [−2,5; 0]. Ответ: -6
Дополнительно. Найдите точку минимума функции y= 2x—ln(x+8)2 . Ответ: -7
Задание 8. Найдите точку минимума функции y= (1-2x)cosx + 2sinx +7 на отрезке 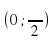
Дополнительно. Найдите точку максимума функции y=(x+5)2⋅e2 − x.
Первообразная.
Первообразной функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции. F‘ (x)= f(x).
Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную.
Пример. Функция F(x)=x3 является первообразной функции f(x)=3x2 так как (x3)’=3x2. Функции F1(x)=x3 +5 и F2(x)=x3 — 7 также являются первообразными функции f(x). Любая функция вида F(x)=x3 +с, где с – произвольное число, является первообразной функции f(x).
Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое.
Задание 9. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 8). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [0; 5]. Ответ:1
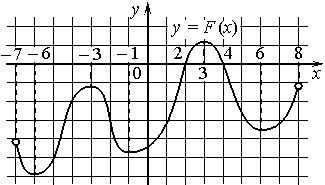
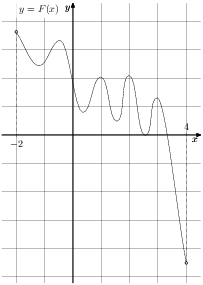
Задание 10. На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f (x) = 0 на отрезке [−1; 3]. Ответ: 6
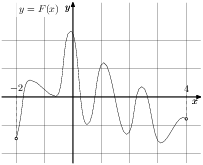
Дополнительно.
1. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 2]. Ответ: 3
2. На рисунке изображён график функции y=F(x) и одной из первообразных некоторой функции f(x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f(x) = 0на отрезке [−1; 3]. Ответ: 7.
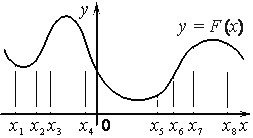
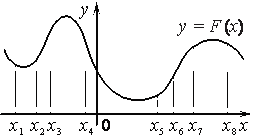
Задание 11. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек функция f(x) отрицательна?
Решение: Т.к f(x)= F`(x), то функция f(x) отрицательна, если F(x) убывает и функция f(x) положительна, если F(x) возрастает. По рисунку определим, сколько точек попали на промежуток убывания F(x). Это точки х1, х4, х8.
Значит, таких точек 3. Ответ: 3
Задание 12. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены десять точек на оси абсцисс: x1,x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек функция f(x) положительна? Ответ:6 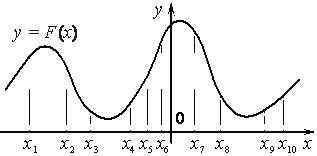
Криволинейная трапеция
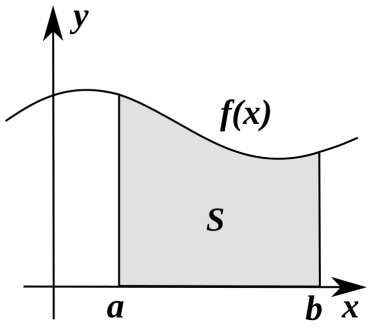
Пусть на отрезке [а; в] задана непрерывная функция, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; в] и прямыми х=а и х=b называют криволинейной трапецией.
Если функция непрерывная и неотрицательная на отрезке [а; в], а F- ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на этом отрезке[а; в].
S= F(b)-F(a)
Задание 13. На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x). Ответ:7
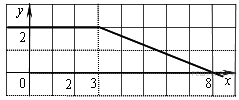
Решение: Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции ABCD. Поэтому
S= F(b) – F(a)= 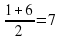
Задание 14. На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(− 1)−F(− 8), где F(x) — одна из первообразных функции f(x). Ответ: 20
Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое. Совокупность всех первообразных данной непрерывной функции называется неопределенным интегралом от этой функции и обозначается 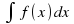
Если F(x) — некоторая первообразная данной функции, то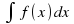
Процесс нахождения неопределенного интеграла называется интегрированием данной функции, или взятием интеграла от данной функции.
Площадь S криволинейной трапеции равна приращению первообразной на отрезке[а; в].
S= F(b)-F(a)=
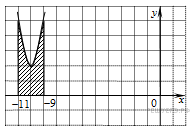
Задание 15. На рисунке изображён график функции y = f(x). Функция F(x)= x3+30x2+302x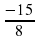
Задание 16. На рисунке изображён график некоторой функции y=f(x). Функция F(x)=12x3−3x2+152x−92 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Ответ: 592
Задание 17. На рисунке изображён график некоторой функции y=f(x). Функция F(x)=− x3−92x2−6x+2 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Ответ: 263
Подборка задач базового ЕГЭ по математике задание №14 — вычисления
Для выполнения задания 14 необходимо уметь выполнять вычисления и преобразования.
Практика ЕГЭ по базовой математике задание №14
| Источник | Варианты заданий |
| time4math.ru | Скачать задания |
| math100.ru | скачать задания |
Коды проверяемых элементов содержания (по кодификатору) — 1.1.1, 1.1.3, 1.4.1
Уровень сложности задания — базовый
Максимальный балл за выполнение задания — 1
Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 5
Смотрите также:
Демоверсия ЕГЭ 2023 по математике — базовый уровень
Тренировочные варианты ЕГЭ 2023 по математике профильного уровня
Тренировочные варианты ЕГЭ 2023 по математике базового уровня
Задание 11 ЕГЭ по математике база — прикладная стереометрия
Задание 12 ЕГЭ по математике база — планиметрия
1. На рисунке изображён график функции 

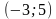
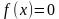
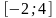
2. На рисунке изображён график некоторой функции 
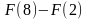
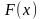

3. На рисунке изображён график функции 
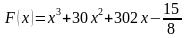

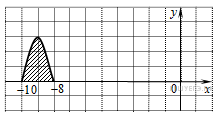
4. На рисунке изображён график некоторой функции 
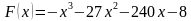


5. На рисунке изображён график функции 

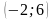

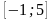



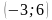

7. На рисунке изображён график функции 


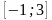
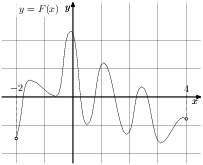


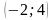

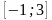

9. На рисунке изображён график функции 

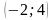

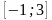

10. На рисунке изображён график функции 

Пользуясь рисунком, определите количество решений уравнения

11. На рисунке изображён график функции 

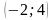

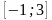
12. . На рисунке изображён график некоторой функции 
, где
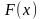

13. На рисунке изображён график некоторой функции 
, где
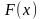

14. . На рисунке изображён график некоторой функции 
, где
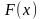

15. На рисунке изображён график функции 

16. На рисунке изображён график функции 
Функция — одна из первообразных функции 
17. На рисунке изображён график функции 

18. На рисунке изображён график функции 

19. На рисунке изображён график функции 

20. На рисунке изображён график функции 

21. На рисунке изображён график функции 

22. На рисунке изображен график некоторой функции 
23. На рисунке изображён график функции 

Найдите количество решений уравнения
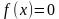
.
24. На рисунке изображён график функции 

. Найдите количество решений уравнения
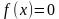
.
Ресурс содержит презентацию и тест для самостоятельной работы. Тест составлен в 4 вариантах. Предназначен для подготовки к ЕГЭ. Цели ресурса: Образовательные: повторить и закрепить знания о первообразной функции и её свойствах, научиться применять знания при решении конкретных задач. Развивающие: развивать умение анализировать условие задачи. Воспитательные: воспитание аккуратности, внимательности, быстроты мышления.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
Подготовка к ЕГЭ Задание №7 (первообразная)
Слайд 2
1) На рисунке изображён график функции y = F( x ) — одной из первообразных функции f ( x ), определённой на интервале (−3; 5). Найдите количество решений уравнения f ( x ) = 0 на отрезке [−2; 4].
Слайд 3
2 ) На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F( x ) — одна из первообразных функции f ( x ).
Слайд 4
3 ) На рисунке изображён график функции y = f ( x ). Функция — одна из первообразных функции y = f ( x ). Найдите площадь закрашенной фигуры.
Слайд 5
4 ) На рисунке изображён график функции y = f ( x ). Функция — одна из первообразных функции y = f ( x ). Найдите площадь закрашенной фигуры.
Слайд 6
5 ) На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл .
Слайд 7
При подготовке презентации были использованы материалы с сайтов: https://www.uchportal.ru / https://ege.sdamgia.ru /
Предварительный просмотр:
|
ФИ_________________________________________________________В 1
Ответ:___________________
Ответ:___________________
Функция Ответ:___________________
Функция Ответ:___________________ |
ФИ_________________________________________________________В 2
Ответ________________________________
Ответ:___________________
Функция Ответ:___________________
Функция Ответ:___________________ |
|
ФИ__________________________________________________________В 3
Ответ_____________________
Ответ_____________________
Функция Ответ:___________________
Функция Ответ:___________________ |
ФИ_________________________________________________________В 4
Ответ____________________
Ответ_____________________
Функция Ответ:___________________
Функция Ответ:___________________ |
По теме: методические разработки, презентации и конспекты
Построение профиля задание С1 ЕГЭ по географии
При выполнении ЕГЭ по географии в задании С1 требуется выполнить профиль по топографической карте. Данный цикл занятий направленный на формирование у одинадцати классников умения выполнять этит тип за…
Варианты ЕГЭ математика (профиль), задания 1-12.
Варианты ЕГЭ математика (профиль), задания 1-12. Задания варианта соответствуют заданиям демоверсии ЕГЭ. При составлении вариантов использованы задания открытого банка заданий ЕГЭ. Ответы прилагаются….
- Мне нравится
Интегралы на ЕГЭ. Первообразные элементарных функций
Вы в школе уже прошли интегралы? Поняли эту тему?:)
А вы знали, что в ЕГЭ тоже могут попасться интегралы? Да-да, открываем кодификатор и видим:
4.3 Первообразная и интеграл
– 4.3.1 Первообразные элементарных функций
– 4.3.2 Примеры применения интеграла в физике и геометрии)
Но не волнуйтесь. В школьной программе интегралы – не сложные. Это не проблема, это скорее возможность получить легкие баллы!!!
И это значит, что пора смотреть наше видео.
Интегралы на ЕГЭ. Первообразные элементарных функций
В этом видео мы расскажем вам, какие типы задач на интегралы и первообразную могут быть в ЕГЭ, и научим их решать.
И да, в институте без знания производной и интегралов делать нечего. Совсем. Там не будет времени разбираться с ней, так что лучше займитесь ей сейчас.
Важно: перед этим уроком повторите производную!
Ведь проходить интегралы без производной – это как вычислять арксинус, не зная, что такое синус:)
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
Что думаете об интегралах на ЕГЭ?
Попадутся или нет на экзамене?
Насколько сложно понять и научиться решать задачи именно для вас?
Будете ли вы учить эту тему перед ЕГЭ.
Напишите нам в комментариях прямо сейчас.
Файл к занятию 29.
Производная. Применение производной. Первообразная.
Угловой коэффициент касательной к графику функции в точке с абсциссой х0 равен производной функции в точке х0.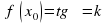
Т.е. производная функции в точке х0 равна тангенсу угла наклона касательной, проведенной к графику функции в точке (х0; f(x0)).
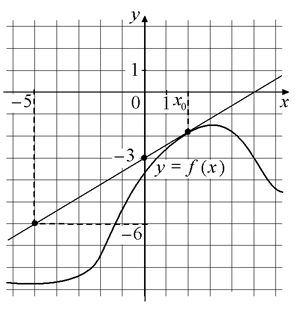
Задание 1. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 0,25
Задание 2. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Ответ: 0,6
Задание 3. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Ответ: -0,25
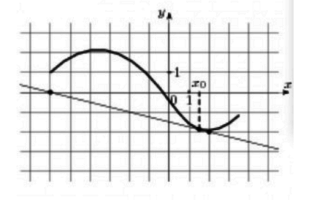
Задание 4. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Ответ: -0,2.
Механический смысл производной.
v ( t0 ) = x’ ( t0 )
скорость – это производная координаты по времени. Аналогично, ускорение – это производная скорости по времени:
a = v’ ( t ).
Задание 5. Материальная точка движется прямолинейно по закону x(t)=12 t2+4 t+27, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=2 с. Ответ: 52
Задание 6. Материальная точка движется прямолинейно по закону x(t)=16 t3+t2−8 t+180, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 42 м/с? Ответ: 1
Достаточный признак возрастания (убывания) функции
1. Если f `(x)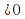
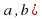
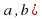
2. Если f `(x)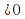
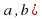
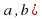
Необходимое условие экстремума
Если точка х0 является точкой экстремума функции и в этой точке существует производная, то f `(x0 )=0
Достаточное условие экстремума
Если f `(x0) = 0 и при переходе через точку x0 значение производной меняет знак с «+» на « — », то x0 является точкой максимума функции.
Если f `(x0) = 0 и при переходе через точку x0 значение производной меняет знак с « — » на «+», то x0 является точкой минимума функции.
Задание 7. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 10). Найдите количество точек минимума функции f(x) на отрезке [−3; 8].
Решение. Точки минимума соответствуют точкам смены знака производной с минуса на плюс. На отрезке [−3; 8] функция имеет одну точку минимума x = 4. Значит, такая точка 1. Ответ: 1.
Задание 8. На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7. В скольких из этих точек производная функции f(x) отрицательна? Ответ: 3
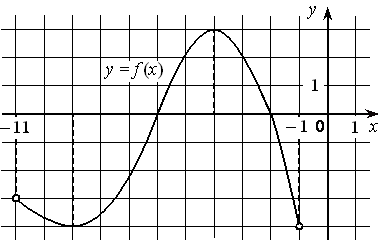
Задание 9. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 11 ; − 1). Найдите точку из отрезка [− 7 ; − 2], в которой производная функции f(x) равна 0. Ответ: -4
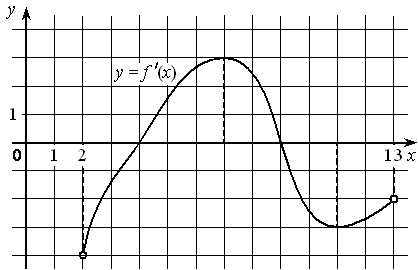
Задание 10. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (2 ; 13). Найдите точку максимума функции f(x). Ответ: 9
Задание 11. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение? Ответ: -2
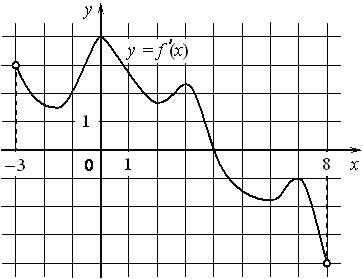
Задание 12. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 2 ; 11). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней. Ответ: 3
Задание 13. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4 ; 6). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y=3x или совпадает с ней. Ответ: 5
Задание 14. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4 ; 13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=− 2x−10 или совпадает с ней. Ответ: 5
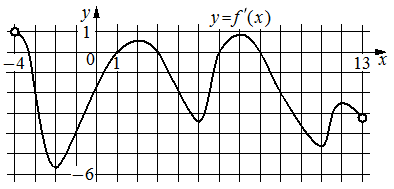
Задание 15. Прямая y=5x-8 является касательной к графику функции 4x2-15x+c. Найдите c. Oтвет: 17.
Первообразная
Первообразной функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции. F‘ (x)= f(x).
Задание 16. На рисунке изображён график y=F (x) одной из первообразных некоторой функции f (x), определённой на интервале (1;13). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке [2;11]. Ответ: 4
Задание 17. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 8). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [0; 5]. Ответ:1
Задание 18. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек функция f(x) отрицательна? Ответ: 3
Задание 19. На рисунке изображён график некоторой функции y=f(x). Функция F(x)=12x3−3x2+152x−92 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Ответ: 592
Алгоритм нахождения точек экстремума
-
Найти область определения функции.
-
Найти производную функции f ‘(x)
-
Найти точки, в которых f ‘(x) = 0.
-
Отметить на числовой прямой область определения функции и все нули производной.
-
Определить знак производной для каждого промежутка. (Для этого подставляем «удобное» значение x из этого промежутка в f ‘(x)).
-
Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере (max или min) в каждой из этих точек.
Задание 20. Найдите точку максимума функции y=(2x−1)cosx−2sinx+5, принадлежащую промежутку (0 ; π/2). Ответ: 0,5
Задание 21. Найдите точку максимума функции y=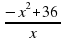
Алгоритм нахождения наибольшего и наименьшего значение функции на отрезке
-
Найти производную функции f ‘(x).
-
Найти точки, в которых f ‘(x) = 0. Проверить принадлежность этих точек отрезку
-
Найти значение функции на концах отрезка и в данных точках.
-
Выбрать из полученных значений наибольшее или наименьшее.
Задание 22. Найдите наименьшее значение функции y=x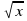
Задание 23. Найдите наименьшее значение функции y=8cosx+30x/π+19 на отрезке [− 2π/3; 0]. Ответ: -5
Дополнительно. 1. Найдите точку максимума функции y=(x−11)2⋅e x − 7.
2. Найдите наибольшее значение функции y=х5-5х3-20х на отрезке [− 9 ; 1]. Ответ:48