Интеграл в заданиях егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Каталог заданий.
Первообразная

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

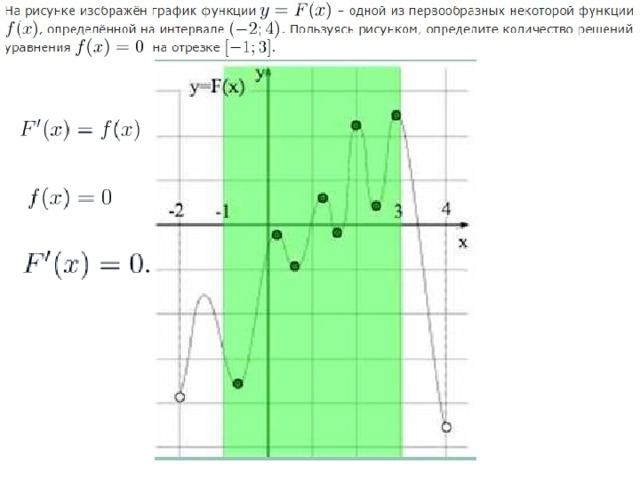
На рисунке изображён график функции y  =  F(x)  — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)  =  0 на отрезке [−2; 4].

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.

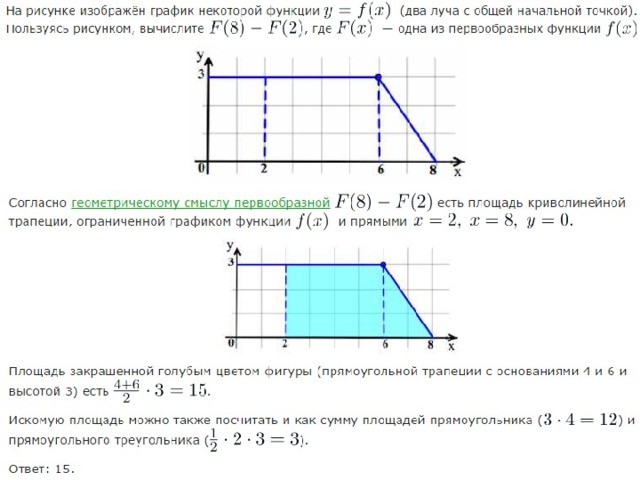
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x)  — одна из первообразных функции f(x).

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.

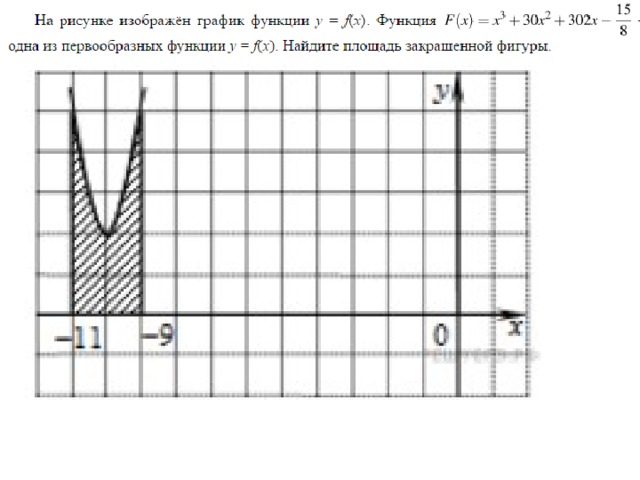
На рисунке изображён график функции y = f(x). Функция   — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

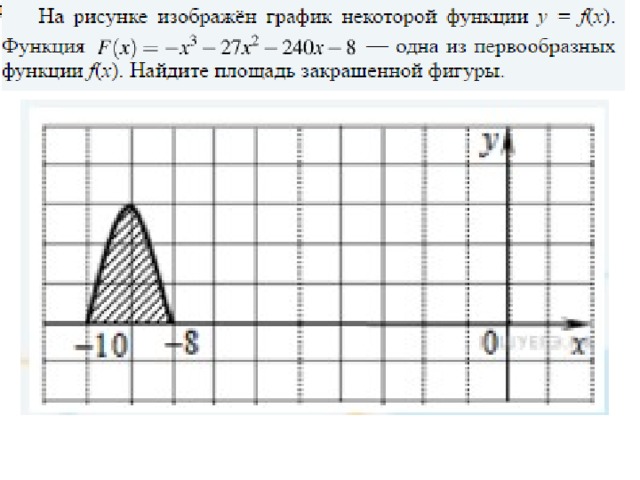
На рисунке изображён график некоторой функции y = f(x). Функция   — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

Пройти тестирование по этим заданиям

Источник

Ресурс содержит презентацию и тест для самостоятельной работы. Тест составлен в 4 вариантах. Предназначен для подготовки к ЕГЭ. Цели ресурса: Образовательные: повторить и закрепить знания о первообразной функции и её свойствах, научиться применять знания при решении конкретных задач. Развивающие: развивать умение анализировать условие задачи. Воспитательные: воспитание аккуратности, внимательности, быстроты мышления.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Подготовка к ЕГЭ Задание №7 (первообразная)

Слайд 2

1) На рисунке изображён график функции y = F( x ) — одной из первообразных функции f ( x ), определённой на интервале (−3; 5). Найдите количество решений уравнения f ( x ) = 0 на отрезке [−2; 4].

Слайд 3

2 ) На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F( x ) — одна из первообразных функции f ( x ).

Слайд 4

3 ) На рисунке изображён график функции y = f ( x ). Функция — одна из первообразных функции y = f ( x ). Найдите площадь закрашенной фигуры.

Слайд 5

4 ) На рисунке изображён график функции y = f ( x ). Функция — одна из первообразных функции y = f ( x ). Найдите площадь закрашенной фигуры.

Слайд 6

5 ) На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл .

Слайд 7

При подготовке презентации были использованы материалы с сайтов: https://www.uchportal.ru / https://ege.sdamgia.ru /

Предварительный просмотр:

ФИ_________________________________________________________В 1

На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−2; 6). Найдите количество решений уравнения f(x) = 0 на отрезке [−1; 5].

Ответ:___________________

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(6) − F(2), где F(x) — одна из первообразных функции f(x).

Ответ:___________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

ФИ_________________________________________________________В 2

На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 6). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 5].

Ответ________________________________

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(5) − F(3), где F(x) — одна из первообразных функции f(x).

Ответ:___________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

ФИ__________________________________________________________В 3

На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−2; 4). Найдите количество решений уравнения f(x) = 0 на отрезке [−1; 3].

Ответ_____________________

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(6) − F(4), где F(x) — одна из первообразных функции f(x).

Ответ_____________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

ФИ_________________________________________________________В 4

На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−2; 4). Найдите количество решений уравнения f(x) = 0 на отрезке [−1; 3].

Ответ____________________

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(6), где F(x) — одна из первообразных функции f(x).

Ответ_____________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

На рисунке изображён график функции y = f(x).

Функция — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Ответ:___________________

По теме: методические разработки, презентации и конспекты

Построение профиля задание С1 ЕГЭ по географии

При выполнении ЕГЭ по географии в задании С1 требуется выполнить профиль по топографической карте. Данный цикл занятий направленный на формирование у одинадцати классников умения выполнять этит тип за…

Варианты ЕГЭ математика (профиль), задания 1-12.

Варианты ЕГЭ математика (профиль), задания 1-12. Задания варианта соответствуют заданиям демоверсии ЕГЭ. При составлении вариантов использованы задания открытого банка заданий ЕГЭ. Ответы прилагаются….

Мне нравится

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Первообразная функции»

Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №1164

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.

Её площадь равна frac{4+3}{2}cdot 3=10,5.

Ответ

10,5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1158

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].

Показать решение

Решение

Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1155

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.

Её площадь равна frac{5+3}{2}cdot 3=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1149

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].

Показать решение

Решение

Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1146

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).

Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №907

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).

Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №307

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

По формуле Ньютона-Лейбница S=F(-1)-F(-5).

F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.

F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.

F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.

Ответ

576

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №306

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.

Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №104

Тип задания: 7
Тема:
Первообразная функции

Условие

На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.

Показать решение

Решение

На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:

intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)

Подставим значение первообразной из условия и получим площадь фигуры:

F(-1)-F(-4)=

=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=

=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5

Ответ

4,5

Задание №103

Тип задания: 7
Тема:
Первообразная функции

Условие

Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].

Показать решение

Решение

Формула первообразной имеет следующий вид:

f(x) = F'(x)

По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.

Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.

На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Блок 1. Физический смысл производной

1	Материальная точка движется прямолинейно по закону x(t) = t^3 — 9t^2 + 2t +30 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени её скорость была равна 50 м/с?	Смотреть видеоразбор
2	Материальная точка движется прямолинейно по закону x(t)=−t^4+6t^3+5t+23, где x−расстояние от точки отсчета в метрах, t−время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.	Смотреть видеоразбор

Блок 2. Анализ графика функции, касательные

3	На графике дифференцируемой функции у=f(x) отмечены семь точек: х1 ,…, х7. Найдите все отмеченные точки, в которых производная функции f(x) равна нулю. В ответе укажите количество этих точек.	Смотреть видеоразбор
4	На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции f(x) отрицательна. В ответе укажите количество найденных точек.	Смотреть видеоразбор
5	На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой X0. Найдите значение производной функции f(x) в точке X0.	Смотреть видеоразбор
6	На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой X0. Найдите значение производной функции f(x) в точке X0.	Смотреть видеоразбор
7	На рисунке изображен график функции y = f(x) и отмечены точки -7, -3, 1, 5. В какой из этих точек значение производной этой функции наибольшее? В ответе укажите эту точку.	Смотреть видеоразбор
8	На рисунке изображен график функции y = f(x), одна из первообразных которой равна F(x). Найдите разность F(4) — F(-1).	Смотреть видеоразбор
9	На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).	Смотреть видеоразбор
10	На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.	Смотреть видеоразбор
11	На рисунке изображен график функции y = f(x). Касательная к этому графику, проведенная в точке с абсциссой -1, проходит через начало координат. Найдите значение производной функции f(x) в точке -1.	Смотреть видеоразбор
12	На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке x0. Уравнение касательной y=-2x-7. Найдите значение производной функции y=-frac{1}{4}f(x)+5x-3 в точке x0.	Смотреть видеоразбор
13	На рисунке изображен график функции y=f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна.	Смотреть видеоразбор
14	На рисунке изображен график функции y=f(x), определенной на интервале (-6;8). Определите количество целых точек, в которых производная функции положительна.	Смотреть видеоразбор
15	На рисунке изображен график функции и шесть точек на оси абсцисс: x_1, x_2, x_3, x_4, x_5, x_6. В скольких из этих точек производная функции отрицательна?	Смотреть видеоразбор
16	Функция f(x) определена на интервале (-4; 6). На рисунке изображен ее график. В скольких целых точках ее производная положительна?	Смотреть видеоразбор

Блок 3. Анализ графика производной

17	На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].	Смотреть видеоразбор
18	На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].	Смотреть видеоразбор
19	На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?	Смотреть видеоразбор
20	На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7; -3] функция f(x) принимает наименьшее значение?	Смотреть видеоразбор
21	На рисунке изображён график y = f′(x) производной функции f(x) и шесть точек на оси абсцисс: x1 , x2 , . . . , x6. В скольких из этих точек функция f(x) возрастает?	Смотреть видеоразбор
22	На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-3; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-2; 15].	Смотреть видеоразбор
23	На рисунке изображен график производной функции f(x) и отмечены одиннадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11. В скольких из этих точек функция f(x) возрастает?	Смотреть видеоразбор
24	На рисунке изображен график производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=-2x-11 или совпадает с ней.	Смотреть видеоразбор
25	На рисунке изображен график производной функции f(x), определенной на интервале (-17; 2). Найдите число точек минимума функции y=f(x).	Смотреть видеоразбор
26	На рисунке изображен график производной функции f(x), определенной на интервале (-4; 4). Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой y=-3x-11 или совпадает с ней.	Смотреть видеоразбор
27	На рисунке изображен график производной функции f(x), определенной на интервале (-6; 8). Найдите количество таких чисел x, что касательная к графику функции f(x) в точке x параллельна прямой y=2x-5 или совпадает с ней.	Смотреть видеоразбор
28	На рисунке изображен график производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7; -2] функция f(x) принимает наибольшее значение?	Смотреть видеоразбор
29	Функция f(x) определена на отрезке [-6; 6]. На рисунке изображен график ее производной. Найдите наибольшую длину промежутка возрастания функции f(x).	Смотреть видеоразбор
30	Функция y = f(x) определена и непрерывна на отрезке [-5; 5]. На рисунке изображен график её производной. Найдите точку x, в которой функция принимает наименьшее значение, если f(-5) больше либо равна f(5).	Смотреть видеоразбор

Блок 4. Задачи на производную без готовых графиков

31	Прямая y=-4x-11 является касательной к графику функции y=x^3+7x^2+7x-6. Найдите абсциссу точки касания.	Смотреть видеоразбор
32	Прямая y=7x-5 параллельна касательной к графику функции y=x^2+6x-8. Найдите абсциссу точки касания.	Смотреть видеоразбор

Блок 5. Первообразная, интеграл

33	На рисунке изображен график функции y=f(x). Функция F(x)=-x^3-21x^2-144x-frac{11}{4} — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.	Смотреть видеоразбор
34	На рисунке изображен график y=F(x) одной из первообразных некоторой функции f(x), определенной на интервале (-8; 7). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-5; 5].	Смотреть видеоразбор
35	На рисунке изображен график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислить F(8)-F(2), где F(x) — одна из первообразных функции f(x).	Смотреть видеоразбор
36	На рисунке изображен график некоторой функции y=f(x). Пользуясь рисунком, вычислите intlimits_{-7}^{-1} f(x)dx	Смотреть видеоразбор
37	На рисунке изображен график некоторой функции y=f(x). Функция F(x) = x^3+30x^2+302x-frac{15}{8} — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.	Смотреть видеоразбор
38	На рисунке изображен график одной из первообразных некоторой функции, определенной на интервале (-3;5). Пользуясь рисунком, определите число корней уравнения на отрезке [-2;4]	Смотреть видеоразбор
39	На рисунке изображен график функции y = f(x). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).	Смотреть видеоразбор
40	На рисунке изображен график функции y=F(x) — одной из первообразных некоторой функции f(x), определенной на интервале (-3; 5). Пользуясь графиком, определите число корней уравнения f(x)=0 на отрезке [-2; 4].	Смотреть видеоразбор
41	На рисунке изображен график функции y=F(x) одной из первообразных некоторой функции f(x), определенной на интервале (-3; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [1; 4].	Смотреть видеоразбор
42	Значение первообразной F(x) функции f(x)=frac{7}{x} в точке 1 равно -11. Найдите F(e^2)	Смотреть видеоразбор

Блок 6. Нестандартные задачи

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №6. Первообразная

ЕГЭ Профиль №6. Первообразнаяadmin2022-08-17T21:08:43+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №6. Первообразная

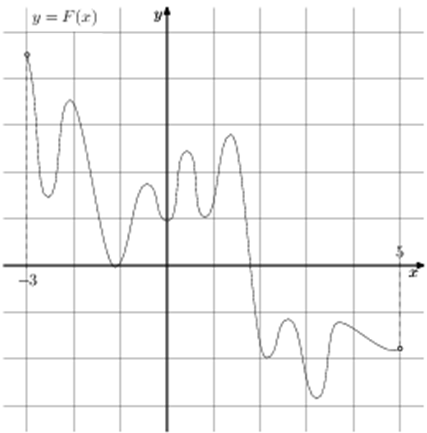
Задача 1. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)), определённой на интервале (left( { — 3;;5} right)). Пользуясь рисунком, определите количество решений уравнения (fleft( x right) = 0) на отрезке (left[ { — 2;;4} right]). Ответ ОТВЕТ: 10.
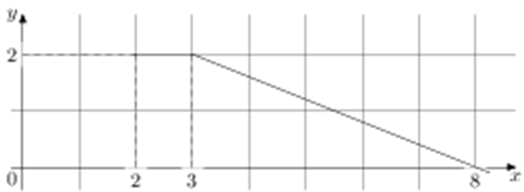
Задача 2. На рисунке изображён график некоторой функции (y = fleft( x right)) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (Fleft( 8 right) — Fleft( 2 right)), где (Fleft( x right))— одна из первообразных функции (fleft( x right)). Ответ ОТВЕТ: 7.
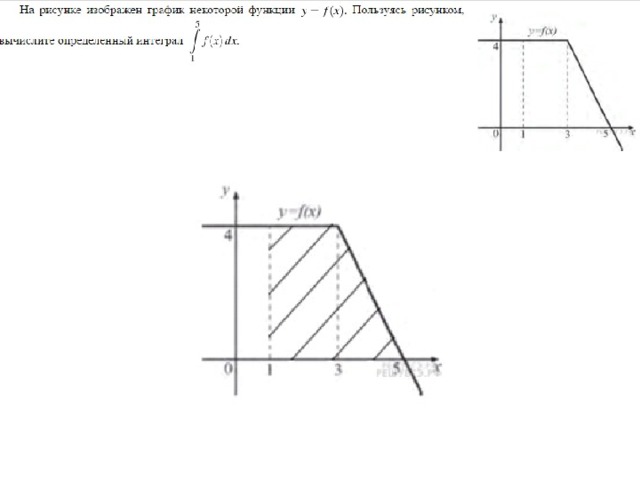
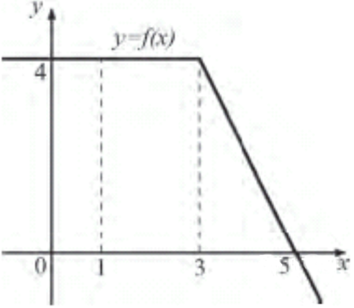
Задача 3. На рисунке изображен график некоторой функции (y = fleft( x right)). Пользуясь рисунком, вычислите определенный интеграл (intlimits_1^5 {fleft( x right)} ,dx) Ответ ОТВЕТ: 12.
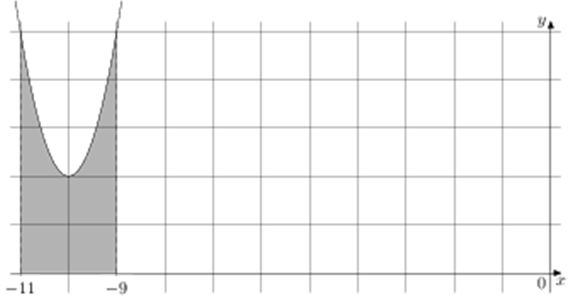
Задача 4. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = {x^3} + 30{x^2} + 302x — frac{{15}}{8}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 6.
Задача 5. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — {x^3} — 27{x^2} — 240x — — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 4.
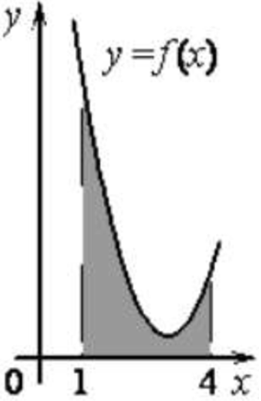
Задача6 . На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = frac{1}{2}{x^3} — frac{9}{2}{x^2} + 14x — 12) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 6.
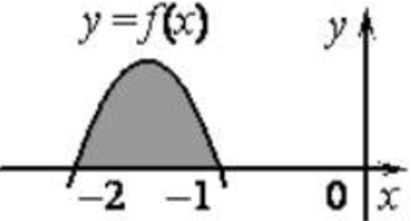
Задача 7. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — {x^3} — frac{9}{2}{x^2} — 6x — frac{{123}}{7}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 0,5.
Задача 8. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)) и отмечены десять точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀. В скольки из этих точек функция (fleft( x right)) положительна? Ответ ОТВЕТ: 7.
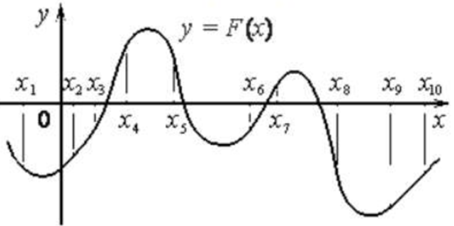Задача 9. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)) и отмечены семь точек на оси абсцисс: x₁, x₂, x₃, x₄, x₅, x₆, x₇. В скольки из этих точек функция (fleft( x right)) отрицательна? Ответ ОТВЕТ: 3.

Источник

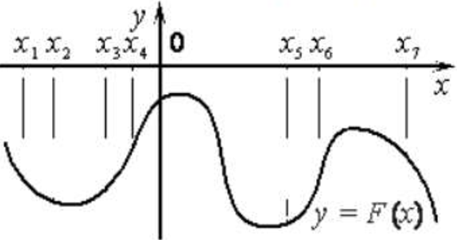Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.

Геометрический смысл производной

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке x_0 равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции f(x) в точке x_0 равна тангенсу угла наклона касательной, проведенной в точке x_0 .

Достроив до прямоугольного треугольника АВС, получим:

Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке x_0 функция убывает, следовательно, её производная отрицательна. Касательная в точке x_0 образует тупой угол alpha с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла varphi , смежного с углом alpha .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку $alpha + varphi = 180^{circ}$ , имеем:

$tg alpha = tg(180^{circ} -varphi ) = - tg varphi = -0, 25.$

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой y=kx+b в точке x_0 .

При x= x_0 значения выражений и kx+b равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

$left{ begin{array}{c}fleft(xright)=kx+b \f^{$

$left{ begin{array}{c}x^3+{7x}^2+7x-6=-4x-11 \{3x}^2+14x+7=-4 end{array}right..$

Из второго уравнения находим x = -1 или $x=-frac{11}{3}.$ Первому уравнению удовлетворяет только x = -1 .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени t = 3 с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени t=3 получим:

Ответ: 3.

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция f (x) возрастает.

Если , то функция f (x) убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

	возрастает	точка максимума	убывает	точка минимума	возрастает
		0		0

5. На рисунке изображен график функции y=f(x) , определенной на интервале Найдите количество точек, в которых производная функции f(x) равна 0.

Производная функции f { в точках максимума и минимума функции f(x). Таких точек на графике 5.

Ответ: 5.

6. На рисунке изображён график y = f — производной функции f(x) , определённой на интервале (-6; 5) . В какой точке отрезка [-1; 3] функция f(x) принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке [-1;3] производная функции f(x) положительна.

Значит, функция f(x) возрастает на этом отрезке. Большим значениям х соответствует большее значение f(x). Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции y= f(x) , определённой на интервале (-3; 8) . Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 1.

Прямая y=1 параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции f(x) , определенной на интервале Найдите количество точек максимума функции f(x) на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке [-6; 9] такая точка всего одна! Это x=7.

Ответ: 1.

9. На рисунке изображен график производной функции f(x) , определенной на интервале Найдите точку экстремума функции f(x) на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке x = -2. В этой точке производная меняет знак с минуса на плюс.

Значит, x= -2 является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция F(x) , для которой f(x) является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции f(x) , определённой на интервале Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке

Функция F(x), для которой f(x) является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку [-4; 4] , в которых производная функции F(x) равна нулю. Это точки максимума и минимума функции F(x). На отрезке [-4; 4] таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник