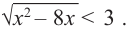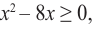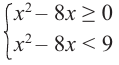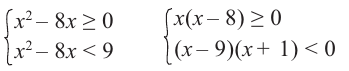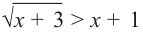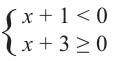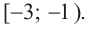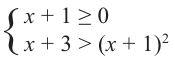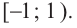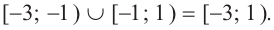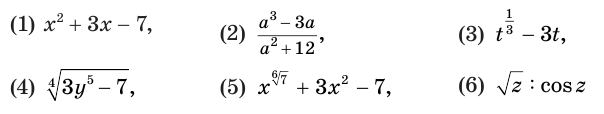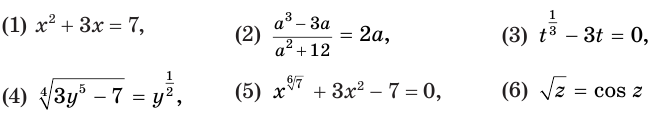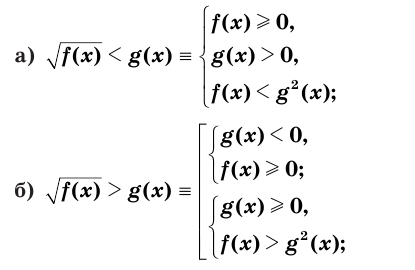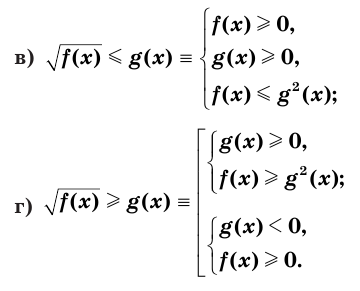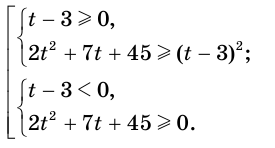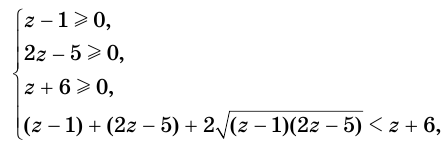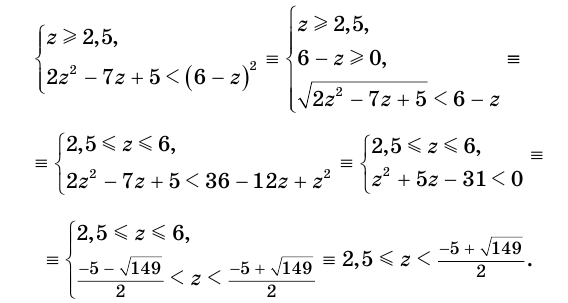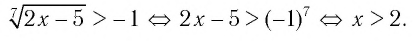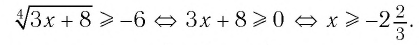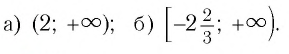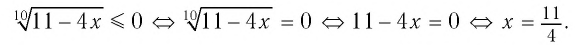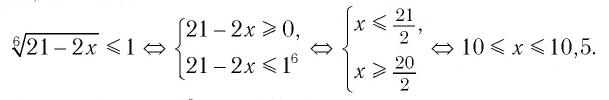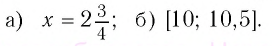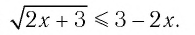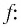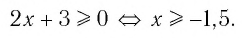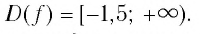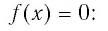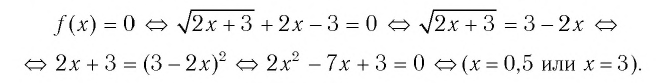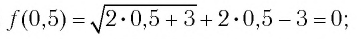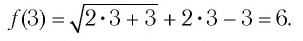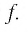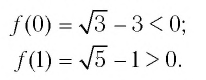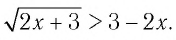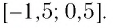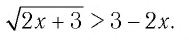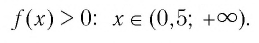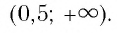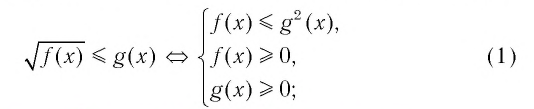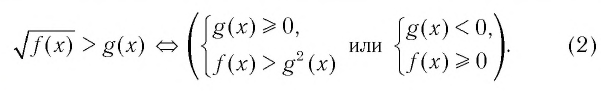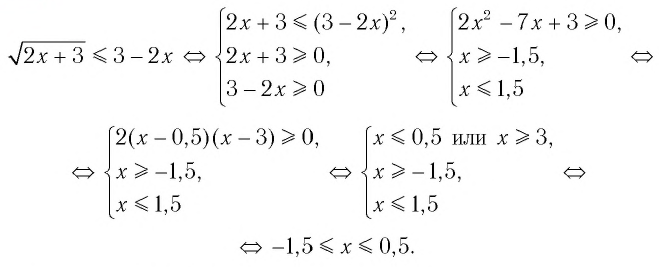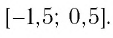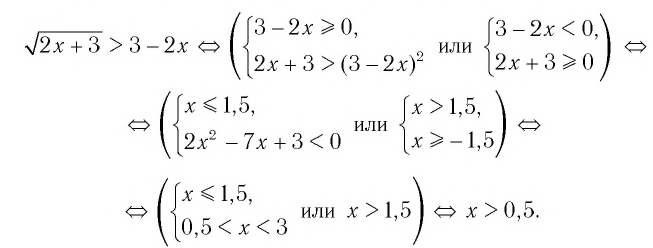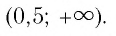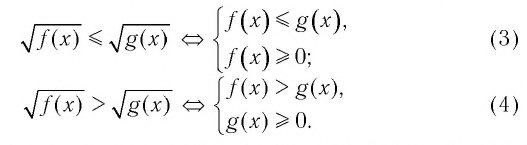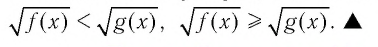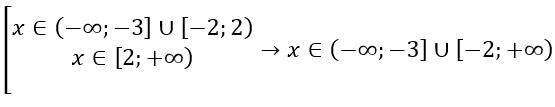Иррациональные неравенства егэ теория

Иррациональные неравенства

Так называются неравенства, содержащие знак корня.

В решении иррациональных неравенств главное – логика и внимательность.

И конечно, надо повторить следующие темы:

1) Арифметический квадратный корень.

2) Решение неравенств. Основные ошибки и полезные лайфхаки.

Напоминаем, что решение лучше всего записывать в виде цепочки равносильных переходов.

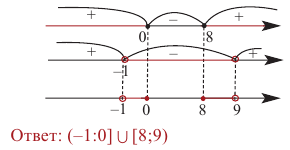
1.Решите неравенство 

Правая часть неравенства неотрицательна:
(по определению корня квадратного).

Поскольку  левая часть положительна: 

Выражение под корнем должно быть неотрицательным. Неравенство равносильно системе:

Ответ: (5;+∞)

2.Решите неравенство .

Как вы думаете – это неравенство такое же, как предыдущее, или отличается от него? Ведь здесь правая часть может быть и положительной, и отрицательной, и равной нулю. И надо рассмотреть все эти случаи.

1) Пусть правая часть неравенства неотрицательна. И левая тоже неотрицательна (по определению арифметического квадратного корня). И подкоренное выражение неотрицательно. Значит, при обе части неравенства можно возвести в квадрат.

Получим:

Разложим выражение на множители. Корни уравнения – это и .

Получаем систему:

2) Пусть теперь правая часть неравенства отрицательна. Если  то неравенство выполняется. В самом деле, по определению. Значит,

Нам нужно только, чтобы подкоренное выражение было неотрицательно: .

Получим:

Объединим полученные интервалы и запишем ответ.

Ответ: .

3.Решите неравенство 

Ответ:

4.Решите неравенство 

Ответ:  

5.Решите неравенство

Сделаем замену , тогда

Ответ:

6. Решите неравенство

Ответ:

Иррациональные неравенства

Привет!

Говоря об иррациональности, может показаться, что сложнее иррациональных уравнений есть лишь одна вещь — иррациональные неравенства.

И сейчас ты поймешь, что это не так!

Если ты хорошо разобрался в предыдущих темах (я скажу, в каких в начале статьи), то иррациональные уравнения покажутся тебе легкими.

Мы рассмотрим все виды неравенств и разберем различные примеры, так, чтобы ты смог решить любое иррациональное неравенство. 

Иррациональные неравенства – коротко о главном

Определение

Иррациональное неравенство – это неравенство, содержащее переменную под корнем

Неравенства вида ( sqrt{A}ge sqrt{B})

( sqrt{A}ge sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}Age B\Bge 0end{array} right.)

или

( sqrt{A}>sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}A>B\Bge 0end{array} right.)

Неравенства вида ( Asqrt{B}>0) или ( Asqrt{B}<0)

( Asqrt{B}>0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A>0end{array} right.)

или

( Asqrt{B}<0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A<0end{array} right.)

Неравенства вида ( Asqrt{B}ge 0)

( Asqrt{B}ge 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Age 0\Bge 0end{array} right.end{array} right.)

или

( Asqrt{B}le 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Ale 0\Bge 0end{array} right.end{array} right.)

Неравенства вида ( sqrt{A}ge B)

( sqrt{A}ge Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}Ble 0\Age 0end{array} right.\left{ begin{array}{l}B>0\Age {{B}^{2}}end{array} right.end{array} right.)

или

( sqrt{A}>Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}B<0\Age 0end{array} right.\left{ begin{array}{l}Bge 0\A>{{B}^{2}}end{array} right.end{array} right.)

Неравенства вида ( sqrt{A}le B)

( sqrt{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\Bge 0\Ale {{B}^{2}}end{array} right.)

или

( sqrt{A}<Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\B>0\A<{{B}^{2}}end{array} right.)

Корни четной степени

Например:

( displaystyle sqrt[4]{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Ale {{B}^{4}}\Bge 0\Age 0end{array} right.)

Корни нечетной степени

Корень нечетной степени можно извлекать из любого числа!

( displaystyle begin{array}{l}sqrt[3]{A}>Btext{ }Leftrightarrow text{ }A>{{B}^{3}}\sqrt[5]{A}<Btext{ }Leftrightarrow text{ }A<{{B}^{5}},end{array}) и т.д.

ОДЗ (Область допустимых значений)

Помнишь, что такое ОДЗ?

ОДЗ (область допустимых значений) неравенства или неравенств – это множество значений переменной, при которых обе части данного неравенства (или неравенств) имеют смысл.

Например, в уравнении ( sqrt{x+2}=3) присутствует квадратный корень. А квадратный корень не имеет смысла, если подкоренное выражение отрицательно.

То есть, в данном случае ОДЗ – это решения неравенства ( x+2ge 0).

Нет необходимости искать ОДЗ в каждой задаче, содержащей корень.

Взять, например, такую задачу:

( sqrt{{{x}^{2}}+3x}>2).

При возведении в квадрат получаем ( {{x}^{2}}+3x>4), то есть подкоренное выражение автоматически неотрицательно! Так зачем лишняя писанина?

Но в некоторых случаях это может быть очень полезно. Более того, иногда можно решить пример, просто найдя ОДЗ. Например:

( sqrt{2{x}-6}>-2).

Но ведь мы помним, что квадратный корень всегда неотрицателен. Поэтому он всегда будет больше ( -2). Значит, решением задачи будет ОДЗ:

( 2{x}-6ge 0text{ }Leftrightarrow text{ }xge 3).

Ответ: ( left[ 3;+infty right)).

Пять видов неравенств и способы их решений

Первый вид неравенств

( sqrt{A}ge sqrt{B})

Естественно, знак неравенства может быть и нестрогим.

Здесь и далее большими буквами ( A), ( B), ( C) и т.д. я буду обозначать не переменные или параметры, а целые выражения, содержащие переменную.

Так, общая запись ( sqrt{A}>sqrt{B}) соответствует, например, уравнению ( sqrt{{{x}^{2}}-{x}-2}>sqrt{{x}-1}).

Здесь ( A={{x}^{2}}-{x}-2) и ( B={x}-1).

Как решить такое неравенство?

Для начала вспомним, что функция ( fleft( x right)=sqrt{x}) – монотонна, то есть, чем больше подкоренное выражение, тем больше сам корень.

Поэтому из двух корней больше тот, у которого подкоренное выражение больше.

Но недаром мы недавно вспоминали про ОДЗ. Есть ли какие-нибудь ограничения в этом неравенстве?

Действительно, чтобы неравенство имело смысл, необходимо, чтобы оба подкоренных выражения были неотрицательны:

( left{ begin{array}{l}Age 0\Bge 0end{array} right.)

Но поскольку первое выражение больше второго, достаточно потребовать неотрицательности только второго:

( sqrt{A}ge sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}Age B\Bge 0end{array} right.)

или

( sqrt{A}>sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}A>B\Bge 0end{array} right.)

Три примера на закрепление материала:

Пример №1. ( sqrt{{{x}^{2}}-{x}+2}>sqrt{{x}+1})

Пример №2. ( sqrt{2{{x}^{2}}-6{x}-17}ge sqrt{{x}-2})

Пример №3. ( sqrt{2{{x}^{2}}-x-6}le sqrt{3{{x}^{2}}-{8x}})

Решение примера №1

Применим только что выученное правило:

( displaystyle sqrt{{{x}^{2}}-x+2}>sqrt{x+1}text{ }Leftrightarrow text{ }left{ begin{array}{l}{{x}^{2}}-x+2>x+1\x+1ge 0end{array} right.text{ }Leftrightarrow text{ }left{ begin{array}{l}{{x}^{2}}-2x+1>0\xge -1end{array} right.Leftrightarrow )

( displaystyle Leftrightarrow text{ }left{ begin{array}{l}{{left( {x}-1 right)}^{2}}>0\xge -1end{array} right.text{ }Leftrightarrow left{ begin{array}{l}xne 1\xge -1end{array} right.text{ }Leftrightarrow text{ }xin left[ -1;1 right)cup left( 1;+infty right)).

Решение примера №2

( displaystyle sqrt{2{{x}^{2}}-6{x}-17}ge sqrt{{x}-2}text{ }Leftrightarrow text{ }left{ begin{array}{l}2{{x}^{2}}-6{x}-17ge {x}-2\{x}-2ge 0end{array} right. Leftrightarrow )

Решение примера №3

( displaystyle sqrt{2{{x}^{2}}-{x}-6}le sqrt{3{{x}^{2}}-8x}text{ }Leftrightarrow text{ }left{ begin{array}{l}3{{x}^{2}}-8xge 2{{x}^{2}}-{x}-6\2{{x}^{2}}-{x}-6ge 0end{array} right.text{ }Leftrightarrow )

( displaystyle Leftrightarrow text{ }left{ begin{array}{l}left( {x}-6 right)left( {x}-1 right)ge 0\2left( {x}-2 right)left( x+frac{3}{2} right)ge 0end{array} right.).

Далее поставим знаки…

Второй вид неравенств

( Asqrt{B}>0) или ( Asqrt{B}<0)

Корень всегда принимает неотрицательные значения, поэтому, он влияет на это неравенство, только если равен нулю. То есть нужно ограничить корень, чтобы он не был равен нулю, а в остальном – дело за выражением ( A).

И не забываем про ОДЗ, подкоренное выражение неотрицательно. А если оно неотрицательно, и при этом не должно быть равно нулю, то оно строго болше нуля:

( Asqrt{B}>0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A>0end{array} right.)

или

( Asqrt{B}<0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A<0end{array} right.)

Три примера на закрепление материала

Пример №1. ( xsqrt{x+5}>0)

Пример №2. ( ({{x}^{2}}-{x}-2)cdot sqrt{{x}-2}<0)

Пример №3. ( ({{x}^{2}}-9)sqrt{{{x}^{2}}-4}>0)

Решение примера №1

( xsqrt{x+5}>0)

( left{ begin{array}{l}x+5>0\x>0end{array} right. Rightarrow left{ begin{array}{l}x>-5\x>0end{array} right.Rightarrow x>0).

Решение примера №2

( ({{x}^{2}}-{x}-2)cdot sqrt{{x}-2}<0)

Решение примера №3

( ({{x}^{2}}-9)sqrt{{{x}^{2}}-4}>0)

Третий вид неравенств

( Asqrt{B}ge 0)

В случае нестрогого неравенства условие, что подкоренное выражение не равно нулю теперь лишнее. Но это только добавило нам проблем, ведь при этом выражение ( displaystyle A) может быть любым. Значит, надо отдельно рассмотреть случай, когда корень равен нулю:

( Asqrt{B}ge 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Age 0\Bge 0end{array} right.end{array} right.)

или

( Asqrt{B}le 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Ale 0\Bge 0end{array} right.end{array} right.)

Три примера на закрепление материала

Пример №1. ( xsqrt{{x}-1}ge 0)

Пример №2. ( left( {{x}^{2}}-4 right)sqrt{x+1}le 0)

Пример №3. ( left( {{x}^{2}}-3{x}-4 right)sqrt{x+1}>0)

Решение примера №1

( xsqrt{{x}-1}ge 0text{ }Leftrightarrow text{ }left[ begin{array}{l}{x}-1=0\left{ begin{array}{l}xge 0\{x}-1ge 0end{array} right.end{array} right.text{ }Leftrightarrow text{ }left[ begin{array}{l}x=1\xge 1end{array} right.text{ }Leftrightarrow text{ }xge 1.).

Решение примера №2

( displaystyle left( {{x}^{2}}-4 right)sqrt{x+1}le 0text{ }Leftrightarrow text{ })

Решение примера №3

( displaystyle left( {{x}^{2}}-3{x}-4 right)sqrt{x+1}>0text{ }Leftrightarrow text{ })

Четвертый вид неравенств

( sqrt{A}le B)

Здесь все немного проще: поскольку корень неотрицателен, то и правая часть этого неравенства должна быть неотрицательной:

( sqrt{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\Bge 0\Ale {{B}^{2}}end{array} right.) или ( sqrt{A}<Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\B>0\A<{{B}^{2}}end{array} right.).

Три примера на закрепление материала

Пример №1. ( sqrt{15-2x}le x)

Пример №2. ( x+3>sqrt{4x})

Пример №3. ( sqrt{x+7}+3x<4{x}-5)

Решение примера №1

( sqrt{15-2x}le x)

( left{ begin{array}{l}15-2x ge 0\xge 0\15-2xle {{x}^{2}}end{array} right.Rightarrow left{ begin{array}{l}x le 7,5\xge 0\{{x}^{2}}+2{x}-15ge 0end{array} right.Rightarrow left{ begin{array}{l}x le 7,5\xge 0\({x}-3)cdot ({x}+5)ge 0end{array} right.Rightarrow )

( left{ begin{array}{l}x le 7,5\xge 0\xin (-infty ;left. -5 right]cup left[ 3 right.;+infty )end{array} right.Rightarrow xin left[ 3; right.left. 7,5 right]).

Решение примера №2

( x+3>sqrt{4x})

Решение примера №3

( sqrt{x+7}+3x<4{x}-5)

Пятый вид неравенств

( sqrt{A}ge B)

Рассмотрим пример:

( sqrt{x+2}ge x)

Тут возможны два варианта. Если ( xle 0), неравенство выполнится при всех допустимых ( x), ведь корень неотрицателен, значит, он автоматически больше (или равен) неположительного числа:

( left{ begin{array}{l}xle 0\x+2ge 0end{array} right.)

Если же правая часть положительна (( x>0)), имеем право возводить в квадрат:

( x+2ge {{x}^{2}}).

ОДЗ, как видим, здесь учтено автоматически. Итак, собираем все в кучу:

( left[ begin{array}{l}left{ begin{array}{l}xle 0\x+2ge 0end{array} right.\left{ begin{array}{l}x>0\x+2ge {{x}^{2}}end{array} right.end{array} right.)

Запомни, прежде чем возводить в квадрат, нужно убедиться, что обе части неравенства неотрицательны! Тоже своего рода ОДЗ.

Итак, правило в общем виде:

( sqrt{A}ge Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}Ble 0\Age 0end{array} right.\left{ begin{array}{l}B>0\Age {{B}^{2}}end{array} right.end{array} right.)

А как будет выглядеть это правило, если неравенство строгое? Вот так:

( sqrt{A}>Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}B<0\Age 0end{array} right.\left{ begin{array}{l}Bge 0\A>{{B}^{2}}end{array} right.end{array} right.)

Подумай сам, почему именно так.

Три примера на закрепление материала

Пример №1. ( sqrt{4x+1}ge {x}-1)

Пример №2. ( sqrt{2{x}-1}-sqrt{x+2}<1)

Пример №3. ( displaystyle 3sqrt{6+2{x}-4{{x}^{2}}}+2>8x)

Решение примера №1

( displaystyle sqrt{4x+1}ge {x}-1text{ }Leftrightarrow )

( displaystyle Leftrightarrow left[ begin{array}{l}left{ begin{array}{l}{x}-1le 0\4x+1ge 0end{array} right.\left{ begin{array}{l}4x+1ge {{x}^{2}}-2x+1\{x}-1>0end{array} right.end{array} right.text{ }Leftrightarrow left[ begin{array}{l}-frac{1}{4}le xle 1\left{ begin{array}{l}xleft( {x}-6 right)le 0\x>1end{array} right.end{array} right.text{ }Leftrightarrow )

( displaystyle Leftrightarrow left[ begin{array}{l}-frac{1}{4}le xle 1\left{ begin{array}{l}0le xle 6\x>1end{array} right.end{array} right.text{ }Leftrightarrow text{ }xin left[ -frac{1}{4};6 right]text{.}).

Решение примера №2

( sqrt{2{x}-1}-sqrt{x+2}<1text{ }Leftrightarrow text{ }sqrt{2{x}-1}<1+sqrt{x+2})

Теперь обе части неравенства неотрицательны, значит, можно возвести их в квадрат (не забыв также, что подкоренное выражение в левой части должно быть неотрицательным):

Решение примера №3

( displaystyle 3sqrt{6+2{x}-4{{x}^{2}}}+2>8x)

Корни степени больше 2

Если же корень в неравенстве не квадратный, важна четность его степени.

Корни чётной степени

Корни ( 2), ( 4), ( 6) и т.д. степеней очень похожи друг на друга, и принцип решения уравнений с ними абсолютно одинаковый. Дело в том, что корень четной степени можно всегда привести к квадратному (вспоминаем тему «Корень и его свойства»!):

( sqrt[4]{x}=sqrt{sqrt{x}};text{ }sqrt[6]{x}=sqrt{sqrt[3]{x}};text{ }sqrt[2k]{x}=sqrt{sqrt[k]{x}})

Например:

( displaystyle sqrt[4]{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Ale {{B}^{4}}\Bge 0\Age 0end{array} right.).

Корни нечётной степени

С нечетными степенями (( 3), ( 5), …) все намного проще!

Дело в том, что корень нечетной степени можно извлекать из любого числа! (И снова, если ты этого не знал, вспомни тему «Корень и его свойства»!)

Что это значит?

Теперь никаких дополнительных условий, никаких ограничений – просто возводим все в нужную степень и решаем:

( displaystyle begin{array}{l}sqrt[3]{A}>Btext{ }Leftrightarrow text{ }A>{{B}^{3}}\sqrt[5]{A}<Btext{ }Leftrightarrow text{ }A<{{B}^{5}},end{array}) и т.д.

Три примера на закрепление материала

Пример №1. ( displaystyle sqrt[5]{2-x}>-2)

Пример №2. ( displaystyle sqrt[3]{{{x}^{3}}+3x+5}ge x)

Пример №3. ( displaystyle sqrt[3]{{{x}^{2}}-{x}-7}<sqrt[3]{1-x})

( displaystyle sqrt[5]{2-x}>-2text{ }Leftrightarrow text{ }2-x>{{left( -2 right)}^{5}}text{ }Leftrightarrow text{ }2-x>-32text{ }Leftrightarrow text{ }x<34).

Решение примера №3

( displaystyle sqrt[3]{{{x}^{2}}-{x}-7}<sqrt[3]{1-x}text{ }Leftrightarrow text{ }{{x}^{2}}-{x}-7<1-xtext{ }Leftrightarrow )

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж – c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
• отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.

21
Окт 2013

Категория: Иррациональные выражения, уравнения и неравенства

Иррациональные неравенства

2013-10-21
2019-08-13

Автор: egeMax |

комментариев 6

Неравенства, содержащие переменную под знаком радикала, называются иррациональными неравенствами.

Содержание:

Решение иррациональных неравенств также ищут на множестве действительных чисел и, используя свойства корня и неравенств, сводится к решению системы рациональных неравенств.

Пример: Решите неравенство

Решение: чтобы найти множество решений данного неравенства на множестве допустимых значений, т. е. при условии

Каждое неравенство системы решим методом интервалов и найдем пересечение полученных решений:

Пример: Решите неравенство

Решение: рассмотрим два случая, в зависимости от знака правой части.

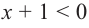
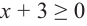
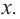
1) при для всех неравенство справедливо для всех Значит, надо решить систему

Ее решением является промежуток

2) при 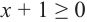обе стороны заданного неравенства можно возвести в квадрат. Тогда получим систему

Ее решением является промежуток

Решением заданного неравенства является

Способы решения иррациональных неравенств 

С действием возведения в степень связаны разные виды выражений. Будем рассматривать выражения с переменными, при образовании которых используются действия сложения, вычитания, умножения, деления и возведения в степень, причем возведение в степень хотя бы один раз применено к выражению с переменной.

Если показатель степени целый, то возникает рациональное выражение, если дробный, то — иррациональное выражение, а если иррациональный, то — трансцендентное выражение.

К трансцендентным выражениям приводят и действия нахождения значений синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса, арккотангенса. Рациональные и иррациональные выражения вместе составляют множество алгебраических выражений.

Из выражений

выражения (1) и (2) являются рациональными, выражения (3) и (4) — иррациональными, выражения (5) и (6) — трансцендентными, а выражения (1)—(4) — алгебраическими.

В зависимости от того, из каких выражений составлено уравнение, говорят о рациональных, иррациональных, трансцендентных уравнениях.

Из уравнений

уравнения (1) и (2) являются рациональными, уравнения (3) и (4) — иррациональными, а уравнения (5) и (6) — трансцендентными.

Так же говорят о рациональных, иррациональных, трансцендентных неравенствах.

В этом параграфе рассматривается решение иррациональных уравнений и неравенств. При их решении нужно следить за тем, какие преобразования выполняются при этом.

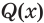
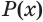
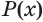
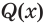
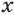
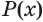
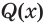
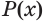
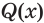
Утверждение равносильно утверждению , если утверждения и истинны при одних и тех же значениях переменной . Равносильность уравнений означает, что они имеют одни и те же корни, а равносильность неравенств — то, что они имеют одни и те же решения. Равносильность утверждений и обозначают = .

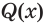
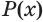
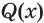
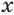
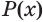
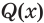
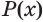
Утверждение следует из утверждения , если утверждение истинно при всех значениях переменной , при которых истинно утверждение . Следование второго уравнения из первого означает, что каждый корень первого уравнения является корнем второго уравнения, но второе уравнение может иметь и дополнительные корни. Так же понимается и следование одного неравенства из другого. Следование утверждения из утверждения обозначают .

Отношения равносильности и следования связаны:

При решении иррациональных неравенств нужно учитывать, что проверка подстановкой найденного множества чисел обычно невозможна из-за его бесконечности. Поэтому при решении неравенств нужно следить за равносильностью проводимых преобразований.

Теорема:

Верны следующие равносильности:

Доказательство проводится по схеме, использованной при доказательстве теоремы 9 с применением соответствующих свойств числовых неравенств.

Пример №1

Решим неравенство 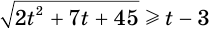. Это неравенство равносильно совокупности неравенств

Первую систему можно заменить равносильной системой 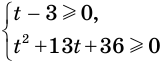, которая равносильна системе , которая, в свою очередь, равносильна неравенству .

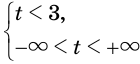
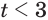
Вторая система совокупности равносильна системе , которая равносильна неравенству .

Решения данного неравенства получим, когда объединим решения и первой и второй систем совокупности, в результате получим множество всех действительных чисел.

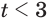
Ответ. .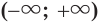

Пример №2

Решим неравенство .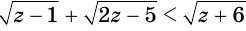

Обратим внимание на то, что на области определения левая и правая части данного неравенства обе неотрицательны, поэтому оно равносильно системе неравенств

решение которой следующее:

Ответ. .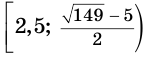

• Заказать решение задач по высшей математике

Какие неравенства называются иррациональными

В этой лекции мы будем рассматривать неравенства, содержащие переменную (неизвестное) под знаком корня. Такие неравенства называются иррациональными.

При решении иррациональных неравенств часто используют подход, который мы уже применяли, решая иррациональные уравнения. Он состоит в замене исходного неравенства равносильным ему неравенством (системой или совокупностью неравенств).

Пример №3

Решить неравенство:

Решение:

а) Учитывая свойства корня нечетной степени, получаем:

б) По определению корня четной степени значения выражения

неотрицательны при всех значениях при которых это

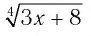
выражение имеет смысл, т. е. когда значения подкоренного выражения неотрицательны. Таким образом, имеем:

Ответ:

Пример №4

Решить неравенство:

Решение:

а) По определению корня четной степени значения выражения 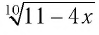отрицательными быть не могут. Поэтому имеем:

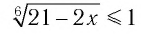
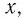
б) Поскольку обе части неравенства неотрицательны при всех значениях при которых его левая часть имеет смысл, то имеем:

Ответ:

При решении иррациональных неравенств часто используется также метод интервалов.

Пример №5

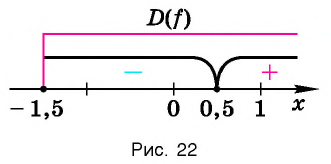
Решить неравенство

Решение:

Обозначим 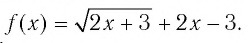Найдем область определения функции

Таким образом,

Найдем нули функции 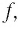т. е. корни уравнения

Проверка:

Значит, 0,5 — единственный нуль функции

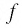
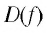
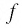
Отметим нуль функции на области определения (рис.22). Определим знаки значений функции на образовавшихся интервалах, для чего вычислим:

Используя рисунок 22, запишем решение неравенства

Ответ:

Пример №6

Решить неравенство

Решение:

Решение этого примера аналогично решению примера 3.

Используя рисунок 22, записываем решение неравенства

Ответ:

▲ При решении иррациональных неравенств часто используются следующие утверждения о равносильности неравенств и систем неравенств:

Решим пример 3, используя равносильность (1):

Ответ:

Решим пример 4, используя равносильность (2):

Ответ:

Для решения заданий такого типа, как, например, в 1.265, можно использовать следующие утверждения о равносильности:

Аналогичные утверждения можно записать и для неравенств

Иррациональные неравенства

Иррациональное неравенство вида (sqrt{mathbf{f}}mathbf{< a})

Здесь можно рассмотреть 2 случая – когда число a справа больше нуля и когда a меньше нуля.

1. (sqrt{mathbf{f}}mathbf{< a, a > 0})

При преобразовании любых неравенств первым делом записываем ОДЗ. В нашем случае ограничения накладываются на подкоренную функцию – она должна быть неотрицательной.

После того, как ограничения добавлены, можно преобразовывать выражение. В данном случае возводим в квадрат обе части неравенства.

(sqrt{f} < a Longleftrightarrow left{ begin{matrix} \ f geq 0 \ f < a^{2} \ \ end{matrix} right. )

Пример №1

(sqrt{x + 2} < 5 Longleftrightarrow left{ begin{matrix} \ x + 2 geq 0 \ x + 2 < 5^{2} \ \ end{matrix} right. )

(left{ begin{matrix} \ x geq — 2 \ x < 25 — 2 \ \ end{matrix} right. )

(left{ begin{matrix} \ x geq — 2 \ x < 23 \ \ end{matrix} right. )

(x in lbrack — 2;23))

1. (sqrt{mathbf{f}}mathbf{< a, a < 0})

Здесь мы имеем с левой стороны неравенства квадратный корень, а значит число заведомо неотрицательное. То есть в неравенстве

(sqrt{f} < a) при (a < 0)

мы получаем ситуацию, когда неотрицательное число меньше отрицательного, чего быть не может. А, значит, наше неравенство решений не имеет.

Пример №2

(sqrt{x + 6} < — 3)

(- 3 < 0)

(x in varnothing)

Иррациональное неравенство вида (sqrt{mathbf{f}}mathbf{> a})

Здесь, так же, как и в предыдущем случае имеет место быть два возможных варианта:

( a > 0) и (a < 0.)

1. (sqrt{mathbf{f}}mathbf{> a, a > 0})

Если действовать по правилам, то сначала мы должны записать ОДЗ, а затем возвести в квадрат, чтобы избавиться от иррациональности. Тогда мы получим систему:

(left{ begin{matrix} \ f geq 0 \ f > a^{2} \ \ end{matrix} right. )

Посмотрим внимательно на получившуюся систему – она «требует», чтобы выражение (f) было больше или равно нуля и в то же время больше (a^{2}). Но (a^{2}) — заведомо неотрицательное число. Если какое-то число больше (a^{2}), то оно и больше нуля автоматически. Это значит, что первое неравенство из системы можно просто убрать.

Значит от исходного неравенства можно сразу сделать переход:

(sqrt{f} > a Longleftrightarrow f > a^{2})

Пример №3

(sqrt{2x + 5} > Longleftrightarrow 2x + 5 > 3^{2})

(2x + 5 > 9)

(2x > 9 — 5)

(x > frac{4}{2})

(x > 2)

(x in (2; + infty))

1. (sqrt{mathbf{f}}mathbf{> a, a < 0})

Здесь снова имеем ситуацию – слева число заведомо неотрицательное, а справа – отрицательное. Только теперь между ними стоит знак «больше». Но, мы точно можем сказать, что любое неотрицательное число всегда больше отрицательного. Значит, в рассмотренном случае нам подойдут любые значения x, удовлетворяющие ОДЗ.

(sqrt{f} > a, a < 0 Longleftrightarrow f geq 0)

Пример №4

(sqrt{x + 6} > — 4)

(- 4 < 0)

ОДЗ: (x + 6 geq 0)

(x geq — 6)

Иррациональное неравенство вида (sqrt{mathbf{f}}mathbf{>}sqrt{mathbf{g}})

По аналогии с предыдущим случаем можно сделать вывод, что если неравенство содержит два корня, то мы возводим квадрат и убираем меньшее ограничение из ОДЗ.

(sqrt{mathbf{f}}mathbf{>}sqrt{mathbf{g}}mathbf{Longleftrightarrow}left{ begin{matrix} mathbf{ } \ mathbf{f > g} \ mathbf{g geq 0} \ mathbf{ } \ end{matrix} right. )

Важно отметить, что ограничение «больше нуля» накладывается на меньшее выражение, а уж какой оно обозначается буквой, неважно. Если вместо (> )будет (geq) , то все выводы проводятся аналогично.

Пример №5

(sqrt{2x + 5} > sqrt{x + 3} Longleftrightarrow left{ begin{matrix} \ 2x + 5 > x + 3 \ x + 3 geq 0 \ \ end{matrix} right. )

(left{ begin{matrix} \ 2x — x > 3 — 5 \ x geq — 3 \ \ end{matrix} right. )

(left{ begin{matrix} \ x > — 2 \ x geq — 3 \ \ end{matrix} right. )

(x in ( — 2; + infty))

Иррациональные неравенства вида (sqrt{mathbf{f}}mathbf{<}mathbf{g})

Будем действовать в соответствии со стандартным алгоритмом: записываем ОДЗ и возводим в квадрат обе части неравенства, принимая во внимание тот факт, что справа теперь тоже находится функция. В ОДЗ идет 2 условия, так как на корень накладывается 2 ограничения.

(sqrt{mathbf{f}}mathbf{<}mathbf{g}mathbf{Longleftrightarrow}left{ begin{matrix} mathbf{ } \ mathbf{f <}mathbf{g}^{mathbf{2}} \ mathbf{f geq 0} \ mathbf{g > 0} \ mathbf{ } \ end{matrix} right. )

Пример №6

(sqrt{x^{2} + 5x + 7} < x + 3 Longleftrightarrow left{ begin{matrix} \ x^{2} + 5x + 7 < left( x + 3 right)^{2} \ x^{2} + 5x + 7 geq 0 \ x + 3 > 0 \ \ end{matrix} right. )

(left{ begin{matrix} \ x^{2} + 5x + 7 < x^{2} + 6x + 9 \ x^{2} + 5x + 7 geq 0, D < 0 \ x > — 3 \ \ end{matrix} right. )

(left{ begin{matrix} \ 5x — 6x < 9 — 7 \ x > — 3 \ \ end{matrix} right. )

(left{ begin{matrix} \ — x < 2 \ x > — 3 \ \ end{matrix} right. )

(left{ begin{matrix} \ x > — 2 \ x > — 3 \ \ end{matrix} right. )

(x in ( — 2; + infty))

Иррациональные неравенства вида(sqrt{mathbf{f}}mathbf{>}mathbf{g})

Здесь у нас будет объединение двух случаев — первый, когда функция стоящая справа отрицательна, второй – неотрицательна.

(sqrt{mathbf{f}}mathbf{>}mathbf{g Longleftrightarrow}leftlbrack begin{matrix} mathbf{ } \ left{ begin{matrix} mathbf{ } \ mathbf{g < 0} \ mathbf{f geq 0} \ mathbf{ } \ end{matrix} right. \ left{ begin{matrix} mathbf{ } \ mathbf{g geq 0} \ mathbf{f >}mathbf{g}^{mathbf{2}} \ mathbf{ } \ end{matrix} right. \ mathbf{ } \ end{matrix} right. )

Пример №7

(sqrt{x^{2} + 5x + 6} > x — 2 Longleftrightarrow leftlbrack begin{matrix} \ left{ begin{matrix} \ x — 2 < 0 \ x^{2} + 5x + 6 geq 0 \ \ end{matrix} right. \ left{ begin{matrix} \ x — 2 geq 0 \ x^{2} + 5x + 6 > left( x — 2 right)^{2} \ \ end{matrix} right. \ \ end{matrix} right. )

Решим каждую из систем по отдельности:

1. (left{ begin{matrix} \ x < 2 \ (x + 3)(x + 2) geq 0 \ \ end{matrix} right. )

(left{ begin{matrix} \ x < 2 \ leftlbrack begin{matrix} \ x leq — 3 rightarrow x in left( — infty; — 3 rightrbrack cup lbrack — 2;2) \ x geq — 2 \ \ end{matrix} right. \ \ end{matrix} right. )

1. (left{ begin{matrix} \ x — 2 geq 0 \ x^{2} + 5x + 6 > x^{2} — 4x + 4 \ \ end{matrix} right. )

(left{ begin{matrix} \ x geq 2 \ 5x + 4x > 4 — 6 \ \ end{matrix} right. )

(left{ begin{matrix} \ x geq 2 \ 9x > — 2 \ \ end{matrix} right. )

(left{ begin{matrix} \ x geq 2 \ x > — frac{2}{9} \ \ end{matrix} right. rightarrow x in lbrack 2; + infty))

Теперь запишем исходную совокупность: