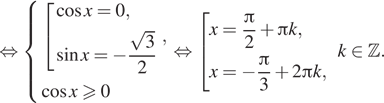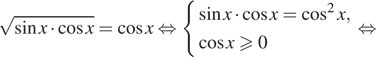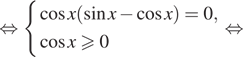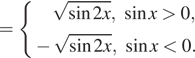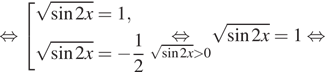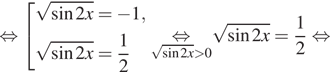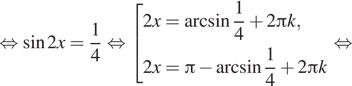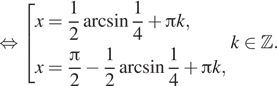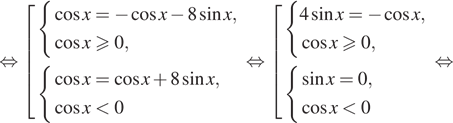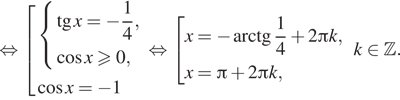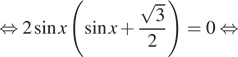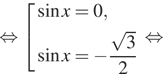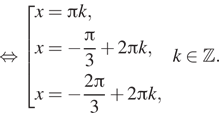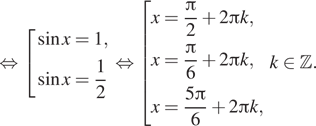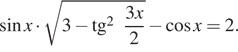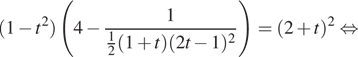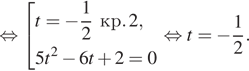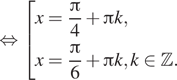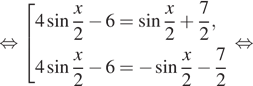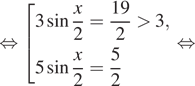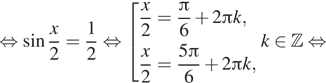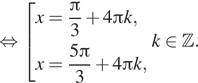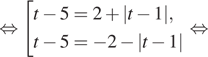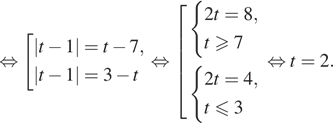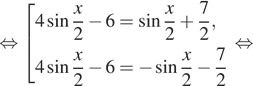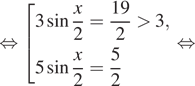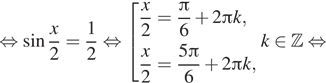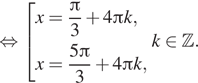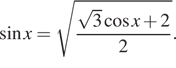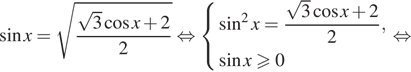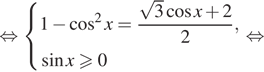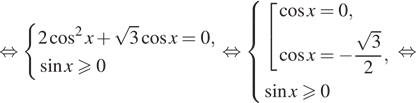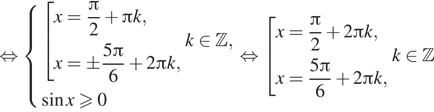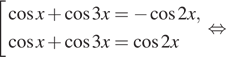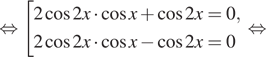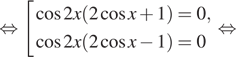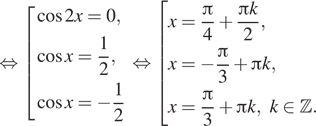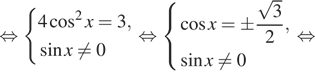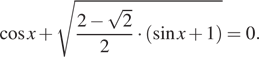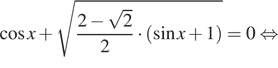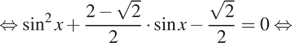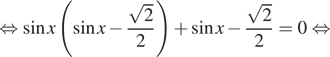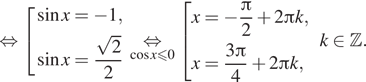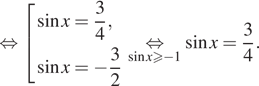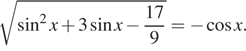Иррациональные тригонометрические уравнения егэ - Помощь в подготовке к экзаменам и поступлению

11
Фев 2014

Категория: 12 (С1) УравненияТ/P A. ЛаринаТригонометрические выражения, уравнения и неравенства

С1 (№15). Иррациональное уравнение с тригонометрическими функциями

2014-02-11
2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №13»

Смотрите также С2(№16), С4(№18), С5(№20) тренировочной работы №63 А. Ларина.

Возможно, вам стоит вспомнить/изучить как осуществляются равносильные переходы в иррациональных уравнениях.

а) Решите уравнение
б) Найдите все корни на промежутке $[-2pi;-frac{pi}{2}]$ .

Решение:

а) Перепишем уравнение следующим образом:

Заметим,

Переходим к равносильной системе уравнений:

$begin{cases} 5sinx+cos2x=4cos^2x,& &-2cosxgeq 0; end{cases}$

Обратите внимание, нет необходимости указывать в системе неравенство .

Раз есть , а , то получается, – все уже оговорено.

Применяем к формулу двойного угла

Также используем для правой части уравнения основное тригонометрическое тождество:

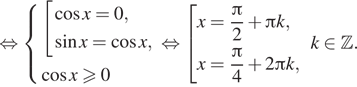
Получаем

$begin{cases} 5sinx+1-2sin^2x=4(1-sin^2x),& &-2cosxgeq 0; end{cases}$

$begin{cases} 2sin^2x+5sinx-3=0,& &cosxleq 0; end{cases}$

$begin{cases} left[begin{gathered} sinx=-3, &sinx=frac{1}{2}; end{gathered}right& &cosxleq 0;& end{cases}&$

$begin{cases} sinx=frac{1}{2};& &cosxleq 0; end{cases}&$

Нас устраивает только серия корней $x=frac{5pi}{6}+2pi n,;nin Z.$

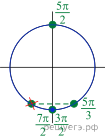
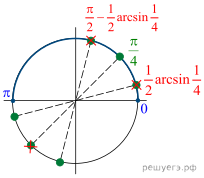
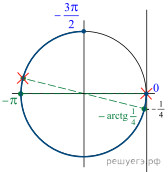
б) Произведем отбор корней из отрезка $[-2pi;-frac{pi}{2}]$ :

В данный отрезок попадает один корень – это $-frac{7pi}{6}.$

Ответ: a) $frac{5pi}{6}+2pi n,;nin Z$ ; б) $-frac{7pi }{6}.$

___________________________________________________________

Полезно порешать

а) Решите уравнение $sqrt{1-2cos^2x}=cosx+sinx;$
б) Найдите все корни на промежутке $[-2pi;-frac{pi}{2}]$ .

Ответ: + показать

Если у вас возникли вопросы, – пожалуйста, пишите в комментариях!

Автор: egeMax |

комментариев 5

Источник

Уравнения
из материалов ЕГЭ профильного уровня смешанного тип

Иррациональные и тригонометрические уравнения.

1. а)  Решите
уравнение

б)  Найдите все корни этого уравнения, принадлежащие
отрезку

Решение. а)  Решим
уравнение

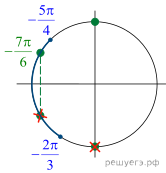
б)  С помощью числовой окружности отберём корни,
принадлежащие отрезку Получим
числа:

Ответ: а) б)

2. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  Воспользуемся
тем, что

и произведем эквивалентые преобразования уравнения:

б)  Отберем корни при помощи единичной окружности.
Подходят

Ответ: а) б)

3. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  Заметим,
что

поэтому, внося под знак корня, необходимо
рассмотреть два случая:

В случае имеем:

Условию удовлетворяет
серия

В случае имеем:

Условию удовлетворяют
серии и

б)  Отберём корни, принадлежащие отрезку при помощи
тригонометрической окружности (см. рис.). Получим

Ответ: а) б)

4. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. Уравнение имеет корни,
только если При этом
условии обе части уравнения неотрицательны и можно возвести их в квадрат.
Выполним преобразования:

Разделим второе
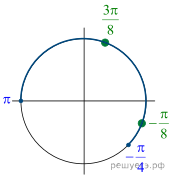
уравнение совокупности на получим это уравнение не имеет
решений. Умножим обе части первого уравнения на −1 и воспользуемся
формулами двойного угла. Получим:

Из найденных серий условию удовлетворяют
только и

Отберем корни при помощи тригонометрической окружности
(см. рис.), получим числа и

Ответ: а) б)
и

5. а)  Решите
уравнение

б)  Укажите корни этого уравнения принадлежащие
отрезку

Решение. а)  Заметим,
что получим
в левой части

Далее, используя формулы перейдем
к половинному аргументу в правой части и сведем уравнение к однородному
тригонометрическому второй степени:

б)  Отберем корни при помощи единичной окружности,
подходят

Ответ: а) б)

6. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  Преобразуем
уравнение с помощью формул приведения и основного тригонометрического
тождества:

б)  Отберём корни. принадлежащие отрезку. Для первой
серии получаем:

откуда корень Для
второй серии имеем:

откуда корень

Ответ: а) б)

7. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. 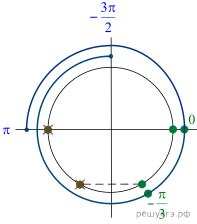а)  При
условии исходное
уравнение равносильно следующим:

Условию удовлетворяет
только

б)  Отберем корни при помощи единичной окружности,
подходят и 0.

Ответ: а) б)
0.

8. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  Левая
часть уравнения обращается в нуль в двух случаях. Если второй множитель равен
нулю:

Или если первый множитель равен нулю, а второй при этом определён.

Решим уравнение:

Решим неравенство:

Неравенству удовлетворяют только корни серии

Объединяя два рассмотренных случая, заключаем, что решениями
уравнения являются и

б)  Для отбора корней воспользуемся тригонометрической
окружностью (см. рис.). На отрезке лежат корни и

Ответ: а) б)

9. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  Перенесем
в правую часть, заметим, что сумма не
принимает отрицательных значений. Следовательно, при условии возведение обеих частей уравнения в квадрат
является равносильным преобразованием. Имеем:

Выразим множители, стоящие в левой части уравнения, через В силу основного тригонометрического тождества Чтобы преобразовать
первый множитель, воспользуемся формулой откуда
получим: 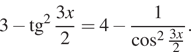Далее
применим формулы косинуса тройного угла и
косинуса половинного угла

Пусть тогда имеем:

Вернемся к исходной переменной, получим уравнение откуда
Учитывая
условие окончательно
получаем:

б)  Чтобы найти корни на заданном отрезке, решим двойное
неравенство:

Так как правая часть
полученного двойного неравенства лежит в интервале (−1; 0). Значения k
целые, поэтому наибольшее значение k = −1. Оценим
левую часть:

Поскольку подходит
также значение k = −2. Поскольку осталось
проверить значение k = −3. Покажем, что

Итак k = −3, k = −2
или k = −1. Найденным значениям k соответствуют
корни и

Ответ: а) б)

10. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. 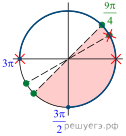а)   При
условии и
исходное уравнение эквивалентно совокупности

Условию удовлетворяют серии корней и

б)  Отберём корни при помощи единичной
тригонометрической окружности. На заданном отрезке лежит только один
корень  — число

Ответ: а) б)

11. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
промежутку

Решение. 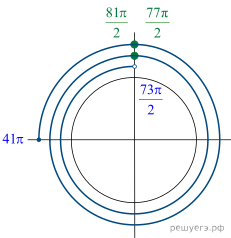a)  Уравнение
равносильно уравнению при
условии Возведем обе
части исходного уравнения в квадрат при условии получим:

Полученный корень удовлетворяет исходному ограничению.

б)  Отберем корни при помощи единичной окружности
(см. рис.), подходят числа и 

Ответ: а) б)

12. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. 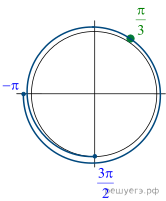а)  Под
знаками обоих радикалов находятся полные квадраты:

б)  Отберём корни при помощи единичной окружности.
Подходит

Ответ: а) б)

13. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  Сделаем
замену переменной тогда:

Таким образом, откуда

б)  Отберем корни при помощи единичной окружности.
Точка удовлетворяет
заданному интервалу.

Ответ: а) б)

Примечание.

Уравнение удобно
решить, используя геометрический смысл модуля. Действительно, с геометрической
точки зрения левая часть уравнения представляет собой разность расстояний от
точки с координатой t до точек с координатами 5 и 1 на числовой
оси. Эта разность равна в точке для точек, лежащих на
числовой оси правее числа 2, эта разность расстояний будет меньше двух, а для
точек, лежащих левее  — больше двух.

14. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. 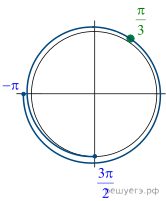а)  Под
знаками обоих радикалов находятся полные квадраты:

б)  Отберём корни при помощи единичной окружности.
Подходит

Ответ: а) б)

15. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  Преобразуем
уравнение:

б)  Отберём корни при помощи единичной окружности.
Подходит

Ответ: а) б)

16. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. 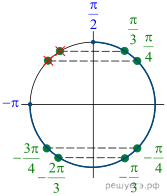а)  Исходное
уравнение имеет смысл только при тогда
это эквивалентно совокупности:

Все найденные серии корней удовлетворяют условию

б)  Отберем корни при помощи единичной окружности
(см. рис.), получим: и

Ответ: а) б)
и

17. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. 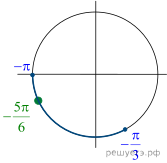а)  Преобразуем
уравнение:

б)  Отберём корни при помощи единичной окружности.
Получим

Ответ: а) б)

18. а)  Решите
уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Решение. а)  При
условии исходное
уравнение эквивалентно следующим:

Каждое из слагаемых в левой части не меньше −1, поэтому их
сумма равна −2 тогда и только тогда, когда каждое слагаемое равно
−1. Решим уравнение получим то есть Проверим
для найденных решений выполнение условия Используем
периодичность синуса, применим формулу приведения, получаем:

Выражение равно −1 для
всех нечетных k и только для них. Следовательно, решениями уравнения
(⁎) являются числа где k  —
любое нечетное число. Эти числа удовлетворяют условию поскольку обращают косинус в нуль. Тем
самым все они являются корнями исходного уравнения.

б)  Решим двойное неравенство:

Следовательно, k = 3 и подходит корень

Ответ: а) б)

Примечание.Ответ к пункту а) можно записать в виде

19. а)  Решите
уравнение

б)  Найдите все корни уравнения, принадлежащие отрезку

Решение. 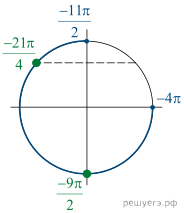а) Заметим, что
уравнение может иметь решения только при Преобразуем его при этом условии:

б)  Отберём корни, принадлежащие отрезку при
помощи тригонометрической окружности. Подходят

Ответ: а) б)

20. а)  Решите
уравнение

б)  Найдите все корни уравнения, принадлежащие отрезку

Решение. а)  Знаменатель
дроби должен быть отличен от нуля, то есть

При этом условии числитель дроби должен быть равен нулю. Применим
формулы и получим:

Если и угол х
лежит в первой четверти, то 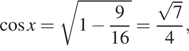а
тогда что
обращает знаменатель в нуль. Если же и угол х
лежит во второй четверти, то 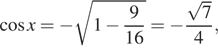а
тогда что
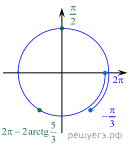
допустимо. Следовательно, решением уравнения является серия

б)  Отберем корни, решая двойное неравенство:

Акрсинус положительного числа лежит в интервале поэтому
левая часть двойного неравенства больше  –5π, а
правая  — меньше –4,5π. Следовательно, число 2πk
лежит в интервале (–5π; –4,5π), а значит, Найденному значению параметра соответствует корень

Ответ: а) б)

Решить
самостоятельно.

1. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие
промежутку

2. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

3. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

4. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

5. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие
промежутку

6. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие
отрезку

7. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

8. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие
отрезку

Ответы.

1. а) б)
(№17)

2. : а) б)
(№40)

3. : а) б)
(№31)

4. : а) б)
(№47)

5. : а) б)
(№55)

6. а) б)
(№67)

7. а) б)
(№68)

8. : а) б)
0. (№71)

Уравнения из материалов ЕГЭ профильного уровня смешанного тип

Отберем корни при помощи единичной окружности

В случае имеем: Условию удовлетворяет серия

Укажите корни этого уравнения, принадлежащие отрезку

Укажите корни этого уравнения принадлежащие отрезку

Отберём корни. принадлежащие отрезку

Решение. а) При условии исходное уравнение равносильно следующим:

Решим неравенство: Неравенству удовлетворяют только корни серии

Пусть тогда имеем:

Ответ: а) б) 10. а)

Полученный корень удовлетворяет исходному ограничению

Отберём корни при помощи единичной окружности

Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку

Решение. а) Исходное уравнение имеет смысл только при тогда это эквивалентно совокупности:

Отберём корни при помощи единичной окружности

Решите уравнение б) Найдите все корни уравнения, принадлежащие отрезку

При этом условии числитель дроби должен быть равен нулю

Решить самостоятельно. 1. а)

Ответы. 1. а) б) (№17) 2

Источник

Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

Опубликовано 16.09.2020Подготовка к ЕГЭ

Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

На сегодняшний день ЕГЭ по математике проходит в форме решения заданий, содержащихся в контрольно-измерительных материалах, при этом, ответы на задания выносят на отдельный бланк.

Уравнения могут быть следующих видов:

В данной статье рассмотрена профильная математика, а именно раздел по видам и системам рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений.

При решении уравнений нужно помнить основные термины:

— Корнем уравнения называют неизвестное число, которое нужно найти;

— Решение уравнения предполагает нахождение его корня;

— Уравнения, у которых совпадают решения называют равносильными;

— ОДЗ – область допустимых значений;

— Если возможно заменить переменные, то нужно это выполнить;

— После решения уравнения необходимо провести проверку на правильность нахождения корня.

Итак, рассмотрим каждый вид уравнений по отдельности, включая примеры решения.

Рациональные уравнения – уравнения, у которых, как правило, слева расположено рациональное выражение, а справа – ноль.

Рациональным уравнением называют уравнение вида r(х)=0.

Если обе части уравнения являются рациональными выражениями, то рациональные уравнения называют целыми.

Дробно-рациональным называют уравнение, которое содержит дробное выражение.

Порядок действий при решении данного вида уравнения должен быть следующий:

— Все члены должны быть переведены в левую часть уравнения;

— Данную часть уравнения нужно представить в виде дроби p(x)/q(x);

— Для полученного решения нужно провести проверку, то есть.

При решение этого рационального уравнения понадобится формула (а-в)2=а2-2ав+в2.

Рассмотрим ещё один пример решения рационального уравнения:

На основе примеров показано, что рациональные уравнения могут быть с разным количеством переменных.

Иррациональными уравнениями считают уравнения с переменной под корнем. Для того, чтобы определить является ли уравнение иррациональным нужно просто посмотреть на корень переменной. Следует учитывать, что в некоторых учебниках по математике иррациональное уравнение определяют другим способом.

Способы решения таких уравнений:

— Возвести в степень обе части уравнения;

— Ввести новые переменные;

Пример решения уравнения по первому способу:

Пример решения по второму способу:

Показательные уравнения

Показательные уравнения – уравнение, содержащее неизвестный показатель.

В учебниках по математике разных авторов определение показательного уравнения может отличаться. Обычно такие отличия касаются незначительных деталей.

Как правило, это уравнения вида af(x)=ag(x), где а не равно одному и число а больше нуля. Из этого следует, что f(x)=g(x).

— Уравнение с одним основанием;

— Уравнение с равными основаниями.

Существует следующие способы решения таких уравнений:

— Использовать метод логарифмов;

— Привести уравнение к квадратному виду;

— Вынести за скобку общий множитель;

— Ввести новую переменную.

Итак, как решить показательное уравнение? Любое по сложности уравнение нужно привести в простую форму.

Рассмотрим наиболее простой пример решения показательного уравнения:

Для решения данного уравнения следует 2 возвести во вторую степень.

Решение даже простейших показательных уравнений имеет большую значимость. Поэтому далее вам будет легче решать уравнения более сложного уровня.

Данная тема является одной из самых сложных, поэтому следует внимательно подойти к изучению данной темы. Известны три формулы тригонометрических уравнений, запомнить которые не составляет особой сложности.

Наиболее простое тригонометрическое уравнение имеет вид sin x=a, cos x=a, tg x=а, а – число действительное.

Способы решения таких уравнений:

— Решение с помощью форму и приведение к простейшему;

— Ввод других переменных;

— Разложить уравнение по множителям.

Пример решения тригонометрического уравнения:

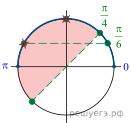
Здесь нужно рисовать окружность, далее выделить точки с координатой ½, соответственно, это точки 5п/6 и п/6. Если пройти по окружности, исходя из данных точек, то х=п/6+2пk, x=5п/6+2пn. При этом синус и косинус принадлежат промежутку [-1;1]. Если при решении уравнения в его правой части стоит число не принадлежащее промежутку, считается, что уравнение не имеет решения.

Также рассмотрим пример решения уравнения, разложив его по множителям.

Нужно применить формулу sin2x = 2sinxcosx.

2sinxcosx – sinx = 0.

sinx (2cosx – 1) = 0.

Таким образом, если один из множителей равен нулю, то решение уравнения также равно нулю.

Далее, sinx=0, x=пk.

Логарифмические уравнения

Особое значение имеет подготовка ЕГЭ по математике логарифмы, это обусловлено тем, что в КИМах чаще всего встречаются именно этого вида уравнения.

Логарифмическое уравнение – это уравнение с неизвестной величиной, находящейся внутри логарифма.

Примерами логарифмических уравнений являются уравнения следующего вида:

Способы решения уравнений данного вида:

— Применять способ уравнивания к единице;

— Применять способ умножать на единицу;

— Применять доступные правила логарифмов;

— Введение другого основания;

— Возвести в степень.

Самым простым логарифмическим уравнением принято считать уравнение вида log a x = b, при этом основание a>0,a≠1.

Пример решения уравнения:

Сначала следует найти значение области, то есть ОДЗ. При этом нужно помнить, что под логарифмом выражение всегда положительное. Воспользуемся логарифмическим определением, представим х степью основания 2 логарифма, степень будет равна 3.

Решение уравнения является ОДЗ, то есть корень уравнения найден.

Таким образом, подобное задание ЕГЭ по математике легко можно решить, зная логарифмы и способы их решения.

Оставить Комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Выбери тему

Самые популярные записи

StudyWay

Помощь

Ты можешь попробовать 3 наших закрытых занятия из курса «Прорыв».

Записаться можно через Instagram

Для этого напиши в Direct (в личку) кодовое слово «Пробный«

Что за курс и что тебя там будет ждать?

12 мощнейших онлайн занятий по 2 часа в формате вебинаров.
Содержание вебинара: повторение предыдущей темы, теория, перерыв и практика.

Воркбук (рабочая тетрадь)абсолютно к каждому уроку со всей необходимой теорией к этой теме и практикой.

Личный куратор — это твой помощник во всех учебных вопросах.
Они занимаются проверкой твоих домашних заданий, поддерживают и мотивируют двигаться дальше, даже когда хочется сдаться.

На собственной онлайн платформе тебя ждут
Домашние задания, которые необходимо решать после каждого занятия.
Все задания построены на базе создателей ЕГЭ — Котова / Лискова.

К каждому тестовому вопросу будет подробный разбор от главного куратора.
А задания, где необходимо оценить ответ (вторая часть) — будет проверять твой личный куратор и писать подробный комментарий про ошибки

Общий чат единомышленников, поделенный на команды.
Название даете совместно (например «Воробушки»)

Ты будешь двигаться сообща с однокурсниками, поддерживая и мотивируя друг друга.
За лучшую командную успеваемость всей команде будут выделены призы в конце каждого месяца (скидка на обучение, стикерпаки и т.д).

Личный помощник — это твой верный друг и помощник, который поможет тебе со всеми техническими вопросами, ответит на вопросы про поступление, да и просто может обсудить какие-то личные вопросы, поделиться переживаниями.

Доступ к уникальной «Академии косатиков».

Там ты сможешь найти:
Банк теории, банк планов, банк аргументов, курсы по работе со всей второй частью, термины, курсы по саморазвитию, полезные лайфхаки и всю подробную информация о ЕГЭ.

Игровая система на нашей платформе StudyWay👇

За выполнение заданий получаешь баллы (XP).

При достижении нового уровня у тебя открываются новые персонажи из Marvel, DC Comics, Игра престолов и Star Wars, а также на каждом новом уровне тебя ждут призы от нашей школы.

Основная ценность курса
1. Изучение теории и практики с учетом изменений в ЕГЭ 2022
2. Заложение фундамента и основы предмета
3. Прохождение всей теории для первой части
4. Нарешивание всех возможных типов заданий
5. Повышение результата с 0 до 60 баллов

Отличия тарифа «Стандарт от «Профи».

Дополнительные домашние задания
необходимо выполнять. Это значительно повысит твою успеваемость и улучшит показатели.

Дополнительное объяснение
твой личный куратор объяснит тебе тему повторно, если останется что-то не понятным

Групповые зачеты
у тебя будут зачеты с твоим личным куратором в мини группах по 5 человек. Там спрашиваются пройденные темы, термины и так далее.

Карта памяти
будешь восполнять все пройденные в удобной интеллект карте и в конце учебы у тебя выйдет файл с полноценной теорией по всем темам и разделам.

Персональный звонок куратору
1 раз в месяц ты можешь позвонить своему куратору и обсудить все волнующие тебя вопросы в течении 20 минут.

Секретный квест
1 раз в месяц ты будешь созваниваться с другим учеником курса и проводить совместные зачеты, тем самым познакомишься с новыми ребятами из других городов, уберешь страхи знакомства, повторишь и закрепишь пройденные темы.

Основные виды тригонометрических уравнений (задание 13)

Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.

(blacktriangleright) Квадратные тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: [<Large>] где (ane 0, f(x)) — одна из функций (sin x, cos x, mathrm,x, mathrm, x) ,
то такое уравнение с помощью замены (f(x)=t) сводится к квадратному уравнению.

Часто при решении таких уравнений используются
основные тождества: [begin <|ccc|>hline sin^2 alpha+cos^2 alpha =1&& mathrm, alpha cdot mathrm, alpha =1\ &&\ mathrm, alpha=dfrac<sin alpha><cos alpha>&&mathrm, alpha =dfrac<cos alpha><sin alpha>\&&\ 1+mathrm^2, alpha =dfrac1 <cos^2 alpha>&& 1+mathrm^2, alpha=dfrac1<sin^2 alpha>\&&\ hline end]
формулы двойного угла: [begin <|lc|cr|>hline sin <2alpha>=2sin alphacos alpha & qquad &qquad & cos<2alpha>=cos^2alpha -sin^2alpha\ sin alphacos alpha =dfrac12sin <2alpha>&& & cos<2alpha>=2cos^2alpha -1\ & & & cos<2alpha>=1-2sin^2 alpha\ hline &&&\ mathrm, 2alpha = dfrac<2mathrm, alpha><1-mathrm^2, alpha> && & mathrm, 2alpha = dfrac<mathrm^2, alpha-1><2mathrm, alpha>\&&&\ hline end]

Пример 1. Решить уравнение (6cos^2x-13sin x-13=0)

С помощью формулы (cos^2alpha=1-sin^2alpha) уравнение сводится к виду:
(6sin^2x+13sin x+7=0) . Сделаем замену (t=sin x) . Т.к. область значений синуса (sin xin [-1;1]) , то (tin[-1;1]) . Получим уравнение:

(6t^2+13t+7=0) . Корни данного уравнения (t_1=-dfrac76, t_2=-1) .

Таким образом, корень (t_1) не подходит. Сделаем обратную замену:
(sin x=-1 Rightarrow x=-dfrac<pi>2+2pi n, ninmathbb) .

Пример 2. Решить уравнение (5sin 2x=cos 4x-3)

С помощью формулы двойного угла для косинуса (cos 2alpha=1-2sin^2alpha) имеем:
(cos4x=1-2sin^22x) . Сделаем эту подстановку и получим:

(2sin^22x+5sin 2x+2=0) . Сделаем замену (t=sin 2x) . Т.к. область значений синуса (sin 2xin [-1;1]) , то (tin[-1;1]) . Получим уравнение:

(2t^2+5t+2=0) . Корни данного уравнения (t_1=-2, t_2=-dfrac12) .

Таким образом, корень (t_1) не подходит. Сделаем обратную замену: (sin 2x=-dfrac12 Rightarrow x_1=-dfrac<pi><12>+pi n, x_2=-dfrac<5pi><12>+pi n, ninmathbb) .

Пример 3. Решить уравнение (mathrm, x+3mathrm,x+4=0)

Т.к. (mathrm,xcdot mathrm,x=1) , то (mathrm,x=dfrac1<mathrm,x>) . Сделаем замену (mathrm,x=t) . Т.к. область значений тангенса (mathrm,xinmathbb) , то (tinmathbb) . Получим уравнение:

(t+dfrac3t+4=0 Rightarrow dfrac=0) . Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Таким образом:

Сделаем обратную замену:

(blacktriangleright) Кубические тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: [<Large>] где (ane 0, f(x)) — одна из функций (sin x, cos x, mathrm,x, mathrm, x) ,
то такое уравнение с помощью замены (f(x)=t) сводится к кубическому уравнению.

Часто при решении таких уравнений в дополнение к предыдущим формулам используются
формулы тройного угла: [begin <|lc|cr|>hline &&&\ sin <3alpha>=3sin alpha -4sin^3alpha &&& cos<3alpha>=4cos^3alpha -3cos alpha\&&&\ hline end]

Пример 4. Решить уравнение (11cos 2x-3=3sin 3x-11sin x)

При помощи формул (sin 3x=3sin x-4sin^3x) и (cos2x=1-2sin^2x) можно свести уравнение к уравнению только с (sin x) :

(12sin^3x-9sin x+11sin x-3+11-22sin^2 x=0) . Сделаем замену (sin x=t, tin[-1;1]) :

(6t^3-11t^2+t+4=0) . Подбором находим, что один из корней равен (t_1=1) . Выполнив деление в столбик многочлена (6t^3-11t^2+t+4) на (t-1) , получим:

((t-1)(2t+1)(3t-4)=0 Rightarrow) корнями являются (t_1=1, t_2=-dfrac12, t_3=dfrac43) .

Таким образом, корень (t_3) не подходит. Сделаем обратную замену:

(blacktriangleright) Однородные тригонометрические уравнения второй степени: [I. quad <Large>, quad ane 0,cne 0]

Заметим, что в данном уравнении никогда не являются решениями те значения (x) , при которых (cos x=0) или (sin x=0) . Действительно, если (cos x=0) , то, подставив вместо косинуса ноль в уравнение, получим: (asin^2 x=0) , откуда следует, что и (sin x=0) . Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если (cos x=0) , то (sin x=pm 1) .

Аналогично и (sin x=0) не является решением такого уравнения.

Значит, данное уравнение можно делить на (cos^2 x) или на (sin^2 x) . Разделим, например, на (cos^2 x) :

Таким образом, данное уравнение при помощи деления на (cos^2x) и замены (t=mathrm,x) сводится к квадратному уравнению:

(at^2+bt+c=0) , способ решения которого вам известен.

Уравнения вида [I’. quad <Large>, quad ane0,cne 0] с легкостью сводятся к уравнению вида (I) с помощью использования основного тригонометрического тождества: [d=dcdot 1=dcdot (sin^2x+cos^2x)]

Заметим, что благодаря формуле (sin2x=2sin xcos x) однородное уравнение можно записать в виде

(asin^2 x+bsin 2x+ccos^2x=0)

Пример 5. Решить уравнение (2sin^2x+3sin xcos x=3cos^2x+1)

Подставим вместо (1=sin^2x+cos^2x) и получим:

(sin^2x+3sin xcos x-4cos^2x=0) . Разделим данное уравнение на (cos^2x) :

(mathrm^2,x+3mathrm,x-4=0) и сделаем замену (t=mathrm,x, tinmathbb) . Уравнение примет вид:

(t^2+3t-4=0) . Корнями являются (t_1=-4, t_2=1) . Сделаем обратную замену:

(blacktriangleright) Однородные тригонометрические уравнения первой степени: [II.quad <Large>, ane0, bne 0]

Заметим, что в данном уравнении никогда не являются решениями те значения (x) , при которых (cos x=0) или (sin x=0) . Действительно, если (cos x=0) , то, подставив вместо косинуса ноль в уравнение, получим: (asin x=0) , откуда следует, что и (sin x=0) . Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если (cos x=0) , то (sin x=pm 1) .

Аналогично и (sin x=0) не является решением такого уравнения.

Значит, данное уравнение можно делить на (cos x) или на (sin x) . Разделим, например, на (cos x) :

(a dfrac<sin x><cos x>+b dfrac<cos x><cos x>=0) , откуда имеем (amathrm, x+b=0 Rightarrow mathrm, x=-dfrac ba)

Пример 6. Решить уравнение (sin x+cos x=0)

Разделим правую и левую части уравнения на (sin x) :

(1+mathrm, x=0 Rightarrow mathrm, x=-1 Rightarrow x=-dfrac<pi>4+pi n, ninmathbb)

(blacktriangleright) Неоднородные тригонометрические уравнения первой степени: [II.quad <Large>, ane0, bne 0, cne 0]

Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:

1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества: (<large<sin x=2sin<dfrac x2>cos<dfrac x2>, qquad cos x=cos^2 <dfrac x2>-sin^2 <dfrac x2>,qquad c=ccdot Big(sin^2 <dfrac x2>+cos^2 <dfrac x2>Big)>>) данное уравнение сведется к уравнению (I) :

Пример 7. Решить уравнение (sin 2x-sqrt3 cos 2x=-1)

Распишем (sin 2x=2sin xcos x, cos 2x=cos^2x-sin^2 x, -1=-sin^2 x-cos^2x) . Тогда уравнение примет вид:

((1+sqrt3)sin^2x+2sin xcos x+(1-sqrt3)cos^2x=0) . Данное уравнение с помощью деления на (cos^2x) и замены (mathrm,x=t) сводится к:

((1+sqrt3)t^2+2t+1-sqrt3=0) . Корнями этого уравнения являются (t_1=-1, t_2=dfrac<sqrt3-1><sqrt3+1>=2-sqrt3) . Сделаем обратную замену:

2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: [begin <|lc|cr|>hline &&&\ sin<alpha>=dfrac<2mathrm, dfrac<alpha>2><1+mathrm^2, dfrac<alpha>2> &&& cos<alpha>=dfrac<1-mathrm^2, dfrac<alpha>2><1+mathrm^2, dfrac<alpha>2>\&&&\ hline end] уравнение сведется к квадратному уравнению относительно (mathrm, dfrac x2)

Пример 8. Решить то же уравнение (sin 2x-sqrt3 cos 2x=-1)

(dfrac<(sqrt3+1)t^2+2t+1-sqrt3><1+t^2>=0 Rightarrow (sqrt3+1)t^2+2t+1-sqrt3=0) (т.к. (1+t^2geqslant 1) при всех (t) , то есть всегда (ne 0) )

Таким образом, мы получили то же уравнение, что и, решая первым способом.

3 СПОСОБ: при помощи формулы вспомогательного угла.
[<large,sin (x+phi),>> quad text <где >cos phi=dfrac a<sqrt>]

Для использования данной формулы нам понадобятся формулы сложения углов: [begin <|lc|cr|>hline &&&\ sin<(alphapm beta)>=sinalphacdot cosbetapm sinbetacdot cosalpha &&& cos<(alphapm beta)>=cosalphacdot cosbeta mp sinalphacdot sinbeta\ &&&\ hline end]

Пример 9. Решить то же уравнение (sin 2x-sqrt3 cos 2x=-1)

Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на (sqrt<1^2+(-sqrt3)^2>=2) :

(dfrac12sin 2x-dfrac<sqrt3>2cos 2x=-dfrac12)

Заметим, что числа (dfrac12) и (dfrac<sqrt3>2) получились табличные. Можно, например, взять за (dfrac12=cos dfrac<pi>3, dfrac<sqrt3>2=sin dfrac<pi>3) . Тогда уравнение примет вид:

(sin 2xcos dfrac<pi>3-sin dfrac<pi>3cos 2x=-dfrac12 Rightarrow sinleft(2x-dfrac<pi>3right)=-dfrac12)

Решениями данного уравнения являются:

Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.

(blacktriangleright) Если тригонометрическое уравнение можно свести к виду [<Large>, text <где >ane 0, bne 0,] то с помощью формулы [<large<(sin xpmcos x)^2=1pm2sin xcos x>> (*)] данное уравнение можно свести к квадратному.

Для этого необходимо сделать замену (t=sin xpm cos x) , тогда (sin xcos x=pm dfrac2) .

Заметим, что формула ((*)) есть не что иное, как формула сокращенного умножения ((Apm B)^2=A^2pm 2AB+B^2) при подстановке в нее (A=sin x, B=cos x) .

Пример 10. Решить уравнение (3sin 2x+3cos 2x=16sin xcos^3x-8sin xcos x) .

Вынесем общий множитель за скобки в правой части: (3sin 2x+3cos 2x=8sin xcos x(2cos^2 x-1)) .
По формулам двойного угла (2sin xcos x=sin 2x, 2cos^2x-1=cos 2x) имеем: [3(sin 2x+cos 2x)=4sin 2xcos 2x] Заметим, что полученное уравнение как раз записано в необходимом нам виде. Сделаем замену (t=sin 2x+cos 2x) , тогда (sin 2xcos 2x=dfrac2) . Тогда уравнение примет вид: [3t=2t^2-2 Rightarrow 2t^2-3t-2=0] Корнями данного уравнения являются (t_1=2, t_2=-dfrac12) .

По формулам вспомогательного аргумента (sin2x+cos 2x=sqrt2sinleft(2x+dfrac<pi>4right)) , следовательно, сделав обратную замену: [left[ begin begin &sqrt2sinleft(2x+dfrac<pi>4right)=2\[1ex] &sqrt2sinleft(2x+dfrac<pi>4right)=-dfrac12 end end right. Rightarrow left[ begin begin &sinleft(2x+dfrac<pi>4right)=sqrt2\[1ex] &sinleft(2x+dfrac<pi>4right)=-dfrac1 <2sqrt2>end end right.] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от (-1) до (1) . Значит: (sinleft(2x+dfrac<pi>4right)=-dfrac1 <2sqrt2>Rightarrow left[ begin begin &2x+dfrac<pi>4=-arcsin <dfrac1<2sqrt2>>+2pi n\[1ex] &2x+dfrac<pi>4=pi+arcsin <dfrac1<2sqrt2>>+2pi n end end right. Rightarrow )
(Rightarrow left[ begin begin &x=-dfrac12arcsin <dfrac1<2sqrt2>>-dfrac<pi>8+pi n\[1ex] &x=dfrac<3pi>8+dfrac12arcsin <dfrac1<2sqrt2>>+pi n end end right. ninmathbb)

(blacktriangleright) Формулы сокращенного умножения в тригонометрическом варианте:

(I) Квадрат суммы или разности ((Apm B)^2=A^2pm 2AB+B^2) :

((sin xpm cos x)^2=sin^2 xpm 2sin xcos x+cos^2x=(sin^2 x+cos^2 x)pm 2sin xcos x=1pm sin 2x)

(II) Разность квадратов (A^2-B^2=(A-B)(A+B)) :

((cos x-sin x)(cos x+sin x)=cos^2x-sin^2x=cos 2x)

(III) Сумма или разность кубов (A^3pm B^3=(Apm B)(A^2mp AB+B^2)) :

(sin^3xpm cos^3x=(sin xpm cos x)(sin^2xmp sin xcos x+cos^2x)=(sin xpm cos x)(1mp sin xcos x)=)

(=(sin xpm cos x)(1mp frac12sin 2x))

(IV) Куб суммы или разности ((Apm B)^3=A^3pm B^3pm 3AB(Apm B)) :

((sin xpm cos x)^3=(sin xpm cos x)(sin xpm cos x)^2=(sin xpm cos x)(1pm sin 2x)) (по первой формуле)

Иррациональные тригонометрические уравнения

Харцызск

Год

Виды тригонометрических уравнений.

1. Простейшие тригонометрические уравнения:

Пример 1. 2sin(3x — p/4) -1 = 0.

Решение. Решим уравнение относительно sin(3x — p/4).

sin(3x — p/4) = 1/2, отсюда по формуле решения уравнения sinx = а находим

3х — p/4 = (-1) n arcsin 1/2 + np, nÎZ.

Зх — p/4 = (-1) n p/6 + np, nÎZ; 3x = (-1) n p/6 + p/4 + np, nÎZ;

x = (-1) n p/18 + p/12 + np/3, nÎZ

Если k = 2n (четное), то х = p/18 + p/12 + 2pn/3, nÎZ.

Если k = 2n + 1 (нечетное число), то х = — p/18 + p/12 + ((2pn + 1)p)/3 =

= p/36 + p/3 + 2pn/3 = 13p/36 + 2pn/3, nÎz.

Ответ: х1 = 5p/6 + 2pn/3,nÎZ, x2 =13p/36 + 2pn/3, nÎZ,

или в градусах: х, = 25° + 120 · n, nÎZ; x, = 65° + 120°· n, nÎZ.

Пример 2. sinx + Öз cosx = 1.

Решение. Подставим вместо Öз значение ctg p/6, тогда уравнение примет вид

sinx + ctg p/6 cosx = 1; sinx + (cosp/6)/sinp/6 · cosx = 1;

sinx sin p/6 + cos p/6 cosx = sin p/6; cos(x — p/6) = 1/2.

По формуле для уравнения cosx = а находим

х — p/6 = ± arccos 1/2 + 2pn, nÎZ; x = ± p/3 + p/6 + 2pn, nÎZ;

x1 = p/3 + p/6 + 2pn, nÎZ; x1 = p/2 + 2pn, nÎZ;

x2 = — p/3 + p/6 + 2pn, nÎZ; x2 = -p/6 + 2pn, nÎZ;

Ответ: x1 = p/2 + 2pn, nÎZ; x2 = -p/6 + 2pn, nÎZ.

2. Двучленные уравнения:

Пример 1. sin3x = sinx.

Решение. Перенесем sinx в левую часть уравнения и полученную разность преобразуем в произведение. sin3x — sinx == 0; 2sinx · cos2x = 0.

Из условия равенства нулю произведения получим два простейших уравнения.

sinx = 0 или cos2x = 0.

x1 = pn, nÎZ, x2 = p/4 + pn/2, nÎZ.

Ответ: x1 = pn, nÎZ, x2 = p/4 + pn/2, nÎZ.

3. Разложение на множители:

Пример 1. sinx + tgx = sin 2 x / cosx

Решение. cosx ¹ 0; x ¹ p/2 + pn, nÎZ.

sinx + sinx/cosx = sin 2 x / cosx . Умножим обе части уравнения на cosx.

sinx · cosx + sinx — sin 2 x = 0; sinx(cosx + 1 — sinx) = 0;

sinx = 0 или cosx — sinx +1=0;

x1 = pn, nÎZ; cosx — cos(p/2 — x) = -1; 2sin p/4 · sin(p/4 — x) = -1;

Ö2 · sin(p/4 — x) = -1; sin(p/4 -x) = -1/Ö2; p/4 — x = (-1) n+1 arcsin 1/Ö2 + pn, nÎZ;

x2 = p/4 — (-1) n+1 · p/4 — pn, nÎZ; x2 = p/4 + (-1) n · p/4 + pn, nÎZ.

Если n = 2n (четное), то x = p/2 + pn, если n = 2n + l (нечетное), то x = pn.

Ответ: x1 = pn, nÎZ; x2 = p/4 + (-I) n · p/4 + pn, nÎZ.

Способ подстановки

Пример 1. 2 sin 2 x = 3cosx.

Решение. 2sin 2 x — 3cosx = 0; 2 (l — cos 2 x) — 3cosx = 0; 2cos 2 x + 3cosx — 2 = 0.

Пусть z = cosx, |z| £ 1. 2z 2 + 32z — 2=0.

Д = 9+16 = 25; ÖД = 5; z1 = (-3 + 5)/4 = 1/2; z2 = (-3-5)/ 4 = -2 —

-не удовлетворяют условию для z. Тогда решим одно простейшее уравнение:

cosx = 1/2; х = ± p/3 + 2pn, nÎZ. Ответ: х = ± p/3 + 2pn, nÎZ.

Однородные уравнения

Однородные тригонометрические уравнения имеют такой вид:

a sin 2 x + b sinxcosx + c cos 2 x = 0 (однородное уравнение 2-й степени) или

a sin 3 x + b sin 2 x cosx + c sinx cos 2 x + d sin 3 x = 0 и т.д.

В этих уравнениях sinx ¹ 0, cosx ¹ 0. Решаются они делением обеих частей уравнения на sin 2 x или на cos 2 x и приводятся к уравнениям относительно tgx или ctgx.

Пример 1. Ö3sin 2 2x — 2sin4x + Ö3cos 2 2x = 0.

Решение. Разложим sin4x по формуле синуса двойного угла.

Получим уравнение Ö3sin 2 2x — 4sin2xcos2x + Ö3cos 2 2x = 0.

Разделим на cos 2 2x. Уравнение примет вид Ö3 tg 2 2x – 4tg2x + Ö3 = 0.

Пусть z = tg2x, тогда Ö3z 2 — 4z + Ö3 = 0; Д = 4; ÖД = 2.

z1 = (4 +2)/2Ö3 = 6/2Ö3 = Ö3; z2 = (4 – 2)/2Ö3 = 1/Ö3

tg2x = Ö3 или tg2x = 1/Ö3

2x = p/3 + pn, nÎZ; 2x = p/6 + pn, nÎZ;

x1 = p/6 + pn/2, nÎZ ; x2 = p/12 + pn/2, nÎz.

Ответ: x1 = p/6 + pn/2, nÎZ ; x2 = p/12 + pn/2, nÎz.

6. Уравнение вида a sinx + b cosx = с

Пример 1. 3sinx + 4cosx = 5.

Решение. Разделим обе части уравнения на 5, тогда 3/5sinx + 4/5cosx = 1.

sinj = 4/5; cosj = 3/5; sin(x+j) = 1, x + j = p/2 + 2pn, nÎZ.

Ответ: x = p/2 — arcsin 4/5 + 2pn, nÎZ.

Дробно-рациональные тригонометрические уравнения

Уравнения, содержащие тригонометрические дроби, называются дробно-рациональными уравнениями. В этих уравнениях требуется следить за областью допустимых значений.

Пример 1. 1/(Ö3-tgx) – 1/(Ö3 +tgx) = sin2x

Решение. Область допустимых значений решений этого уравнения

tgx ¹ ± Ö3, х ¹ ± p/8 + pn, nÎZ и х ¹ ± p/2 + pn, nÎZ.

Левую часть уравнения приведем к общему знаменателю, а правую преобразуем с помощью формулы выражения синуса угла через тангенс половинного угла.

(Ö3 + tgx — Ö3 + tgx)/3 — tg 2 x = 2tgx/ (1 + tg 2 x); 2tgx / (3 — tg 2 x) = 2tgx/(1 + tg 2 x)

Второе уравнение имеет вид

2tg 2 x — 2 = 0; tg 2 x = 1; tgx = ±1; x2 = ± p/4 + pn, nÎZ.

Ответ: x1 = pn, nÎZ; х2 = ± p/4 + pn, nÎZ.

Иррациональные тригонометрические уравнения

Если в уравнении тригонометрическая функция находится под знаком радикала, то такое тригонометрическое уравнение будет иррациональным. В таких уравнениях следует соблюдать все правила, которыми пользуются при решении обычных иррациональных уравнений (учитывается область допустимых значений как самого уравнения, так и при освобождении от корня четной степени).

Пример 1. Ö( cos 2 x + ½) + Ö( sin 2 x + ½) = 2.

Решение. Уравнение имеет смысл при любом х. Возведем обе части уравнения в квадрат.

cos 2 x + ½ + 2 Ö(( cos 2 x + ½) ( sin 2 x + ½)) + sin 2 x + ½ = 4

Ö(( cos 2 x + ½) ( sin 2 x + ½)) = 1; ( cos 2 x + ½) ( sin 2 x + ½) = 1

( ½ + ½ cos2x + ½)( ½ — ½ cos2x + ½) = 1; (1 + ½ cos2x) (1 — ½ cos2x) = 1;

1 – ¼ cos 2 2x = 1; cos2x=0; x = p/4 + pn/2, nÎz

Ответ: x = p/4 + pn/2, nÎz.

9. Тригонометрические уравнения, в которых под знаком тригонометрической функции находится функция

Особого внимания заслуживают тригонометрические уравнения со сложной зависимостью, когда под знаком тригонометрической функции находится какая-либо другая функция. Эти уравнения требуют дополнительного исследования множества решений.

Пример 1. tg(x 2 + 5x)ctg 6=1.

Решение. Запишем уравнение в виде tg(x 2 +5x)=tg 6. Учитывая, что аргументы равных тангенсов отличаются на свои периоды теп, имеем х 2 + 5х = 6 + pn, nÎZ; х 2 + 5х — (6+pn) = 0, nÎz;

Д = 25 + 4(6 + pn) = 49 + 4pn, nÎZ; х1,2 = (-5 ± Ö(49 + 4pn))/2, nÎz

Решение имеет смысл, если 49 + 4pn > 0, т.е. n ³ -49/4p; n ³ -3.

“Математика” Р. Л . Вейцман, Л . Р. Вейцман, 2000 г.

“Алгебра начала анализа 10-11” А . Н . Колмогоров,

А . М . Абрамов, Ю . П . Дудницын, Б . М . Ивлев,

источники:

http://shkolkovo.net/theory/24

http://poisk-ru.ru/s51199t16.html

Источник