Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на (–1, 2)
ПОВТОРИ … РАЗ
сместиться на (…, …)
сместиться на (–1, –2)
КОНЕЦ ПОВТОРИ
сместиться на (–24, –12)
КОНЕЦ
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
2
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
НАЧАЛО
сместиться на (30, −10)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (−11, −12)
КОНЕЦ ПОВТОРИ
сместиться на (−3, 100)
КОНЕЦ
Укажите наименьшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
3
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
НАЧАЛО
сместиться на (30, 30)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (15, −9)
КОНЕЦ ПОВТОРИ
сместиться на (2, −10)
КОНЕЦ
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
4
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на (5, 2)
ПОВТОРИ … РАЗ
сместиться на (…, …)
сместиться на (−1, −2)
КОНЕЦ ПОВТОРИ
сместиться на (−25, −12)
КОНЕЦ
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
5
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на (−1, −2)
ПОВТОРИ … РАЗ
сместиться на (…, …)
сместиться на (−1, −2)
КОНЕЦ ПОВТОРИ
сместиться на (−20, −33)
КОНЕЦ
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
Пройти тестирование по этим заданиям
12 задание ЕГЭ по информатике обычно решает только половина выпускников. Оно правда такое сложное? Нет, если заранее изучить каждый из трех прототипов. Из этой статьи вы узнаете, как справиться с Редактором, Роботом и Чертежником — и как можно сделать это еще проще, используя программирование.
Прототипы задания 12 и их сложности
12 задание ЕГЭ по информатике относится к повышенному уровню сложности. На экзамене за него можно получить один первичный балл.
Это задание — часть блога «Алгоритмизация». Чтобы решить его, нужно уметь работать с алгоритмами и анализировать их. В этом задании могут встретиться три прототипа заданий: Редактор, Робот и Чертежник. Причем Редактор встречается на экзамене в последнее время чаще других прототипов.
Редактор — это прототип на работу с цепочками цифр или букв. Нам дают алгоритм и строку, содержащую некоторое количество знаков. Нужно узнать, какая строка получится после выполнения программы или посчитать количество символов в строке.
Если решать подобные задания аналитически, нужно искать закономерности изменения цепочки, чтобы получить ответ. Именно в этом и заключается сложность задания, ведь не все могут правильно найти нужную закономерность.
Робот — прототип на работу с клетчатой плоскостью и алгоритмом. Вам дают алгоритм и плоскость, содержащую 36 клеток. Нужно найти количество клеток, удовлетворяющее определенному условию. Сложность в том, что ученики начинают проверять все 36 клеток. Делать это не нужно, если проанализировать алгоритм из условия.
Чертежник — прототип на работу с алгоритмом, где исполнитель перемещается по координатной плоскости. Чаще всего в таких заданиях в алгоритме есть пропуски в командах. Нужно найти наибольшее количество повторений цикла. Сложностей обычно здесь не так много, основная — невнимательность при выполнении вычислений.
Самостоятельно подготовиться к ЕГЭ непросто. На то, чтобы разобраться со всеми темами, понадобится много времени. Но и это не решит проблему! Например, если вы запомнили какое-то решение из интернета, а оно оказалось неправильным, можно на пустом месте потерять баллы. Если хотите научиться решать все задания ЕГЭ по информатике, обратите внимание на онлайн-курсы MAXIMUM! Наши специалисты уже проанализировали сотни вариантов ЕГЭ и подготовили для вас вас максимально полезные занятия.
Приходите к нам на консультацию — вы сможете пройти диагностику по выбранным предметам ЕГЭ, поставить цели и составить стратегию подготовки, чтобы получить на экзамене высокие баллы. Все это абсолютно бесплатно!
Редактор — как решать?
Задания с прототипом «Редактор» можно решать как аналитически, так и с помощью компьютера, если у вас все хорошо с программированием. Мы рассмотрим с вами оба способа решения и убедимся, что они дают одинаковые ответы.
Пример 1 (Редактор)
Исполнитель Редактор получает на вход строку цифр и преобразовывает ее.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 88 идущих подряд цифр 4? В ответе запишите полученную строку.
Аналитическое решение
Алгоритм сначала заменяет в цепочке цифр все четверки на единицы. Потом начинает заменять назад единицы на четверки, но как только в цепочке образуются 3 четверки, алгоритм заменяет их на единицу. Порядок замены имеет значение при поиске ответа, поэтому его нужно обязательно учитывать. Также важно, что замена выполняется всегда в начале цепочки.
Сначала уберем по возможности все четверки из цепочки.
88 / 3 = 29 и 1 в остатке.
Получается, что из цепочки уйдет 29 блоков по 3 четверки и образуется 29 единиц, 1 четверка останется в цепочке в самом конце.
Теперь будем последовательно убирать единицы из цепочки.
29 “1” + 1 “4”
1 “4” + 27 “1” + 1 “4”
2 “4” + 25 “1” + 1 “4”
3 “4” + 23 “1” + 1 “4”
24 “1” + 1 “4”
Как только в цепочке появились 3 четверки, алгоритм заменил их назад на единицу. Суммарно из цепочки ушло 5 единиц. Это действие будет повторяться циклически, поэтому можно посчитать, сколько блоков по 5 единиц уйдет из цепочки.
29 / 5 = 5 и 4 в остатке
Получается, что в цепочке останется 4 единицы и 1 четверка.
11114 → 4114 → 444 → 1
В итоге в цепочке останется только единица.
Решение с помощью компьютера
В самом задании у нас уже написана программа. Остается перевести ее на конкретный язык программирования. Напишем программу на Python.
Она будет выглядеть следующим образом:
Создаем строку, содержащую 88 четверок. Далее запускаем цикл, который будет проверять, есть ли в строке 3 четверки или 2 единицы. Пропиваем условие и замену в строке. Важно в методе replace() указать третий параметр, который отмечает, сколько замен нужно выполнить. По умолчанию replace() сразу заменит все цифры в строке, а нам нужно выполнять замены по одной.
При запуске данной программы мы также получим ответ 1.
Ответ: 1
Пример 2 (Редактор)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
На вход приведенной ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 25 цифр 1, 45 цифр 2 и 10 цифр 3, расположенных в произвольном порядке.
Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы.
Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
Аналитическое решение
Цифры 1, 2 и 3 находятся в строке в произвольном порядке. Все, что нам нужно сделать, чтобы получить ответ — это понять, сколько цифр образовалось в результате замен.
Каждую единицу алгоритм заменит на тройку. Если изначально было 25 единиц, то в результате замен образуется 25 троек, и их сумма будет равна 25 * 3 = 75.
Каждую двойку алгоритм заменит на 2 единицы. Изначально было 45 двоек, значит, в результате замен образуется 90 единиц. Их сумма будет равна 90.
Каждую тройку алгоритм заменит на 2 тройки. Было 10 троек, станет 20. Сумма составит 20 * 3 = 60.
Итоговая сумма всех цифр цепочки будет равна 75 + 90 + 60 = 225.
Решение с помощью компьютера
Перенесем алгоритм на язык программирования Python.
Получаем следующую программу:
Сначала мы задали строку, содержащую знак “>” и нужное количество всех цифр. Далее в цикле проверяем наличие знака “>” и цифр и выполняем замену. Как только программа вышла из цикла, считаем количество единиц, двоек и троек в строке — и находим сумму. При запуске программы также получается ответ 225.
В данном задании написание программы может занять больше времени, чем аналитическое решение. Поэтому всегда оценивайте временные затраты на написание кода.
Ответ: 225
Робот — как решать?
Второй прототип, который включает в себя 12 задание ЕГЭ по информатике — Робот. Этот прототип точно придётся решать аналитически, поэтому давайте разбираться, как сделать это с минимальными затратами времени.
Пример 3 (Робот)
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа и 4 команды проверки условия.
Команды-приказы: вверх, вниз, влево, вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится, и программа прервется.
Другие 4 команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно, снизу свободно, слева свободно, справа свободно
Цикл
ПОКА < условие > команда
Выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится, и программа прервется.
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ уцелеет и остановится в той же клетке, с которой он начал движение?
НАЧАЛО
ПОКА < снизу свободно > вправо
ПОКА < справа свободно > вверх
ПОКА < сверху свободно > влево
ПОКА < слева свободно > вниз
КОНЕЦ
Решение
Чтобы не проверять все 36 клеток плоскости, нужно проанализировать программу. В алгоритме 4 цикла, но нам важен только последний. Робот будет выполнять действия и остановится только в той клетке плоскости, где слева есть стена, так как в последнем цикле мы проверяем именно это условие. Поэтому необходимо проверить только те клетки, где слева есть стена. В остальных клетках плоскости Робот просто не сможет остановиться, поэтому и начинать движение из них мы тоже не будем.
Проверяем по алгоритму 12 отмеченных клеток.
Из всех отмеченных клеток нам подойдет только клетка В5. Если начать движение из нее, Робот вернется в эту же точку. Остальные клетки не подойдут, так как Робот либо разобьется, либо остановится в другой клетке.
Ответ: 1
Прототип Чертежник — как решать?
Последний прототип, который составители включили в 12 задание ЕГЭ по информатике — это Чертежник. Здесь при решении важно правильно составить систему уравнений и найти наибольший/наименьший делитель двух чисел. Посмотрим, как это сделать.
Пример 4 (Чертежник)
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и величины смещения в первой из повторяемых команд неизвестны):
В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Решение
Чтобы решить это задание, необходимо обозначить неизвестными пропуски в алгоритме.
Далее составим систему уравнений. Нам известно, как перемещался Чертежник, и сказано, что он вернулся в начальную точку. Получается, его перемещение равно 0.
Теперь мы можем найти n — наибольшее количество повторений цикла. Число n должно быть делителем как 24, так и 16, то есть нам нужно найти НОД(24, 16). Он равен 8. Это и будет ответом к заданию.
Ответ: 8
Что нужно запомнить?
- Если вам попадется Редактор, можете написать программу, которая найдет ответ вместо вас. Но всегда рассчитывайте, что будет рациональнее: аналитическое решение или компьютерное. Если останется время, можно проверить себя вторым способом.
- Решая задание с Роботом, не нужно проверять все клетки — это долго. Проанализируйте алгоритм и проверяйте только те клетки, которые действительно могут подойти под условия.
- Чтобы разобраться с Чертежником, внимательно составляйте систему уравнений. Ищите НОД, если нужно найти наибольшее количество повторений цикла.
- Если в конце экзамена осталось время, вернитесь к заданию и проверьте его — ребята часто теряют баллы из-за невнимательности. Особенно рекомендую перепроверить Робота — решите его заново.
Теперь вы знаете, как решать 12 задание ЕГЭ по информатике! Обязательно прочитайте наш гайд по этому экзамену, если хотите разобраться с остальными темами и заданиями. Там вы найдете структуру экзамена, актуальные прототипы, тематические блоки и лайфхаки от наших преподавателей. Желаем удачи в подготовке 🙂
Сегодня научимся решать 12 задание из ЕГЭ по информатике 2022.
В основном 12 задание решается шаблонно с помощью Питона, но есть и задачи, в которых нужен особый подход.
Перейдём к классической задачке из ЕГЭ по информатике 2022.
Задача (Классическая)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (2222) ИЛИ нашлось (666)
ЕСЛИ нашлось (2222)
ТО заменить (2222, 6)
ИНАЧЕ заменить (666, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 239 идущих подряд цифр 6? В ответе запишите полученную строку.
Решение:
Решим задачу с помощью программы на Python’е.
s = '6'*239 while ('2222' in s) or ('666' in s): if '2222' in s: s = s.replace('2222', '6', 1) else: s = s.replace('666', '2', 1) print(s)
Здесь в начале формируется строка, состоящая из 239 шестёрок. Потом эта строка подаётся в программу. Программу переводим с русского языка на язык Питон.
Третий параметр в функции replace обозначает, что замену нужно производить один раз. Это в точности соответствует предложенной функции заменить.
Ответ получается 2266.
Ответ: 2266
В следующей типовой задаче из ЕГЭ по информатике 2022 нужно сообразить один момент.
Задача (Нужно сообразить)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (21) ИЛИ нашлось (31) ИЛИ нашлось (23)
ЕСЛИ нашлось (21)
ТО заменить (21, 12)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (31)
ТО заменить (31, 13)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (23)
ТО заменить (23, 32)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, содержащая 50 цифр 1, 50 цифр 2 и 50 цифр 3, расположенных в произвольном порядке. Запишите без разделителей символы, которые имеют порядковые номера 10, 90 и 130 в получившейся строке.
Решение:
Здесь сказали, что начальный порядок цифр в строке неизвестен. А просят написать конкретные данные на выходе. Отсюда делаем вывод, что любой порядок в начале приводит к одному и тому же результату.
В строке заведём цифры по порядку: в начале единицы, потом двойки, потом тройки.
s = '1'*50 + '2'*50 + '3'*50 while ('21' in s) or ('31' in s) or ('23' in s): if '21' in s: s = s.replace('21', '12', 1) if '31' in s: s = s.replace('31', '13', 1) if '23' in s: s = s.replace('23', '32', 1) print(s[9] + s[89] + s[129])
Чтобы обратится к конкретному символу в строке, используем конструкцию s[позиция символа]. Но нумерация начинается с нуля.
В ответе запишем 132.
Ответ: 132
В следующей примерной задаче из ЕГЭ по информатике 2022 опять используем Питон.
Задача (Снова программируем)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
НАЧАЛО ПОКА нашлось (111) заменить (111, 22) заменить (222, 11) КОНЕЦ ПОКА КОНЕЦ
Известно, что исходная строка содержала более 70 единиц и не содержала других цифр. Укажите минимально возможную длину исходной строки, при которой в результате работы этой программы получится строка, содержащая максимально возможное количество единиц.
Решение:
Здесь мы попробуем с помощью программы формировать строчки с разной длиной и смотреть, какое количество единиц получится на выходе.
for i in range(71, 1000): s = '1'*i while '111' in s: s = s.replace('111', '22', 1) s = s.replace('222', '11', 1) print(i, s.count('1'))
Посмотрев результаты, понимаем, что максимальное количество единиц в окончательной строке равно 4. А минимальное количество единиц в изначальной строке, чтобы получилось в итоге 4 единицы, равно 73.
Ответ: 73
Ещё один частый гость в тренировочных вариантах из ЕГЭ по информатике 2022.
Задача (Сумма цифр + непонятный символ)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>1)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>3)
ТО заменить (>3, 1>2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 28 цифр 1, 18 цифр 2 и 35 цифр 3, расположенных в произвольном порядке. Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
Решение:
Здесь снова результат будет одним и тем же независимо от того, как будут расположены числа в начале.
s = '>' + '1'*28 + '2'*18 + '3'*35 while ('>1' in s) or ('>2' in s) or ('>3' in s): if '>1' in s: s = s.replace('>1', '22>', 1) if '>2' in s: s = s.replace('>2', '2>1', 1) if '>3' in s: s = s.replace('>3', '1>2', 1) # Находим сумму цифр в строке sm=0 for i in range(0, len(s)): if s[i]!='>': sm = sm + int(s[i]) print(sm)
Чтобы найти сумму цифр, мы пробегаем по всей строке с помощью цикла range. Если символ не равен «>», то превращаем его в число с помощью функции int() и суммируем в переменную sm.
Получается 465.
Ответ: 465
Задача (Трудно запрограммировать)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (11)
ЕСЛИ нашлось(112)
ТО заменить (112, 5)
ИНАЧЕ заменить (11, 3)
КОНЕЦ ПОКА
КОНЕЦ
Исходная строка содержит 23 единицы и 5 двоек, других цифр нет, точный порядок расположения цифр неизвестен. Какую наибольшую сумму цифр может иметь строка, которая получится после выполнения программы?
Решение:
Здесь не важно, по какой ветке будет идти программа, прирост в сумме цифр будет всегда равен 1. Поэтому можно расположить в начале только 1, а затем все двойки в исходной строке.
Одиннадцать раз символы ’11’ превратятся в ‘3’. Тогда 11 * 3 = 33. Останутся цифры ‘122222’. Их сумма равна 11.
В ответе получается 33 + 11 = 44.
Ответ: 44
Задача (Крепкий орешек)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (01) или нашлось (02)
заменить (01, 2202)
заменить (02, 10)
КОНЕЦ ПОКА
КОНЕЦ
Известно, что начальная строка начиналась с нуля, а далее содержала только единицы и двойки. После выполнения данной программы получилась строка, содержащая 40 единиц и 64 двойки. Сколько двоек было в исходной строке ?
Решение:
Посмотрим, во что превращается 1:
01 -> 2202 -> 2210
Посмотрим, во что превращается 2:
02 -> 10
Т.е. в окончательном результате двойки могли возникнуть только из 1. Двоек получается в два раза больше, чем было изначально единиц.
Получается, что изначальное количество единиц равно 64 / 2 = 32. Эти 32 единицы так же принесли 32 единицы. Всего 40 единиц стало. Значит, ещё 8 единиц получилось в результате преобразования 02 -> 10. Т.е. двоек будет 8.
Теперь попробуем решить задачу с помощью программы. Здесь неизвестно количество единиц и двоек. Поэтому придётся создавать вложенные циклы. Предположим, что количество единиц и двоек меньше 100, чтобы программа отработала за адекватное время.
for i in range(1, 100): for j in range(1, 100): s = '0' + '1'*i + '2'*j while ('01' in s) or ('02' in s): s = s.replace('01', '2202', 1) s = s.replace('02', '10', 1) if s.count('1')==40 and s.count('2')==64: print(j)
Получается количество двоек равно восьми.
Ответ: 8
Решим задачу про Робота, которая в последнее время редко встречается на экзамене по информатике.
Задача (Робот)
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх , вниз , влево , вправо .
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно | снизу свободно | слева свободно | справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
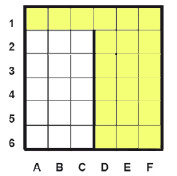
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободнo
ТО вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
|
|
Решение:
Проанализируем внимательно программу для Робота.
В программе есть главный цикл, внутри цикла проверяется сначала возможность двигаться вправо. Если есть такая возможность, робот будет двигаться до упора с помощью ещё одного цикла. Потом после того как больше нет возможности двигаться вправо, с помощью основного цикла и записанного условия будет перемещаться вниз, пока есть такая возможность.
Если нет возможности двигаться ни вправо, ни вниз, то Робот завершает программу.
Поняв этот алгоритм не сложно отметить те клетки, стартовав с которых, Робот остановится на клетке F6.
Ещё раз, Робот до упору будет двигаться вправо, потом до упору вниз, насколько это возможно. Вот алгоритм в двух словах.
Важно в этих задачах простыми словами сформулировать алгоритм, чтобы можно было проверять целые блоки лабиринта.
Количество клеток, удовлетворяющие условию будет 21.
Ответ: 21
12 Задание из ЕГЭ по информатике 2021 выглядит обычно объёмным, но на деле описываются обычные конструкции (Циклы и условия), которые есть в большинстве языках программирования.
Задача (Чертёжник)
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнить команду сместиться на(a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на(2, -3) переместит Чертёжника в точку (6, -1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (число повторений и величины смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на(8, -60)
ПОВТОРИ ... РАЗ
сместиться на(..., ...)
сместиться на(4, -6)
КОНЕЦ ПОВТОРИ
сместиться на(-35, -3)
КОНЕЦ
В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшие число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ» ?
Решение:
Эта задача похоже на задачу Кузнечик, которую рассматривали в 5 задании.
Напишем для переменной x уравнение.
8 + n * x + n * 4 — 35 = 0
Всё выражение приравниваем к нулю, т.к. Чертёжник возвращается в исходную точку, т.е. как ни ходил Чертёжник, он никуда в итоге не сдвинулся.
n — положительное целое число, количество повторений.
x — целое число, смещение по координате x.
n * x + n * 4 = 27
n * ( x + 4 ) = 27
Нужно подобрать x и n, чтобы равенство было верным.
Число n может быть 27, 9, 3, 1. Нам нужно выбрать число n, как можно больше.
Проверим число 27! Тогда выражение x + 4 = 1 => x = -3. Теперь нужно проверить это число для координаты y.
-60 + n * y — n * 6 — 3 = 0
27 * y — 27 * 6 = 63
27 * ( y — 6 ) = 63
Видим, что нельзя подобрать такое целое число для 27, чтобы при умножении получалось 63.
Проверим число 9! Тогда выражение x + 4 = 3 => x = -1. Теперь нужно проверить это число для координаты y.
-60 + n * y — n * 6 — 3 = 0
9 * y — 9 * 6 = 63
9 * ( y — 6 ) = 63
Видим, что можно подобрать такое целое число для 9, чтобы при умножении получалось 63. Это число 7. Значит, y — 6 = 7 => y = 13
Мы подобрали все нужные числа и нашли наибольшее число n=9.
Ответ: 9
Некоторые формулировки задач были взяты с сайтов:
https://kpolyakov.spb.ru/
https://inf-ege.sdamgia.ru/
Счастливых экзаменов по информатике!
почему 5-ую задачу сложно запрограммировать? тут ведь тоже произвольный порядок
я пробовал в программе ставить сначала единицы, а потом двойки и наоборот — сначала двойки а потом единицы
печатаю s и суммирую цифры
получается везде 44
Если бы сама программа была немного другая, то могло и не получится. Т.е. тут нужно самостоятельно провести анализ, при каком расположении цифр сумма будет максимальной.
Обожаю ваш сайт! Спасибо за пояснение усложненных задач.
Задание 14. Алгоритмы с циклами и условиями: Разбор досрочного егэ по информатике 2018, Демонстрационный вариант ЕГЭ по информатике 2018; государственный выпускной экзамен 2018; тренировочные варианты ЕГЭ по информатике, тематические тестовые задания и задачи из тренажера по информатике 2018
14 задание. Демоверсия ЕГЭ 2018 информатика:
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x,y) в точку с координатами (x + a, y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (число повторений и величины смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на (4, 6)
ПОВТОРИ … РАЗ
сместиться на (…, …)
сместиться на (4, -6)
КОНЕЦ ПОВТОРИ
сместиться на (-28, -22)
КОНЕЦ
В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку.
Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
📹 Видеоразбор
Решение 14 задания ЕГЭ по информатике (контрольный вариант № 2 экзаменационной работы 2018 года, С.С. Крылов, Д.М. Ушаков):
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает 4 команды-приказа и 4 команды проверки условия.
Команды-приказы:
вверх вниз влево вправо
Другие четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
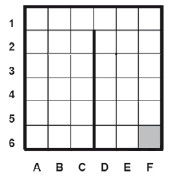
Сколько клеток приведенного лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО ПОКА < снизу свободно ИЛИ справа свободно > ЕСЛИ < справа свободно > ТО вправо КОНЕЦ ЕСЛИ ПОКА < снизу свободно > вниз КОНЕЦ ПОКА КОНЕЦ ПОКА КОНЕЦ

✍ Показать решение:
- Рассмотрим тело внешнего цикла и операторы, которые в нем находятся:
- 1. В цикле выполняется проверка ЕСЛИ справа свободно ТО вправо: что означает движение на один шаг вправо (если это возможно).
- 2. Затем располагается цикл с условием пока снизу свободно вниз: что означает движение до конца вниз (пока это возможно).
- После чего внешний цикл повторяется.
- Таким образом, отметим «тупиковые» клетки, т.е. те, которые не позволят двигаться роботу к цели:
A5, A6, B1, B2, B6, C1, C2, D1, D2, D3, D4, D5, E3, E4, E5
36 - 15 = 21
Результат: 21
Решение 14 задания ЕГЭ по информатике, вариант 1 (ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С.С. Крылов, Т.Е. Чуркина):
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w)
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Б) нашлось (v)
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка при этом не изменяется.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 250 идущих подряд цифр 1? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (88) ИЛИ нашлось (1111)
ЕСЛИ нашлось (1111)
ТО заменить (1111, 8)
ИНАЧЕ заменить (88, 1)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
📹 Видеоразбор
✍ Показать решение:
- Схематично изобразим исходную строку:
- Каждый проход цикла появляется одна цифра 8 и отнимается 4 единицы. Вернемся к пункту 1 и посчитаем, сколько единиц и восьмерок останется после выполнения всех условий
ЕСЛИ нашлось (1111)(т.е. пока есть стоящие подряд 1111): - Затем будет выполняться условие
ИНАЧЕ заменить (88, 1). После 4 проходов цикла получаем: - Опять работает условие
ЕСЛИ нашлось (1111): - Вернемся к пункту 3, за 4 прохода получим:
- Исходя из пункта 3 и 5 получаем, что за 5 проходов количество восьмерок уменьшается на 7 раз.
- Вернемся к пункту 3 и вычислим сколько восьмерок останется:
- Возвращаясь к третьему пункту, подсчитаем количество цифр 8:
- За три дальнейших прохода получаем:
- Последний проход:
1...1 250
Рассмотрим, что произойдет после выполнения исполнителем 1-й и 2-й итерации (шага) цикла:
81..1 -> 1 проход 246 (250-4) 881..1 -> 2 проход 242
250 / 4 = 62 и 2 в остатке
т.е. получаем:
8...811 (две единицы в конце - это остаток)
62
11118...811
54 (62-8)
88...811 -> 8...811 54 55
11118...811
47
8...811 (11 - остаток) 62 11118...8 :четыре прохода 62-8 8 8...8 :пятый проход ИТОГО: за пять проходов уменьшение на 7 восьмерок
62 / 7 = 8 и 6 остаток
Т.е. получим:
88888811 (6 восьмерок - остаток)
88888811 -> 11111
11111 -> 81
Результат: 81
Решение 14 задания ЕГЭ по информатике, вариант 5 (ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С.С. Крылов, Т.Е. Чуркина):
Исполнитель Чертежник перемещается на координатной плоскости, оставляя след в виде линии. Чертежник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертежника из точки с координатами (x, y) в точку с координатами (x+a, y+b).
Цикл ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертежнику был дан для исполнения следующий алгоритм (число повторений и величины смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на (35, -20)
ПОВТОРИ ... РАЗ
сместиться на (..., ...)
сместиться на (2, -3)
КОНЕЦ ПОВТОРИ
сместиться на (-105, -8)
КОНЕЦ
В результате выполнения этого алгоритма Чертежник возвращается в исходную точку.
Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Досрочный егэ по информатике 2018, вариант 1. Задание 14:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
1. заменить (v, w)
2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь».
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из одной единицы и 75 стоящих справа от нее нулей? В ответе запишите сколько нулей будет в конечной строке.
НАЧАЛО ПОКА нашлось (10) ИЛИ нашлось (1) ЕСЛИ нашлось (10) ТО заменить (10, 001) ИНАЧЕ заменить (1, 00) КОНЕЦ ЕСЛИ КОНЕЦ ПОКА КОНЕЦ
📹 Видеоразбор
✍ Показать решение:
Результат: 152
ЕГЭ по информатике -> ЕГЭ 2018 -> ЕГЭ 2018 — 14
12. Сложные исполнители и алгоритмы
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Исполнитель «Чертёжник»
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ((c, d)), где (c) и (d) — целые числа, которык перемещают Чертёжника из точки с координатами ((x, y)) в точку с координатами ((x+c, y+d)).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
Означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм:
НАЧАЛО
сместиться на (-32, -73)
ПОВТОРИ (k) РАЗ
сместиться на ((c, d))
сместиться на ((246,; -114))
КОНЕЦ ПОВТОРИ
сместиться на ((-16,; 13))
КОНЕЦ
Укажите количество чисел (k>1), для которых найдутся такие значения чисел (c) и (d), что после выполнения программы Чертёжник возвратится в исходную точку.
Будем обозначать изменение первой координаты из скобки за (Delta x,) второй – за (Delta y.)
Запишем изменения координат:
(Delta x = -32 + k(c+246)-16;)
(Delta y = -73 + k(d-114)+13.)
Возвращение исполнителя в исходную точку для математической записи изменения координат значит, что должно выполняться равенство нулю.
Таким образом, мы имеем систему из двух уравнений:
[begin{cases}
-32 + k(c+246)-16 = 0 \
-73 + k(d-114)+13 = 0
end{cases}]
Преобразуем выражение:
[begin{cases}
k(c+246) = 48 \
k(d-114) = 60
end{cases}]
Можно заметить, что нам требуется определить количество чисел k, которые являются делителем и 48, и 60. Таких чисел пять – 2, 3, 4, 6 и 12.
Ответ: 5
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ((c, d)), где (c) и (d) — целые числа, которык перемещают Чертёжника из точки с координатами ((x, y)) в точку с координатами ((x+c, y+d)).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
Означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм:
НАЧАЛО
сместиться на (-29, -100)
ПОВТОРИ (k) РАЗ
сместиться на ((c, 87))
сместиться на ((32,; d))
КОНЕЦ ПОВТОРИ
сместиться на ((-25,; 19))
КОНЕЦ
Укажите максимальное значение числа (k>1), для которого найдутся такие значения чисел (c) и (d), что после выполнения программы Чертёжник возвратится в исходную точку.
Будем обозначать изменение первой координаты из скобки за (Delta x,) второй – за (Delta y.)
Запишем изменения координат:
(Delta x = -29 + k(c+32)-25;)
(Delta y = -100 + k(87+d)+19.)
Возвращение исполнителя в исходную точку для математической записи изменения координат значит, что должно выполняться равенство нулю.
Таким образом, мы имеем систему из двух уравнений:
[begin{cases}
-29 + k(c+32)-25 = 0 \
-100 + k(87+d)+19 = 0
end{cases}]
Преобразуем выражение:
[begin{cases}
k(c+32) = 54 \
k(87+d) = 81
end{cases}]
Можно заметить, что нам требуется такое максимальное число k, чтобы оно было делителем и 81, и 54, т.е. НОД этих чисел. НОД(81,54)=27.
Ответ: 27
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ((c, d)), где (c) и (d) — целые числа, которык перемещают Чертёжника из точки с координатами ((x, y)) в точку с координатами ((x+c, y+d)).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
Означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм:
НАЧАЛО
сместиться на (-15, -144)
ПОВТОРИ (k) РАЗ
сместиться на ((c, 300))
сместиться на ((200,; d))
КОНЕЦ ПОВТОРИ
сместиться на ((-25,; 72))
КОНЕЦ
Укажите количество чисел (k>1), для которых найдутся такие значения чисел (c) и (d), что после выполнения программы Чертёжник возвратится в исходную точку.
Будем обозначать изменение первой координаты из скобки за (Delta x,) второй – за (Delta y.)
Запишем изменения координат:
(Delta x = -15 + k(c+200)-25;)
(Delta y = -144 + k(300+d)+72.)
Возвращение исполнителя в исходную точку для математической записи изменения координат значит, что должно выполняться равенство нулю.
Таким образом, мы имеем систему из двух уравнений:
[begin{cases}
-15 + k(c+200)-25 = 0 \
-144 + k(300+d)+72 = 0
end{cases}]
Преобразуем выражение:
[begin{cases}
k(c+200) = 40 \
k(300+d) = 72
end{cases}]
Можно заметить, что нам требуется определить количество чисел k, которые являются делителем и 40, и 72. Таких чисел три – 2, 4 и 8.
Ответ: 3
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ((c, d)), где (c) и (d) — целые числа, которык перемещают Чертёжника из точки с координатами ((x, y)) в точку с координатами ((x+c, y+d)).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
Означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм:
НАЧАЛО
сместиться на (-15, -144)
ПОВТОРИ (k) РАЗ
сместиться на ((c, 300))
сместиться на ((200,; d))
КОНЕЦ ПОВТОРИ
сместиться на ((-25,; 72))
КОНЕЦ
Укажите максимальное значение числа (k>1), для которого найдутся такие значения чисел (c) и (d), что после выполнения программы Чертёжник возвратится в исходную точку.
Будем обозначать изменение первой координаты из скобки за (Delta x,) второй – за (Delta y.)
Запишем изменения координат:
(Delta x = -15 + k(c+200)-25;)
(Delta y = -144 + k(300+d)+72.)
Возвращение исполнителя в исходную точку для математической записи изменения координат значит, что должно выполняться равенство нулю.
Таким образом, мы имеем систему из двух уравнений:
[begin{cases}
-15 + k(c+200)-25 = 0 \
-144 + k(300+d)+72 = 0
end{cases}]
Преобразуем выражение:
[begin{cases}
k(c+200) = 40 \
k(300+d) = 72
end{cases}]
Можно заметить, что нам требуется такое максимальное число k, чтобы оно было делителем и 40, и 72, т.е. НОД этих чисел. НОД(40,72)=8.
Ответ: 8
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ((c, d)), где (c) и (d) — целые числа, которык перемещают Чертёжника из точки с координатами ((x, y)) в точку с координатами ((x+c, y+d)).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
Означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм:
НАЧАЛО
сместиться на (-29, -100)
ПОВТОРИ (k) РАЗ
сместиться на ((c, 87))
сместиться на ((32,; d))
КОНЕЦ ПОВТОРИ
сместиться на ((-25,; 19))
КОНЕЦ
Укажите количество чисел (k>1), для которых найдутся такие значения чисел (c) и (d), что после выполнения программы Чертёжник возвратится в исходную точку.
Будем обозначать изменение первой координаты из скобки за (Delta x,) второй – за (Delta y.)
Запишем изменения координат:
(Delta x = -29 + k(c+32)-25;)
(Delta y = -100 + k(87+d)+19.)
Возвращение исполнителя в исходную точку для математической записи изменения координат значит, что должно выполняться равенство нулю.
Таким образом, мы имеем систему из двух уравнений:
[begin{cases}
-29 + k(c+32)-25 = 0 \
-100 + k(87+d)+19 = 0
end{cases}]
Преобразуем выражение:
[begin{cases}
k(c+32) = 54 \
k(87+d) = 81
end{cases}]
Можно заметить, что нам требуется определить количество чисел k, которые являются делителем и 54, и 81.Таких чисел три – 3, 9, 27.
Ответ: 3
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ((c, d)), где (c) и (d) — целые числа, которык перемещают Чертёжника из точки с координатами ((x, y)) в точку с координатами ((x+c, y+d)).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
Означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм:
НАЧАЛО
сместиться на (-32, -73)
ПОВТОРИ (k) РАЗ
сместиться на ((c, d))
сместиться на ((246,; -114))
КОНЕЦ ПОВТОРИ
сместиться на ((-16,; 13))
КОНЕЦ
Укажите максимальное значение числа (k>1), для которого найдутся такие значения чисел (c) и (d), что после выполнения программы Чертёжник возвратится в исходную точку.
Будем обозначать изменение первой координаты из скобки за (Delta x,) второй – за (Delta y.)
Запишем изменения координат:
(Delta x = -32 + k(c+246)-16;)
(Delta y = -73 + k(d-114)+13.)
Возвращение исполнителя в исходную точку для математической записи изменения координат значит, что должно выполняться равенство нулю.
Таким образом, мы имеем систему из двух уравнений:
[begin{cases}
-32 + k(c+246)-16 = 0 \
-73 + k(d-114)+13 = 0
end{cases}]
Преобразуем выражение:
[begin{cases}
k(c+246) = 48 \
k(d-114) = 60
end{cases}]
Можно заметить, что нам требуется такое максимальное число k, чтобы оно было делителем и 48, и 60, т.е. НОД этих чисел. НОД(48,60)=12.
Ответ: 12
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ((c, d)), где (c) и (d) — целые числа, которык перемещают Чертёжника из точки с координатами ((x, y)) в точку с координатами ((x+c, y+d)).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
Означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм:
НАЧАЛО
сместиться на (-30, -110)
ПОВТОРИ (k) РАЗ
сместиться на ((c, d))
сместиться на ((76,; -93))
КОНЕЦ ПОВТОРИ
сместиться на ((0,; 5))
КОНЕЦ
Укажите количество чисел (k>1), для которых найдутся такие значения чисел (c) и (d), что после выполнения программы Чертёжник возвратится в исходную точку.
Будем обозначать изменение первой координаты из скобки за (Delta x,) второй – за (Delta y.)
Запишем изменения координат:
(Delta x = -30 + k(c+76)+0;)
(Delta y = -110 + k(d-93)+5.)
Возвращение исполнителя в исходную точку для математической записи изменения координат значит, что должно выполняться равенство нулю.
Таким образом, мы имеем систему из двух уравнений:
[begin{cases}
-30 + k(c+76)+0 = 0 \
-110 + k(d-93)+5 = 0
end{cases}]
Преобразуем выражение:
[begin{cases}
k(c+76) = 30 \
k(d-93) = 105
end{cases}]
Можно заметить, что нам требуется определить количество чисел k, которые являются делителем и 30, и 105. Таких чисел три – 3, 5 и 15.
Ответ: 3

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Автор материалов — Лада Борисовна Есакова.
В этой задаче используется, в основном, описание алгоритмов на псевдокоде (условном алгоритмическом языке, включающем в себя и элементы языка программирования, и элементы обычного естественного языка).
Основные конструкции псевдокода описаны перед текстом задачи.
Исполнитель чертежник
Пример 1.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, -3) переместит Чертёжника в точку (6, -1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n>1):
НАЧАЛО
сместиться на (60, 100)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (33, 44)
КОНЕЦ ПОВТОРИ
сместиться на (13, 200)
сместиться на (-1, 60)
КОНЕЦ
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
Решение:
В результате выполнения алгоритма Чертежник переместится
по оси х на:
60 + n*a + n*33 + 13 – 1
по оси y на:
100 + n*b + n*44 + 200 + 60
Известно, что в результате перемещения Чертежник вернулся в исходную точку, т.е. перемещение по оси х равно нулю, и перемещение по оси y равно нулю:
60 + n*a + n*33 + 13 – 1 = 0
100 + n*b + n*44 + 200 + 60 = 0
Т.е.
n*(a + 33) = -72
n*(b + 44) = -360
Наибольшее n – это наибольший общий делитель чисел -72 и -360. Это число 72.
Ответ: 72
Исполнитель робот
Пример 2.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно (по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно ПОКА справа свободно
вправо
КОНЕЦ ПОКА
вниз
КОНЕЦ ПОКА
КОНЕЦ
1) 22
2) 19
3) 15
4) 12
Решение:
В данной программе РОБОТ сначала проверяет, свободна ли клетка справа или снизу от него. Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом цикле пока у правой стороны клетки, в которой находится РОБОТ, нет стены, он продолжает двигаться вправо. Как только это условие перестанет выполняться, он переходит ко второму действию внутри цикла. Второе действие, заключается в следующем: РОБОТ передвигается на одну клетку вниз. После чего возвращается к началу внешнего цикла.
Проверив последовательно все клетки по правилу движения РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи равно 15 (вся первая строчка, весь столбец F, клетки D2, E2, D4, D6, E4).
Правильный ответ указан под номером 3.
Ответ: 3
Исполнитель редактор
Пример 3.
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 68 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось (888)
ЕСЛИ нашлось (222)
ТО заменить (222, 
ИНАЧЕ заменить (888, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Решение:
Обозначим строку из 68 восьмерок — 68«8»,
строку из двойки и 65 восьмерок – 1«2»65«8» и т.д.
Отработаем 4 первых цикла программы:
68«8» → 1«2»65«8» → 2«2»62«8» → 3«2»59«8» → 60«8»
В результате количество восьмерок уменьшилось на 8. Не сложно понять, что строка будет уменьшаться на 8 восьмерок каждые 4 итерации. В результате останется строка из 4 восьмерок. Доработаем программу:
…→ 4«8» → 1«2»1«8» = 28
Ответ: 28
Исполнитель черепашка
Пример 4.
Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:
Вперед n, где n – целое число, вызывающее передвижение черепашки на n шагов в направлении движения.
Направо m, где m – целое число, вызывающее изменение направления движения на m градусов по часовой стрелке.
Запись Повтори 5 [Команда1 Команда2] означает, что последовательность команд в скобках повторится 5 раз.
Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [Повтори 4 [Вперед 40 Направо 90] Направо 120]
Какая фигура появится на экране?
Решение:
Последовательность действий Вперед 40 Направо 90 рисует отрезок длиной 40 шагов, а затем меняет направление на 90 градусов по часовой стрелке. Тогда последовательность Повтори 4 [Вперед 40 Направо 90] нарисует квадрат, а направление вернется в исходное.
Затем выполняется команда Направо 120, она изменит направление на 120 градусов от исходного.
Если повторить все рассмотренные действия 5 раз:
Повтори 5 [Повтори 4 [Вперед 40 Направо 90] Направо 120], то будет 5 раз нарисован квадрат. Причем каждый следующий повернут вокруг вершины относительно предыдущего на 120 градусов. Не сложно заметить, что 4-й квадрат будет нарисован поверх первого (120*3 = 360, сделан поворот на целый круг, возврат в исходное положение), а 5-й поверх второго.
Результат изображен под номером 3.
Ответ: 3
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №14. Выполнение алгоритма.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Выполнения алгоритмов для исполнителя робот
Исполнитель чертёжник
№1. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 2 раз
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
Конец
Сместиться на (−6, −4)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −1)
2) Сместиться на (1, 1)
3) Сместиться на (−4, −2)
4) Сместиться на (2, 1)
№2. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 4 paз
Команда1 Сместиться на (3, 3) Сместиться на (1,−2)
Конец
Сместиться на (−8, 12)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −4)
2) Сместиться на (4,−13)
3) Сместиться на (2, 4)
4) Сместиться на (−8, −16)
№3. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Команда1 Сместиться на (1, 3) Сместиться на (1, −2)
Конец
Сместиться на (3, 9)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (3, 4)
2) Сместиться на (−5, −10)
3) Сместиться на (−9, −12)
4) Сместиться на (−3, −4)
№4. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
Конец
Сместиться на (−9, −6)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−6, −3)
2) Сместиться на (4, 3)
3) Сместиться на (−2, −1)
4) Сместиться на (2, 1)
№5. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 2 paз
Команда1 Сместиться на (3, 3) Сместиться на (1, −2)
Конец
Сместиться на (4, −6)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (6, −2)
2) Сместиться на (−8, 5)
3) Сместиться на (−12, 4)
4) Сместиться на (−6, 2)
№6. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 4 paз
Команда1 Сместиться на (1, 3) Сместиться на (1, −2)
Конец
Сместиться на (−4, −12)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (1,−2)
2) Сместиться на (12, 4)
3) Сместиться на (2, 11)
4) Сместиться на (−1, 2)
№7. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 4 paз
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
Конец
Сместиться на (−12, −8)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−8, −4)
2) Сместиться на (−2, −1)
3) Сместиться на (7, 5)
4) Сместиться на (2, 1)
№8. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Команда1 Сместиться на (3, 3) Сместиться на (1, −2)
Конец
Сместиться на (−6, 9)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−6, −12)
2) Сместиться на (2, −10)
3) Сместиться на (2, 4)
4) Сместиться на (−2, −4)
№9. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 2 paз
Команда1 Сместиться на (1, 3) Сместиться на (1, −2)
Конец
Сместиться на (2, 6)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (− 6, − 
2) Сместиться на (3, 4)
3) Сместиться на (− 4, − 7)
4) Сместиться на (− 3, − 4)
№10. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Сместиться на (−2, −1) Сместиться на (3, 2) Сместиться
на (2,1) Конец
На какую одну команду можно заменить этот алгоритм,
чтобы Чертёжник оказался в той же точке, что и после выполнения алгоритма?
1) Сместиться на (−9, −6)
2) Сместиться на (6, 9)
3) Сместиться на (−6, −9)
4) Сместиться на (9, 6)
Остановка в заданой клетке. циклы с оператором пока
№1. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА<справа свободно ИЛИ снизу свободно >
ПОКА < снизу свободно >
вниз
КОНЕЦ ПОКА
ПОКА < справа свободно >
вправо
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
1) 14
2) 17
3) 19
4) 21
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому внутреннему циклу. В этом
цикле пока у нижней стороны клетки в которой находится РОБОТ нет стены
он продолжает двигаться вниз. Как только это условие перестанет выполняться
он переходит ко второму внутреннему циклу. Этот внутренний цикл аналогичен
первому, только теперь проверяется отсутствие стены у правой стороны
клетки.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 19.
Правильный ответ указан под номером 3.
№2. Исполнитель РОБОТ умеет перемещаться
по прямоугольному лабиринту, начерченному на плоскости, разбитой
на клетки. Между соседними по сторонам клетками может стоять стена.
Клетка в лабиринте может быть чистая или закрашенная.
Закрашенные клетки на рисунке выделены серым цветом.
Система команд исполнителя РОБОТ содержит восемь
команд. Четыре команды – это команды перемещения:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие>
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ <условие>
ТО команда
КОНЕЦ ЕСЛИ
выполняется команда только, если условие истинно.
В противном случае ничего не происходит.
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА<справа свободно ИЛИ снизу свободно>
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 22
3) 26
4) 30
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле, пока снизу клетки в которой находится РОБОТ нет стены, он продолжает
двигаться вниз. Как только это условие перестанет выполняться, он переходит
ко второму действию внутри цикла. Второе действие, заключается в следующем:
РОБОТ передвигается на одну клетку вправо, до тех пор, пока справа свободно.
После чего возвращается к началу внешнего цикла.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся. Проверив все клетки
по выведенному нами правилу движения РОБОТА выясняем, что число
клеток, удовлетворяющих условию задачи равно 26.
Правильный ответ указан под номером 3.
№3. Исполнитель РОБОТ умеет перемещаться
по прямоугольному лабиринту, начерченному на плоскости, разбитой
на клетки. Между соседними по сторонам клетками может стоять стена.
Клетка в лабиринте может быть чистая или закрашенная.
Закрашенные клетки на рисунке выделены серым цветом.
|
1 |
|||||||
|
2 |
|||||||
|
3 |
|||||||
|
4 |
|||||||
|
5 |
|||||||
|
6 |
|||||||
|
A |
B |
C |
D |
E |
F |
Система команд исполнителя РОБОТ содержит восемь
команд. Четыре команды – это команды перемещения:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие>
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ <условие>
ТО команда
КОНЕЦ ЕСЛИ
выполняется команда только, если условие истинно.
В противном случае ничего не происходит.
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА<справа свободно ИЛИ снизу свободно>
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 21
3) 24
4) 27
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами а не по одной.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока справа клетки в которой находится РОБОТ нет стены он продолжает
двигаться вправо. Как только это условие перестанет выполняться он
переходит ко второму циклу. Он, заключается в следующем: РОБОТ передвигается
на одну клетку вниз, до тех пор, пока снизу свободно.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 21.
№4. Исполнитель РОБОТ умеет перемещаться
по прямоугольному лабиринту, начерченному на плоскости, разбитой
на клетки. Между соседними по сторонам клетками может стоять стена.
Система команд исполнителя РОБОТ содержит восемь
команд. Четыре команды — это команды перемещения:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если
на пути РОБОТа окажется стена, он разрушится.
Четыре команды проверяют отсутствие стены у каждой
стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА <условие>
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкциях ПОКА условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ.
Начало формы
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА <снизу свободно ИЛИ справа
свободно>
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
вправо
КОНЕЦ ПОКА
КОНЕЦ
1) 8
2) 12
3) 17
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока снизу клетки в которой находится РОБОТ нет стены он продолжает
двигаться вниз. Как только это условие перестанет выполняться он переходит
ко второму действию цикла. Второе действие, заключается в следующем:
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла. У робота есть возможность разбиться: например,
стартовав из любой клетки столбца F робот разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 12.
Правильный ответ указан под номером 2.
№5. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКАснизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
вниз
КОНЕЦ ПОКА
КОНЕЦ
1) 22
2) 19
3) 15
4) 12
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у правой стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вправо. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ передвигается на одну
клетку вниз. После чего возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток А6,B6,C6. Проверив
все клетки по выведенному нами правилу движения РОБОТА выясняем,
что число клеток, удовлетворяющих условию задачи равно 15 (вся первая
строчка, весь столбец F, клетки D2, E2, D4, D6, E4).
Правильный ответ указан под номером 3.
№6. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКАснизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
вправо
КОНЕЦ ПОКА
КОНЕЦ
1) 7
2) 12
3) 17
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ передвигается на одну
клетку вправо. После чего возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток С1,Е1,А3.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 7 (В5,С5,В6,С6,D6,E6,F6).
№7. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия.
Команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится, и программа прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно)
или команда2 (если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка А1)?
НАЧАЛО
ПОКА слева свободно ИЛИ сверху
свободно
ЕСЛИ слева свободно
ТО влево
ИНАЧЕ вверх
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 13
2) 15
3) 21
4) 27
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной. В данной программе РОБОТ поступает следующим
образом: сперва РОБОТ проверяет, свободна ли клетка слева или сверху
от него. Если это так, то РОБОТ переходит к первому действию внутри
цикла. В этом цикле если у левой стороны клетки, в которой находится
РОБОТ, нет стены, он двигается влево, в противном случае он перемещается
вверх. После этого возвращается к началу внешнего цикла. Проанализировав
эту программу, приходим к выводу, что РОБОТ не может разбиться.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 21: A1-A6, A6-F6, A1-D1, E3, F3, D2-F2, B2, C2.
Правильный ответ указан под номером 3.
№8. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия. Команды-приказы: вверх,вниз, влево, вправо.
При выполнении любой из этих команд РОБОТ перемещается на одну клетку
соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если РОБОТ начнёт движение
в сторону находящейся рядом с ним стены, то он разрушится, и программа
прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ: сверху
свободно, снизу свободно, слева свободно, справа
свободно.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно. В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно)
или команда2 (если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
вправо
КОНЕЦ ПОКА
КОНЕЦ
1) 10
2) 13
3) 16
4) 20
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка снизу или справа от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вниз, далее делает один шаг вправо. После этого возвращается
к началу внешнего цикла.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 13: все клетки столбца E, D3−D6, C4, C5.
Правильный ответ указан под номером 2.
№9. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия. Команды-приказы: вверх,вниз, влево, вправо.
При выполнении любой из этих команд РОБОТ перемещается на одну клетку
соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если РОБОТ начнёт движение
в сторону находящейся рядом с ним стены, то он разрушится, и программа
прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ: сверху
свободно, снизу свободно, слева свободно, справа
свободно.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
вниз
КОНЕЦ ПОКА
КОНЕЦ
1) 6
2) 10
3) 13
4) 16
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка снизу или справа от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у правой стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вправо, далее делает один шаг вниз. После этого возвращается
к началу внешнего цикла.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 16.
Правильный ответ указан под номером 4.
нестандартные задачи
№1. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
МАШИНКА (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно> вниз
ПОКА <справа свободно> вправо
вверх
вправо
КОНЕЦ
1) 10
2) 14
3) 3
4) 22
Пояснение.
Начав движение из любой клетки столбца А, клеток
В7, В8, С7, С8 Машинка разобьется, выполняя команду вправо. Стартовав
из клеток В1−В3, Машинка уцелеет. Начав движение из любой клетки первых
двух строк, начиная со столбца С и до столбца I, Машинка разобьется.
Стартовав из любой клетки столбца J, Машинка разобьется, выполняя команду
вверх. Начав движение из любой клетки столбца K, L, M, N Машинка разобьется,
выполняя команду вправо.
Проанализировав «пещеру» (участок лабиринта в центре,
из которого только один выход), приходим к выводу, что Машинка не
разобьется, стартовав из столбцов D и E, H, I. В каждом из них по три
клетки, а в столбце I — 2. Следовательно, ответ 3 + 9 + 2 = 14.
Правильный ответ указан под номером 2.
№2. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 12
2) 13
3) 15
4) 17
Пояснение.
Стартовав из любой клетки столбцов A, B, D, I, K, M, N,
O и клеток F1−F2, G1−G2, I2−N2 кораблик разобьётся, выполнив команду
вверх. Начав из любой клетки столбца С клетки E8 и клеток F4-F8, I4-I8, J4,
G4 и H4, кораблик не разобьётся. Таким образом, число клеток, стартовав
из которых кораблик не разбивается, равно 17.
Правильный ответ указан под номером 4.
№3. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку. При попытке передвижения на любую
серую клетку КОРАБЛИК разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 5
2) 4
3) 3
4) 2
Пояснение.
Эффективным приёмом решения является проверка клеток
группами. Начав движение из любой клетки столбца А, клеток В7, В8 Машинка
разобьется, выполняя команду вверх. Стартовав из любой клетки первой
строки, Машинка разобьется, выполняя команду вверх. Начав движение
из любой клетки столбцов C, D, E, G, H, J, K, L, M, I Машинка разобьется,
выполняя команду вверх.
Начав движение из клетки F8 Машинка не разобьется.
Начав движение из клеток N7, N8, O7, O8 Машинка не разобьется.
Таким образом, правильный ответ указан под номером 1.
№4. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для удобства
идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
вверх
влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Эффективным приёмом решения является проверка клеток
группами. Если Кораблик начнет движение из клеток H6, I6, D7, D8 он не
разобьется. Начав движение из любой другой клетки, Кораблик разобьется,
выполняя последние две команды: вверх, влево.
Правильный ответ указан под номером 4.
№5. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <справа свободно> вправо
ПОКА <слева свободно> влево
вверх
влево
КОНЕЦ
1) 10
2) 9
3) 12
4) 11
Пояснение.
Разбиться Кораблик может только при выполнении команд
«вверх» и «влево». Начав из любой клетки строк 1, 3, 4, 5,
7, столбца А и клеток E6−J6 кораблик разобьётся, выполняя команду
влево. Стартовав из клеток С2, E2, G2, I2, K2, M2, O2, O4, O6, O8 кораблик
уцелеет.
Правильный ответ указан под номером 1.
№6. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную. ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <слева свободно> влево
ПОКА <справа свободно> вправо
вверх
вправо
КОНЕЦ
1) 0
2) 5
3) 15
4) 25
Пояснение.
Разбиться Кораблик может только при выполнении команд
«вверх» и «вправо». Начав из любой клетки строк 1, 3 и
клеток A3−A7, С3−С7, G5−O5 кораблик разобьётся, выполняя команду вверх.
Стартовав из любой клетки строки 8, кроме клетки O8 и клеток A2, C2, E2,
G2, I2, K2, M2, E6−J6, I4−K4 кораблик уцелеет.
Правильный ответ указан под номером 4.
№7. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится МАШИНКА (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободо> вниз
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 1
2) 13
3) 21
4) 40
Пояснение.
Разбиться Машинка может только при выполнении команд
«вверх» и «вправо». Начав из любой клетки рядов столбцов
А, C, O и клеток B8, D1, K1−L1, J3−J4, I4−I6, машинка разобьётся, выполняя
команду вправо. Начав из любой клетки столбцов E, F, G, M и клеток H8,
I8, J6−J8, L3−L8, I1−I2 машинка не разобьётся.
Правильный ответ указан под номером 4.
№8. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится МАШИНКА (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно> вниз
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 10
2) 13
3) 15
4) 17
Пояснение.
Разбиться Машинка может только при выполнении команд
«вверх» и «вправо». Начав из любой клетки столбцов A, G,
H, I, O, и клеток B2−F2, D4, J4−J6, K5−K6, L6, L4, машинка разобьётся, выполняя
команду вправо. Стартовав из клеток B4−B6, C4−C5, N4−N6, М4−М5 машинка
не разобьётся.
Правильный ответ указан под номером 1.
№9. Исполнитель
МАШИНКА «живет» в ограниченном прямоугольном лабиринте на клетчатой
плоскости, изображенном на рисунке. Серые клетки — возведенные
стены, светлые — свободные клетки, по которым МАШИНКА может свободно
передвигаться. По краю поля лабиринта также стоит возведенная стенка
с нанесенными номерами и буквами для идентификации клеток в лабиринте.
Система команд исполнителя
МАШИНКА:
При выполнении
любой из этих команд МАШИНКА перемещается на одну клетку соответственно
(по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды
проверяют истинность условия отсутствия стены у каждой стороны той
клетки, где находится МАШИНКА (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие>
команда
выполняется,
пока условие истинно, иначе происходит переход на следующую строку.
При попытке передвижения
на любую серую клетку МАШИНКА разбивается о стенку.
Сколько клеток приведенного
лабиринта соответствуют требованию, что, стартовав в ней и выполнив
предложенную ниже программу, МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно>
вниз
ПОКА <слева свободно>
влево
вверх
влево
КОНЕЦ
1) 1
2) 7
3) 17
4) 21
Пояснение.
Разбиться Машинка
может только при выполнении команд «вверх» и «влево».
Начав из любой клетки столбцов A, C, E, G, H, J, O и клеток B8, D1, F7 − F8,
I1 − I2, L1, L3 − L4, N1 машинка разобьётся, выполняя команду влево. Стартовав
из любой клетки столбца M, клеток I1, I2, I4 − I6, L6 − L8, K7 машинка не
разобьётся.
Правильный
ответ указан под номером 3.
№10. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится МАШИНКА (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно> вниз
ПОКА <справа свободно> вправо
вверх
вправо
КОНЕЦ
1) 0
2) 7
3) 1
4) 3
Пояснение.
Разбиться Машинка может только при выполнении команд
«вверх» и «вправо». Стартовав из любой клетки из столбца
А, машинка разобьется на последнем шаге, аналогично для клеток С7, С8
и А8 − J8. Начав движение из любой клетки с С1 по С5 машинка не разобьется,
аналогично для клеток I1, I2 (см. рисунок).
Правильный ответ указан под номером 2.
Остановка в заданной клетке, циклы с операторами ПОКА и ЕСЛИ
№1.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном
лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа
и 4 команды проверки условия. Команды-приказы: вверх, вниз, влево, вправо.
При выполнении любой из этих команд РОБОТ перемещается на одну клетку
соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если РОБОТ начнёт движение
в сторону находящейся рядом с ним стены, то он разрушится, и программа
прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ: сверху
свободно, снизу свободно, слева свободно, справа
свободно. Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно. В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно). В конструкциях
ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И,
ИЛИ, НЕ.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА <снизу свободно ИЛИ справа свободно>
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
ЕСЛИ <снизу свободно>
ТО вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 12
2) 15
3) 18
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у правой стороны клетки, в которой находится РОБОТ, нет стены,
он продолжает двигаться вправо. Как только это условие перестанет выполняться,
он переходит ко второму действию внутри цикла. Второе действие, заключается
в следующем: РОБОТ проверяет, есть ли стена у нижней стороны клетки,
в которой он находится, и если снизу свободно, РОБОТ передвигается
на одну клетку вниз. После чего возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу, что РОБОТ будет
двигаться вправо или вниз, пока у него есть такая возможность. РОБОТ при
данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 18.
№2. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия.
Команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится, и программа прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка А1)?
НАЧАЛО
ПОКА < слева свободно ИЛИ сверху свободно >
ЕСЛИ < слева свободно >
ТО влево
ИНАЧЕ вверх
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 8
2) 12
3) 17
4) 21
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами а не по одной.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка сслева или сверху от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока слева клетки в которой находится РОБОТ нет стены он продолжает
двигаться влево. В противном случае он двигается вверх.
Проверив все клетки группами выясняем, что число клеток,
удовлетворяющих условию задачи равно 21.
№3. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх , вниз
, влево
, вправо
.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции. Если РОБОТ начнёт движение в сторону находящейся рядом с
ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ЕСЛИ снизу свободно
ТО
вниз
КОНЕЦ ЕСЛИ
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 19
3) 20
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому условию. По этому условию,
пока у нижней стороны клетки в которой находится РОБОТ нет стены, он
продолжает двигаться вниз. Как только это условие перестанет выполняться,
он переходит ко второму условию. Это условие аналогично первому,
только теперь проверяется отсутствие стены у правой стороны клетки.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Видно, что существует всего 2 места, в которых робот
может остановиться: нужная нам 6F и 3F. Робот может прийти в клетку 3F
только если он находится в области 1B:3F и клетках 1A и 2A, количество
клеток в этой области равно 17. Общее количество клеток лабиринта
равна 36, следовательно, 36 − 17 = 19.
Правильный ответ указан под номером 2.
№4. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх , вниз
, влево
, вправо
.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
ТО
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободнo
ТО
вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 19
3) 20
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому условию. По этому условию,
пока у правой стороны клетки в которой находится РОБОТ нет стены, он
продолжает двигаться вправо. Как только это условие перестанет выполняться,
он переходит ко второму условию. Это условие аналогично первому,
только теперь проверяется отсутствие стены у нижней стороны клетки.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Видно, что существует всего 2 места, в которых робот
может остановиться: нужная нам 6F и 6C. Робот может прийти в клетку 6С,
только если он находится в области 2А:6С, количество клеток в этой области
равно 15. Общее количество клеток лабиринта равно 36, следовательно,
36 − 15 = 21.
Правильный ответ указан под номером 4.
№5. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх вниз
влево
вправо
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в данной клетке и выполнив предложенную программу,
РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦl
1) 18
2) 24
3) 27
4) 30
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ проверяет, есть ли стена у
правой стороны клетки, в которой он находится, и если справа свободно,
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ будет двигаться вниз или вправо, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 30 (все клетки за исключением E1:F3).
№6. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх вниз
влево
вправо
Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в данной клетке и выполнив предложенную программу,
РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦl
1) 6
2) 14
3) 18
4) 30
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной.
При данной программе РОБОТ поступает следующим образом:
вначале РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ проверяет, есть ли стена у
правой стороны клетки, в которой он находится, и если справа свободно,
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла.
Поэтому РОБОТ будет двигаться вправо или вниз, пока у
него есть такая возможность. РОБОТ при данной программе никогда не
разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 14.
Ответ: 2.
№7. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх вниз
влево
вправо
Четыре команды проверяют
истинность условия отсутствия стены у каждой стороны той клетки, где
находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в данной клетке и выполнив предложенную программу,
РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 6
2) 10
3) 13
4) 18
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной.
При данной программе РОБОТ поступает следующим образом:
вначале РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ проверяет, есть ли стена у
правой стороны клетки, в которой он находится, и если справа свободно,
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла.
Поэтому РОБОТ будет двигаться вправо или вниз, пока у
него есть такая возможность. РОБОТ при данной программе никогда не
разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 13 (вся шестая строчка, клетки A, B четвертой и пятой строчки, клетки
C, D, E пятой строчки).
Ответ: 3.
№8. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то
он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ЕСЛИ снизу свободно
ТО вниз
ИНАЧЕ вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 16
2) 20
3) 25
4) 28
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле если у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вниз, в противном случае он перемещается вправо.
После этого возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток C1, A5, C5.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 16 (весь столбец F, E1-E5, клетки D1, D2, D3, D4, D5).
№9. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ЕСЛИ справа свободно
ТО вправо
ИНАЧЕ вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 19
2) 22
3) 25
4) 28
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле если у правой стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вправо, в противном случае он перемещается
вниз. После этого возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток А4, B4, C6.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 22 (вся первая и пятая строчка, весь столбец F, клетки D2-D4, E2-E4,
F2 и. т. д.).
№10. Система команд исполнителя РОБОТ,
«живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит
из 8 команд. Четыре команды −
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится, и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно ЕСЛИ
снизу свободно
ТО
вниз
КОНЕЦ ЕСЛИ
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 12
2) 16
3) 20
4) 24
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле если у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вниз, в противном случае, если у правой стороны
клетки нет стены, он перемещается вправо. После этого возвращается к
началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ не может разбиться.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 12 (клетки А4-6, B4-6, C5-6, D5-6, E6, F6).
Правильный ответ указан под номером 1.
Остановка в клетке, из которой начатодвижение
№1. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на
одну клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА < снизу свободно > вниз
ПОКА < слева свободно > влево
ПОКА < сверху свободно > вверх
ПОКА < справа свободно > вправо
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Программа заканчивается
командой «ПОКА < справа свободно > вправо», следовательно,
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка справа (условие 1). Этому
условию удовлетворяют все клетки правой стенки лабиринта и еще пять
клеток кроме нее.
Предпоследняя команда: «ПОКА < сверху свободно
> вверх», значит у клетки в которой он прекратит выполнение
должно быть ограничение стенкой сверху. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться на одной строчке с клеткой, с которой
он начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего две:
Г3 и Д1, если нумеровать цифрами сверху вниз, а буквами слева направо.
Представив себе движение робота в том случае когда он стартует из этих
клеток, увидим, что в них он и вернется.
Правильный ответ указан под номером 2.
№2. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <справа свободно> вправо
ПОКА <снизу свободно> вниз
ПОКА <слева свободно> влево
ПОКА <сверху свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <сверху свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка сверху (условие 1).
Этому условию удовлетворяют все клетки верхней стенки лабиринта и
еще пять клеток кроме нее.
Предпоследняя команда: «ПОКА <слева свободно>
влево», значит у клетки в которой он прекратит выполнение должно
быть ограничение стенкой слева. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одном столбце с клеткой, с которой он
начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего две:
А1 и Б2 если нумеровать цифрами сверху вниз, а буквами слева направо.
И клетка, из которой движение невозможно начать Д4.
Правильный ответ указан под номером 3.
№3. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
ПОКА<снизу свободно> вниз
ПОКА<справа свободно> вправо
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <справа свободно> вправо», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка справа (условие 1). Этому
условию удовлетворяют все клетки правой стенки лабиринта и еще пять
клеток кроме нее. Предпоследняя команда: «ПОКА<снизу свободно>
вниз», следовательно, у клетки в которой он прекратит выполнение
должно быть ограничение стенкой снизу. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одной строке с клеткой, с которой он
начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего три:
Е6, Е5 и Б2, если нумеровать цифрами сверху вниз, а буквами слева направо.
Правильный ответ указан под номером 3.
№4. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на
од-ну клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА<снизу свободно> вниз
ПОКА<справа свободно> вправо
ПОКА<сверху свободно> вверх
ПОКА<слева свободно> влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА<слева свободно> влево», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева (условие 1). Этому
условию удовлетворяют все клетки левой стенки лабиринта и еще восемь
клеток кроме нее.
Предпоследняя команда: «ПОКА<сверху свободно>
вверх», значит у клетки в которой он прекратит выполнение должно
быть ограничение стенкой сверху. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одной строке с клеткой, с которой он
начал движение (условие 2). Клеток, удовлетворяющих условиям 1 и 2,
всего три: В1, А1 и А3, если нумеровать цифрами сверху вниз, а русскими
буквами слева направо.
Правильный ответ указан под номером 3.
№5. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на
од-ну клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> влево
ПОКА <сверху свободно> вверх
ПОКА <справа свободно> вправо
ПОКА <снизу свободно> вниз
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <снизу свободно> вниз», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка снизу. Этому условию удовлетворяют
все клетки нижней стенки лабиринта и еще шесть клеток кроме нее.
Предпоследняя команда: «ПОКА <справа свободно>
вправо», значит у клетки в которой он прекратит выполнение должно
быть ограничение стенкой справа. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одном столбце с клеткой, с которой он
начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего одна:
Г5, если нумеровать цифрами сверху вниз, а буквами слева направо.
Правильный ответ указан под номером 1.
№6. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вправо
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
ПОКА <слева свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <слева свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева. Этому условию удовлетворяют
все клетки левой стенки лабиринта и еще пять клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию 1.
Обратим внимание, что возможны зацикливания, например, если начать
движение из клетки А6, если нумеровать цифрами сверху вниз, а буквами
слева направо.
Ответ: одна клетка Г1.
№7. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вправо
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
ПОКА <слева свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <слева свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева. Этому условию удовлетворяют
все клетки левой стенки лабиринта и еще пять клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию 1.
Обратим внимание, что возможны зацикливания, например, если начать
движение из клетки А1, если нумеровать цифрами сверху вниз, а буквами
слева направо.
Ответ: две клетки Д1 и В2.
№8. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> вниз
ПОКА <снизу свободно> вправо
ПОКА <справа свободно> вверх
ПОКА <сверху свободно> влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Так как программа заканчивается командой «ПОКА
<сверху свободно> влево», для того, чтобы робот остановился в
той же клетке, с которой он начал движение, необходимо, чтобы у этой
клетки была стенка сверху. Этому условию удовлетворяют все клетки верхней
стенки лабиринта и еще пять клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию.
Обратите внимание, что возможны зацикливания, например, если начать
движение из клетки Д1 (если нумеровать цифрами сверху вниз, а русскими
буквами слева направо).
Ответ: две клетки Г4 и А2.
№9. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вправо
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
ПОКА <слева свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <слева свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева. Этому условию удовлетворяют
все клетки левой стенки лабиринта и еще семь клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию. Обратите
внимание, что возможны зацикливания, например, если начать движение
из клетки из любой клетки левой стенки.
Ответ: две клетки: Д1 и В2, если нумеровать цифрами
сверху вниз, а буквами слева направо.
№10. Система команд исполнителя РОБОТ,
«живущего» в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> вниз
ПОКА <снизу свободно> вправо
ПОКА <справа свободно> вверх
ПОКА <сверху свободно> влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо для того, чтобы РОБОТ остановился
в той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <сверху свободно> влево», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка сверху. Этому условию удовлетворяют
все клетки верхней стенки лабиринта и еще шесть клеток кроме нее. Проверим
каждую клетку, удовлетворяющую условию. Обратим внимание, что возможны
зацикливания, например, если начать движение из клетки А1, Б1, если
нумеровать цифрами сверху вниз, а буквами слева направо.
Ответ: три клетки В1, А2 и Д3.