Исследование частных решу егэ математика

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Исследование частных

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 11 № 77467

Найдите точку максимума функции

Аналоги к заданию № 77467: 129843 129871 523993 524020 548510 548529 129845 129847 129849 129851 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на бесконечном промежутке

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77468

Найдите точку минимума функции

Аналоги к заданию № 77468: 129873 129899 129901 129875 129877 129879 129881 129883 129885 129887 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 77469

Найдите наименьшее значение функции на отрезке

Аналоги к заданию № 77469: 129903 129931 129905 129907 129909 129911 129913 129915 129917 129919 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77470

Найдите наибольшее значение функции на отрезке

Аналоги к заданию № 77470: 129933 129961 129935 129937 129939 129941 129943 129945 129947 129949 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77471

Найдите точку максимума функции

Аналоги к заданию № 77471: 129965 129963 130011 129967 129969 129971 129973 129975 129977 129979 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

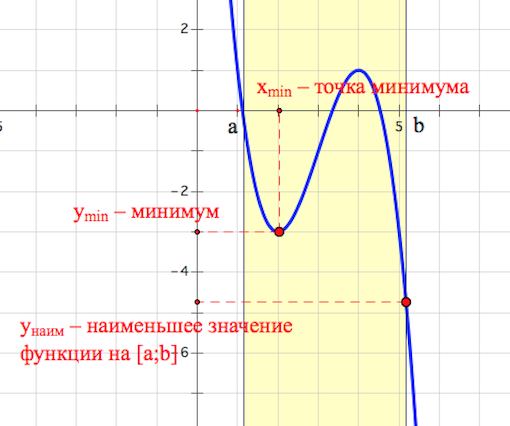
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Исследование частных решу егэ математика

Найдите точку максимума функции

Решение. Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Заметим, что функция имеет разрыв при (при X = 0), и ее значение в точке минимума (при X = −17) больше, чем значение в точке максимума (при X = 17).

Найдите точку минимума функции

Решение. Область определения функции:

Найдём производную заданной функции:

Найдём нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума

Найдите наименьшее значение функции на отрезке

Решение. Найдем производную заданной функции:

Производная обращается в нуль в точках 5 и −5. Определим знаки производной функции и изобразим на рисунке поведение функции на заданном отрезке:

Наименьшим значением функции на заданном отрезке будет ее значение в точке 5. Найдем его:

Найдите наибольшее значение функции на отрезке

Решение. Найдем производную заданной функции:

Производная обращается в нуль в точках 5 и −5, заданному отрезку принадлежит только число −5.

Наибольшим значением функции на заданном отрезке будет наибольшее из чисел и Найдем их:

Найдите точку максимума функции

Решение. Область определения функции:

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Внимательный читатель может заметить, что значение функции в точке X = −4 меньше, чем в точке X = 4. Тем не менее точка −4 является точкой максимума, поскольку слева от нее функция возрастает, а справа убывает, а точка 4 является точкой минимума. Значение в точке максимума оказалось меньше, чем в точке минимума, поскольку функция имеет разрыв при X = 0.

Тем не менее точка 4 является точкой максимума, поскольку слева от нее функция возрастает, а справа убывает, а точка 4 является точкой минимума.

Ege. sdamgia. ru

12.12.2020 20:45:45

2020-12-12 20:45:45

Источники:

Https://ege. sdamgia. ru/test? theme=83&print=true

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Исследование частных решу егэ математика

Задание 11 № 77467

Найдите точку максимума функции

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Задание 11 № 77468

Найдите точку минимума функции

Область определения функции:

Найдём производную заданной функции:

Найдём нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума

У меня получается при х=-1 значение функции=2.

А при х=1, значение функции= -2,

То есть точка минимума х=1.

Объясните, пожалуйста, в чём моя ошибка.

Вопрос о точке минимума, а не о минимальном значении функции

Задание 11 № 77469

Найдите наименьшее значение функции на отрезке

Найдем производную заданной функции:

Наименьшим значением функции на заданном отрезке будет ее значение в точке 5. Найдем его:

Задание 11 № 77470

Найдите наибольшее значение функции на отрезке

Найдем производную заданной функции:

Производная обращается в нуль в точках 5 и −5, заданному отрезку принадлежит только число −5.

Наибольшим значением функции на заданном отрезке будет наибольшее из чисел и Найдем их:

Задание 11 № 77471

Найдите точку максимума функции

Область определения функции:

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Задание 11 № 77469

Задание 11 № 77470

Найдите наименьшее значение функции на отрезке.

Ege. sdamgia. ru

10.03.2019 17:14:26

2019-03-10 17:14:26

Источники:

Https://ege. sdamgia. ru/test? theme=83

Исследование частных решу егэ математика

Задание 6 № 6401

На рисунке изображен график функции определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой

Поскольку касательная параллельна прямой Y = 10 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. Производная равна нулю в точках экстремума функции. На заданном интервале функция имеет 3 максимума и 3 минимума, итого 6 экстремумов. Таким образом, касательная к графику функции параллельна прямой y = 10 или совпадает с ней в 6 точках.

Задание 6 № 7321

Поскольку касательная параллельна прямой Y = −6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. Производная равна нулю в точках экстремума функции. На заданном интервале функция имеет 3 максимума и 4 минимума, итого 7 экстремумов. Таким образом, касательная к графику функции параллельна прямой y = −6 или совпадает с ней в 7 точках.

Задание 6 № 512487

На рисунке изображён график функции Y = F(X), определённой на интервале (−3; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой Y = 1.

Поскольку касательная параллельна прямой Y = 1 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. Производная равна нулю в точках экстремума функции. На заданном интервале функция имеет 7 экстремумов. Таким образом, касательная к графику функции параллельна прямой Y = 1 или совпадает с ней в 7 точках.

Задание 6 № 512497

На рисунке изображён график функции Y = F(X), определённой на интервале (−4; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой Y = 18.

Поскольку касательная параллельна прямой Y = 18 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. Производная равна нулю в точках экстремума функции. На заданном интервале функция имеет 6 экстремумов. Таким образом, касательная к графику функции параллельна прямой y = 18 или совпадает с ней в 6 точках.

Задание 6 № 6407

На рисунке изображен график производной функции определенной на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = X − 7 или совпадает с ней, их угловые коэффициенты равны 1. Найдем количество точек, в которых F ‘(X0) = 1, это соответствует количеству точек пересечения графика производной с прямой Y = 1. На данном интервале таких точек 4.

Задание 6 № 40131

На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику параллельна оси абсцисс или совпадает с ней.

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, она имеет вид и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка

Разве угловой коэффициент равен нулю не в точках с абциссой 1 и 4?

На рисунке изображен график ПРОИЗВОДНОЙ

Задание 6 № 54801

На рисунке изображен график функции Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная проходит через начало координат, ее уравнение имеет вид Прямая проходит через точку (10; −6), значит, Поскольку угловой коэффициент равен значению производной в точке касания получаем:

Аналоги к заданию № 40129: 54801 Все

Задание 6 № 500248

На рисунке изображён график дифференцируемой функции Y = F(X). На оси абсцисс отмечены девять точек: X1, X2, X3, . X9. Среди этих точек найдите все точки, в которых производная функции F(X) отрицательна. В ответе укажите количество найденных точек.

Две из отмеченных точек являются точками экстремума функции F(X). Это точки X3 и X6 (выделены красным). В них производная функции F(X) равна нулю.

В точках X1, X2, X7 и X8 функция F(X) возрастает (выделены синим). В этих четырёх точках производная функции F(X) положительна.

В точках X4, X5 и X9 функция F(X) убывает (выделены оранжевым). В этих Трёх точках производная функции F(X) отрицательна.

Источник: Демонстрационная версия ЕГЭ—2013 по математике., Проект демонстрационной версии ЕГЭ—2014 по математике.

Задание 6 № 512487

Задание 6 № 7321

Поскольку касательная проходит через начало координат, ее уравнение имеет вид Прямая проходит через точку 10; 6 , значит, Поскольку угловой коэффициент равен значению производной в точке касания получаем.

Math-ege. sdamgia. ru

04.11.2018 23:14:34

2018-11-04 23:14:34

Источники:

Https://math-ege. sdamgia. ru/search? keywords=1&cb=1&search=4.2.1%20%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9%20%D0%BA%20%D0%B8%D1%81%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8E%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B9%20%D0%B8%20%D0%BF%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D1%8E%20%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA%D0%BE%D0%B2

Источник

Старый каталог

Каталог заданий по типам по темам

?

Т3. Начала теории вероятностей

4. Вероятности сложных событий

Т5. Простейшие уравнения

Т6. Вычисления и преобразования

213

Т7. Производная и первообразная

Т8. Задачи с прикладным содержанием

Т11. Наибольшее и наименьшее значение функций

166

13. Стереометрическая задача

279

15. Финансовая математика

234

16. Планиметрическая задача

290

17. Задача с параметром

412

18. Числа и их свойства

333

Дополнительные задания для подготовки

ТЗадания Д1. Чтение графиков и диаграмм

ТЗадания Д2. Простейшие текстовые задачи

Задания Д3. Выбор оптимального варианта

ТЗадания Д4. Квадратная решётка, координатная плоскость

124

Задания Д5. Планиметрия: вычисление длин и площадей

Задания Д6. Планиметрия

254

Задания Д7. Задачи с прикладным содержанием

Задания Д8 C1. Уравнения, системы уравнений

332

Задания Д9 C2. Стереометрическая задача

157

Задания Д10 C2. Сложная стереометрия

310

Задания Д11 C3. Простые системы неравенств

105

Задания Д12 C3. Сложные неравенства

189

Задания Д13 C3. Системы сложных неравенств

Задания Д14 C4. Планиметрическая задача

123

Задания Д15 C4. Сложная планиметрия

300

Задания Д16 C5. Сложные практические задачи

201

Задания Д17 C6. Сложные задачи с параметром

281

Задания Д18 C7. Числа и их свойства

Задания Д19 C7. Сложные задания на числа и их свойства

242

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.admin2023-03-05T21:56:54+03:00

Используйте LaTeX для набора формулы

Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.

Тренировочные варианты ЕГЭ 2022 по математике (профиль)

egemath.ru
Вариант 1	скачать
Вариант 2	скачать
Вариант 3	скачать
Вариант 4	скачать
Вариант 5	скачать
Вариант 6	скачать
Вариант 7	скачать
variant 8	скачать
variant 9	скачать
variant 10	скачать
variant 11	скачать
variant 12	скачать
variant 13	скачать
variant 14	скачать
variant 15	скачать
variant 16	скачать
variant 17	скачать
variant 18	скачать
variant 19	скачать
variant 20	скачать
yagubov.ru
вариант 21	ege2022-yagubov-prof-var21
вариант 22	ege2022-yagubov-prof-var22
вариант 23	ege2022-yagubov-prof-var23
вариант 24	ege2022-yagubov-prof-var24
вариант 25	ege2022-yagubov-prof-var25
вариант 26	ege2022-yagubov-prof-var26
вариант 27	ege2022-yagubov-prof-var27
вариант 28	ege2022-yagubov-prof-var28
Досрочный Москва 28.03.2022	скачать
egemathschool.ru
вариант 1	ответ
вариант 2	ответ
вариант 3	ответ
вариант 4	ответ
ЕГЭ 100 баллов (с решениями)
Вариант 1	скачать
Вариант 2	скачать
Вариант 3	скачать
Вариант 4	скачать
Вариант 5	скачать
Вариант 6	скачать
Вариант 7	скачать
Вариант 8	скачать
Вариант 9	скачать
Вариант 10	скачать
variant 11	скачать
variant 12	скачать
variant 13	скачать
variant 14	скачать
variant 15	скачать
variant 16	скачать
variant 17	скачать
variant 18	скачать
variant 20	скачать
variant 21	скачать
variant 23	скачать
variant 24	скачать
variant 25	скачать
variant 26	скачать
variant 29	скачать
variant 30	скачать
math100.ru (с ответами)
Вариант 140	скачать
Вариант 141	скачать
Вариант 142	скачать
Вариант 143	math100-ege22-v143
Вариант 144	math100-ege22-v144
Вариант 145	math100-ege22-v145
Вариант 146	math100-ege22-v146
variant 147	math100-ege22-v147
variant 148	math100-ege22-v148
variant 149	math100-ege22-v149
variant 150	math100-ege22-v150
variant 151	math100-ege22-v151
variant 152	math100-ege22-v152
variant 153	math100-ege22-v153
variant 154	math100-ege22-v154
variant 155	math100-ege22-v155
variant 156	math100-ege22-v156
variant 157	math100-ege22-v157
variant 158	math100-ege22-v158
variant 159	math100-ege22-v159
variant 160	math100-ege22-v160
variant 161	math100-ege22-v161
variant 162	math100-ege22-v162
variant 163	math100-ege22-v163
variant 164	math100-ege22-v164
variant 165	math100-ege22-v165
variant 166	math100-ege22-v166
variant 167	math100-ege22-v167
variant 168	math100-ege22-v168
variant 169	math100-ege22-v169
variant 170	math100-ege22-v170
variant 171	math100-ege22-v171
variant 172	math100-ege22-v172
variant 173	math100-ege22-v173
variant 174	math100-ege22-v174
alexlarin.net
Вариант 358	скачать
Вариант 359	скачать
Вариант 360	скачать
Вариант 361	скачать
Вариант 362	проверить ответы
Вариант 363	проверить ответы
Вариант 364	проверить ответы
Вариант 365	проверить ответы
Вариант 366	проверить ответы
Вариант 367	проверить ответы
Вариант 368	проверить ответы
Вариант 369	проверить ответы
Вариант 370	проверить ответы
Вариант 371	проверить ответы
Вариант 372	проверить ответы
Вариант 373	проверить ответы
Вариант 374	проверить ответы
Вариант 375	проверить ответы
Вариант 376	проверить ответы
Вариант 377	проверить ответы
Вариант 378	проверить ответы
Вариант 379	проверить ответы
Вариант 380	проверить ответы
Вариант 381	проверить ответы
Вариант 382	проверить ответы
Вариант 383	проверить ответы
Вариант 384	проверить ответы
Вариант 385	проверить ответы
Вариант 386	проверить ответы
Вариант 387	проверить ответы
Вариант 388	проверить ответы
vk.com/ekaterina_chekmareva (задания 1-12)
Вариант 1	ответы
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7	ответы
Вариант 8
Вариант 9
Вариант 10
vk.com/matematicalate
Вариант 1	matematikaLite-prof-ege22-var1
Вариант 2	matematikaLite-prof-ege22-var2
Вариант 3	matematikaLite-prof-ege22-var3
Вариант 4	matematikaLite-prof-ege22-var4
Вариант 5	matematikaLite-prof-ege22-var5
Вариант 6	matematikaLite-prof-ege22-var6
Вариант 7	matematikaLite-prof-ege22-var7
Вариант 8	matematikaLite-prof-ege22-var8
vk.com/pro_matem
variant 1	pro_matem-prof-ege22-var1
variant 2	pro_matem-prof-ege22-var2
variant 3	pro_matem-prof-ege22-var3
variant 4	разбор
variant 5	разбор
vk.com/murmurmash
variant 1	otvet
variant 2	otvet
→ Купить сборники тренировочных вариантов ЕГЭ 2022 по математике

Структура варианта КИМ ЕГЭ

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:

– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;

– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).

Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.

Связанные страницы:

Средний балл ЕГЭ 2021 по математике

Решение задач с параметром при подготовке к ЕГЭ

Изменения в КИМ ЕГЭ 2022 года по математике

Купить сборники типовых вариантов ЕГЭ по математике

Как решать экономические задачи ЕГЭ по математике профильного уровня?

Математика Профильный уровень

Об экзамене

Профильная математика – довольно коварная, обманчивая вещь. Вроде бы смотришь на задания первой части, думаешь, лол, что это за детский сад? А потом открываешь вторую часть, и в голове начинают крутиться совершенно другие мысли… И ведь подсознательно понимаешь, что это далеко не самые сложные вещи, но сколько всевозможных тонких моментов, о которые начинаешь сходу спотыкаться. Так что не впадайте в крайности, готовьтесь планомерно, по чуть-чуть повышайте сложность заданий и стремитесь к большему! Ведь профильная математика – это круто!

Структура

Часть 1 содержит 8 заданий (задания 1–8) с кратким ответом; часть 2 содержит 4 задания (задания 9–12) с кратким ответом заданий (задания 13–19) с развернутым ответом. По уровню сложности задания распределяются следующим образом: задания 1–8 имеют базовый уровень; задания 9–17 – повышенный уровень; задания 18 и 19 относятся к высокому уровню сложности.

На выполнение экзаменационной работы отводится 3 часа 55 минут (235 минут).

Пояснения к оцениванию заданий

Правильное решение каждого из заданий 1–12 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби. Решения заданий с развернутым ответом оцениваются от 0 до 4 баллов. Полное правильное решение каждого из заданий 13–15 оценивается 2 баллами; каждого из заданий 16 и 17 – 3 баллами; каждого из заданий 18 и 19 – 4 баллами. Проверка выполнения заданий 13–19 проводится разработанной системы критериев оценивания.

	Тема	Результат
1.	Простейшие текстовые задачи Вычисления Округление с недостатком Округление с избытком Проценты Проценты и округление	Не изучена	Отработать	PDF
2.	Чтение графиков и диаграмм Определение величины по графику Определение величины по диаграмме Вычисление величин по графику или диаграмме	Не изучена	Отработать	PDF
3.	Планиметрия: вычисление длин и площадей Многоугольники: вычисление длин и углов Многоугольники: вычисление площадей Круг и его элементы Координатная плоскость	Не изучена	Отработать	PDF
4.	Начала теории вероятностей Классическое определение вероятности Теоремы о вероятностях событий	Не изучена	Отработать	PDF
5.	Простейшие уравнения Линейные, квадратные, кубические уравнения Рациональные уравнения Иррациональные уравнения Показательные уравнения Логарифмические уравнения Тригонометрические уравнения	Не изучена	Отработать	PDF
6.	Планиметрия Прямоугольные треугольники Равнобедренные треугольники Треугольники общего вида Параллелограмм Трапеция Центральные и вписанные углы Касательная, хорда, секущая Вписанные окружности Описанные окружности	Не изучена	Отработать	PDF
7.	Производная и первообразная Физический смысл производной Производная и касательная Применение производной к исследованию функций Определение свойств производной по заданной функции Определение свойств функции по заданной производной Первообразная	Не изучена	Отработать	PDF
8.	Стереометрия Куб Прямоугольный параллелепипед Элементы составных многогранников Площадь поверхности составного многогранника Объем составного многогранника Призма Пирамида Комбинации тел Цилиндр Конус Сфера, шар	Не изучена	Отработать	PDF
9.	Вычисления и преобразования Алгебраические выражения Рациональные выражения Иррациональные выражения Степенные выражения Логарифмические выражения Тригонометрические выражения	Не изучена	Отработать	PDF
10.	Задачи с прикладным содержанием Разные задачи Линейные уравнения и неравенства Квадратные и степенные уравнения и неравенства Иррациональные уравнения и неравенства Рациональные уравнения и неравенства Логарифмические уравнения и неравенства Тригонометрические уравнения и неравенства Показательные уравнения и неравенства	Не изучена	Отработать	PDF
11.	Текстовые задачи Задачи на сплавы и смеси Задачи на движение по прямой Задачи на движение по окружности Задачи на движение по воде Задачи на производительность Задачи на прогрессии Задачи на проценты	Не изучена	Отработать	PDF
12.	Наибольшее и наименьшее значение функций Исследование степенных и иррациональных функций Исследование частных Исследование произведений Исследование показательных и логарифмических функций Исследование тригонометрических функций Исследование функций без помощи производной	Не изучена	Отработать	PDF
Часть 2
13.	Уравнения Рациональные и иррациональные уравнения Логарифмические и показательные уравнения Тригонометрические уравнения Тригонометрические уравнения, исследование ОДЗ Уравнения смешанного типа		Отработать	PDF
14.	Углы и расстояния в пространстве Задача на доказательство и вычисление Угол между скрещивающимися прямыми Угол между прямой и плоскостью Угол между плоскостями Расстояние от точки до прямой и до плоскости Расстояние между прямыми и плоскостями Сечения многогранников Объёмы многогранников Тела вращения: цилиндр, конус, шар		Отработать	PDF
15.	Неравенства Рациональные неравенства Иррациональные неравенства Показательные неравенства Логарифмические неравенства Неравенства с логарифмами по переменному основанию Неравенства с модулем Смешанные неравенства		Отработать	PDF
16.	Планиметрическая задача Многоугольники и их свойства Окружности и треугольники Окружности и четырёхугольники Окружности и системы окружностей Задача на доказательство и вычисление		Отработать	PDF
17.	Практические задачи Банки, вклады, акции Кредиты (с установленными размерами платежей) Кредиты (с установленной схемой уменьшения долга) Задачи на оптимальный выбор Разные задачи		Отработать	PDF
18.	Уравнения, неравенства, системы с параметром Комбинация «кривых» Кусочное построение графика функции Комбинация прямых Координаты (x, a) Левая и правая части в качестве отдельных графиков Перебор случаев Подвижная галочка Расстояние между точками Симметрия в решениях Уравнение окружности Функции, зависящие от параметра Уравнения с параметром Расположение корней квадратного трехчлена Использование симметрий, оценок, монотонности		Отработать	PDF
19.	Числа и их свойства Числа и их свойства Числовые наборы на карточках и досках Последовательности и прогрессии Сюжетные задачи		Отработать	PDF

Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу.
Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.

Ознакомьтесь с подробной видеоинструкцией по использованию модуля.

Источник

Задача 1. Найдите точку максимума функции

Решение: + показать

Задача 2. Найдите точку минимума функции

Решение: + показать

Задача 3. Найдите наименьшее значение функции на отрезке .

Решение: + показать

Задача 4. Найдите наибольшее значение функции $y=2+9x-frac{x^3}{3}$ на отрезке

Решение: + показать

Задача 5. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 6. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 7. Найдите точку максимума функции $y=6+12x-2x^{frac{3}{2}}.$

Решение: + показать

Задача 8. Найдите наибольшее значение функции $y=-frac{2}{3}xsqrt x+3x+8$ на отрезке

Решение: + показать

Задача 9. Найдите точку минимума функции $y=-frac{x^2+25}{x}$ .

Решение: + показать

Задача 10. Найдите наименьшее значение функции $y=frac{x^2+900}{x}$ на

Решение: + показать

Задача 11. Найдите точку максимума функции $y=frac{441}{x}+x+18.$

Решение: + показать

Задача 12. Найдите точку минимума функции $y=(3x^2-15x+15)e^{x-15}.$

Решение: + показать

Задача 13. Найдите точку максимума функции $y=(x+11)^2cdot e^{3-x}.$

Решение: + показать

Задача 14. Найдите наименьшее значение функции на отрезке .

Решение: + показать

Задача 15. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 16. Найдите наименьшее значение функции на отрезке $[frac{1}{12};frac{5}{12}].$

Решение: + показать

Задача 17. Найдите наименьшее значение функции на отрезке $[frac{3}{4};frac{5}{4}].$

Решение: + показать

Задача 18. Найдите наименьшее значение функции $y=e^{2x}-11e^x-1$ на отрезке .

Решение: + показать

Задача 19. Найдите наибольшее значение функции на отрезке $[0;frac{pi}{2}].$

Решение: + показать

Задача 20. Найдите наименьшее значение функции на отрезке $[-frac{pi}{3};frac{pi}{3}].$

Решение: + показать

Задача 21. Найдите наибольшее значение функции на отрезке $[-frac{3pi}{2};0]$ .

Решение: + показать

Задача 22. Найдите наименьшее значение функции $y=4cosx+frac{15}{pi}x+9$ на отрезке $[-frac{2pi}{3};0].$

Решение: + показать

Задача 23. Найдите наименьшее значение функции на отрезке $[0;frac{pi}{4}].$

Решение: + показать

Задача 24. Найдите точку минимума функции принадлежащую промежутку $(0;frac{pi}{2})$ .

Решение: + показать

* Замечание. Важно!

Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!

Например, на рисунке ниже наименьшее значение функции на отрезке достигается на конце отрезка , а именно, в точке .

То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке следует выбрать наименьшую из величин:

1) $y(x_{min})$ (их может быть несколько) из рассматриваемого отрезка

2) ,

При нахождении наибольшего значения функции на отрезке следует выбрать большую из величин:

1) $y(x_{max})$ (их может быть несколько) из рассматриваемого отрезка

2) ,

Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.

Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.

В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.

Вы можете пройти тест “Исследование функции при помощи производной”

Источник


3647	Найдите точку минимума функции y= x^3-27x^2+13 Решение График	Найдите точку минимума функции y= x3 -27×2 +13 ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 11

3632	Найдите точку максимума функции y= -(x^2+196)/x Решение График	Найдите точку максимума функции y= — x2 + 196 / x ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 11

3592	Найдите точку максимума функции y= (x+35)e^(35-x) Решение	Найдите точку максимума функции y= (x+35)e^(35-x) ! 36 вариантов ФИПИ Ященко 2023 Вариант 19 Задание 11

3587	Найдите наибольшее значение функции y= 2x^2-12x+8ln(x)-5 на отрезке [12/13; 14/13]. Решение График	Найдите наибольшее значение функции y= 2×2 -12x + 8lnx — 5 на отрезке [12/13; 14/13] ! 36 вариантов ФИПИ Ященко 2023 Вариант 18 Задание 11

3571	Найдите наименьшее значение функции y= 10x-10ln(x+4)+23 на отрезке [-3,5; 0] Решение График	Найдите наименьшее значение функции y= 10x -10ln(x+4) +23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 11 Вариант МА2210209

3562	Найдите точку минимума функции y= x^3-8.5x^2+10x-13 Решение График	Найдите точку минимума функции y= x3 -8,5×2 +10x -13 ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 11

3537	Найдите точку максимума функции y= (4x^2-36x+36)e^(33-x) Решение График	Найдите точку максимума функции y= (4×2 -36x +36)e^ 33 -x ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 11

3529	Найдите наименьшее значение функции y= 6x-6sin(x)+17 на отрезке [0; pi/2]. Решение График	Найдите наименьшее значение функции y = 6x-6sinx+17 на отрезке ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 11

3518	Найдите точку максимума функции y= (2x-1)cos(x)-2sin(x)+9, принадлежащую промежутку (0; pi/2). Решение График	Найдите точку максимума функции y= (2x-1)cosx — 2sinx +9, принадлежащую промежутку! 36 вариантов ФИПИ Ященко 2023 Вариант 7 Задание 11

3506	Найдите наименьшее значение функции y= x^3+18x^2+81x+56 на отрезке [-7; 0]. Решение График	Найдите наименьшее значение функции y= x3 +18×2 + 81x +56 на отрезке ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 11

Источник

Задание №11 решу ЕГЭ 2022 по математике 11 класс профильный уровень (профиль) все задания с ответами и решением, которые могут попасться на реальном ЕГЭ 2022.

Степенные иррациональные функции
Логарифмические функции
Показательные функции
Тригонометрические функции
Исследование функции без производной

Задание 11 часть 1 профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной. Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке

Степенные иррациональные функции ЕГЭ 2022 профиль математика:

Логарифмические функции ЕГЭ 2022 профиль математика:

Показательные функции ЕГЭ 2022 профиль математика:

Тригонометрические функции ЕГЭ 2022 профиль математика:

Исследование функции ЕГЭ 2022 профиль математика:

Видео как решать 11 задание в ЕГЭ по математике профиль:

1)Найдите наименьшее значение функции y=−2ln(x+3)5+10x на отрезке [−2,5;−1].

2)Найдите наибольшее значение функции y=ln(x+7)3−3x на отрезке [−6,5;−4].

3)Найдите наибольшее значение функции y=ln(4−2x)+2x−7 на отрезке [0;1,7].

4)Найдите точку максимума функции y=−8√x+12ln(x−4)−11.

5)Найдите точку максимума функции y=2lnx−√x−17.

6)Найдите наибольшее значение функции y=√−2log0,5(5x+1) на отрезке [12,6;51].

7)Найдите точку минимума функции y=x2−21x+6+55lnx.

8)Найдите точку максимума функции y=x2−11x−17+15lnx.

9)Найдите точку максимума функции y=(5×2−3x−3)ex+5.

10)Найдите наименьшее значение функции y=−4x−4cosx+5 на отрезке [−π;0].

Тренировочные варианты ЕГЭ 2022 по математике профиль 11 класс

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Исследование частных решу егэ математика

Источники:

Исследование частных решу егэ математика

Исследование частных решу егэ математика

Источники:

Исследование частных решу егэ математика

Исследование частных решу егэ математика

Источники:

Каталог заданий по типам по темам ?

Дополнительные задания для подготовки

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.

Математика Профильный уровень

Об экзамене

Структура

Пояснения к оцениванию заданий

* Замечание. Важно!

Степенные иррациональные функции ЕГЭ 2022 профиль математика:

Логарифмические функции ЕГЭ 2022 профиль математика:

Показательные функции ЕГЭ 2022 профиль математика:

Тригонометрические функции ЕГЭ 2022 профиль математика:

Исследование функции ЕГЭ 2022 профиль математика:

Видео как решать 11 задание в ЕГЭ по математике профиль:

Тренировочные варианты ЕГЭ 2022 по математике профиль 11 класс

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Каталог заданий по типам по темам

?