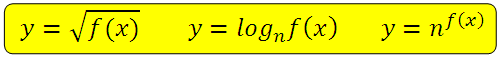Исследование функции без помощи производной решу егэ

ЕГЭ Профиль №11. Исследование функций без помощи производнойadmin2023-01-27T15:47:53+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №11. Исследование функций без помощи производной

Задача 1. Найдите точку максимума функции    (y = sqrt {4 — 4x — {x^2}} ) Ответ ОТВЕТ: — 2. Решение Функция  (y = sqrt x )  является возрастающей при  (x ge 0.)  Графиком функции  (fleft( x right) = 4 — 4x — {x^2})  является парабола ветвями направленными вниз. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 4}}{{2 cdot left( { — 1} right)}} =  — 2)  является точкой максимума функции  (fleft( x right).)  Так как функция  (y = sqrt {4 — 4x — {x^2}} )  определена в точке  (x =  — 2)  (left( {,,yleft( { — 2} right) = sqrt {4 — 4 cdot left( { — 2} right) — {{left( { — 2} right)}^2}}  = sqrt 8 ,,} right),)  то  (x =  — 2)  является её точкой максимума. Ответ:  – 2.

Задача 2. Найдите точку минимума функции     (y = sqrt {{x^2} — 6x + 11} ) Ответ ОТВЕТ: 3. Решение Функция  (y = sqrt x )  является возрастающей при  (x ge 0.)  Графиком функции  (fleft( x right) = {x^2} — 6x + 11)  является парабола ветвями направленными вверх. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 6}}{2} = 3)  является точкой минимума функции  (fleft( x right).)  Так как функция  (y = sqrt {{x^2} — 6x + 11} )  определена в точке  (x = 3)  (left( {,,yleft( 3 right) = sqrt {{3^2} — 6 cdot 3 + 11}  = sqrt 2 ,,} right),)  то  (x = 3)  является её точкой минимума. Ответ:  3.

Задача 3. Найдите наименьшее значение функции     (y = sqrt {{x^2} — 6x + 13} ) Ответ ОТВЕТ: 2. Решение Функция  (y = sqrt x )  является возрастающей при  (x ge 0.)  Графиком функции  (fleft( x right) = {x^2} — 6x + 13)  является парабола ветвями направленными вверх. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 6}}{2} = 3)  является точкой минимума функции  (fleft( x right)), а так же и точкой минимума функции  (y = sqrt {{x^2} — 6x + 11} ). Следовательно, наименьшее значение исходной функции будет в точке  (x = 3:)   (yleft( 3 right) = sqrt {{3^2} — 6 cdot 3 + 13}  = 2.) Ответ:  2.

Задача 4. Найдите наибольшее значение функции     (y = sqrt {5 — 4x — {x^2}} ) Ответ ОТВЕТ: 3. Решение Функция  (y = sqrt x )  является возрастающей при  (x ge 0.)  Графиком функции  (fleft( x right) = 5 — 4x — {x^2})  является парабола ветвями направленными вниз. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 4}}{{2 cdot left( { — 1} right)}} =  — 2)  является точкой максимума функции  (fleft( x right)), а так же и точкой максимума функции  (y = sqrt {5 — 4x — {x^2}} ). Следовательно, наибольшее значение исходной функции будет в точке  (x =  — 2:)   (yleft( { — 2} right) = sqrt {5 — 4 cdot left( { — 2} right) — {{left( { — 2} right)}^2}}  = 3.) Ответ:  3.

Задача 5. Найдите точку максимума функции    (y = {log _2}left( {2 + 2x — {x^2}} right) — 2) Ответ ОТВЕТ: 1. Решение Логарифмическая функция  (y = {log _2}x)  является возрастающей при  (x > 0.)  Графиком функции  (fleft( x right) = 2 + 2x — {x^2})  является парабола ветвями направленными вниз. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{2}{{2 cdot left( { — 1} right)}} = 1)  является точкой максимума функции  (fleft( x right).)  Так как функция  (y = {log _2}left( {2 + 2x — {x^2}} right) — 2)  определена в точке  (x = 1)  (left( {,,yleft( 1 right) = {{log }_2}left( {2 + 2 — 1} right) — 2 =  — 2 + {{log }_2}3,,} right),)  то  (x = 1)  является её точкой максимума. Ответ:  1.

Задача 6. Найдите точку минимума функции     (y = {log _5}left( {{x^2} — 6x + 12} right) + 2) Ответ ОТВЕТ: 3. Решение Логарифмическая функция  (y = {log _5}x)  является возрастающей при  (x > 0.)  Графиком функции  (fleft( x right) = {x^2} — 6x + 12)  является парабола ветвями направленными вверх. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 6}}{2} = 3)  является точкой минимума функции  (fleft( x right).)  Так как функция  (y = {log _5}left( {{x^2} — 6x + 12} right) + 2)  определена в точке  (x = 3)  (left( {,,yleft( 3 right) = {{log }_5}left( {9 — 18 + 12} right) + 2 = 2 + {{log }_5}3,,} right),)  то  (x = 3)  является её точкой минимума. Ответ:  3.

Задача 7. Найдите наименьшее значение функции  (y = {log _3}left( {{x^2} — 6x + 10} right) + 2) Ответ ОТВЕТ: 2. Решение Логарифмическая функция  (y = {log _3}x)  является возрастающей при  (x > 0.)  Графиком функции  (fleft( x right) = {x^2} — 6x + 10)  является парабола ветвями направленными вверх. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 6}}{2} = 3)  является точкой минимума функции  (fleft( x right)), а так же и точкой минимума функции  (y = {log _3}left( {{x^2} — 6x + 10} right) + 2). Следовательно, наименьшее значение исходной функции будет в точке  (x = 3:)   (yleft( 3 right) = {log _3}left( {9 — 18 + 10} right) + 2 = 2 + {log _3}1 = 2.)

Задача 8. Найдите наибольшее значение функции    (y = {log _5}left( {4 — 2x — {x^2}} right) + 3) Ответ ОТВЕТ: 4. Решение Логарифмическая функция  (y = {log _5}x)  является возрастающей при  (x > 0.)  Графиком функции  (fleft( x right) = 4 — 2x — {x^2})  является парабола ветвями направленными вниз. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 2}}{{2 cdot left( { — 1} right)}} =  — 1)  является точкой максимума функции  (fleft( x right)), а так же и точкой максимума функции  (y = {log _5}left( {4 — 2x — {x^2}} right) + 3). Следовательно, наибольшее значение исходной функции будет в точке  (x =  — 1:)   (yleft( { — 1} right) = {log _5}left( {4 + 2 — 1} right) + 3 = 3 + {log _5}5 = 4.) Ответ:  4.

Задача 9. Найдите точку максимума функции    (y = {11^{6x — {x^2}}}) Ответ ОТВЕТ: 3. Решение Показательная функция  (y = {11^x})  является возрастающей, так основание 11 больше 1.  Графиком функции  (fleft( x right) = 6x — {x^2})  является парабола ветвями направленными вниз. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{6}{{2 cdot left( { — 1} right)}} = 3)  является точкой максимума функции  (fleft( x right),) а так же и точкой максимума исходной функция  (y = {11^{6x — {x^2}}}.) Ответ:  3.

Задача 10. Найдите точку минимума функции    (y = {7^{{x^2} + 2x + 3}}) Ответ ОТВЕТ: — 1. Решение Показательная функция  (y = {7^x})  является возрастающей, так основание 7 больше 1.  Графиком функции  (fleft( x right) = {x^2} + 2x + 3)  является парабола ветвями направленными вверх. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{2}{2} =  — 1)  является точкой минимума функции  (fleft( x right),) а так же и точкой минимума исходной функция  (y = {7^{{x^2} + 2x + 3}}.) Ответ:  – 1.

Задача 11. Найдите наименьшее значение функции    (y = {2^{{x^2} + 2x + 5}}) Ответ ОТВЕТ: 16. Решение Показательная функция  (y = {2^x})  является возрастающей, так основание 2 больше 1.  Графиком функции  (fleft( x right) = {x^2} + 2x + 5)  является парабола ветвями направленными вверх. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{2}{2} =  — 1)  является точкой минимума функции  (fleft( x right),) а так же и точкой минимума исходной функция  (y = {7^{{x^2} + 2x + 5}}.) Следовательно, наименьшее значение исходной функции будет в точке (x =  — 1:)  (yleft( { — 1} right) = {2^{1 — 2 + 5}} = {2^4} = 16.) Ответ:  16.

Задача 12. Найдите наибольшее значение функции    (y = {3^{ — 7 — 6x — {x^2}}}) Ответ ОТВЕТ: 9. Решение Показательная функция  (y = {3^x})  является возрастающей, так основание 3 больше 1.  Графиком функции  (fleft( x right) =  — 7 — 6x — {x^2})  является парабола ветвями направленными вниз. Следовательно, её вершина  ({x_B} =  — frac{b}{{2a}} =  — frac{{ — 6}}{{2 cdot left( { — 1} right)}} =  — 3)  является точкой максимума функции  (fleft( x right),) а так же и точкой максимума исходной функция  (y = {3^{ — 7 — 6x — {x^2}}}.) Следовательно, наибольшее значение исходной функции будет в точке (x =  — 3:)  (yleft( { — 3} right) = {3^{ — 7 + 18 — 9}} = {3^2} = 9.) Ответ:  9.

28
Ноя 2013

Категория: 11 Исследование функции

2013-11-28
2021-09-24

Автор: egeMax |

комментариев 28

29 января 2012

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f (x) называется монотонно возрастающей на отрезке [a; b], если для любых точек x₁ и x₂ этого отрезка выполняется следующее:

x₁ < x₂ ⇒ f (x₁) < f (x₂).

Функция f (x) называется монотонно убывающей на отрезке [a; b], если для любых точек x₁ и x₂ этого отрезка выполняется следующее:

x₁ < x₂ ⇒ f (x₁) > f (x₂).

Другими словами, для возрастающей функции чем больше x, тем больше f (x). Для убывающей функции все наоборот: чем больше x, тем меньше f (x).

Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 < a < 1. Не забывайте про область допустимых значений логарифма: x > 0.

f (x) = log_a x (a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 < a < 1. Но в отличие от логарифма, показательная функция определена для всех чисел, а не только для x > 0:

f (x) = a ^x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax² + bx + c. Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх (при a > 0) или вниз (a < 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a < 0) значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x₀ тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x₀ для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [a; b] в условии задачи отсутствует. Следовательно, вычислять f (a) и f (b) не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы x₀, координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы y = ax² + bx + c и найти ее вершину по формуле: x₀ = −b/2a;
2. Найти значение исходной функции в этой точке: f (x₀). Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

Под корнем стоит квадратичная функция y = x² + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.

Вершина параболы:

x₀ = −b/(2a) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке x₀ = −3 функция y = x² + 6x + 13 принимает наименьшее значение.

Корень монотонно возрастает, значит x₀ — точка минимума всей функции. Имеем:

Задача. Найдите наименьшее значение функции:

y = log ₂ (x² + 2x + 9)

Под логарифмом снова квадратичная функция: y = x² + 2x + 9. График — парабола ветвями вверх, т.к. a = 1 > 0.

Вершина параболы:

x₀ = −b/(2a) = −2/(2 · 1) = −2/2 = −1

Итак, в точке x₀ = −1 квадратичная функция принимает наименьшее значение. Но функция y = log ₂ x — монотонная, поэтому:

y_min = y(−1) = log ₂ ((−1)² + 2 · (−1) + 9) = … = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

В показателе стоит квадратичная функция y = 1 − 4x − x². Перепишем ее в нормальном виде: y = −x² − 4x + 1.

Очевидно, что график этой функции — парабола, ветви вниз (a = −1 < 0). Поэтому вершина будет точкой максимума:

x₀ = −b/(2a) = −(−4)/(2 · (−1)) = 4/(−2) = −2

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x₀ = −2:

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

1. Аргумент логарифма должен быть положительным:

   y = log_a f (x) ⇒ f (x) > 0

2. Арифметический квадратный корень существует только из неотрицательных чисел:

   

3. Знаменатель дроби не должен равняться нулю:

   

Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

Под корнем снова квадратичная функция: y = 3 − 2x − x². Ее график — парабола, но ветви вниз, поскольку a = −1 < 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2x − x² ≥ 0 ⇒ x² + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Теперь найдем вершину параболы:

x₀ = −b/(2a) = −(−2)/(2 · (−1)) = 2/(−2) = −1

Точка x₀ = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x₀, а также на концах ОДЗ:

y(−3) = y(1) = 0

Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

y = log _0,5 (6x − x² − 5)

Внутри логарифма стоит квадратичная функция y = 6x − x² − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6x − x² − 5 > 0 ⇒ x² − 6x + 5 < 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.

Ищем вершину параболы:

x₀ = −b/(2a) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: x₀ = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x₀:

y_min = y(3) = log _0,5 (6 · 3 − 3² − 5) = log _0,5 (18 − 9 − 5) = log _0,5 4 = −2

Смотрите также:

1. Показательные функции в задаче B15: хитрости решения
2. Задача B15: работаем с показательной функцией без производной
3. Тест к уроку «Сложные выражения с дробями» (легкий)
4. Четырехугольная пирамида в задаче C2
5. Задача B5: площадь кольца
6. Решение задач на движение по воде

Здравствуйте! В этой статье речь пойдёт о задачах, которые можно решать без нахождения производной. В данной рубрике мы уже рассмотрели некоторые примеры с логарифмами, числом е, функции  с произведениями. Смысл заданий тот же –  требуется найти либо точку максимума (минимума) функции, либо определить максимальное (минимальное) значение функции. 

В чём суть и каков «стандартный» алгоритм решения — можно посмотреть в этой статье. Но не для всех заданий применение этого алгоритма будет рационально. Если следовать ему в представленных ниже примерах, то процесс решения будет «перегружен» вычислениями. А потеря времени на экзамене вам не нужна. Так какие же задания имеются ввиду?

В условии дана иррациональная, логарифмическая или показательная функция:

при чём под корнем, под знаком логарифма или в показателе находится квадратичная функция вида:

Рассмотрим подход без нахождения производной. Вы увидите, что такие задачи можно решать устно.

Что необходимо знать? Свойство параболы, напомним его:

Если а > 0, то её ветви направлены вверх.

Если а < 0, то её ветви направлены вниз.

Далее вспомним  координату  (абсциссу)  вершины параболы:

То есть, это точка экстремума квадратичной функции – в ней функция меняет своё поведение с возрастания на убывание или наоборот.

Следующий важный факт (ключевой для этих задач):

Если исходная функция монотонна (непрерывно возрастает или убывает), для нее указанная точка «х» также будет точкой экстремума.

Почему? Давайте рассмотрим отдельно функции подробнее.

Квадратичная функция в показателе степени (при чём n>1):

Смотрите! Представим, что ax²+bx+c=z. Можем записать:

Получается что значение z изменяется следующим образом.

Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a  z уменьшается, в точке –b/2a значение будет минимальным, далее при х от –b/2a  до бесконечности z увеличивается.

Это означает, что и сама функция у=n^f(x) будет имет минимальное значение в точке х=–b/2a, так как при минимуме в показателе получится минимум в результате.

Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до  –b/2a  z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a  до бесконечности z уменьшается.

Это означает, что и сама функция у=n^f(x) будет иметь максимальное значение в точке х=–b/2a, так как при максимуме в показателе получится максимум в результате.

Квадратичная функция под знаком логарифма (при чём n>1):

Представим, что ax²+bx+c=z. Можем записать:

Получается что значение z изменяется следующим образом:

Вариант когда a>0 (ветви параболы направлены вверх) –  при х от минус бесконечности до  –b/2a  z уменьшается, в точке –b/2a значение будет минимальным, далее при х от–b/2a  до бесконечности z увеличивается.

Это означает, что и сама функция log_nz будет имет минимальное значение в точке х=–b/2a. Так как логарифмическая функция уменьшается при уменьшении аргумента (видно по графику).

Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до  –b/2a  z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a  до бесконечности z уменьшается.

Это означает, что и сама функция log_nz будет имеет максимальное значение в точке х=–b/2a. Так как логарифмическая функция увеличивается при увеличении аргумента (видно по графику).

Квадратичная функция под знаком корня:

Представим, что ax²+bx+c=z. Можем записать:

Получается что:

При a>0 значение z минимально в точке х=–b/2a, а значит и сама функция будет иметь минимальное значение. *Корень из наименьшего значения в результате даст наименьшее число.

При a<0 значение z максимально в точке х=–b/2a, а значит и сама функция будет иметь максимальное значение.

Таким образом, сформулируем ключевое правило:

ВНИМАНИЕ! Конечно, если глубже уйти в тему, то возможны варианты когда сложная функция имеет отрицательный знак, когда логарифм находится в знаменателе дроби, когда основание логарифма или основание степени находится в пределах от 0 до 1. Разумеется,  важно понимать как ведёт себя данная в условии функция (возрастает или убывает). Но для решения типовых заданий экзамена указанного вывода вам будет вполне достаточно.

И конечно, не теряйте из виду область допустимых значений заданной функции:

— выражение стоящее под знаком корня, больше или равно нулю (число неотрицательное).

— выражение стоящее под знаком  логарифма, есть положительное число.

— выражение стоящее в знаменателе дроби не равно нулю.

В подобных задачах на нахождение наибольшего и наименьшего значения функции, я бы посоветовал находить область определения в любом случае (даже не смотря на то, что в представленных ниже примерах это ничего важного нам не даёт и не влияет на ответ).

Рассмотрим примеры:

Найдите точку максимума функции 

Под корнем  квадратичная функция  13+6х–х². Ее график — парабола, ветви направлены вниз, поскольку  а=–1<0. Значит максимальное значение  функция приобретает в точке:

Проверим чему равно подкоренное выражение при х=3 То есть будет ли оно числом неотрицательным:

13 + 6∙3 – 3² = 13 + 18 – 9 = 22 > 0 

Почему необходимо это сделать? Дело в том, что при полученной абсциссе квадратичная функция теоретически может дать отрицательное значение, то есть график такой параболы будет лежать ниже оси ох. Это  будет означать что решения (таких вариантов заданий на самом ЕГЭ не будет).

Ответ: 3

Решите самостоятельно:

Найдите точку максимума функции

Посмотреть решение

Найдите наименьшее значение функции

Под корнем  квадратичная функция   х² + 8х + 185.

Ее график — парабола,  ветви направлены вверх,  поскольку а =  1 > 0

Абсцисса вершины параболы:

Так как  ветви параболы направлены вверх, то в точке  х = – 4 функция

х² + 8х + 185 принимает наименьшее значение.

Функция кважратного корня монотонно возрастает, значит х = 4 точка минимума  всей функции, вычислим  её наименьшее  значение:

Ответ: 13

Решите самостоятельно:

Найдите наименьшее значение функции

Посмотреть решение

Найдите точку максимума функции у=log₇(–2 – 12х – х²) + 10. 

Под знаком логарифма квадратичная функция    –2 – 12х – х².

График — парабола, ветви направлены  вниз, так как а = – 1 < 0 

Абсцисса вершины параболы:

Проверим, принадлежит ли полученное значение х области определения (выражение под знаком логарифма должно быть число положительное):

– 2 – 12∙(–6) – (–6)² = – 2 + 72 – 36 = 34 > 0

То есть, в точке х = – 6

функция f (х) = – 2 – 12х – х²   будет иметь  максимальное значение.

Значит, и у=log₇(–2–12х–х²)+10  в этой точке так же будет иметь максимальное значение.

Ответ: – 6.

Решите самостоятельно:

Найдите точку максимума функции у=log₂(2 + 2х – х²) – 2

Посмотреть решение

Найдите наименьшее значение функции  у=log₉ (х² – 10х + 754) + 3

Под корнем  квадратичная функция   х² – 10х+754.

Ее график — парабола,  ветви направлены вверх,  поскольку а = 1 > 0

Абсцисса вершины параболы:

То есть, в точке х = 5 функция f (x) = х²  – 10х + 754 принимает наименьшее значение.  

Функция log₉х  монотонная, значит у =log₉ (х² – 10х + 754) + 3  в точке х = 5 также принимает наименьшее значение, вычислим его:

Ответ: 6

Решите самостоятельно:

Найдите наименьшее значение функции  у=log₃(х² – 6х + 10) + 2

Посмотреть решение

Найдите точку максимума функции 

В показателе стоит квадратичная функция   – 30 + 12х – х².     

График — парабола, ветви направлены  вниз, так как а = –1 < 0.

Абсцисса вершины параболы:

То есть, в точке х = 6 функция f (х) = – 30 + 12х – х² приобретёт максимальное значение. Значит и данная функция в этой точке будет иметь также максимальное значение.

Ответ: 6

Решите самостоятельно:

Найдите точку максимума функции: 

Посмотреть решение

Найдите наименьшее значение функции

В показателе стоит   квадратичная функция  х²  + 16х + 66.

Ее график — парабола,  ветви направлены вверх,  поскольку а = 1 > 0

Абсцисса вершины параболы:

То есть, в точке х = – 8 функция х²  + 16х + 66 принимает наименьшее значение.

Показательная  функция монотонна, поэтому её наименьшее значение будет также в точке х = – 8, вычислим его  

Ответ: 36

Решите самостоятельно:

Найдите наименьшее значение функции

Посмотреть решение

Разумеется,  что  это краткая схема решения и, конечно же, нужно понимать свойства квадратичной, показательной, логарифмической, дробно-рациональной функции,  но эта схема работает.

В данной рубрике мы ещё рассмотрим задания с тригонометрическими функциями, не пропустите! Успеха вам!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции

Найдем производную функции.

Приравняем производную к нулю. Получим:

Исследуем знаки производной.

В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

Определим знаки производной.

В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции

Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция монотонно возрастает, точка максимума функции будет при том же , что и точка максимума функции А ее найти легко.

при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при

Ответ: — 4.

4. Найдите абсциссу точки максимума функции

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции

Это вершина квадратичной параболы

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

Найдем знаки производной.

В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю.

при

Найдем знаки производной.

Точка — точка минимума функции . Точка не лежит на отрезке Поэтому

 и  Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при

Если  то  Если , то 

Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке

Найдем производную функции

Приравняем производную к нулю:

. Поскольку если

Найдем знаки производной на отрезке

При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и

Мы нашли, что

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

Найдем производную функции

если Тогда

 При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке

Как всегда, возьмем производную функции и приравняем ее к нулю.

По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки

В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю.  — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что  для всех , и функция монотонно возрастает при

Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при

Ответ: 6

ЕГЭ Профиль

Наибольшее и наименьшее значение функций

Исследование функций без помощи производной

Задание 1102

Найдите точку минимума функции $$sqrt[3]{(x+5)^{2}}-sqrt[3]{(x+5)^{5}}$$

Ответ: -5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную этой функции. Представим, что

$$sqrt[3]{(x+5)^{2}}=(x+5)^{frac{2}{3}}$$

$$ sqrt[3]{(x+5)^{5}}=(x+5)^{frac{5}{3}}$$

Тогда $$f_{‘}(x)=frac{2}{3}*(x+5)^{-frac{1}{3}}-frac{5}{3}*(x+5)^{frac{2}{3}}=0$$

$$0=frac{1}{3}*(2(x+5)^{-frac{1}{3}}-5*(x+5)^{frac{2}{3}})$$

$$0=2(x+5)^{-frac{1}{3}}-5*(x+5)^{frac{2}{3}}$$ Вынесем $$(x+5)^{-frac{1}{3}}$$ за скобки:

$$(x+5)^{-frac{1}{3}}(2-5*(x+5))=0$$

Получаем, что x = -4.6 и x = -5. 

Если начертить координатную прямую и расставить на ней знаки производной, то увидим, что на промежутках (-∞;-5] и [-4.6;+∞) производная отрицательна, а на промежутке [-5;-4.6] — положительна. Значит x = -5 точка минимума

Задание 3247

Найдите наименьшее значение функции: $$f(x)=6-log_{2}(16x-x^{2})$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$f(x)=6-log_{2}(16x-x^{2})$$ $$x_{0}=frac{-16}{-2}=8$$ $$f(8)=6-log_{2}(16cdot8-8^{2})=f(8)=6-log_{2}64=6-6=0$$

Задание 4571

Найдите наименьшее значение функции $$y=4^{x}-8cdot2^{x}+1$$ на отрезке [1; 3].

Ответ: -15

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Пусть $$2^{x}=a$$: $$y=a^{2}-8a+1$$ — это квадратичная функция, ее наименьшее значение там, где вершина параболы: $$a_{0}=-frac{-8}{2}=4$$; $$2^{x}=4$$ $$Rightarrow$$ $$x=2$$; $$y(2)=4^{2}-8cdot2^{2}+1=16-32+1=-15$$

Задание 4667

Найдите наименьшее значение функции $$y=7|x-3|-2|x+5|-|4x-3|+5$$ на отрезке $$[1;6]$$

Ответ: -20

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

На данном отрезке второе и третье подмодульные выражения положительны, следовательно, модули раскроются не поменяв знаки: $$y=7|x-3|-2x-10-4x+3+5=7|x-3|-6x-2$$ В данном случае получаем график (выглядит как галочка) вершина которого ( в том числе и наименьшее значение) в точке x=3. Тогда наименьшее значение функции: $$y(3)=7|3-3|-2|3+5|-|4*3-3|+5=-16-9+5=-20$$

Задание 6228

Найти наименьшее значение функции $$y=sqrt{x^{2}-2x+2}+sqrt{x^{2}-10x+29}$$

Ответ: 5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Воспользуемся неравенством: $$left | bar{a} right |+left | bar{b} right |geq left | bar{a}+bar{b} right |$$ Рассмотрим правило треугольника : $$AB=left | bar{a} right |; BC=left | bar{b} right |; AC=left | bar{a}+bar{b} right |$$. По свойству треугольника: $$ACleq AB+BC$$ При этом Знак равно $$(left | bar{a} right |+left | bar{b} right |=left | bar{a}+bar{b}right |)$$ только тогда, когда $$bar{a}$$ и $$bar{b}$$ сонаправлены , т.е. когда $$frac{x_{1}}{x_{2}}=frac{y_{1}}{y_{2}}$$ (где $$bar{a}(x;y));bar{b}(x_{2};y_{2})$$) Выделим полные квадраты под корнями: $$x^{2}-2x+2=x^{2}-2x+1+1=(x-1)^{2}+1$$ $$x^{2}-10x+29=x^{2}-10x+25+4=(x-5)^{2}+4$$ Найдем наименьшее значение: $$y=sqrt{(x-1)^{2}+1}+sqrt{(x-5)^{2}+4}$$ Пусть: $$bar{a}=(1-x; 1); bar{b}(x-5; 2)$$ (Если найти длины векторов, получим подкоренные выражения) Тогда: $$left | bar{a} right |=sqrt{(1-x)^{2}+1}=sqrt{(x-1)^{2}+1}$$ и $$left | bar{b} right |=sqrt{(x-5)^{2}+4}$$ Каждая координата суммарного вектора, равна сумме соответствующих координат первоначальных векторов: $$bar{a}+bar{b} =(1-x+x-5, 1+2)=(-4 ;3)$$ Тогда его длина: $$left | bar{a}+bar{b} right |=sqrt{(-4)^{2}+3^{2}}=5$$ В таком случае получаем: $$left | bar{a} right |+left | bar{b} right |geq left | bar{a}+bar{b} right |, y(x)geq 5$$ То есть минимальное значение данной функции равно 5.

Задание 6324

Найти наименьшее значение функции $$y=log_{0,5} (frac{sqrt{4x^{4}-3x^{2}+9}-sqrt{4x^{4}-8x^{2}+9}}{x})$$ на интервале $$(0;infty)$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

     При x>0: $$sqrt{4x^{4}=3x^{2}+9}>sqrt{4x^{4}-8x^{2}+9}$$

     Пусть $$t=frac{sqrt{4x^{4}-3x^{2}+9}-sqrt{4x^{4}-8x^{2}+9}}{x}=$$$$frac{4x^{4}-3x^{2}+9-(4x^{4}-8x^{2}+9)}{x(sqrt{4x^{4}-3x^{2}+9}+sqrt{4x^{4}-8x^{2}+9})}=$$$$frac{5x^{2}}{sqrt{4x^{4}-3x^{2}+9}+sqrt{4x^{4}-8x^{2}+9}}=$$$$frac{5}{sqrt{4x^{4}-frac{9}{x^{2}}-3}+sqrt{4x^{4}-frac{9}{x^{2}}-8}}$$

     Учтем, что $$a^{2}+b^{2}geq 2ab$$. Пусть $$a^{2}=4x^{2}, b^{2}=frac{9}{x^{2}}$$. Тогда: $$4x^{2}+frac{9}{x^{2}}geq 2sqrt{4x^{2}*frac{9}{x^{2}}}=2*6=12(1)$$

     Следовательно $$sqrt{4x^{4}-frac{9}{x^{2}}-3}+sqrt{4x^{4}-frac{9}{x^{2}}-8}(2)$$ минимальна при выполнении (1):

$$sqrt{12-3}+sqrt{12-8}=3+2=5$$. Чем меньше (2), тем больше t и тем меньше: $$log_{0,5}tRightarrow log_{0,5}frac{5}{5}=log_{0,5}1=0$$

Задание 6371

Найдите наименьшее на отрезке [1;6] значение функции $$y=7|x-3|-2|x+5|-|4x-3|+5$$

Ответ: -20

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

На промежутке [1;6] x+5>0 4x-3>0, тогда: $$y=7left | x-3 right |-2x-10-4x+3+5=$$$$7left | x-3 right |-6x-2$$

Вершина полученного графика будет находиться в точке, где подмодульное выражение равно 0, то есть $$x=3Rightarrow$$ $$y_{min}=y(3)$$

$$y(3)=7left | 3-3 right |-6*3-2=-20$$

Задание 6418

Найдите наименьшее значение выражения $$z=sqrt{(2x-1)^{2}+(3y-1)^{2}}+sqrt{(2x-3y)^{2}+9y^{2}}$$

Ответ: 1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

     Пусть $$bar{a}: (2x-1; 3y-1);bar{b}: (3y-2x ; -3y)$$

     Из неравенства $$left | bar{a} right |+left | bar{b} right |geq left | bar{a}+bar{b} right |$$, и учитывая , что $$bar{a}+bar{b}:(2x-1+3y-2x;3y-1-3y)=(3y-1;-1)$$, и $$z=left | bar{a} right |+left | bar{b} right |$$ получим : $$zgeq left | bar{a}+bar{b} right |=sqrt{(3y-1)^{2}+(-1)^{2}}$$

     Рассмотрим $$(3y-1)^{2}+(-1)^{2}=g$$ .Т.к. $$(3y-1)^{2}geq 0$$ при любом y,  $$grightarrow min$$, только тогда, когда $$3y-1rightarrow 0$$, следовательно, $$g_{min}=1$$. Т.е. $$zgeq sqrt{1}=1$$

Задание 6803

Найдите наименьшее значение функции $$y=|x^{2}-x|+|x+1|$$

Ответ: 1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Раскроем модули :

1) $$x in (-infty ;-1]Rightarrow$$ $$y=x^{2}-x-x-1=x^{2}-2x-1$$

2) $$x in (-1,0]cup [1;+infty )Rightarrow$$ $$y=x^{2}-x+x+1=x^{2}+1$$

3) $$x in (0;1)Rightarrow$$ $$y=-x^{2}+x+x+1=-x^{2}+2x+1$$

Следовательно , $$y _{min}=1$$

Задание 6874

Найдите наименьшее значение выражения x²-x+y²-y

Ответ: -0,5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Рассмотрим выражение по частям : Пусть $$f(x)=x^{2}-x$$; $$g(y)=y^{2}-y$$ (функции одинаковы, следовательно, минимальные значения будут так же одинаковы) $$f_{min}=f(x_{0}); x_{0}=-frac{-1}{2}=0,5$$$$Rightarrow$$ $$f(x_{0})=0,5^{2}-0,5=-0,25$$ $$g(y_{0})=0,5^{2}=0,5=-0,25$$$$Rightarrow$$ $$f_{min}+g_{min}=-0,25-0,25=-0,5$$

Задание 6970

Найдите наименьшее значение функции $$f(x)=4^{x}-2^{x+4}+100$$

Ответ: 36

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$f(x)=4^{x}-2^{x+4}+100=2^{2x}-16*2^{x}+100$$ Пусть $$2^{x}=y>0$$, тогда $$f(y)=y^{2}-16y+100$$ — график парабола, ветви направлены вверх: Найдем вершину параболы (в ней будет $$f_{min}(y)$$ при y>0): $$y_{0}=-frac{-16}{2}=8Rightarrow$$ $$f(18)=8^{2}-16*8+100=36$$

Задание 8870

Найдите наибольшее значение функции: $$y=x(sqrt{1-9x^{2}}+3sqrt{4-x^{2}})$$

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10071

Найдите наибольшее значение функции: $$y=sqrt{-x^2+4}+1$$

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10094

Найдите наименьшее значение функции $$f(x)=(2-cos^2 x-cos^{4} x)(1+ctg^{2}x)$$

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10191

Найти наименьшее значение функции

$$f(x)=|sqrt{-x^{2}+6x-5}-3|+sqrt{-x^{2}+6x-5}+x^{3}+6x^{2}$$

Ответ: 10

Скрыть

1


Как решать В-14 без производной. Подготовка к ЕГЭ МБОУ СОШ 46,г. Хабаровск. Учитель математики – Кочерга Г.Н.

2


Иногда в задачах B14 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ. В этом случае работают другие приемы, один из которых монотонность. Определение Функция f (x) называется монотонно возрастающей на отрезке [a; b], если для любых точек x 1 и x 2 этого отрезка выполняется следующее: x 1 < x 2 f (x 1 ) < f (x 2 ).

3


Определение. Функция f (x) называется монотонно убывающей на отрезке [a; b], если для любых точек x 1 и x 2 этого отрезка выполняется следующее: x 1 f (x 2 ). Другими словами, для возрастающей функции чем больше x, тем больше f (x). Для убывающей функции все наоборот: чем больше x, тем меньше f (x).

4


Примеры. Логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 0. f (x) = log a x (a > 0; a 1; x > 0)

5


Примеры. Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

6


Примеры. Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 0:

7


Примеры. Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

8


Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит сейчас разберем.

9


Координаты вершины параболы Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график стандартная парабола, в которой нас интересуют ветви: Ветви параболы могут уходить вверх (при a > 0) или вниз (a < 0). Они задают направление, в котором функция может принимать бесконечные значения; Вершина параболы точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a < 0) значение.

10


Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

11


Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x 0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

12


Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x 0 для квадратного трехчлена, а на функцию забить.

13


Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

14


Отрезок [a; b] в условии задачи отсутствует. Следовательно, вычислять f (a) и f (b) не требуется. Остается рассмотреть лишь точки экстремума; Но таких точек всего одна это вершина параболы x 0, координаты которой вычисляются буквально устно и без всяких производных.

15


Таким образом, решение задачи резко упрощается и сводится всего к двум шагам: Выписать уравнение параболы и найти ее вершину по формуле: Найти значение исходной функции в этой точке: f (x 0 ). Если никаких дополнительных условий нет, это и будет ответом.

16


На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

17


Рассмотрим настоящие задачи из пробного ЕГЭ по математике именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B-14 становятся почти устными.

18


Найдите наименьшее значение функции : Решение: Под корнем стоит квадратичная функция График этой функции парабола ветвями вверх, поскольку коэффициент a = 1 > 0. Вершина параболы: x 0 = b/(2a) = 6/(2 · 1) = 6/2 = 3

19


Поскольку ветви параболы направлены вверх, в точке x 0 = 3 функция принимает наименьшее значение. Корень монотонно возрастает, значит x 0 точка минимума всей функции. Имеем: Ответ: 2

20


Найдите наименьшее значение функции: Решение Под логарифмом снова квадратичная функция.График парабола ветвями вверх, т.к. a = 1 > 0. Вершина параболы: x 0 = b/(2a) = 2/(2 · 1) = 2/2 = 1

21


Итак, в точке x 0 = 1 квадратичная функция принимает наименьшее значение. Но функция y = log 2 x монотонная, поэтому: y min = y(1) = log 2 ((1)2 + 2 · (1) + 9) =… = log 2 8 = 3 Ответ: 3

22


Найдите наибольшее значение функции: Решение: В показателе стоит квадратичная функция Перепишем ее в нормальном виде: Очевидно, что график этой функции парабола, ветви вниз (a = 1 < 0). Поэтому вершина будет точкой максимума: x 0 = b/(2a) = (4)/(2 · (1)) = 4/(2) = 2

23


Исходная функция показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x 0 = 2: Ответ: 11

24


Внимательный ученик наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

25


Следствия из области определения функции Иногда для решения задачи B14 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

26


1. Аргумент логарифма должен быть положительным: y = log a f (x) f (x) > 0 2. Арифметический квадратный корень существует только из неотрицательных чисел: 3.Знаменатель дроби не должен равняться нулю:

27


Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби никогда. Посмотрим, как это работает на конкретных примерах: Найдите наибольшее значение функции:

28


Решение Под корнем снова квадратичная функция. Ее график парабола, но ветви направлены вниз, поскольку a = 1 < 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

29


Выписываем область допустимых значений (ОДЗ):

30


Теперь найдем вершину параболы: x 0 = b/(2a) = (2)/(2 · (1)) = 2/(2) = 1 Точка x 0 = 1 принадлежит отрезку ОДЗ и это хорошо. Теперь считаем значение функции в точке x 0, а также на концах ОДЗ: y(3) = y(1) = 0 Итак, получили числа 2 и 0. Нас просят найти наибольшее это число 2. Ответ: 2

31


Найдите наименьшее значение функции:

32


Решение Внутри логарифма стоит квадратичная функция. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

33


Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают. Ищем вершину параболы: x 0 = b/(2a) = 6/(2 · (1)) = 6/(2) = 3 Вершина параболы подходит по ОДЗ: x 0 = 3 (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x 0 :

34


y min = y(3) = log 0,5 (6 · ) = = log 0,5 (18 9 5) = log 0,5 4 = 2 Ответ: -2