Исследование функции егэ профильного уровня - Помощь в подготовке к экзаменам и поступлению

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Исследование степенных и иррациональных функций

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 11 № 77419

Найдите точку максимума функции

Аналоги к заданию № 77419: 124217 124229 124261 124265 526251 124219 124221 124223 124225 124227 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 77421

Найдите наименьшее значение функции на отрезке

Аналоги к заданию № 77421: 124317 124361 124365 124319 124321 124323 124325 124327 124329 124331 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 77422

Найдите наибольшее значение функции на отрезке

Аналоги к заданию № 77422: 124367 124415 124369 124371 124373 124375 124377 124379 124381 124383 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77423

Найдите точку максимума функции

Аналоги к заданию № 77423: 124417 124515 124419 124421 124423 124425 124427 124429 124431 124433 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77424

Найдите точку минимума функции

Аналоги к заданию № 77424: 124517 124615 509563 509605 635963 124519 124521 124523 124525 124527 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Исследование функций с помощью производной

Задание
1

#2390

Уровень задания: Легче ЕГЭ

Найдите точку максимума функции (y = -x^2).

ОДЗ: (x) – произвольный.

1) [y’ = -2x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2x = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

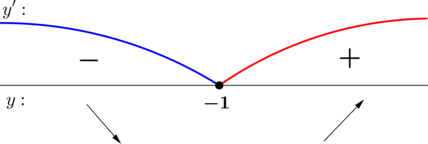
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = 0) – точка максимума функции (y).

Ответ: 0

Задание
2

#2391

Уровень задания: Легче ЕГЭ

Найдите точку минимума функции (y = x^2 + 2x + 2) на отрезке ([-2; 2]).

ОДЗ: (x) – произвольный.

1) [y’ = 2x + 2]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x + 2 = 0qquadLeftrightarrowqquad x = -1,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

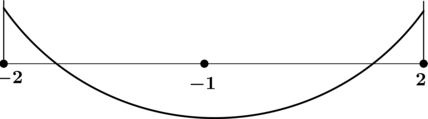
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-2; 2]):

4) Эскиз графика на отрезке ([-2; 2]):

Таким образом, (x = -1) – точка минимума функции (y) на ([-2; 2]).

Ответ: -1

Задание
3

#2392

Уровень задания: Легче ЕГЭ

Найдите точку минимума функции (y = 3x^2 — 6x + pi) на отрезке ([-3; 3]).

ОДЗ: (x) – произвольный.

1) [y’ = 6x — 6]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [6x — 6 = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

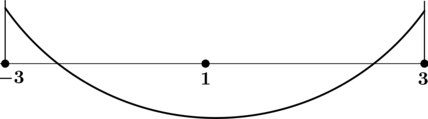
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-3; 3]):

4) Эскиз графика на отрезке ([-3; 3]):

Таким образом, (x = 1) – точка минимума функции (y) на ([-3; 3]).

Ответ: 1

Задание
4

#2691

Уровень задания: Равен ЕГЭ

Найдите точку локального минимума функции (y = x^3 — 3x).

ОДЗ: (x) – произвольный.

1) [y’ = 3x^2 — 3]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3x^2 — 3 = 0qquadLeftrightarrowqquad x = pm 1,.] Производная существует при любом (x).

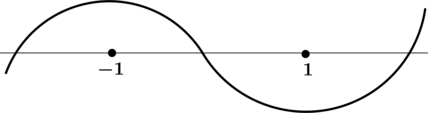
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 1) – точка локального минимума функции (y).

Ответ: 1

Задание
5

#2710

Уровень задания: Равен ЕГЭ

Найдите точку локального максимума функции

(y = x^3 — 15x^2 + 48x + e).

1) (y’ = 3x^2 — 30x + 48 = 3(x^2 — 10x + 16)).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):

[3(x^2 — 10x + 16) = 0qquadLeftrightarrowqquad x^2 — 10x + 16 = 0,] откуда находим (x_1 = 2, x_2 = . Таким образом, [y’ = 3(x — 2)(x — 8).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 2) – точка локального максимума функции (y).

Ответ: 2

Задание
6

#869

Уровень задания: Равен ЕГЭ

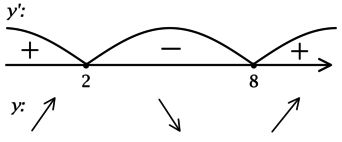
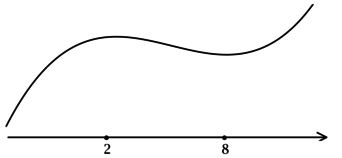
Найдите точку локального максимума функции (y = dfrac{1}{3}x^3 — 8x^2 + 55x + 11).

1) (y’ = x^2 — 16x + 55).

(x^2 — 16x + 55 = 0), откуда находим корни (x_1 = 5, x_2 = 11). Таким образом, [y’ = (x-5)(x-11).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 5) – точка локального максимума функции (y).

Ответ: 5

Задание
7

#868

Уровень задания: Равен ЕГЭ

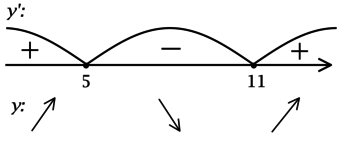
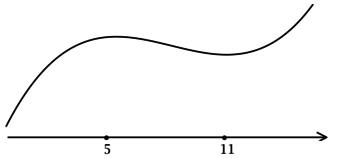
Найдите точку локального минимума функции (y = dfrac{1}{3}x^3 — 3x^2 + 8x + 2).

1) (y’ = x^2 — 6x + .

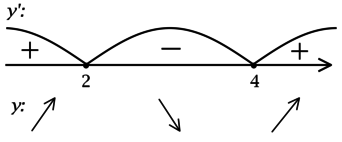
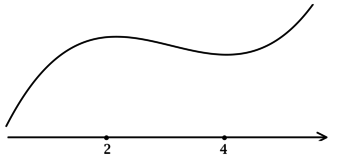
(x^2 — 6x + 8 = 0), откуда находим корни (x_1 = 2, x_2 = 4). Таким образом, [y’ = (x-2)(x-4).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 4) – точка локального минимума функции (y).

Ответ: 4

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №7. Применение производной к исследованию функций

ЕГЭ Профиль №7. Применение производной к исследованию функцийadmin2018-11-29T18:58:03+03:00

Источник

Задача 1. Найдите точку максимума функции

Решение: + показать

Задача 2. Найдите точку минимума функции

Решение: + показать

Задача 3. Найдите наименьшее значение функции на отрезке .

Решение: + показать

Задача 4. Найдите наибольшее значение функции $y=2+9x-frac{x^3}{3}$ на отрезке

Решение: + показать

Задача 5. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 6. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 7. Найдите точку максимума функции $y=6+12x-2x^{frac{3}{2}}.$

Решение: + показать

Задача 8. Найдите наибольшее значение функции $y=-frac{2}{3}xsqrt x+3x+8$ на отрезке

Решение: + показать

Задача 9. Найдите точку минимума функции $y=-frac{x^2+25}{x}$ .

Решение: + показать

Задача 10. Найдите наименьшее значение функции $y=frac{x^2+900}{x}$ на

Решение: + показать

Задача 11. Найдите точку максимума функции $y=frac{441}{x}+x+18.$

Решение: + показать

Задача 12. Найдите точку минимума функции $y=(3x^2-15x+15)e^{x-15}.$

Решение: + показать

Задача 13. Найдите точку максимума функции $y=(x+11)^2cdot e^{3-x}.$

Решение: + показать

Задача 14. Найдите наименьшее значение функции на отрезке .

Решение: + показать

Задача 15. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 16. Найдите наименьшее значение функции на отрезке $[frac{1}{12};frac{5}{12}].$

Решение: + показать

Задача 17. Найдите наименьшее значение функции на отрезке $[frac{3}{4};frac{5}{4}].$

Решение: + показать

Задача 18. Найдите наименьшее значение функции $y=e^{2x}-11e^x-1$ на отрезке .

Решение: + показать

Задача 19. Найдите наибольшее значение функции на отрезке $[0;frac{pi}{2}].$

Решение: + показать

Задача 20. Найдите наименьшее значение функции на отрезке $[-frac{pi}{3};frac{pi}{3}].$

Решение: + показать

Задача 21. Найдите наибольшее значение функции на отрезке $[-frac{3pi}{2};0]$ .

Решение: + показать

Задача 22. Найдите наименьшее значение функции $y=4cosx+frac{15}{pi}x+9$ на отрезке $[-frac{2pi}{3};0].$

Решение: + показать

Задача 23. Найдите наименьшее значение функции на отрезке $[0;frac{pi}{4}].$

Решение: + показать

Задача 24. Найдите точку минимума функции принадлежащую промежутку $(0;frac{pi}{2})$ .

Решение: + показать

* Замечание. Важно!

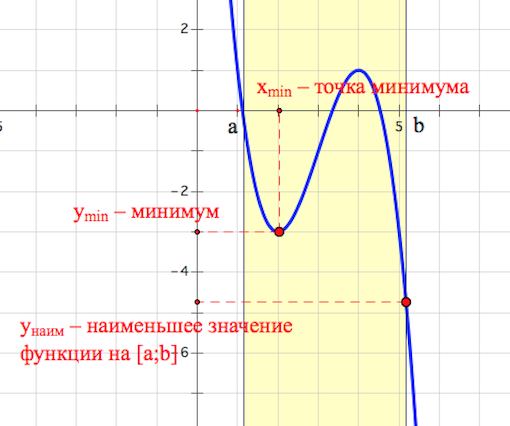
Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!

Например, на рисунке ниже наименьшее значение функции на отрезке достигается на конце отрезка , а именно, в точке .

То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке следует выбрать наименьшую из величин:

1) $y(x_{min})$ (их может быть несколько) из рассматриваемого отрезка

2) ,

При нахождении наибольшего значения функции на отрезке следует выбрать большую из величин:

1) $y(x_{max})$ (их может быть несколько) из рассматриваемого отрезка

2) ,

Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.

Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.

В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.

Вы можете пройти тест “Исследование функции при помощи производной”

Источник


3647	Найдите точку минимума функции y= x^3-27x^2+13 Решение График	Найдите точку минимума функции y= x3 -27×2 +13 ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 11

3632	Найдите точку максимума функции y= -(x^2+196)/x Решение График	Найдите точку максимума функции y= — x2 + 196 / x ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 11

3592	Найдите точку максимума функции y= (x+35)e^(35-x) Решение	Найдите точку максимума функции y= (x+35)e^(35-x) ! 36 вариантов ФИПИ Ященко 2023 Вариант 19 Задание 11

3587	Найдите наибольшее значение функции y= 2x^2-12x+8ln(x)-5 на отрезке [12/13; 14/13]. Решение График	Найдите наибольшее значение функции y= 2×2 -12x + 8lnx — 5 на отрезке [12/13; 14/13] ! 36 вариантов ФИПИ Ященко 2023 Вариант 18 Задание 11

3571	Найдите наименьшее значение функции y= 10x-10ln(x+4)+23 на отрезке [-3,5; 0] Решение График	Найдите наименьшее значение функции y= 10x -10ln(x+4) +23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 11 Вариант МА2210209

3562	Найдите точку минимума функции y= x^3-8.5x^2+10x-13 Решение График	Найдите точку минимума функции y= x3 -8,5×2 +10x -13 ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 11

3537	Найдите точку максимума функции y= (4x^2-36x+36)e^(33-x) Решение График	Найдите точку максимума функции y= (4×2 -36x +36)e^ 33 -x ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 11

3529	Найдите наименьшее значение функции y= 6x-6sin(x)+17 на отрезке [0; pi/2]. Решение График	Найдите наименьшее значение функции y = 6x-6sinx+17 на отрезке ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 11

3518	Найдите точку максимума функции y= (2x-1)cos(x)-2sin(x)+9, принадлежащую промежутку (0; pi/2). Решение График	Найдите точку максимума функции y= (2x-1)cosx — 2sinx +9, принадлежащую промежутку! 36 вариантов ФИПИ Ященко 2023 Вариант 7 Задание 11

3506	Найдите наименьшее значение функции y= x^3+18x^2+81x+56 на отрезке [-7; 0]. Решение График	Найдите наименьшее значение функции y= x3 +18×2 + 81x +56 на отрезке ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 11

Источник

Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:

$f'(x_0)={lim}↙{△x→0}{△f(x_0)}/{△x}$

Дифференцированием называют операцию нахождения производной.

Таблица производных некоторых элементарных функций

Функция	Производная
$c$	$0$
$x$	$1$
$x^n$	$nx^{n-1}$
${1}/{x}$	$-{1}/{x^2}$
$√x$	${1}/{2√x}$
$e^x$	$e^x$
$lnx$	${1}/{x}$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$

Производная суммы (разности) равна сумме (разности) производных.

$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

Найти производную $f(x)=4x·cosx$

$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

$f(x)= cos(5x)$

$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Решение:

Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$

Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.

Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)

$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$

$f'(x_0) = tg ВАС = 0,25$

Ответ: $0,25$

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.

В ответ запишите количество данных точек.

Решение:

Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.

В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.

Ответ: $2$

Источник